Epidemiological Analysis of Symmetry in Transmission of the Ebola Virus with Power Law Kernel
Abstract
:1. Introduction
2. Fundamental Fractional Operator Concepts
3. Fractional-Order Model of Ebola with Treatment
3.1. Model Description
3.2. Model Assumptions
- 1.
- People who have not been exposed to the illness pathogen are placed in the susceptible class .
- 2.
- Those that reside in this class have the disease pathogen but do not exhibit overt clinical symptoms. They are not yet able to spread infection. This is the incubation phase. People then proceed to the infectious class at the conclusion of this phase.
- 3.
- People begin exhibiting clinical symptoms and potentially spread an infection to others . Authorities place infectious patients under sanitary care after the infectious period, which is the average amount of time a person spends in this class and then classify them as hospitalized.
- 4.
- Although they are receiving treatment, the individuals in this class are still contagious. After the hospital stay, patients have two options: heal (and move into the recovered class) or pass away (dead class). We specifically state that there are no hospitalized patients who are no longer able to spread disease in class H. They are classified as described below as “recovered”.
- 5.
- People who have died from the disease but have not yet been buried are still contagious to others through touch. The body is interred after a predetermined amount of time.
- 6.
- This class consists of survivors of the virus. In this class, people are naturally immune to the disease-causing agent and stop being contagious.
4. Well Posedness of the Model
5. Qualitative Analysis of the Proposed Model
5.1. Equilibrium Point of the Model
5.2. Positivity of Proposed Model with Nonlocal Operator
5.3. Invariant Region
5.4. Existence and Uniqueness
- , for all and for all , which has a unique solution whenever .
- 1.
- , provided that .
- 2.
- is continuous and compact.
- 3.
- is the mapping contraction.
- and .
6. Analysis of the Proposed Model’s Stability
7. Numerical Dynamics
Numerical Scheme with Power Law Kernel
8. Discussions and Numerical Simulations
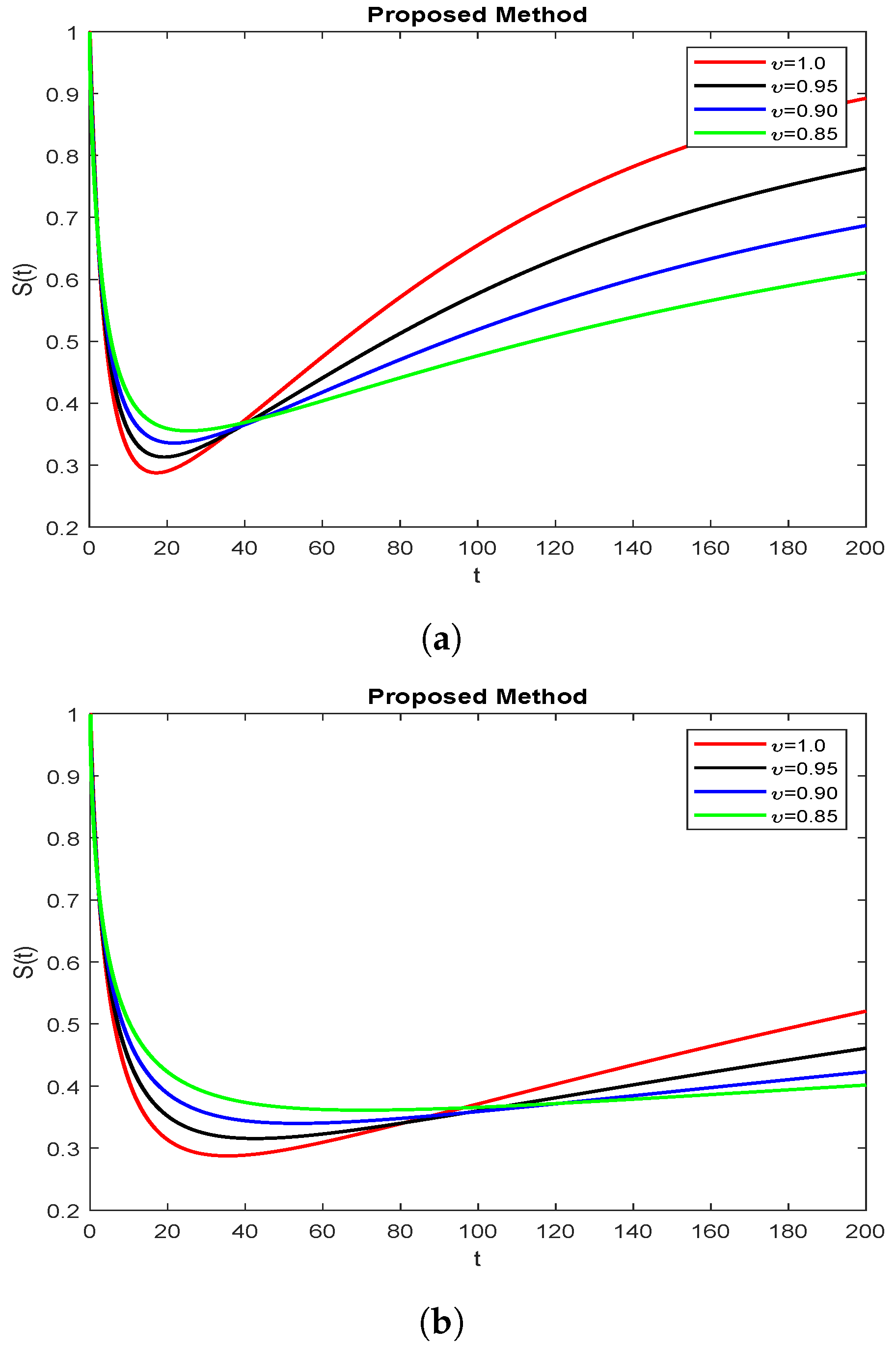
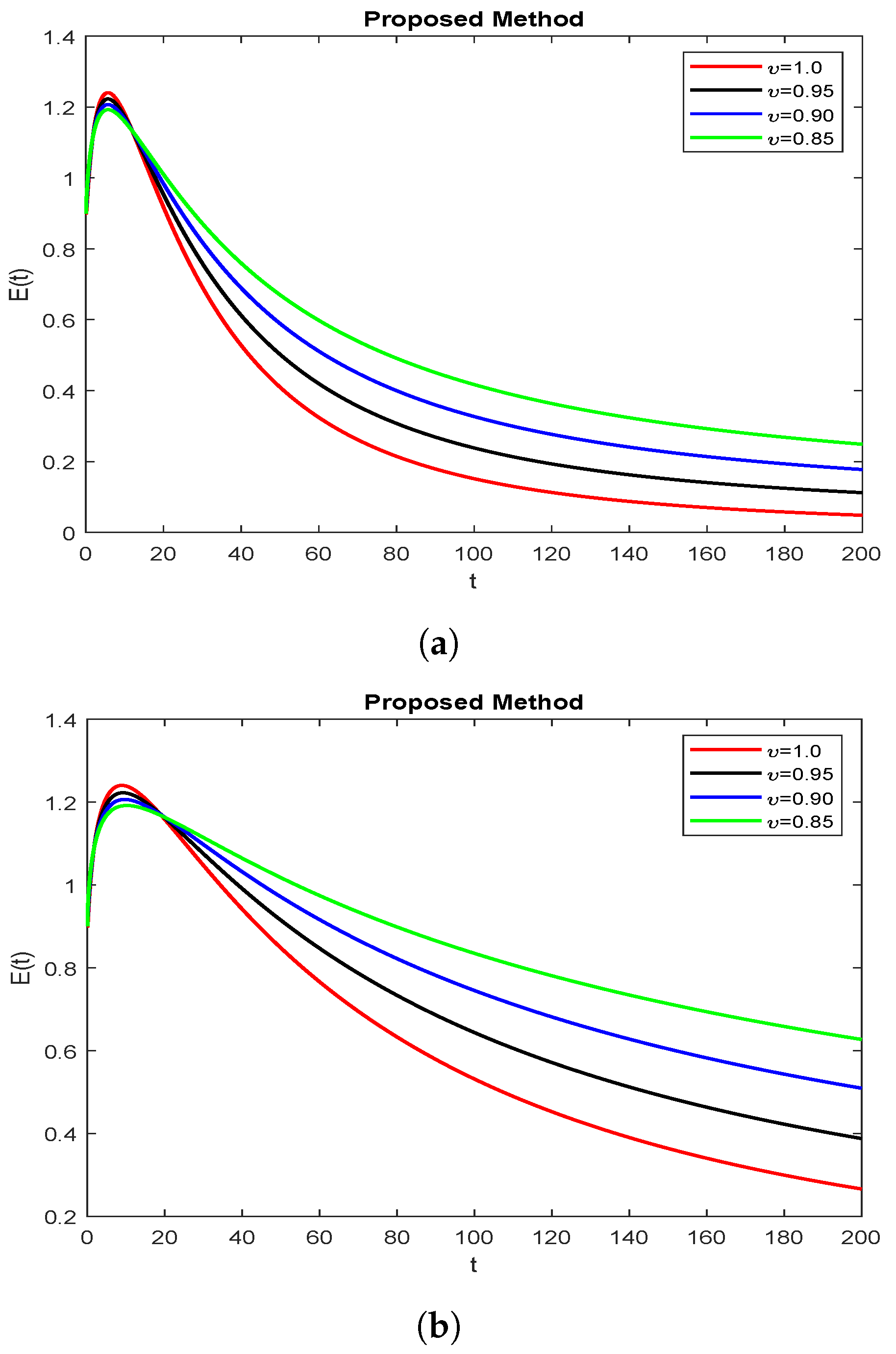
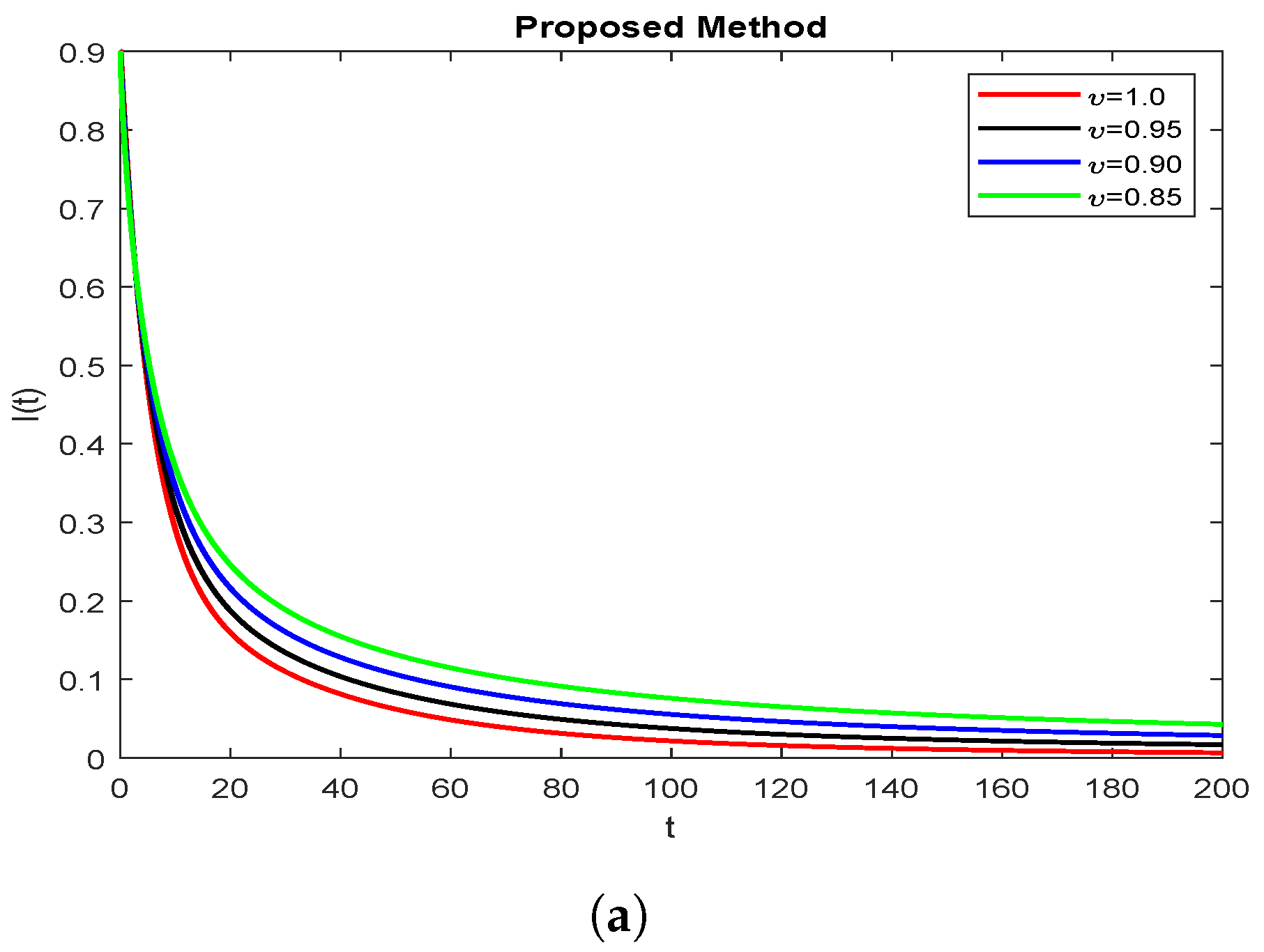
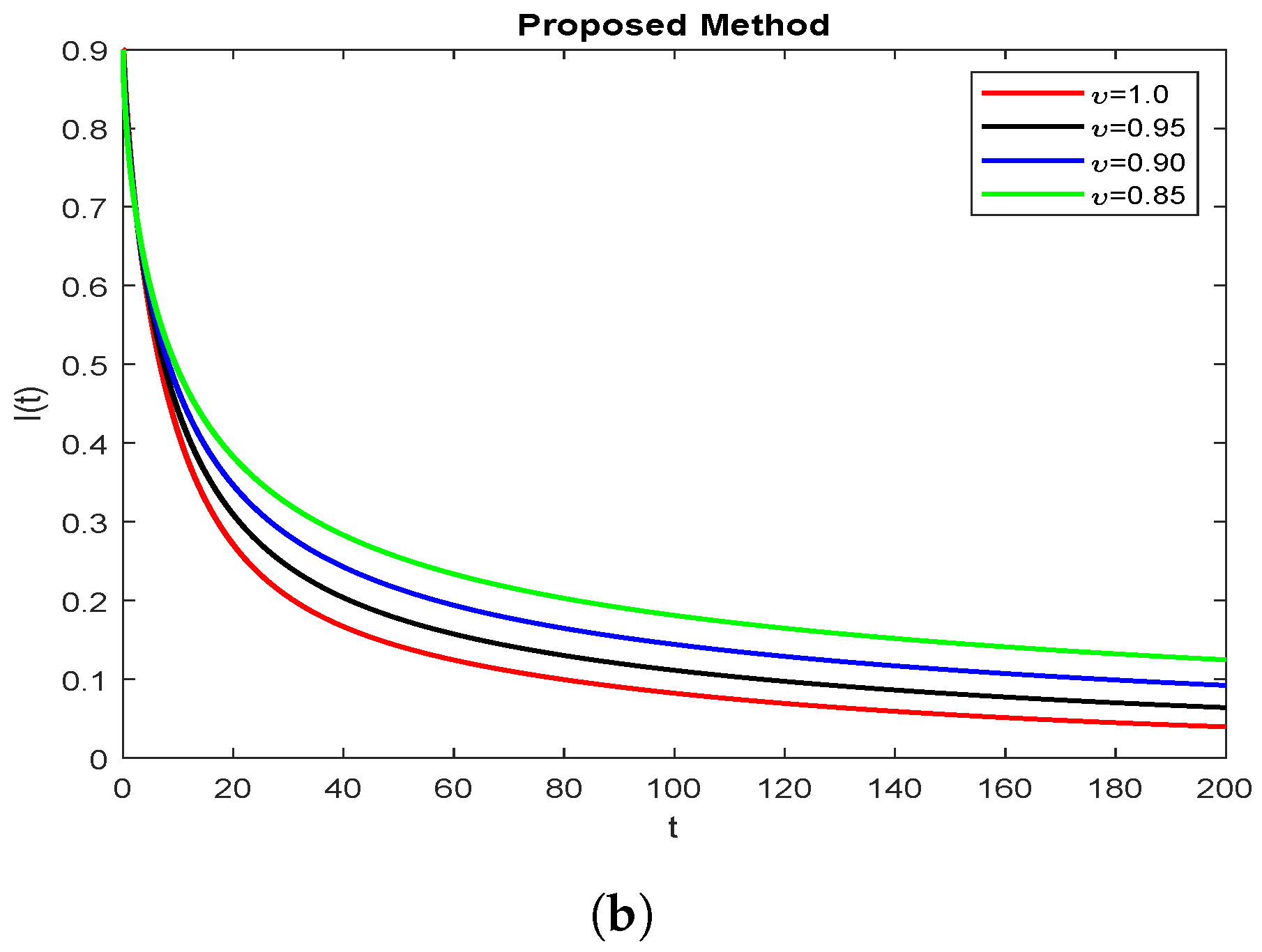
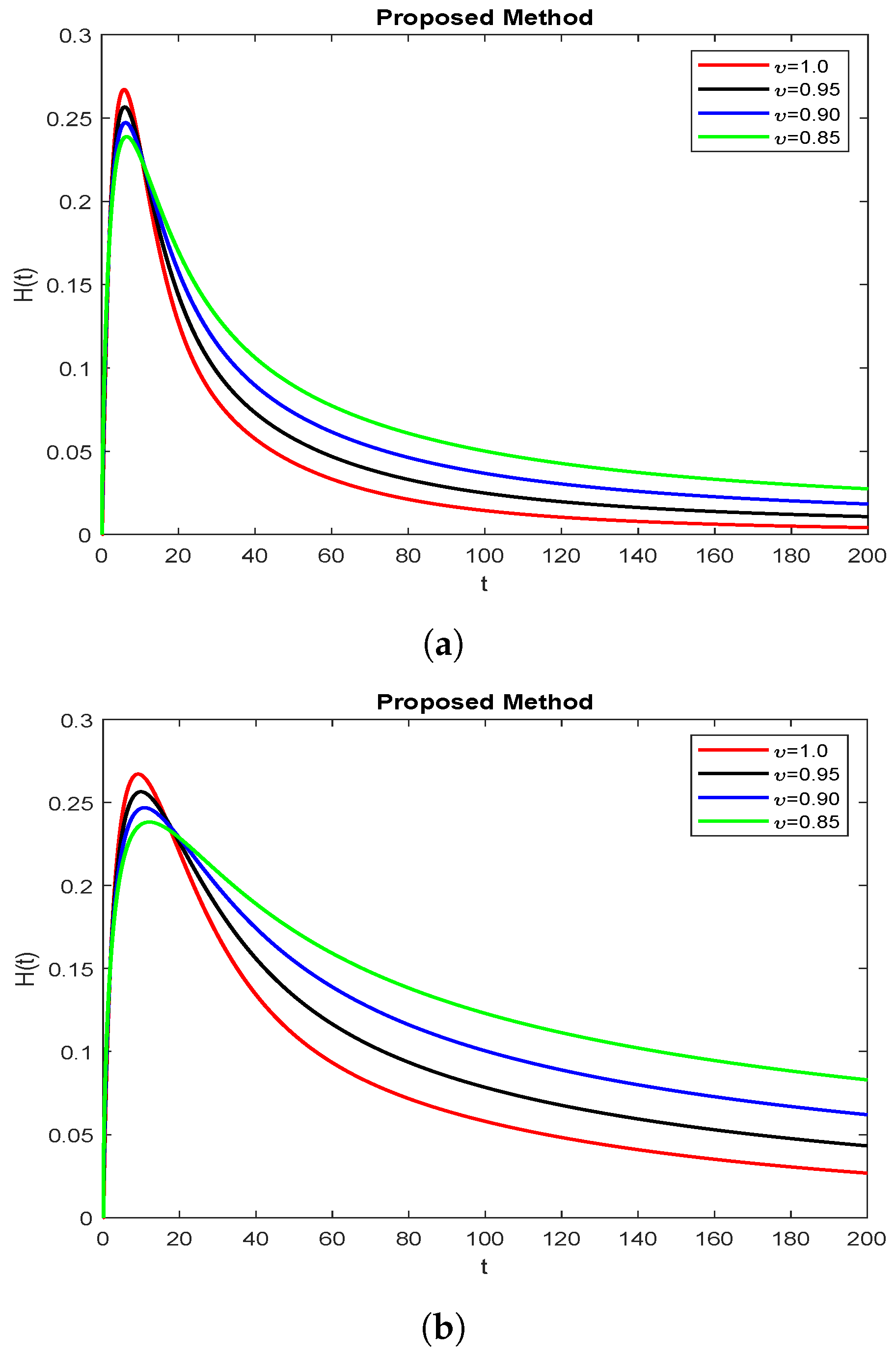

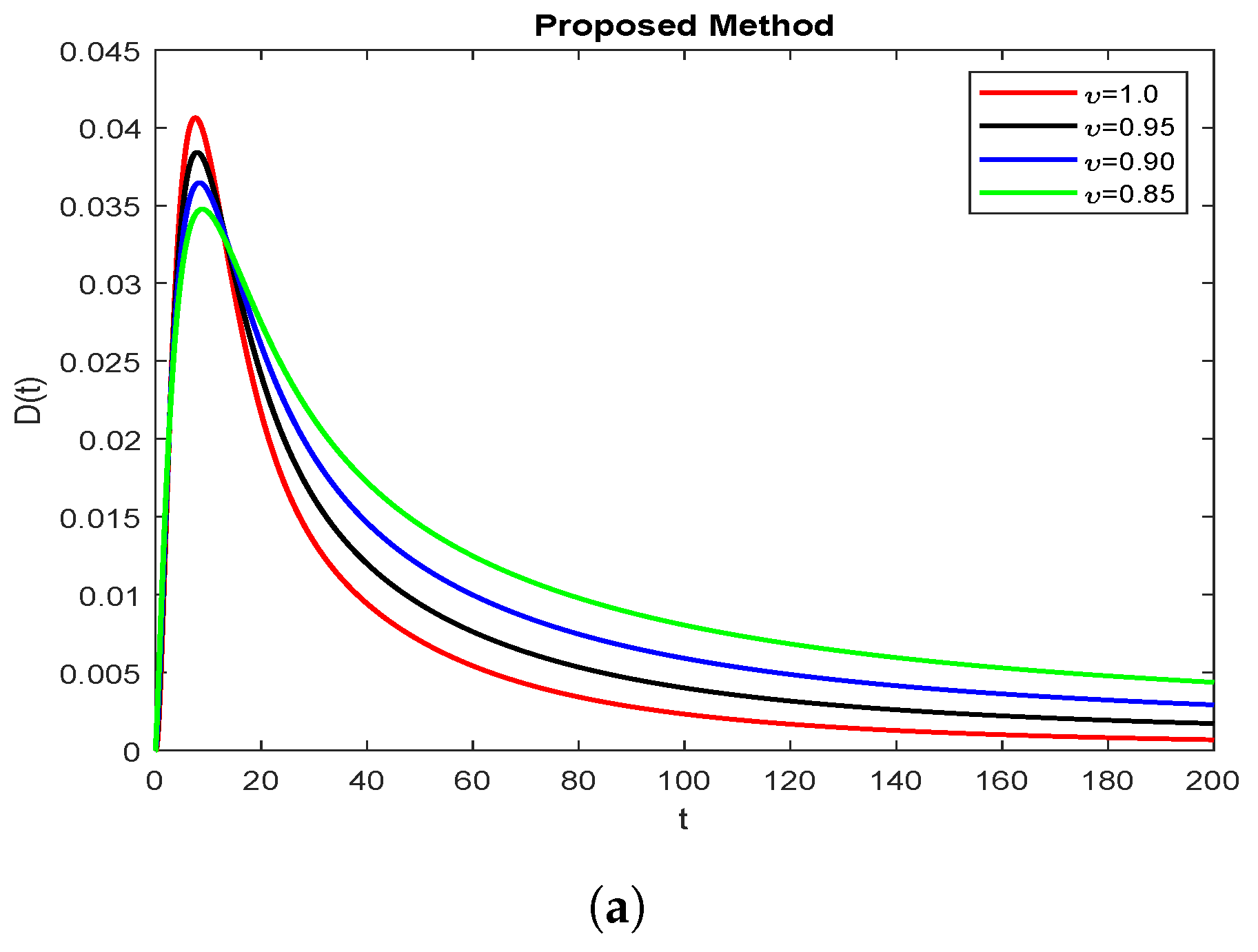
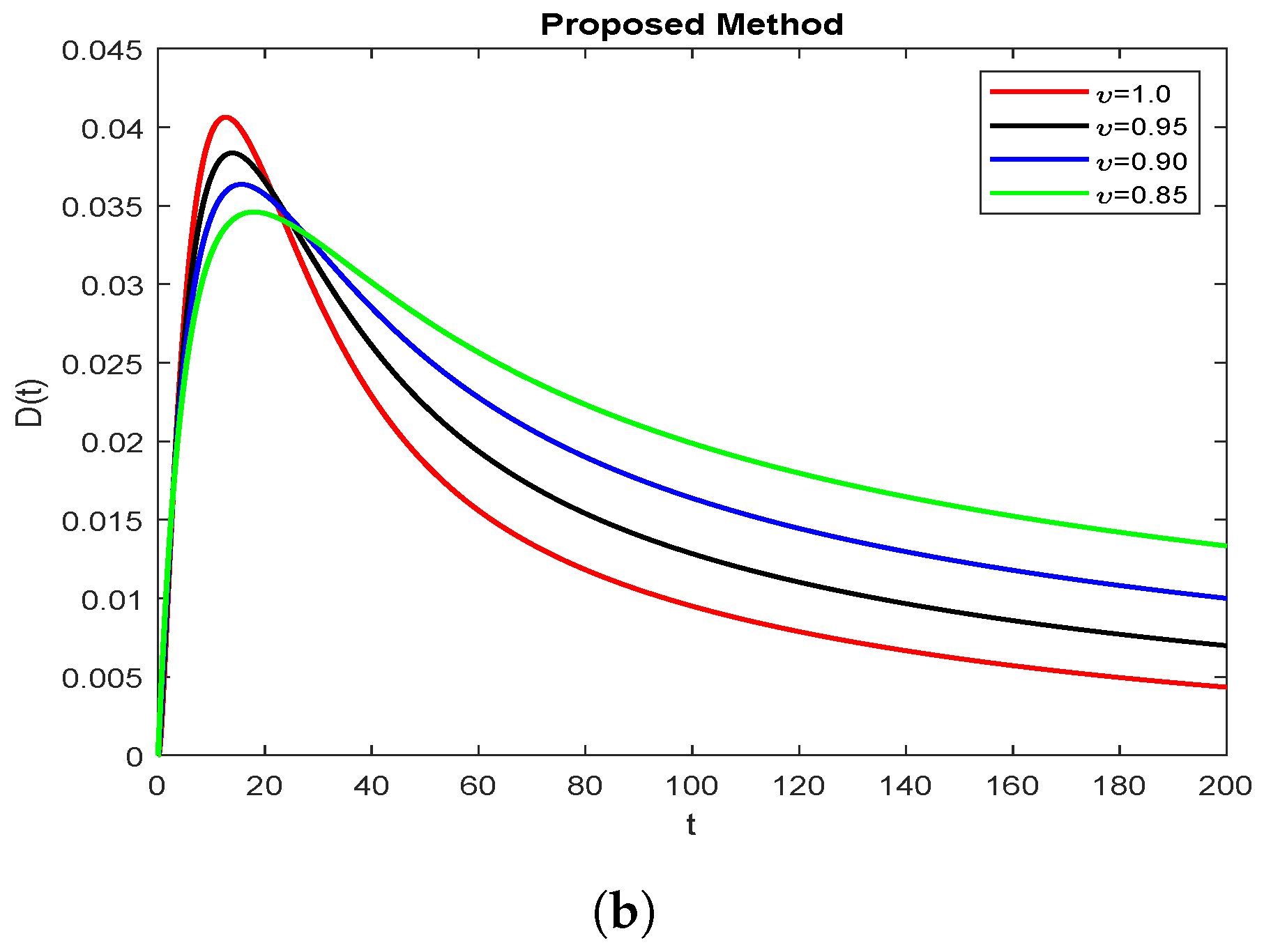
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baseler, L.; Chertow, D.S.; Johnson, K.M.; Feldmann, H.; Morens, D.M. The pathogenesis of Ebola virus disease. Ann. Rev. Pathol. 2017, 12, 387–418. [Google Scholar] [CrossRef]
- Sullivan, N.J.; Sanchez, A.; Rollin, P.E.; Yang, Z.Y.; Nabel, G.J. Development of a preventive vaccine for Ebola virus infection in primates. Nature 2000, 408, 605–609. [Google Scholar] [CrossRef]
- Rachah, A.; Torres, D.F. Mathematical modelling, simulation, and optimal control of the 2014 Ebola outbreak in West Africa. Discr. Dyn. Nat. Soc. 2015. [Google Scholar] [CrossRef]
- Area, I.; Batarfi, H.; Losada, J.; Nieto, J.J.; Shammakh, W.; Torres, A. On a fractional order Ebola epidemic model. Adv. Diff. Equ. 2015, 2015, 278. [Google Scholar] [CrossRef]
- Rachah, A.; Torres, D.F. Predicting and controlling the Ebola infection. Math. Methods Appl. Sci. 2017, 40, 6155–6164. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Akg, A. A novel method for a fractional derivative with non-local and non-singular kernel. Chaos. Solitons Fractals 2018, 114, 478–482. [Google Scholar]
- Akg, E.K. Solutions of the linear and nonlinear differential equations within the generalized fractional derivatives. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 023108. [Google Scholar]
- Diethelm, K.; Ford, N.J. Multi-order fractional differential equations and their numerical solution. Appl. Math. Comput. 2004, 154, 621–640. [Google Scholar] [CrossRef]
- Fernandez, A.; Baleanu, D.; Fokas, A.S. Solving PDEs of fractional order using the unified transform method. Appl. Math. Comput. 2018, 339, 738–749. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. arXiv 2016, arXiv:1602.03408. [Google Scholar] [CrossRef]
- Atangana, A.; Goufo, E.F.D. On the mathematical analysis of Ebola hemorrhagic fever: Deathly infection disease in west african countries. BioMed Res. Int. 2014, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Koca, I. Modelling the spread of ebola virus with Atangana-Baleanu fractional operators. Eur. Phys. J. Plus 2018, 133, 100. [Google Scholar] [CrossRef]
- Latha, V.P.; Rihan, F.A.; Rakkiyappan, R.; Velmurugan, G. A fractional-order model for Ebola virus infection with delayed immune response on heterogeneous complex networks. J. Comput. Appl. Math. 2018, 339, 134–146. [Google Scholar] [CrossRef]
- Singh, H. A new numerical algorithm for fractional model of Bloch equation in nuclear magnetic resonance. Alexandria Eng. J. 2016, 55, 2863–2869. [Google Scholar] [CrossRef]
- Singh, H. Operational matrix approach for approximate solution of fractional model of Bloch equation. J. King Saud Univ.-Sci. 2017, 29, 235–240. [Google Scholar] [CrossRef]
- Dokuyucu, M.A.; Celik, E.; Bulut, H.; Baskonus, H.M. Cancer treatment model with the Caputo-Fabrizio fractional derivative. Eur. Phys. J. Plus 2018, 133, 92. [Google Scholar] [CrossRef]
- Xu, C.; Farman, M.; Hasan, A.; Akgl, A.; Zakarya, M.; Albalawi, W.; Park, C. Lyapunov Stability and Wave Analysis of COVID-19 Omicron Variant of Real Data with Fractional Operator. Alex. Eng. J. 2022, 61, 11787–11802. [Google Scholar] [CrossRef]
- Farman, M.; Akg, A.; Abdeljawad, T.; Naik, P.A.; Bukhari, N.; Ahmad, A. Modeling and analysis of fractional order Ebola virus model with Mittag–Leffler kernel. Alex. Eng. J. 2022, 61, 2062–2073. [Google Scholar] [CrossRef]
- Farman, M.; Akg, l.A.; Nisar, K.S.; Ahmad, D.; Ahmad, A.; Kamangar, S.; Saleel, C.A. Epidemiological analysis of fractional order COVID-19 model with Mittag–Leffler kernel. AIMS Math. 2022, 7, 756–783. [Google Scholar] [CrossRef]
- Farman, M.; Akg, A.; Tekin, M.T.; Akram, M.M.; Ahmad, A.; Mahmoud, E.E.; Yahia, I.S. Fractal fractional-order derivative for HIV/AIDS model with Mittag–Leffler kernel. Alex. Eng. J. 2022, 61, 10965–10980. [Google Scholar] [CrossRef]
- Farman, M.; Saleem, M.U.; Ahmad, A.; Ahmad, M.O. Analysis and numerical solution of SEIR epidemic model of measles with non-integer time fractional derivatives by using Laplace Adomian Decomposition Method. Ain Shams Eng. J. 2018, 9, 3391–3397. [Google Scholar] [CrossRef]
- Amin, M.; Farman, M.; Akg, A.; Partohaghighi, M.; Jarad, F. Computational analysis of COVID-19 model outbreak with singular and nonlocal operator. AIMS Math. 2022, 7, 16741–16759. [Google Scholar] [CrossRef]
- Seck, R.; Ngom, D.; Ivorra, B.; Ramos, M. An optimal control model to design strategies for reducing the spread of the Ebola virus disease. Math. Biosci. Eng. 2022, 19, 1746–1774. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. New numerical surfaces to the mathematical model of cancer chemotherapy effect in Caputo fractional derivatives. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 013119. [Google Scholar] [CrossRef]
| Group of vulnerable individuals | |
| Group of infected people | |
| Group of contagion carriers | |
| Class of hospitalized people | |
| Class of dead people | |
| Class of recovered people |
| Rate of recruitment of individuals in state S | |
| The death rate | |
| The effective contact rates for diseases among those in compartment I | |
| People in class H’s rates of effective disease contact | |
| The effective contact rates for diseases among those in compartment D | |
| Rate of change from compartment E to I | |
| Rate of change from compartment E to compartment I | |
| The result of the sickness mortality rate multiplied by the compartment H to compartment D transition rate | |
| The percentage of illnesses that survive multiplied by the transition rate from condition H to compartment R | |
| The percentage of Ebola victims buried | |
| The daily percentage of persons departing the nation in states S, E, and R |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasan, A.; Akgül, A.; Farman, M.; Chaudhry, F.; Sultan, M.; De la Sen, M. Epidemiological Analysis of Symmetry in Transmission of the Ebola Virus with Power Law Kernel. Symmetry 2023, 15, 665. https://doi.org/10.3390/sym15030665
Hasan A, Akgül A, Farman M, Chaudhry F, Sultan M, De la Sen M. Epidemiological Analysis of Symmetry in Transmission of the Ebola Virus with Power Law Kernel. Symmetry. 2023; 15(3):665. https://doi.org/10.3390/sym15030665
Chicago/Turabian StyleHasan, Ali, Ali Akgül, Muhammad Farman, Faryal Chaudhry, Muhammad Sultan, and Manuel De la Sen. 2023. "Epidemiological Analysis of Symmetry in Transmission of the Ebola Virus with Power Law Kernel" Symmetry 15, no. 3: 665. https://doi.org/10.3390/sym15030665
APA StyleHasan, A., Akgül, A., Farman, M., Chaudhry, F., Sultan, M., & De la Sen, M. (2023). Epidemiological Analysis of Symmetry in Transmission of the Ebola Virus with Power Law Kernel. Symmetry, 15(3), 665. https://doi.org/10.3390/sym15030665








