Kirchhoff Index and Additive Kirchhoff Index Based on Multiplicative Degree for a Random Polyomino Chain

Abstract

Several topological indices are known to have widespread implications in a variety of research areas. Over the years, the Kirchhoff index has turned out to be an extremely significant and efficient index. In this paper, we propose the exact formulas for the expected values of the random polyomino chain to construct the multiplicative degree-Kirchhoff index and the additive degree-Kirchhoff index. We also carefully examine the highest degree of the expected values for a random polyomino chain through the multiplicative degree-Kirchhoff index and additive degree-Kirchhoff index.

1. Introduction

Resistance distance is regarded as the distance graph function, which is essential for random walk of the graph and the spring network. Based on the idea of electrical networks, Klein and Randić [1] proposed the notion of the Kirchhoff index and resistance distance of graphs in 1993. Suppose $\mathcal{G}$ as a symmetric graph with the vertex set $\{{\breve{\upsilon }}_1,{\breve{\upsilon }}_2,{\breve{\upsilon }}_3,\dots ,{\breve{\upsilon }}_{\eta }\},$ and the corresponding electrical network $\mathcal{N}$ is obtained when each edge of the graph is replaced by a fixed resistance (unit resistance). For a graph $\mathcal{G}$, the resistance distance between any two vertices is denoted by $\breve{\gamma }({\breve{\upsilon }}_i,{\breve{\upsilon }}_j)$, where ${\breve{\upsilon }}_i,{\breve{\upsilon }}_j\in \mathcal{G}$. However, in electrical networks, the resistance distance is known as effective resistance between nodes. The effective resistance can be calculated from Kirchhoff’s circuit laws and Ohm’s laws. The sum of all pairs of vertices of resistance distances is known as the Kirchhoff index of $\mathcal{G}$, represented as $\mathcal{K}\mathfrak{f}\left(\mathcal{G}\right)$, and written as

$$\mathcal{K}\mathfrak{f}\left(\mathcal{G}\right)=\sum _{i<j}\breve{\gamma }({\breve{\upsilon }}_i,{\breve{\upsilon }}_j)=\frac{1}{2}\sum _{i=1}^{\eta }\sum _{j=1}^{\eta }\breve{\gamma }({\breve{\upsilon }}_i,{\breve{\upsilon }}_j)=\frac{1}{2}\sum _{i=1}^{\eta }\breve{\gamma }\left({\breve{\upsilon }}_i\right|\left(\mathcal{G}\right),$$

(1)

where

$$\breve{\gamma }\left({\breve{\upsilon }}_i\right|\left(\mathcal{G}\right)=\sum _{j=1}^{\eta }\breve{\gamma }({\breve{\upsilon }}_i,{\breve{\upsilon }}_j).$$

(2)

Chen and Zhang [2] introduced a modern graph invariant in 2007, which is stated as

$$\mathcal{K}{\mathfrak{f}}^{*}\left(\mathcal{G}\right)=\sum _{1\le i<j\le \eta }{\breve{\delta }}_i{\breve{\delta }}_j\breve{\gamma }({\breve{\upsilon }}_i,{\breve{\upsilon }}_j)=\frac{1}{2}\sum _{i=1}^{\eta }\sum _{j=1}^{\eta }{\breve{\delta }}_i{\breve{\delta }}_j\breve{\gamma }({\breve{\upsilon }}_i,{\breve{\upsilon }}_j),$$

(3)

where ${\breve{\delta }}_i$ indicates the vertex’s degree ${\breve{\upsilon }}_i$ of the graph $\mathcal{G}$.

Gutman et al. [3] introduced the idea of the additive degree-Kirchhoff index in 2012, defined as

$$\mathcal{K}{\mathfrak{f}}^{+}\left(\mathcal{G}\right)=\sum _{1\le i<j\le \eta }({\breve{\delta }}_i+{\breve{\delta }}_j)\breve{\gamma }({\breve{\upsilon }}_i,{\breve{\upsilon }}_j).$$

(4)

Many studies have been carried out to compute Kirchhoff indices for specific classes of graphs, to find bounds for the Kirchhoff indices of graphs, and to find the characteristic extremal graphs [4,5,6,7,8,9,10]. Recently, a study has been made to explore the Kirchhoff index based on the degree of vertices regarding irregular polygonal chains. These efforts led to the expected values of the degree-Kirchhoff indices (both additive and multiplicative), Gutman index, and Schultz index of a random polyphenylene chain being obtained [11]. For extended studies on random polygonal chains, mostly readers referred to the recent papers [12,13,14,15]. The motivation of the purposed study can be elaborated as:

• Some scholars study the calculation methods of degree-Kirchhoff index for some special classes of graphs such as linear hexagonal chain, hexagonal chain, ladder diagram, ladder chain, linear polynomial chain, linear hexagon chain, and so on. This work was still unattended for a random polyomino chain.
• In [2], the authors have established a beautiful relation between the multiplicative degree-Kirchhoff index and the eigenvalues of the normalized Laplacian matrix.

Inspired by the above literature, this paper is dedicated to establish the exact formulas for the expected values of the additive and multiplicative degree-Kirchhoff indices via a random polyomino chain. Moreover, the highest degree of the expected values of these indices is also characterized.

The graph of polyominoes [16] (also known as chessboards [17] or arrangements that use square cells [18]) is a symmetrical geometric graph that is attained when two congruent ordinary squares (have either a common edge or are disjoint) with sides of distance 1 (known as a cell) are arranged in a plane. Polyomino graphs have numerous applications in structural chemistry and statistical physics. An irregular polyomino chain is known as a subgraph of a polyomino graph [19]. A polyomino chain ${\mathcal{Q}}_{\eta }$ having “$\eta$” squares, that is to be considered as a polyomino chain ${\mathcal{Q}}_{\eta -1}$ having “$\eta -1$” squares adjacent to a indicated in picture, a new terminal square by a cut edge as shown in Figure 1.

If ${\mathcal{Q}}_{\eta }={\breve{ϝ}}_1,{\breve{ϝ}}_2,\cdots ,{\breve{ϝ}}_{\eta }$ is a polyomino chain having $\eta (\ge 2)$ squares, ${\breve{ϝ}}_{\kappa }$ as the $\kappa$th square of ${\mathcal{Q}}_{\eta }$ connected to ${\breve{ϝ}}_{\kappa -1}$ with a cut edge ${\breve{\mu }}_{\kappa -1}{\breve{\omega }}_{\kappa }$, where ${\breve{\mu }}_{\kappa -1}\in {\breve{ϝ}}_{\kappa -1}\mathrm{and}{\breve{\omega }}_{\kappa }\in {\breve{ϝ}}_{\kappa }$, $(2\le \kappa \le \eta )$. A vertex $\breve{\upsilon }$ is known as ortho-vertex $\left({\breve{o}}_{\kappa }\right)$ and para-vertex $\left({\breve{p}}_{\kappa }\right)$ of ${\breve{ϝ}}_{\kappa }$ if the distance between $\breve{\upsilon }$ and ${\breve{\omega }}_{\kappa }$ is one and two, respectively. It is easy to establish that ${\breve{\omega }}_{\eta }={\breve{\lambda }}_1$, ${\breve{o}}_{\eta }={\breve{\lambda }}_2,{\breve{\lambda }}_4$, and ${\breve{p}}_{\eta }={\breve{\lambda }}_3$ in ${\breve{ϝ}}_{\eta }$ (see Figure 1).

A polyomino chain ${\mathcal{Q}}_{\eta }$ is known as a polyomino ortho-chain ${\mathcal{Q}}_{\eta }^o$ and polyomino para-chain ${\mathcal{Q}}_{\eta }^p$ if ${\breve{\mu }}_{\kappa }={\breve{o}}_{\kappa }$ and ${\breve{\mu }}_{\kappa }={\breve{p}}_{\kappa }$ with $2\le \kappa \le \eta -1,$ respectively.

Two distinct connections to the para- or ortho-vertices are possible for the ending square $\eta \ge 2$ to provide the local arrangements, written as ${\mathcal{Q}}_{\eta +1}^1{\mathcal{Q}}_{\eta +1}^2$ (see Figure 2).

A polyomino chain is known as polyomino chain $\mathcal{Q}(\eta ,\mathfrak{t})$ with $\eta$ squares if the terminal squares are added gradually. At each stage $\kappa =(3,4,\cdots ,\eta )$, a random choice is made from the following constructions:

1.

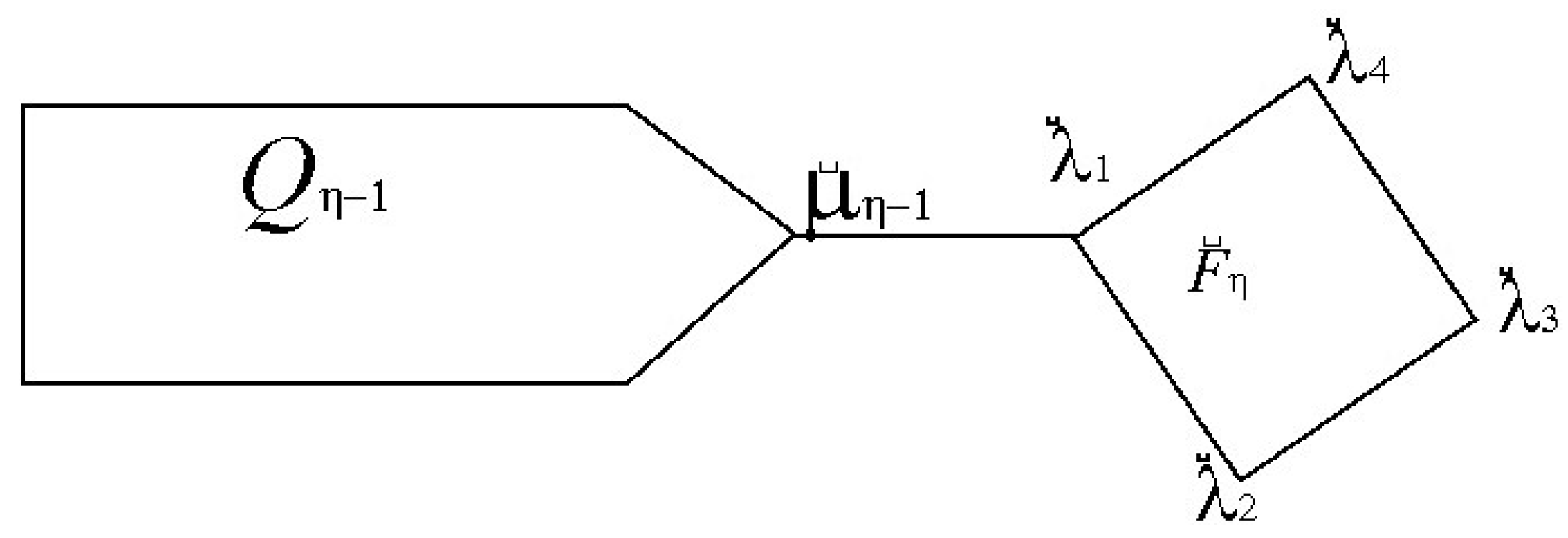
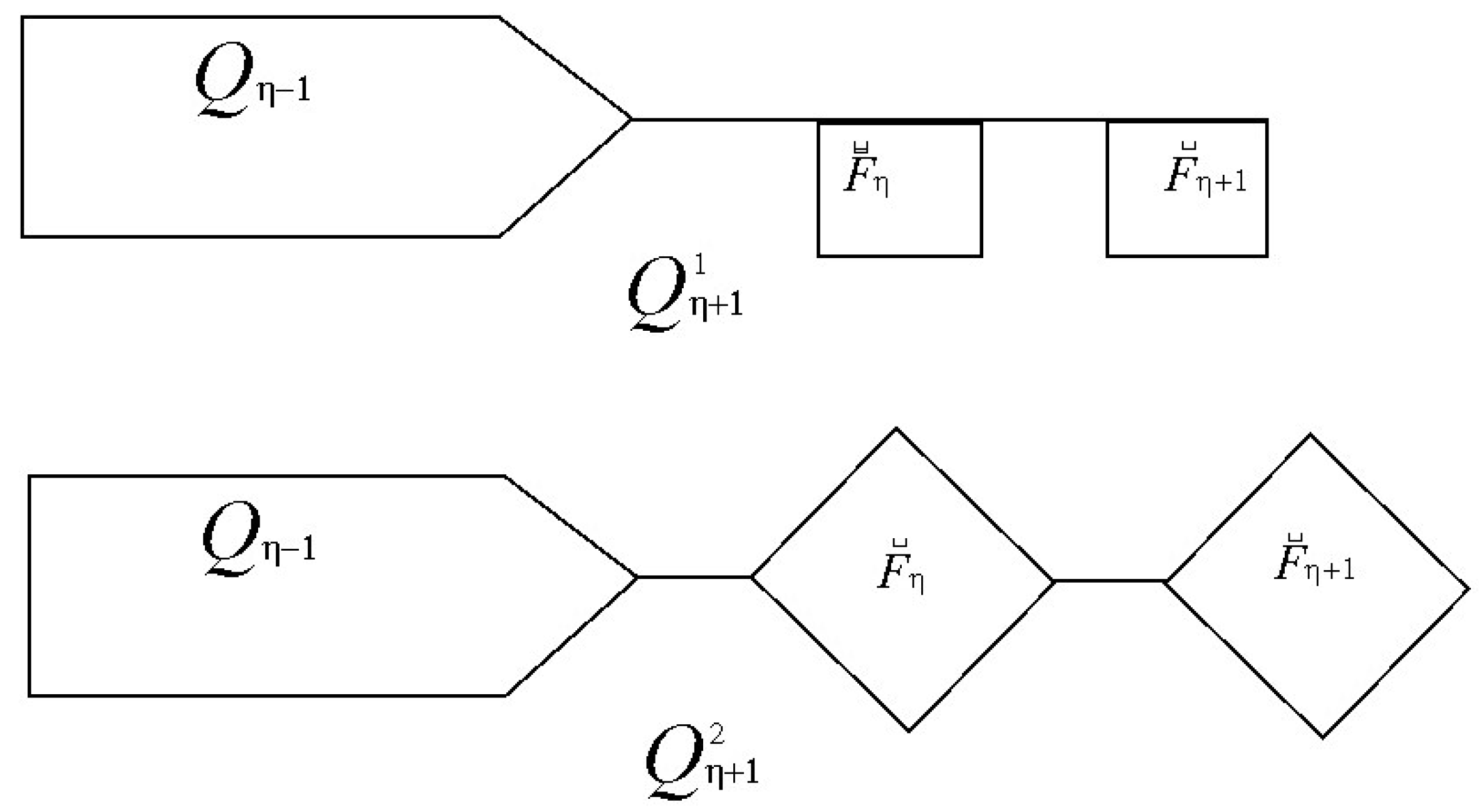
${\mathcal{Q}}_{\kappa -1}\to Q_{\kappa }^1$ with probability $\mathfrak{t}$,

2.

${\mathcal{Q}}_{\kappa -1}\to Q_{\kappa }^2$ with probability $1-\mathfrak{t},$

where probability $\mathfrak{t}$ is constant, independent of the step parameter $\kappa$. Particularly, the irregular polyomino chain $\mathcal{Q}(\eta ,1)$ is known as the polyomino ortho-chain ${\mathcal{Q}}_{\eta }^o$. Additionally, $\mathcal{Q}(\eta ,0)$ is termed as the polyomino para-chain ${\mathcal{Q}}_{\eta }^p$.

2. The Expected Value of the Multiplicative Degree-Kirchhoff Index of a Random Polyomino Chain

The multiplicative degree-Kirchhoff index $\mathcal{K}{\mathfrak{f}}^{*}\left({\mathcal{Q}}_{\eta }\right)$ for a random polyomino chain ${\mathcal{Q}}_{\eta }$ is a random variable. Here, we propose a precise formula for its expected value $E\left(\mathcal{K}{\mathfrak{f}}^{*}\left({\mathcal{Q}}_{\eta }\right)\right)$.

Let the terminal square is spanned by vertices $\{{\breve{\lambda }}_1,{\breve{\lambda }}_2,{\breve{\lambda }}_3,{\breve{\lambda }}_4\}$ and a new edge is labeled as ${\breve{\mu }}_{\eta }{\breve{\lambda }}_1$ (as shown in Figure 1). For each $\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}$, we have

$$\breve{\gamma }({\breve{\lambda }}_1,\breve{\upsilon })=\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })+1,\breve{\gamma }({\breve{\lambda }}_2,\breve{\upsilon })=\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })+1+\frac{3}{4},$$

(5)

$$\breve{\gamma }({\breve{\lambda }}_3,\breve{\upsilon })=\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })+1+1,\breve{\gamma }({\breve{\lambda }}_4,\breve{\upsilon })=\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })+1+\frac{3}{4},$$

(6)

$$\sum _{\breve{\upsilon }\in {\mathcal{V}}_{Q_{\eta }}}{\breve{\delta }}_{{\mathcal{Q}}_{\eta +1}}\left(\breve{\upsilon }\right)=10\eta -1.$$

(7)

Meanwhile,

$$\begin{array}{cc}\hfill \sum _{i=1}^4\breve{\delta }\left({\breve{\lambda }}_i\right)\breve{\gamma }({\breve{\lambda }}_1,{\breve{\lambda }}_i)=& 2\times \frac{3}{4}+2\times 1+2\times \frac{3}{4}=5,\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill \sum _{i=1}^4\breve{\delta }\left({\breve{\lambda }}_i\right)\breve{\gamma }({\breve{\lambda }}_2,{\breve{\lambda }}_i)=& 3\times \frac{3}{4}+2\times \frac{3}{4}+2\times 1=\frac{23}{4},\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill \sum _{i=1}^4\breve{\delta }\left({\breve{\lambda }}_i\right)\breve{\gamma }({\breve{\lambda }}_3,{\breve{\lambda }}_i)=& 3\times 1+2\times \frac{3}{4}+2\times \frac{3}{4}=6,\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill \sum _{i=1}^4\breve{\delta }\left({\breve{\lambda }}_i\right)\breve{\gamma }({\breve{\lambda }}_4,{\breve{\lambda }}_i)=& 3\times \frac{3}{4}+2\times 1+2\times \frac{3}{4}=\frac{23}{4}.\hfill \end{array}$$

(11)

Theorem 1. 

The expected value (for $\eta \ge 1$) is provided as the multiplicative degree-Kirchhoff index of an arbitrary polyomino chain

$$E\left(\mathcal{K}{\mathfrak{f}}^{*}\left({\mathcal{Q}}_{\eta }\right)\right)=(\frac{100}{3}-\frac{25}{6}t){\eta }^3+(\frac{25}{2}t-10){\eta }^2+(-\frac{25}{3}t-\frac{7}{3})\eta -1.$$

(12)

Proof. 

By Equation (3), it is clear that

$$\mathcal{K}{\mathfrak{f}}^{*}\left({\mathcal{Q}}_{\eta +1}\right)=\sum _{\{\breve{\mu },\breve{\upsilon }\}\subseteq {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\breve{\delta }\left(\breve{\mu }\right)\breve{\delta }\left(\breve{\upsilon }\right)\breve{\gamma }(\breve{\mu },\breve{\upsilon })+\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\sum _{{\breve{\lambda }}_i\in {\mathcal{V}}_{{\breve{ϝ}}_{\eta +1}}}\breve{\delta }\left(\breve{\upsilon }\right)\breve{\delta }\left({\breve{\lambda }}_i\right)\breve{\gamma }(\breve{\upsilon },{\breve{\lambda }}_i)+\sum _{\{{\breve{\lambda }}_i,{\breve{\lambda }}_j\}\subseteq {\mathcal{V}}_{{\breve{ϝ}}_{\eta +1}}}\breve{\delta }\left({\breve{\lambda }}_i\right)\breve{\delta }\left({\breve{\lambda }}_j\right)\breve{\gamma }({\breve{\lambda }}_i,{\breve{\lambda }}_j).$$

(13)

Note that

$$\begin{array}{cc}\hfill \sum _{\{\breve{\mu },\breve{\upsilon }\}\subseteq {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\breve{\delta }\left(\breve{\mu }\right)\breve{\delta }\left(\breve{\upsilon }\right)\breve{\gamma }(\breve{\mu },\breve{\upsilon })=& \sum _{\{\breve{\mu },\breve{\upsilon }\}\subseteq {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}\setminus \left\{{\breve{\mu }}_{\eta }\right\}}\breve{\delta }\left(\breve{\mu }\right)\breve{\delta }\left(\breve{\upsilon }\right)\breve{\gamma }(\breve{\mu },\breve{\upsilon })+\hfill \\ & \sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}\setminus \left\{{\breve{\mu }}_{\eta }\right\}}\breve{\delta }\left(\breve{\upsilon }\right){\breve{\delta }}_{{\mathcal{Q}}_{\eta +1}}\left({\breve{\mu }}_{\eta }\right)\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon }),\hfill \\ \hfill =& \sum _{\{\breve{\mu },\breve{\upsilon }\}\subseteq {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}\setminus \left\{{\breve{\mu }}_{\eta }\right\}}\breve{\delta }\left(\breve{\mu }\right)\breve{\delta }\left(\breve{\upsilon }\right)\breve{\gamma }(\breve{\mu },\breve{\upsilon })+\hfill \\ \hfill & \sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}\setminus \left\{{\breve{\mu }}_{\eta }\right\}}\breve{\delta }\left(\breve{\upsilon }\right)({\breve{\delta }}_{{\mathcal{Q}}_{\eta }}\left({\breve{\mu }}_{\eta }\right)+1)\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon }),\hfill \\ \hfill =& \mathcal{K}{\mathfrak{f}}^{*}\left({\mathcal{Q}}_{\eta }\right)+\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\breve{\delta }\left(\breve{\upsilon }\right)\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon }).\hfill \end{array}$$

By Equations (5) and (6), we obtain

$$\begin{array}{cc}\hfill \sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\sum _{{\breve{\lambda }}_i\in {\mathcal{V}}_{{\breve{ϝ}}_{\eta }+1}}\breve{\delta }\left(\breve{\upsilon }\right)\breve{\delta }\left({\breve{\lambda }}_i\right)\breve{\gamma }(\breve{\upsilon },{\breve{\lambda }}_i)=& \sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\breve{\delta }\left(\breve{\upsilon }\right)[3(\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })+1)+2(\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })+1+\frac{3}{4})\hfill \\ \hfill & +2(\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })+1+1)+2(\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })+1+\frac{3}{4})]\hfill \\ \hfill =& \sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\breve{\delta }\left(\breve{\upsilon }\right)[9\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })+14],\hfill \\ \hfill =& 9\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\breve{\delta }\left(\breve{\upsilon }\right)\left(\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })\right)+14\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\breve{\delta }\left(\breve{\upsilon }\right),\hfill \\ \hfill =& 9\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\breve{\delta }\left(\breve{\upsilon }\right)\left(\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })\right)+14(10\eta -1).\hfill \end{array}$$

$$\begin{array}{cc}\hfill \sum _{({\breve{\lambda }}_i,{\breve{\lambda }}_j)\subseteq {\mathcal{V}}_{{\breve{ϝ}}_{\eta +1}}}\breve{\delta }\left({\breve{\lambda }}_i\right)\breve{\delta }\left({\breve{\lambda }}_j\right)\breve{\gamma }({\breve{\lambda }}_i,{\breve{\lambda }}_j)=& \frac{1}{2}\sum _{i=1}^4\sum _{j=1}^4\breve{\delta }\left({\breve{\lambda }}_i\right)\breve{\delta }\left({\breve{\lambda }}_j\right)\breve{\gamma }({\breve{\lambda }}_i,{\breve{\lambda }}_j),\hfill \\ \hfill =& \frac{1}{2}\sum _{i=1}^4\breve{\delta }\left({\breve{\lambda }}_i\right)\sum _{j=1}^4\breve{\delta }\left({\breve{\lambda }}_j\right)\breve{\gamma }({\breve{\lambda }}_i,{\breve{\lambda }}_j),\hfill \\ \hfill =& \frac{1}{2}(3.5+2.\frac{23}{4}+2.6+2.\frac{23}{4}),\hfill \\ \hfill =& 25.\hfill \end{array}$$

Then,

$$\mathcal{K}{\mathfrak{f}}^{*}\left({\mathcal{Q}}_{\eta +1}\right)=\mathcal{K}{\mathfrak{f}}^{*}\left(Q_{\eta }\right)+10\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\breve{\delta }\left(\breve{\upsilon }\right)\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })+14(10\eta -1)+25.$$

(14)

For a random polyomino chain ${\mathcal{Q}}_{\eta }$, a random variable is given as ${\sum }_{v\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\breve{\delta }\left(\breve{\upsilon }\right)\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })$. We write ${\mathcal{R}}_{\eta }=E\left({\sum }_{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\breve{\delta }\left(\breve{\upsilon }\right)\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })\right)$ to represent its expected value. Consider these two significant situations, for instance:

• Case 1: ${\mathcal{Q}}_{\eta }\to {\mathcal{Q}}_{\eta +1}^1$
  Here, ${\breve{\mu }}_{\eta }$ correlates to the vertex labeled ${\breve{\lambda }}_2$ or ${\breve{\lambda }}_4$. As a result, ${\sum }_{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\breve{\delta }\left(\breve{\upsilon }\right)\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })$ is equivalent to ${\sum }_{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\breve{\delta }\left(\breve{\upsilon }\right)\breve{\gamma }({\breve{\lambda }}_2,\breve{\upsilon }).$
• Case 2: ${\mathcal{Q}}_{\eta }\to {\mathcal{Q}}_{\eta +1}^2$
  Here, ${\breve{\mu }}_{\eta }$ correlates to the vertex labeled ${\breve{\lambda }}_3.$ As a result, ${\sum }_{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\breve{\delta }\left(\breve{\upsilon }\right)\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })$ is equivalent to ${\sum }_{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\breve{\delta }\left(\breve{\upsilon }\right)\breve{\gamma }({\breve{\lambda }}_3,\breve{\upsilon }).$

Since the probabilities for the above mentioned two cases in random polyomino chains are $\mathfrak{t}$ and $1-\mathfrak{t}$, respectively, we can determine the expected value ${\mathcal{R}}_{\eta }$ as:

$$\begin{array}{cc}\hfill {\mathcal{R}}_{\eta }=& E\left(\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\breve{\delta }\left(\breve{\upsilon }\right)\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })\right).\hfill \\ \hfill =& t\left(\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\breve{\delta }\left(\breve{\upsilon }\right)\breve{\gamma }({\breve{\lambda }}_2,\breve{\upsilon })\right)+(1-t)\left(\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\breve{\delta }\left(\breve{\upsilon }\right)\breve{\gamma }({\breve{\lambda }}_3,\breve{\upsilon })\right),\hfill \\ \hfill =& t\left\{\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta -1}}}\breve{\delta }\left(\breve{\upsilon }\right)[\breve{\gamma }({\breve{\mu }}_{\eta -1},\breve{\upsilon })+1+\frac{3}{4}]+\sum _{\breve{\upsilon }\in {\breve{ϝ}}_{\eta }}\breve{\delta }\left(\breve{\upsilon }\right)\left[\breve{\gamma }({\breve{\lambda }}_2,\breve{\upsilon })\right]\right\}\hfill \\ \hfill & +(1-t)\left\{\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta -1}}}\breve{\delta }\left(\breve{\upsilon }\right)[\breve{\gamma }({\breve{\mu }}_{\eta -1},\breve{\upsilon })+1+1]+\sum _{\breve{\upsilon }\in {\breve{ϝ}}_{\eta }}\breve{\delta }\left(\breve{\upsilon }\right)\left[\breve{\gamma }({\breve{\lambda }}_3,\breve{\upsilon })\right]\right\},\hfill \\ \hfill =& t\left\{\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta -1}}}\breve{\delta }\left(\breve{\upsilon }\right)\left[\breve{\gamma }({\breve{\mu }}_{\eta -1},\breve{\upsilon })\right]+\frac{7}{4}\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta -1}}}\breve{\delta }\left(\breve{\upsilon }\right)+\frac{23}{4}\right\}\hfill \\ \hfill & +(1-t)\left\{\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta -1}}}\breve{\delta }\left(\breve{\upsilon }\right)\breve{\gamma }({\breve{\mu }}_{\eta -1},\breve{\upsilon })+2\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta -1}}}\breve{\delta }\left(\breve{\upsilon }\right)+6\right\},\hfill \\ \hfill =& t\left\{\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta -1}}}\breve{\delta }\left(\breve{\upsilon }\right)\breve{\gamma }({\breve{\mu }}_{\eta -1},\breve{\upsilon })+\frac{7}{4}(10\eta -11)+\frac{23}{4}\right\}\hfill \\ & +(1-t)\left\{\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta -1}}}\breve{\delta }\left(\breve{\upsilon }\right)\breve{\gamma }({\breve{\mu }}_{\eta -1},\breve{\upsilon })+2(10\eta -11)+6\right\},\hfill \\ \hfill =& \sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta -1}}}\breve{\delta }\left(\breve{\upsilon }\right)\breve{\gamma }({\breve{\mu }}_{\eta -1},\breve{\upsilon })+(20-\frac{5}{2}t)\eta +\frac{5}{2}t-16.\hfill \end{array}$$

Now, by applying the properties of mathematical expectation and check that $E\left({\mathcal{R}}_{\eta }\right)={\mathcal{R}}_{\eta }$, we obtain

$${\mathcal{R}}_{\eta }={\mathcal{R}}_{\eta -1}+(20-\frac{5}{2}\mathfrak{t})\eta +\frac{5}{2}\mathfrak{t}-16.$$

(15)

The boundary condition is

$${\mathcal{R}}_1=E\left(\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_1}}\breve{\delta }\left(\breve{\upsilon }\right)\breve{\gamma }({\breve{\mu }}_1,\breve{\upsilon })\right)=5.$$

Using the recurrence relation in Equation (15), we obtain

$$\begin{array}{cc}\hfill {\mathcal{R}}_{\eta }=& {\mathcal{R}}_1+(20-\frac{5}{2}\mathfrak{t})[\eta +(\eta -1)+\dots +2]+(\eta -1)(\frac{5}{2}\mathfrak{t}-16),\hfill \\ \hfill =& (10-\frac{5}{4}\mathfrak{t}){\eta }^2+(\frac{5}{4}\mathfrak{t}-6)\eta +1.\hfill \end{array}$$

Through the use of the expectation operator and Equation (14), we obtain

$$\begin{array}{ccc}\hfill E\left(\mathcal{K}{\mathfrak{f}}^{*}\left({\mathcal{Q}}_{\eta +1}\right)\right)& =& E\left(\mathcal{K}{\mathfrak{f}}^{*}\left({\mathcal{Q}}_{\eta }\right)\right)+10{\mathcal{R}}_{\eta }+14(10\eta -1)+25,\hfill \\ & =& E\left(\mathcal{K}{\mathfrak{f}}^{*}\left({\mathcal{Q}}_{\eta }\right)\right)+10[(10-\frac{5}{4}\mathfrak{t}){\eta }^2+(\frac{5}{4}\mathfrak{t}-6)\eta +1]+140\eta +11,\hfill \\ & =& E\left(\mathcal{K}{\mathfrak{f}}^{*}\left({\mathcal{Q}}_{\eta }\right)\right)+(100-\frac{25}{2}\mathfrak{t}){\eta }^2+(\frac{25}{2}\mathfrak{t}+80)\eta +21.\hfill \end{array}$$

(16)

The used condition is

$$\begin{array}{cc}\hfill E\left(\mathcal{K}{\mathfrak{f}}^{*}\left({\mathcal{Q}}_1\right)\right)=& \frac{1}{2}\sum _{i=1}^4\sum _{j=1}^4\breve{\delta }\left({\breve{\lambda }}_i\right)\breve{\delta }\left({\breve{\lambda }}_j\right)\breve{\gamma }({\breve{\lambda }}_i,{\breve{\lambda }}_j).\hfill \\ \hfill =& \frac{1}{2}\sum _{i=1}^4\breve{\delta }\left({\breve{\lambda }}_i\right)\sum _{j=1}^4\breve{\delta }\left({\breve{\lambda }}_j\right)\breve{\gamma }({\breve{\lambda }}_i,{\breve{\lambda }}_j),\hfill \\ \hfill =& \frac{1}{2}\left[2(5+5+5+5)\right],\hfill \\ \hfill =& 20.\hfill \end{array}$$

and Equation (16) can be rewritten as

$$E\left(\mathcal{K}{\mathfrak{f}}^{*}\left({\mathcal{Q}}_{\eta }\right)\right)=E\left(\mathcal{K}{f}^{*}\left({\mathcal{Q}}_{\eta -1}\right)\right)+(100-\frac{25}{2}\mathfrak{t}){(\eta -1)}^2+(\frac{25}{2}\mathfrak{t}+80)(\eta -1)+21.$$

Using the recurrence relation in above equation, we obtain

$$\begin{array}{cc}\hfill E\left(\mathcal{K}{\mathfrak{f}}^{*}\left({\mathcal{Q}}_{\eta }\right)\right)=& E\left(\mathcal{K}{\mathfrak{f}}^{*}\left({\mathcal{Q}}_1\right)\right)+(100-\frac{25}{2}\mathfrak{t})[{(\eta -1)}^2+{(\eta -2)}^2+\dots +1^2]\hfill \\ \hfill & +(\frac{25}{2}\mathfrak{t}+80)[(\eta -1)+(\eta -2)+\dots +1]+21(\eta -1),\hfill \\ \hfill =& E\left(\mathcal{K}{f}^{*}\left({\mathcal{Q}}_1\right)\right)+(100-\frac{25}{2}\mathfrak{t})\frac{\eta (\eta -1)(2\eta -1)}{6}+(\frac{25}{2}\mathfrak{t}+80)\frac{\eta (\eta -1)}{2}+21(\eta -1),\hfill \\ \hfill =& (\frac{100}{3}-\frac{25}{6}\mathfrak{t}){\eta }^3+(\frac{25}{2}\mathfrak{t}-10){\eta }^2+(-\frac{25}{3}\mathfrak{t}-\frac{7}{3})\eta -1.\hfill \end{array}$$

Particularly,

• If $\mathfrak{t}=1,E\left(\mathcal{K}{\mathfrak{f}}^{*}\left({\mathcal{Q}}_{\eta }^o\right)\right)=\frac{175}{6}{\eta }^3+\frac{5}{2}{\eta }^2-\frac{32}{3}\eta -1$.
• If $\mathfrak{t}=0,E\left(\mathcal{K}{\mathfrak{f}}^{*}\left({\mathcal{Q}}_{\eta }^p\right)\right)=\frac{100}{3}{\eta }^3-10{\eta }^2-\frac{7}{3}\eta -1$.

□

Corollary 1. 

Let ${\mathcal{Q}}_{\eta }(\eta \ge 3)$ be a random polyomino chain. Then,

$$E\left(\mathcal{K}{\mathfrak{f}}^{*}\left({\mathcal{Q}}_{\eta }^o\right)\right)\le E\left(\mathcal{K}{\mathfrak{f}}^{*}\left({\mathcal{Q}}_{\eta }\right)\right)\le E\left(\mathcal{K}{\mathfrak{f}}^{*}\left({\mathcal{Q}}_{\eta }^p\right)\right).$$

Proof. 

With reference to Theorem 1, we have

$$E\left(\mathcal{K}{\mathfrak{f}}^{*}\left({\mathcal{Q}}_{\eta }\right)\right)=(-\frac{25}{6}{\eta }^3+\frac{25}{2}{\eta }^2-\frac{25}{3}\eta )\mathfrak{t}+\frac{100}{3}{\eta }^3-10{\eta }^2-\frac{7}{3}\eta -1.$$

Note that $\eta \ge 3$, by a direct calculation, one has

$$\frac{\partial E\left(\mathcal{K}{\mathfrak{f}}^{*}\left({\mathcal{Q}}_{\eta }\right)\right)}{\partial \mathfrak{t}}=-\frac{25}{6}{\eta }^3+\frac{25}{2}{\eta }^2-\frac{25}{3}\eta =-\frac{25}{6}\eta ({\eta }^2-3\eta +2)<0.$$

• If $\mathfrak{t}=1$, the polyomino ortho-chain ${\mathcal{Q}}_{\eta }^o$ realizes a minimum of $E\left(\mathcal{K}{\mathfrak{f}}^{*}\left({\mathcal{Q}}_{\eta }\right)\right)$.
• If $\mathfrak{t}=0$, the polyomino para-chain ${\mathcal{Q}}_{\eta }^p$ realizes a maximum of $E\left(\mathcal{K}{\mathfrak{f}}^{*}\left({\mathcal{Q}}_{\eta }\right)\right)$.

□

3. The Expected Value of the Additive Degree-Kirchhoff Index of a Random Polyomino Chain

Theorem 2. 

The expected value of the additive degree-Kirchhoff index of a random polyomino chain for $\eta \ge 1$ is

$$E\left(\mathcal{K}{\mathfrak{f}}^{+}\left({\mathcal{Q}}_{\eta }\right)\right)=(\frac{80}{3}-\frac{10}{3}\mathfrak{t}){\eta }^3+(10\mathfrak{t}-36){\eta }^2-(\frac{20}{3}\mathfrak{t}+\frac{23}{3})\eta .$$

Proof. 

As described above, the polyomino chain ${\mathcal{Q}}_{\eta +1}$ is obtained by joining ${\mathcal{Q}}_{\eta }$ to a new terminal polyomino with a cutting edge, as shown in Figure 2. By using Equation (4), one has

$$\mathcal{K}{\mathfrak{f}}^{+}\left({\mathcal{Q}}_{\eta +1}\right)={\Delta }_1+{\Delta }_2+{\Delta }_3.$$

(17)

where;

$$\begin{array}{cc}\hfill {\Delta }_1=& \sum _{\{\breve{\mu },\breve{\upsilon }\}\subseteq {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}(\breve{\delta }\left(\breve{\mu }\right)+\breve{\delta }\left(\breve{\upsilon }\right))\breve{\gamma }(\breve{\mu },\breve{\upsilon }),\hfill \\ \hfill {\Delta }_2=& \sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\sum _{{\breve{\lambda }}_i\in {\mathcal{V}}_{{\breve{ϝ}}_{\eta +1}}}(\breve{\delta }\left(\breve{\upsilon }\right)+\breve{\delta }\left({\breve{\lambda }}_i\right))\breve{\gamma }(\breve{\upsilon },{\breve{\lambda }}_i),\hfill \\ \hfill {\Delta }_3=& \sum _{({\breve{\lambda }}_i,{\breve{\lambda }}_j)\subseteq {\mathcal{V}}_{{\breve{ϝ}}_{\eta +1}}}(\breve{\delta }\left({\breve{\lambda }}_i\right)+\breve{\delta }\left({\breve{\lambda }}_j\right))\breve{\gamma }({\breve{\lambda }}_i,{\breve{\lambda }}_j).\hfill \end{array}$$

Put $\breve{\gamma }\left({\breve{\mu }}_{\eta }\right|{\mathcal{Q}}_{\eta })={\sum }_{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })$, as discussed in Theorem 1, one has

$$\begin{array}{cc}\hfill {\Delta }_1=& \sum _{\{\breve{\mu },\breve{\upsilon }\}\subseteq {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}(\breve{\delta }\left(\breve{\mu }\right)+\breve{\delta }\left(\breve{\upsilon }\right))\breve{\gamma }(\breve{\mu },\breve{\upsilon }),\hfill \\ \hfill =& \sum _{\{\breve{\mu },\breve{\upsilon }\}\subseteq {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}\setminus {\breve{\mu }}_{\eta }}(\breve{\delta }\left(\breve{\mu }\right)+\breve{\delta }\left(\breve{\upsilon }\right))\breve{\gamma }(\breve{\mu },\breve{\upsilon })+\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}\setminus {\breve{\mu }}_{\eta }}(\breve{\delta }\left(\breve{\upsilon }\right)+{\breve{\delta }}_{{\mathcal{Q}}_{\eta +1}}\left({\breve{\mu }}_{\eta }\right))\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon }),\hfill \\ \hfill =& \sum _{\{\breve{\mu },\breve{\upsilon }\}\subseteq {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}\setminus {\breve{\mu }}_{\eta }}(\breve{\delta }\left(\breve{\mu }\right)+\breve{\delta }\left(\breve{\upsilon }\right))\breve{\gamma }(\breve{\mu },\breve{\upsilon })+\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}\setminus {\breve{\mu }}_{\eta }}(\breve{\delta }\left(\breve{\upsilon }\right)+{\breve{\delta }}_{{\mathcal{Q}}_{\eta }}\left({\breve{\mu }}_{\eta }\right)+1)\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon }),\hfill \\ \hfill =& \mathcal{K}{\mathfrak{f}}^{+}\left({\mathcal{Q}}_{\eta }\right)+\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon }),\hfill \\ \hfill =& \mathcal{K}{\mathfrak{f}}^{+}\left({\mathcal{Q}}_{\eta }\right)+\breve{\gamma }\left({\breve{\mu }}_{\eta }\right|{\mathcal{Q}}_{\eta }).\hfill \end{array}$$

By Equations (5) and (6), one has

$$\begin{array}{cc}\hfill {\Delta }_2=& \sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\sum _{{\breve{\lambda }}_i\in {\mathcal{V}}_{{\breve{ϝ}}_{\eta +1}}}(\breve{\delta }\left(\breve{\upsilon }\right)+\breve{\delta }\left({\breve{\lambda }}_i\right))\breve{\gamma }(\breve{\upsilon },{\breve{\lambda }}_i)=\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\sum _{{\breve{\lambda }}_i\in {\mathcal{V}}_{{\breve{ϝ}}_{\eta +1}}}\breve{\delta }\left(\breve{\upsilon }\right)\breve{\gamma }(\breve{\upsilon },{\breve{\lambda }}_i)+\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\sum _{{\breve{\lambda }}_i\in {\mathcal{V}}_{{\breve{ϝ}}_{\eta +1}}}\breve{\delta }\left({\breve{\lambda }}_i\right)\breve{\gamma }(\breve{\upsilon },{\breve{\lambda }}_i),\hfill \\ \hfill =& \sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\breve{\delta }\left(\breve{\upsilon }\right)[\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })+1+\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })+1+\frac{3}{4}+\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })+1+1+\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })+1+\frac{3}{4}]+\hfill \\ \hfill & \sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\{3[\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })+1]+2[\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })+1+\frac{3}{4}]+2[\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })+1+1]+2[\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })+1+\frac{3}{4}]\},\hfill \\ \hfill =& 4\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\breve{\delta }\left(\breve{\upsilon }\right)\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })+\frac{13}{2}\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\breve{\delta }\left(\breve{\upsilon }\right)+9\breve{\gamma }\left({\breve{\mu }}_{\eta }\right|{\mathcal{Q}}_{\eta })+56\eta ,\hfill \\ \hfill =& 4\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\breve{\delta }\left(\breve{\upsilon }\right)\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })+\frac{13}{2}(10\eta -1)+9r\left({\breve{\mu }}_{\eta }\right|{\mathcal{Q}}_{\eta })+56\eta .\hfill \end{array}$$

Note that,

$$\sum _{i=1}^4({\breve{\lambda }}_{\kappa },{\breve{\lambda }}_i)=\frac{5}{2}(where\kappa =1,2,3,4).$$

$$\begin{array}{cc}\hfill {\Delta }_3=& \sum _{({\breve{\lambda }}_i,{\breve{\lambda }}_j)\subseteq {\mathcal{V}}_{{\breve{ϝ}}_{\eta +1}}}(\breve{\delta }\left({\breve{\lambda }}_i\right)+\breve{\delta }\left({\breve{\lambda }}_j\right))\breve{\gamma }({\breve{\lambda }}_i,{\breve{\lambda }}_j)=\frac{1}{2}\sum _{i=1}^4\sum _{j=1}^4(\breve{\delta }\left({\breve{\lambda }}_i\right)+\breve{\delta }\left({\breve{\lambda }}_j\right))\breve{\gamma }({\breve{\lambda }}_i,{\breve{\lambda }}_j),\hfill \\ \hfill =& \sum _{i=1}^4\sum _{j=1}^4\breve{\delta }\left({\breve{\lambda }}_i\right)\breve{\gamma }({\breve{\lambda }}_i,{\breve{\lambda }}_j),\hfill \\ \hfill =& \sum _{i=1}^4\breve{\delta }\left({\breve{\lambda }}_i\right)\sum _{j=1}^4\breve{\gamma }({\breve{\lambda }}_i,{\breve{\lambda }}_j),\hfill \\ \hfill =& \frac{5}{2}\sum _{i=1}^4\breve{\delta }\left({\breve{\lambda }}_i\right),\hfill \\ \hfill =& \frac{45}{2}.\hfill \end{array}$$

Then, Equation (17) can be rewritten as

$$\mathcal{K}{\mathfrak{f}}^{+}\left({\mathcal{Q}}_{\eta +1}\right)=\mathcal{K}{\mathfrak{f}}^{+}\left({\mathcal{Q}}_{\eta }\right)+4\sum _{\breve{\upsilon }\in {\mathcal{V}}_{{\mathcal{Q}}_{\eta }}}\breve{\delta }\left(\breve{\upsilon }\right)\breve{\gamma }({\breve{\mu }}_{\eta },\breve{\upsilon })+10\breve{\gamma }\left({\breve{\mu }}_{\eta }\right|{\mathcal{Q}}_{\eta })+121\eta +16.$$

(18)

For a random polyomino chain ${\mathcal{Q}}_{\eta },\breve{\gamma }\left({\breve{\mu }}_{\eta }\right|{\mathcal{Q}}_{\eta })$ is a random variable with expected value

$$D_{\eta }=E\left(\breve{\gamma }\left({\breve{\mu }}_{\eta }\right|{\mathcal{Q}}_{\eta })\right).$$

The following two possible cases helped us to proceed our work further.

• Case 1: ${\mathcal{Q}}_{\eta }\to {\mathcal{Q}}_{\eta +1}^1$
  Here, ${\breve{\mu }}_{\eta }$ coincides with the vertices ${\breve{\lambda }}_2$ or ${\breve{\lambda }}_4$. Consequently, $\breve{\gamma }\left({\breve{\mu }}_{\eta }\right|{\mathcal{Q}}_{\eta })$ is given by $\breve{\gamma }\left({\breve{\lambda }}_2\right|{\mathcal{Q}}_{\eta }).$
• Case 2: ${\mathcal{Q}}_{\eta }\to {\mathcal{Q}}_{\eta +1}^2$
  Here, ${\breve{\mu }}_{\eta }$ coincides with the vertex ${\breve{\lambda }}_3$. Consequently, $\breve{\gamma }\left({\breve{\mu }}_{\eta }\right|{\mathcal{Q}}_{\eta })$ is given by $\breve{\gamma }\left({\breve{\lambda }}_3\right|{\mathcal{Q}}_{\eta }).$

Since the aforementioned in irregular polyomino chains with probability, two scenarios happen, $\mathfrak{t}$ and $1-\mathfrak{t}$, respectively, we can obtain the following result:

$$\begin{array}{cc}\hfill D_{\eta }=& E\left(\breve{\gamma }\left({\breve{\mu }}_{\eta }\right|{\mathcal{Q}}_{\eta })\right),\hfill \\ \hfill =& \mathfrak{t}\breve{\gamma }\left({\breve{\lambda }}_2\right|{\mathcal{Q}}_{\eta })+(1-\mathfrak{t})\breve{\gamma }\left({\breve{\lambda }}_3\right|{\mathcal{Q}}_{\eta }),\hfill \\ \hfill =& \mathfrak{t}[\breve{\gamma }\left({\breve{\mu }}_{\eta -1}\right|{\mathcal{Q}}_{\eta -1})+4(\eta -1)(1+\frac{3}{4})+\frac{5}{2}]+(1-\mathfrak{t})[\breve{\gamma }\left({\breve{\mu }}_{\eta -1}\right|{\mathcal{Q}}_{\eta -1})+4(\eta -1)(1+1)+\frac{5}{2}],\hfill \\ \hfill =& \breve{\gamma }\left({\breve{\mu }}_{\eta -1}\right|{\mathcal{Q}}_{\eta -1})+(8-\mathfrak{t})\eta +\mathfrak{t}-\frac{11}{2}.\hfill \end{array}$$

By applying the properties of mathematical expectation to the equation mentioned above and noting that $E\left(D_{\eta }\right)=D_{\eta }$, we obtain

$$D_{\eta }=D_{\eta -1}+(8-\mathfrak{t})\eta +\mathfrak{t}-\frac{11}{2}.$$

(19)

The boundary condition is

$$D_1=E\left(\breve{\gamma }\left({\breve{\mu }}_1\right|{\mathcal{Q}}_1)\right)=\frac{5}{2}.$$

Using the recurrence relation in Equation (19), one has

$$\begin{array}{cc}\hfill D_{\eta }=& D_1+(8-\mathfrak{t})[\eta +(\eta -1)+\dots +2]+(\eta -1)(\mathfrak{t}-\frac{11}{2}),\hfill \\ \hfill =& (8-\mathfrak{t})\frac{{\eta }^2}{2}+(\frac{\mathfrak{t}}{2}-\frac{3}{2})\eta .\hfill \end{array}$$

By applying the properties of mathematical expectation to Equation (18), we obtain

$$\begin{array}{cc}\hfill E\left(\mathcal{K}{\mathfrak{f}}^{+}\left({\mathcal{Q}}_{\eta +1}\right)\right)=& E\left(\mathcal{K}{\mathfrak{f}}^{+}\left({\mathcal{Q}}_{\eta }\right)\right)+10D_{\eta }+4{\mathcal{R}}_{\eta }+121\eta +16,\hfill \\ \hfill =& E\left(\mathcal{K}{\mathfrak{f}}^{+}\left({\mathcal{Q}}_{\eta }\right)\right)+10[(8-\mathfrak{t})\frac{{\eta }^2}{2}+(\frac{\mathfrak{t}}{2}-\frac{3}{2})\eta ]+4[(10-\frac{5}{4}\mathfrak{t}){\eta }^2+(\frac{5}{4}\mathfrak{t}-6)\eta +1]+121\eta +16,\hfill \\ \hfill =& E\left(\mathcal{K}{\mathfrak{f}}^{+}\left({\mathcal{Q}}_{\eta }\right)\right)+(80-10\mathfrak{t}){\eta }^2+(10\mathfrak{t}+82)\eta +20.\hfill \end{array}$$

Thus,

$$E\left(\mathcal{K}{\mathfrak{f}}^{+}\left({\mathcal{Q}}_{\eta }\right)\right)=E\left(\mathcal{K}{\mathfrak{f}}^{+}\left({\mathcal{Q}}_{\eta -1}\right)\right)+(80-10\mathfrak{t}){(\eta -1)}^2+(10\mathfrak{t}+82)(\eta -1)+20.$$

(20)

The boundary condition is given as

$$E\left(\mathcal{K}{\mathfrak{f}}^{+}\left({\mathcal{Q}}_1\right)\right)=20.$$

Using the recurrence relation in Equation (20) and the boundary condition, we obtain

$$\begin{array}{cc}\hfill E\left(\mathcal{K}{\mathfrak{f}}^{+}\left({\mathcal{Q}}_{\eta }\right)\right)=& E\left(\mathcal{K}{f}^{+}\left({\mathcal{Q}}_1\right)\right)+(80-10\mathfrak{t})[{(\eta -1)}^2+{(\eta -2)}^2+\dots +1^2]\hfill \\ \hfill & +(10\mathfrak{t}+82)\left[\right(\eta -1)+(\eta -2)+...+1]+20(\eta -1),\hfill \\ \hfill =& 20+(80-10\mathfrak{t})\frac{\eta (\eta -1)(2\eta -1)}{6}+(10\mathfrak{t}+82)\frac{\eta (\eta -1)}{2}+20(\eta -1),\hfill \\ \hfill =& (\frac{80}{3}-\frac{10}{3}\mathfrak{t}){\eta }^3+(10\mathfrak{t}+1){\eta }^2-(\frac{20}{3}\mathfrak{t}+\frac{23}{3})\eta .\hfill \end{array}$$

In particular,

• If $\mathfrak{t}=1,E\left(\mathcal{K}{\mathfrak{f}}^{+}\left({\mathcal{Q}}_{\eta }^o\right)\right)=\frac{70}{3}{\eta }^3+11{\eta }^2-\frac{43}{3}\eta .$
• If $\mathfrak{t}=0,E\left(\mathcal{K}{\mathfrak{f}}^{+}\left({\mathcal{Q}}_{\eta }^p\right)\right)=\frac{80}{3}{\eta }^3+{\eta }^2-\frac{23}{3}\eta .$

□

Corollary 2. 

Let ${\mathcal{Q}}_{\eta }(\eta \ge 3)$ be a random polyomino chain. Then,

$$E\left(\mathcal{K}{\mathfrak{f}}^{+}\left({\mathcal{Q}}_{\eta }^o\right)\right)\le E\left(\mathcal{K}{\mathfrak{f}}^{+}\left({\mathcal{Q}}_{\eta }\right)\right)\le E\left(\mathcal{K}{\mathfrak{f}}^{+}\left({\mathcal{Q}}_{\eta }^p\right)\right).$$

Proof. 

According to Theorem 2, we have

$$E\left(\mathcal{K}{\mathfrak{f}}^{+}\left({\mathcal{Q}}_{\eta }\right)\right)=(-\frac{10}{3}{\eta }^3+10{\eta }^2-\frac{20}{3}\eta )\mathfrak{t}+\frac{80}{3}{\eta }^3+{\eta }^2-\frac{23}{3}\eta .$$

Note that for $\eta \ge 3$, by a direct calculation, we have

$$\frac{\partial E\left(\mathcal{K}{\mathfrak{f}}^{+}\left({\mathcal{Q}}_{\eta }\right)\right)}{\partial \mathfrak{t}}=-\frac{10}{3}{\eta }^3+10{\eta }^2-\frac{20}{3}\eta =-\frac{10}{3}\eta ({\eta }^2-3\eta +2)<0.$$

• If $\mathfrak{t}=1$, the polyomino ortho-chain ${\mathcal{Q}}_{\eta }^o$ realizes a minimum of $E\left(\mathcal{K}{\mathfrak{f}}^{+}\left({\mathcal{Q}}_{\eta }\right)\right)$.
• If $\mathfrak{t}=0$, the polyomino para-chain ${\mathcal{Q}}_{\eta }^p$ realizes a maximum of $E\left(\mathcal{K}{\mathfrak{f}}^{+}\left({\mathcal{Q}}_{\eta }\right)\right)$.

□

4. Conclusions

In this article, we computed the exact formulae for a highly specific category of a polyomino graph, known as subgraphs or polyomino chains by using topological indices, namely the multiplicative degree-Kirchhoff index and the additive degree-Kirchhoff index. This study also characterizes the highest degree of the expected value for the mentioned graph. The given strategy allows the computation of the expected value for the Schultz index and Gutman index, which is extremely viable for a random polyomino chain. These results are restricted to random polyomino chains. In the future, we hope to create some new structures/graphs and then study their topological indices to better understand their underlying topologies.