Voronoi Diagrams Generated by the Archimedes Spiral: Fibonacci Numbers, Chirality and Aesthetic Appeal

Abstract

Voronoi mosaics inspired by seed points placed on the Archimedes Spirals are reported. Voronoi (Shannon) entropy was calculated for these patterns. Equidistant and non-equidistant patterns are treated. Voronoi tessellations generated by the seeds located on the Archimedes spiral and separated by linearly growing radial distance demonstrate a switch in their chirality. Voronoi mosaics built from cells of equal size, which are of primary importance for the decorative arts, are reported. The pronounced prevalence of hexagons is inherent for the patterns with an equidistant and non-equidistant distribution of points when the distance between the seed points is of the same order of magnitude as the distance between the turns of the spiral. Penta- and heptagonal “defected” cells appeared in the Voronoi diagrams due to the finite nature of the pattern. The ordered Voronoi tessellations demonstrating the Voronoi entropy larger than 1.71, reported for the random 2D distribution of points, were revealed. The dependence of the Voronoi entropy on the total number of seed points located on the Archimedes Spirals is reported. Voronoi tessellations generated by the phyllotaxis-inspired patterns are addressed. The aesthetic attraction of the Voronoi mosaics arising from seed points placed on the Archimedes Spirals is discussed.

1. Introduction

Quantification of order in 2D patterns remains the challenging task [1,2,3,4,5,6,7,8,9,10,11,12,13]. In our paper we address quantification of ordering in spiral patterns. A spiral is a curve which emanates from a point, which moves farther away as it revolves around an origin point. Spirals inspiring wonder and curiosity abound in nature, mathematics, art, and decoration [6,7,8]. A spiral-like curve was found in Mezine, Ukraine, as part of a decorative object dated to 10,000 BCE. Spiral motifs resembling an evergreen shrub appear on an altar found in the Temples of Malta (3000 BC), also, they are inherent in the Celtic megalithic culture. They are often seen on Minoan pottery in Egypt. Many famous spirals were created by Leonardo da Vinci. Spirals are inspiring modern artists such as Robert Smithson and Francisco Infante-Arana. On a microscopic scale, DNA molecules twist around in the form of two helices, whereas on the largest possible scale, the arms of galaxies curl around in the form of logarithmic spirals [9]. The physical world exhibits a startling repetition of spiral patterns [6,7,8]. Biological patterns often demonstrate spiral-like structures. In particular, geometric models of phyllotaxis were used to generate realistic images of flowers and fruits with spiral patterns [14].

In our paper, we focus on patterns generated by the Archimedes (or Archimedean) spiral, used for generating Voronoi partitions. The Archimedean spiral (abbreviated for brevity AS) is a spiral with the polar equation $r=a{\theta }^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.}$, where r is the radial distance, $\theta$ the polar angle, and n is a constant which determines how tightly the spiral is ‘‘wrapped’’ [15]. When this constant n = 1, the resulting spiral is given by $r=a\theta$. In this case, any ray from the origin of coordinates crosses successive turnings of the spiral at points with constant separation (which equals 2πa if θ is measured in radians), which is why this spiral is also called the “arithmetic spiral”.

There are numerous natural and technological exemplifications of the AS. For example, the drawing of an AS (spirography) is commonly used in the evaluation of patients with pathologic tremors and other movement disorders [16]. Interlocked AS supplied a relief-cutting method to turn rigid planar surfaces into flexible ones using meander patterns [17]. Archimedes’ spiral grooves produced on silver films supplied a selective chirality to surface plasmons [18]. Artistic space-filling designs based on spiral packing were reported [19,20,21].

We exploited AS for generating Voronoi partitions, demonstrating interesting mathematical properties and aesthetic appeal. Voronoi partitions (or tessellations) enable quantification (the expression or measurement) of ordering in sets of points [2,22,23]. The idea of what is now called the Voronoi tessellation was proposed by Johannes Kepler and Rene Descartes [10,24]. Descartes used these tessellations to verify that the distribution of matter in the universe forms vortices centered at fixed stars [10,24]. The idea was developed by Dirichlet in the context of his works on quadratic forms [11].

Let us explain the idea of the Voronoi diagram (tessellation). The tessellation or tiling of a plane is the arrangement of figures that fill the plane with no overlaps and no gaps. A Voronoi tessellation shows the partitioning of a plane into cells based on the distance to a specified discrete set of points (called seeds, nuclei, or generators) [2,23]. For each nucleus, there is a corresponding region consisting of all points closer to that seed than to any other [2,23]. The Voronoi polyhedron of a point nucleus in space is the smallest polyhedron formed by the perpendicularly bisecting planes between a given seed and all the other seeds [2,23]. The Voronoi tessellation divides a region into a space-filling, non-overlapping convex polyhedral. Voronoi diagrams represent planar graphs [2,23]. The topological properties of Voronoi diagrams are surveyed in Ref. [23].

The Voronoi tessellation enables quantification of the ordering of a 2D structure by the calculation of the so-called Voronoi entropy, defined as:

$$S_{vor}=-\sum _i{P}_{i}ln{P}_i$$

(1)

where i is the number of polygon types, and P_i is the fraction of polygons possessing n sides (edges) inherent for a given Voronoi diagram (also called the coordination number of the polygon) [2,12,22,23]. The Voronoi entropy becomes zero for a perfectly ordered structure (when we have polygons of only a single kind), and it is increased with the number of types of polygons. For a typical case of fully random 2D distribution, the value of S_vor = 1.71 was reported [25,26]; six types of polygons are inherent in these patterns. Equation (1) is similar in its form to the statistical measure of information and entropy in statistical mechanics [27]. That is why it was called “the Voronoi entropy”, which is also labeled in the literature as the Shannon entropy. We also address the aesthetic appeal of the Voronoi patterns generated by Archimedes’ spiral [28].

Consider some simple exemplifications of the Voronoi tessellation (see Figure 1). Figure 1A represents a regular array of points (left) that leads to a regular array of square tiles (right) with the Voronoi entropy $S_{vor}$ which equals zero (indeed $P_1=1;ln{P}_1=0$ in Equation (1)). Figure 1B represents the pattern (left) giving rise to the Voronoi tessellation built from irregular (distorted) hexagons (right). The corresponding Voronoi entropy of the tessellation, demonstrated in Figure 1B also equals zero (again $P_1=1;ln{P}_1=0$ is true for this pattern). Figure 1C, in turn, depicts a semi-regular set of points (left) resulting in a twin-tile tessellation (i.e., regular hexagons and smaller squares, right). The Voronoi entropy of the tessellation shown in Figure 1C (left) is $S_{vor}=\frac{1}{3}ln\frac{1}{3}+\frac{2}{3}ln\frac{2}{3}=0.6365$ (two hexagons per one square). Figure 1D demonstrates the pattern emerging from 75 randomly placed points (left) and the Voronoi tessellation (right) arising from this pattern. The Voronoi entropy of this pattern $S_{vor}=1.6959$ is close to the value S_vor = 1.71 established for the randomly distributed sets of points [25,26]. We will demonstrate that tessellations with S_vor > 1.71 are possible. Figure 1E exemplifies a regular pattern of 80 points (left), giving rise to the Voronoi tessellation (right) with an entropy larger than that inherent for randomly distributed points.

The topological argument, arising from the Euler equation for the Voronoi diagrams is that in the limit of a large system, the average number of edges surrounding a cell is six. This leads to the prevalence of hexagons in Voronoi diagrams emerging from large, random sets of points [23].

2. Voronoi Partitions Generated by the AS

MATLAB software was used for the calculation of the coordinates of points on an AS and the subsequent generation and processing of the corresponding Voronoi patterns. To create the Voronov diagrams, we used moduli of the program developed at the Department of Physics and Astronomy at the University of California (Department of Physics and Astronomy University of California, Irvine) (https://www.physics.uci.edu/~foams/do_all.html, accessed on 1 January 2022).

The AS with various parameters (points density and quantity) was generated with MATLAB software Version 9.6, (See Appendix A and Figure A1, Figure A2 and Figure A3 for detailed explanation). Coordinates of points on the AS in a rectangular coordinate system were defined by the following equations:

x = r·cos(φ),
    y = r·sin(φ).

(2)

Consider first the equidistant distribution of the points along the given AS. Parameters r and φ were varied in a way providing a given distance between the neighboring points along the spiral (p) and the coils of the spiral (q) (See Appendix A, Figure A3). The Voronoi tessellations and Voronoi entropy were established for the aforementioned points. In the case of a linear increase of distance between neighboring points (abbreviated in the text NP) on the spiral, Formulae (2) were transformed into Equation (3) (see Appendix A, this transformation was made to obtain a finite set of points and for the convenience of further calculations):

x_n = t_n·cos(t_n),
    y_n = t_n·sin(t_n),

(3)

where x_n and y_n are the coordinates of a single point on the spiral. The variable t is an array of values that alter discretely from b to d with a step of c. Parameters b, c, and d determine a finite set of coordinates for developing different AS. Parameter b sets a value for the spiral starting point coordinates. For the sake of simplicity, we adopt b = 0 for all of the studied patterns; this assumption corresponds to spirals starting from the coordinates’ origin. Modification of the parameters c and d enables the generation of points located on the AS with controlled distances between them. The aforementioned parameters p and q denoting linear dimensions were given in millimeters, and parameters b, c, d, and t were dimensionless. Note that from the “physical point of view”, the dimensionless parameter $\xi =\frac{p}{q}$ appears. The ratio $\frac{p}{q}$ controls the shape of the spiral and defines the distribution of points on it. Thus, the value of $\xi$ influences the properties of the Voronoi tessellation, as demonstrated below.

Consider first the tessellations where the distance between the seed points and the distance between the turns of the spiral are of the same order of magnitude (in other words, the condition $\xi \cong 1$ takes place). Voronoi tessellations arising from the AS with constant and linearly increasing p, and the different total points number of 60, 200, and 600 are displayed in Figure 2. It is seen that for the equidistant distribution of points on a spiral (depicted in Figure 2A,C,E,G), the type of pattern does not change with an increase in the total number of points N. The configuration of external (boundary) polygons changes with the growth in the total number of points N on the spiral for the patterns with a linear increase of NP distance.

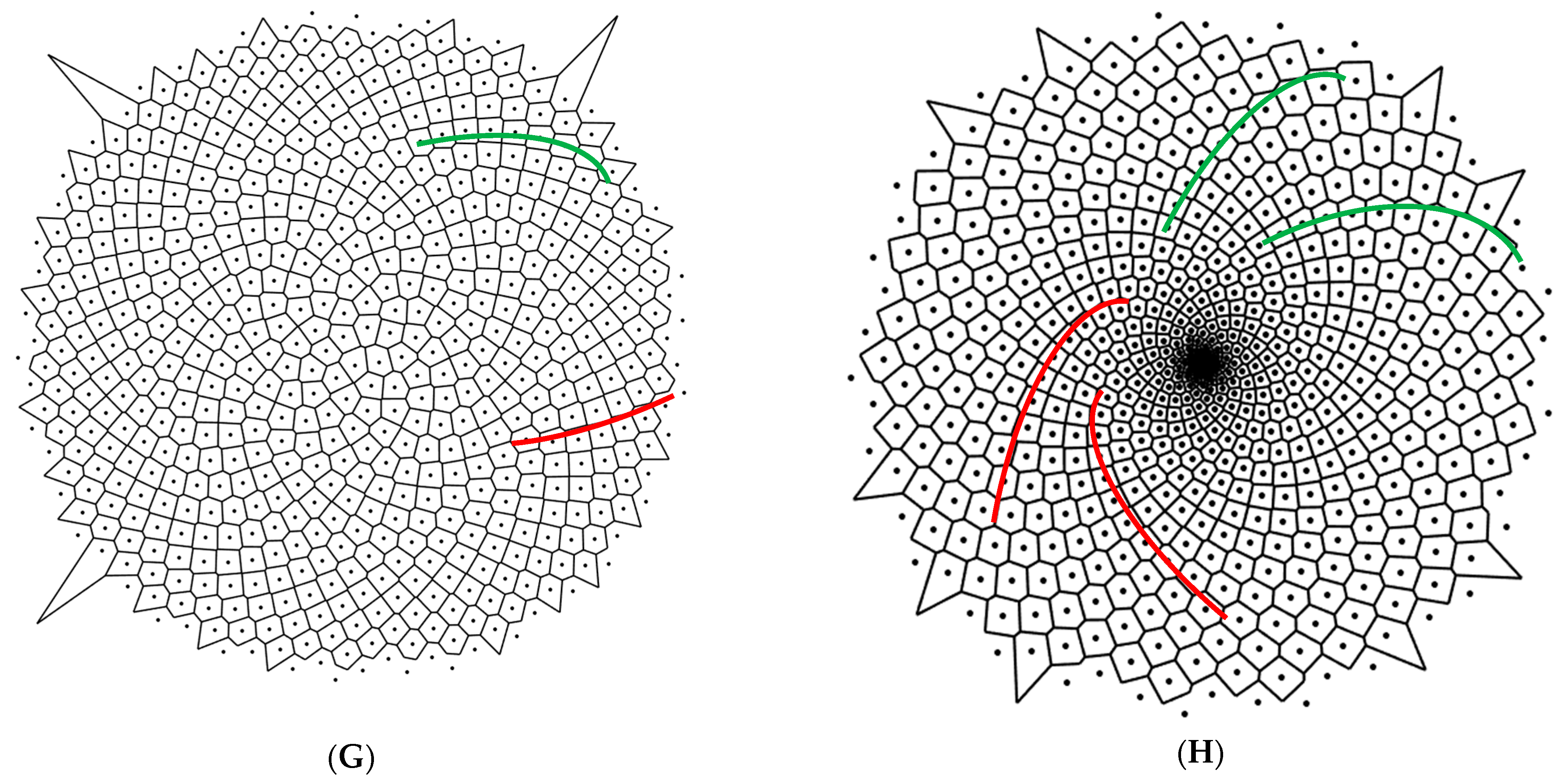
Perhaps, the most surprising observations, emerge from the analysis of the pattern, depicted in Figure 2F–H, in which both clockwise and counterclockwise twisted spirals are distinctly recognized. Figure 2H demonstrates the Voronoi diagram resulting from the seeds separated by the linearly increasing distance. In this case, the counterclockwise oriented spirals (shown with red solid lines) appear along with the clockwise oriented spirals (shown with green solid lines). Recall, that the pristine pattern is generated by the points located on the clockwise-oriented Archimedes spiral. Thus, the increasing distance between the seed points results in the generation of spirals with different chirality. This is exactly the case inherent for the location of the sunflower seeds [29,30,31]. The appearance of spirals with opposite chirality for the spiral with the constant radial shift of successive points was reported in ref. [32]; the same is true for the Voronoi tessellations emerging from such patterns, shown in Figure 2H. The ratio of the number of spirals $\chi =\frac{N_{+}}{N_{-}}$ (where $N_{+}$ and $N_{-}$ are the number clockwise twisted spirals correspondingly) for the pattern depicted in Figure 2F equals $\chi =1.923,$ which is close but not equal to the Fibonacci number (also known as the golden ratio) $\Phi =\frac{1+\sqrt{5}}{2}\cong 1.618$.

Figure 2G,H, in turn, depict the Voronoi tessellations arising from Phyllotactic spirals based on a simple mathematical model of sunflower seed rows [29,30,31]. Phyllotactic spirals emerge from Equation (2), when φ = 2πNΦ, Φ is the golden ratio and r = N^α, α = 0.5 in Figure 2G and α = 1 in Figure 2H. The numbers of clockwise and counterclockwise spirals in Figure 2G,H are 55/89 and 21/34, correspondingly. These numbers appear as consequent ones in the Fibonacci sequence.

Now we address the Voronoi (Shannon) entropy calculated for the tessellations presented in Figure 2. The distinct prevalence of hexagons is obvious for the patterns with an equidistant distribution of points. This is an immediate consequence of Euler’s equation in two dimensions [31]. Let us introduce the number (abbreviated NR) and the area ratios (abbreviated AR) of polygons on the pattern as follows: $NR=\frac{N_e}{N}\times 100\%$; $AR=\frac{A_e}{A}\times 100\%$, where N_e and A_e are the number and area of polygons with e edges respectively, and N and A are the total number and area covered by polygons correspondingly.

The area ratio AR of hexagons increases with the increase in the number of points from 73% for 600 points pattern to 94% for 12,000 points pattern (as illustrated in Figure 3A,B and Figure 4A,B). For the tessellations based on spirals with linearly increasing distance between NP, hexagons also occupied most of the area of the pattern. For example, for the 600 points pattern (c = 0.5, d = 300) hexagons cover up to 60% of the area, as shown in

Table 1. Polygon distribution characteristics and Voronoi entropy.

Number of Polygon Sides, e	NR, %				AR, %
	Figure 2A, 600 Points (p = 1, q = 1)	Figure 2B, 12,000 Points (p = 1, q = 1)	Figure 2C, 600 Points (c = 0.5, d = 300)	Figure 2D, 12,000 Points (b = 0, c = 1, d = 12,000)	Figure 2A, 600 Points (p = 1, q = 1)	Figure 2B, 12,000 Points (p = 1, q = 1)	Figure 2C, 600 points (c = 0.5, d = 300)	Figure 2D, 12,000 Points (c = 1, d = 12,000)
3	0	0	0	0	0	0	0	0
4	0	0.01	2.15	0.01	0	3.25 × 10−2	6.522	2.63 × 10−6
5	13.73	3.21	16.52	4.55	13.73	3.21	18.1123	8.5875
6	73.31	93.61	67.68	92.36	73.07	93.56	61.5241	89.8156
7	12.77	3.17	13.46	3.09	12.85	3.18	13.8391	1.5969
8	0	0	0	0	0	0	0	0
9	0	0	0	0	0	0	0	0
10	0.19	0.01	0.18	0	0.35	1.55 × 10−2	2.41 × 10−3	0
$S_{vor}$	0.775	0.283	0.926	0.322	0.785	0.256	1.099	0.307

. The AR of the hexagons increases with an increase in the total number of polygons forming the mosaic (Figure 3C,D and Figure 4C,D).

Equation (1) enabled the calculation of the Voronoi entropy for a given pattern. The Voronoi entropy values were obtained for spirals with different densities of N points. The Voronoi entropy $S_{vor}$ depended markedly on the entire number of points for both the equidistant and linearly increasing distance points distribution. Consider first the patterns arising from spirals with equidistant NP shown in Figure 2B and Figure 3A,B demonstrates that the Voronoi entropy $S_{vor}$ is mainly determined by the contributions of the blue heptagons bordering yellow pentagons (which may be called “the defects”). Indeed, the contribution of closely packed hexagons too $S_{vor}$ is negligible. Hence, the value of $S_{vor}$ mainly results from the secondary spiral-like pattern created by the pairs of heptagons bordering pentagons, as illustrated in Figure 3A,B.

Similar Voronoi mosaics, arising from the analysis of the Benard-Marangoni cells, were reported, and discussed in Ref. [33] by Rivier et al. It was noted in ref. [33] that penta- and heptagonal cells represent positive or negative disclinations (corresponding to rotational dislocations, well-known in crystallography) and that they are topologically defined objects which are structurally stable; in other words, they keep their identity under small deformation. Rivier et al. related their appearance to the finite nature of the studied pattern. The defects are a necessary ingredient of the finite mosaic [33]. The reported finite mosaics are necessarily restricted by the origin (the area adjacent to the origin is “defected”, as shown in Figure 2A,B) and the boundary points. Thus, the boundary conditions are crucial for the formation of the resulting pattern [33]. In our case, the boundary conditions are prescribed by the location of the seeds on the AS, given by Equations (2) and (3). Indeed, it is recognized from Figure 3B that the larger the pattern is, the smaller the number and area ratios of the defects. It is also seen from Figure 3A–D that pentagons attract heptagons, as reported in Ref. [33].

Consider now the dependence $S_{vor}\left(N\right)$. In the case of the equidistant location of the seed points along the spiral (p = const), the Voronoi entropy is decreasing monotonously with the increase of the total number of points N, with the exception of the initial part of the curve $S_{vor}\left(N\right)$ as can be seen in Figure 5. For the pattern with p = 3, q = 3, we calculated $S_{vor}\left({10}^4\right)\cong 0.3$, $S_{vor}\left(2.5\times {10}^4\right)\cong 0$.2. The initial jump in the curve $S_{vor}\left(N\right)$ is due to the large density of “defects” (presented as yellow pentagons and blue heptagons in Figure 3A) appearing at the initial stage of spiral formation. The density of these “defects” decreases with the growth of the total number of points N, leading to the monotonic decrease in the resulting Voronoi entropy of the pattern.

The Voronoi entropy for the patterns based on a spiral with the linear increase of distance between neighboring points demonstrates a saw-like pattern, depicted in Figure 6A, while tending to decrease with the increase of the entire number of points N. The saw-like behavior of the curve $S_{vor}\left(N\right)$ is reasonably explained as follows: the bordering heptagons and pentagons form the ring-like secondary pattern, contributing markedly to the $S_{vor}\left(N\right)$. The appearance of these rings (introducing geometrical disorder into the pattern) increases the value of $S_{vor}\left(N\right)$, resulting in the saw-like dependence of the function $S_{vor}\left(N\right)$.

We relate the origin of these peaks’ appearance to the appearance of irregularities on the Voronoi diagrams. Two kinds of irregularities (defects) inherent in AS-inspired Voronoi diagrams should be distinguished, the first of which is the fringe of a Voronoi pattern formed by open (incomplete) polygons. The fringe effect on the Voronoi entropy is essential for patterns consisting of a small number of points (polygons, respectively). The second type of irregularity is represented by the aforementioned “defected areas” of a pattern (colored blue and yellow in Figure 3D). These irregularities appear as circles of pentagons bordering heptagons recognized on the background filled with hexagons [33]. The well-ordered nature of the defective areas are noteworthy. With an increase in the number of points, the distance between irregular circles is growing, as shown in Figure 3B. The growth of the distance between blue/yellow circles leads to a consequent decrease in the Voronoi entropy of the entire pattern.

It is also noteworthy that in the case of linearly increasing distance between the adjacent seed points, it is possible to select values of parameters c and d (for example consider the case of c = 20, d = 40,000) resulting in the disappearance of irregularities built of pentagons and heptagons (this occurs for N > N*, where N* is the threshold value of points, corresponding to two or three central rings). In this case, the value of the Voronoi entropy falls faster and asymptotically tends to zero. When N → ∞ the role of the central area of the spiral becomes negligible and S_vor → (0 + 1/∞). Consequently, the Voronoi entropy S_vor(N) does not show the saw-like behavior when the “defected circles” are absent, as shown in Figure 6B. This possibility to fill a plane with cells of equal size is of primary importance for phyllotaxis (leaf or floret arrangement) and for decorative arts [33].

3. The Aboav and Lewis Laws for the Patterns Inspired by the Archimedes Spiral

The Aboav law validity for the mosaics generated by AS was verified. This law, which was obtained empirically first for grains in polycrystals, has also been shown to be valid for soap froth and some living cells [1,5,34,35]. It describes the regularities of the mutual arrangement of the different polygons on a two-dimensional plane. The Aboav law states that the mean number of sides of polygons (labeled m_n) bordering the polygon with n-edges is given by Equation (4) [1]:

$$m_n=5+\frac{8}{n}$$

(4)

In other words, the few-edged cells have a remarkable tendency to be in contact with many-edged cells and vice versa. The critics, derivation, and consequences of the Aboav law are discussed in Refs [1,24,30,31]. The values of m_n were calculated for the pattern with a linear increase of distance between NP (c = 1, d = 500) and the pattern with equidistant points distribution (p = 3, q = 3, N = 500). All of the obtained m_n values were lower than those calculated with Formula (4) as shown in Figure 7. Thus, the Aboav law, supplied by Equation (4) does not work for the Voronoi patterns inspired by AS. We relate this observation to the non-random distribution of points on the studied mosaics.

On the other hand, the mean values of m_n for the AS-inspired patterns tend to decrease with the increase in the number of sides of the corresponding polygon, as qualitatively predicted by the Aboav law [1,5,23,35].

Another important statistical law, established for 2D patterns, is the Lewis law, reported for natural and artificial patterns [5,36,37]. The Lewis law predicts a linear relationship between the average area of a typical n-cell, A_n and n in a random pattern:

A_n = α(n − 2),

(5)

where α is a proportionality constant, whose meaning and precise value can be found in Ref. [35]. The Lewis law quite expectably does not work for mosaics generated by AS when p ~ q. For the patterns based on equidistant NP distribution, polygon areas have a constant mean value of 9.0 ± 0.01 mm² all over the pattern. In the case of patterns with linearly increasing NP distance, the areas of polygons on spiral coils grow with the distance from the origin of a spiral.

4. Patterns Generated by Archimedes Spirals and the Maximal Voronoi Entropy

Consider patterns with an equidistant distribution of points, in which the NP distance p is much greater (an order of magnitude) than the distance between the turns of a spiral q. When p >> q and correspondingly $\xi \gg 1$ takes place, we assume $\phi =k\pi +\mathsf{\Delta }\phi$, where k is a positive integer. Two examples of such patterns are shown in Figure 8A,B. Such patterns contain more kinds of polygons than patterns, where $p\cong q$ and correspondingly $\xi \cong 1$ is adopted. Eight types of polygons constituting these mosaics were registered, when $\xi \gg 1$. It should be emphasized that hexagons do not prevail when $\xi \gg 1$ takes place (see Figure 8A,B,E,F).

The patterns, where p >> q, are interesting because while not being random, they show high Voronoi entropy values that are close to the value of 1.71, which is considered as maximum inherent for a random pattern [25,26]. Figure 8A depicts the pattern demonstrating the Voronoi Entropy S_vor = 1.825. The maximal value of the Voronoi entropy S_vor = 1.888 was registered for the pattern (p = 24.6131, q = 3, N = 80), presented in Figure 9A, which is markedly higher than the value reported for random patterns [25,26]. The value of the Voronoi entropy may even be extended to larger values. Consider the pattern arising from the seven-fold X and sevenfold Y translation of the pattern shown in Figure 9A. Such a procedure gave rise to the Voronoi diagram shown in Figure 9B built from 8 types of polygons and characterized by the Voronoi entropy $S_{vor}=1.9327$, which is much larger than that, established for random point patterns [25,26].

This finding poses the following fundamental question: it is well-accepted that the Voronoi Entropy quantifies ordering in 2D patterns [2,10,22,23]. It is reasonable to conjecture that the maximal disorder corresponds to the random distribution of seed points over the plane. Hence, the maximal possible Voronoi Entropy is expected for the random distribution of points. At the same time, patterns depicted in Figure 9 are ordered, however possessing the Voronoi Entropy markedly higher than $S_{vor}=1.71$, established for the random patterns [25,26]. How is this possible? This question calls for additional theoretical insights. Actually, it is well-known that the Voronoi entropy may be larger than 1.71. The maximal value of the Voronoi entropy for the mosaics built from n kinds of polygons corresponds to a pattern at which equipartition of polygons takes place (their appear $\frac{1}{n}$ of all kinds of n-polygons in the pattern) [27]. In this case, the maximal value of the Voronoi entropy is given by $S_{vor}^{max}=ln\left(n\right)$ [27], and it obviously may be larger than $S_{vor}=1.71$, inherent for a random 2D pattern [25,26].

Table 2. Typical distributions of the polygons for tessellations considered in the text $S_{vor}<1.71$, $S_{vor}\approx 1.71$ и $S_{vor}>1.71$ are considered.

$${\mathit{S}}_{\mathit{v}\mathit{o}\mathit{r}}$$	Distribution of Polygons for the Considered Patterns (“3” Denotes Triangles, “4”—Quadrangles, etc.)								Total Number of Polygons in the Given Pattern.
	3	4	5	6	7	8	9	10
0.6365		25		50					75
1.6959	1	9	14	11	10	3	2		50
1.7104	3	10	20	22	17	7	2		81
1.8878	6	10	9	10	7	6	3		51
1.9327	301	532	855	684	463	588	219	84	3726

displays the typical distributions of polygons in the tessellations discussed in the text, where the Voronoi entropy ranges from 0.64 to 1.93.

We also have checked the validity of the Lewis law [5,36,37] for the patterns characterized by the p >> q interrelation (see Figure 10). In this case, the dependence $An\left(n\right)$ demonstrates the linear part, predicted by the Lewis law (see Equation (5)), as shown in Figure 10.

5. Voronoi Diagrams Arising from Archimedes Spirals Demonstrating an Aesthetic Appeal

The Voronoi diagrams depicted in Figure 11A–D demonstrate definite aesthetic appeal. The aesthetic attractiveness of the AS was already known to Neolithic artists [38]. Remarkably AS holds its aesthetic appeal in the XXI century [3]. The very question is why do the spirals demonstrate obvious aesthetic appeal. The true answer could not be covered by physics and mathematics only, but also enrooted in psychology [20]. We allow ourselves to put forward the following hypothesis: the aesthetic appeal and abundance of spirals in nature are probably related to their simplicity and self-similarity (the equation describing AS is one of the simplest possible). Simplicity and self-similarity are not synonymous but bordering notions [19,21,28,39]. Mathematicians have customarily regarded a proof as beautiful if it conformed to the classical ideals of brevity and simplicity [39]. Similarly, Michael Atiyah claims that “elegance is more or less synonymous with simplicity” [39]. We are quoting from Ref. [19] “The mathematical concept of similarity holds one of the keys to understanding the processes of growth in the natural world. As a member of a species grows to maturity, it generally transforms in such a way that its parts maintain approximately the same proportion concerning each other, and this is probably a reason why nature is often constrained to exhibit self-similar spiral growth”. AS and AS-inspired Voronoi mosaics exemplify simple, self-similar structures. This at least partially explains their aesthetic appeal. The concept of “beauty as simplicity” was strongly criticized recently [39]; thus, additional insights into the understanding of the aesthetic appeal of spiral-inspired patterns are necessary.

6. Discussion

Patterns, depicted in Figure 10 and Figure 11 create a sense of inherent “order”. In our discussion, we address the following fundamental question: how orders may be quantified? In other words: which of n given patterns is more ordered? It turns out, that an answer to this question has a fine structure, and different measures of order appearing in 2D patterns were already suggested. Between these measures are the Voronoi (Shannon) entropy, continuous measure of symmetry [40,41], the areal disorder factor [42] and the shape factor [42,43,44,45]. For example, the shape factor of the i-th Voronoi cell is defined as:

$${\mathit{\psi }}_{\mathit{i}}=\frac{{\mathit{p}}_{\mathit{i}}^2}{4\mathit{\pi }{\mathit{A}}_{\mathit{i}}}$$

(6)

where $p_i$ is the circumference of the i-th cell and $A_i$ is its area [42,43,44,45]. The shape factor is a dimensionless quantity that describes the shape of the cell, independently of its size (which is sensitive to the inter-particle distance) and characterizes the circularity of a cell because ${\psi }_i=1$ for a circle and ${\psi }_i>1$ for any other polygonal shape [42,43,44,45].

It was already demonstrated that the continuous measure of symmetry and the Voronoi (Shannon) entropy is not necessarily correlated [46,47]. Moreover, they may demonstrate anti-correlation [46,47]. The very question is: what is the correlation between the shape factor, Voronoi entropy and continuous measure of symmetry? We plan to address this question in our future research. Meanwhile, we conclude that the ordering of 2D patterns has a fine structure and could not be quantified with a single numerical parameter.

7. Conclusions

We conclude that the Voronoi diagrams generated by seed points located on the Archimedes Spirals demonstrate non-trivial mathematical properties and aesthetic attraction. Equidistant seed point distribution and points separated by linearly increasing distance generated very different Voronoi diagrams. Voronoi entropy calculated for the equidistant seed points located on the Archimedes Spiral decreased monotonously with the increase in the number of seeds. The Voronoi entropy calculated for points separated by linearly increasing distance demonstrated a saw-like behavior. It is possible to fill a plane with Voronoi mosaics built from cells of equal size which is of primary importance for phyllotaxis and the decorative arts.

The properties of the Voronoi tessellation are, too much extent, governed by the parameter $\xi =\frac{p}{q}$ where p and q are the distance between the points neighboring the spiral and the separation between the coils of the spiral, respectively. When the condition $\xi \cong 1$ is assumed, hexagons dominate the mosaic; whereas eight types of polygons were registered when the condition $\xi \gg 1$ was prescribed. For the patterns characterized by $\xi \gg 1$ the ordered patterns were revealed, demonstrating Voronoi entropy markedly larger than that of 1.71, reported for the random distribution of points [25,26].

The situation becomes more interesting for non-equidistant patterns, in which seed points are separated by the linearly growing radial distance. In this case, the switch of chirality of spirals constituting the pattern was observed; both clockwise and counterclockwise spirals were observed. Thus, patterns resembling phyllo-tactic (sunflower-like) ones were generated [29,30,31].

Archimedes Spirals can generate Voronoi diagrams that fill a plane with equal size cells. This possibility is also of primary importance for phyllotaxis (as exemplified by leaf or floret arrangement) [33]. Voronoi tessellations generated by the phyllotaxis-inspired patterns are addressed. The Aboav and Lewis laws generally do not hold for the Voronoi mosaics generated by the Archimedes Spirals. We explain this observation by the non-random distribution of seed points inherent in the studied patterns. The presented analysis applies to a diversity of soft matter problems, in which Archimedes Spirals appear. In particular, it was demonstrated, that confined chemical garden patterns formed an Archimedean spiral structure [48]. Propagating Archimedes spiral waves, form as a result of this strong complex light-matter interaction in anisotropic soft matter systems [49]. Non-point nature of real physical objects, such as sunflower grains impose limitations on the Voronoi tessellations analysis [50,51,52].

The Voronoi mosaics inspired by Archimedes’ Spirals demonstrate definite aesthetic appeal [3,20,28,38]. We relate, at least partially, the aesthetic attraction of the reported mosaics to their simplicity and self-similarity [16,21]. In our future work, we plan to consider symmetry considerations applied to the analysis of Voronoi diagrams inspired by the Archimedes Spirals.