A Numerical Solution of Symmetric Angle Ply Plates Using Higher-Order Shear Deformation Theory
Abstract
:1. Introduction
2. Solution of Problem
Method of Solution
3. Results and Discussion
3.1. Convergence Study
3.2. Validation
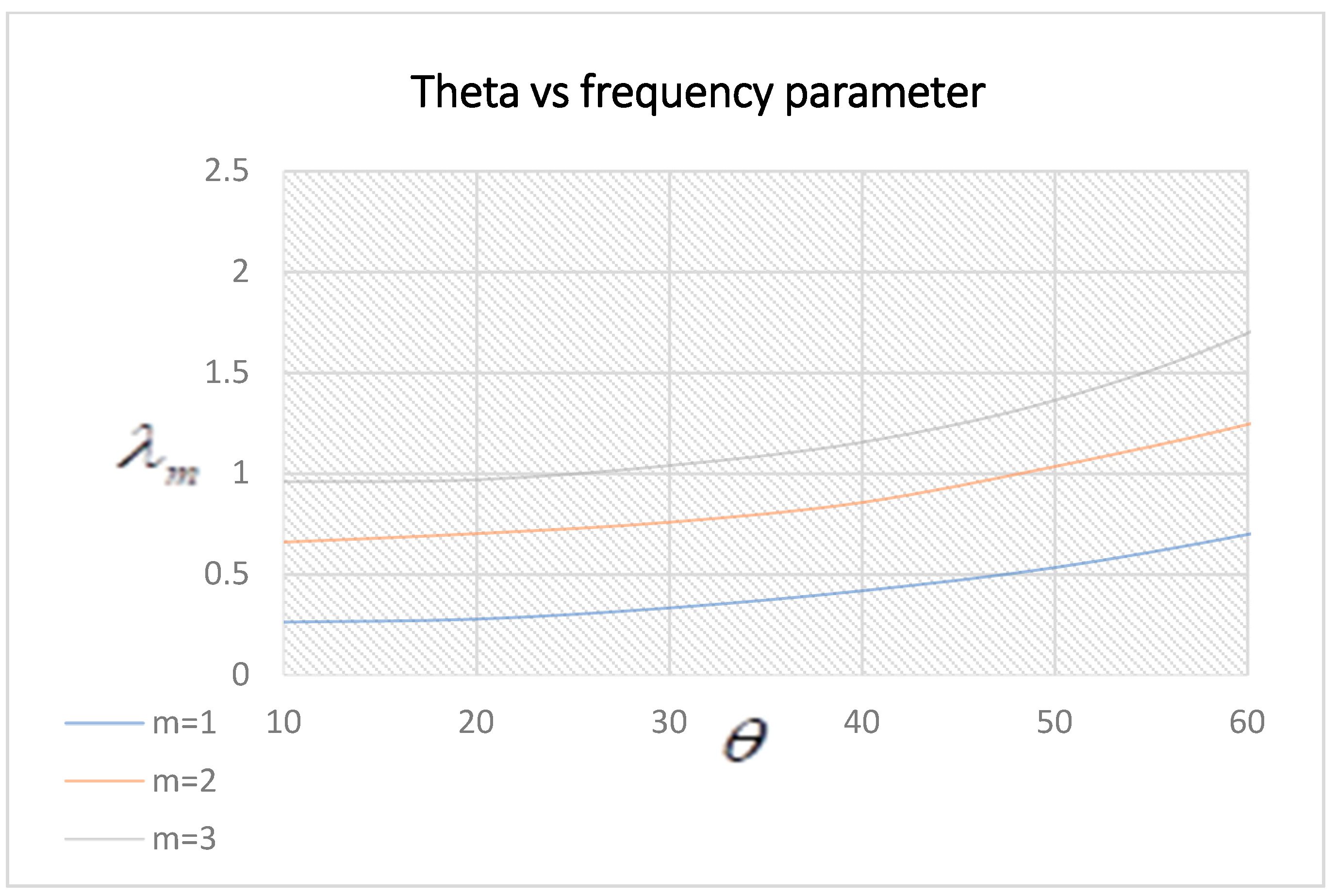
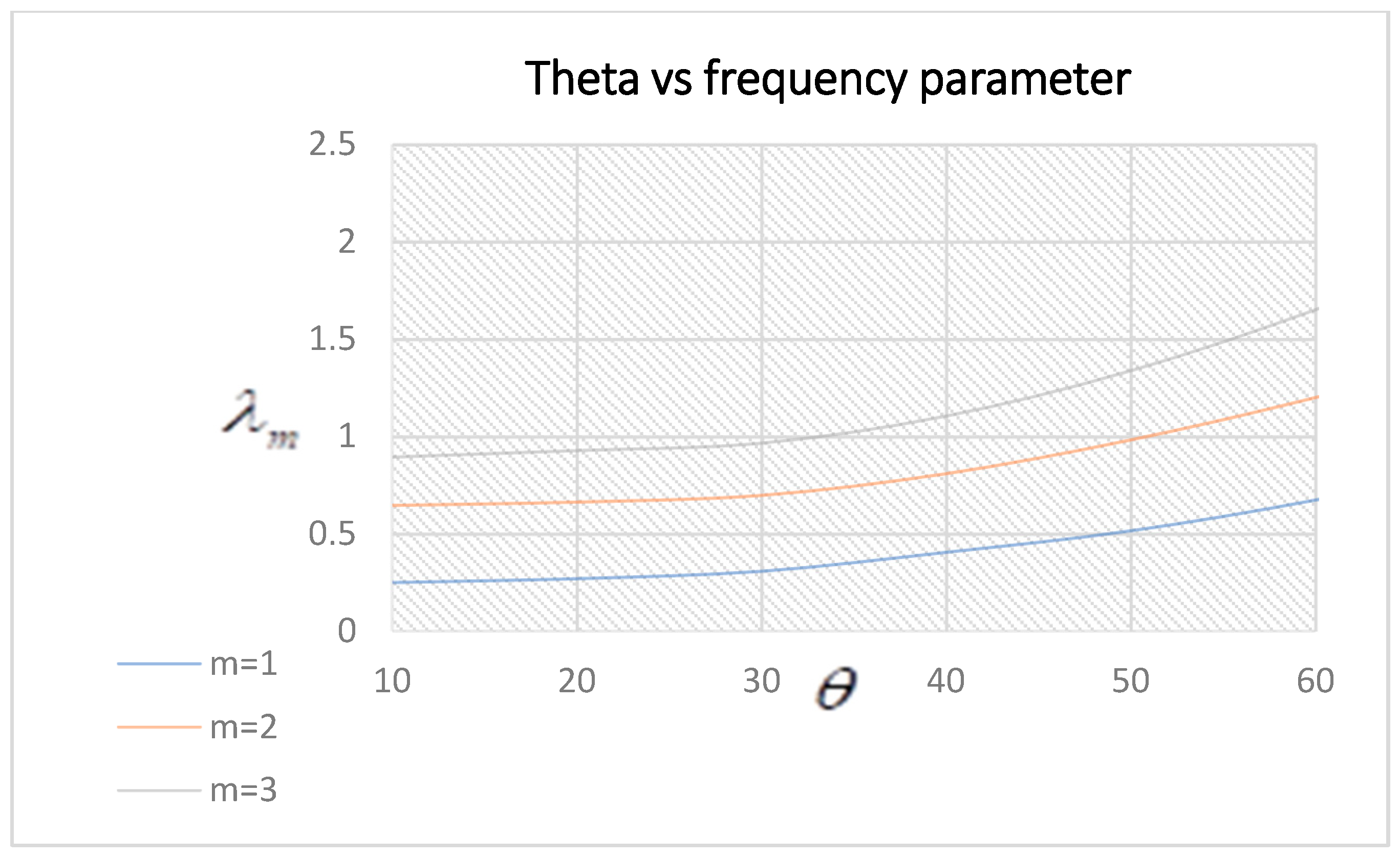
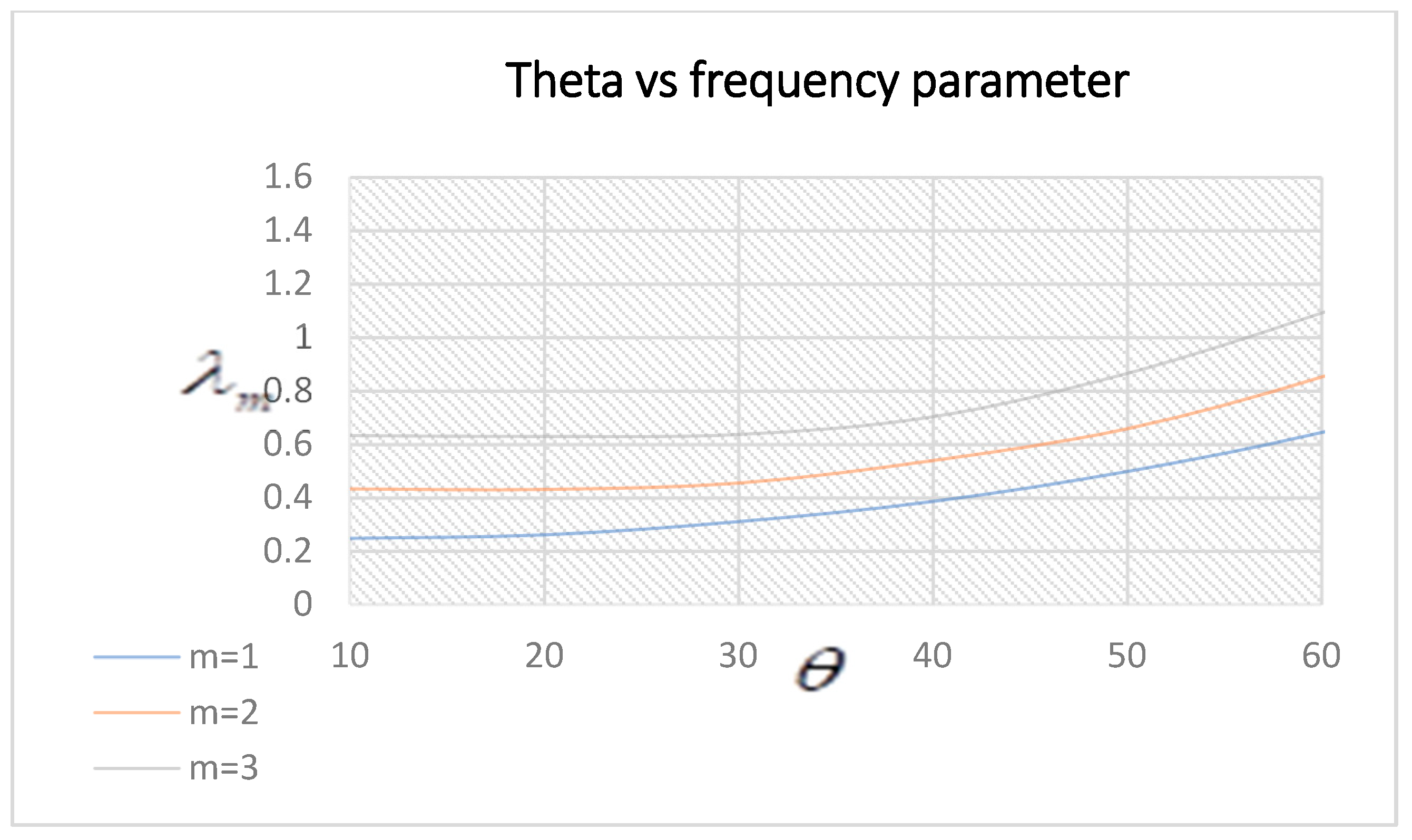
3.3. Frequency Parameter Variation under Different Ply Angles of Symmetric Plates
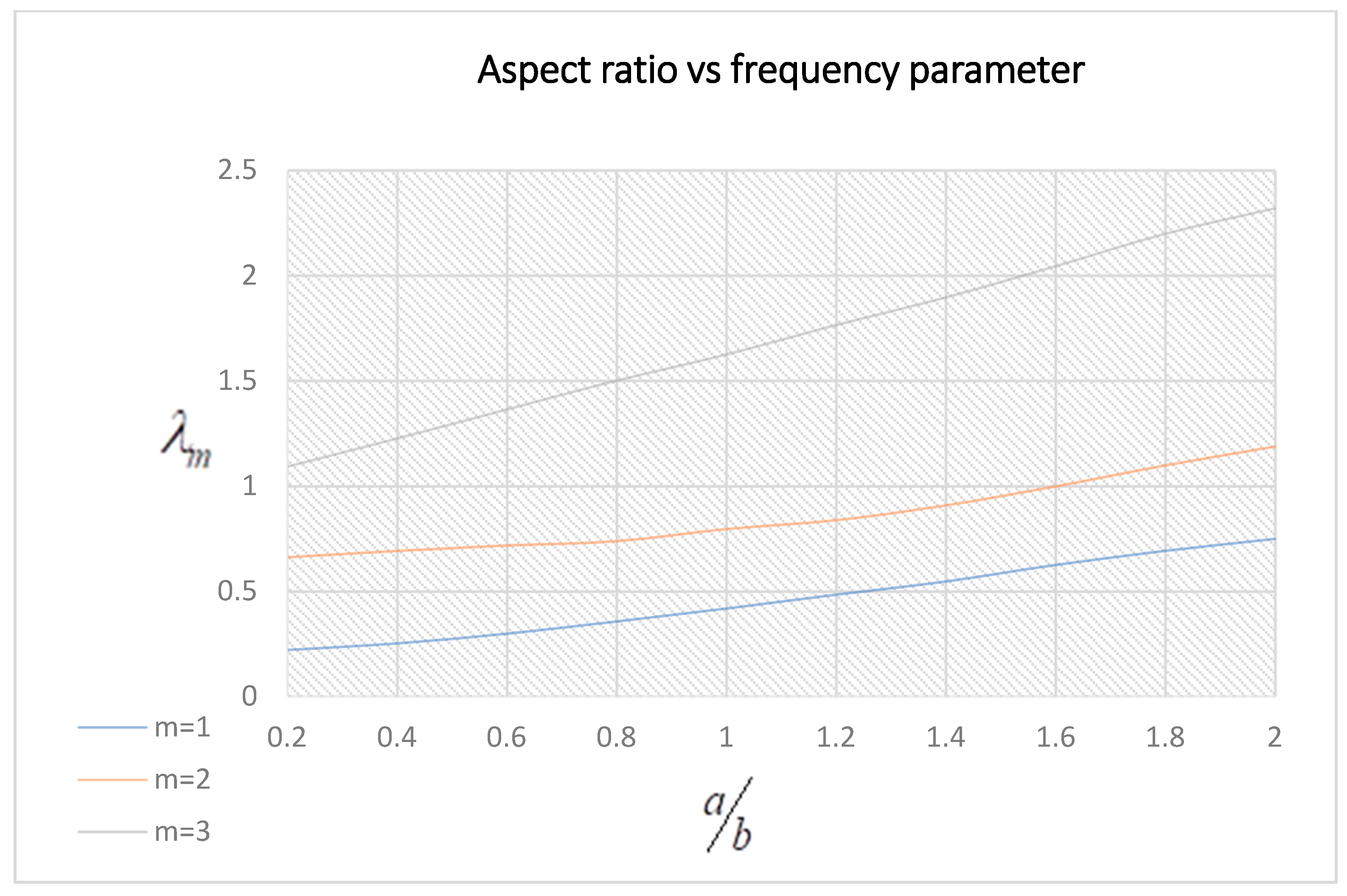
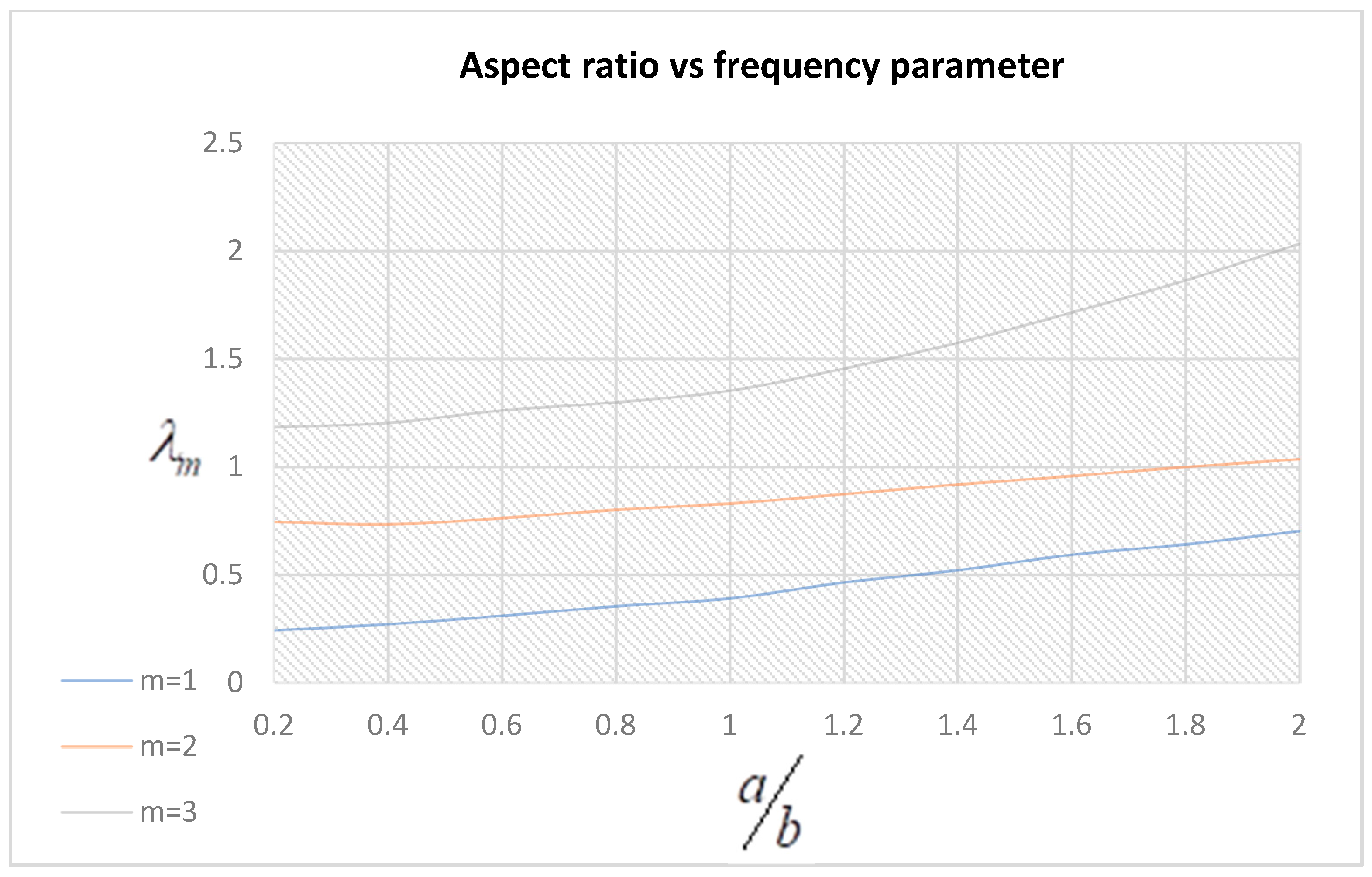
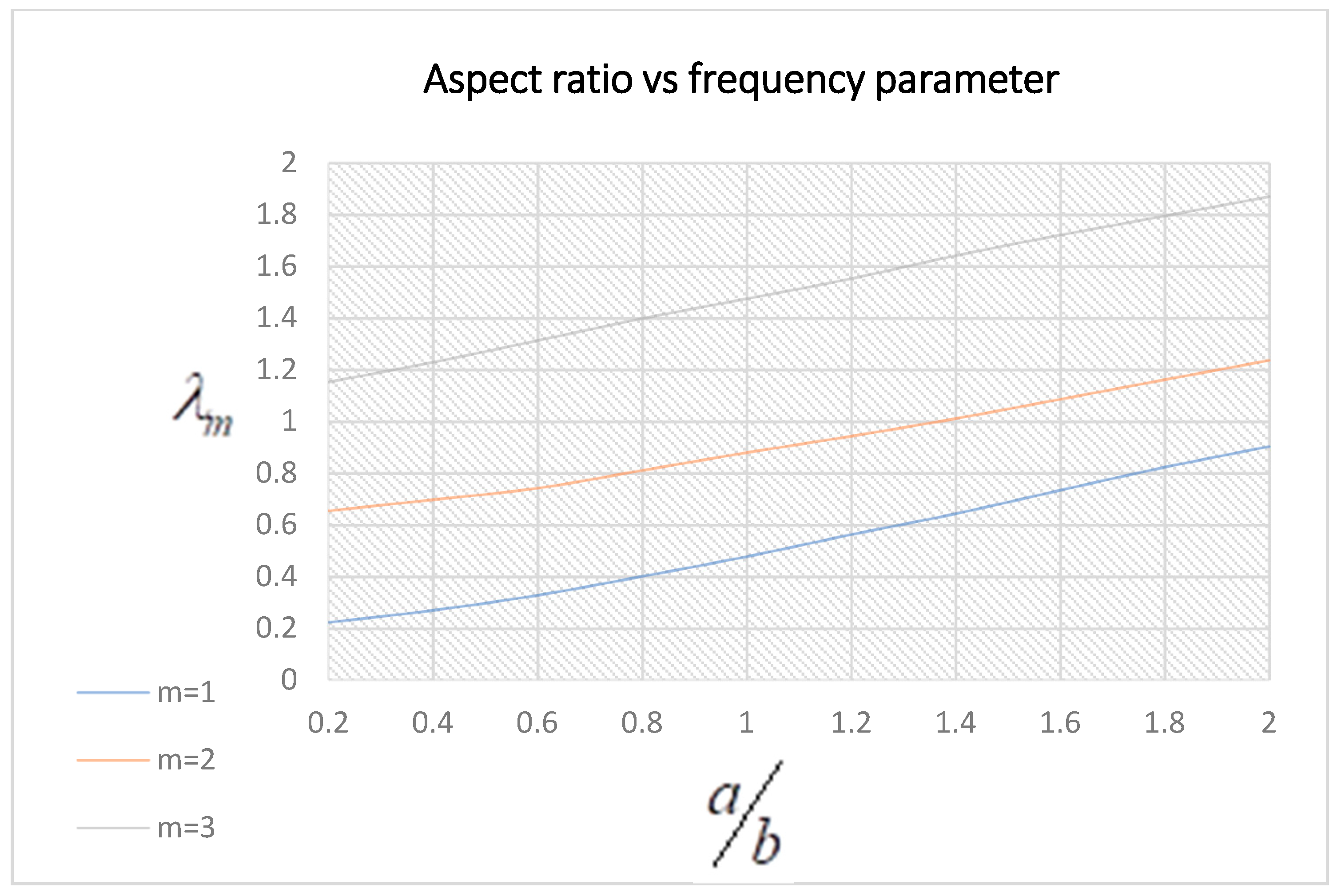
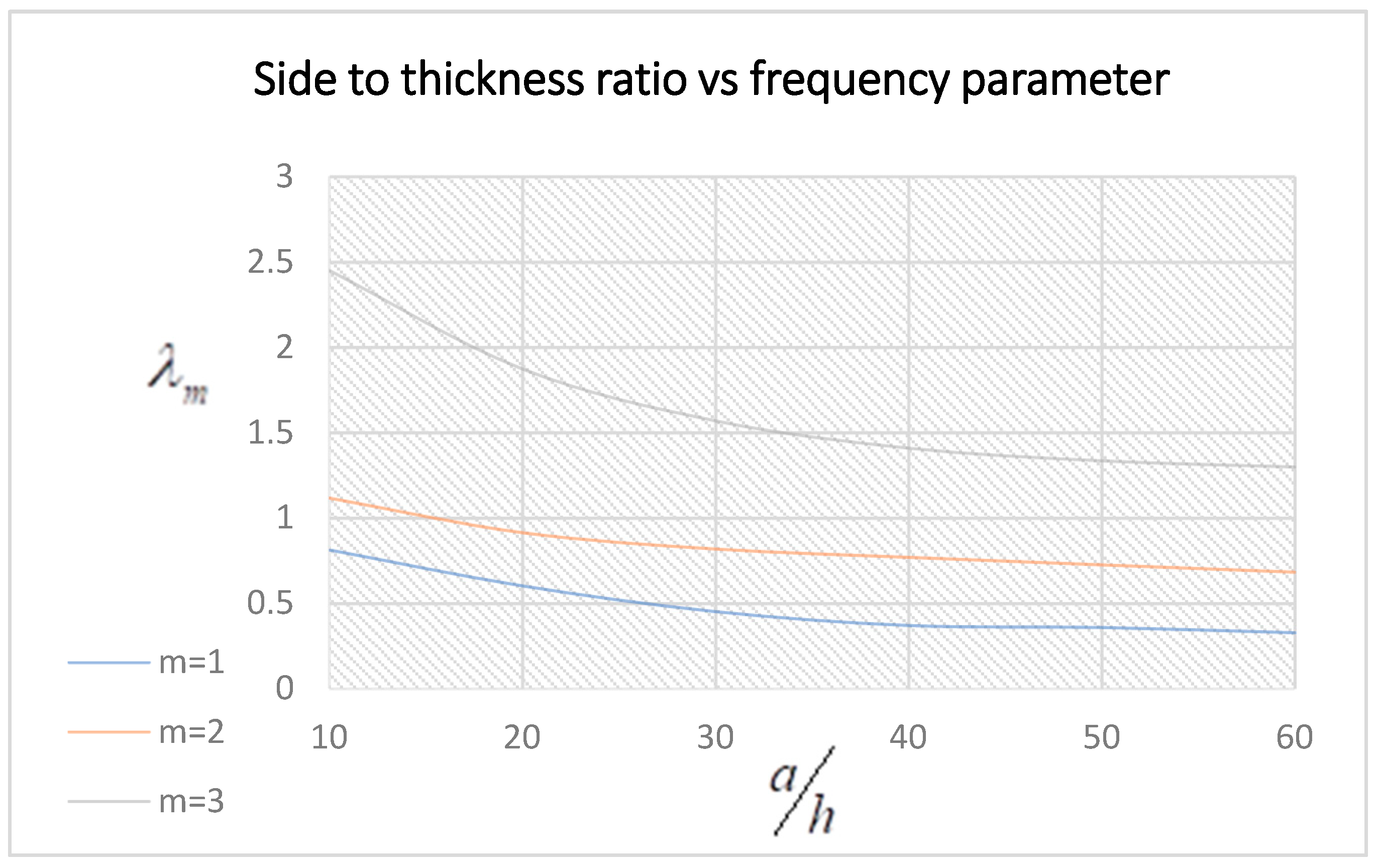
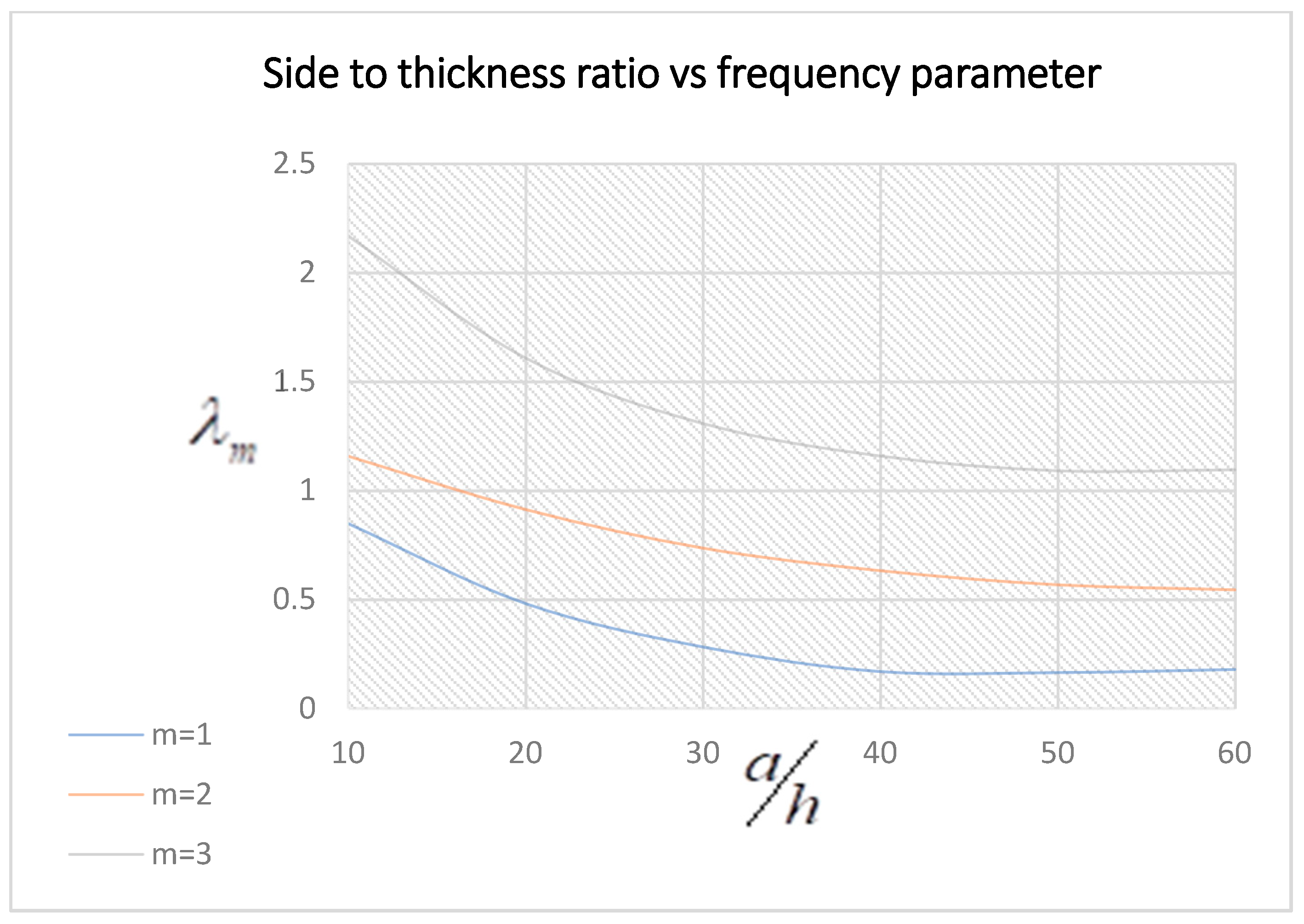
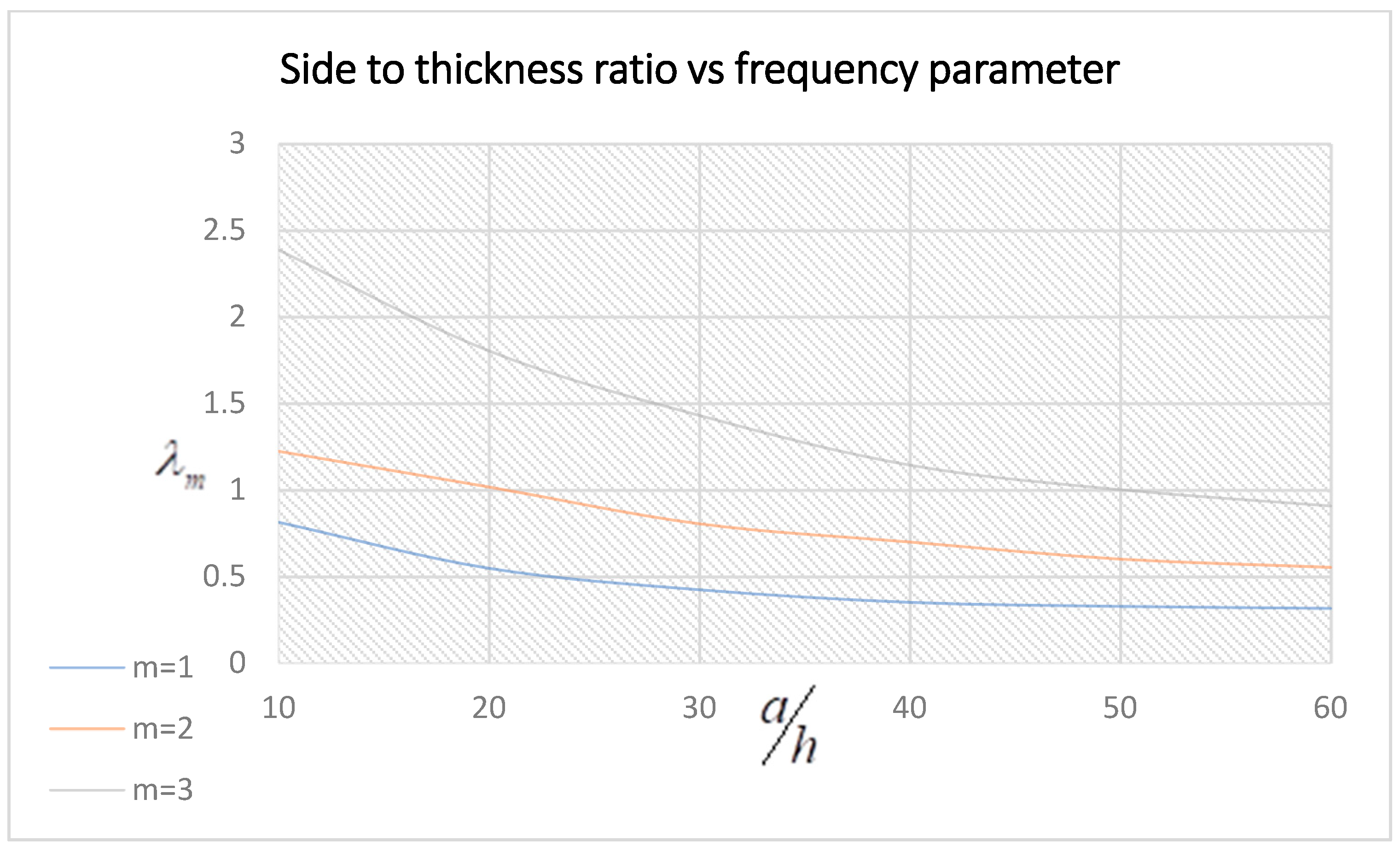
3.4. Frequency Parameter Variation under the Effect of the Aspect Ratio, Side-to-Thickness Ratio, and Ply Angle of Symmetric Plates
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Elastic coefficients representing the extensional rigidity | |
| Elastic coefficients representing the bending–stretching coupling rigidity | |
| Elastic coefficients representing the bending rigidity | |
| Shear modulus in the respective directions of the k-th layer | |
| Side-to-thickness ratio | |
| The Heaviside step function | |
| Normal inertia coefficient | |
| Rotary inertia coefficients | |
| Length parameter | |
| Moment resultants in the respective directions of the plate | |
| Stress results in the respective direction of the plate | |
| Number of intervals of spline interpolation | |
| Elements of the stiffness matrix for the material of the k-th layer | |
| Elements of the transformed stiffness matrix for the material of the k-th layer | |
| Transverse shear resultants in the respective directions of the plate | |
| Displacement functions in the , , and directions of the plate | |
| Nondimensionalized distance co-ordinate of the plate | |
| The equally spaced knots of spline interpolation | |
| , | Length and width of the plates |
| , | Spline coefficients |
| The total thickness of the plate | |
| The thickness of the k-th layer of the plate | |
| Summation or general indices | |
| , , and displacements of the plate | |
| The in-plane displacements of the reference surface | |
| Length coordinate of the plate | |
| Width coordinate of the plate | |
| Normal coordinate of any point on the plate | |
| Distance of the top of the k-th layer from the reference surface | |
| Product of of the plate | |
| The relative layer thickness of the -th layer | |
| Normal strain in the respective directions | |
| Shear strain in the respective directions of the plate | |
| The changes in the curvature of the reference surface during deformation in the respective directions of the plate Non-dimensional frequency parameter | |
| Shear rotations of any point on the middle surface of the plate | |
| Shear rotational functions of the plate | |
| Non-dimensionalized shear rotations of the plate | |
| The mass density of the material of the plate or shell | |
| Normal stress in the respective directions of the plate | |
| Shear stress at a point on the reference surface of the plate | |
| Ply orientation angle |
Appendix A
Appendix A.1. Components of the Stiffness Matrix for the of k-th Layer of Plate Material
Appendix A.2. Components of the Transformed Stiffness Matrix for the k-th Layer Material
References
- Vinson, J.R. Sandwich Structures. Appl. Mech. Rev. 2001, 54, 201–214. [Google Scholar] [CrossRef]
- Noor, A.K.; Burton, W.S.; Bert, C.W. Computational models for sandwich panels and shells. Appl. Mech. Rev. 1996, 49, 155–199. [Google Scholar] [CrossRef]
- Yang, P.C.; Nooris, C.H.; Stavsky, Y. Elastic wave propogation in heterogeneous plates. Int. J. Solids Struct. 1966, 2, 665–684. [Google Scholar] [CrossRef]
- Reddy, J.N. Theory and Analysis of Elastic Plates and Shells; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Ghiamy, A.; Amoushahi, H. Dynamic stability of different kinds of sandwich plates using third order shear deformation theory. Thin-Walled Struct. 2022, 172, 108822. [Google Scholar] [CrossRef]
- Parida, S.P.; Jena, P.C. Free and forced vibration analysis of flyash/graphene filled laminated composite plates using higher order shear deformation theory. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 4648–4659. [Google Scholar] [CrossRef]
- Zhao, Y.; Qin, B.; Wang, Q.; Liang, X. A unified Jacobi–Ritz approach for the FGP annular plate with arbitrary boundary conditions based on a higher-order shear deformation theory. J. Vib. Control 2022. [Google Scholar] [CrossRef]
- Tian, Y.; Li, Q.; Wu, D.; Chen, X.; Gao, W. Nonlinear dynamic stability analysis of clamped and simply supported organic solar cells via the third-order shear deformation plate theory. Eng. Struct. 2022, 252, 113616. [Google Scholar] [CrossRef]
- Belkhodja, Y.; Ouinas, D.; Fekirini, H.; Olay, J.A.; Achour, B.; Touahmia, M.; Boukendakdji, M. A new hybrid HSDT for bending, free vibration, and buckling analysis of FGM plates (2D & quasi-3D). Smart Struct. Syst. 2022, 29, 395–420. [Google Scholar]
- Eskandari Shahraki, M.; Shariati, M.; Asiaban, N.; Davar, A.; Heydari Beni, M.; Eskandari Jam, J. Assessment of Third-order Shear Deformation Graphene Nanoplate Response under Static Loading Using Modified Couple Stress Theory. J. Mod. Process. Manuf. Prod. 2022, 11, 41–57. [Google Scholar]
- Shi, P.; Dong, C. A refined hyperbolic shear deformation theory for nonlinear bending and vibration isogeometric analysis of laminated composite plates. Thin-Walled Struct. 2022, 174, 109031. [Google Scholar] [CrossRef]
- Javani, M.; Kiani, Y.; Eslami, M.R. On the free vibrations of FG-GPLRC folded plates using GDQE procedure. Compos. Struct. 2022, 286, 115273. [Google Scholar] [CrossRef]
- Sayyad, A.S.; Avhad, P.V. A new higher order shear and normal deformation theory for the free vibration analysis of sandwich curved beams. Compos. Struct. 2022, 280, 114948. [Google Scholar] [CrossRef]
- Ellali, M.; Bouazza, M.; Amara, K. Thermal buckling of a sandwich beam attached with piezoelectric layers via the shear deformation theory. Arch. Appl. Mech. 2022, 92, 657–665. [Google Scholar] [CrossRef]
- Nguyen, N.D.; Nguyen, T.N.; Nguyen, T.K.; Vo, T.P. A new two-variable shear deformation theory for bending, free vibration and buckling analysis of functionally graded porous beams. Compos. Struct. 2022, 282, 115095. [Google Scholar] [CrossRef]
- Peng, L.X.; Chen, S.Y.; Wei, D.Y.; Chen, W.; Zhang, Y.S. Static and free vibration analysis of stiffened FGM plate on elastic foundation based on physical neutral surface and MK method. Compos. Struct. 2022, 290, 115482. [Google Scholar] [CrossRef]
- Pham, Q.H.; Tran, T.T.; Tran, V.K.; Nguyen, P.C.; Nguyen-Thoi, T. Free vibration of functionally graded porous non-uniform thickness annular-nanoplates resting on elastic foundation using ES-MITC3 element. Alex. Eng. J. 2022, 61, 1788–1802. [Google Scholar] [CrossRef]
- Hung, P.T.; Phung-Van, P.; Thai, C.H. A refined isogeometric plate analysis of porous metal foam microplates using modified strain gradient theory. Compos. Struct. 2022, 289, 115467. [Google Scholar] [CrossRef]
- Sharma, N.; Swain, P.K.; Maiti, D.K.; Singh, B.N. Static and free vibration analyses and dynamic control of smart variable stiffness laminated composite plate with delamination. Compos. Struct. 2022, 280, 114793. [Google Scholar] [CrossRef]
- Cho, J.R. Nonlinear free vibration of functionally graded CNT-reinforced composite plates. Compos. Struct. 2022, 281, 115101. [Google Scholar] [CrossRef]
- Zang, Q.; Liu, J.; Ye, W.; Yang, F.; Hao, C.; Lin, G. Static and free vibration analyses of functionally graded plates based on an isogeometric scaled boundary finite element method. Compos. Struct. 2022, 288, 115398. [Google Scholar] [CrossRef]
- Ghosh, S.; Haldar, S. Free Vibration analysis of isotropic and laminated composite plate on elastic point supports using finite element method. In Recent Advances in Computational and Experimental Mechanics; Springer: Singapore, 2022; Volume II, pp. 371–384. [Google Scholar]
- Milazzo, A. Free vibrations analysis of cracked variable stiffness composite plates by the extended Ritz method. Mech. Adv. Mater. Struct. 2022. [Google Scholar] [CrossRef]
- Saiah, B.; Bachene, M.; Guemana, M.; Chiker, Y.; Attaf, B. On the free vibration behavior of nanocomposite laminated plates contained piece-wise functionally graded graphene-reinforced composite plies. Eng. Struct. 2022, 253, 113784. [Google Scholar] [CrossRef]
- Singh, A.; Karathanasopoulos, N. Three-dimensional analytical elasticity solution for the mechanical analysis of arbitrarily-supported, cross and angle-ply composite plates under patch loads. Compos. Struct. 2023, 310, 116752. [Google Scholar] [CrossRef]
- Belardi, V.G.; Fanelli, P.; Vivio, F. Application of the Ritz method for the bending and stress analysis of thin rectilinear orthotropic composite sector plates. Thin-Walled Struct. 2023, 183, 110374. [Google Scholar] [CrossRef]
- Zhong, R.; Hu, S.; Liu, X.; Qin, B.; Wang, Q.; Shuai, C. Vibro-acoustic analysis of a circumferentially coupled composite laminated annular plate backed by double cylindrical acoustic cavities. Ocean. Eng. 2022, 257, 111584. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, X.; Gao, H.; Yuan, T.; Liu, X.; Zhang, W. Effects of alkali-treated plant wastewater on the properties and microstructures of alkali-activated composites. Ceram. Int. 2023, 49, 8583–8597. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, G.; Ye, J.; Lin, Y. Crushing and parametric studies of polygonal substructures based hierarchical cellular honeycombs with non-uniform wall thickness. Compos. Struct. 2022, 299, 116087. [Google Scholar] [CrossRef]
- Zhang, H.; Ouyang, Z.; Li, L.; Ma, W.; Liu, Y.; Chen, F.; Xiao, X. Numerical study on welding residual stress distribution of corrugated steel webs. Metals 2022, 12, 1831. [Google Scholar] [CrossRef]
- Peng, J.; Xu, C.; Dai, B.; Sun, L.; Feng, J.; Huang, Q. Numerical Investigation of Brittleness Effect on Strength and Microcracking Behavior of Crystalline Rock. Int. J. Geomech. 2022, 22, 04022178. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanis of Laminated Composite Plates and Shells; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Schoenberg, I.J.; Whitney, A. On Pólya frequence functions. III. The positivity of translation determinants with an application to the interpolation problem by spline curves. Trans. Am. Math. Soc. 1953, 74, 246–259. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.W.; Nakatani, A.; Kitagawa, H. Vibration analysis of fully clamped arbitrarily laminated plate. Compos. Struct. 2004, 63, 115–122. [Google Scholar] [CrossRef]
- Xiang, S.; Jiang, S.X.; Bi, Z.Y.; Jin, Y.X.; Yang, M.S. A nth-order meshless generalization of Reddy’s third-order shear deformation theory for the free vibration on laminated composite plates. Compos. Struct. 2011, 93, 299–307. [Google Scholar] [CrossRef]

| % Change | % Change | % Change | ||||
|---|---|---|---|---|---|---|
| 4 | 0.547064 | - | 1.260471 | - | 2.0610 | - |
| 6 | 0.511985 | −6.41222 | 1.12029 | −11.12131 | 1.894131 | −8.09650 |
| 8 | 0.499459 | −2.46555 | 1.069711 | −4.51481 | 1.761941 | −6.97892 |
| 10 | 0.493624 | −1.16826 | 1.046288 | −2.18965 | 1.700053 | −3.51248 |
| 12 | 0.490446 | −0.64380 | 1.033585 | −1.21410 | 1.666535 | −1.97158 |
| Method | Mode 1 | 2 | 3 | |
|---|---|---|---|---|
| 10 | Shi et al. [34] Xiang et al. [35] Present | 17.433 17.225 17.333 | 22.506 22.261 22.576 | 30.905 30.631 30.981 |
| 20 | Shi et al. [34] Xiang et al. [35] Present | 23.979 23.745 23.854 | 30.407 30.041 30.342 | 41.937 41.295 41.821 |
| 100 | Shi et al. [34] Xiang et al. [35] Present | 28.946 28.572 28.734 | 36.772 36.184 36.634 | 50.721 49.791 50.612 |
| 6-Layered | 5-Layered | 3-Layered | |
|---|---|---|---|
| 0.262205 | 0.249637 | 0.246888 | |
| 0.276866 | 0.269521 | 0.259949 | |
| 0.332592 | 0.307604 | 0.309678 | |
| 0.417498 | 0.404969 | 0.385188 | |
| 0.53254 | 0.515285 | 0.497382 | |
| 0.696845 | 0.673437 | 0.643287 | |
| 0.899267 | 0.869292 | 0.83807 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Javed, S. A Numerical Solution of Symmetric Angle Ply Plates Using Higher-Order Shear Deformation Theory. Symmetry 2023, 15, 767. https://doi.org/10.3390/sym15030767
Javed S. A Numerical Solution of Symmetric Angle Ply Plates Using Higher-Order Shear Deformation Theory. Symmetry. 2023; 15(3):767. https://doi.org/10.3390/sym15030767
Chicago/Turabian StyleJaved, Saira. 2023. "A Numerical Solution of Symmetric Angle Ply Plates Using Higher-Order Shear Deformation Theory" Symmetry 15, no. 3: 767. https://doi.org/10.3390/sym15030767
APA StyleJaved, S. (2023). A Numerical Solution of Symmetric Angle Ply Plates Using Higher-Order Shear Deformation Theory. Symmetry, 15(3), 767. https://doi.org/10.3390/sym15030767






