Sweeping Surfaces according to Type-3 Bishop Frames in Euclidean 3-Space

Abstract

The aim of this work is to investigate sweeping surfaces and their local singularities due to type-3 Bishop frames in Euclidean 3-space, ${\mathbb{E}}^3$. A sweeping surface a is surface that is designed from a section curve positioned along a path, which acts as the vertebral column or spine curve, and it has symmetrical characteristics. In this work, we have specified a sweeping surface and have examined its geometry and singularity. Thereafter, we deduced the circumstances required for this surface to be a developable surface. In great detail, we concentrated on the fundamental discussion on whether the resulting developable surface is a cylindrical, cone or tangent surface. Meanwhile, examples are detailed to explain the applications of the notional outcomes.

1. Introduction

A sweeping surface is a surface that is traced by a section curve positioned over a path which acts as the spine curve. Sweeping is an indispensable tool in geometric modeling. The primary idea revolves around choosing distinct geometrical matters (such as generators) that move with the spine curve (trajectory) in the space. This upgrowth involves movement in the space together with intrinsic metamorphosis, resulting in the sweeping goal. Therefore, wiping the curve with a different curve creates the sweeping surface. Commonly used names for the sweeping surface are tubular surface, pipe surface, string and canal surface [1,2,3,4,5,6,7]. A noteworthy fact with regard to sweeping surfaces is that they can be developable ruled surfaces [7]. Developable ruled surfaces are widely applied in geometric modeling, such as leather, cloth, metal plates, etc., and they can also be seen in modern automotive design, aircraft wing design and upper styling. There are three types of developable ruled surfaces: cylindrical, cones and tangent surfaces [8,9,10,11,12].

However, to best of the authors knowledge, we cannot find any work on natural mates of a curve as the original object, nor can we find work addressing the singularities and convexity of sweeping surfaces. To serve such a need, and motivated by the work of the second author [7], in this work, we develop a new version of a Bishop frame, comparable with the well known Bishop and Frenet–Serret frames, utilizing a mutual tangent vector field to a natural mate of a curve, and name this frame the type-3 Bishop frame. By employing this frame, we drive the parametrization of a sweeping surface. We also show that the parametric curves on this surface are curvature lines, and study the local singularities and convexity. Therefore, conditions in which a sweeping surface is a developable ruled surface are attained. Meanwhile, examples are given to explain the applications of the notional outcomes.

2. Preliminaries

For our task, we have used [1,2,3,4] as generic references. Let $\mathit{\alpha }=\mathit{\alpha }\left(s\right)$ be a unit speed curve in ${\mathbb{E}}^3$. We denote the natural curvature and torsion of $\mathit{\alpha }=$$\mathit{\alpha }\left(s\right)$ by $\kappa \left(s\right)$ and $\tau \left(s\right)$, respectively. We set ${\mathit{\alpha }}^{″}\left(s\right)\ne$ 0 for all $s\in [0,T]$, since this would give us a straight line. In this study, ${\mathit{\alpha }}^{\prime }\left(s\right)$ denotes the derivative of $\mathit{\alpha }$ with respect to the arc length parameter, s. For all points of $\mathit{\alpha }\left(s\right)$, the set $\{{\mathit{\xi }}_1,{\mathit{\xi }}_2,{\mathit{\xi }}_3\}$ is the Frenet–Serret frame, where ${\mathit{\xi }}_1\left(s\right)={\mathit{\alpha }}^{\prime }\left(s\right)$, ${\mathit{\xi }}_2\left(s\right)={\mathit{\alpha }}^{″}\left(s\right)/∥{\mathit{\alpha }}^{″}\left(s\right)∥$ and ${\mathit{\xi }}_3\left(s\right)={\mathit{\xi }}_1\left(s\right)\times {\mathit{\xi }}_2\left(s\right)$ are the unit tangent, principal normal and binormal vectors of the curve at point $\mathit{\alpha }\left(s\right)$, respectively. The Frenet–Serret frame formula is:

$$\left(\begin{array}{c}{\mathit{\xi }}_1^{{}^{\prime }}\hfill \\ {\mathit{\xi }}_2^{{}^{\prime }}\hfill \\ {\mathit{\xi }}_3^{{}^{\prime }}\hfill \end{array}\right)=\left(\begin{array}{ccc}0\hfill & \kappa \left(s\right)\hfill & 0\hfill \\ -\kappa \left(s\right)\hfill & 0\hfill & \tau \left(s\right)\hfill \\ 0\hfill & -\tau \left(s\right)\hfill & 0\hfill \end{array}\right)\left(\begin{array}{c}{\mathit{\xi }}_1\hfill \\ {\mathit{\xi }}_2\hfill \\ {\mathit{\xi }}_3\hfill \end{array}\right).$$

(1)

Definition 1.

Let curve $\mathit{\beta }\left(s_n\right)$ be the integral curve of the principal normal vector ${\mathit{\xi }}_2\left(s\right)$; that is, $\mathit{\beta }\left(s_n\right)=\underset{0}{\stackrel{s}{\int }}{\mathit{\xi }}_2\left(s\right)ds$, where the curve $\mathit{\beta }\left(s_n\right)$ is named the natural mate curve of $\mathit{\alpha }\left(s\right)$, and the pair$\left\{\mathit{\alpha }\right(s)$, $\mathit{\beta }\left(s_n\right)\}$ is named the conjugate pair [13].

It can be furthermore displayed that the arc length parameter, $s_n$, of the curve $\mathit{\beta }\left(s_n\right)$ can be displayed as $s_n=s+c$, where c is a constant. Without loss of generality, we can choose $c=0$, i.e., $s=s_n$. Let $\{{\mathit{e}}_1\left(s\right),$${\mathit{e}}_2\left(s\right)$, ${\mathit{e}}_3\left(s\right)\}$ be the movable Frenet–Serret frame on $\mathit{\beta }\left(s\right)$, such that ${\mathit{e}}_1\left(s\right)$, ${\mathit{e}}_2\left(s\right)$ and ${\mathit{e}}_3\left(s\right)$ are the unit tangent, the principal normal and the binormal vector fields, respectively. Then, the Frenet–Serret frame of $\mathit{\beta }\left(s\right)$ satisfies the following formula:

$$\left(\begin{array}{c}{\mathit{e}}_1\hfill \\ {\mathit{e}}_2\hfill \\ {\mathit{e}}_3\hfill \end{array}\right)=\left(\begin{array}{ccc}0\hfill & 1\hfill & 0\hfill \\ -cos\psi \hfill & 0\hfill & sin\psi \hfill \\ sin\psi \hfill & 0\hfill & cos\psi \hfill \end{array}\right)\left(\begin{array}{c}{\mathit{\xi }}_1\hfill \\ {\mathit{\xi }}_2\hfill \\ {\mathit{\xi }}_3\hfill \end{array}\right),$$

(2)

where $\psi ={tan}^{-1}\left(\frac{\tau }{\kappa }\right)$. Then,

$$\left(\begin{array}{c}{\mathit{e}}_1^{{}^{\prime }}\hfill \\ {\mathit{e}}_2^{{}^{\prime }}\hfill \\ {\mathit{e}}_3^{{}^{\prime }}\hfill \end{array}\right)=\left(\begin{array}{ccc}0\hfill & {ϵ}_1\left(s\right)\hfill & 0\hfill \\ -{ϵ}_1\left(s\right)\hfill & 0\hfill & {ϵ}_2\left(s\right)\hfill \\ 0\hfill & -{ϵ}_2\left(s\right)\hfill & 0\hfill \end{array}\right)\left(\begin{array}{c}{\mathit{e}}_1\hfill \\ {\mathit{e}}_2\hfill \\ {\mathit{e}}_3\hfill \end{array}\right)=\mathit{\omega }\left(s\right)\times \left(\begin{array}{c}{\mathit{e}}_1\hfill \\ {\mathit{e}}_2\hfill \\ {\mathit{e}}_3\hfill \end{array}\right),$$

(3)

where

$${ϵ}_1\left(s\right)=\sqrt{{\kappa }^2+{\tau }^2}\mathrm{and}{ϵ}_2\left(s\right)=\frac{{\kappa }^2}{{\kappa }^2+{\tau }^2}{\left(\frac{\tau }{\kappa }\right)}^{{}^{\prime }}$$

(4)

and $\mathit{\omega }\left(s\right)={ϵ}_2{\mathit{e}}_1+{ϵ}_1{\mathit{e}}_3$ is the angular velocity vector of the Frenet–Serret frame.

Definition 2.

An orthonormal movable frame $\{{\mathit{\chi }}_1,{\mathit{\chi }}_2$, ${\mathit{\chi }}_3\}$ over a space curve $\mathit{\gamma }\left(s\right)$ is a rotation minimizing frame (RMF) with respect to ${\mathit{\chi }}_1$ if its angular velocity ω satisfies $<{\mathit{\omega },\mathit{\chi }}_1>=0$ or, equally, if the derivatives of ${\mathit{\chi }}_2$ and ${\mathit{\chi }}_3$ are both parallel to ${\mathit{\chi }}_1$. A comparable characterization holds when ${\mathit{\chi }}_2$ or ${\mathit{\chi }}_3$ is chosen as the reference direction.

Via Definition 2, we observe that $\{{\mathit{e}}_1\left(s\right),$${\mathit{e}}_2\left(s\right)$, ${\mathit{e}}_3\left(s\right)\}$ is the RMF for ${\mathit{e}}_2$, but not for ${\mathit{e}}_1$ and ${\mathit{e}}_3$. In the reality that $\{{\mathit{e}}_1\left(s\right),$${\mathit{e}}_2\left(s\right)$, ${\mathit{e}}_3\left(s\right)\}$ is not the RMF for ${\mathit{e}}_1$, one can readily derive such an RMF from it. New plane vectors (${\mathit{\zeta }}_1$,${\mathit{\zeta }}_2$) are given by rotating (${\mathit{e}}_2$,${\mathit{e}}_3$) via

$$\left(\begin{array}{c}{\mathit{e}}_1\left(s\right)\hfill \\ {\mathit{\zeta }}_1\left(s\right)\hfill \\ {\mathit{\zeta }}_2\left(s\right)\hfill \end{array}\right)=\left(\begin{array}{ccc}1\hfill & 0\hfill & 0\hfill \\ 0\hfill & cos\vartheta \hfill & sin\vartheta \hfill \\ 0\hfill & -sin\vartheta \hfill & cos\vartheta \hfill \end{array}\right)\left(\begin{array}{c}{\mathit{e}}_1\left(s\right)\hfill \\ {\mathit{e}}_2\left(s\right)\hfill \\ {\mathit{e}}_3\left(s\right)\hfill \end{array}\right),$$

(5)

where $\vartheta \left(s\right)\ge 0$. Then, we have the alternate frame equations

$$\left(\begin{array}{c}{\mathit{e}}_1^{{}^{\prime }}\left(s\right)\hfill \\ {\mathit{\xi }}_1^{{}^{\prime }}\left(s\right)\hfill \\ {\mathit{\zeta }}_2^{{}^{\prime }}\left(s\right)\hfill \end{array}\right)=\left(\begin{array}{ccc}0\hfill & {\kappa }_1\left(s\right)\hfill & -{\kappa }_2\left(s\right)\hfill \\ -{\kappa }_1\left(s\right)\hfill & 0\hfill & 0\hfill \\ {\kappa }_2\left(s\right)\hfill & 0\hfill & 0\hfill \end{array}\right)\left(\begin{array}{c}{\mathit{e}}_1\left(s\right)\hfill \\ {\mathit{\zeta }}_1\left(s\right)\hfill \\ {\mathit{\zeta }}_2\left(s\right)\hfill \end{array}\right),$$

(6)

where

$$\left.\begin{array}{c}{\kappa }_1={ϵ}_{1}cos\vartheta ,{\kappa }_2={ϵ}_{1}sin\vartheta ,\vartheta \left(s\right)={tan}^{-1}\left(\frac{{\kappa }_2}{{\kappa }_1}\right);{\kappa }_1\ne 0,\hfill \\ \vartheta ={\vartheta }_0-\underset{s_0}{\stackrel{s}{\int }}{ϵ}_{2}ds,\mathrm{and}{\vartheta }_0=\vartheta \left(s_0\right).\hfill \end{array}\right\}$$

(7)

The frame $\{{\mathit{e}}_1,{\mathit{\zeta }}_1,$${\mathit{\zeta }}_2\}$ has angular velocity $\mathit{\psi }={\kappa }_2\left(s\right){\mathit{\zeta }}_1\left(s\right)+{\kappa }_1\left(s\right){\mathit{\zeta }}_2\left(s\right)$, fulfilling $<\mathit{\psi },{\mathit{e}}_1>=0$, and this frame is the RMF for ${\mathit{e}}_1$. Since the vectors (${\mathit{\zeta }}_1$,${\mathit{\zeta }}_2$) span the normal plane and display no instantaneous rotation on ${\mathit{e}}_1$ to that plane along $\mathit{\beta }=\mathit{\beta }\left(s\right)$, similar to what was reported in [6,7,14], the set $\{{\mathit{e}}_1,{\mathit{\zeta }}_1,$${\mathit{\zeta }}_2\}$ is a type-3 Bishop frame or conjugate rotation minimizing frame.

3. Sweeping Surfaces with Type-3 Bishop Frame

A sweeping surface with conjugate mate curve $\mathit{\beta }\left(s\right)$ is a surface described by [7]:

$$M:\mathit{q}(s,u)=\mathit{\beta }\left(s\right)+A\left(s\right)\mathit{x}\left(u\right)=\mathit{\beta }\left(s\right)+x_1\left(u\right){\mathit{\zeta }}_1\left(s\right)+x_2\left(u\right){\mathit{\zeta }}_2\left(s\right),$$

(8)

where $\mathit{\beta }\left(s\right)$ is the spine curve (at least $C^1$ is continuous), $0\le s\le \mathit{t}$ and s is the arc length parameter. $x\left(u\right)$ is the planar profile (cross-section) curve assigned by $x\left(u\right)=(0,$ $x_1\left(u\right),x_2{\left(u\right))}^{\mathit{t}}$, where the symbol T denotes transposition, with the other parameter $u\in I\subseteq \mathbb{R}$. The orthogonal matrix $A\left(s\right)=\{{\mathit{e}}_1\left(s\right),{\mathit{\zeta }}_1\left(s\right)$,${\mathit{\zeta }}_2\left(s\right)\}$ designates the type-3 Bishop frame over $\mathit{\beta }\left(s\right)$.

The sweeping surface $\mathit{q}(s,u)$ is traced by moving the profile curve $\mathit{x}\left(u\right)$ over the spine curve $\mathit{\beta }\left(s\right)$ with the parameters given by $A\left(s\right)$. The profile curve $\mathit{x}\left(u\right)$ is in the 2D or 3D space which moves the spine curve $\mathit{\beta }\left(s\right)$ through sweeping. Evidently, the sweeping method leaves the decorator with one degree of freedom, as it is still conceivable to rotate the type-3 Bishop frame ${\mathit{e}}_1$.

Remark 1.

Evidently, if $\mathit{\beta }\left(s\right)$ is a straight line, the sweeping surface is a circular cylinder with $\mathit{\beta }\left(s\right)$ as the symmetry axis. Furthermore, if $\mathit{\beta }\left(s\right)$ is a circle, the sweeping surface is a torus.

We now resolve the correlation through the regularity of $\mathit{\beta }\left(s\right)$ and the appropriate sweeping surface. Next, we can presume the profile curve x(u) is a unit speed curve, i.e., ${\stackrel{.}{x}}_1^2+{\stackrel{.}{x}}_2^2=1$. In the following, we employ a “dot” to indicate the differentiation regarding the arc length parameter of $\mathit{x}\left(u\right)$. Then,

$$\left.\begin{array}{c}{\mathit{q}}_s(s,u)=(1-x_1{\kappa }_1+x_2{\kappa }_2){\mathit{e}}_1,\\ {\mathit{q}}_u(s,u)={\stackrel{.}{x}}_1{\mathit{\zeta }}_1+{\stackrel{.}{x}}_2{\mathit{\zeta }}_2,\end{array}\right\}$$

(9)

and

$$\mathit{n}(s,u):=\frac{{\mathit{q}}_u\times {\mathit{q}}_s}{∥{\mathit{q}}_u\times {\mathit{q}}_s∥}={\stackrel{.}{x}}_2{\mathit{\zeta }}_1-{\stackrel{.}{x}}_1{\mathit{\zeta }}_2.$$

(10)

Since $<{\mathit{n},\mathit{e}}_1>=0$, the above equation shows that the surface normal $\mathit{n}(s,u)$ lies in the normal plane of $\mathit{\beta }\left(s\right)$. Thus, the surface normal and the principal normal of $\mathit{x}\left(u\right)$ are identical. Hence, the profile curve $\mathit{x}\left(u\right)$ is a geodesic curve on M.

Proposition 1.

Let x be a point in the normal plane of the spine curve $\mathit{\beta }\left(s\right)$. The tangent vector of its trajectory $\mathit{\beta }\left(s\right)+A\left(s\right)\mathit{x}\left(u\right)$, which is created by the type-3 Bishop frame, is constantly parallel to the tangent vector ${\mathit{e}}_1$ of the spine curve $\mathit{\beta }\left(s\right)$.

From Equation (9), the coefficients of the first fundamental form $g_{11}$, $g_{12}$ and $g_{22}$ are specified by

$$\left.\begin{array}{c}{g}_{11}=<{\mathit{q}}_{\mathit{s}},{\mathit{q}}_{\mathit{s}}>={(1-x_1{\kappa }_1+x_2{\kappa }_2)}^2,\hfill \\ g_{12}=<{\mathit{q}}_s,{\mathit{q}}_u>=0,g_{22}=<{\mathit{q}}_u,{\mathit{q}}_u>=1.\hfill \end{array}\right\}$$

Furthermore, we have

$$\left.\begin{array}{c}{\mathit{q}}_{ss}=\left(-x_1{\kappa }_1^{{}^{\prime }}+x_2{\kappa }_2^{{}^{\prime }}\right){\mathit{e}}_1+(1-x_1{\kappa }_1+x_2{\kappa }_2)({\kappa }_1{\mathit{\zeta }}_1-{\kappa }_2{\mathit{\zeta }}_2),\hfill \\ {\mathit{q}}_{su}=(-{\stackrel{.}{x}}_1{\kappa }_1+{\stackrel{.}{x}}_2{\kappa }_2){\mathit{e}}_1,\hfill \\ {\mathit{q}}_{uu}={\stackrel{..}{x}}_1{\mathit{\zeta }}_1+{\stackrel{..}{x}}_2{\mathit{\zeta }}_2.\hfill \end{array}\right\}$$

Then, the coefficients of the second fundamental form $h_{11}$, $h_{12}$ and $h_{22}$ are specified by

$$\left.\begin{array}{c}{h}_{11}=<{\mathit{q}}_{ss},n>=(1-x_1{\kappa }_1+x_2{\kappa }_2)({\kappa }_1{\stackrel{.}{x}}_2+{\stackrel{.}{x}}_1{\kappa }_2),\hfill \\ h_{12}=<{\mathit{q}}_{su},n>=0,h_{22}=<{\mathit{q}}_{uu},n>={\stackrel{.}{x}}_2{\stackrel{..}{x}}_1-{\stackrel{.}{x}}_1{\stackrel{..}{x}}_2.\hfill \end{array}\right\}$$

Then, the u and s curves of M are curvature lines ($g_{12}=0$ and $h_{12}=0$). Furthermore, the curve

$$\pi \left(u\right):\mathit{\zeta }\left(u\right):=\mathit{q}(u,s_0)=\mathit{\beta }\left(s_0\right)+x_1\left(u\right){\mathit{\zeta }}_1\left(s_0\right)+x_2\left(u\right){\mathit{\zeta }}_2\left(s_0\right)$$

(11)

is a planar unit speed curvature line. Equation (11) describes a set of one-parameter pencil of planes in ${\mathbb{E}}^3$. It is clear that

$${\mathit{t}}_{\mathit{\zeta }}\left(u\right)={\stackrel{.}{x}}_1\left(u\right){\mathit{\zeta }}_1\left(s_0\right)+{\stackrel{.}{x}}_2\left(u\right){\mathit{\zeta }}_2\left(s_0\right)$$

is the unit tangent vector to $\mathit{\zeta }\left(u\right)$. Thus, the principal unit normal vector is specified by

$${\mathit{n}}_{\mathit{\zeta }}\left(u\right)={\mathit{t}}_{\mathit{\zeta }}\left(u\right)\times {\mathit{e}}_1\left(s_0\right)={\stackrel{.}{x}}_2{\mathit{\zeta }}_1-{\stackrel{.}{x}}_1{\mathit{\zeta }}_2=\mathit{n}(s_0,u).$$

Hence, we have $\mathit{n}(s_0,u)\Vert {\mathit{n}}_{\mathit{\zeta }}\left(u\right)$; that is, the curve $\mathit{\zeta }\left(u\right)$ is a geodesic planar curvature line on $\mathit{q}(u,s_0)$. Surfaces for which parametric curves are curvature lines have a distinct impact on geometric layout [2,3,4,5,6]. In the case of sweeping surfaces, the offset surfaces ${\mathit{q}}_f(u,s)=\mathit{q}(u,s)+f\mathit{n}(s,u)$ of a specified surface $\mathit{q}(u,s)$ must be at a specific distance f. As a consequence, the offsetting style of a sweeping surface can be turned into the offsetting of planar profile curve, which is much simpler to deal with.

Hence, we can state the following proposition.

Proposition 2.

Suppose that ${\mathit{x}}_f\left(u\right)$ is the planar offset of the profile $\mathit{x}\left(u\right)$ at distance f. Then, the offset surface ${\mathit{q}}_f(u,s)$ is still a sweeping surface created due to the profile curve ${\mathit{x}}_f\left(u\right)$ and spine curve $\mathit{\beta }\left(s\right)$.

3.1. Singularity and Convexity

Singularity and convexity are beneficial for sweeping surfaces. We can specify that M has singular points if and only if

$$∥{\mathit{q}}_u\times {\mathit{q}}_s∥=1-x_1{\kappa }_1+x_2{\kappa }_2=0,$$

from which we have

$$\sigma -x_{1}cos\vartheta +x_{2}sin\vartheta =0,$$

where $\sigma \left(s\right)={ϵ}_1{}^{-1}$ is the radius of curvature of $\mathit{\beta }\left(s\right)$. By $\sigma \left(s\right)$, we have

$$x_1=\sigma \left(s\right)cos\vartheta ,x_2=\sigma \left(s\right)sin\vartheta .$$

Via its kinematic characteristics, the singular points occur at the intersection between the profile curve $\mathit{x}=\mathit{x}\left(u\right)$ and the curvature axis (alternation axis); that is,

$$L\left(u\right)=\{(x_1,x_2)\mid \sigma -x_{1}cos\vartheta +x_{2}sin\vartheta =0).$$

Thus, the sweeping surface has 2nd order osculation with the revolving surface traced by rotating the profile curve $x=x\left(u\right)$ about $L\left(u\right)$. Hence, we attain the following corollary.

Corollary 1.

The sweeping surface M specified by Equation (8) has no singular points if

$$\sigma -x_{1}cos\vartheta +x_{2}sin\vartheta \ne 0$$

is satisfied for all s and u.

In computer-aided geometric design, the situations that lead to the convexity of a surface are preferable in particular applications (such as industrialization of sculptured surfaces or layered processing). For the sweeping surface M, convexity can be only be designed with the assistance of differential geometric characteristics. Therefore, we studied the Gaussian curvature $K(s,u)={\chi }_1{\chi }_2$; ${\chi }_i(s,u)$ ($i=1,2$) as the principal curvature in the following. Since $g_{12}=h_{12}=0$, the value of one principal curvature is

$${\chi }_1(s_0,u)=\frac{∥\stackrel{.}{x}\times \stackrel{..}{x}∥}{{∥\stackrel{.}{x}∥}^2}={\stackrel{.}{x}}_1{\stackrel{..}{x}}_2-{\stackrel{.}{x}}_2{\stackrel{..}{x}}_1.$$

(12)

The curvature of the isoparametric s-curves (u-constant) is

$$\chi (s,u_0)=\frac{∥{\mathit{q}}_s\times {\mathit{q}}_{ss}∥}{{∥{\mathit{q}}_s∥}^2}=\frac{1}{\sigma -x_{1}cos\vartheta +x_{2}sin\vartheta }.$$

(13)

From Equations (5) and (10), we have:

$$\mathit{n}(s,u)=cos\phi {\mathit{e}}_2+sin\phi {\mathit{e}}_3,\mathrm{with}\phi ={tan}^{-1}\left(\frac{{\stackrel{.}{x}}_{2}sin\vartheta -{\stackrel{.}{x}}_{1}cos\vartheta }{{\stackrel{.}{x}}_{2}cos\vartheta +{\stackrel{.}{x}}_{1}sin\vartheta }\right).$$

(14)

In view of Meusnier’s Theorem, the principal curvature ${\chi }_2(s,u)$ is linked to $\chi (s,u)$ as [1,2,3]:

$${\chi }_2=\chi (s,u)cos\phi ;\phi ={tan}^{-1}\left(\frac{{\stackrel{.}{x}}_{2}sin\vartheta -{\stackrel{.}{x}}_{1}cos\vartheta }{{\stackrel{.}{x}}_{2}cos\vartheta +{\stackrel{.}{x}}_{1}sin\vartheta }\right).$$

(15)

Hence, the Gaussian curvature $K(s,u)$ can be described as:

$$K(s,u)=\frac{h_{11}{h}_{22}-h_{12}^2}{g_{11}{g}_{22}-g_{12}^2}={\chi }_1(s,u)\chi (s,u)cos\phi .$$

(16)

We now aim to locate the curves on M that are created by parabolic curves; that is, points with $K(s,u)=0$. These curves separate elliptic ($K>0$, locally convex) and hyperbolic ($K<0$, non-convex) sections of the surface. Then, from Equation (16), it follows that

$$K(s,u)=0\iff {\chi }_1(s,u)\chi (s,u)cos\phi =0.$$

(17)

It can be considered that there are three cases which output parabolic curves. Case (1) occurs when ${\chi }_1=0$. If ${\chi }_1=0$, the profile curve $\mathit{x}=\mathit{x}\left(u\right)$ becomes a straight line. From Equation (13), it can be considered that

$${\chi }_1=0\iff \stackrel{.}{\mathit{x}}\times \stackrel{..}{\mathit{x}}=\mathbf{0}\iff \stackrel{.}{\mathit{x}}\Vert \stackrel{..}{\mathit{x}},$$

which infers that an inflection or flat point in the profile curve creates a parabolic curve where $s=$ const. on portions of the surface. Case (2) occurs when $\chi (s,u)=0$. Thus, an infection or flat point of the spine curve produces an isoparametric parabolic curve where u = const. on the sweeping surface. Case (3) occurs when $\phi =\pi /2$. Owing to Equations (12) and (15), these parabolic curves are characterized by

$${\stackrel{.}{x}}_{2}sin\vartheta +{\stackrel{.}{x}}_{1}cos\vartheta =0$$

(18)

for all s and u. In this case, the spine curve $\mathit{\beta }$ is not only a curvature line but also a geodesic curve on the surface. By means of integrating Equation (18), the following can be obtained

$$x_{2}sin\vartheta +x_{1}cos\vartheta =h\left(s\right),$$

where $h=h\left(s\right)$ is any differentiable function. Then, we have the solutions

$$x_1=h\left(s\right)cos\vartheta ,x_2=h\left(s\right)sin\vartheta .$$

(19)

If Equation (19) is substituted into Equation (8), using Equation (4), we instantly find that the parabolic curve is

$$\mathit{\gamma }\left(s\right)=\mathit{\beta }\left(s\right)+h\left(s\right){\mathit{e}}_3\left(s\right).$$

(20)

From the above analysis, the following conclusions can be reached.

Corollary 2.

Let M be a sweeping surface with spine and profile curves with non-vanishing curvatures anywhere. Then, M has one fully parabolic curve if and only if the spine curve is a geodesic curvature line.

3.2. Developable Surfaces

A developable surface can be briefly described as a specific case of a ruled surface. Such a surface has particular applications, for instance, in the manufacture of automobile body parts and ship hulls. Then, we investigate the case that the profile curve $\mathit{x}=\mathit{x}\left(u\right)$ is reduced into a line, i.e., $\mathit{x}\left(u\right)=(0,$$u,0)$. In this case, Equation (8) can be written as

$$S:\mathit{y}(s,u)=\mathit{\beta }\left(s\right)+u{\mathit{\zeta }}_2\left(s\right),u\in \mathbb{R}.$$

(21)

It is evident that S is a developable ruled surface, i.e.,

$$\det ({\mathit{\beta }}^{{}^{\prime }}\left(s\right),{\mathit{\xi }}_2\left(s\right),{\mathit{\xi }}_2^{{}^{\prime }}\left(s\right))=0.$$

Via Proposition 1, all tangent vectors ${\mathit{y}}_s(s,u)$ of the ruled surface for a fixed s are parallel to ${\mathit{\beta }}^{{}^{\prime }}\left(s\right)$. Furthermore, the creators of S are the curvature lines. Hence, we are led to the following proposition.

Proposition 3.

If the profile curve $\mathit{x}\left(u\right)$ becomes a straight line, then the sweeping surface is a developable surface.

Furthermore, from Equation (8), we obtain the developable surface

$$S^{\perp }:{\mathit{y}}^{\perp }(s,u)=\mathit{\beta }\left(s\right)+u{\mathit{\zeta }}_1\left(s\right),u\in \mathbb{R}.$$

(22)

It is clear that $\mathit{y}(s,0)=\mathit{\beta }\left(s\right)$ (${\mathit{y}}^{\perp }(s,0)=\mathit{\beta }\left(s\right)$), $0\le s\le L$; that is, the surface S ($S^{\perp }$) interpolates the curve $\mathit{\beta }\left(s\right)$. In addition, since

$${\mathit{y}}_s\times {\mathit{y}}_u:=-\left(1-u{ϵ}_2\right){\mathit{\zeta }}_1\left(s\right),$$

(23)

then $S^{\perp }$ is the normal developable surface of S along $\mathit{\beta }\left(s\right)$. Thus, the surface S ($S^{\perp }$) interpolates the curve $\mathit{\beta }\left(s\right)$, and $\mathit{\beta }\left(s\right)$ is a curvature line of S ($S^{\perp }$).

Theorem 1.

Let M be the sweeping surface in Equation (8). Then,

(1)S and $S^{\perp }$ intersect at a right angle along $\mathit{\beta }\left(s\right)$ and(2)$\mathit{\beta }\left(s\right)$ is a mutual curvature line of S and $S^{\perp }$.

Theorem 2

(Existence and uniqueness). Let S be a developable surface, Equation (21). Then, there exists a unique developable surface described by Equation (21).

Proof. 

The existence it is clear. We have the developable surface represented by Equation (21). For the uniqueness, we suppose that

$$\left.\begin{array}{c}S:\mathit{y}(s,u)=\mathit{\beta }\left(s\right)+u\mathit{\eta }\left(s\right),u\in \mathbb{R},\hfill \\ \\ \mathit{\eta }\left(s\right)={\eta }_1\left(s\right){\mathit{\zeta }}_1+{\eta }_2\left(s\right){\mathit{\zeta }}_2+{\eta }_3\left(s\right){\mathit{e}}_1,\hfill \\ \\ {∥\mathit{\eta }\left(s\right)∥}^2={\eta }_1^2+{\eta }_2^2+{\eta }_3^2=1,{\mathit{\eta }}^{{}^{\prime }}\left(s\right)\ne \mathbf{0}.\hfill \end{array}\right\}$$

(24)

Since S is developable, then we have

$$det({\mathit{\beta }}^{\prime },\mathit{\eta },{\mathit{\eta }}^{\prime })=0\iff {\eta }_1{\eta }_2^{{}^{\prime }}-{\eta }_2{\eta }_1^{{}^{\prime }}-{\eta }_3\tau \left({\eta }_{2}cos\vartheta +{\eta }_{1}sin\vartheta \right)=0.$$

(25)

On the other hand, in Equation (23), we have:

$$\left({\mathit{y}}_s\times {\mathit{y}}_u\right)\left(s,u\right)=-\varphi \left(s,u\right){\mathit{\zeta }}_1,$$

(26)

where $\varphi =\varphi \left(s,u\right)$ is a differentiable function. Then, the normal vector ${\mathit{y}}_s\times {\mathit{y}}_v$ at the point $(s,0)$ is

$$\left({\mathit{y}}_s\times {\mathit{y}}_u\right)(s,0)=-{\eta }_2{\mathit{\zeta }}_1+{\eta }_1{\mathit{\zeta }}_2.$$

(27)

Thus, from Equations (26) and (27), one finds that

$${\eta }_1=0\mathrm{and}{\eta }_2=\psi \left(s,0\right),$$

(28)

which, following from Equation (25), implies that ${\eta }_2{\eta }_3\tau cos\vartheta =0$, leading to ${\eta }_2{\eta }_3=0$, with $\tau \ne 0$. If $(s,0)$ is a regular point (i.e., $\varphi \left(s,0\right)\ne 0$), then ${\eta }_2\left(s\right)\ne 0$ and ${\eta }_3=0$. Thence, we attain $\mathit{\eta }\left(s\right)={\mathit{\zeta }}_2$. This suggests that the orientation of $\mathit{\eta }\left(s\right)$ is equal to the orientation of ${\mathit{\zeta }}_2\left(s\right)$.

However, let M have a singular point at $(s_0,0)$. Then, $\varphi \left(s_0,0\right)={\eta }_2\left(s_0\right)={\eta }_1\left(s_0\right)=0$, and we have $\mathit{\eta }\left(s_0\right)={\eta }_3\left(s_0\right){\mathit{e}}_2\left(s_0\right)$. If the singular point $\mathit{\beta }\left(s_0\right)$ in the closure of the set of points where S is developable on $\mathit{\beta }\left(s\right)$ is regular, then there exists a point $\mathit{\beta }\left(s\right)$ in any neighborhood of $\mathit{\beta }\left(s_0\right)$ such that the uniqueness of S holds at $\mathit{\beta }\left(s\right)$. Beyond the limit $s\to s_0$, the developable surface is unique at $s_0$. Suppose that there exists an open interval J$\subseteq I$ such that S is singular at $\mathit{\beta }\left(s\right)$ for any $s\in J$. Then, $y(s,u)=\mathit{\beta }\left(s\right)+u{\eta }_3\left(s\right){\mathit{e}}_1\left(s\right)$ for any $s\in J$. This suggests that ${\eta }_1\left(s\right)={\eta }_2\left(s\right)=0$ for $s\in J$. It follows that

$$\left({\mathit{y}}_s\times {\mathit{y}}_u\right)(s,u)=\tau u{\eta }_2^2\left(cos\vartheta {\mathit{\zeta }}_2+sin\vartheta {\mathit{\zeta }}_1\right).$$

Thus, the above vector is directed to ${\mathit{\zeta }}_1$, i.e., ${\mathit{y}}_s\times {\mathit{y}}_u\Vert {\mathit{\zeta }}_1\left(s\right)$, if and only if $\vartheta =\pi /2$ for any $s\in J$. In this case, $\mathit{\eta }\left(s\right)=\pm {\mathit{\zeta }}_2$. This suggests that uniqueness holds. □

For a developable surface S, as an application (such as cylindrical milling or flank milling), by the movement of the type-3 Bishop frame, a cylindrical cutter can be rigidly joined with this frame. Then, the equation of a pencil of cylindrical cutters, which is located by the movement of the cylindrical cutter on $\mathit{\beta }\left(s\right)$, can be obtained as follows:

$$S_f:\overline{\mathit{y}}(s,u)=\mathit{y}(s,u)+f{\mathit{\zeta }}_1\left(s\right),$$

(29)

where f indicates the cylindrical cutter radius. This surface is a developable surface offset of the surface $\mathit{y}(s,u)$. The equation of $S_f$ can then be written as

$$S_f:\overline{\mathit{y}}(s,u)=\mathit{\beta }\left(s\right)+u{\mathit{\zeta }}_2\left(s\right)+f{\mathit{\zeta }}_1\left(s\right).$$

(30)

The normal vector of cylindrical cutter can be obtained as:

$${\mathit{n}}_f(s,0)=\frac{{\overline{\mathit{y}}}_s\times {\overline{\mathit{y}}}_u}{∥{\overline{\mathit{y}}}_s\times {\overline{\mathit{y}}}_u∥}={\mathit{\zeta }}_1(s).$$

(31)

In addition, from Equation (29), we have:

$$S:\mathit{y}(s,u)=\overline{\mathit{y}}(s,u)-f{\mathit{\zeta }}_1\left(s\right).$$

(32)

The derivative of Equation (30) with respect to s can be obtained by:

$${\overline{\mathit{y}}}_s(s,u)={\mathit{y}}_s(s,u)-\left(f\mathit{\psi }\right)\times {\mathit{\zeta }}_1.$$

(33)

From Equation (30), we can see that the vector ${\overline{\mathit{y}}}_s(s,u)$ is orthogonal to the normal vector ${\mathit{\zeta }}_1$. Furthermore, the vector ${\mathit{\zeta }}_1$ is orthogonal to the tool axis vector ${\mathit{e}}_1\left(s\right)$. As a result of this equation, the envelope surface of the cylindrical cutter and the developable surface $\mathit{y}(s,u)$ have a mutual normal vector and the distance between the two surfaces is the cylindrical cutter radius f.

Hence, we can come to the following conclusion.

Proposition 4.

Let $S_f$ be the envelope surface of cylindrical cutter at distance f. Then, the two surfaces S and $S_f$ are offset developable surfaces.

Now, once more, since S is a developable surface, then

$$det({\mathit{\beta }}^{{}^{\prime }},{\mathit{\zeta }}_2{,\mathit{\zeta }}_2^{{}^{\prime }})=0\iff <{\mathit{\beta }}^{{}^{\prime }},{\mathit{\zeta }}_2\times {\mathit{\zeta }}_2^{{}^{\prime }}>=0.$$

(34)

Hence, two main cases occur when developabilty are treated. Case (a) occurs when

$${\mathit{\zeta }}_2\times {\mathit{\zeta }}_2^{{}^{\prime }}=0\iff {ϵ}_{1}sin\vartheta {\mathit{\zeta }}_1=0.$$

(35)

In this case, the surface M is a cylindrical surface. Since ${\mathit{\zeta }}_1$ is a non-zero unit vector, then S is a cylindrical surface if and only if $sin\vartheta =0\iff \vartheta \left(s\right)=0$ or $\pi$. However, in any case, we have ${\vartheta }^{{}^{\prime }}=0$, then ${ϵ}_2\left(s\right)=0$. Consequently, $\mathit{\beta }$ is a plane curve and the surface S is a binormal surface.

Corollary 3.

S is a cylindrical surface if and only if $\vartheta \left(s\right)=0$.

Case (b) occurs when

$${\mathit{\zeta }}_2\times {\mathit{\zeta }}_2^{{}^{\prime }}\ne 0.$$

(36)

In this case, S is a non-cylindrical surface. The 1st differentiation of the directrix is

$${\mathit{\beta }}^{{}^{\prime }}\left(s\right)=c^{{}^{\prime }}\left(s\right)+\mu \left(s\right){\mathit{\zeta }}_2^{{}^{\prime }}\left(s\right)+{\mu }^{{}^{\prime }}\left(s\right){\mathit{\zeta }}_2\left(s\right),$$

(37)

where $c^{{}^{\prime }}$ is the 1st differentiation of the striction curve and $\mu \left(s\right)$ is a smooth function [1, 2]. Substituting Equation (37) into Equation (34) gives:

$$<{\mathit{\zeta }}_2\times {\mathit{\zeta }}_2^{{}^{\prime }},c^{{}^{\prime }}>=0.$$

(38)

It can be considered that there are two cases that Equation (38) can be true for all values of s. The first case is when $c^{{}^{\prime }}=0$. Geometrically, this case suggests that the striction curve becomes a point and S turns into a cone; the striction point of the cone is generally designated as the vertex. In this case, from Equation (37), we obtain $\mu {\kappa }_2=1$ and ${\mu }^{{}^{\prime }}=0$, which implies that

$$\mu =const.=\frac{1}{{ϵ}_{1}sin\vartheta }\iff {ϵ}_{1}sin\vartheta ={ϵ}_{1_0}sin{\vartheta }_0,$$

(39)

where ${\vartheta }_0=\vartheta \left(0\right)$ and ${ϵ}_{1_0}={ϵ}_1\left(0\right)$. Then, if $\vartheta$ is a stationary, i.e., ${ϵ}_2=0$, then the curve is a plane curve with a stationary curvature. Similarly, if ${ϵ}_1$ is also stationary, we can have ${ϵ}_2=0$ and $\vartheta$ as stationary. Then, the curve $\mathit{\beta }\left(s\right)$ is the arc of a circle.

Corollary 4.

S is a cone if and only if ${ϵ}_{1}sin\vartheta ={ϵ}_{1_0}sin{\vartheta }_0$, ${\vartheta }_0=\vartheta \left(0\right)$ and ${ϵ}_{1_0}={ϵ}_1\left(0\right)$.

The second case is when $c^{{}^{\prime }}\ne 0$, i.e., ${ϵ}_{1}sin\vartheta \ne {ϵ}_{1_0}sin{\vartheta }_0$. From Equation (38), $c^{{}^{\prime }}$ is orthogonal to ${\mathit{\zeta }}_2\times {\mathit{\zeta }}_2^{{}^{\prime }}$, and therefore $c^{{}^{\prime }}$ is in the plane spanned by ${\mathit{\zeta }}_2$ and ${\mathit{\zeta }}_2^{{}^{\prime }}$. The condition for c to be striction curve is thus suggestive that $<c^{\prime },{\mathit{\zeta }}_2^{\prime }>=0$. Thus, we may infer that the creator is parallel to the first derivative of the striction curve, which is also the tangent of the striction curve. This ruled surface is named a tangent ruled surface.

Corollary 5.

S is a tangent surface if and only if ${ϵ}_{1}sin\vartheta \ne {ϵ}_{1_0}sin{\vartheta }_0$${\vartheta }_0=\vartheta \left(0\right)$ and ${ϵ}_{1_0}={ϵ}_1\left(0\right)$.

3.3. Application

In what follows, as an implementation of our major results, we give the following examples.

Example 1.

Let us take the unit speed circular helix

$$\mathit{\alpha }\left(s\right)=\frac{1}{\sqrt{2}}(-coss,-sins,s),-\pi \le s\le \pi .$$

Then,

$$\left.\begin{array}{c}{\mathit{\xi }}_1\left(s\right)=\frac{1}{\sqrt{2}}(sins,-coss,1),\hfill \\ {\mathit{\xi }}_2\left(s\right)=(coss,sins,0),\hfill \\ {\mathit{\xi }}_3\left(s\right)=\frac{1}{\sqrt{2}}(-sins,coss,1),\hfill \\ \kappa \left(s\right)=\tau \left(s\right)=\frac{1}{\sqrt{2}}.\hfill \end{array}\right\}$$

Via Definition 1 and Equation (2), we have

$$\left.\begin{array}{c}\mathit{\beta }\left(s\right)=(sins,-coss,0),\hfill \\ {\mathit{e}}_1\left(s\right)=(coss,sins,0),\hfill \\ {\mathit{e}}_2\left(s\right)=(-sins,coss,0),\hfill \\ {\mathit{e}}_3\left(s\right)=(0,0,1),\hfill \\ {ϵ}_1\left(s\right)=1,\mathrm{and}{ϵ}_2\left(s\right)=0.\hfill \end{array}\right\}$$

(40)

Now, we will gain the type-3 Bishop frame $\{{\mathit{e}}_1\left(s\right),{\mathit{\zeta }}_1\left(s\right),$${\mathit{\zeta }}_2\left(s\right)\left)\right\}$ in the following. From ${ϵ}_1\left(s\right)=1$ and ${ϵ}_2\left(s\right)=0$, we find $\vartheta \left(s\right)$ is a stationary. Clearly, if $\vartheta \left(s\right)=0$ or $\pi$, the developable surface S is a cylinder.

(A) By letting $\vartheta \left(s\right)=0$, for example, the type-3 Bishop frame can be gained as ${\mathit{\zeta }}_1\left(s\right)={\mathit{e}}_2\left(s\right),$${\mathit{\zeta }}_2\left(s\right)={\mathit{e}}_3\left(s\right)$. The parametric form of the sweeping surface family can be written as

$$M:\mathit{q}(s,u)=(sins-x_{1}sins,-coss+x_{1}coss,x_2).$$

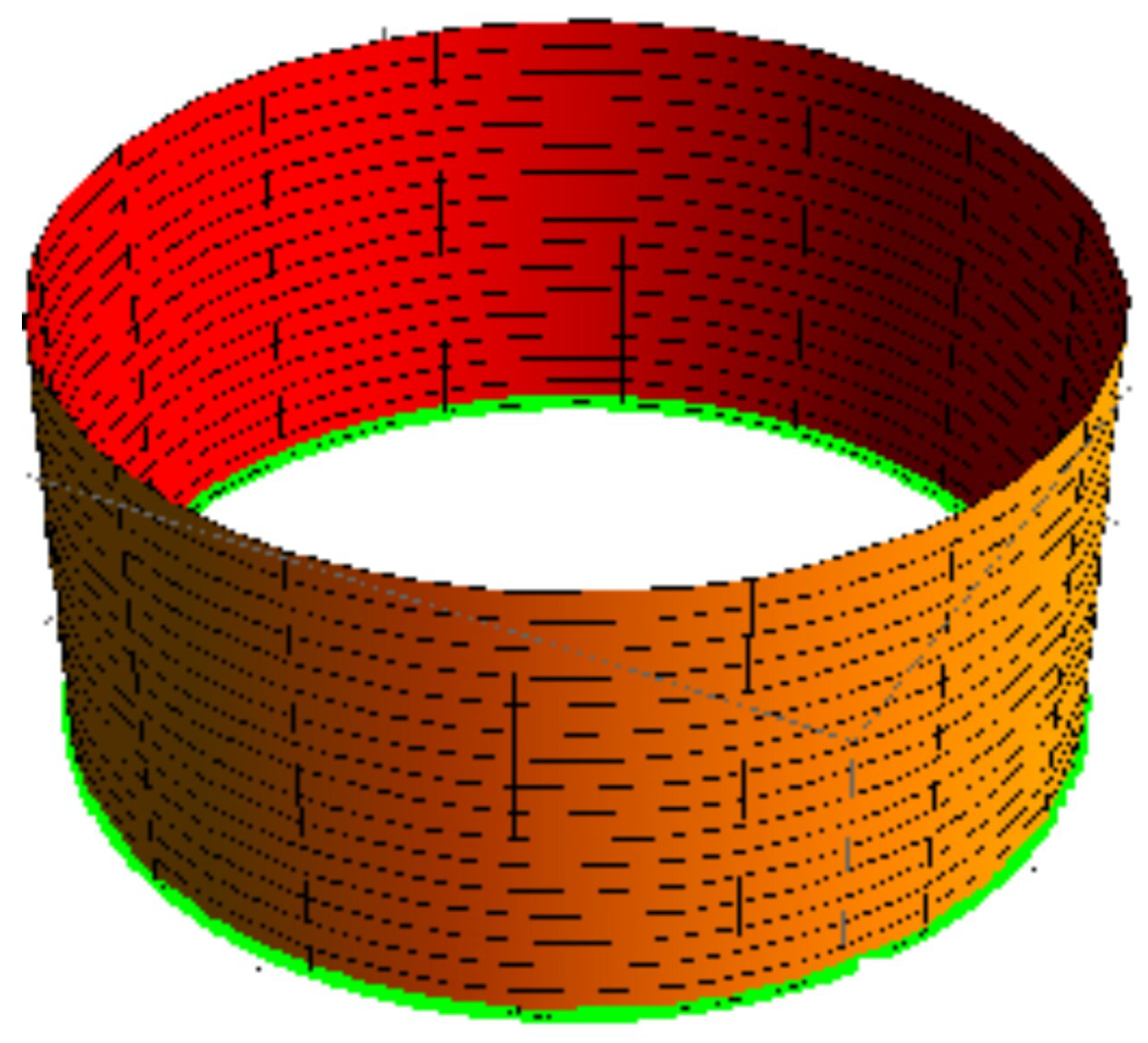
For $x_1\left(u\right)=cosu,$$x_2\left(u\right)=sinu$ and $0\le s,u\le 2\pi$, the sweeping surface is displayed in Figure 1. The developable surface

$$S:\mathit{y}(s,u)=(sins,-coss,u)$$

is a cylinder, where for $0\le s\le 2\pi$ and $0\le u\le 1$, the surface is shown in Figure 2.

(B) For $\vartheta \left(s\right)=\frac{\pi }{4}$, the type-3 Bishop frame can be obtained as

$$\left(\begin{array}{c}{\mathit{e}}_1\left(s\right)\hfill \\ {\mathit{\zeta }}_1\left(s\right)\hfill \\ {\mathit{\zeta }}_2\left(s\right)\hfill \end{array}\right)=\left(\begin{array}{ccc}1\hfill & 0\hfill & 0\hfill \\ 0\hfill & \frac{1}{\sqrt{2}}\hfill & \frac{1}{\sqrt{2}}\hfill \\ 0\hfill & -\frac{1}{\sqrt{2}}\hfill & \frac{1}{\sqrt{2}}\hfill \end{array}\right)\left(\begin{array}{c}{\mathit{e}}_1\left(s\right)\hfill \\ {\mathit{e}}_2\left(s\right)\hfill \\ {\mathit{e}}_3\left(s\right)\hfill \end{array}\right).$$

(41)

Hence, from Equations (40) and (41), we have

$${\mathit{\zeta }}_1\left(s\right)=\frac{1}{\sqrt{2}}(-sins,coss,1),\mathrm{and}{\mathit{\zeta }}_2\left(s\right)=\frac{1}{\sqrt{2}}(sins,-coss,-1).$$

Thus, the parametric form of the sweeping surface family can be written as

$$M:\mathit{q}(s,u)=\left(sins,-coss,0\right)+\frac{1}{\sqrt{2}}\left(\begin{array}{c}\sqrt{2}\left(-x_1+x_2\right)sins\hfill \\ \left(x_1-x_2\right)sins\hfill \\ x_1-x_2\hfill \end{array}\right).$$

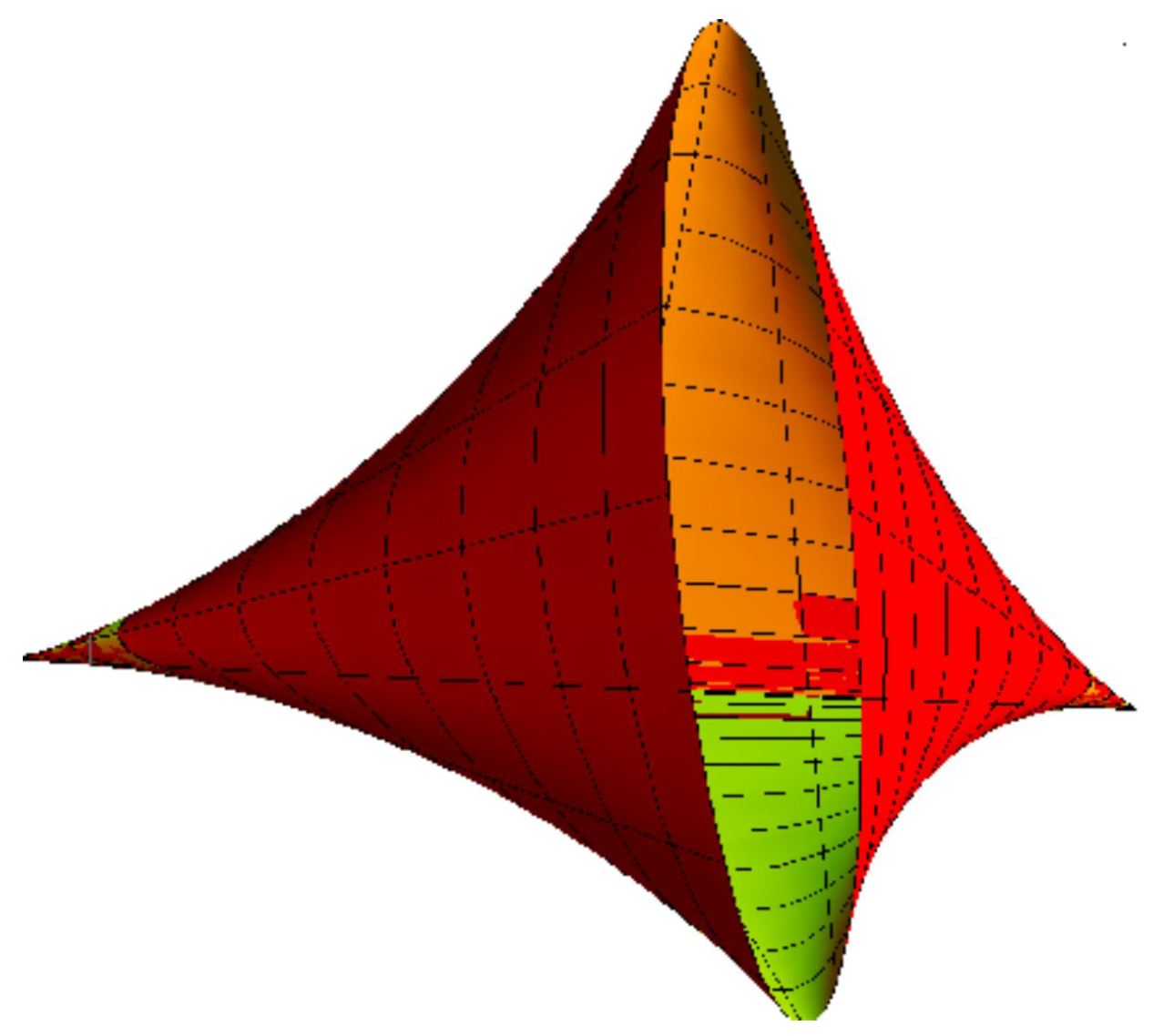
For $x_1\left(u\right)=cosu,$$x_2\left(u\right)=sinu$ and $0\le s,u\le 2\pi$, the sweeping surface is shown in Figure 3. Furthermore, the developable surface

$$S:\mathit{y}(s,u)=\left(\left(1+\frac{u}{\sqrt{2}}\right)sins,-\left(1+\frac{u}{\sqrt{2}}\right)coss,-\frac{u}{\sqrt{2}}\right)$$

is a cone, where for $0\le u\le 1$, the surface is shown in Figure 4.

Example 2.

Given the slant helix

$$\mathit{\alpha }\left(s\right)=(\frac{3coss}{4}+\frac{cos3s}{12},\frac{3sins}{4}+\frac{sin3s}{12},-\frac{\sqrt{3}coss}{2}),$$

then,

$$\left.\begin{array}{c}{\mathit{\xi }}_1\left(s\right)=\left(\frac{-3sins-sin3s}{4},\frac{3coss+cos3s}{4},\frac{\sqrt{3}sins}{2}\right),\hfill \\ {\mathit{\xi }}_2\left(s\right)=(\frac{-\sqrt{3}cos2s}{2},\frac{-\sqrt{3}sin2s}{2},\frac{1}{2}),\hfill \\ {\mathit{\xi }}_3\left(s\right)=\left(\frac{3coss-cos3s}{4},{sin}^{3}s,\frac{\sqrt{3}coss}{2}\right),\hfill \\ \kappa \left(s\right)=\sqrt{3}coss,\tau \left(s\right)=-\sqrt{3}sins.\hfill \end{array}\right\}$$

Similarly, we have:

$$\left.\begin{array}{c}\mathit{\beta }\left(s\right)=\left(\frac{-\sqrt{3}sin2s}{2},\frac{\sqrt{3}cos2s}{2},\frac{s}{2}\right),\hfill \\ {\mathit{e}}_1\left(s\right)=\left(\frac{-\sqrt{3}cos2s}{2},\frac{-\sqrt{3}sin2s}{2},\frac{1}{2}\right),\hfill \\ {\mathit{e}}_2\left(s\right)=\left(\frac{sin4s}{4},\frac{-3-cos4s}{4},-\frac{\sqrt{3}sin2s}{2}\right),\hfill \\ {\mathit{e}}_3\left(s\right)=\left(\frac{3-cos4s}{4},\frac{-coss-cos3s}{2},\frac{\sqrt{3}coss}{2}\right),\hfill \\ {ϵ}_1\left(s\right)=\sqrt{3}coss,\mathrm{and}{ϵ}_2\left(s\right)=-1.\hfill \end{array}\right\}$$

(42)

Then, $\vartheta \left(s\right)=s+{\vartheta }_0$. If we choose ${\vartheta }_0=0$, for example, the type-3 Bishop frame can be expressed as

$$\left(\begin{array}{c}{\mathit{e}}_1\left(s\right)\hfill \\ {\mathit{\zeta }}_1\left(s\right)\hfill \\ {\mathit{\zeta }}_2\left(s\right)\hfill \end{array}\right)=\left(\begin{array}{ccc}1\hfill & 0\hfill & 0\hfill \\ 0\hfill & cos\vartheta \hfill & sin\vartheta \hfill \\ 0\hfill & -sin\vartheta \hfill & cos\vartheta \hfill \end{array}\right)\left(\begin{array}{c}{\mathit{e}}_1\hfill \\ {\mathit{e}}_2\hfill \\ {\mathit{e}}_3\hfill \end{array}\right).$$

(43)

From this we find

$$\begin{array}{ccc}\hfill {\mathit{\zeta }}_1& =& \left(\begin{array}{c}{\zeta }_{11}\hfill \\ {\zeta }_{12}\hfill \\ {\zeta }_{13}\hfill \end{array}\right)=\left(\begin{array}{c}coss\frac{sin4s}{4}+\left(\frac{3-cos4s}{4}\right)sins\hfill \\ -\left(\frac{3+cos4s}{4}\right)coss-\left(\frac{coss+cos3s}{2}\right)sins\hfill \\ -\frac{\sqrt{3}}{2}sin2scoss+\frac{\sqrt{3}}{2}sinscoss\hfill \end{array}\right),\hfill \\ \hfill {\mathit{\zeta }}_2& =& \left(\begin{array}{c}{\zeta }_{21}\hfill \\ {\zeta }_{22}\hfill \\ {\zeta }_{23}\hfill \end{array}\right)=\left(\begin{array}{c}-sins\frac{sin4s}{4}+\left(\frac{3-cos4s}{4}\right)coss\hfill \\ -\left(\frac{3+cos4s}{4}\right)sins-\left(\frac{coss+cos3s}{2}\right)coss\hfill \\ -\frac{\sqrt{3}}{2}sin2ssins+\frac{\sqrt{3}}{2}cosssins\hfill \end{array}\right).\hfill \end{array}$$

By a similar procedure as in Example (1), the sweeping surface family can be written as

$$M:\mathit{q}(s,u)=\left(\frac{-\sqrt{3}sin2s}{2},\frac{\sqrt{3}cos2s}{2},\frac{s}{2}\right)+x_1\left(\begin{array}{c}{\zeta }_{11}\hfill \\ {\zeta }_{12}\hfill \\ {\zeta }_{13}\hfill \end{array}\right)+x_2\left(\begin{array}{c}{\zeta }_{21}\hfill \\ {\zeta }_{22}\hfill \\ {\zeta }_{23}\hfill \end{array}\right).$$

Figure 5 shows the surface when $x_1\left(u\right)=cosu,$$x_2\left(u\right)=sinu$ and $0\le s,u\le 2\pi$. Since we have ${ϵ}_{1}sin\vartheta \ne {ϵ}_{1_0}sin{\vartheta }_0$, the surface

$$S:\mathit{y}(s,u)=\left(\frac{-\sqrt{3}sin2s}{2},\frac{\sqrt{3}cos2s}{2},\frac{s}{2}\right)+u\left(\begin{array}{c}{\zeta }_{21}\hfill \\ {\zeta }_{22}\hfill \\ {\zeta }_{23}\hfill \end{array}\right)$$

is a tangent surface, where $0\le s\le \pi$ and $0\le u\le 1$ (see Figure 6).

4. Conclusions

This paper inspects the properties of sweeping surfaces due to type-3 Bishop frames at each point of the natural mate of a space curve. Consequently, we have resolved the problem of requiring a surface that is both a sweeping surface and a developable surface. Moreover, examples to illustrate the applications of the obtained formula are presented. There are different directions for further work. The methodology used here can be applied to sweeping surfaces in different spaces such as Lorentz–Minkowski spaces, isotropic spaces, etc. The authors plan to extend the study to different spaces and examine the classification of singularities as reported in [15,16,17,18].