Resolvability in Subdivision Graph of Circulant Graphs

Abstract

Circulant networks are a very important and widely studied class of graphs due to their interesting and diverse applications in networking, facility location problems, and their symmetric properties. The structure of the graph ensures that it is symmetric about any line that cuts the graph into two equal parts. Due to this symmetric behavior, the resolvability of these graph becomes interning. Subdividing an edge means inserting a new vertex on the edge that divides it into two edges. The subdivision graph G is a graph formed by a series of edge subdivisions. In a graph, a resolving set is a set that uniquely identifies each vertex of the graph by its distance from the other vertices. A metric basis is a resolving set of minimum cardinality, and the number of elements in the metric basis is referred to as the metric dimension. This paper determines the minimum resolving set for the graphs $H_l[1,k]$ constructed from the circulant graph $C_l[1,k]$ by subdividing its edges. We also proved that, for $k=2,3$, this graph class has a constant metric dimension.

1. Introduction and Preliminary Results

Metric dimension is a significant parameter in metric graph theory that has been employed in a wide range of graph theory applications, including facility location problems, pharmaceutical chemistry [1,2], long-range navigation aids, robot navigation in networks [3], combinatorial optimization [4], and sonar and coast guard Loran [5]. The metric dimension is the extension of affine dimension to any metric space (assuming a resolving set exists).

The distance $d(x,y)$ between two vertices $u,v\in V\left(G\right)$ in a connected graph G is the length of the shortest path between them. Let $W=\{x_1,x_2,x_3,\dots ,x_k\}$ represent an ordered set of G vertices and v represent an arbitrary G vertex. If each vertex of G can be uniquely identified by its distance from the vertices of W, the k-tuple $(d(v,x_1),d(v,x_2),d(v,x_3),\dots ,d(v,x_k))$ is the $r\left(v\right|W)$ representation of v with respect to W. If different vertices of G have different representations with respect to W, then W is known as a resolving set [1] or a locating set [5]. A basis for G is a resolving set of minimal cardinality, where cardinality is the metric dimension of G.

In response to the problem of uniquely identifying an intruder in a network, Slater [5,6] introduced the concept of metric dimension. Harary and Melter conducted independent research on the same concept in [7]. This invariant is discussed in [3] for network robot navigation, ref. [1] for chemistry, and [8] for pattern recognition and image processing problems, some of which involve the use of hierarchical data structures.

If all of the graphs in F have the same metric dimension (which is separate to l), F is identified as a family with a constant metric dimension.

Whenever the graph is a path, the metric dimension is one, and the metric dimension is two if the graph is cycle $C_l$. In [9,10,11], the metric dimension of some classes of regular graphs with constant metric dimensions is investigated.

Inserting a new vertex on an edge splits it in half. In the graph, this is referred to as subdivision. A subdivision graph G has edges that are subdivided. Subdivision is a method for reducing a complicated graph to a simple graph. A barycentric graph subdivision is one where every vertex is subdivided. A planar graph is one with no intersecting edges that can be drawn in a plane. Planar graphs require graph subdivision to be described. A planar graph G has only planar subdivisions.

The subdivision operation in planar graphs is demonstrated in the following theorem.

Theorem 1

([12]). A graph is planar if and only if it does not have a $K_5$ or $K_{3,3}$ subdivision.

In [9,13], the subdivision graphs are constructed from the circulant graph $C_l[1,k]$ and it is shown that this subdivision graph has a constant metric dimension for some values of l and k. In this paper, a new subdivision graph is constructed from the circulant graph $C_l[1,k]$ for $k\ge 2$. It is demonstrated that this subdivision graph has a constant metric dimension when $k=2$.

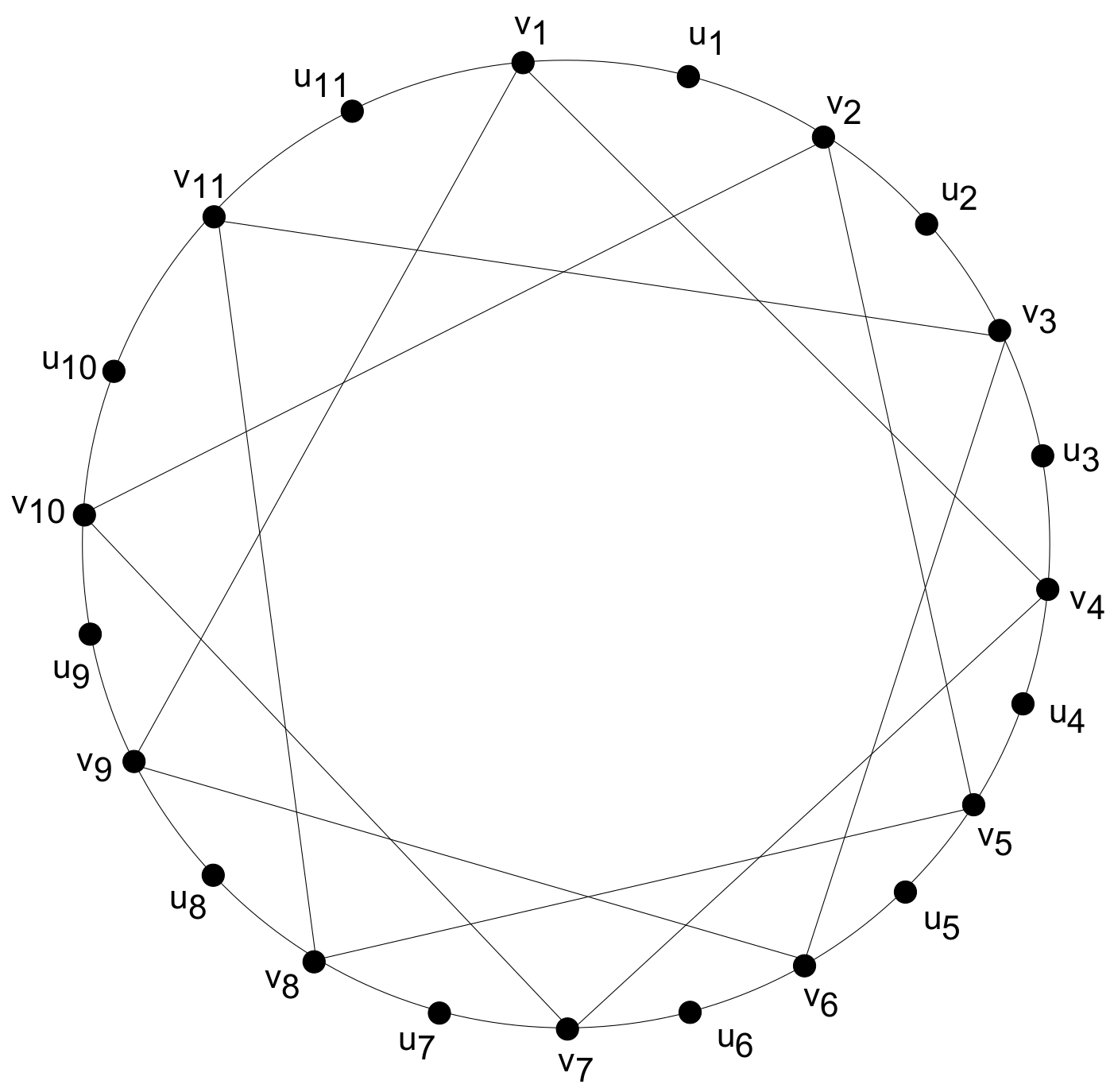
1.1. Metric Dimension of Subdivision of Circulant Graph $C_l[1,2]$

Circulant graphs are a popular type of graph in local area networks. Circulant graphs are defined as follows:

Let $n,m$ be natural numbers and $x_1,x_2,...,x_m$ be positive integers, with $1\le x_p\le \lfloor \frac{l}{2}\rfloor$ and $x_p\ne x_q$ for all $1\le p<q\le m$. The circulant graph is an undirected graph with the vertices $V=\{v_1,\dots ,v_l\}$ and the edge set $E=\{v_{p+x_q}:1\le p\le l,1\le q\le m$ (the indices are taken modulo l) and is denoted by $C_l[x_1,x_2...,x_m]$. The numbers $(x_1,x_2,\dots ,x_m)$ are known as generators. It is critical to observe that the circulant graphs are regular.

The graph $H_l[1,k]$ is formed by subdividing edges of the type $v_p{v}_{p+1}$. Let $u_p$ be the additional vertex in each edge $v_p{v}_{p+k}$. As a result, the graph $H_l[1,k]$ contains $2l$ vertices and $3l$ edges.

If $x_p$ and $x_q$ are two vertices of $H_l[1,k]$, then the distance between them is defined as $|p-q|$, where $1\le p<q\le l$. The vertices of the graph can be divided into two groups: U and V, where U is the set of added vertices and V is the set of vertices of type $v_p$.

The first theorem establishes that the metric dimension of the graph $H_l[1,2]$ is constant.

The following lemma offer a choice of the resolving set and will be useful in proving the main result of this section Figure 1.

Lemma 1.

If W is a resolving set of the graph $H_l[1,2]$, then at least one vertex from each of the set $\{v_1,v_3,v_5,\dots ,v_l\}$ and $\{v_2,v_4,v_6,\dots ,v_{l-1}\}$ must belong to W.

Proof. 

Assume, for the sake of argument, that l is odd. Now, if none of the vertexes in the set $\{v_2,v_4,v_6,\dots ,v_{l-1}\}$ belongs to W, then the representation of the following vertices will be the same:

$$\left\{\begin{array}{cc}r\left(u_l\right)=r\left(v_{l-1}\right)\hfill & \mathrm{if}{v}_2,v_4,v_6,\dots ,v_{\lceil \frac{l}{2}-1\rceil }\notin W\hfill \\ r(u_{\lceil \frac{l}{2}\rceil -1})=r(v_{\lceil \frac{l}{2}\rceil -2})\hfill & \mathrm{if}{v}_{\lceil \frac{l}{2}\rceil },\dots ,v_{l-1}\notin W\hfill \end{array}\right.$$

If none of the vertices in the set $\{v_1,v_3,v_5,\dots ,v_l\}$ belongs to W, then the representation of the following vertices will be the same:

$$\left\{\begin{array}{cc}r\left(u_1\right)=r\left(v_l\right)\hfill & \mathrm{if}{v}_1,v_3,v_5,\dots ,v_{\lceil \frac{l-1}{2}\rceil }\notin W\hfill \\ r\left(u_1\right)=r\left(v_3\right)\hfill & \mathrm{if}{v}_{\lceil \frac{l+1}{2}\rceil },\dots ,v_{l-1}\hfill \end{array}\right.$$

The proof is now complete. □

Theorem 2.

For $l\le 3$,

$dim\left(H_l[1,2]\right)=\left\{\begin{array}{cc}3\hfill & \mathrm{if}n=4t-1;t\in \mathbb{N}\hfill \\ 4\hfill & \mathrm{otherwise}\hfill \end{array}\right.$

Proof. 

Case 1: $l\equiv 3\left(mod4\right)$.

Let $W=\{u_1,u_2,u_{\lceil \frac{l+1}{2}\rceil }\}$ be subset of the $V\left(H_l(1,2)\right)$. A representation of the vertices of $H_l(1,2)$ concerning W is given below:

$r\left(v_1\right)=(1,2,4)$, $r\left(v_2\right)=(1,1,3)$, $r\left(u_1\right)=(0,2,3)$,$r\left(u_2\right)=(2,0,3)$.

$$r\left(v_p\right|W)=\left\{\begin{array}{cc}(\lceil \frac{p+1}{2}\rceil ,\lceil \frac{p-1}{2}\rceil ,\lceil \frac{l-2p+5}{4}\rceil )\hfill & \mathrm{for}3\le p\le \lceil \frac{l+1}{2}\rceil \mathrm{and}p=2t-1;t\in \mathbb{N}\hfill \\ (\lceil \frac{p}{2}\rceil ,\lceil \frac{p}{2}\rceil ,\lceil \frac{l-2p+5}{4}\rceil )\hfill & \mathrm{for}3\le p\le \lceil \frac{l+1}{2}\rceil \mathrm{and}p=2t;t\in \mathbb{N}\hfill \\ (\lceil \frac{l+5}{4}\rceil ,\lceil \frac{l+1}{4}\rceil ,1)\hfill & \mathrm{for}p=\lceil \frac{l+1}{2}\rceil +1\hfill \\ (\lceil \frac{l-p+3}{2}\rceil ,\lceil \frac{l-p+4}{2}\rceil ,\lceil \frac{2p-l+1}{4}\rceil )\hfill & \mathrm{for}\lceil \frac{l+1}{2}\rceil +3\le p\le l\hfill \end{array}\right.$$

$$r\left(u_p\right|W)=\left\{\begin{array}{cc}(\lceil \frac{p+2}{2}\rceil ,\lceil \frac{p+1}{2}\rceil ,\lceil \frac{p+1}{2}\rceil )\hfill & \mathrm{for}3\le p\le \lceil \frac{l+1}{2}\rceil \hfill \\ (\lceil \frac{l+2}{4}\rceil ,\lceil \frac{l+2}{4}\rceil ,\lceil \frac{l-p-2}{4}\rceil )\hfill & \mathrm{for}p=\lceil \frac{l+1}{2}\rceil +1\hfill \\ (\lceil \frac{l-p+4}{2}\rceil ,\lceil \frac{l-p+5}{2}\rceil ,\lceil \frac{2p-l+5}{4}\rceil )\hfill & \mathrm{for}\lceil \frac{l+1}{2}\rceil +2\le p\le l\hfill \end{array}\right.$$

The above representations demonstrate that each vertex has a distinct representation. As a result, W must be a resolving set. and that $dim\left(H_l[1,2]\right)=3.$ To demonstrate that $dim\left(H_l[1,2]\right)\ge 3$, it is sufficient to demonstrate that there is no resolving set with cardinality two.

On the other hand, suppose there is a resolving set A with cardinality 2. Then, by Lemma 1, both vertices of A belong to $v_p$. One vertex can be assumed to be $v_1$. Thus, one can suppose that $A=\{v_1,v_p:2\le p\le \lceil \frac{l+1}{2}\rceil \}$.

In this case, the vertices that have same representations for every choice of A are stated below:

$$\left\{\begin{array}{c}r\left(u_1\right)=r\left(v_l\right)\mathrm{for}p=1\hfill \\ r\left(v_l\right)=r\left(u_2\right)=(2,\frac{p}{2})p\ge 2,\mathrm{and}p=2t;t\in \mathbb{N}\hfill \\ r\left(u_1\right)=r\left(u_l\right)=(1,\frac{p+1}{2})p\ge 2,\mathrm{and}p=2t-1;t\in \mathbb{N}\hfill \end{array}\right.$$

As a result, no resolving set with cardinality two exists, and $dim\left(Hn\right[1,2\left]\right)\ge 3$.

The result can be obtained by combining the lower and upper bounds.

Case 2: $l\equiv 0,1,2\left(mod4\right)$.

• $l\equiv 1,2\left(mod4\right)$.

Let $W=\{v_1,v_2,u_2,v_3\}$ be a set of graph vertices. Each vertex’s representation regarding this set W is as follows:

$r\left(v_1\right)=(0,2,2,2)$, $r\left(v_2\right)=(2,0,1,2)$.

For $3\le p\le l$

$$r\left(v_p\right|W)=\left\{\begin{array}{cc}(\lceil \frac{p-1}{2}\rceil ,\lceil \frac{p-2}{2}\rceil +1,\lceil \frac{p-2}{2}\rceil ,\lceil \frac{p-2}{2}\rceil )\hfill & \mathrm{if}3\le p\le \lceil \frac{l+1}{2}\rceil andp=2t-1;t\in \mathbb{N}\hfill \\ (\lceil \frac{p+1}{2}\rceil ,\lceil \frac{p-2}{2}\rceil ,\lceil \frac{p-1}{2}\rceil ,\lceil \frac{p-2}{2}\rceil )\hfill & \mathrm{if}3\le p\le \lceil \frac{l+1}{2}\rceil \mathrm{and}p=2t;t\in \mathbb{N}\hfill \\ (\lceil \frac{l-4}{4}\rceil ,\lceil \frac{l-4}{4}\rceil ,\lceil \frac{l}{4}\rceil ,\lceil \frac{l-4}{4}\rceil )\hfill & \mathrm{if}p=\lceil \frac{l+1}{2}\rceil +1\mathrm{and}p=2t-1;t\in \mathbb{N}\hfill \\ (\lceil \frac{l-4}{4}\rceil ,\lceil \frac{l+4}{4}\rceil ,\lceil \frac{l}{4}\rceil ,\lceil \frac{l}{4}\rceil )\hfill & \mathrm{if}p=\lceil \frac{l+1}{2}\rceil +1\mathrm{and}p=2t;t\in \mathbb{N}\hfill \\ (\lceil \frac{l}{4}\rceil ,\lceil \frac{l}{4}\rceil -1,\lceil \frac{l}{4}\rceil ,\lceil \frac{l}{4}\rceil )\hfill & \mathrm{if}p=\lceil \frac{l+1}{2}\rceil +2\mathrm{and}p=2t-1;t\in \mathbb{N}\hfill \\ (\lceil \frac{l}{4}\rceil ,\lceil \frac{l-4}{4}\rceil ,\lceil \frac{l}{4}\rceil ,\lceil \frac{l}{4}\rceil )\hfill & \mathrm{if}p=\lceil \frac{l+1}{2}\rceil +2\mathrm{and}p=2t;t\in \mathbb{N}\hfill \\ (\lceil \frac{l-p+1}{2}\rceil ,\lceil \frac{l-p+3}{2}\rceil ,\lceil \frac{l-p+4}{2}\rceil ,\lceil \frac{l-p+4}{2}\rceil )\hfill & \mathrm{if}\lceil \frac{l+1}{2}\rceil +3\le p\le l\mathrm{and}p=2t-1;t\in \mathbb{N}\hfill \\ (\lceil \frac{l-p}{2}\rceil -2,\lceil \frac{l-p}{2}\rceil +1,\lceil \frac{l-p}{2}\rceil +2,\lceil \frac{l-p}{2}\rceil +3)\hfill & \mathrm{if}\lceil \frac{l+1}{2}\rceil +3\le p\le l\mathrm{and}p=2t;t\in \mathbb{N}\hfill \end{array}\right.$$

$r\left(u_1\right)=(1,1,2,3)$, $r\left(u_2\right)=(2,1,0,2)$ and $r\left(u_3\right)=(2,2,2,0)$.

For $4\le p\le l$

$$r\left(u_p\right|W)=\left\{\begin{array}{cc}(\lceil \frac{p+1}{2}\rceil ,\lceil \frac{p}{2}\rceil ,\lceil \frac{p+1}{2}\rceil ,\lceil \frac{p}{2}\rceil )\hfill & \mathrm{if}4\le p\le \lceil \frac{l}{2}\rceil \hfill \\ (\lceil \frac{l+2}{4}\rceil ,\lceil \frac{l+2}{2}\rceil ,\lceil \frac{l+6}{4}\rceil ,\lceil \frac{l+2}{4}\rceil )\hfill & \mathrm{if}p=\lceil \frac{l}{2}\rceil +1\hfill \\ (\lceil \frac{l-3}{4}\rceil ,\lceil \frac{l+2}{4}\rceil ,\lceil \frac{l+6}{2}\rceil ,\lceil \frac{l+6}{2}\rceil )\hfill & \mathrm{if}p=\lceil \frac{l}{2}\rceil +2\hfill \\ (\lceil \frac{l-p+2}{2}\rceil ,\lceil \frac{l-p+2}{2}\rceil ,\lceil \frac{l-p+5}{2}\rceil ,\lceil \frac{l-p+6}{2}\rceil )\hfill & \mathrm{if}\lceil \frac{l}{2}\rceil +3\le p\le l\hfill \end{array}\right.$$

The above representations demonstrate that each vertex has a distinct representation. This can be explained by the existence of a resolving set W and

$$dim\left(H_l[1,2]\right)\le 4$$

(1)

• $l\equiv 0\left(mod4\right)$.

Let $W=\{v_1,v_2,u_2,v_3\}$ be a set of graph vertices of $H_l[1,2]$. It will be shown that this set is a resolving set by proving that the representation of each vertex is unique. The representations of each vertex are shown below:

$r\left(v_1\right)=(0,2,2,1)$, $r\left(v_2\right)=(2,0,1,2)$.

For $3\le p\le l$, we have

$$r\left(v_p\right|W)=\left\{\begin{array}{cc}(\lceil \frac{p-1}{2}\rceil ,\lceil \frac{p-2}{2}\rceil +2,\lceil \frac{p-1}{2}\rceil ,\lceil \frac{p-3}{2}\rceil )\hfill & \mathrm{if}3\le p\le \lceil \frac{l+1}{2}\rceil \mathrm{and}p=2t-1;t\in \mathbb{N}\hfill \\ (\lceil \frac{p-1}{2}\rceil ,\lceil \frac{p-3}{2}\rceil ,\lceil \frac{p}{2}\rceil ,\lceil \frac{p}{2}\rceil )\hfill & \mathrm{if}3\le p\le \lceil \frac{l+1}{2}\rceil \mathrm{and}p=2t;t\in \mathbb{N}\hfill \\ (\lceil \frac{l+4}{4}\rceil ,\lceil \frac{l}{4}\rceil ,\lceil \frac{l+4}{4}\rceil ,\lceil \frac{l+4}{4}\rceil )\hfill & \mathrm{if}p=\lceil \frac{l+1}{2}\rceil +1\mathrm{and}p=2t;t\in \mathbb{N}\hfill \\ (\lceil \frac{l-4}{4}\rceil ,\lceil \frac{l+1}{4}\rceil ,\lceil \frac{l+1}{4}\rceil ,\lceil \frac{l}{4}\rceil )\hfill & \mathrm{if}p=\lceil \frac{l+1}{2}\rceil +1i\mathrm{and}p=2t-1;t\in \mathbb{N}\hfill \\ (\lceil \frac{l-p}{2}\rceil +2,\lceil \frac{l-p}{2}\rceil +1,\lceil \frac{l-p}{2}\rceil +2,\lceil \frac{l-p}{2}\rceil +3)\hfill & \mathrm{if}\lceil \frac{l+1}{2}\rceil +2\le p\le l\mathrm{and}p=2t;t\in \mathbb{N}\hfill \\ (\lceil \frac{l-p+1}{2}\rceil ,\lceil \frac{l-p+4}{2}\rceil ,\lceil \frac{l-p+4}{2}\rceil ,\lceil \frac{l-p+3}{2}\rceil )\hfill & \mathrm{if}\lceil \frac{l+1}{2}\rceil +2\le p\le l\mathrm{and}p=2t-1;t\in \mathbb{N}\hfill \end{array}\right.$$

$u_1(1,1,2,2)$, $u_2(2,1,0,1)$ and $u_3(2,2,2,1)$.

For $4\le p\le l$, we have

$$r\left(u_p\right|W)=\left\{\begin{array}{cc}(\lceil \frac{p+1}{2}\rceil ,\lceil \frac{p}{2}\rceil ,\lceil \frac{p+1}{2}\rceil ,\lceil \frac{p-1}{2}\rceil )\hfill & \mathrm{if}4\le p\le \lceil \frac{l}{2}\rceil \hfill \\ (\lceil \frac{l+2}{4}\rceil ,\lceil \frac{l+2}{4}\rceil ,\lceil \frac{l+2}{4}\rceil ,\lceil \frac{l}{4}\rceil )\hfill & \mathrm{if}p=\lceil \frac{l}{2}\rceil +1\hfill \\ (\lceil \frac{l-p+2}{2}\rceil ,\lceil \frac{l-p+3}{2}\rceil ,\lceil \frac{l-p+5}{2}\rceil ,\lceil \frac{l-p+4}{2}\rceil )\hfill & \mathrm{if}\lceil \frac{l}{2}\rceil +2\le p\le l\hfill \end{array}\right.$$

The above representations show that each vertex has a unique representation. As a result, W is a resolving set. Hence,

$$dim\left(H_l[1,2]\right)\le 4$$

(2)

To prove the other bound, it is sufficient to demonstrate that the resolving set has at least four elements. Assume, on the other hand, that W is a resolving set of $Hn[1,2]$ such that $\left|W\right|=3$. According to the Lemma 1, W must have two vertices $v_p$ and $v_q$ with different parities. Because the third vertex of W belongs to either $v_p$ or $u_p$, we consider the following possibilities:

• If all the vertices of W belong to $v_p$.

In this case, without loss of generality, suppose that $W=\{v_1,v_p,v_q:1\le p<q\le \lceil \frac{l+1}{2}\rceil \}$. The vertices that have a representation for each choice of i and j are listed below:

$$\left\{\begin{array}{cc}r\left(u_{q-2}\right)=r\left(v_{q+1}\right)\hfill & \mathrm{if}p=2t-1;t\in \mathbb{N}\mathrm{and}q=2t;t\in \mathbb{N}\hfill \\ r(u_{\lceil \frac{l}{2}\rceil -2})=r(v_{\lceil \frac{l}{2}\rceil +1})\hfill & \mathrm{if}p,q=2t;t\in \mathbb{N}\hfill \\ r\left(u_{q+11}\right)=r\left(v_{q+9}\right)\hfill & \mathrm{if}p=2t-1;t\in \mathbb{N}\mathrm{and}q=2t;t\in \mathbb{N}\hfill \end{array}\right.$$

• If W contain one vertex from $u_p$. Assume, without being too specific, that $W=\{v_1,v_p,u_q:1\le p\le q\le \lceil \frac{l+1}{2}\rceil \}$. The vertices that have representation for each choice of i and j are listed below:

$$\left\{\begin{array}{cc}r\left(u_p\right)=r\left(v_{p+2}\right)=(\frac{p+2}{2},\frac{p}{2}-\lceil \frac{q}{2}\rceil +2,1)\hfill & \mathrm{if}1\le q\le p\le \lceil \frac{l-1}{2}\rceil \hfill \\ r\left(u_{p-1}\right)=r\left(v_{p-2}\right)=(\frac{p}{2},1,\lceil \frac{q}{2}\rceil -\frac{p}{2}+2)\hfill & \mathrm{if}1\le p\le q\le \lceil \frac{l+1}{2}\rceil \hfill \end{array}\right.$$

Thus, $H_l[1,2]$ does not contain any resolving set of cardinality 3 for $l\equiv 0,1,2\left(mod4\right)$. This implies that

$$dim\left(H_l[1,2]\right)\ge 4$$

(3)

From Equations (1)–(3), we can obtain

$$dim\left(H_l[1,2]\right)=4.$$

 □

1.2. Metric Dimension of Subdivision of Circulant Graph $C_l[1,3]$

In this section, the metric dimension of the subdivision graph $H_l[1,3]$ is investigated. The following lemma gives a choice of the resolving set and will be useful in proving the main result of this section.

Lemma 2.

If W is a resolving set of the graph $H_l[1,3]$, then at least one vertex from each of the set $U=\{u_p:1\le p\le l\}$ and $V=\{v_p:1\le p\le l\}$ must belong to W.

Proof. 

The distance of the vertices $u_l$, $v_{l-2}$, $u_{l-1}$ and $u_{l-2}$ from the vertices $u_p$ and $v_p$ for $1\le p\le \lceil \frac{l}{2}\rceil$ are given below:

For $l\equiv 0\left(mod3\right)$.

$$\left\{\begin{array}{c}\mathrm{If}1\le p\le \lceil \frac{l}{2}\rceil \hfill \\ d(u_l,u_p)=d(u_{l-1},u_p)=\frac{p+6}{3},d(u_l,v_p)=d(u_{l-1},v_p)=\frac{p+3}{3}\hfill & \mathrm{for}p=3t;t\in \mathbb{N}\hfill \\ d(u_{l-1},u_p)=d(u_{l-2},u_p)=\lceil \frac{p+7}{3}\rceil ,d(u_{l-1},v_p)=d(u_{l-2},v_p)=\lceil \frac{p+4}{3}\rceil \hfill & \mathrm{for}p\equiv 1,2\left(mod3\right)\hfill \end{array}\right.$$

For $l\equiv 1\left(mod3\right)$.

$$\left\{\begin{array}{c}\mathrm{If}1\le p\le \lceil \frac{l}{2}\rceil -2\hfill \\ d(u_{l-2},u_p)=d(u_{l-1},u_p)=\frac{p+5}{2},d(u_{l-1},v_p)=d(u_{l-2},v_p)=\frac{p+3}{2}\hfill & \mathrm{for}p=2t-1;t\in \mathbb{N}\hfill \\ d(u_l,u_p)=d(v_{l-2},u_p)=\frac{p+4}{2},d(u_l,v_p)=d(v_{l-2},v_p)=\frac{p+2}{2}\hfill & \mathrm{for}p=2t;t\in \mathbb{N}\hfill \\ \mathrm{If}p=\lceil \frac{l}{2}\rceil -1\hfill \\ d(u_l,u_p)=d(u_{l-1},u_p)=\frac{p+4}{2},d(u_l,v_p)=d(u_{l-1},v_p)=\frac{p+2}{2}.\hfill \\ \mathrm{If}p=\lceil \frac{l}{2}\rceil \hfill \\ d(u_l,u_p)=d(u_{l-1},u_p)=\frac{p+1}{2},d(u_{l-1},v_p)=d(u_{l-2},v_p)=\frac{p+1}{2}.\hfill \end{array}\right.$$

For $l\equiv 2\left(mod3\right)$.

$$\left\{\begin{array}{c}\mathrm{If}1\le p\le \lceil \frac{l}{2}\rceil -1\hfill \\ d(u_l,u_p)=d(v_{l-2},u_p)=\frac{p+6}{3},d(u_l,v_p)=d(u_{l-1},v_p)=\frac{p+3}{3}\hfill & \mathrm{for}p=3t;t\in \mathbb{N}\hfill \\ d(u_l,u_p)=d(v_{l-2},u_p)=\frac{p+5}{3},d(u_l,v_p)=d(v_{l-2},v_p)=\frac{p+2}{3}\hfill & \mathrm{for}p=3t-2;t\in \mathbb{N}\hfill \\ d(u_l,u_p)=d(u_{l-1},u_p)=\frac{p+7}{3},d(u_l,v_p)=d(v_{l-2},v_p)=\frac{p+7}{3}\hfill & \mathrm{for}p=3t-1;t\in \mathbb{N}\hfill \\ \mathrm{If}p=\lceil \frac{l}{2}\rceil -1\hfill \\ d(u_l,u_p)=d(u_{l-1},u_p)=\frac{p+7}{3},d(u_l,v_p)=d(v_{l-2},v_p)=\frac{p+4}{3}.\hfill \\ \mathrm{If}p=\lceil \frac{l}{2}\rceil \hfill \\ d(u_{l-1},u_p)=d(u_{l-2},u_p)=\frac{p+3}{3},d(u_l,v_p)=d(u_{l-1},v_p)=\frac{p+3}{3}.\hfill \end{array}\right.$$

The above distances show that, to resolve the vertices $u_l$, $v_{l-2}$, $u_{l-1}$ and $u_{l-2}$, it is necessary to include at least one vertex from the set U and V Figure 2. □

Theorem 3.

Let G denote the graph of $H_l[1,3]$. Then, for $l\le 12$

$$dim\left(G\right)\le 4.$$

Proof. 

Case 1: $l\equiv 0\left(mod4\right)$.

Let $W=\{v_1,v_2,v_3,u_4\}$ be a set of vertices of $H_l[1,3]$. It will be shown that this set is a resolving set by proving that the representation of each vertex is unique. The representations of each vertex are stated below:

For $1\le p\le \lceil \frac{l}{2}\rceil +1$

$$r\left(u_p\right|W)=\left\{\begin{array}{cc}(1,1,3,3)\hfill & \mathrm{if}\mathrm{p}=1\hfill \\ (\lceil \frac{p+2}{3}\rceil ,\lceil \frac{p+6}{3}\rceil ,\lceil \frac{p}{3}\rceil ,\lceil \frac{p+1}{3}\rceil )\hfill & \mathrm{if}p=3t;t\in \mathbb{N}\hfill \\ (\lceil \frac{p+2}{3}\rceil ,\lceil \frac{p}{3}\rceil ,\lceil \frac{p+8}{3}\rceil ,\lceil \frac{p}{3}\rceil )\hfill & \mathrm{if}p=3t-2;t\in \mathbb{N}\hfill \\ (\lceil \frac{p+7}{3}\rceil ,\lceil \frac{p}{3}\rceil ,\lceil \frac{p}{3}\rceil ,\lceil \frac{p+1}{3}\rceil )\hfill & \mathrm{if}p=3t-1;t\in \mathbb{N}\hfill \end{array}\right.$$

$$r\left(v_p\right|W)=\left\{\begin{array}{cc}\lceil \frac{p-4}{3}\rceil ,\lceil \frac{p+3}{3}\rceil ,\lceil \frac{p-3}{3}\rceil ,\lceil \frac{p+3}{3}\rceil \hfill & \mathrm{if}p=3t;t\in \mathbb{N}\hfill \\ \lceil \frac{p+4}{3}\rceil ,\lceil \frac{p-2}{3}\rceil ,\lceil \frac{p+2}{3}\rceil ,\lceil \frac{p+3}{3}\rceil \hfill & \mathrm{if}p=3t-1;t\in \mathbb{N}\hfill \\ \lceil \frac{p-1}{3}\rceil ,\lceil \frac{p+3}{3}\rceil ,\lceil \frac{p+2}{3}\rceil ,\lceil \frac{p+3}{3}\rceil \hfill & \mathrm{if}p=3t-2;t\in \mathbb{N}\hfill \end{array}\right.$$

And for $\frac{l}{2}\rceil +1\le p\le \lceil n$

$$r\left(u_p\right|W)=\left\{\begin{array}{cc}(1,1,3,3)\hfill & \mathrm{if}\mathrm{p}=1\hfill \\ (\lceil \frac{l-p+3}{3}\rceil ,\lceil \frac{l-p+9}{3}\rceil ,\lceil \frac{l-p+6}{3}\rceil ,\lceil \frac{l-p+9}{3}\rceil )\hfill & \mathrm{if}p=3t;t\in \mathbb{N}\hfill \\ (\lceil \frac{l-p+6}{3}\rceil ,\lceil \frac{l-p+6}{3}\rceil ,\lceil \frac{l-p+6}{3}\rceil ,\lceil \frac{l-p-6}{3}\rceil )\hfill & \mathrm{if}p=3t-1;t\in \mathbb{N}\hfill \\ (\lceil \frac{l-p+3}{3}\rceil ,\lceil \frac{l-p+6}{3}\rceil ,\lceil \frac{l-p+4}{3}\rceil ,\lceil \frac{l-p+3}{3}\rceil )\hfill & \mathrm{if}p=3t-2;t\in \mathbb{N}\hfill \end{array}\right.$$

$$r\left(v_p\right|W)=\left\{\begin{array}{cc}(\lceil \frac{l-p+6}{3}\rceil ,\lceil \frac{l-p+7}{3}\rceil ,\lceil \frac{l-p+3}{3}\rceil ,\lceil \frac{l-p+12}{3}\rceil )\hfill & \mathrm{if}p=3t;t\in \mathbb{N}\hfill \\ (\lceil \frac{l-p+6}{3}\rceil ,\lceil \frac{l-p-3}{3}\rceil ,\lceil \frac{l-p+1}{3}\rceil ,\lceil \frac{l-p+6}{3}\rceil )\hfill & \mathrm{if}p=3t-1;t\in \mathbb{N}\hfill \\ (\lceil \frac{l-p+1}{3}\rceil ,\lceil \frac{l-p+7}{3}\rceil ,\lceil \frac{l-p+2}{3}\rceil ,\lceil \frac{l-p+6}{3}\rceil )\hfill & \mathrm{if}p=3t-2;t\in \mathbb{N}\hfill \end{array}\right.$$

The above representations show that each of the vertex has unique representation. This implies that W is a resolving set and $dim\left(H_l[1,3]\right)\le 4$.

Case 2: $l\equiv 1,2\left(mod4\right)$.

Let $W=\{u_1,u_3,u_5,v_7\}$ be a set of vertices of G. It will be shown that this set is a resolving set by proving that the representation of each vertex is unique. The representations of each vertex are presented below:

For $1\le p\le \lceil \frac{l+1}{2}\rceil$

$$r\left(u_p\right|W)=\left\{\begin{array}{cc}(1,1,3,3)\hfill & \mathrm{if}\mathrm{p}=1\hfill \\ (\lceil \frac{p+3}{3}\rceil ,\lceil \frac{p+3}{3}\rceil ,\lceil \frac{p}{3}\rceil ,\lceil \frac{p-4}{3}\rceil )\hfill & \mathrm{if}p=3t;t\in \mathbb{N}\hfill \\ (\lceil \frac{p+3}{3}\rceil ,\lceil \frac{p+3}{3}\rceil ,\lceil \frac{p+2}{3}\rceil ,\lceil \frac{p-4}{3}\rceil )\hfill & \mathrm{if}p=3t-1;t\in \mathbb{N}\hfill \\ (\lceil \frac{p+5}{3}\rceil ,\lceil \frac{p+2}{3}\rceil ,\lceil \frac{p+2}{3}\rceil ,\lceil \frac{p-4}{3}\rceil )\hfill & \mathrm{if}p=3t-2;t\in \mathbb{N}\hfill \end{array}\right.$$

$$r\left(v_p\right|W)=\left\{\begin{array}{cc}\lceil \frac{p}{3}\rceil ,\lceil \frac{p-2}{3}\rceil ,\lceil \frac{p-3}{3}\rceil ,\lceil \frac{p}{3}\rceil \hfill & \mathrm{if}p=3t;t\in \mathbb{N}\hfill \\ \lceil \frac{p+1}{3}\rceil ,\lceil \frac{p}{3}\rceil ,\lceil \frac{p-3}{3}\rceil ,\lceil \frac{p-2}{3}\rceil \hfill & \mathrm{if}p=3t-1;t\in \mathbb{N}\hfill \\ \lceil \frac{p+1}{3}\rceil ,\lceil \frac{p-2}{3}\rceil ,\lceil \frac{p+2}{3}\rceil ,\lceil \frac{p-7}{3}\rceil \hfill & \mathrm{if}p=3t-2;t\in \mathbb{N}\hfill \end{array}\right.$$

And for $\frac{l}{2}\rceil +1\le p\le \lceil n$

$$r\left(u_p\right|W)=\left\{\begin{array}{cc}(\lceil \frac{l-p+7}{3}\rceil ,\lceil \frac{l-p+10}{3}\rceil ,\lceil \frac{l-p+10}{3}\rceil ,\lceil \frac{l-p+10}{3}\rceil )\hfill & \mathrm{if}p=3t;t\in \mathbb{N}\hfill \\ (\lceil \frac{l-p+5}{3}\rceil ,\lceil \frac{l-p+8}{3}\rceil ,\lceil \frac{l-p+10}{3}\rceil ,\lceil \frac{l-p+1}{3}\rceil )\hfill & \mathrm{if}p=3t-1;t\in \mathbb{N}\hfill \\ (\lceil \frac{l-p+7}{3}\rceil ,\lceil \frac{l-p+8}{3}\rceil ,\lceil \frac{l-p+10}{3}\rceil ,\lceil \frac{l-p-4}{3}\rceil )\hfill & \mathrm{if}p=3t-2;t\in \mathbb{N}\hfill \end{array}\right.$$

$$r\left(v_p\right|W)=\left\{\begin{array}{cc}(\lceil \frac{l-p+4}{3}\rceil ,\lceil \frac{l-p+6}{3}\rceil ,\lceil \frac{l-p+13}{3}\rceil ,\lceil \frac{l-p+7}{3}\rceil )\hfill & \mathrm{if}p=3t;t\in \mathbb{N}\hfill \\ (\lceil \frac{l-p+7}{3}\rceil ,\lceil \frac{l-p+6}{3}\rceil ,\lceil \frac{l-p+7}{3}\rceil ,\lceil \frac{l-p+12}{3}\rceil )\hfill & \mathrm{if}p=3t-1;t\in \mathbb{N}\hfill \\ (\lceil \frac{l-p+5}{3}\rceil ,\lceil \frac{l-p+9}{3}\rceil ,\lceil \frac{l-p+7}{3}\rceil ,\lceil \frac{l-p+14}{3}\rceil )\hfill & \mathrm{if}p=3t-2;t\in \mathbb{N}\hfill \end{array}\right.$$

The above representations show that each of the vertices has a unique representation. This implies that W is a resolving set and $dim\left(H_l[1,3]\right)\le 4$.

Case 3: $l\equiv 3\left(mod4\right)$.

Let $W=\{v_1,v_2,v_3,u_{\frac{l-1}{2}}\}$ be a set of vertices of G. It will be shown that this set is a resolving set by proving that the representation of each vertex is unique. The representations of each vertex are given below:

$r\left(u_4\right)=(2,1,3,)$ For $1\le p\le \lceil \frac{l+1}{2}\rceil$

$$r\left(u_p\right|W)=\left\{\begin{array}{cc}(1,1,3,3)\hfill & \mathrm{if}\mathrm{p}=1\hfill \\ (\lceil \frac{p+2}{3}\rceil ,\lceil \frac{p+6}{3}\rceil ,\lceil \frac{p}{3}\rceil ,\lceil \frac{p+1}{3}\rceil )\hfill & \mathrm{if}p=3t;t\in \mathbb{N}\hfill \\ (\lceil \frac{p+2}{3}\rceil ,\lceil \frac{p}{3}\rceil ,\lceil \frac{p+8}{3}\rceil ,\lceil \frac{p}{3}\rceil )\hfill & \mathrm{if}p=3t-2;t\in \mathbb{N}\hfill \\ (\lceil \frac{p+7}{3}\rceil ,\lceil \frac{p}{3}\rceil ,\lceil \frac{p}{3}\rceil ,\lceil \frac{p+1}{3}\rceil )\hfill & \mathrm{if}p=3t-1;t\in \mathbb{N}\hfill \end{array}\right.$$

$$r\left(v_p\right|W)=\left\{\begin{array}{cc}\lceil \frac{p+4}{3}\rceil ,\lceil \frac{p+3}{3}\rceil ,\lceil \frac{p-3}{3}\rceil ,\lceil \frac{k-p+3}{3}\rceil \hfill & \mathrm{if}p=3t;t\in \mathbb{N}\hfill \\ \lceil \frac{p}{3}\rceil ,\lceil \frac{p+3}{3}\rceil ,\lceil \frac{p+2}{3}\rceil ,\lceil \frac{k-p+8}{3}\rceil \hfill & \mathrm{if}p=3t-2;t\in \mathbb{N}\hfill \\ \lceil \frac{p+4}{3}\rceil ,\lceil \frac{p-2}{3}\rceil ,\lceil \frac{p+2}{3}\rceil ,\lceil \frac{k-p+3}{3}\rceil \hfill & \mathrm{if}p=3t-1;t\in \mathbb{N}\hfill \end{array}\right.$$

And for $\frac{l}{2}\rceil +1\le p\le \lceil n$

$$r\left(u_p\right|W)=\left\{\begin{array}{cc}(\lceil \frac{l-p+3}{3}\rceil ,\lceil \frac{l-p+9}{3}\rceil ,\lceil \frac{l-p+6}{3}\rceil ,\lceil \frac{l-p+9}{3}\rceil )\hfill & \mathrm{if}p=3t;t\in \mathbb{N}\hfill \\ (\lceil \frac{l-p+6}{3}\rceil ,\lceil \frac{l-p+6}{3}\rceil ,\lceil \frac{l-p+4}{3}\rceil ,\lceil \frac{l-p+9}{3}\rceil )\hfill & \mathrm{if}p=3t-2;t\in \mathbb{N}\hfill \\ (\lceil \frac{l-p+6}{3}\rceil ,\lceil \frac{l-p+6}{3}\rceil ,\lceil \frac{l-p+6}{3}\rceil ,\lceil \frac{l-p+9}{3}\rceil )\hfill & \mathrm{if}p=3t-1;t\in \mathbb{N}\hfill \end{array}\right.$$

$$r\left(v_p\right|W)=\left\{\begin{array}{cc}(\lceil \frac{l-p+6}{3}\rceil ,\lceil \frac{l-p}{3}\rceil ,\lceil \frac{l-p+8}{3}\rceil ,\lceil \frac{p-k+7}{3}\rceil )\hfill & \mathrm{if}p=3t;t\in \mathbb{N}\hfill \\ (\lceil \frac{l-p+6}{3}\rceil ,\lceil \frac{l-p+7}{3}\rceil ,\lceil \frac{l-p+3}{3}\rceil ,\lceil \frac{p-k+1}{3}\rceil )\hfill & \mathrm{if}p=3t-2;t\in \mathbb{N}\hfill \\ (\lceil \frac{l-p}{3}\rceil ,\lceil \frac{l-p+7}{3}\rceil ,\lceil \frac{l-p+8}{3}\rceil ,\lceil \frac{p-k+1}{3}\rceil )\hfill & \mathrm{if}p=3t-1;t\in \mathbb{N}\hfill \end{array}\right.$$

The above representations show that each of the vertices has a unique representation. This concludes that W is a resolving set and $dim\left(H_l[1,3]\right)\le 4$. □

2. Conclusions

Circulant graphs are very useful graph and often used in local area networks. Various authors [10,11,14,15] had discussed the resolvability of circulant graphs $C_l[1,2,\dots ,k]$. Subdividing an edge is the process of inserting a new vertex into an existing edge and dividing it into two edges. The subdivision graph is a graph comprising edge subdivisions. Ahmad et al. [9] examined the metric dimension of barycentric subdivisions of circulant graphs; they proved that some of these families have constant metric dimensions. Later, Wei et al. [13] computed the metric dimension of a subdivision graph of circulant graphs, which is denoted by $G_l[1,k]$ for $2\le k\le 4$. In this article, another subdivision graph of circulant graph $H_l[1,k]$ was constructed. It was shown that this class of graphs has a constant metric dimension for $k=2,3$. We also think that the metric dimension will remain constant with increase in value of k. In this context, the following problem arises.

Open Problem: Calculate the exact metric dimension value for the subdivision of circulant graphs. $H_l[1,k]$ when $k=4$.