Superradiant (In)stability, Greybody Radiation, and Quasinormal Modes of Rotating Black Holes in Non-Linear Maxwell f(R) Gravity
Abstract
1. Introduction
2. Rotating BHs in Nonlinear Maxwell Gravity
3. Scalar Perturbation
4. Superradiance Phenomenon
4.1. Case of Magnetic Field Absence:
4.2. Case of Magnetic Field Presence
5. Semi-Analytical Greybody Radiation
6. QNMs
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Braidotti, M.C.; Faccio, D.; Wright, E.M. Penrose Superradiance in nonlinear optics. Phys. Rev. Lett. 2020, 125, 193902. [Google Scholar] [CrossRef] [PubMed]
- Hawking, S.W. Black hole explosions. Nature 1974, 248, 30. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199, Erratum in Commun. Math. Phys. 1976, 46, 206. [Google Scholar] [CrossRef]
- Mc Caughey, E. Hawking radiation screening and Penrose process shielding in the Kerr black hole. Eur. Phys. J. C 2016, 76, 179. [Google Scholar] [CrossRef]
- Dicke, R. Coherence in spontaneous radiation processes. Phys. Rev. 1954, 93, 99110. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B. Generation of waves by a rotating body. Sov. J. Exp. Theor. Phys. Lett. 1971, 14, 180. [Google Scholar]
- Zel’dovich, Y.B. Amplification of cylindrical electromagnetic waves reflected from a rotating body. Sov. J. Exp. Theor. Phys. Lett. 1972, 35, 1085. [Google Scholar]
- Press, W.H.; Teukolsky, S.A. Floating orbits, superradiant scattering and the black-hole bomb. Nature 1972, 238, 211. [Google Scholar] [CrossRef]
- Brito, R.; Cardoso, V.; Pani, P. Superradiance. Lect. Notes Phys. 2015, 906, 1. [Google Scholar]
- Cardoso, V.; Dias, O.J.C.; Lemos, J.P.S.; Yoshida, S. The black hole bomb and superradiant instabilities. Phys. Rev. D 2004, 70, 044039, Erratum in Phys. Rev. D 2004, 70, 049903. [Google Scholar] [CrossRef]
- Damour, T.; Deruelle, N.; Ruffini, R. On quantum resonances in stationary geometries. Lett. Nuovo Cim. 1976, 15, 257. [Google Scholar] [CrossRef]
- Brito, R.; Cardoso, V.; Pani, P. Black holes as particle detectors: Evolution of superradiant instabilities. Class. Quantum Gravity 2015, 32, 134001. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Press, W.H.; Teukolsky, S.A. Rotating black holes: Locally nonrotating frames, energy extraction, and scalar synchrotron radiation. Astrophys. J. 1972, 178, 347. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Amplification of waves reflected from a rotating “black hole”. Sov. Phys. JETP 1973, 37, 28. [Google Scholar]
- Teukolsky, S.A.; Press, W.H. Perturbations of a rotating black hole. III. Interaction of the hole with gravitational and electromagnetic radiation. Astrophys. J. 1974, 193, 443. [Google Scholar] [CrossRef]
- Dolan, S.R. Scattering by a draining bathtub vortex. Phys. Rev. D 2013, 87, 124026. [Google Scholar] [CrossRef]
- Xu, J.H.; Zheng, Z.H.; Luo, M.J.; Huang, J.H. Analytic study of superradiant stability of Kerr–Newman black holes under charged massive scalar perturbation. Eur. Phys. J. C 2021, 81, 402. [Google Scholar] [CrossRef]
- Biswas, S. Massive scalar perturbation of extremal rotating braneworld black hole: Superradiant stability analysis. Phys. Lett. B 2021, 820, 136597. [Google Scholar] [CrossRef]
- Brito, R.; Cardoso, V.; Pani, P. Superradiance: New frontiers in black hole physics. Lect. Notes Phys. 2020, 971, 1. [Google Scholar]
- Bekenstein, J.D.; Schiffer, M. The many faces of superradiance. Phys. Rev. D 1998, 58, 064014. [Google Scholar] [CrossRef]
- Cardoso, V.; Dias, O.J.C. Small Kerr-anti-de Sitter black holes are unstable. Phys. Rev. D 2004, 70, 084011. [Google Scholar] [CrossRef]
- Hawking, S.W.; Reall, H.S. Charged and rotating AdS black holes and their CFT duals. Phys. Rev. D 2000, 61, 024014. [Google Scholar] [CrossRef]
- Cardoso, V. Black hole bombs and explosions: From astrophysics to particle physics. Gen. Relativ. Gravit. 2013, 45, 2079. [Google Scholar] [CrossRef]
- Pani, P.; Cardoso, V.; Gualtieri, L.; Berti, E.; Ishibashi, A. Black hole bombs and photon mass bounds. Phys. Rev. Lett. 2012, 109, 131102. [Google Scholar] [CrossRef]
- Arvanitaki, A.; Dubovsky, S. Exploring the string axiverse with precision black hole physics. Phys. Rev. D 2011, 83, 044026. [Google Scholar] [CrossRef]
- Kapadia, S.J.; Kennefick, D.; Glampedakis, K. Do floating orbits in extreme mass ratio binary black holes exist? Phys. Rev. D 2013, 87, 044050. [Google Scholar] [CrossRef]
- Yunes, N.; Pani, P.; Cardoso, V. Gravitational waves from quasicircular extreme mass-ratio inspirals as probes of scalar-tensor theories. Phys. Rev. D 2012, 85, 102003. [Google Scholar] [CrossRef]
- Cardoso, V.; Carucci, I.P.; Pani, P.; Sotiriou, T.P. Matter around Kerr black holes in scalar-tensor theories: Scalarization and superradiant instability. Phys. Rev. D 2013, 88, 044056. [Google Scholar] [CrossRef]
- Friedman, J.L. Ergosphere instability. Commun. Math. Phys. 1978, 63, 243. [Google Scholar] [CrossRef]
- Moschidis, G. A proof of Friedman’s ergosphere instability for scalar waves. Commun. Math. Phys. 2018, 358, 437–520. [Google Scholar] [CrossRef]
- Maartens, R. Brane-world gravity. Living Rev. Relativ. 2004, 7, 7. [Google Scholar] [CrossRef] [PubMed]
- Dvali, G.R.; Gabadadze, G.; Porrati, M. 4D gravity on a brane in 5D Minkowski space. Phys. Lett. B 2000, 485, 208. [Google Scholar] [CrossRef]
- Jacobson, T.; Mattingly, D. Gravity with a dynamical preferred frame. Phys. Rev. D 2001, 64, 024028. [Google Scholar] [CrossRef]
- Pasqua, A.; Gashti, S.N. Einstein-aether scalar-tensor anisotropic constant-roll inflationary scenario in noncommutative phase space. J. Hologr. Appl. Phys. 2022, 2, 63–81. [Google Scholar]
- Bekenstein, J.D. Are there hyperentropic objects? Phys. Rev. D 2004, 70, 083509. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Introduction to modified gravity and gravitational alternative for dark energy. Int. J. Geom. Methods Mod. Phys. 2007, 4, 115. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) theories of gravity. Rev. Mod. Phys. 2010, 82, 451. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S. f(R) Theories. Living Rev. Relativ. 2010, 13, 3. [Google Scholar] [CrossRef]
- Nojiri, S.I.; Odintsov, S.D. Unified cosmic history in modified gravity: From f(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59. [Google Scholar] [CrossRef]
- Buchdahl, H.A. Non-linear Lagrangians and cosmological theory. Mon. Not. R. Astron. Soc. 1970, 150, 1. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Liberati, S. The metric-affine formalism of f(R) gravity. J. Phys. Conf. Ser. 2007, 68, 012022. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Liberati, S. Metric-affine f(R) theories of gravity. Ann. Phys. 2007, 322, 935. [Google Scholar] [CrossRef]
- Frolov, A.V. Singularity Problem with f(R) Models for Dark Energy. Phys. Rev. Lett. 2008, 101, 061103. [Google Scholar] [CrossRef] [PubMed]
- Upadhye, A.; Hu, W. Existence of relativistic stars in f(R) gravity. Phys. Rev. D 2009, 80, 064002. [Google Scholar] [CrossRef]
- Cooney, A.; DeDeo, S.; Psaltis, D. Neutron stars in f(R) gravity with perturbative constraints. Phys. Rev. D 2010, 82, 064033. [Google Scholar] [CrossRef]
- Bamba, K.; Nojiri, S.; Odintsov, S.D. The future of the universe in modified gravitational theories: Approaching a finite-time future singularity. J. Cosmol. Astropart. Phys. 2008, 2008, 045. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Disappearing cosmological constant in f(R) gravity. JETP Lett. 2007, 86, 157. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Transition from a matter-dominated era to a dark energy universe. Phys. Rev. D 2006, 74, 086005. [Google Scholar] [CrossRef]
- Capozziello, S.; Vignolo, S. A comment on “The Cauchy problem of f(R) gravity”. Class. Quantum Gravity 2009, 26, 168001. [Google Scholar] [CrossRef]
- Faraoni, V. Reply to ‘A comment on ‘The Cauchy problem of f(R) gravity’’. Class. Quantum Gravity 2009, 26, 168002. [Google Scholar] [CrossRef]
- Olmo, G.J.; Singh, P. Covariant effective action for loop quantum cosmology à la Palatini. J. Cosmol. Astropart. Phys. 2009, 2009, 030. [Google Scholar] [CrossRef]
- Faraoni, V.; Lanahan-Tremblay, N. Breakdown of the initial value formulation of scalar-tensor gravity and its physical meaning. Phys. Rev. D 2008, 78, 064017. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified gravity theories on a nutshell: Inflation, bounce and late-time evolution. Phys. Rep. 2017, 692, 1. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Capozziello, S. Effective field description of the Anton-Schmidt cosmic fluid. Phys. Rev. D 2019, 99, 104018. [Google Scholar] [CrossRef]
- Hollenstein, L.; Lobo, F.S.N. Exact solutions of f(R) gravity coupled to nonlinear electrodynamics. Phys. Rev. D 2008, 78, 124007. [Google Scholar] [CrossRef]
- Bajardi, F.; D’Agostino, R.; Benetti, M.; Falco, V.D.; Capozziello, S. Early and late time cosmology: The f(R) gravity perspective. Eur. Phys. J. Plus 2022, 137, 1239. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. Extended theories of gravity. Phys. Rep. 2011, 509, 167. [Google Scholar] [CrossRef]
- Nashed, G.G.; Saridakis, E.N. Barrow holographic dark energy. Phys. Rev. D 2020, 102, 124072. [Google Scholar] [CrossRef]
- Sakallı, İ.; Kanzi, S. Topical review: Greybody factors and quasinormal modes for black holes in various theories—Fingerprints of invisibles. Turk. J. Phys. 2022, 46, 51. [Google Scholar] [CrossRef]
- Rocha, J.V. Evaporation of large black holes in AdS: Greybody factor and decay rate. J. High Energy Phys. 2009, 2009, 027. [Google Scholar] [CrossRef]
- Harmark, T.; Natario, J.; Schiappa, R. Greybody factors for d-dimensional black holes. Adv. Theor. Math. Phys. 2010, 14, 727. [Google Scholar] [CrossRef]
- Ford, L. Quantization of a scalar field in the Kerr spacetime. Phys. Rev. D 1975, 12, 2963. [Google Scholar] [CrossRef]
- Creek, S.; Efthimiou, O.; Kanti, P.; Tamvakis, K. Greybody factors in a rotating black-hole background: Fermions and gauge bosons. Phys. Rev. D 2007, 76, 104013. [Google Scholar] [CrossRef]
- Iyer, S. Black-hole normal modes: A WKB approach. II. Schwarzschild black holes. Phys. Rev. D 1987, 35, 12. [Google Scholar] [CrossRef] [PubMed]
- Iyer, S.; Will, C.M. Black-hole normal modes: A WKB approach. I. Foundations and application of a higher-order WKB analysis of potential-barrier scattering. Phys. Rev. D 1987, 35, 3621. [Google Scholar] [CrossRef] [PubMed]
- Kanzi, S.; Sakallı, İ. GUP-modified Hawking radiation and transmission/reflection coefficients of rotating polytropic black hole. Eur. Phys. J. Plus 2022, 137, 14. [Google Scholar] [CrossRef]
- Shankaranarayanan, S. Temperature and entropy of Schwarzschild–de Sitter space-time. Phys. Rev. D 2003, 67, 084026. [Google Scholar] [CrossRef]
- Boonserm, P.; Visser, M. Analytic bounds on transmission probabilities. Ann. Phys. 2010, 325, 1328–1339. [Google Scholar] [CrossRef]
- Kanzi, S.; Sakallı, İ. GUP modified Hawking radiation in bumblebee gravity. Nucl. Phys. B 2019, 946, 114703. [Google Scholar] [CrossRef]
- Al-Badawi, A.; Sakallı, İ.; Kanzi, S. Solution of Dirac equation and greybody radiation around a regular Bardeen black hole surrounded by quintessence. Ann. Phys. 2020, 412, 168026. [Google Scholar] [CrossRef]
- Al-Badawi, A.; Kanzi, S.; Sakallı, İ. Effect of quintessence on geodesics and Hawking radiation of Schwarzschild black hole. Eur. Phys. J. Plus 2020, 135, 219. [Google Scholar] [CrossRef]
- Kanzi, S.; Mazharimousavi, S.H.; Sakallı, İ. Greybody factors of black holes in dRGT massive gravity coupled with nonlinear electrodynamics. Ann. Phys. 2020, 422, 168301. [Google Scholar] [CrossRef]
- Teukolsky, S.A. Perturbations of a rotating black hole. I. Fundamental equations for gravitational, electromagnetic, and neutrino-field perturbations. Astrophys. J. 1973, 185, 635–647. [Google Scholar] [CrossRef]
- Vishveshwara, C.V. Scattering of gravitational radiation by a Schwarzschild black-hole. Nature 1970, 227, 936–938. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, V.; Mashhoon, B. New approach to the quasinormal modes of a black hole. Phys. Rev. D 1984, 30, 295–304. [Google Scholar] [CrossRef]
- Horowitz, G.T.; Hubeny, V.E. Quasinormal modes of AdS black holes and the approach to thermal equilibrium. Phys. Rev. D 2000, 62, 024027. [Google Scholar] [CrossRef]
- Berti, E.; Kokkotas, K.D. Quasinormal modes of Reissner–Nordström–anti-de Sitter black holes: Scalar, electromagnetic, and gravitational perturbations. Phys. Rev. D 2003, 67, 064020. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Panotopoulos, G. Electromagnetic quasinormal modes of the nearly-extremal higher-dimensional Schwarzschild–de Sitter black hole. Mod. Phys. Lett. A 2018, 33, 1850130. [Google Scholar] [CrossRef]
- Destounis, K.; Fontana, R.D.B.; Mena, F.C. Accelerating black holes: Quasinormal modes and late-time tails. Phys. Rev. D 2020, 102, 044005. [Google Scholar] [CrossRef]
- Kanzi, S.; Sakallı, İ. Greybody radiation and quasinormal modes of Kerr-like black hole in Bumblebee gravity model. Eur. Phys. J. C 2021, 81, 501. [Google Scholar] [CrossRef]
- Kanzi, S.; Sakallı, İ. Reply to “Comment on ‘Greybody radiation and quasinormal modes of Kerr-like black hole in Bumblebee gravity model’”. Eur. Phys. J. C 2022, 82, 93. [Google Scholar] [CrossRef]
- Kanzi, S.; Alipour, M.R. Quasinormal modes of Dirac particle near Reissner-Nordstrom black hole. J. Hologr. Appl. Phys. 2022, 2, 101–110. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GW190425: Observation of a compact binary coalescence with total mass 3.4M⊙. Astrophys. J. Lett. 2020, 892, L3. [Google Scholar] [CrossRef]
- Berti, E.; Cardoso, V.; Starinets, A.O. Quasinormal modes of black holes and black branes. Class. Quant. Grav. 2009, 26, 163001. [Google Scholar] [CrossRef]
- Konoplya, R.A. Quasinormal modes of a small Schwarzschild–anti-de Sitter black hole. Phys. Rev. D 2002, 66, 044009. [Google Scholar] [CrossRef]
- Lemos, J.P.S. Cylindrical black hole in general relativity. Phys. Lett. B 1995, 353, 46. [Google Scholar] [CrossRef]
- Awad, A.M.; Nashed, G.G.L.; Hanafy, W.E. Rotating charged AdS solutions in quadratic f(T) gravity. Eur. Phys. J. C 2019, 79, 668. [Google Scholar] [CrossRef]
- Gonzales, P.A.; Rincon, A.; Saavedra, J.; Vasquez, Y. Superradiant instability and charged scalar quasinormal modes for (2+1)-dimensional Coulomb-like AdS black holes from nonlinear electrodynamics. Phys. Rev. D 2021, 104, 084047. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Oxford University Press: New York, NY, USA, 1983. [Google Scholar]
- Miao, Y.G.; Xu, Z.M. Hawking radiation of five-dimensional charged black holes with scalar fields. Phys. Lett. B 2017, 772, 542. [Google Scholar] [CrossRef]
- Mashhoon, B.B. Proceedings of the Third Marcel Grossmann Meeting on General Relativity; Science Press: North-Holland, The Netherlands, 1983; pp. 599–608. [Google Scholar]
- Konoplya, R.A.; Zhidenko, A.; Zinhailo, A.F. Higher order WKB formula for quasinormal modes and grey-body factors: Recipes for quick and accurate calculations. Class. Quantum Gravity 2019, 36, 155002. [Google Scholar] [CrossRef]
- Upadhyay, S.; ul Islam, N.; Ganai, P.A. A modified thermodynamics of rotating and charged BTZ black hole. J. Hologr. Appl. Phys. 2022, 1, 25–48. [Google Scholar]



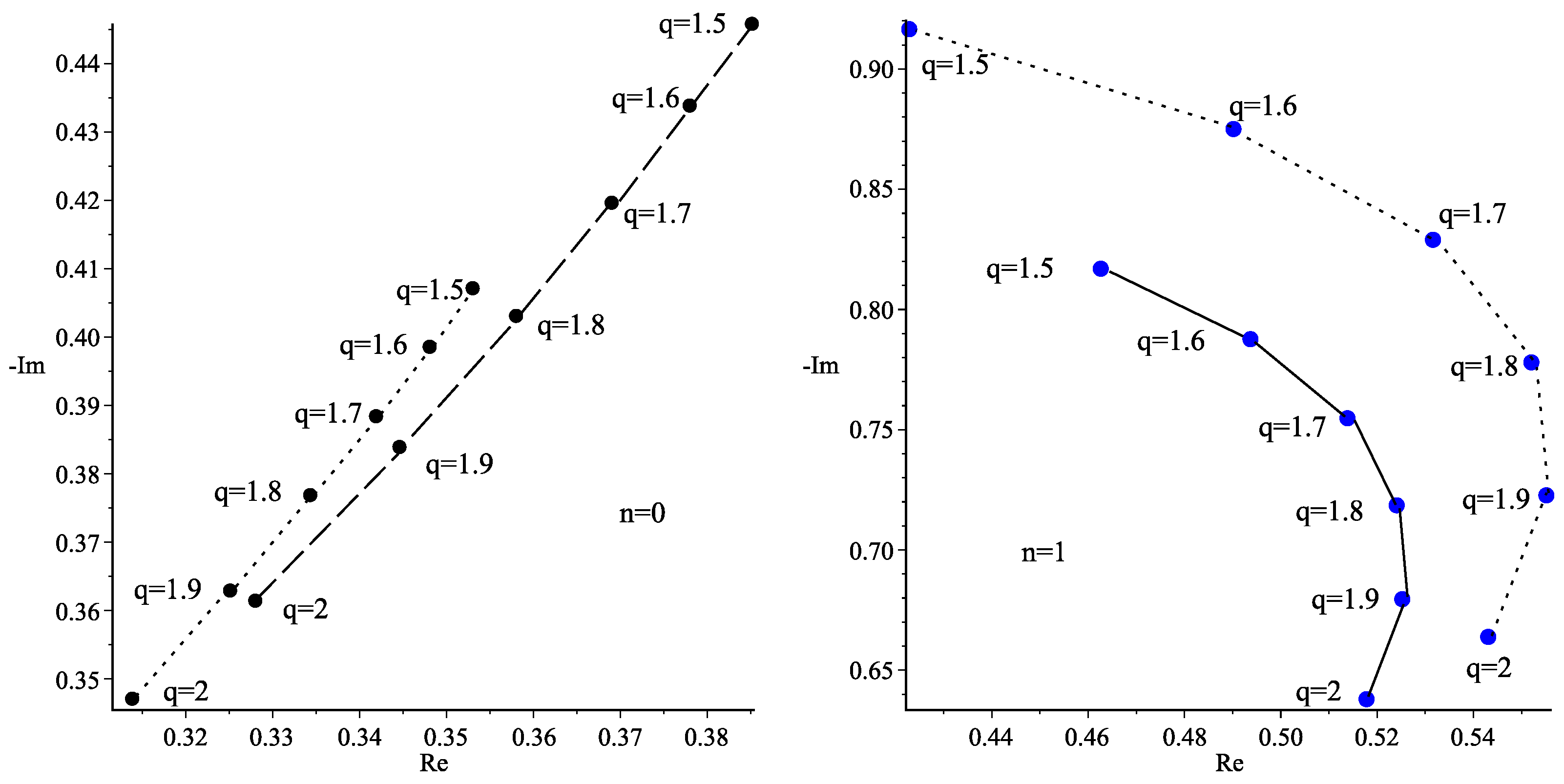
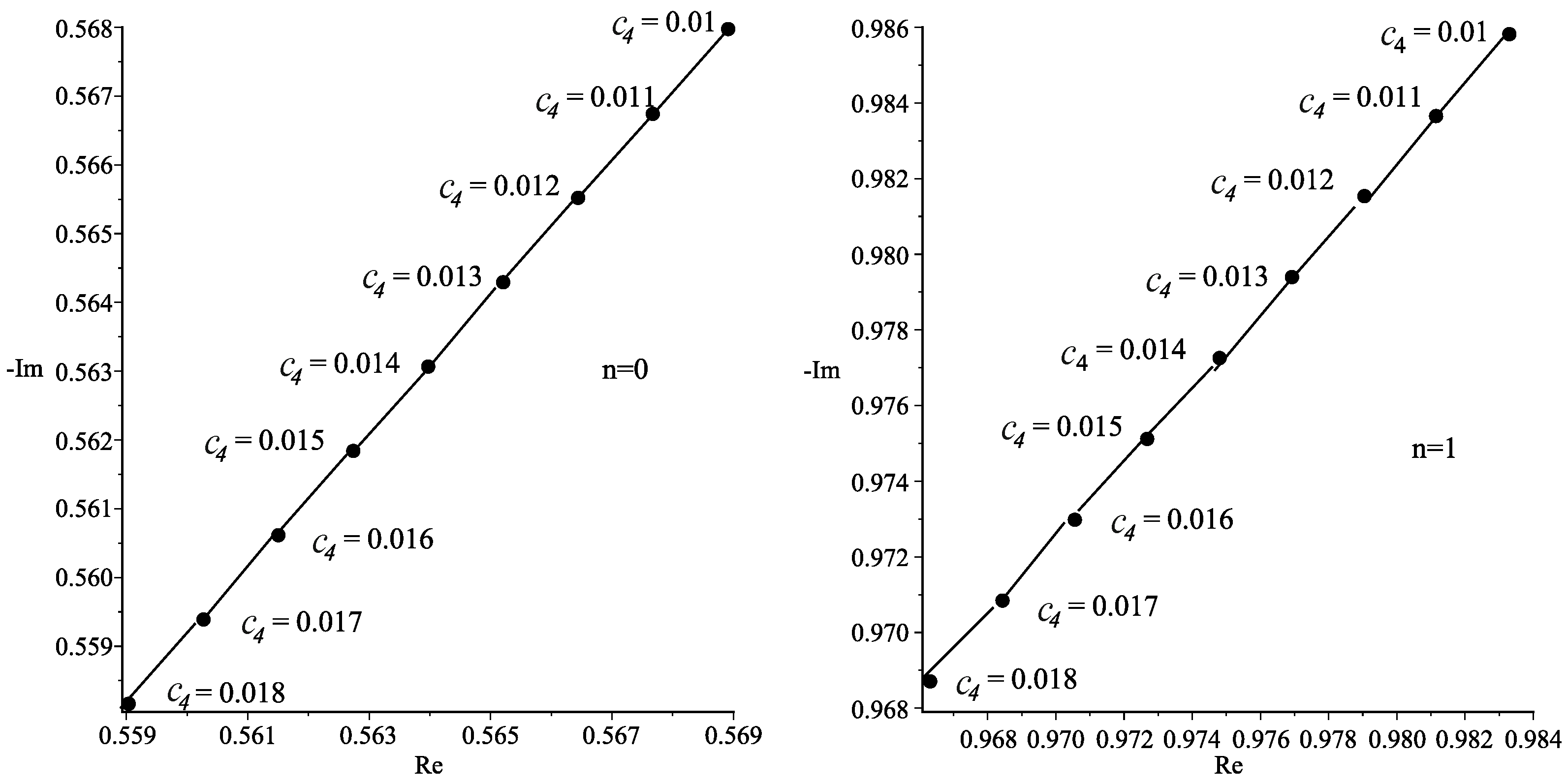
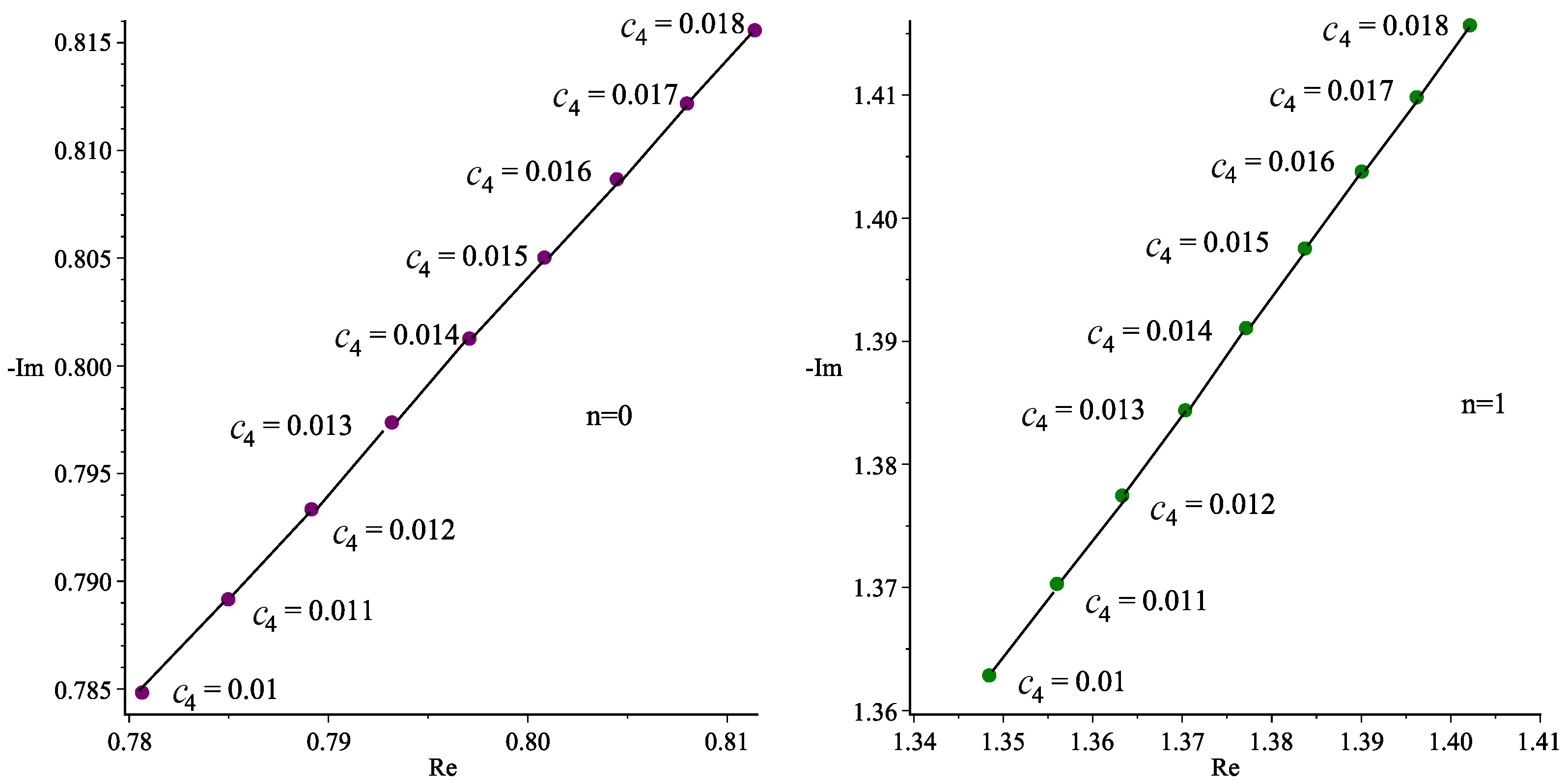
| l | n | c | q | n | q | ||
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1.9 | 1.5 | 0.3531092772–0.4070157966i | 1 | 1.5 | 0.4628156990–0.8165375596i |
| 1.6 | 0.3481646244–0.3984431959i | 1.6 | 0.4939092271–0.7872487864i | ||||
| 1.7 | 0.3419910035–0.3882796385i | 1.7 | 0.5140501121–0.7543542970i | ||||
| 1.8 | 0.3344221195–0.3764501224i | 1.8 | 0.5242699290–0.7181651739i | ||||
| 1.9 | 0.3252048163–0.3627849969i | 1.9 | 0.5254316095–0.6791172459i | ||||
| 2 | 0.3139459780–0.3469628546i | 2 | 0.5180125636–0.6375332598i | ||||
| 1.8 | 1.5 | 0.4171149837–0.4733886692i | 1.5 | 0.4883526041–0.9338811423i | |||
| 1.6 | 0.4079913458–0.4593160345i | 1.6 | 0.5382395015–0.8962742366i | ||||
| 1.7 | 0.3965522968–0.4425772439i | 1.7 | 0.5699039647–0.8530833387i | ||||
| 1.8 | 0.3822146829–0.4227292265i | 1.8 | 0.5845200557–0.8033010248i | ||||
| 1.9 | 0.3639735647–0.3989634900i | 1.9 | 0.5823209373–0.7458662456i | ||||
| 2 | 0.3398557041–0.3697577443i | 2 | 0.5612257904–0.6787904390i | ||||
| 1.7 | 1.5 | 0.3852295784–0.445685725i | 1.5 | 0.4230520984–0.9161599009i | |||
| 1.6 | 0.3780735086–0.4337333922i | 1.6 | 0.4903805959–0.8746300965i | ||||
| 1.7 | 0.3690969050–0.4195188351i | 1.7 | 0.5318064233–0.8285691459i | ||||
| 1.8 | 0.3581027910–0.4029669396i | 1.8 | 0.5522314188–0.7775780030i | ||||
| 1.9 | 0.3446888390–0.3837822213i | 1.9 | 0.5553476661–0.7223112093i | ||||
| 2 | 0.3281070990–0.3613035399i | 2 | 0.5432743870–0.6634326053i |
| l | n | q | n | ||||
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 0.01 | 0.5689309522–0.5679607840i | 1 | 0.01 | 0.9833280391–0.9857933522i |
| 0.011 | 0.5676889204–0.5667273000i | 0.011 | 0.9811788557–0.9836281427i | ||||
| 0.012 | 0.5664589707–0.5655057950i | 0.012 | 0.9790776944–0.9815108377i | ||||
| 0.013 | 0.5652237736–0.5642789170i | 0.013 | 0.9769537380–0.9793708001i | ||||
| 0.014 | 0.5639890661–0.5630524167i | 0.014 | 0.9748305274–0.9772315143i | ||||
| 0.015 | 0.5627548196–0.5618262697i | 0.015 | 0.9727080152–0.9750929361i | ||||
| 0.016 | 0.5615210087–0.5606004477i | 0.016 | 0.9705861561–0.9729550175i | ||||
| 0.017 | 0.5602875984–0.559374939322i | 0.017 | 0.9684648987–0.9708177181i | ||||
| 0.018 | 0.5590545741–0.5581496853i | 0.018 | 0.9663442042–0.9686809854i | ||||
| 2 | 0.01 | 0.7806931526–0.7847869409i | 1 | 0.01 | 1.348548830–1.362771574i | ||
| 0.011 | 0.7850205043–0.7891179837i | 0.011 | 1.356111851–1.370209477i | ||||
| 0.012 | 0.7891946437–0.7932951529i | 0.012 | 1.363406512–1.377383600i | ||||
| 0.013 | 0.7932235382–0.7973263608i | 0.013 | 1.370446745–1.384307536i | ||||
| 0.014 | 0.7971145023–0.8012189424i | 0.014 | 1.377245378–1.390993848i | ||||
| 0.015 | 0.8008742877–0.8049796989i | 0.015 | 1.383814279–1.397454164i | ||||
| 0.016 | 0.8045091827–0.8086149183i | 0.016 | 1.390164462–1.403699260i | ||||
| 0.017 | 0.8080250159–0.8121304478i | 0.017 | 1.396306156–1.409739150i | ||||
| 0.018 | 0.8114272287–0.8155317201i | 0.018 | 1.402248881–1.415583157i |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanzi, S.; Sakallı, İ.; Pourhassan, B. Superradiant (In)stability, Greybody Radiation, and Quasinormal Modes of Rotating Black Holes in Non-Linear Maxwell f(R) Gravity. Symmetry 2023, 15, 873. https://doi.org/10.3390/sym15040873
Kanzi S, Sakallı İ, Pourhassan B. Superradiant (In)stability, Greybody Radiation, and Quasinormal Modes of Rotating Black Holes in Non-Linear Maxwell f(R) Gravity. Symmetry. 2023; 15(4):873. https://doi.org/10.3390/sym15040873
Chicago/Turabian StyleKanzi, Sara, İzzet Sakallı, and Behnam Pourhassan. 2023. "Superradiant (In)stability, Greybody Radiation, and Quasinormal Modes of Rotating Black Holes in Non-Linear Maxwell f(R) Gravity" Symmetry 15, no. 4: 873. https://doi.org/10.3390/sym15040873
APA StyleKanzi, S., Sakallı, İ., & Pourhassan, B. (2023). Superradiant (In)stability, Greybody Radiation, and Quasinormal Modes of Rotating Black Holes in Non-Linear Maxwell f(R) Gravity. Symmetry, 15(4), 873. https://doi.org/10.3390/sym15040873







