Early Identification of Gait Asymmetry Using a Dual-Channel Hybrid Deep Learning Model Based on a Wearable Sensor
Abstract
:1. Introduction
2. Materials and Methods
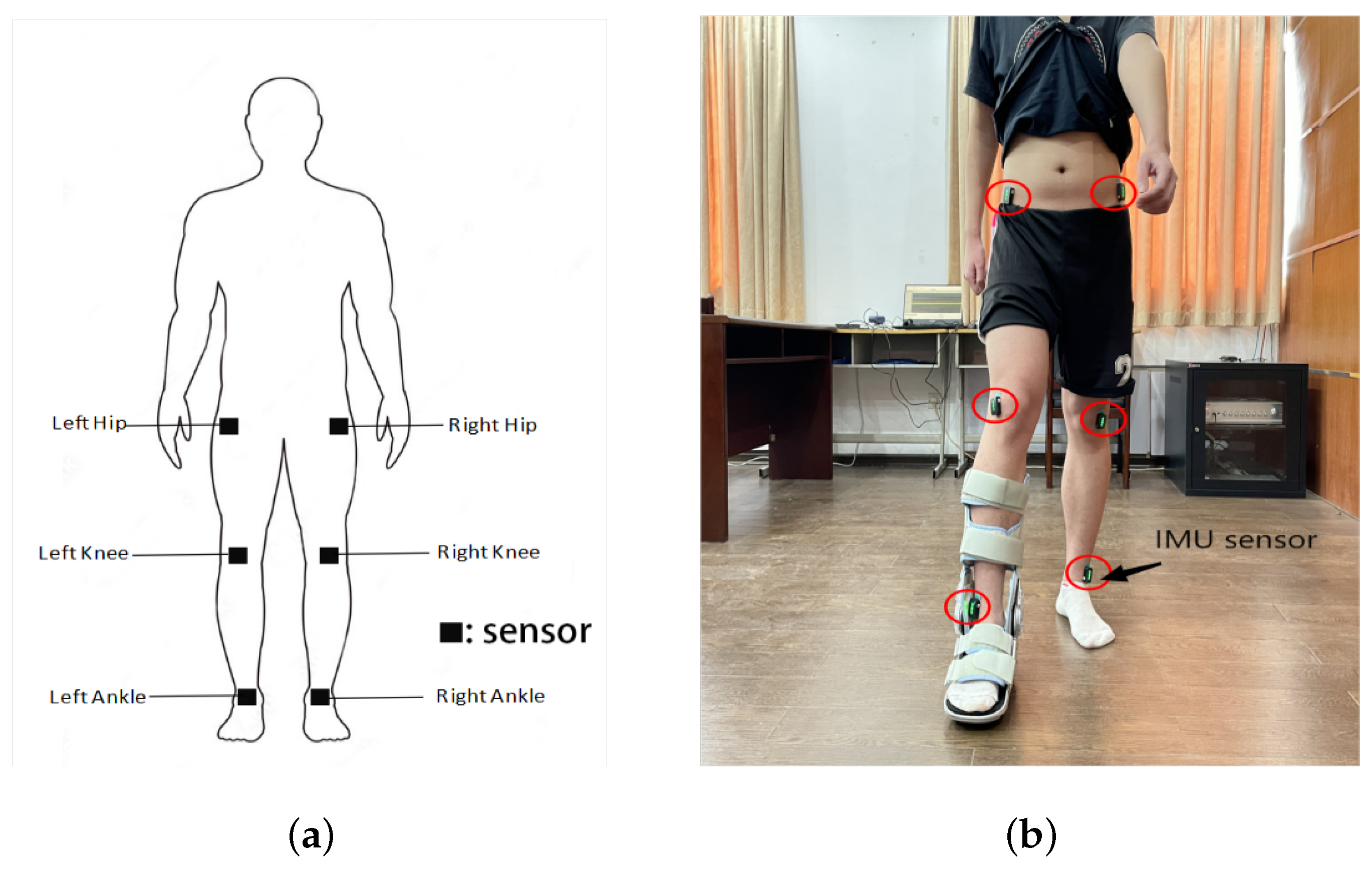
2.1. Acquisition of Multi-Sensor Data
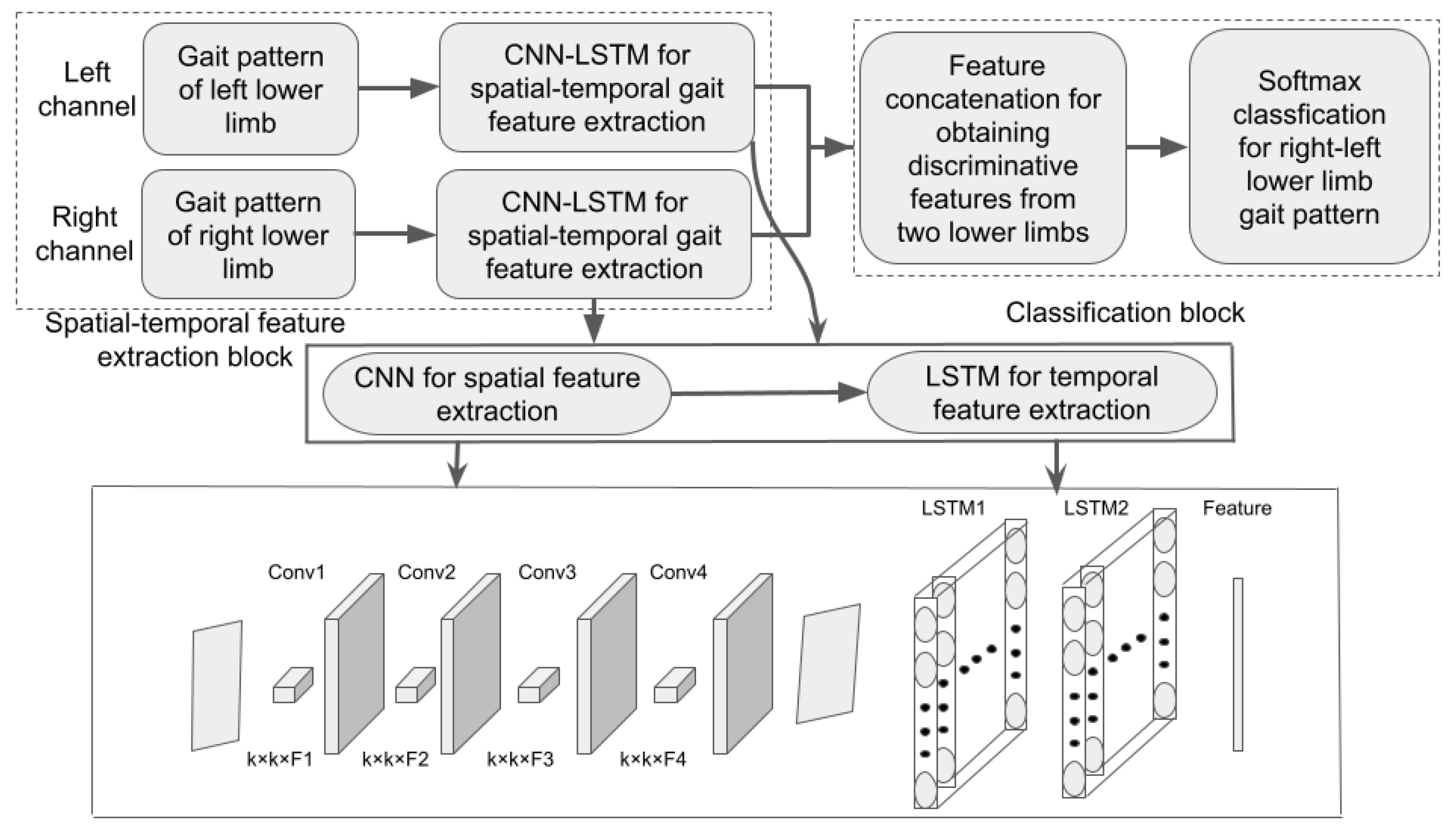
2.2. Cnn-Lstm Hybrid Deep Learning Gait Classification Model
2.2.1. Definition of Gait Pattern of a Lower Limb
2.2.2. Cnn for Spatial Gait Feature Extraction
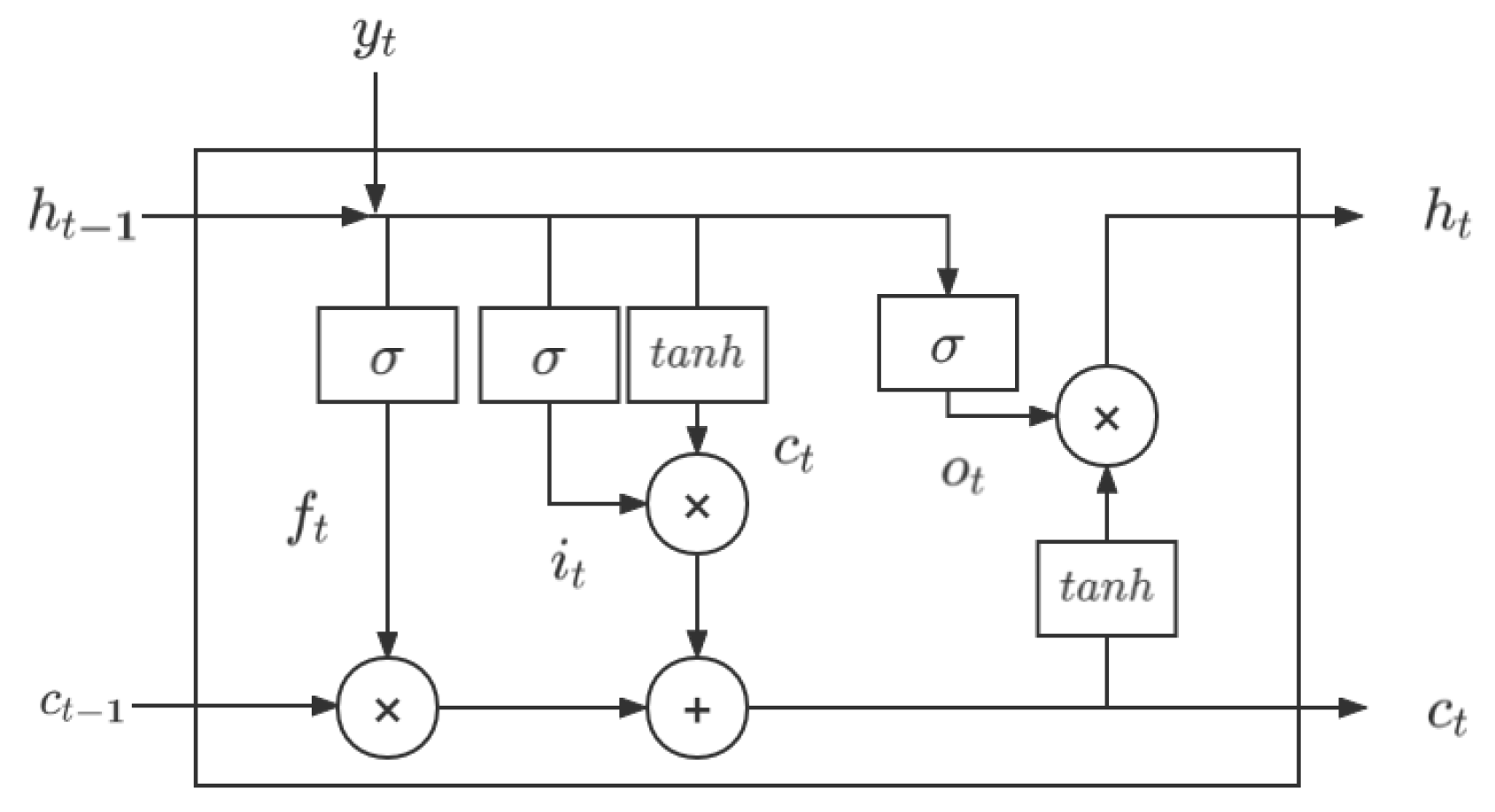
2.2.3. LSTM for Capturing Temporal Dependence Hidden in Gait Spatial Features
2.2.4. Classification of Lower Limb Gait Patterns from Dual-Channels
3. Results
3.1. Construction of Sample Data Set
3.2. Training and Testing Scheme
3.3. Generalization Performance Measurement
- 1.
- Accuracy
- 2.
- Recall
- 3.
- Precision
- 4.
- F1-score
3.4. Evaluation Results of the Accurate Identification of Asymmetric Gait
3.5. Measurement Results of the Generalization Performance
3.6. Evaluation of the Effect of Coupling across Joints of the Lower Limb on Generalization Ability
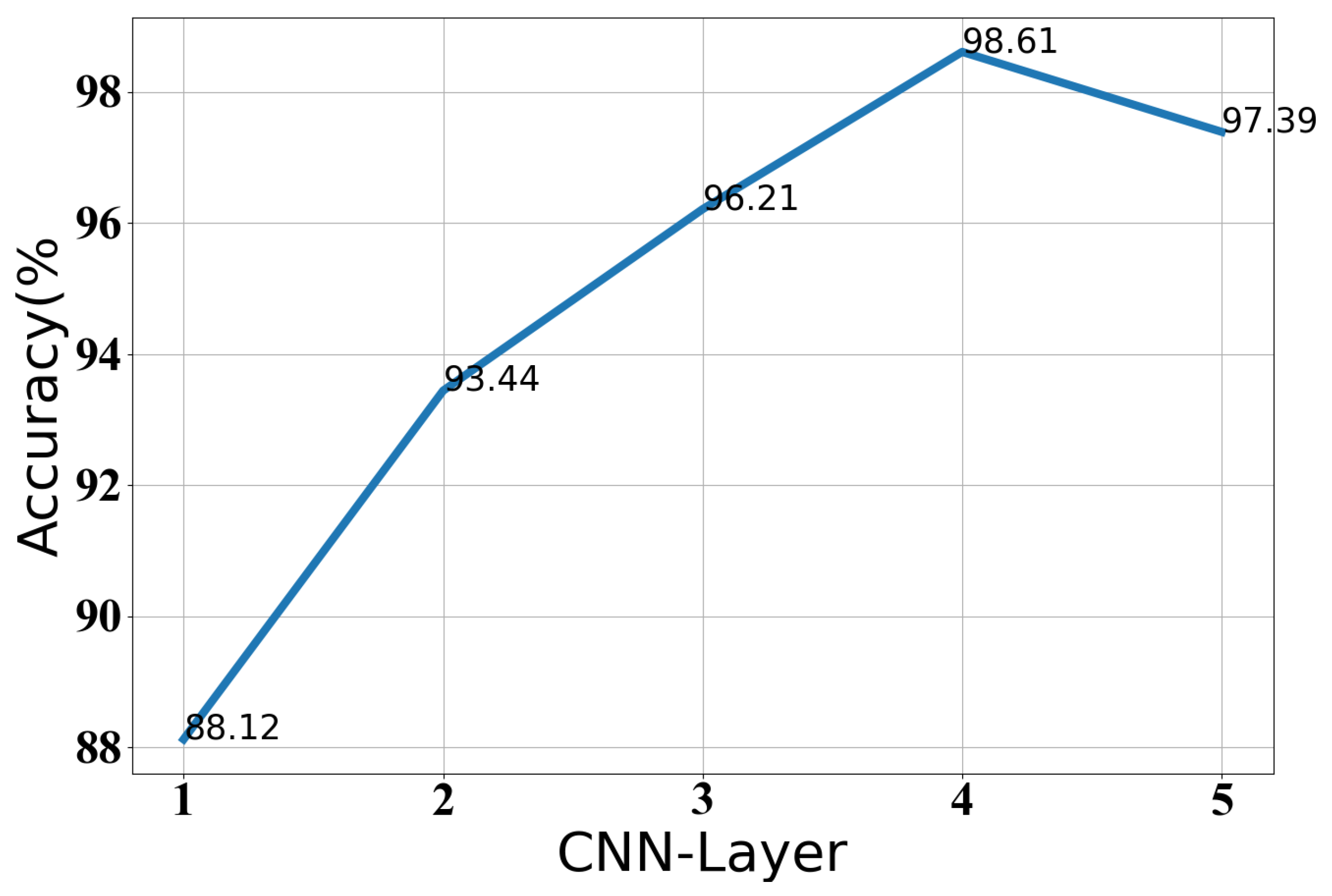
3.7. The Selection of the Optimal Parameters of Our Classification Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CNN | Convolutional Neural Networks |
| LSTM | Long Short-Term Memory |
| RNN | Recurrent Neural Network |
| RF | Random Forest |
| ANN | Artificial Neural Network |
| KNN | K-Nearest Neighbor |
| SVM | Support Vector Machine |
| IMU | Inertial Measurement Unit |
| PCA | Principal Component Analysis |
| MEMS | Micro-Electro-Mechanical System |
References
- Sadeghi, H.; Allard, P.; Prince, F. Symmetry and limb dominance in able-bodied gait: A review. Gait Posture 2000, 12, 34–45. [Google Scholar] [CrossRef] [PubMed]
- Gimunová, M.; Vodička, T.; Bozděch, M.; Vespalec, T. Changes in plantar pressure, contact area and contact time symmetry during the gait 4 weeks before and 12 and 24 weeks after unilateral total hip arthroplasty. Clin. Biomech. 2021, 89, 105473. [Google Scholar] [CrossRef] [PubMed]
- Jørgensen, L.; Crabtree, N.J.; Reeve, J.; Jacobsen, B.K. Ambulatory level and asymmetrical weight bearing after stroke affects bone loss in the upper and lower part of the femoral neck differently: Bone adaptation after decreased mechanical loading. Bone 2000, 27, 701–707. [Google Scholar] [CrossRef] [PubMed]
- Block, J.A.; Shakoor, N. Lower limb osteoarthritis: Biomechanical alterations and implications for therapy. Curr. Opin. Rheumatol. 2010, 22, 544–550. [Google Scholar] [CrossRef]
- Verghese, J.; Wang, C.; Lipton, R.B. Quantitative gait dysfunction and risk of cognitive decline and dementia. J. Neurol. Neurosur. Psychiatry 2007, 78, 929–935. [Google Scholar] [CrossRef] [PubMed]
- Beauchet, O.; Annweiler, C.; Dubost, V. Stops walking when talking: A predictor of falls in older adults? Eur. J. Neurol. 2009, 16, 786–795. [Google Scholar] [CrossRef] [PubMed]
- Wall, J.C.; Turnbull, G.I. Gait asymmetries in residual hemiplegia. Arch. Phys. Med. Rehabil. 1986, 67, 550–553. [Google Scholar]
- Wang, Y.; Mukaino, M.; Ohtsuka, K. Gait characteristics of post-stroke hemiparetic patients with different walking speeds. Int. J. Rehabil. Res. 2020, 43, 69–75. [Google Scholar] [CrossRef]
- Kiwon, P.; Ryan, T.; Jonathan, M. Effects of aging and Parkinson’s disease on joint coupling, symmetry, complexity and variability of lower limb movements during gait. Clin. Biomech. 2016, 33, 92–97. [Google Scholar]
- Xia, Y.; Ye, Q.; Gao, Q. Symmetry analysis of gait between left and right limb using cross-fuzzy entropy. Comput. Math. Methods Med. 2016, 2016, 1737953. [Google Scholar] [CrossRef] [Green Version]
- Viteckova, S.; Khandelwal, S.; Kutilek, P. Gait symmetry methods: Comparison of waveform-based methods and recommendation for use. Biomed. Signal Process. 2020, 55, 101643. [Google Scholar] [CrossRef]
- Ghaderyan, P.; Beyrami, S.M. Neurodegenerative diseases detection using distance metrics and sparse coding: A new perspective on gait symmetric features. Comput. Biol. Med. 2020, 120, 103736. [Google Scholar] [CrossRef] [PubMed]
- Robinson, R.O.; Herzog, W.; Nigg, B.M. Use of force platform variables to quantify the effects of chiropractic manipulation on gait symmetry. J. Manip. Physiol. Ther. 1987, 10, 172–176. [Google Scholar]
- Viteckova, S.; Kutilek, P.; Svoboda, Z. Gait symmetry measures: A review of current and prospective methods. Biomed. Signal Process. Control 2018, 42, 89–100. [Google Scholar] [CrossRef]
- Clemens, S.; Kim, K.J.; Gailey, R.; Kirk-Sanchez, N.; Kristal, A.; Gaunaurd, I. Inertial sensor-based measures of gait symmetry and repeatability in people with unilateral lower limb amputation. Clin. Biomech. 2020, 72, 102–107. [Google Scholar] [CrossRef] [PubMed]
- Caldas, R.; Mundt, M.; Potthast, W. A systematic review of gait analysis methods based on inertial sensors and adaptive algorithms. Gait Posture 2017, 57, 204–210. [Google Scholar] [CrossRef]
- Chen, S.; Lach, J.; Lo, B. Toward pervasive gait analysis with wearable sensors: A systematic review. IEEE J. Biomed. Health 2016, 20, 1521–1537. [Google Scholar] [CrossRef]
- Vienne, A.; Barrois, R.P.; Buffat, S. Inertial sensors to assess gait quality in patients with neurological disorders: A systematic review of technical and analytical challenges. Front. Psychol. 2017, 8, 817. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wafai, L.; Zayegh, A.; Woulfe, J. Automated Classification Of Plantar Pressure Asymmetry During Pathological Gait Using Artificial Neural Network. In Proceedings of the 2nd Middle East Conference on Biomedical Engineering, Doha, Qatar, 17–20 February 2014. [Google Scholar]
- Lemoyne, R.; Heerinckx, F.; Aranca, T. Wearable body and wireless inertial sensors for machine learning classification of gait for people with Friedreich’s ataxia. In Proceedings of the IEEE 13th International Conference on Wearable and Implantable Body Sensor Networks (BSN), San Francisco, CA, USA, 14–17 June 2016. [Google Scholar]
- Hoerzer, S.; Federolf, P.A.; Maurer, C.; Baltich, J.; Nigg, B.M. Footwear Decreases Gait Asymmetry during Running. PLoS ONE 2015, 10, e0138631. [Google Scholar] [CrossRef]
- Nouriani, A.; McGovern, R.A.; Rajamani, R. Step length estimation with wearable sensors using a switched-gain nonlinear observer. Biomed. Signal Process. Control 2021, 69, 102822. [Google Scholar] [CrossRef]
- Watanabe, T.; Saito, H.; Koike, E.; Nitta, K. A preliminary test of measurement of joint angles and stride length with wireless inertial sensors for wearable gait evaluation system. Comput. Intell. Neurosci. 2011, 2011, 975193. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cudejko, T.; Button, K.; Al-Amri, M. Validity and reliability of accelerations and orientations measured using wearable sensors during functional activities. Sci. Rep. 2022, 12, 14619. [Google Scholar] [CrossRef] [PubMed]
- Kulurkar, P.; kumar Dixit, C.; Bharathi, V.C.; Monikavishnuvarthini, A.; Dhakne, A.; Preethi, P. AI based elderly fall prediction system using wearable sensors: A smart home-care technology with IOT. Meas. Sens. 2023, 25, 100614. [Google Scholar] [CrossRef]
- AbdelMaseeh, M.; Chen, T.; Stashuk, D.W. Extraction and Classification of Multichannel Electromyographic Activation Trajectories for Hand Movement Recognition. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 662–673. [Google Scholar] [CrossRef]
- Allen, J.L.; Kautz, S.A.; Neptune, R.R. Step length asymmetry is representative of compensatory mechanisms used in post-stroke hemiparetic walking. Gait Posture 2011, 33, 538–543. [Google Scholar] [CrossRef] [Green Version]
- Gulgin, H.; Hall, K.; Luzadre, A. 3D gait analysis with and without an orthopedic walking boot. Gait Posture 2018, 59, 76–82. [Google Scholar] [CrossRef]
- Khan, A.; Sung, J.E.; Kang, J.W. Multi-channel fusion convolutional neural network to classify syntactic anomaly from language-related ERP components. Inf. Fusion 2019, 52, 53–61. [Google Scholar] [CrossRef]
- Soulard, J.; Vaillant, J.; Balaguier, R. Spatio-temporal gait parameters obtained from foot-worn inertial sensors are reliable in healthy adults in single-and dual-task conditions. Sci. Rep. 2021, 11, 10229. [Google Scholar] [CrossRef] [PubMed]
- Błażkiewicz, M.; Lann vel Lace, K.; Hadamus, A. Gait symmetry analysis based on dynamic time warping. Symmetry 2021, 13, 836. [Google Scholar] [CrossRef]
- McHenry, B.D.; Exten, E.L.; Cross, J.A.; Kruger, K.M.; Law, B.; Fritz, J.M.; Harris, G. Sagittal Subtalar and Talocrural Joint Assessment During Ambulation With Controlled Ankle Movement (CAM) Boots. Foot Ankle Int. 2017, 38, 1260–1266. [Google Scholar] [CrossRef] [PubMed]
- Hammerla, N.; Halloran, S.; Ploetz, T. Deep, convolutional, and recurrent models for human activity recognition using wearable sensor. J. Sci. Comput. 2016, 61, 454–476. [Google Scholar]
- Alex, K.; IIya, S.; Geoffrey, H. Image net classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NA, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural. Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Ramakrishnan, T.; Lahiff, C.A.; Reed, K.B. Comparing gait with multiple physical asymmetries using consolidated metrics. Front. Neurorobotics 2018, 12, 2. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Steinmetzer, T.; Wilberg, S.; Bönninger, I. Analyzing gait symmetry with automatically synchronized wearable sensors in daily life. Microprocess. Microsyst. 2020, 77, 103118. [Google Scholar] [CrossRef]
- Mitchell, E.; Ahmadi, A.; O’Connor, N.E. Automatically Detecting Asymmetric Running Using Time And Frequency Domain Features. In Proceedings of the IEEE 12th International Conference on Wearable and Implantable Body Sensor Networks (BSN), Beijing, China, 9–12 July 2015. [Google Scholar]
- Rovini, E.; Maremmani, C.; Moschetti, A. Comparative motor pre-clinical assessment in Parkinson’s disease using supervised machine learning approaches. Ann. Biomed. Eng. 2018, 46, 2057–2068. [Google Scholar] [CrossRef]
- Abdulhay, E.; Arunkumar, N.; Narasimhan, K. Gait and tremor investigation using machine learning techniques for the diagnosis of Parkinson disease. Future Gener. Comp. Syst. 2018, 83, 366–373. [Google Scholar] [CrossRef]
- Severin, A.C.; Gean, R.P.; Barnes, S.G. Effects of a corrective heel lift with an orthopaedic walking boot on joint mechanics and symmetry during gait. Gait Posture 2019, 73, 233–238. [Google Scholar] [CrossRef]
- Lann Vel Lace, K.; Błazkiewicz, M. A review of the effect of a Walker ankle-foot orthosis on gait biomechanics in healthy individuals. Postep. Rehabil. 2021, 35, 40. [Google Scholar] [CrossRef]



| Walking Patterns | Classification Model | Classification Results | |||
|---|---|---|---|---|---|
| Precision (%) | Recall (%) | F1 (%) | Accuracy (%) | ||
| wearing a boot with 30 degrees of adjustment | CNN-LSTM | 99.59 | 99.62 | 99.72 | 99.59 |
| wearing a boot with 20 degrees of adjustment | CNN-LSTM | 99.45 | 99.59 | 99.66 | 99.62 |
| wearing a boot with 0 degrees of adjustment | CNN-LSTM | 98.80 | 98.41 | 98.60 | 98.61 |
| wearing no boot | CNN-LSTM | 52.94 | 44.53 | 48.37 | 52.47 |
| Classification Models | Classification Results | |||
|---|---|---|---|---|
| Precision (%) | Recall (%) | F1 (%) | Accuracy (%) | |
| CNN–LSTM | 98.80 | 98.41 | 98.60 | 98.61 |
| CNN | 93.18 | 88.08 | 90.56 | 92.38 |
| LSTM | 89.97 | 75.39 | 82.04 | 83.49 |
| PCA–SVM | 66.60 | 69.02 | 67.79 | 68.35 |
| SVM | 66.21 | 53.47 | 59.16 | 54.29 |
| Classification Models | SVM | ANN | RF | Our Model |
|---|---|---|---|---|
| Accuracy (%) | 63.28 | 74.21 | 81.54 | 93.35 |
| Models | CNN Layers | LSTM Layers | Kernel Size | Hidden Cell | Learning Rate | Dropout |
|---|---|---|---|---|---|---|
| CNN | 4 | / | 5 × 5 | / | 0.01 | 0.5 |
| LSTM | / | 2 | / | 18 | 0.01 | 0.5 |
| CNN–LSTM | 4 | 2 | 3 × 3 | 24 | 0.01 | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Liu, Y.; Wu, X. Early Identification of Gait Asymmetry Using a Dual-Channel Hybrid Deep Learning Model Based on a Wearable Sensor. Symmetry 2023, 15, 897. https://doi.org/10.3390/sym15040897
Wu J, Liu Y, Wu X. Early Identification of Gait Asymmetry Using a Dual-Channel Hybrid Deep Learning Model Based on a Wearable Sensor. Symmetry. 2023; 15(4):897. https://doi.org/10.3390/sym15040897
Chicago/Turabian StyleWu, Jianning, Yuanbo Liu, and Xiaoyan Wu. 2023. "Early Identification of Gait Asymmetry Using a Dual-Channel Hybrid Deep Learning Model Based on a Wearable Sensor" Symmetry 15, no. 4: 897. https://doi.org/10.3390/sym15040897
APA StyleWu, J., Liu, Y., & Wu, X. (2023). Early Identification of Gait Asymmetry Using a Dual-Channel Hybrid Deep Learning Model Based on a Wearable Sensor. Symmetry, 15(4), 897. https://doi.org/10.3390/sym15040897






