Numerical Simulation for COVID-19 Model Using a Multidomain Spectral Relaxation Technique
Abstract
:1. Introduction
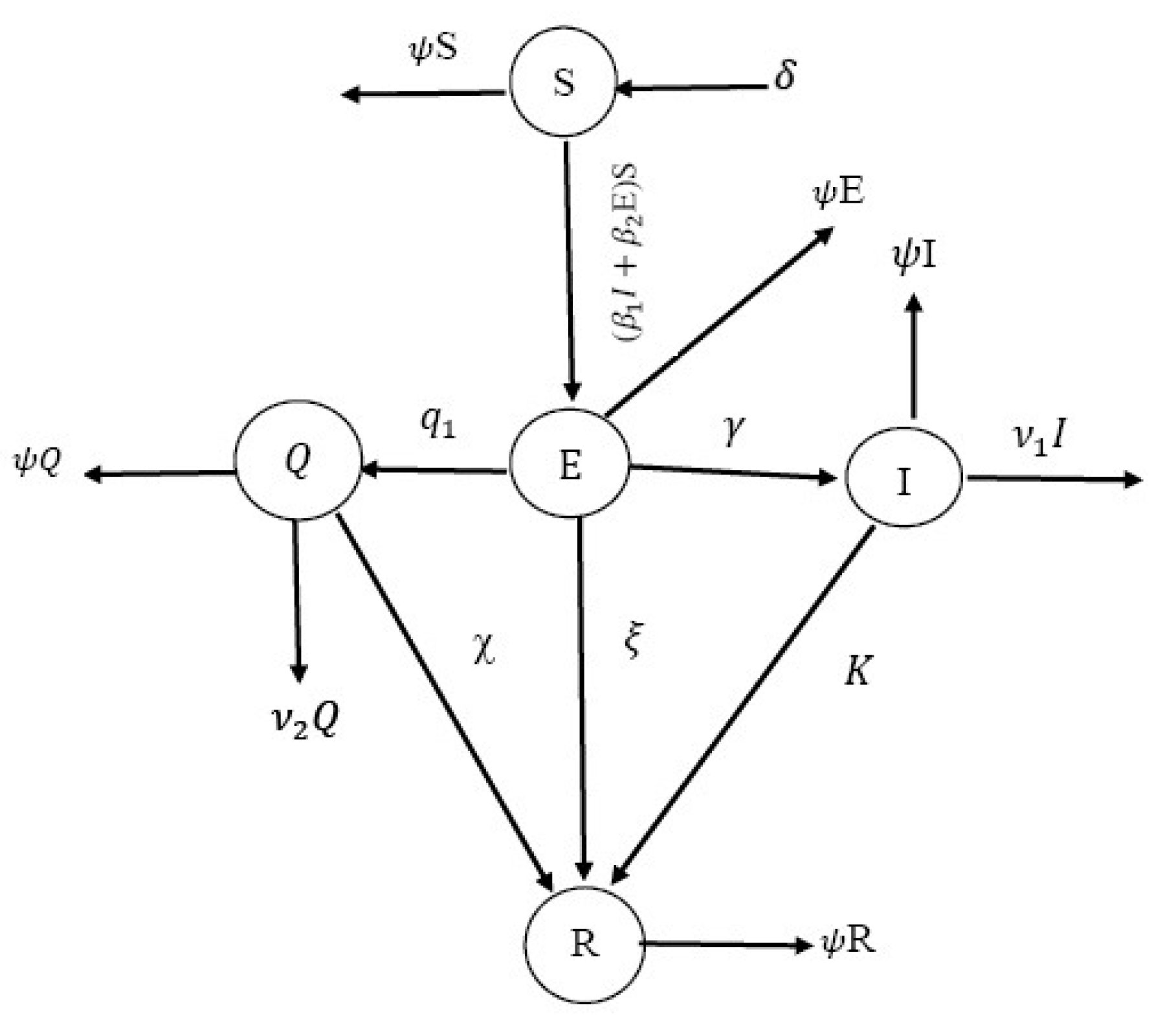
2. General Observations and Notions
2.1. Some Concepts on the COVID-19 Model
- If there is no COVID-19, the model is an equilibrium point.
- In general, the equilibrium takes the form , where
2.2. Non-Negative Solutions, Equilibrium Points and Stability
- 1.
- is the unique solution of (1) and leftover in .
- 2.
- If , then the disease free equilibrium point is locally asymptotically stable (LAS).
- 3.
- The endemic equilibrium point is LAS iff .
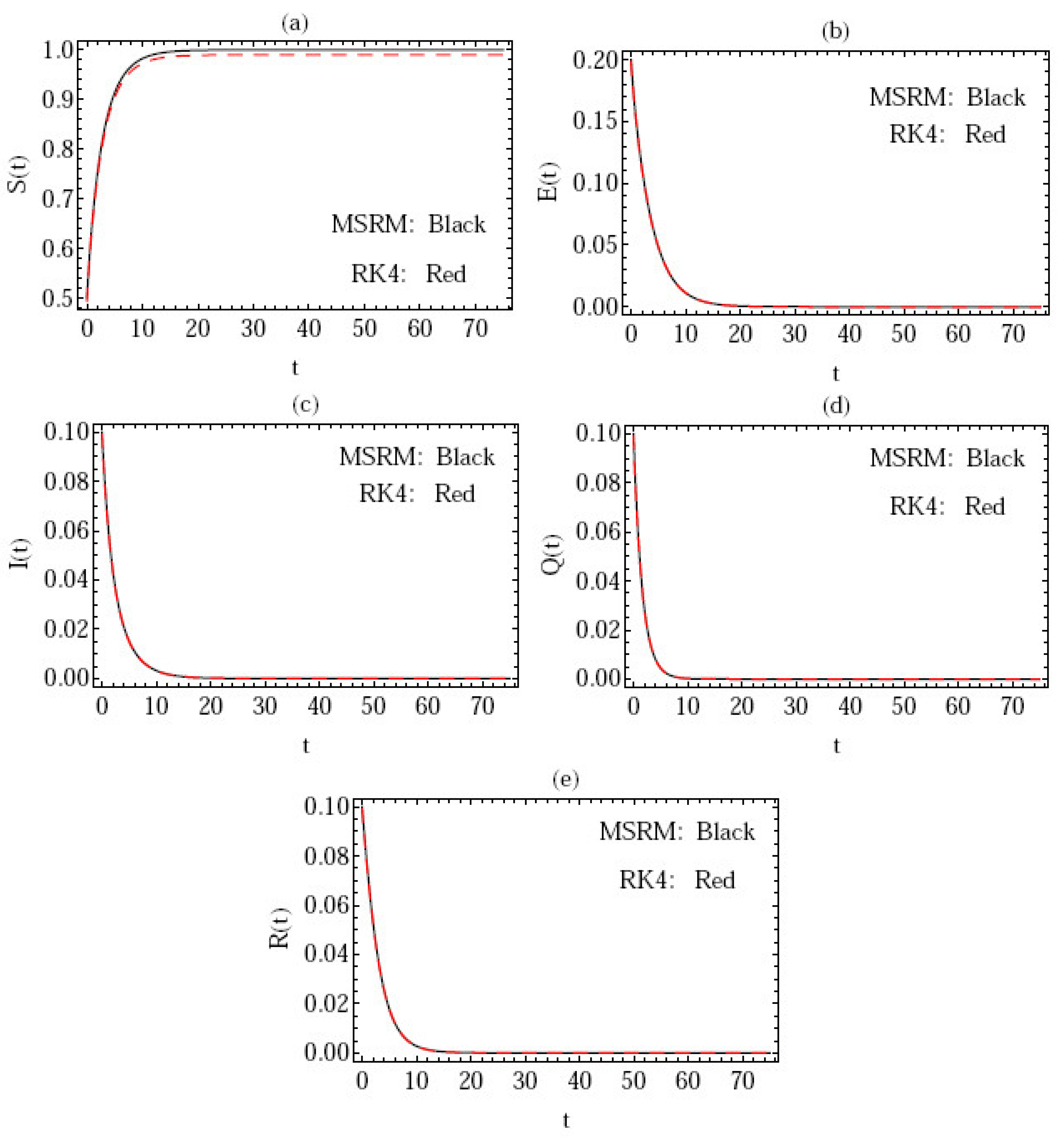
3. Numerical Implementation of the MSRM
4. Error Analysis
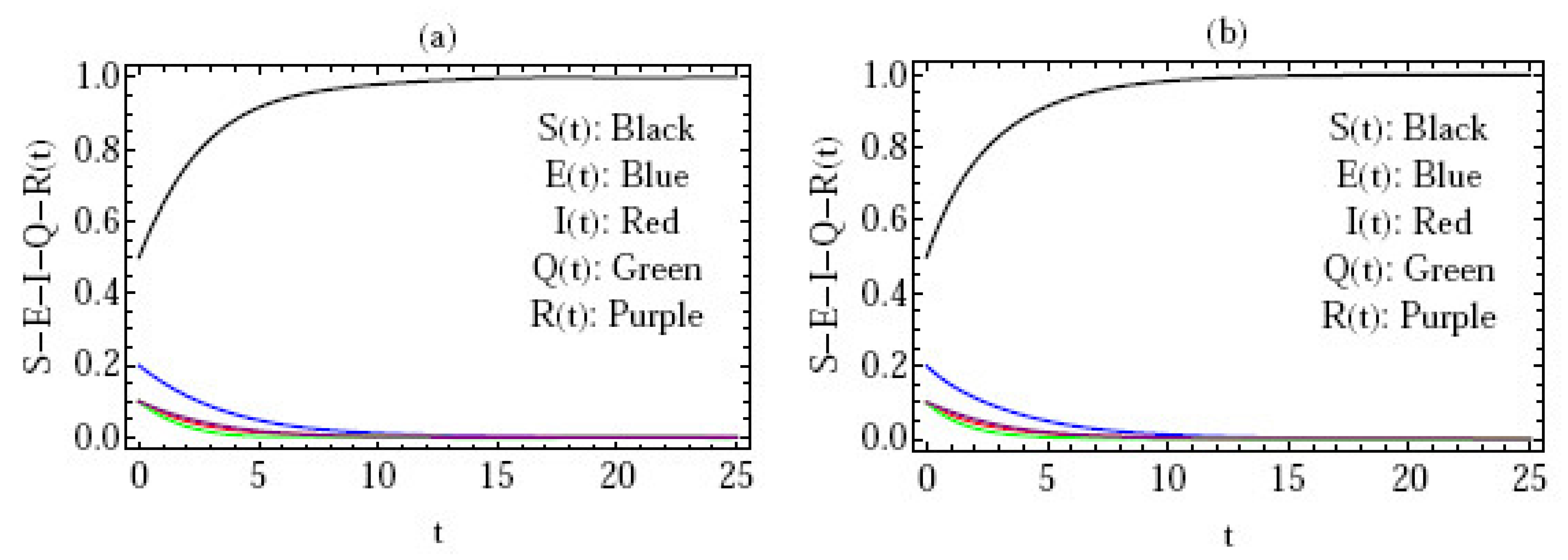
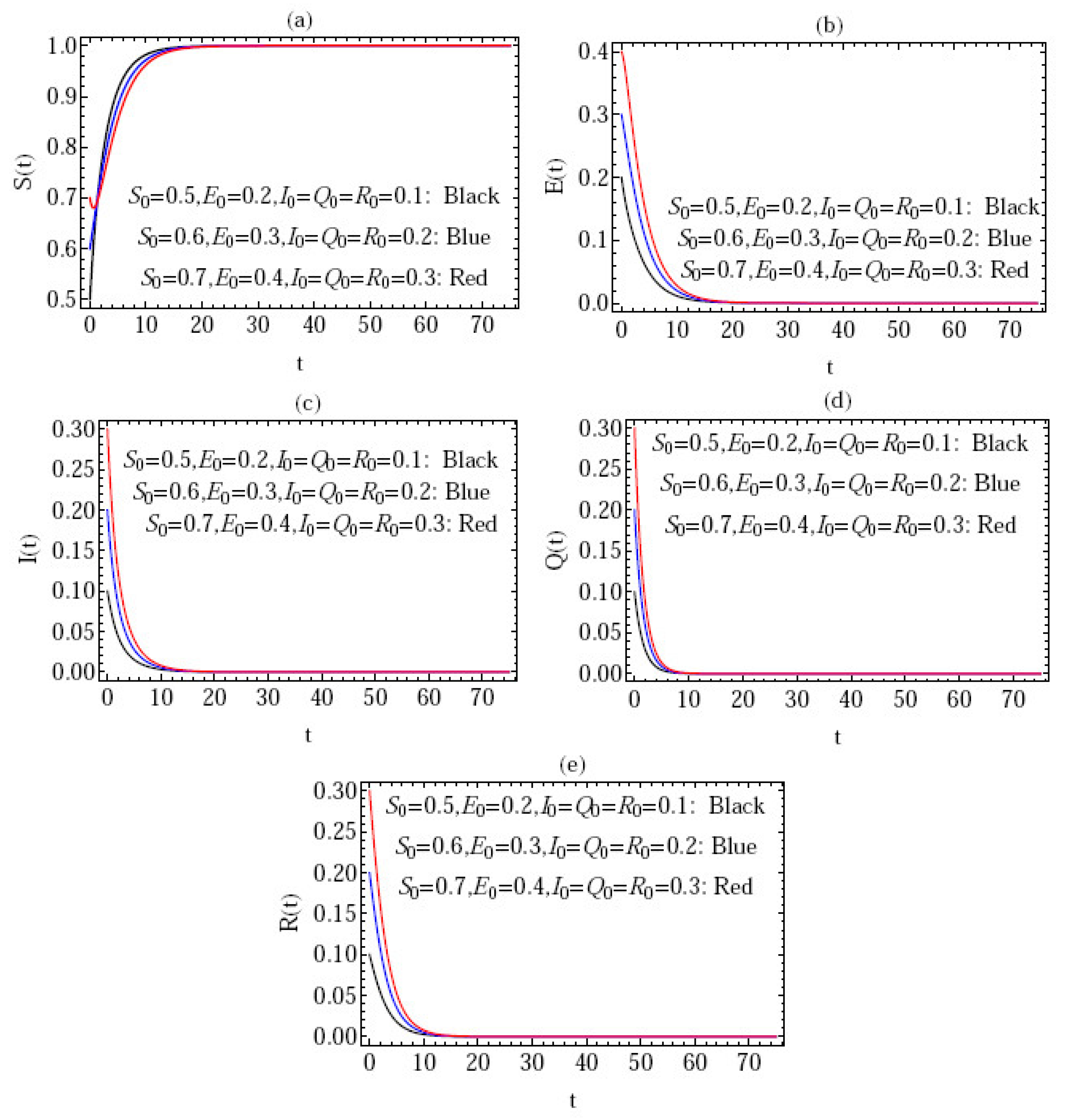
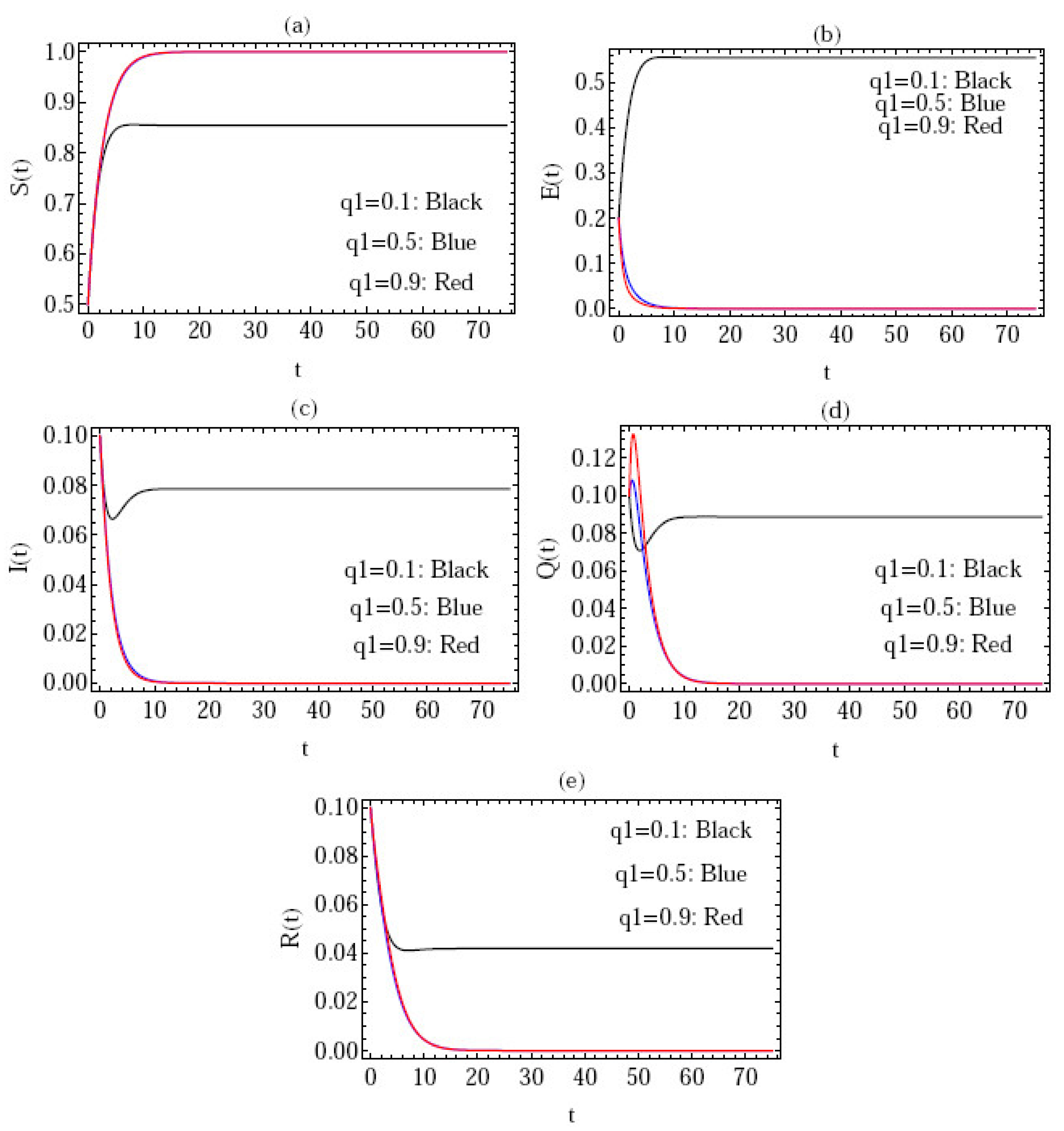
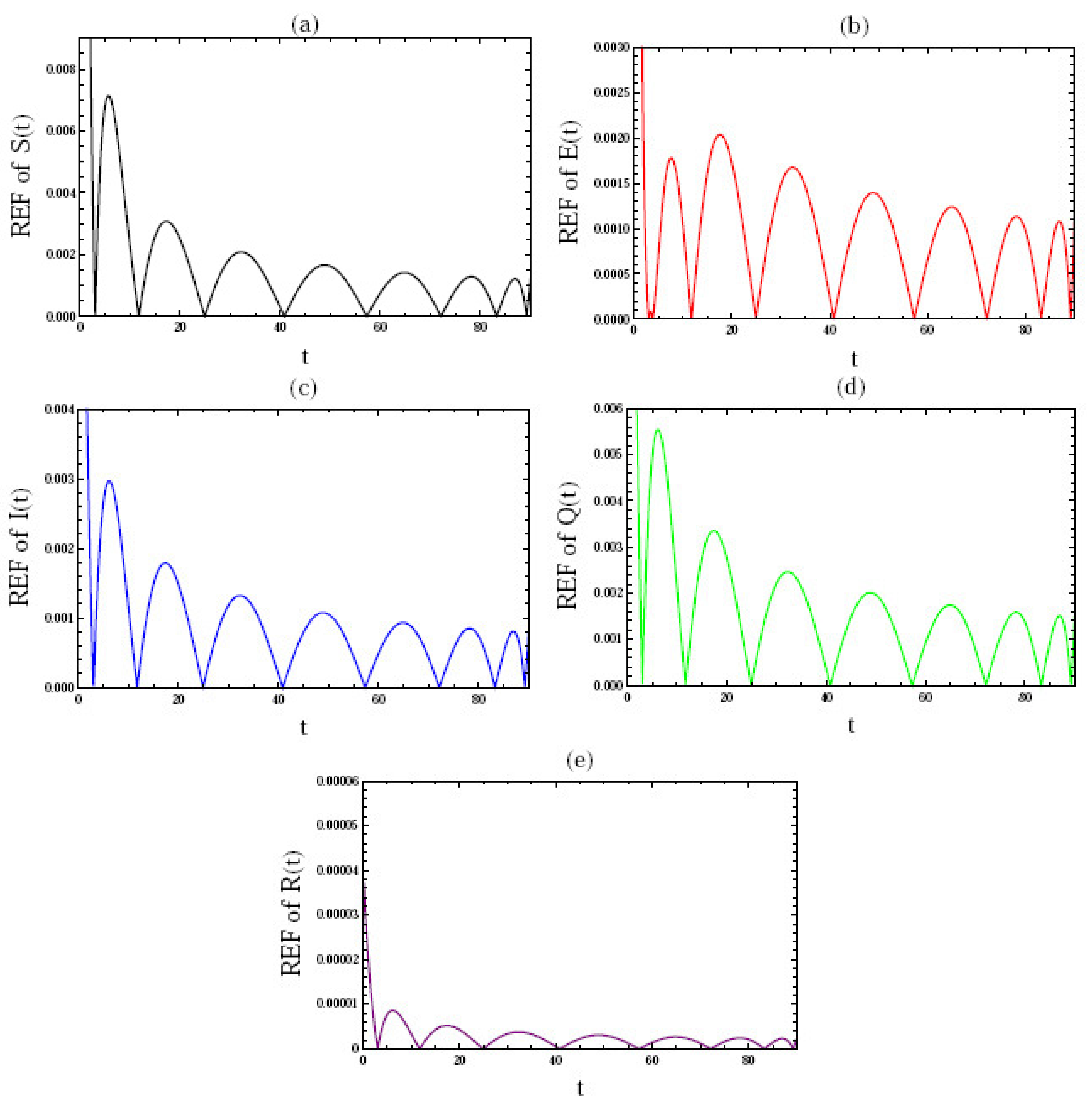
5. Numerical Simulation
- Figure 3 gives the behavior of the approximate solution under the distinct initial solution with in the interval (), and the parameters ; where are plotted in Figure 3a–e, respectively. Here, we give the following three cases:
- i.
- ;
- ii.
- ;
- iii.
- .
In the above three cases, we can confirm that the condition of stability is satisfied, i.e., .
6. Conclusions
- The suggested approach is efficient and reliable.
- The approach has the capacity to apply a limited number of series solution terms to produce precise results.
- There are several benefits to using this approach to solve this kind of problem.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ahmed, I.; Modu, G.U.; Yusuf, A.; Kumam, P.; Yusuf, I. A mathematical model of Coronavirus Disease (COVID-19) containing asymptomatic and symptomatic classes. Results Phys. 2021, 21, 103776. [Google Scholar] [CrossRef]
- Sen, M.D.; Ibeas, A.; Agarwal, R.P. On confinement and quarantine concerns on an SEIAR epidemic model with simulated parameterizations for the COVID-19 pandemic. Symmetry 2020, 12, 1646. [Google Scholar] [CrossRef]
- Srinivasa, K.; Baskonus, H.M.; Sanchez, Y.G. Numerical solutions of the mathematical models on the digestive system and COVID-19 pandemic by Hermite wavelet technique. Symmetry 2021, 13, 2428. [Google Scholar] [CrossRef]
- World Health Organization. Report of the WHO—China Joint Mission on Coronavirus Disease: 2019 (COVID-19); World Health Organization: Geneva, Switzerland, 2020. [Google Scholar]
- Agarwal, P.; Agarwal, R.P.; Ruzhansky, M. Special Functions and Analysis of Differential Equations; Chapman and Hall/CRC: Boca Raton, FL, USA, 2020. [Google Scholar]
- Basti, B.; Hammami, N.; Berrabah, I.; Nouioua, F.; Djemiat, R.; Benhamidouche, N. Stability analysis and existence of solutions for a modified SIRD model of COVID-19 with fractional derivatives. Symmetry 2021, 13, 1431. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M. Novel expressions for the derivatives of sixth kind Chebyshev polynomials: Spectral solution of the non-linear one-dimensional Burgers’ equation. Fractal Fract. 2021, 5, 53. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Khader, M.M.; Adel, M. On the fundamental equations for modeling neuronal dynamics. J. Adv. Res. 2014, 5, 253–259. [Google Scholar] [CrossRef]
- Khader, M.M.; Sweilam, N.H.; Mahdy, A.M.S.; Moniem, N.K.A. Numerical simulation for the fractional SIRC model and influenza A. Appl. Math. Inf. Sci. 2014, 8, 1029–1036. [Google Scholar] [CrossRef]
- Aslan, M.F.; Sabanci, K.; Ropelewska, E. A new approach to COVID-19 detection: An ANN proposal optimized through tree-seed algorithm. Symmetry 2022, 14, 1310. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M. Helminth infections of humans: Mathematical models, population dynamics. and control. Adv. Parasitol. 1985, 24, 1–101. [Google Scholar]
- Meng, X.; Zhao, S.; Feng, T.; Zhang, T. Dynamics of a novel nonlinear stochastic SIS epidemic model with the double epidemic hypothesis. J. Math. Anal. Appl. 2016, 433, 227–242. [Google Scholar] [CrossRef]
- Kabir, K.A.; Kuga, K.; Tanimoto, J. Analysis of SIR epidemic model with information spreading of awareness. Chaos Solitons Fract. 2019, 119, 118–125. [Google Scholar] [CrossRef]
- Dokuyucu, M.A.; Celik, E.; Bulut, H.; Baskonus, H.M. Cancer treatment model with the Caputo-Fabrizio fractional derivative. Eur. Phys. J. Plus 2018, 133, 92. [Google Scholar] [CrossRef]
- Gunwehan, H.; Kaabar, K.A.K.; Celik, E. Novel Analytical and Approximate-Analytical Methods for Solving the Nonlinear Fractional Smoking Mathematical Model. Sigma J. Eng. Nat. Sci. 2022. [Google Scholar] [CrossRef]
- Adel, M.; Sweilam, N.H.; Khader, M.M.; Ahmed, S.M.; Ahmad, H.; Botmart, T. Numerical simulation using the non-standard weighted average FDM for 2Dim variable-order Cable equation. Results Phys. 2022, 39, 105682. [Google Scholar] [CrossRef]
- Dokuyucu, M.A.; Celik, E. Analyzing a novel coronavirus model (COVID-19) in the sense of Caputo-Fabrizio fractional operator. Appl. Comput. Math. 2021, 20, 49–69. [Google Scholar]
- Agarwal, P.; Nieto, J.J.; Ruzhansky, M.; Torres, D.F.M. Analysis of Infectious Disease Problems (COVID-19) and their Global Impact; Springer: Singapore, 2021. [Google Scholar]
- Batiha, I.M.; Obeidat, A.; Alshorm, S.; Alotaibi, A.; Alsubaie, H.; Momani, S.; Albdareen, M.; Zouidi, F.; Jahanshahi, S.M.E.H. A numerical confirmation of a fractional-order COVID-19 Model’s efficiency. Symmetry 2022, 14, 2583. [Google Scholar] [CrossRef]
- Abuasbeh, K.; Shafqat, R.; Alsinai, A.; Awadalla, M. Analysis of the mathematical modeling of COVID-19 by using mild solution with delay Caputo operator. Symmetry 2023, 15, 286. [Google Scholar] [CrossRef]
- Butt, A.I.K.; Imran, M.; Batool, S.; Nuwairan, M.A. Theoretical analysis of a COVID-19 CF-fractional model to optimally control the spread of pandemic. Symmetry 2023, 15, 380. [Google Scholar] [CrossRef]
- Khader, M.M.; Adel, M. Chebyshev wavelet procedure for solving FLDEs. Acta Appl. Math. 2018, 158, 1–10. [Google Scholar] [CrossRef]
- Chowdhury, M.S.H.; Hashim, I.; Momani, S. The multistage homotopy-perturbation method: A powerful scheme for handling the Lorenz system. Chaos Solitons Fractals 2009, 40, 1929–1937. [Google Scholar] [CrossRef]
- Motsa, S.S.; Dlamini, P.; Khumalo, M. A new multistage spectral relaxation method for solving chaotic initial value systems. Nonlinear Dyn. 2013, 72, 265–283. [Google Scholar] [CrossRef]
- Motsa, S.S.; Dlamini, P.G.; Khumalo, M. Solving hyperchaotic systems using the spectral relaxation method. Abstr. Appl. Anal. 2012, 2012, 203461. [Google Scholar] [CrossRef]
- Khan, M.S.; Khan, M.I. A novel numerical algorithm based on Galerkin-Petrov time-discretization method for solving chaotic nonlinear dynamical systems. Nonlinear Dyn. 2018, 91, 1555–1569. [Google Scholar] [CrossRef]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods in Fluid Dynamics; Springer: New York, NY, USA, 1988. [Google Scholar]
- Kouagou, J.N.; Dlamini, P.G.; Simelane, S.M. On the multi-domain compact finite difference relaxation method for high dimensional chaos: The nine-dimensional Lorenz system. Alex. Eng. J. 2020, 59, 2617–2625. [Google Scholar] [CrossRef]
- Ibrahim, Y.; Khader, M.M.; Megahed, A.; Abdelsalam, F.; Adel, M. An efficient numerical simulation for a fractional COVID-19 model by using the GRK4M together with and the fractional FDM. Fractal Fract. 2022, 12, 304. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Youssri, Y.H. Sixth-kind Chebyshev spectral approach for solving fractional differential equations. Int. J. Nonlinear Sci. Numer. Simul. 2019, 20, 191–203. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M. New Galerkin operational matrix of derivatives for solving Lane-Emden singular-type equations. Eur. Phys. J. Plus 2015, 130, 52. [Google Scholar] [CrossRef]
- Trefethen, L.N. Spectral Methods in MATLAB; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Rafiq, M.; Macias-Diaz, J.E.; Raza, A.; Ahmed, N. Design of a nonlinear model for the propagation of COVID-19 and its efficient nonstandard computational implementation. Appl. Math. Model. 2021, 89, 1835–1846. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.A.P.; Metz, J.A. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990, 14, 365–382. [Google Scholar]
- Khader, M.M.; Adel, M. Modeling and numerical simulation for covering the fractional COVID-19 model using spectral collocation-optimization algorithm. Fractal Fract. 2022, 6, 363. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, S. A new fractional modeling on Susceptible-Infected-Recovered equations with constant vaccination rate. Nonlinear Eng. 2014, 3, 11–16. [Google Scholar] [CrossRef]
- Khan, M.A.; Atangana, A. Modeling the dynamics of novel coronavirus (2019-nCoV) with fractional derivative. Alex. Eng. J. 2020, 56, 2379–2389. [Google Scholar] [CrossRef]
- Dlamini, P.; Simelane, S. An efficient spectral method-based algorithm for solving a high-dimensional chaotic Lorenz system. J. Appl. Comput. Mech. 2021, 7, 225–234. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adel, M.; Khader, M.M.; Assiri, T.A.; Kallel, W. Numerical Simulation for COVID-19 Model Using a Multidomain Spectral Relaxation Technique. Symmetry 2023, 15, 931. https://doi.org/10.3390/sym15040931
Adel M, Khader MM, Assiri TA, Kallel W. Numerical Simulation for COVID-19 Model Using a Multidomain Spectral Relaxation Technique. Symmetry. 2023; 15(4):931. https://doi.org/10.3390/sym15040931
Chicago/Turabian StyleAdel, Mohamed, Mohamed M. Khader, Taghreed A. Assiri, and Wajdi Kallel. 2023. "Numerical Simulation for COVID-19 Model Using a Multidomain Spectral Relaxation Technique" Symmetry 15, no. 4: 931. https://doi.org/10.3390/sym15040931
APA StyleAdel, M., Khader, M. M., Assiri, T. A., & Kallel, W. (2023). Numerical Simulation for COVID-19 Model Using a Multidomain Spectral Relaxation Technique. Symmetry, 15(4), 931. https://doi.org/10.3390/sym15040931





