Heat and Mass Transfer on Magnetohydrodynamics Casson Carbon Nanotubes Nanofluid Flow in an Asymmetrical Channel via Porous Medium
Abstract
1. Introduction
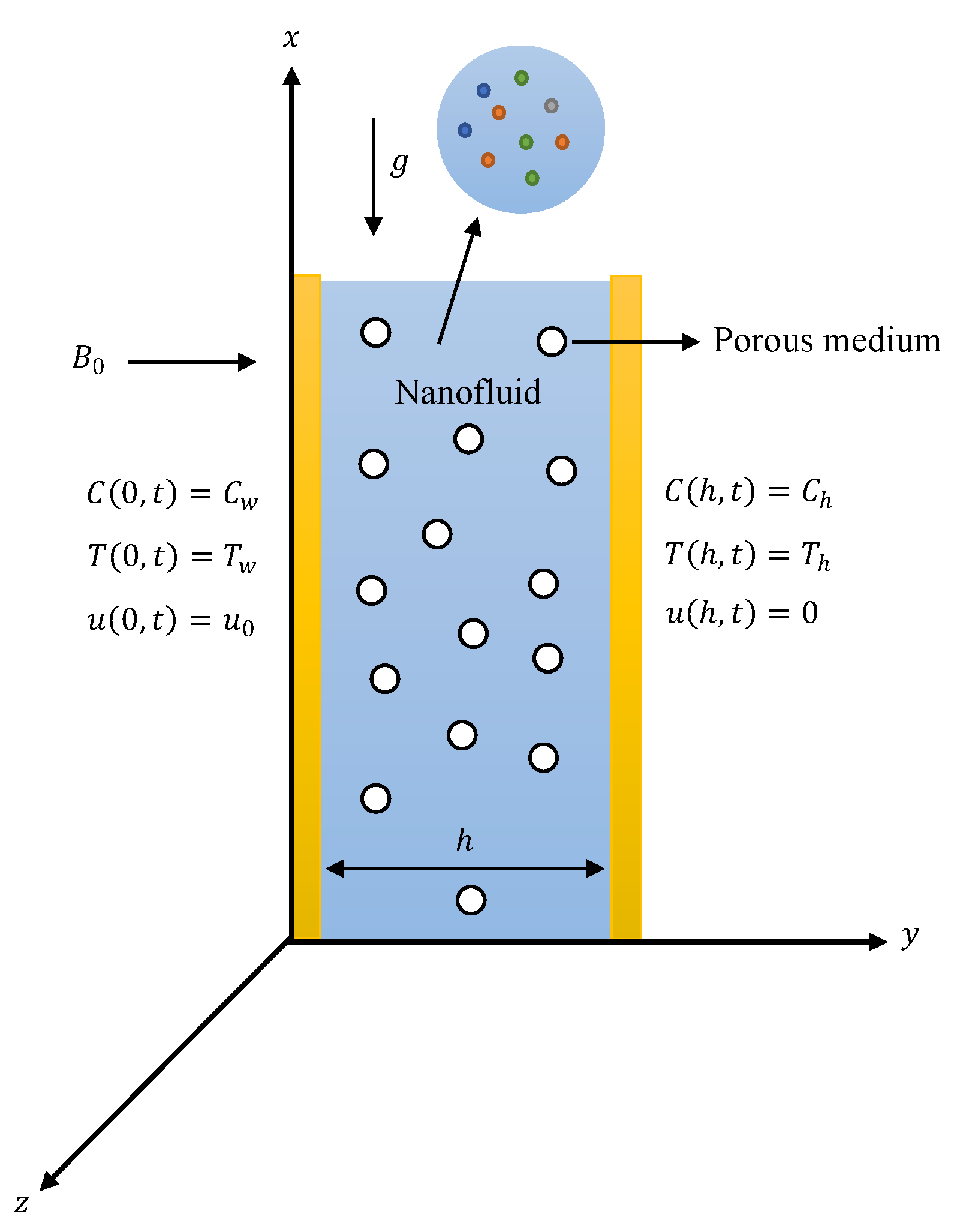
2. Mathematical Formulation
3. Problem Solution
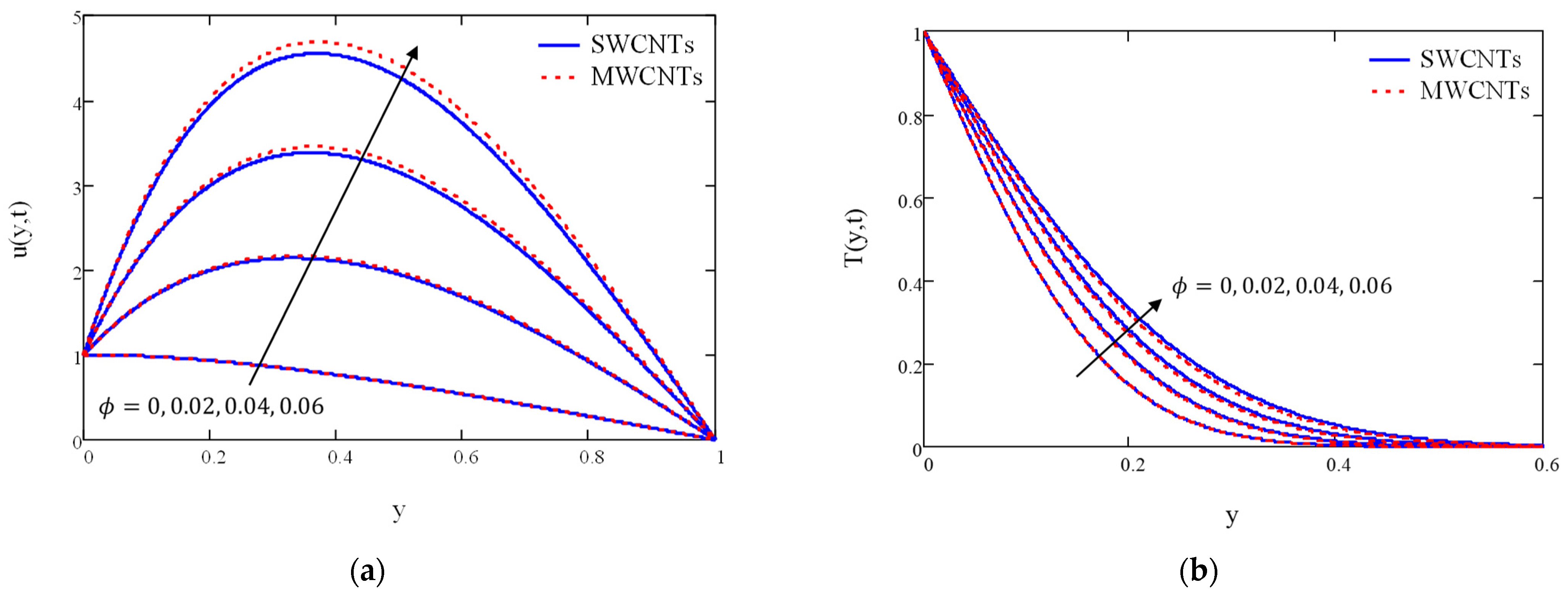
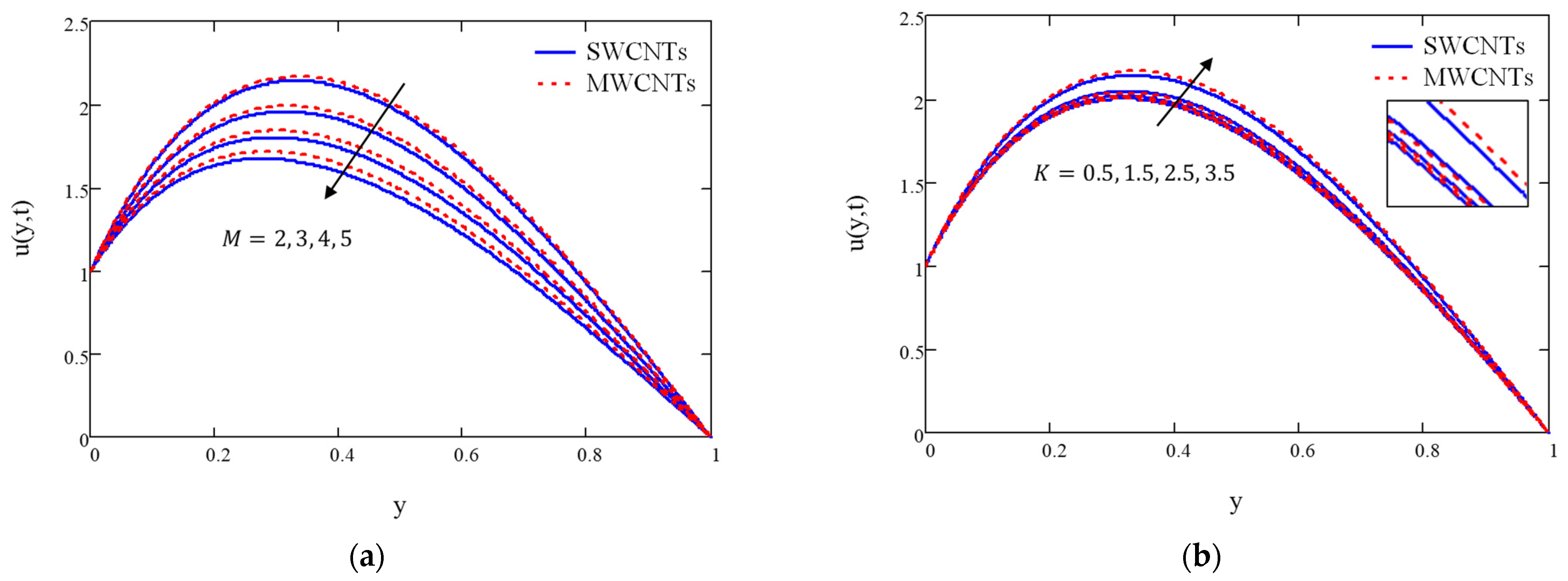
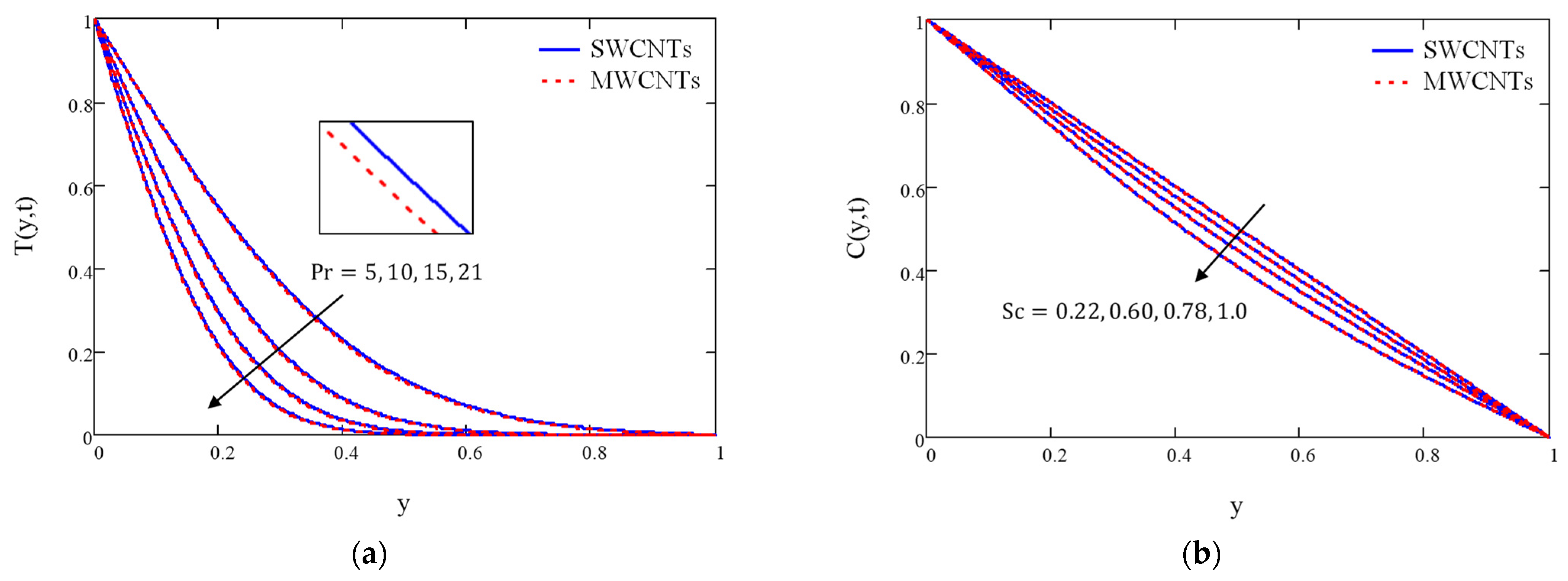
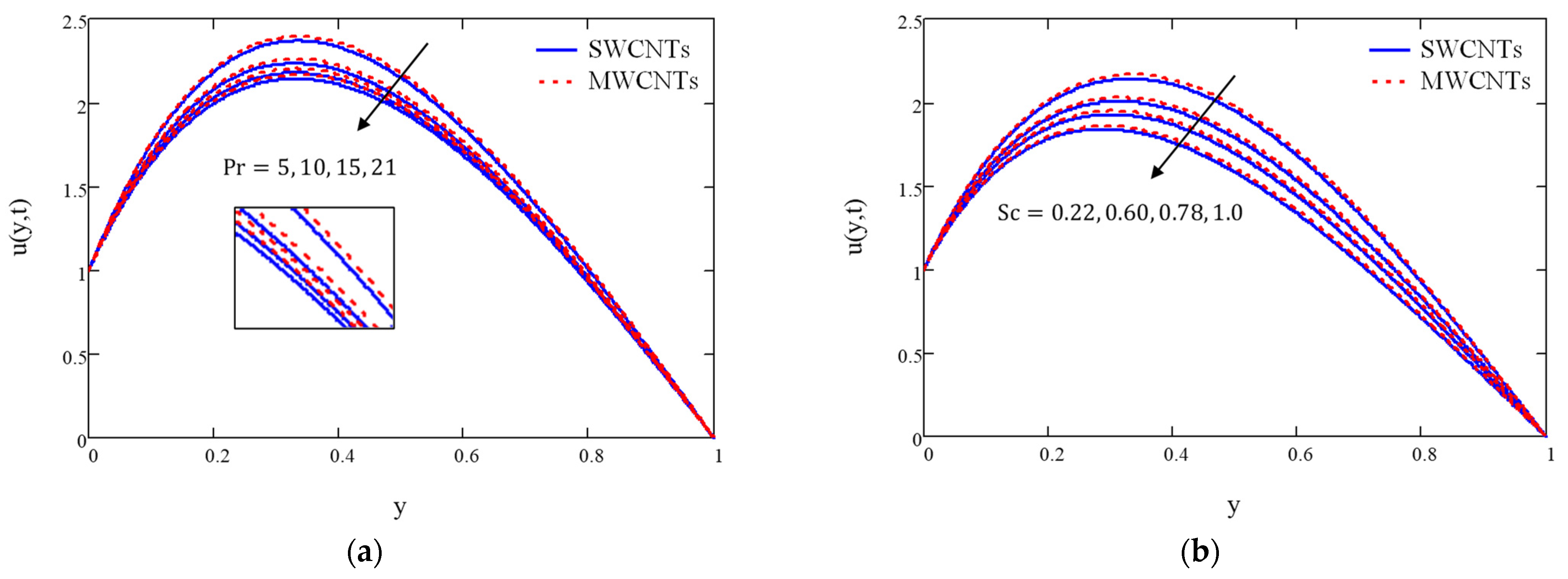
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pattnaik, J.R.; Dash, G.C.; Singh, S. Radiation and mass transfer effects on MHD flow through porous medium past an exponentially accelerated inclined plate with variable temperature. Ain. Shams Eng. J. 2017, 8, 67–75. [Google Scholar] [CrossRef]
- Roa, S.R.; Vidyasagar, G.; Deekshitulu, G.V.S.R. Unsteady MHD free convection Casson fluid flow past an exponentially accelerated infinite vertical porous plate through porous medium in the presence of radiation absorption with heat generation/absorption. Mater. Today Proc. 2020, 42, 1608–1616. [Google Scholar]
- Mohamad, A.Q.; Khan, I.; Shafie, S.; Isa, Z.M.; Ismail, Z. Non-coaxial rotating flow of viscous fluid with heat and mass transfer. Neural Comput. Appl. 2017, 30, 2759–2769. [Google Scholar] [CrossRef]
- Noranuar, W.N.N.; Mohamad, A.Q.; Shafie, S.; Khan, I. Accelerated non-coaxial rotating flow of MHD viscous fluid with heat and mass transfer. IOP Conf. Ser. Mater. Sci. Eng. 2021, 012044, 1051. [Google Scholar] [CrossRef]
- Zulkiflee, F.; Shafie, S.; Mohamad, A.Q. Radiation effect on free convection flow between oscillating parallel plates with mass diffusion. Mal. J. Fund. Appl. Sci. 2021, 17, 1–16. [Google Scholar] [CrossRef]
- Sehra; Haq, S.U.; Shah, S.I.A.; Nisar, K.S.; Jan, S.U.; Khan, I. Convection heat mass transfer and MHD flow over a vertical plate with chemical reaction, arbitrary shear stress and exponential heating. Sci. Rep. 2021, 11, 4265. [Google Scholar] [CrossRef]
- Abbas, S.; Nazar, M.; Nisa, Z.U.; Amjad, M.S.; Din, M.E.; Alanzi, A.M. Heat and mass transfer analysis of MHD Jeffrey fluid over a vertical plate with CPC Fractional derivative. Symmetry 2022, 14, 2491. [Google Scholar] [CrossRef]
- Riaz, M.B.; Rehman, A.U.; Awrejcewicz, J.; Jarad, F. Double diffusive magneto-free-convection flow of Oldroyd-B Fluid over a vertical plate with heat and mass flux. Symmetry 2022, 14, 209. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Makinde, O.D. Entropy generation due to heat and mass transfer in a flow of dissipative elastic fluid through a porous medium. J. Heat Transf. 2019, 141, 022002. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Gireesha, B.J.; Gorla, R.S.R. Heat and mass transfer effects on the mixed convective flow of chemically reacting nanofluid past a moving/stationary vertical plate. Alex. Eng. J. 2016, 55, 569–581. [Google Scholar] [CrossRef]
- Madhura, K.R.; Babitha, S.S.I. Impact of heat and mass transfer on mixed convective flow of nanofluid through porous medium. Int. J. Appl. Comput. Math. 2017, 3, 1361–1384. [Google Scholar] [CrossRef]
- Farooq, A.; Rehman, S.; Alharbi, A.N.; Kamran, M.; Botmart, T.; Khan, I. Closed-form solution of oscillating Maxwell nano-fluid with heat and mass transfer. Sci. Rep. 2022, 12, 12205. [Google Scholar] [CrossRef] [PubMed]
- Siddique, I.; Sadiq, K.; Jaradat, M.M.M.; Ali, R.; Jarad, F. Engine oil based MoS2 Casson nanofluid flow with ramped boundary conditions and thermal radiation through a channel. Case Stud. Therm. Eng. 2022, 35, 102118. [Google Scholar] [CrossRef]
- Arulmohzi, S.; Sukkiramathi, K.; Santra, S.S.; Edwan, R.; Gamiz, U.F.; Noeiaghdam, S. Heat and mass transfer analysis of radiative and chemical reactive effects on MHD nanofluid over an infinite moving vertical plate. Results Eng. 2022, 14, 100394. [Google Scholar] [CrossRef]
- Prabavathi, B.; Reddy, P.S.; Vijaya, R.B. Heat and mass transfer enhancement of SWCNTs and MWCNTs based Maxwell nanofluid flow over a vertical cone with slip effects. Powder Technol. 2018, 340, 253–263. [Google Scholar] [CrossRef]
- Sreedevi, P.; Reddy, P.S.; Chamkha, A.J. Magneto-hydrodynamics heat and mass transfer analysis of single and multi-wall carbon nanotubes over vertical cone with convective boundary condition. Int. J. Mech. Sci. 2018, 135, 646–655. [Google Scholar] [CrossRef]
- Reddy, Y.R.O.; Reddy, M.S. Heat and mass transfer analysis of single walled carbon nanotubes and multi walled carbon nanotubes-water nanofluid flow over porous inclined plate with heat generation/absorption. J. Nanofluids 2019, 8, 1147–1157. [Google Scholar] [CrossRef]
- Javed, F.; Riaz, M.B.; Iftikhar, N.; Awrejcewicz, J.; Akgül, A. Heat and mass transfer impact on differential type nanofluid with carbon nanotubes: A study of fractional order system. Fractal Fract. 2021, 5, 231. [Google Scholar] [CrossRef]
- Noranuar, W.N.N.; Mohamad, A.Q.; Shafie, S.; Khan, I.; Jiann, L.Y. Heat and mass transfer in non-coaxial rotation of radiative MHD Casson carbon nanofluid flow past a porous medium. Data Anal. Appl. Math. 2021, 2, 37–51. [Google Scholar] [CrossRef]
- Saqib, M.; Khan, I.; Shafie, S. Application of Atangana–Baleanu fractional derivative to MHD channel flow of CMC-based-CNT’s nanofluid through a porous medium. Chaos Solitons Fractals 2018, 116, 79–85. [Google Scholar] [CrossRef]
- Kumar, P.; Poonia, H.; Ali, L.; Areekara, S. The numerical simulation of nanoparticle size and thermal radiation with the magnetic field effect based on tangent hyperbolic nanofluid flow. Case Stud. Therm. Eng. 2022, 37, 102247. [Google Scholar] [CrossRef]
- Rehman, S.U.; Ali, B.; Imran, M.; Ali, L.; Shah, N.H.; Chung, I.C. The Casson dusty nanofluid: Significance Darcy-Forchheime law, magnetic field, and non-Fourier heat flux model subject to stretch surface. Mathematics 2022, 10, 2887. [Google Scholar] [CrossRef]
- Ali, L.; Ali, B.; Ghori, M.B. Melting effect on Cattaneo-Christov and thermal radiation features for aligned MHD nanofluid flow comprising microorganisms to leading edge: FEM approach. Comput. Math. Appl. 2022, 109, 260–269. [Google Scholar] [CrossRef]
- Ramzan, M.; Nazar, M.; Nisa, Z.U.; Ahmad, M.; Shah, N.A. Unsteady free convective magnetohydrodynamics flow of a Casson fluid through a channel with double diffusion and ramp temperature and concentration. Math. Meth. Appl. Sci. 2021, 1, 1–20. [Google Scholar] [CrossRef]
- Azmi, W.F.W.; Mohamad, A.Q.; Hoe, Y.S.; Isa, Z.M.; Shafie, S. Effects of Magnetohydrodynamics and Heat Transfer in Casson Fluid Through a Channel. Mal. J. Fund. Appl. Sci. 2021, 17, 416–429. [Google Scholar] [CrossRef]
- Sadiq, K.; Siddique, I.; Ali, R.; Jarad, F. Impact of ramped concentration and temperature on MHD Casson nanofluid flow through a vertical channel. J. Nanomater. 2021, 2021, 3743876. [Google Scholar] [CrossRef]
- Asifa; Kumam, P.; Shah, Z.; Watthayu, W.; Anwar, T. Radiative MHD unsteady Casson fluid flow with heat source/sink through a vertical channel suspended in porous medium subject to generalized boundary conditions. Phys. Scr. 2021, 96, 075213. [Google Scholar] [CrossRef]
- Krishna, M.V.; Vajravelu, K. Rotating MHD flow of second grade fluid through porous medium between two vertical plates with chemical reaction, radiation absorption, Hall, and ion slip impacts. Biomass Convers. Biorefinery 2022, 1–15. [Google Scholar] [CrossRef]
- Khalid, A.; Khan, I.; Khan, A.; Shafie, S.; Tlili, I. Case study of MHD blood flow in a porous medium with CNTs and thermal analysis. Case Stud. Therm. Eng. 2018, 12, 374–380. [Google Scholar] [CrossRef]
- Saeed, A.; Alsubie, A.; Kumam, P.; Nasir, S.; Gul, T.; Kumam, W. Blood based hybrid nanofluid flow together with electromagnetic field and couple stresses. Sci. Rep. 2021, 11, 12865. [Google Scholar] [CrossRef]
- Apmann, K.; Fulmer, R.; Soto, A.; Vafaei, S. Thermal Conductivity and Viscosity: Review and Optimization of Effects of Nanoparticles. Materials 2021, 14, 1291. [Google Scholar] [CrossRef] [PubMed]
- Farahani, S.D.; Amiri, M.; Majd, B.K.; Mosavi, A. Effect of magnetic field on heat transfer from a channel: Nanofluid flow and porous layer arrangement. Case Stud. Therm. Eng. 2021, 28, 101675. [Google Scholar] [CrossRef]


| Human blood | 1053 | 3594 | 0.492 | 0.8 | 0.18 |
| SWCNTs | 2600 | 425 | 6600 | 106–107 | 27 |
| MWCNTs | 1600 | 796 | 3000 | 1.9 × 10−4 | 44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noranuar, W.N.N.; Mohamad, A.Q.; Shafie, S.; Jiann, L.Y. Heat and Mass Transfer on Magnetohydrodynamics Casson Carbon Nanotubes Nanofluid Flow in an Asymmetrical Channel via Porous Medium. Symmetry 2023, 15, 946. https://doi.org/10.3390/sym15040946
Noranuar WNN, Mohamad AQ, Shafie S, Jiann LY. Heat and Mass Transfer on Magnetohydrodynamics Casson Carbon Nanotubes Nanofluid Flow in an Asymmetrical Channel via Porous Medium. Symmetry. 2023; 15(4):946. https://doi.org/10.3390/sym15040946
Chicago/Turabian StyleNoranuar, Wan Nura’in Nabilah, Ahmad Qushairi Mohamad, Sharidan Shafie, and Lim Yeou Jiann. 2023. "Heat and Mass Transfer on Magnetohydrodynamics Casson Carbon Nanotubes Nanofluid Flow in an Asymmetrical Channel via Porous Medium" Symmetry 15, no. 4: 946. https://doi.org/10.3390/sym15040946
APA StyleNoranuar, W. N. N., Mohamad, A. Q., Shafie, S., & Jiann, L. Y. (2023). Heat and Mass Transfer on Magnetohydrodynamics Casson Carbon Nanotubes Nanofluid Flow in an Asymmetrical Channel via Porous Medium. Symmetry, 15(4), 946. https://doi.org/10.3390/sym15040946






