Fluctuating Flexoelectric Membranes in Asymmetric Viscoelastic Media: Power Spectrum through Mechanical Network and Transfer Function Models
Abstract
:1. Introduction
- (1)
- To deduce a new general asymmetric electro rheological model for a flexoelectric membrane attached to a circular capillary tube that contains Maxwell’s viscoelastic fluids and is subjected to a fluctuating small amplitude electric field of arbitrary frequency;
- (2)
- To compute the flow and stress complex transfer functions vs. frequency as a function of the applied frequency and the material properties of the thermodynamic system;
- (3)
- To use the modeling results to characterize the complex loops of the flow and stress transfer functions;
- (4)
- To identify the numerical values of the dimensionless groups that lead to electromechanical force-flow conversion of potential interest to the functioning biological systems.
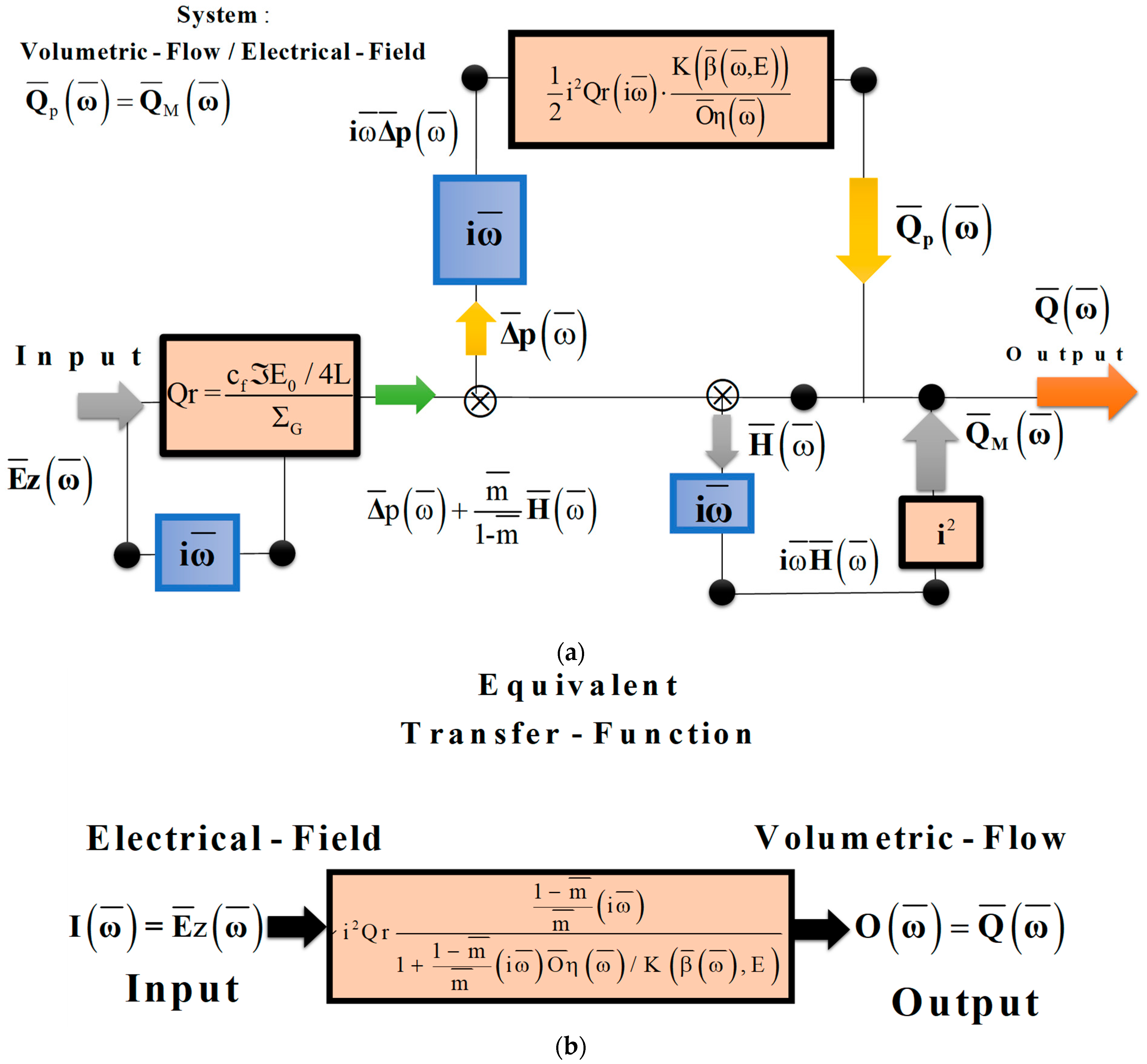
2. Mechanical Network Model
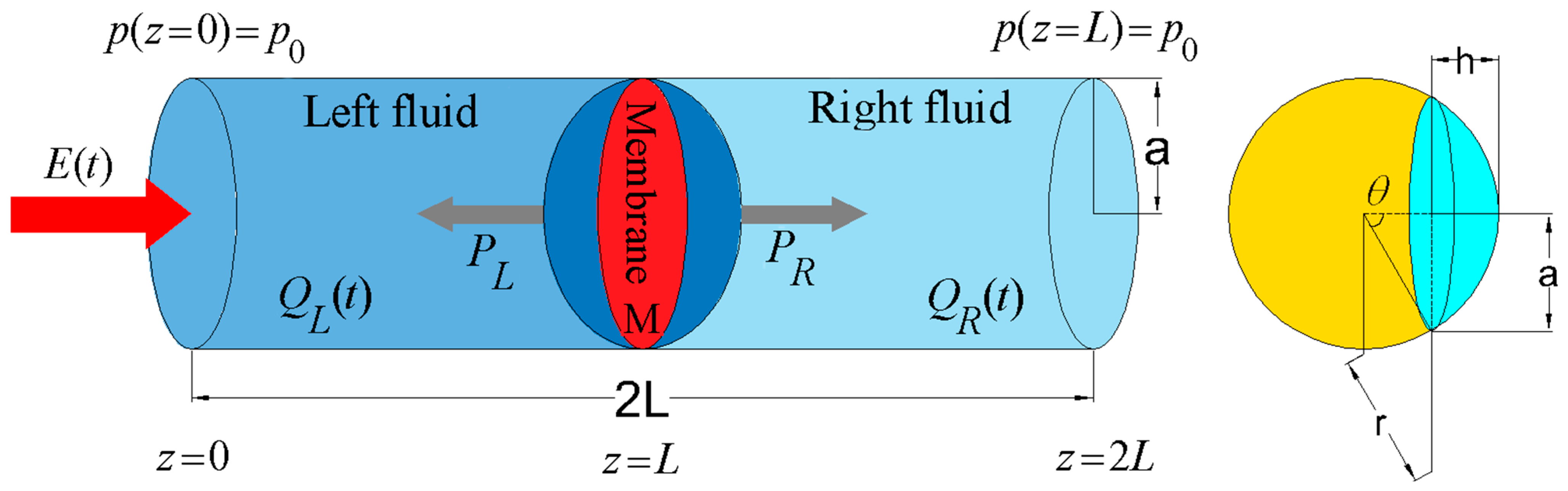
2.1. Device Material Structure and Geometry
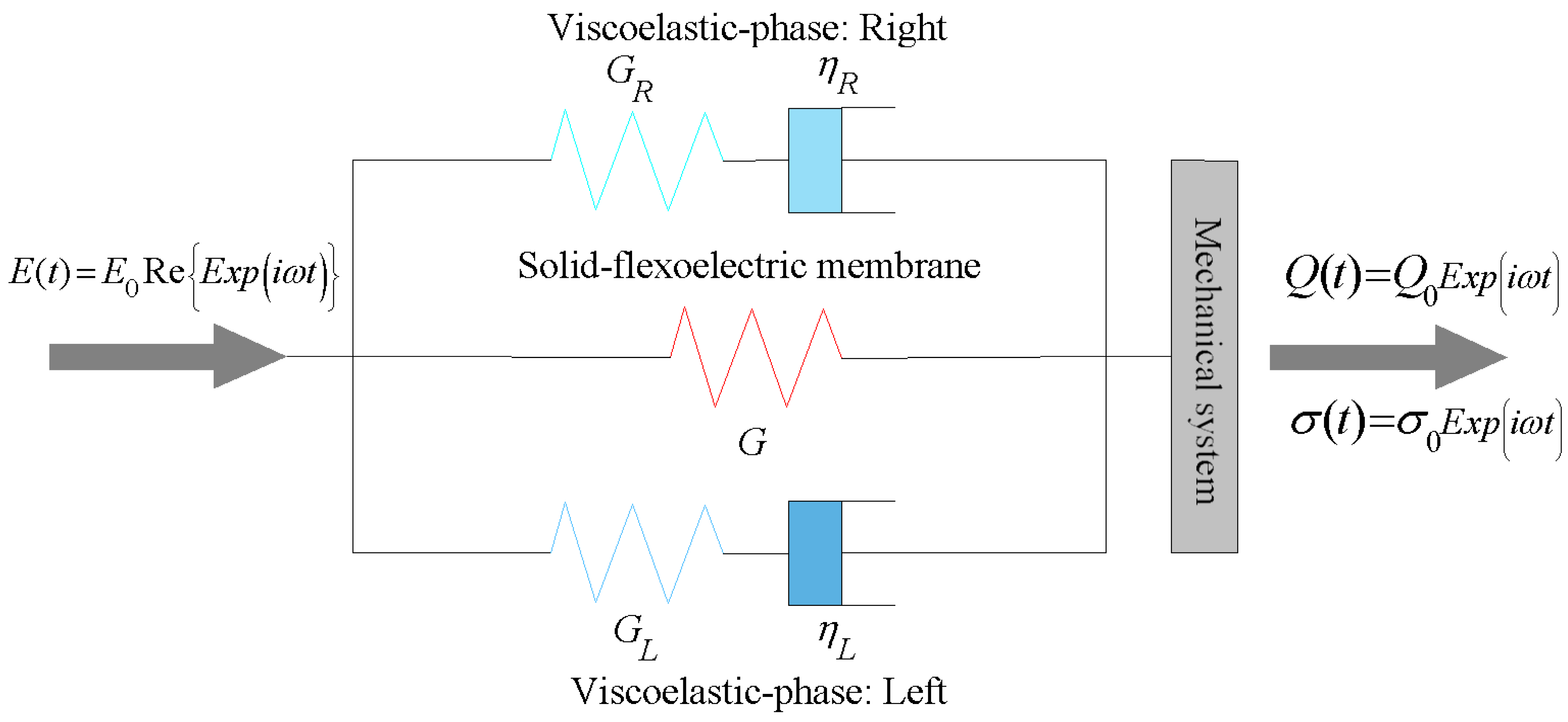
2.2. Mechanical Analogue
3. Transfer Functions from the Fourier Domain
3.1. Continuity and Transport Momentum Equations
3.2. Complex Axial Velocity and Boundary Conditions
3.3. Formulation in the Fourier Domain and Complex Wave Vector β(ω)
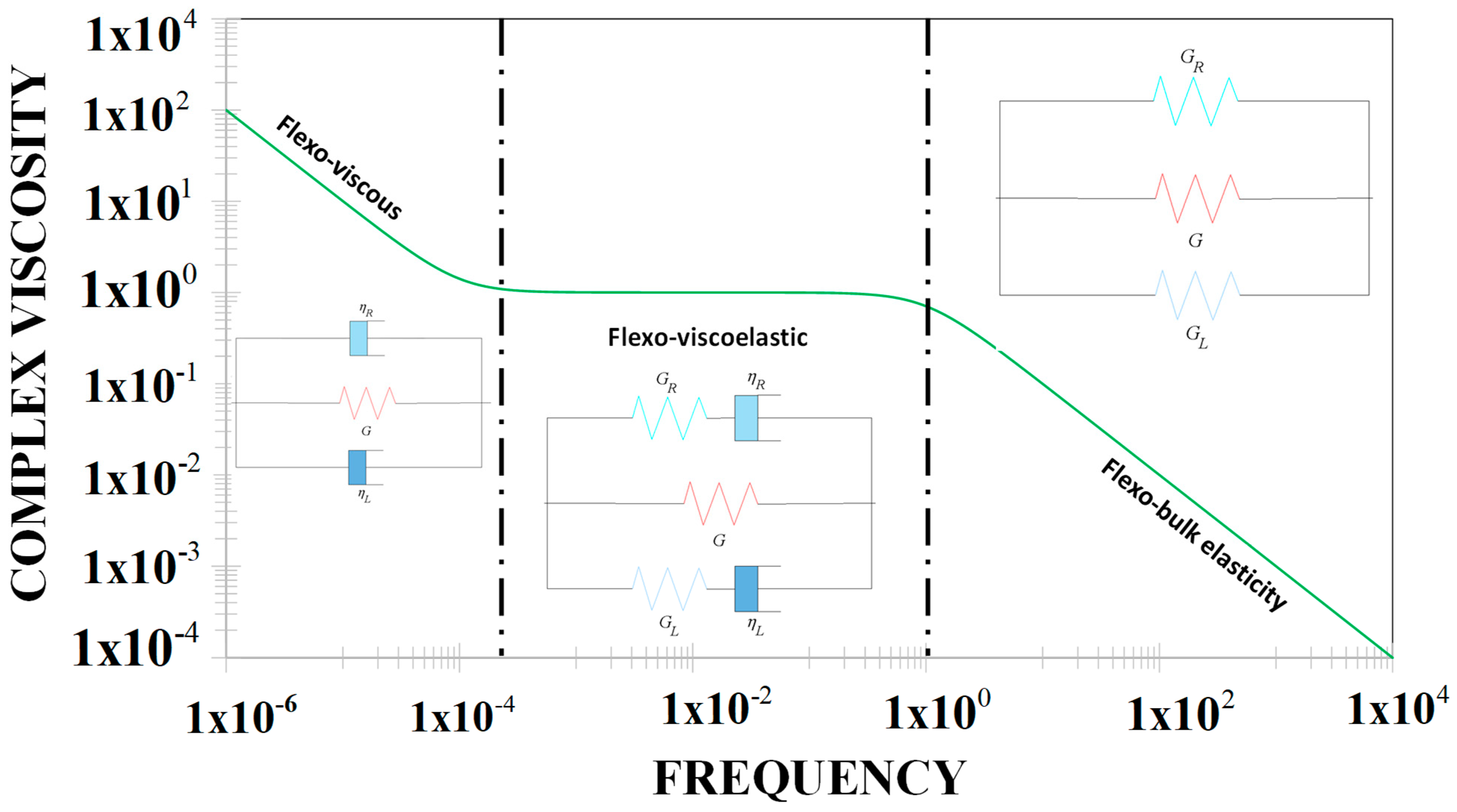
3.4. Scales, Dimensionless Numbers, and Device Mode Classification Based on Kinematics and Rheology
- (a)
- Scales and dimensionless numbers
- (b)
- Device mode classification based on flow kinematics
- (c)
- Device mode classification based on rheology
3.5. Complex Axial Velocity
3.6. Complex Volumetric Flow Rate and Transfer Functions
3.7. Flow Transfer Function ()
3.8. Stress Transfer Function (Ts)
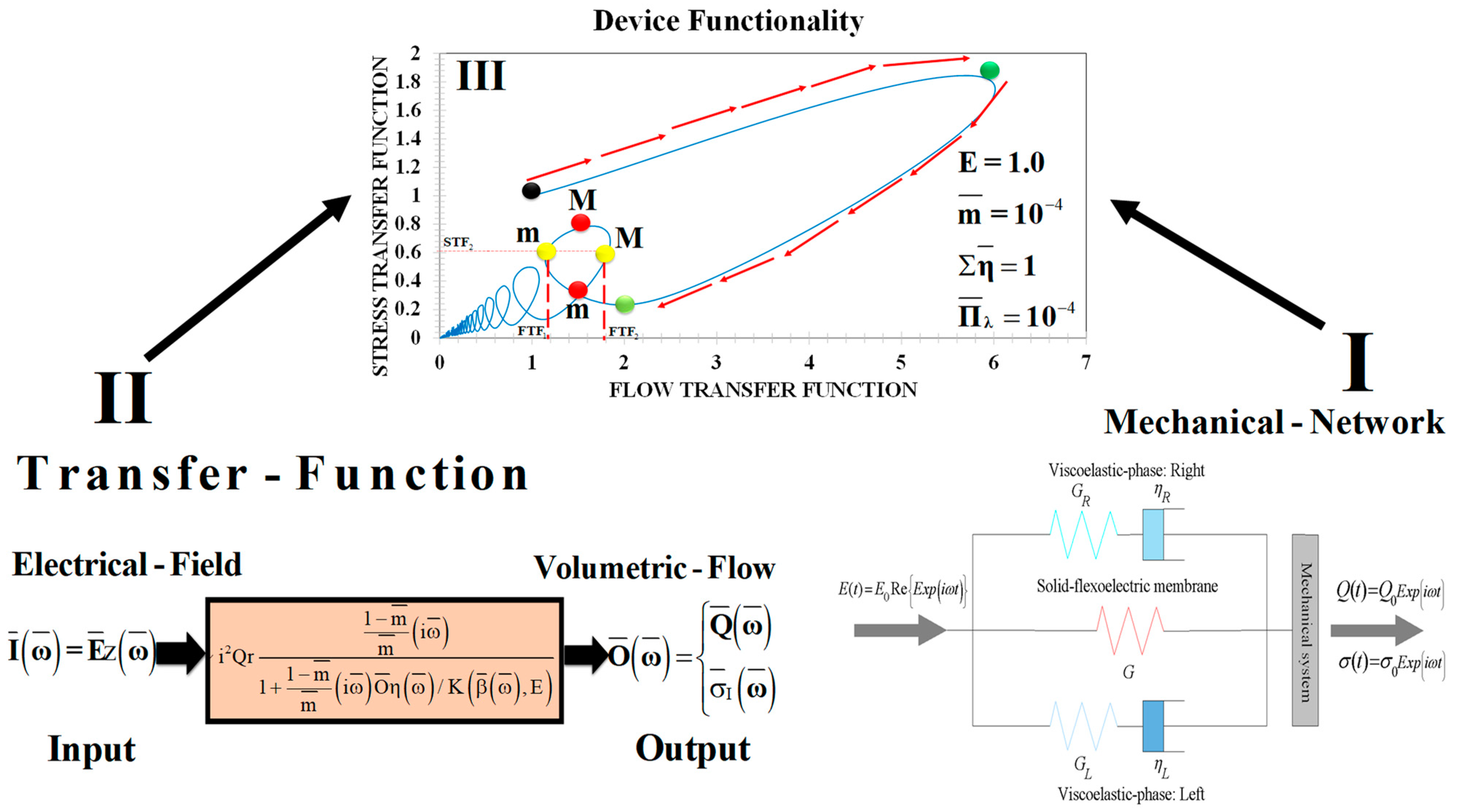
4. Device Functionality: Flow and Force Generation
5. Computational Results
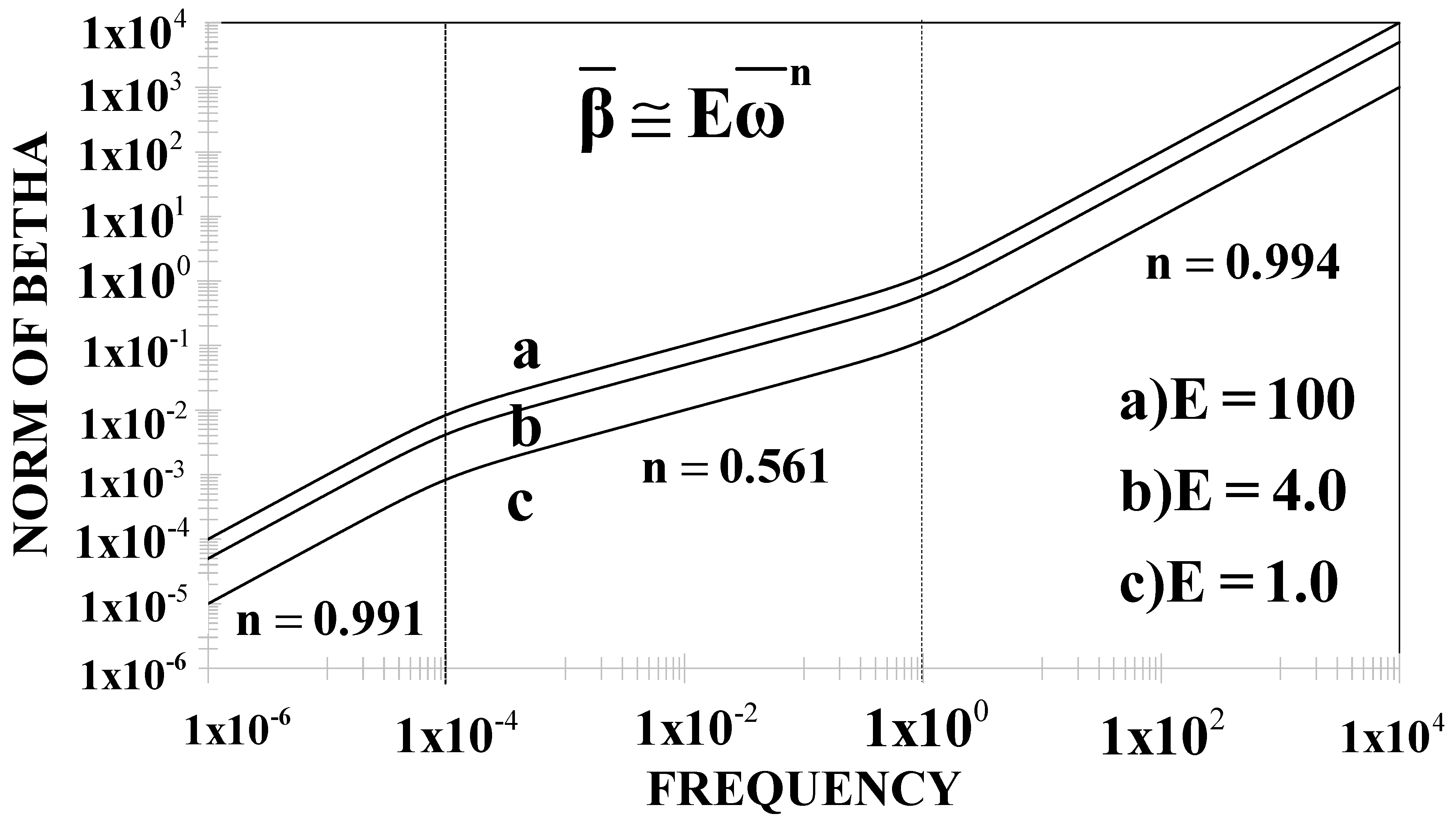
5.1. Elastic Number E
5.2. Membrane Elasticity
5.3. Velocity Profile
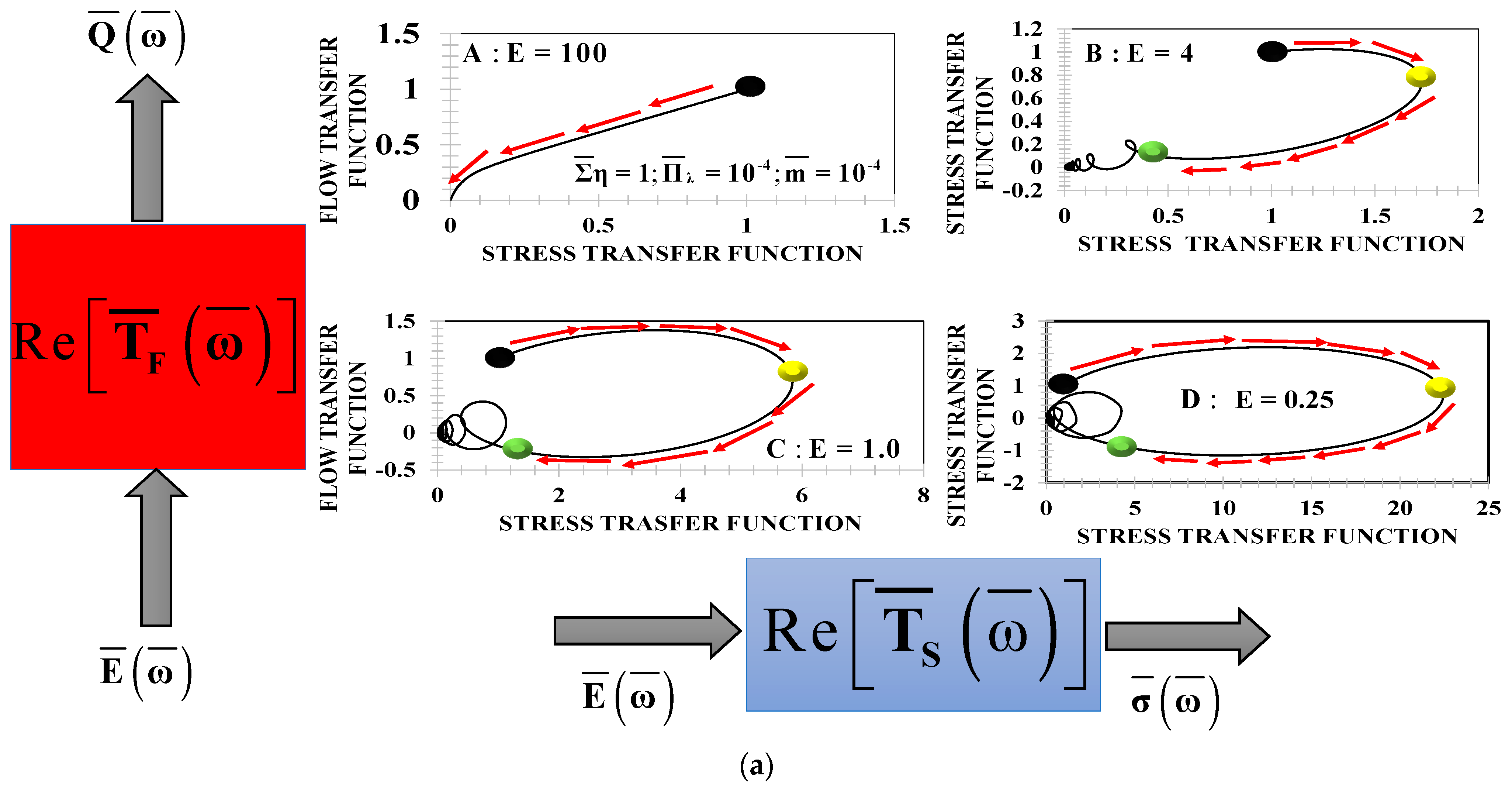
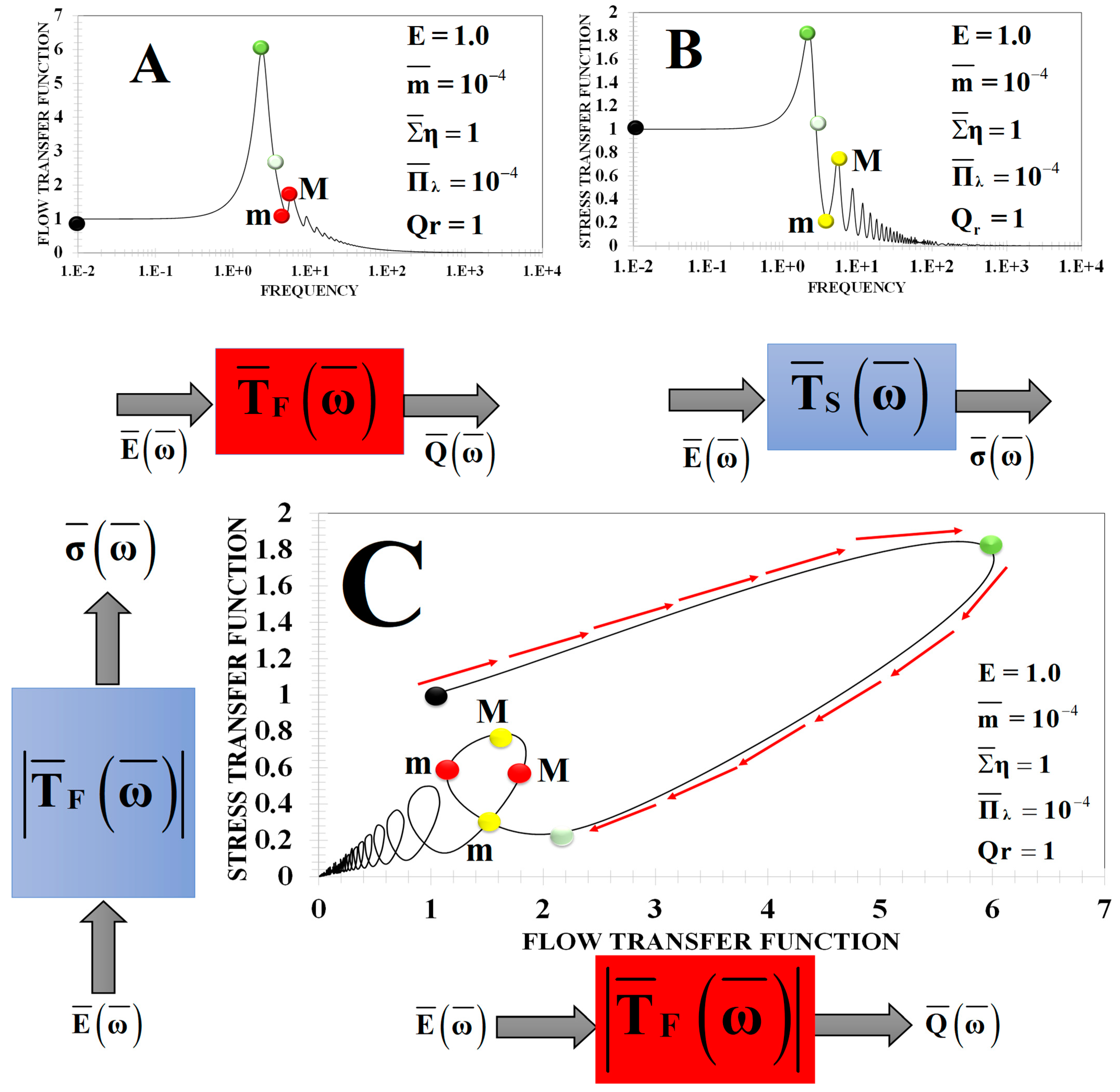
5.4. Flow-Stress Loop Diagrams
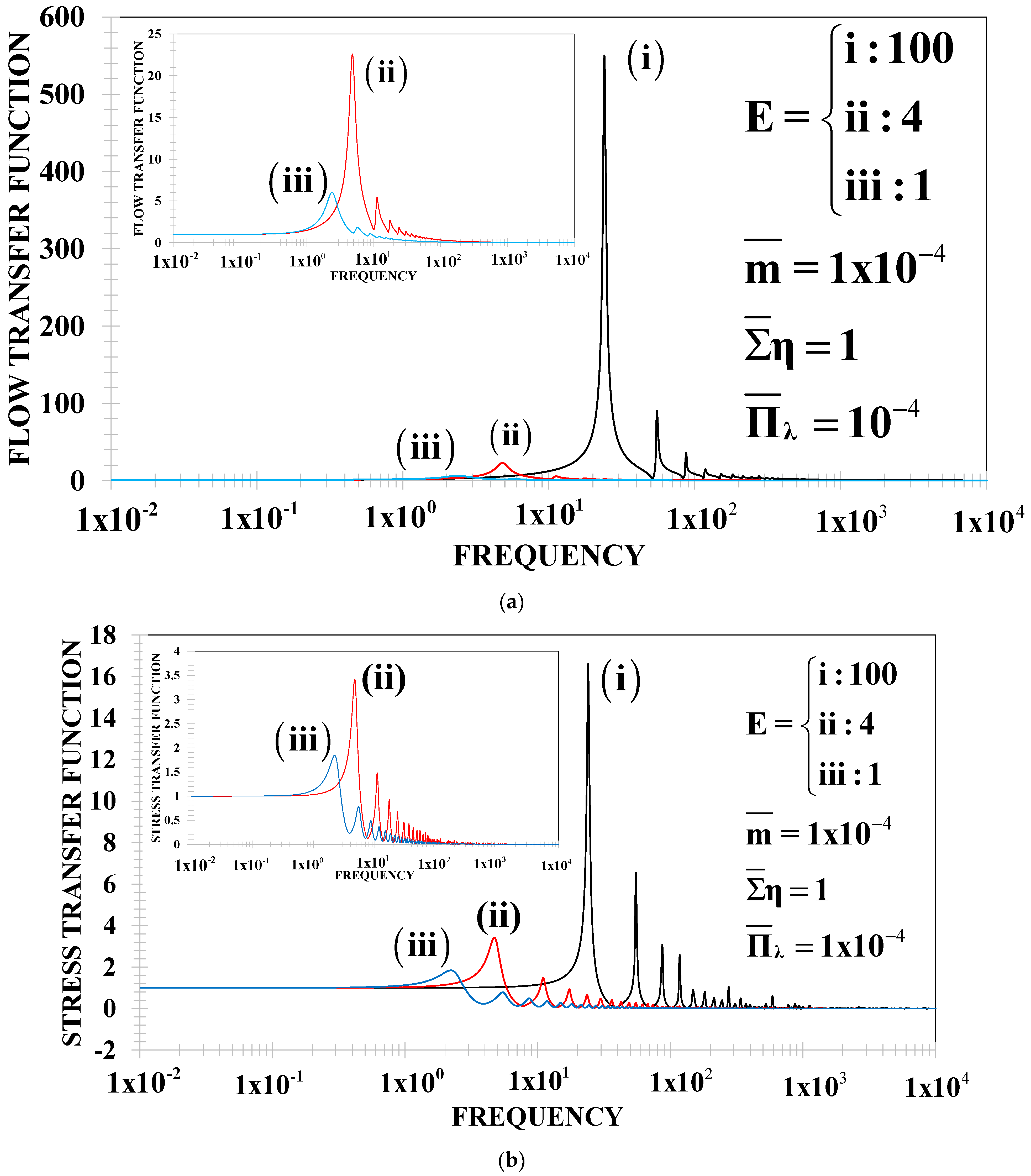
5.5. Force–Flow Loops: Resonances and Transitions
- (a)
- The material conditions needed to observe multiple resonance peaks in the FTF spectrum are: (i) an asymmetry in the viscoelastic liquid phases, i.e., one of them is totally viscoelastic and the other weakly viscoelastic, i.e., , ε << 1. This means that one of the viscoelastic relaxation times is close to the unit , and the other one is very small, ε =1 × 10−4. (ii) The system has large viscosity, i.e., . (iii) The membrane elasticity m = ε = 1 × 10−4. (iv) E is greater than zero, i.e., viscoelastic mechanisms (Weissenberg number We) (viscoelastic forces) dominate over the inertial and viscous forces (Reynolds number Re), E = We/Re > 0.
- (b)
- The maximum resonance peak is linked to the inertia, viscoelastic, and flexo-elastic processes, and its magnitude depends on the elastic number E = We/Re.
- (c)
- The multiple peaks are associated with a possible change in the roots of the ratio of the Bessel functions from real to complex values. The nature of these oscillations depends on coupled mechanisms associated with the inertia, viscous, elastic, and flexoelectric through the dimensionless numbers.
- (d)
- The global peak is found at a critical frequency whose value depends on the main Maxwell relaxation time, and this time is related with the frequency through . The secondary peak corresponds to the less dominant relaxation time, i.e., .
- (e)
- The adequate model to predict resonance behavior is a new asymmetric rheological model, which is a variant of Burgers’ constitutive equation (Equation (10)). Other models (Jeffreys, Burgers, fractional derivative models) contribute to modify the resonance behavior through the viscosity operator defined in Equations (11) and (12) [3,4].
- (f)
- Multiple resonance peaks are found in other biological and complex systems [39,40]. For example, in biorheology, the pulsating pressure-driven force increases the volumetric flow, and its effect is dominated by dynamic permeability [41,42,43,44,45]. In veins with central and peripherical occlusions [46], the frequency can be tuned to obtain the maximum pulsating volumetric flow rate [46], as well as in oil recovery operations with surfactants such as worm-like micellar solutions [13,47,48,49,50].
- (g)
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Notation | |
| a | Radius of the pipe [m] |
| cf | Membrane flexoelectric coefficient [C] |
| {C1, C2} | Constants [1] |
| E (ω) | Frequency-input electrical field [N/C] |
| E0 | Amplitude of the electrical field [N/C] |
| F (ω) | Fourier transform |
| ez | Unit vector [1] |
| F(t) | Fourier transform |
| G | Elastic flexoelectric membrane [Pa] |
| Gb, Gt | Elastic moduli defined in the bottom and the top [Pa] |
| h | Height of the spherical dome [m] |
| H(t) | Average membrane curvature [m−1] |
| J0 | Bessel function of the first kind [1] |
| Y0 | Bessel function of the second kind [1] |
| k0, k1 | Membrane bending rigidity and torsion elastic moduli [J] |
| K | Dynamic permeability |
| L | Characteristic axial length of the capillary [m] |
| m | Elastic ratio [1] |
| Q (ω) | Output volumetric flow rate [m3/s] |
| Δp(z,t) | Pressure, constant pressure at z = 0 and z = 2L, and pressure difference [Pa] |
| PR, pL | Pressure defined at the top and the bottom [Pa] |
| p0 | Constant pressure at the top in the bottom [Pa] |
| Q(t) | Volumetric flow rate [m3/s] |
| Q (ω) | Frequency-volumetric flow rate [m3/s] |
| QR(t), QL(t) | Top and bottom volumetric flow rate [m3/s] |
| r | Radial coordinate [m] |
| Re [TF (ω)] | Real part of the transfer function [m3s−1/NC−1] |
| Im [TF (ω)] | Imaginary part of the transfer function [m3s−1/NC−1] |
| TF (ω) | Complex flow transfer function [m3s−1/NC−1] |
| TS (ω) | Complex stress transfer function [m3s−1/NC−1] |
| t | Time coordinate [s] |
| ti | Inertial time [s] |
| Vz | Axial velocity [m/s] |
| Operators | |
| Dt = ∂/∂t | Time differential operator [1/s] |
| OΦ(Dt) | Viscosity operator [Pas] |
| OηR(Dt), OηL(Dt) | Right and left viscosity operators [Pas] |
| Other symbols | |
| (r,ϕ,z) | Cylindrical coordinates [m,1, m] |
| ℑ | Shape factor [1/m2] |
| ⊗ | Dyadic product [1] |
| ∇ | Gradient operator [1/m] |
| Δ | Delta operator [1] |
| Vectors and tensors | |
| D | Rate of deformation tensor [1/s] |
| E | Electrical field vector [N/C] |
| G | Acceleration of the gravitational forces [m/s2] |
| k | Outer unit normal vector [1] |
| kk | Dyadic product of the outer unit normal vector [1] |
| T | Total stress tensor [Pa] |
| I | Unit tensor [1] |
| V | Velocity field [ms−1] |
| ∇V | Velocity gradient [s−1] |
| Δ | Delta [1] |
| Greek vectors and tensors | |
| σ | Total stress tensor [Pa] |
| σR, σL | Right and left stress tensors [Pa] |
| σM | Membrane stress tensors [Pa] |
| σw | Wall stress [Pa] |
| Greek letters | |
| β | Complex wave vector [1/m] |
| ε | Small parameters [1] |
| ρx | Density of the viscoelastic liquid phases [kg/m3] |
| γ0 | Interfacial surface tension at zero electric field [F/m] |
| γ | Total shear strain in the system [1] |
| γt | Top deformation of the Maxwell element [1] |
| γb | Bottom deformation of the Maxwell element [1] |
| γ0 | Interfacial surface tension at zero electric field [F/m] |
| ηL, ηR | Left and right viscosities [Pas] |
| λL, λR | Left and right viscoelastic relaxation times [s] |
| σrz | rz component of the shear stress tensor [Pa] |
| ω | Angular frequency [rad/s] |
| Σρ | Total liquid density [kg/m3] |
| ΣG | Total bulk elasticity [Pa] |
| Σλ | Total Maxwell relaxation times [s] |
| Ση | Total bulk viscosities [Pas] |
| ΦE | Electrical potential [J/C] |
| Dimensionless variables | |
| Constants [1] | |
| Radial coordinate [1] | |
| Process time [1] | |
| Axial velocity [1] | |
| Electric field [1] | |
| Volumetric flow rate [1] | |
| Elastic membrane [1] | |
| Frequency [1] | |
| Viscoelastic shear stress [1] | |
| Flexoelectric stress [1] | |
| Fluidity operator [1] | |
| Dimensionless numbers | |
| E | Elastic [1] |
| De | Deborah [1] |
| Wo | Womersley [1] |
| Membrane elastic ratio [1] | |
| Elastic ratio [1] | |
| Memory [1] | |
| Other symbols | |
| (r,ϕ,z) | Cylindrical coordinates [m,1, m] |
| e−iωt | Complex negative exponential function [1] |
| π | Pi constant [1] |
| ∂Vz/∂r | Shear strain [1/s] |
| {∂/∂z, ∂/∂t} | Spatial and temporal time derivatives [m−1,s−1] |
| |·| | Absolute value [1] |
| Subscripts | |
| {L, R} | Refers to the left and the right fluids [1] |
| Superscripts | |
| ( )T | Refers to the transport of a tensor [1] |
| Abbreviators | |
| LC | Liquid crystal |
| NLC | Nematic liquid crystal |
| OHC | Outer hair cell |
| SAOS | Small amplitude oscillatory shear |
Appendix A
Dimensionless Variables
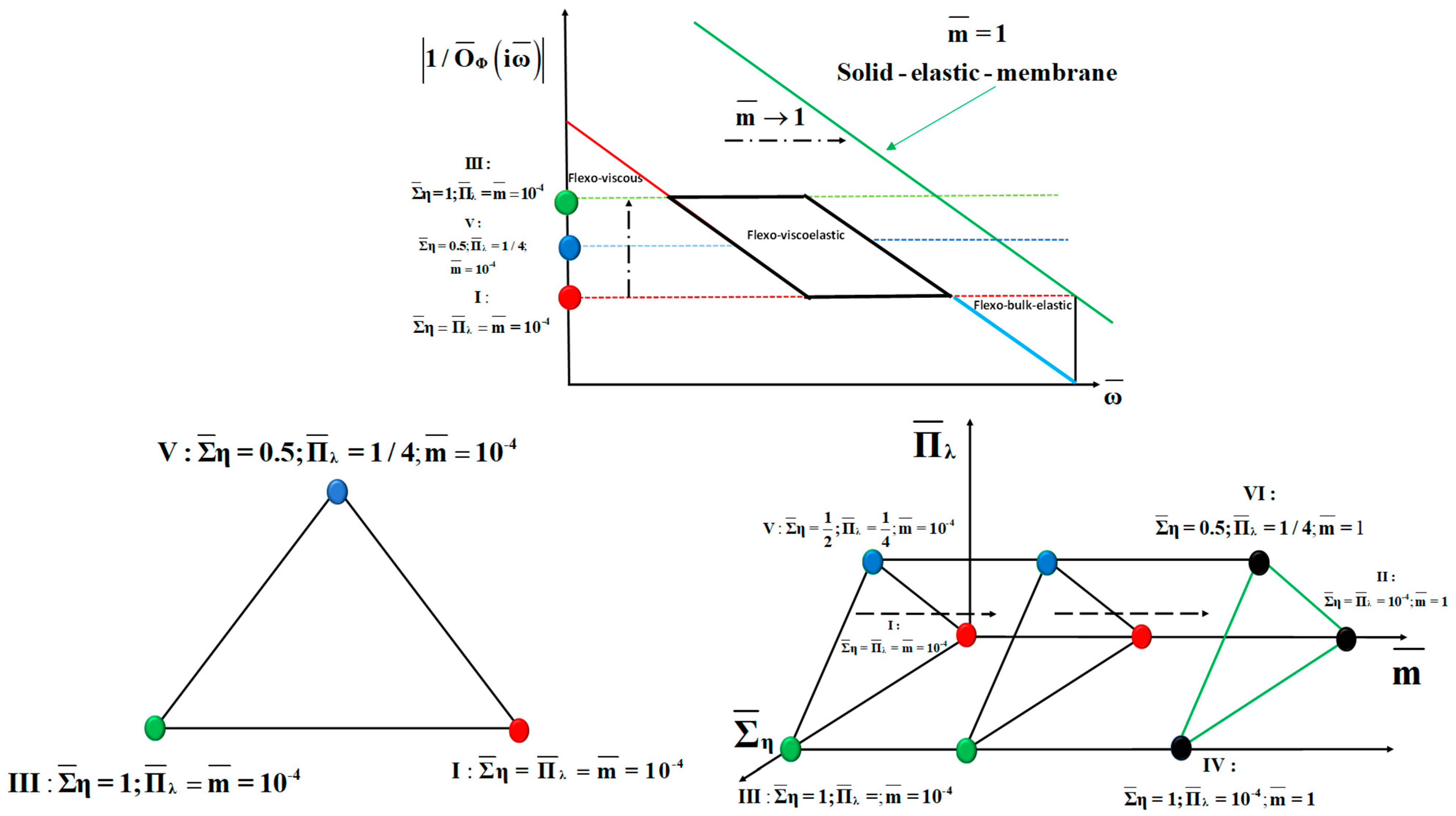
Appendix B
Parametric Material Space
Appendix C
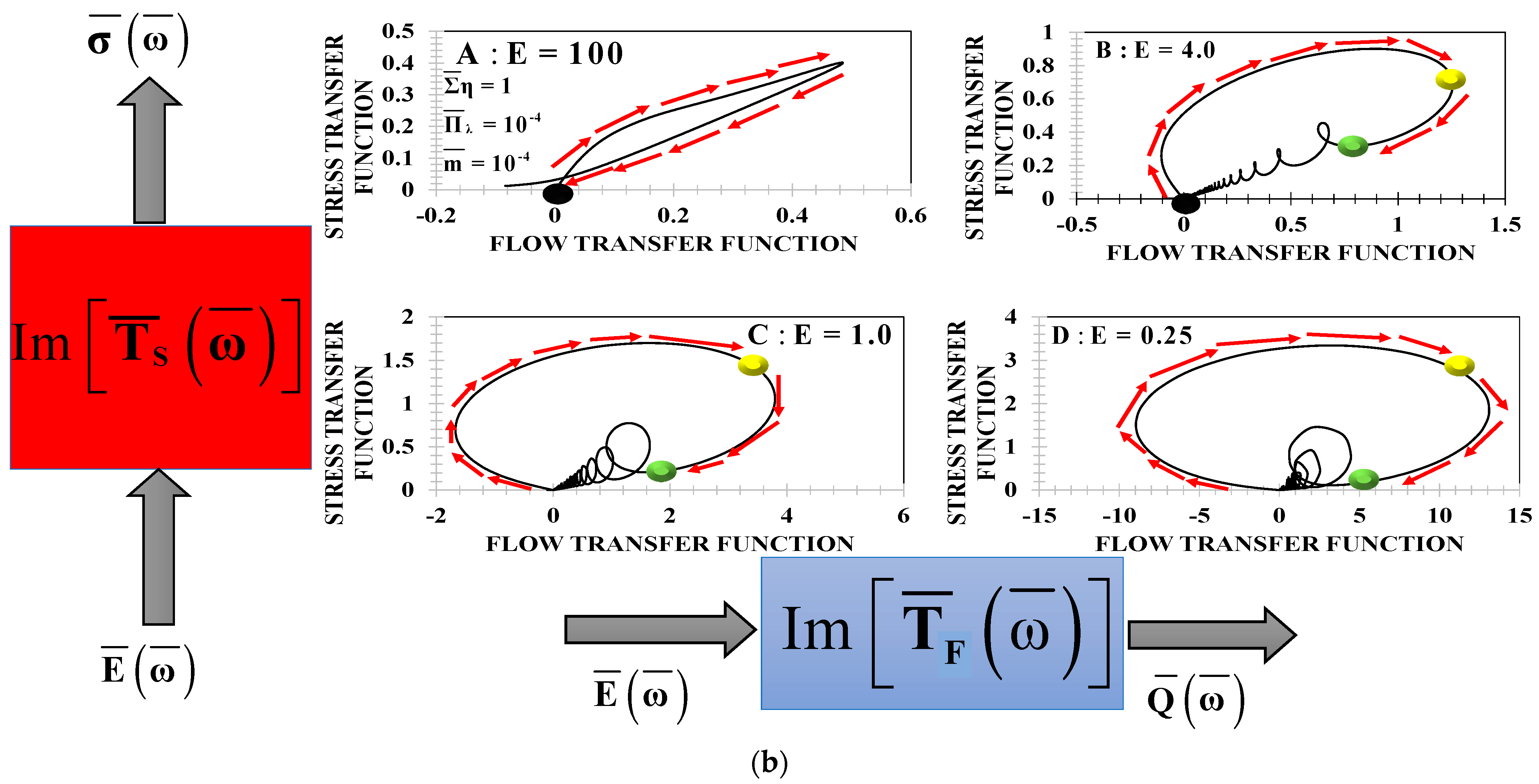
Appendix C.1. Transfer Function
Appendix C.2. Flexoelectric Transfer Function
Appendix C.3. Time Operator: Electrical Field
Appendix C.4. Rheological Transfer Function
Appendix C.5. Time Operator: Average Membrane Curvature
Appendix C.6. Total Transfer Function
Appendix D
- (a)
- The stress and flow transfer functions are coupled and for a critical frequency, where the system shows a stress saturation (peak resonance);
- (b)
- The viscoelastic forces control the shape, magnitude, and orientation of the force–flow loops;
- (c)
- At small frequency, the real stress and flow transfer functions have the same magnitude, at a value 1 (membrane mode); hence, the imaginary part of the stress and flow rate starts from zero value.
Appendix E
Appendix F
References
- Wang, Z.; Servio, P.; Rey, A.D. Pattern formation, structure and functionalities of wrinkled liquid crystals surfaces: A soft matter biomimicry platform. Front. Soft Matter 2023, 3, 1123324. [Google Scholar] [CrossRef]
- Petrov, A.G. The Lyotropic State of Matter: Molecular Physics and Living Matter Physics; Gordon and Breach Science Publisher: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Herrera-Valencia, E.E.; Rey, A.D. Electrorheological model based on liquid crystals membranes with applications to outer hair cells. Fluids 2018, 3, 35. [Google Scholar] [CrossRef]
- Herrera-Valencia, E.E.; Rey, A.D. Mechano-electric transduction performance of actuation device based on liquid crystal membrane flexoelectricity. Phil. Trans. R. Soc. A 2014, 372, 20130369. [Google Scholar] [CrossRef]
- Rey, A.D. Nonlinear actuator model for flexoelectric membranes. Int. J. Des. Nat. Ecodynam. 2008, 3, 28–38. [Google Scholar] [PubMed]
- Petrov, A.G. Flexoelectricity of model and living membranes. BBA-Biomembr. 2001, 1561, 1–25. [Google Scholar] [CrossRef] [PubMed]
- Petrov, A.G. Electricity and mechanics of biomembrane systems: Flexoelectricity in living membranes. Anal. Chim. Acta 2006, 568, 70–83. [Google Scholar] [CrossRef]
- Lee, D. Flexoelectricity in thin films and membranes of complex solids. APL Mater. 2020, 8, 090901. [Google Scholar] [CrossRef]
- Rey, A.D.; Servio, P.; Herrera-Valencia, E.E. Stress-Sensor Device Based on Flexoelectric Liquid Crystalline Membranes. ChemPhysChem 2014, 15, 1405–1412. [Google Scholar] [CrossRef]
- Rey, A.D.; Servio, P.; Herrera-Valencia, E.E. Bioinspired model of mechanical energy harvesting based on flexoelectric membranes. Phys. Rev. E 2013, 87, 022505. [Google Scholar] [CrossRef]
- Rey, A.D. Linear viscoelastic model for bending and torsional modes in fluid membranes. Rheol. Acta 2008, 47, 861–871. [Google Scholar] [CrossRef]
- Aguilar-Gutierrez, O.F.; Herrera-Valencia, E.E.; Rey, A.D. Generalized Boussinesq-Scriven surface fluid model with curvature dissipation for liquid surfaces and membranes. J. Coll. Int. Sci. 2017, 503, 103–114. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Servio, P.; Herrera-Valencia, E.E.; Rey, A.D. Thermal fluctuation spectrum of flexoelectric viscoelastic semiflexible filaments and polymers: A line liquid crystal model. Can. J. Chem. Eng. 2022, 100, 3162–3173. [Google Scholar] [CrossRef]
- Rabbitt, R.D.; Clifford, S.; Breneman, K.D.; Farrell, B.; Brownell, W.E. Power efficiency of outer hair cell somatic electromotility. PLoS Comput. Biol. 2009, 5, e1000444. [Google Scholar] [CrossRef] [PubMed]
- Dewey, J.W.; Altoe, A.; Shera, C.A.; Oghalai, J.S. Cochlear outer hair cell electromotility enhances organ of Corti motion on a cycle-by-cycle basis at high frequencies in vivo. Proc. Natl. Acad. Sci. USA 2021, 118, e2025206118. [Google Scholar] [CrossRef]
- Oghalai, J.S.; Zhao, H.B.; Kutz, J.W.; Brownell, W.E. Voltage-and tension-dependent lipid mobility in the outer hair cell plasma membranes. Science 2000, 287, 658–661. [Google Scholar] [CrossRef]
- Brownell, W.E. Evoked mechanical responses of isolated cochlear outer hair cells. Science 1985, 227, 194–196. [Google Scholar] [CrossRef] [PubMed]
- Levic, S.; Lukaskina, V.A.; Simoes, P.; Lukashkin, A.N.; Russell, I.J. A gap-junction mutation reveals that outer hair cell estracellular receptor potentials drive high-frequency cochlear amplification. J. Neurosci. 2022, 19, 7875–7884. [Google Scholar] [CrossRef]
- Altoe, A.; Shera, C.A. The long outer-hair-cell RC time constant: A feature, not a bug, of the Mammalian Cochlea. J. Assoc. Res. Otolaryngol. 2023, 24, 129–145. [Google Scholar] [CrossRef]
- Yeh, W.H.; Shubina-Oleinik, O.; Levy, J.M.; Pan, B.; Newby, G.A.; Wornow, M.; Burt, R.; Chen, J.C.; Holt, J.R.; Liu, D.R. In vivo base editing restores sensory transduction and transient improves auditory function in a mouse model of recessive deafness. Sci. Transl. Med. 2020, 12, eaay9101. [Google Scholar] [CrossRef]
- Torbati, M.; Mozaffari, K.; Liu, L.; Sharma, P. Coupling of mechanical deformation and electromagnetic fields in biological cells. Rev. Mod. Phys. 2022, 94, 025003. [Google Scholar] [CrossRef]
- Lahlou, G.; Calvet, C.; Giorgi, M.; Lecomte, M.J.; Safieddine, S. Towards the clinical application of gene therapy for genetic inner ear diseases. J. Clin. Med. 2023, 12, 1046. [Google Scholar] [CrossRef]
- Bowling, T.; Lemons, C.; Meaud, L. Reducing tectorial membrane viscoelasticity enhances spontaneous otoacoustic emissions and compromises the detection of low-level sound. Sci. Rep. 2019, 9, 7494. [Google Scholar] [CrossRef] [PubMed]
- Rabbitt, R.D. The cochlear outer hair cell speed paradox. Proc. Natl. Acad. Sci. USA 2020, 117, 21880–21888. [Google Scholar] [CrossRef] [PubMed]
- Mussel, M.; Schneider, M.F. It sounds like an action potential: Unification of electrical, chemical and mechanical aspects of acoustic pulses in lipids. J. R. Soc. Interface 2019, 16, 20180743. [Google Scholar] [CrossRef]
- Mao, X.; Shokef, Y. Introduction to force transmission by nonlinear biomaterials. Soft Matter 2021, 17, 10172–10176. [Google Scholar] [CrossRef] [PubMed]
- Ronceray, P.; Broedersz, C.P.; Lenz, M. Stress-dependent amplification of active force in non-linear elastic media. Soft Matter 2019, 15, 331. [Google Scholar] [CrossRef] [PubMed]
- Bird, R.B.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids; Fluid Mechanics Wiley: New York, NY, USA, 1977; Volume 1. [Google Scholar]
- Shankar, V.; Subramanian, G. A linear route to elasto-inertial turbulence. Sci. Talks 2022, 3, 100051. [Google Scholar] [CrossRef]
- Castillo-Sánchez, H.A.; de Souza, L.F.; Castelo, A. Numerical Simulation of Rheological Models for Complex Fluids Using Hierarchical Grids. Polymers. Polymers 2022, 14, 4958. [Google Scholar] [CrossRef]
- Castillo Sánchez, H.A.; Jovanovic, M.R.; Kumar, S.; Morozov, A.; Shakar, V.; Subramanian, G.; Wilson, H.J. Understanding viscoelasticity flow instabilities: Oldroyd Band beyond. J. Non-Newton. Fluid Mech. 2022, 302, 104742. [Google Scholar] [CrossRef]
- Jeonghun, N.; Hyunjung, L.; Dookon, K.; Hyunwook, J.; Sehyun, S. Continuous separation of microparticles in a microfluidic channel via the elasto inertial effect of non-Newtonian fluid. Lab Chip 2012, 12, 1347. [Google Scholar]
- Fernandez-Feria, R.; Alaminos-Quesada, J. Purely pulsating flow of a viscoelastic fluid in a pipe revisited: The limit of large Womersley number. J. Non-Newton. Fluid Mech. 2015, 217, 32–36. [Google Scholar] [CrossRef]
- Simpson, J.P.; Leylek, J.H. The influence of Womersley number on non-Newtonian effects: Transient computational study of blood rheology. J. Fluids. Eng. 2023, 145, 011206. [Google Scholar] [CrossRef]
- Loudon, C.; Tordesillas, A. The use of the dimensionless Womersley number to characterize the unsteady nature of internal flow. J. Theor. Biol. 1998, 191, 63–78. [Google Scholar] [CrossRef] [PubMed]
- Park, N.; Nam, J. Analysis of pulsatile shear-thinning flows in rectangular channels. Phys. Rev. Fluids 2022, 7, 123301. [Google Scholar] [CrossRef]
- Peralta, M.; Arcos, J.; Mendez, F.; Bautista, O. Mass transfer through a concentric annulus microchannel driven by an oscillatory electroosmotic flow of a Maxwell fluid. J. Non-Newton Fluid Mech. 2020, 279, 104281. [Google Scholar] [CrossRef]
- Rath, S.; Mahapatra, B. Low Reynolds number pulsatile flow of a viscoelastic fluid through a Channel: Effects of fluid rheology and pulsation parameters. J. Fluid Eng. 2022, 144, 021201. [Google Scholar] [CrossRef]
- Castro, M.; Bravo-Gutiérrez, M.E.; Hernández-Machado, A.; Corvera-Poiré, E. Dynamic characterization of permeabilities and flows in microchannels. Phys. Rev. Lett. 2008, 101, 224501. [Google Scholar] [CrossRef]
- Yañez, D.; Travasso, R.D.M.; Corvera-Poiré, E. Resonances in the response of fluidic networks inherent to the cooperation between elasticity and bifurcations. R. Soc. Open Sci. 2019, 6, 190661. [Google Scholar] [CrossRef]
- Flores, J.; Corvera-Poiré, E.; Del Rio, J.A.; López de Haro, M. A plausible explanation for heart rates in mammals. J. Theor. Biol. 2010, 265, 599. [Google Scholar] [CrossRef]
- Flores, J.; Alastruey, J.; Corvera-Poiré, E. A novel analytical approach to pulsatile blood flow in the arterial network. Ann. Biomed. Eng. 2016, 44, 3047–3068. [Google Scholar]
- Lindner, A.; Bonn, D.; Corvera-Poiré, E.; Ben Amar, M.; Meunier, J. Viscous fingering in non-Newtonian fluids. J. Fluid Mech. 2002, 469, 237–256. [Google Scholar] [CrossRef]
- Torres-Rojas, A.M.; Pagonabarraga, I.; Corvera-Poiré, E. Resonances of Newtonian fluids in elastomeric microtubes. Phys. Fluids 2017, 29, 122003. [Google Scholar] [CrossRef]
- Torres-Herrera, U. Dynamic permeability of fluids in rectangular and square microchannels: Shift and coupling of viscoelastic bidimensional resonances. Phys. Fluids 2021, 33, 012016. [Google Scholar] [CrossRef]
- Collepardo-Guevara, J.; Corvera Poiré, E. Controlling viscoelastic flow by tunning frequency. Phys. Rev. E 2007, 76, 026301. [Google Scholar] [CrossRef]
- Pasquino, R.; Avallone, P.R.; Constanzo, S.; Inbal, I.; Danino, D.; Ianniello, V.; Ianniruberto, G.; Marrucci, G.; Grizzuti, N. On the startup behavior of wormlike micellar networks: The effect of different salts bound to the same surfactant molecule. J. Rheol. 2023, 67, 353–364. [Google Scholar] [CrossRef]
- Kang, W.; Mushi, S.J.; Yang, H.; Wang, P.; Hou, X. Development of smart viscoelastic surfactants and its applications in fracturing fluid: A review. J. Pet. Sci. Eng. 2020, 190, 107107. [Google Scholar] [CrossRef]
- Sullivan, P.F.; Panga, M.K.; Lafitte, V. Applications of wormlike micelles in the oilfield industry. Soft Matter 2017, 2017, 330–352. [Google Scholar]
- Rothstein, J.P.; Mohammadigoushki, H. Complex flows of viscoelastic wormlike micelle solutions. J. Non-Newton. Fluid Mech. 2020, 285, 104382. [Google Scholar] [CrossRef]





| Mechanisms/Materials | Device/Process | Source |
|---|---|---|
| Membrane flexoelectricity | Force pump actuation device and mechano-electric transduction | Herrera-Valencia and Rey (2014, 2018) [3,4] |
| Flexoelectric membranes | Nonlinear actuator | Rey, A.D. (2008) [5] |
| Flexoelectric liquid crystalline membranes | Stress sensor devices (signal detecting stress) | Rey, A.D. et al. (2014) [9] |
| Flexoelectric rods | Energy harvesting | Rey, A.D. et al. (2013) [10] |
| Membrane dissipation | Linear viscoelasticity for bending and torsion | Rey, A.D. (2008) [11] |
| Flexo-dissipation | Curvature dissipation | Aguilar-Gutierrez et al. (2017) [12] |
| Flexoelectric viscoelastic semiflexible filaments and polymers | Thermal fluctuation spectrum | Wang, Z. et al. (2022) [13] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Herrera-Valencia, E.E.; Rey, A.D. Fluctuating Flexoelectric Membranes in Asymmetric Viscoelastic Media: Power Spectrum through Mechanical Network and Transfer Function Models. Symmetry 2023, 15, 1004. https://doi.org/10.3390/sym15051004
Herrera-Valencia EE, Rey AD. Fluctuating Flexoelectric Membranes in Asymmetric Viscoelastic Media: Power Spectrum through Mechanical Network and Transfer Function Models. Symmetry. 2023; 15(5):1004. https://doi.org/10.3390/sym15051004
Chicago/Turabian StyleHerrera-Valencia, Edtson Emilio, and Alejandro D. Rey. 2023. "Fluctuating Flexoelectric Membranes in Asymmetric Viscoelastic Media: Power Spectrum through Mechanical Network and Transfer Function Models" Symmetry 15, no. 5: 1004. https://doi.org/10.3390/sym15051004