New Study on the Quantum Midpoint-Type Inequalities for Twice q-Differentiable Functions via the Jensen–Mercer Inequality
Abstract
:1. Introduction
2. Description of Quantum Calculus
3. New Mercer Quantum Midpoint-Type Auxiliary Results
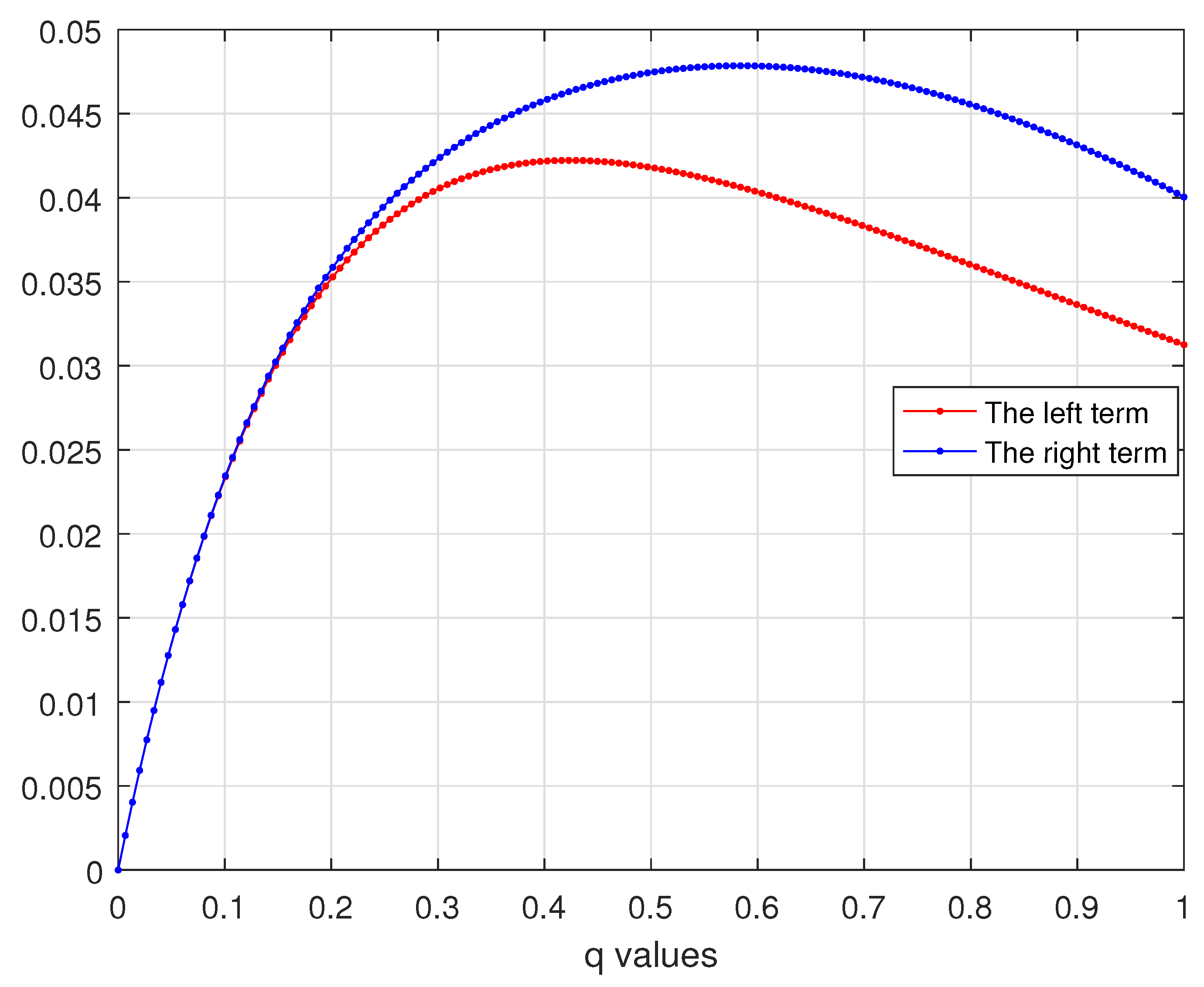
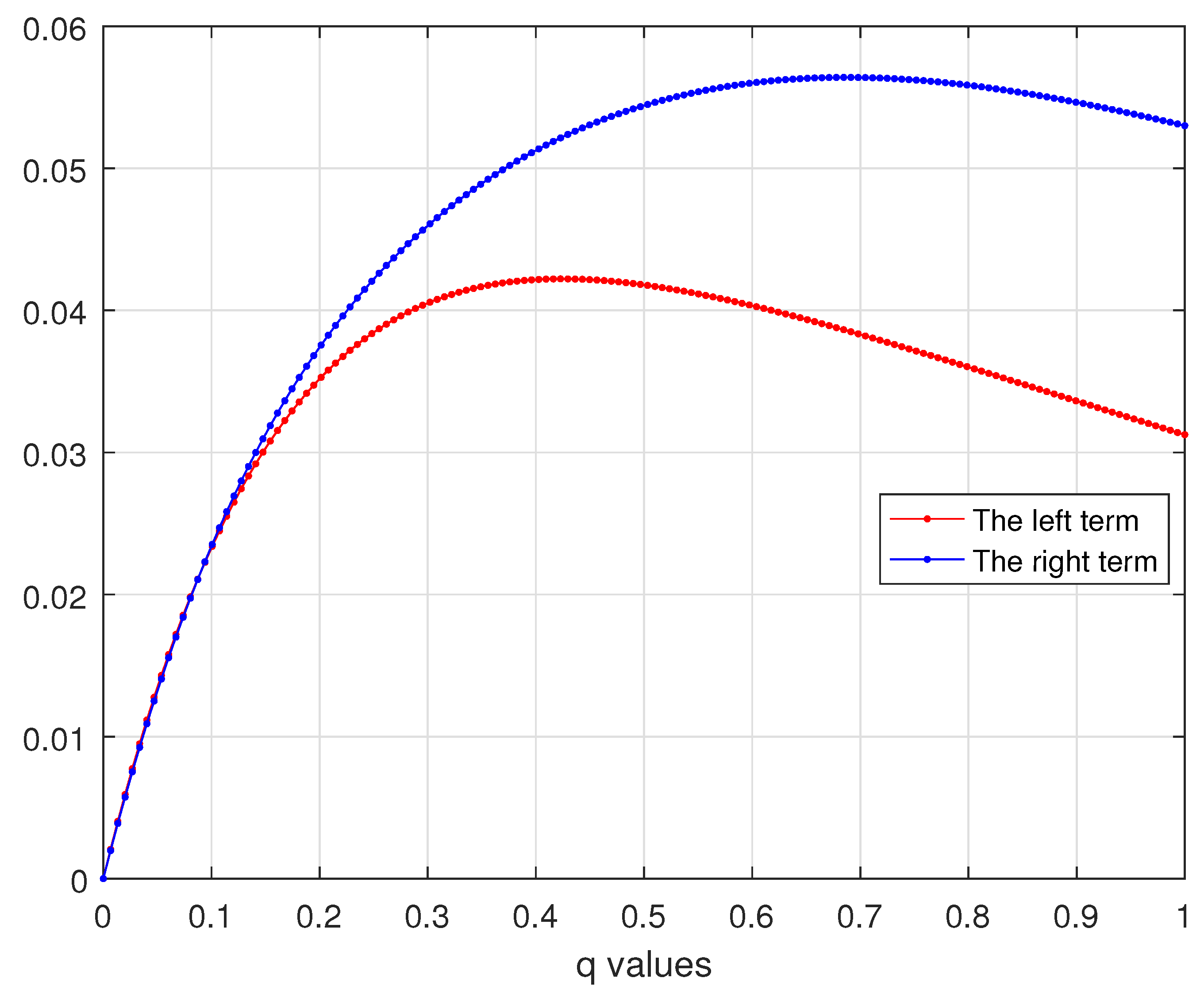
New Quantum Mercer Midpoint-Type Estimates
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mitrinović, D.S.; Pexcxarixcx, J.E.; Fink, A.M. Classical and New Inequalities in Analysis. In Mathematics and Its Applications (East and European Series); Kluwer Academic Publishers Group: Dordecht, The Netherlands, 1993. [Google Scholar]
- Liu, L.; Wang, J.; Zhang, L.; Zhang, S. Multi-AUV Dynamic Maneuver Countermeasure Algorithm Based on Interval Information Game and Fractional-Order DE. Fractal Fract. 2022, 6, 235. [Google Scholar] [CrossRef]
- He, Y.; Zhang, L.; Tong, M.S. Microwave Imaging of3D Dielectric-Magnetic Penetrable Objects Based on Integral Equation Method. IEEE Trans. Antennas Propag. 2023. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, X. The Impact of Contract Enforcement Efficiency on Debt Maturity Structure Using Mathematical Derivation and Comparative Static Analysis. J. Comput. Methods Sci. Eng. 2022, 22, 97–108. [Google Scholar] [CrossRef]
- Shen, Q.; Yang, Z. Applied mathematical analysis of organizational learning culture and new media technology acceptance based on regression statistical software and a moderated mediator model. J. Comput. Methods Sci. Eng. 2021, 21, 1825–1842. [Google Scholar] [CrossRef]
- Mehmood, N.; Butt, S.I.; Pećarixcx, D.; Pexcxarixcx, J. Generalizations of Cyclic Refinements of Jensen’s Inequality by Lidstone’s Polynomial with Applications in Information Theory. J. Math. Inequal. 2019, 14, 249–271. [Google Scholar] [CrossRef]
- Khan, S.; Khan, M.A.; Butt, S.I.; Chu, Y.M. A New Bound for the Jensen Gap Pertaining Twice Differentiable Functions with Applications. Adv. Differ. Equ. 2020, 2020, 333. [Google Scholar] [CrossRef]
- Mercer, A.M. A Variant of Jensens Inequality. J. Inequalities Pure Appl. Math. 2003, 4, 73. [Google Scholar]
- Kian, M.; Moslehian, M.S. Refinements of the Operator Jensen–Mercer Inequality. Electron. J. Linear Algebra 2013, 26, 742–753. [Google Scholar] [CrossRef]
- Anjidani, E. Jensen–Mercer Operator Inequalities Involving Superquadratic Functions. Mediterr. J. Math. 2018, 15, 31. [Google Scholar] [CrossRef]
- Moradi, H.R.; Furuichi, S. Improvement and Generalization of Some Jensen–Mercer–Type Inequalities. J. Math. Inequalities 2020, 14, 377–383. [Google Scholar] [CrossRef]
- Khan, M.A.; Husain, Z.; Chu, Y.M. New Estimates for Csiszar Divergence and Zipf-Mandelbrot Entropy via Jensen-Mercer’s Inequality. Complexity 2020, 2020, 8928691. [Google Scholar]
- Ernst, T. The History Of q-Calculus and New Method; Department of Mathematics, Uppsala University: Uppsala, Sweden, 2000. [Google Scholar]
- Gauchman, H. Integral Inequalities in q-Calculus. Comput. Math. Appl. 2004, 47, 281–300. [Google Scholar] [CrossRef]
- Jackson, F.H. On a q-Definite Integrals. Q. J. Pure Appl. Math. 1910, 41, 193–203. [Google Scholar]
- Kac, V.; Cheung, P. Quantum Calculus, Universitext; Springer: New York, NY, USA, 2002. [Google Scholar]
- Rajkovic, P.M.; Stankovic, M.S.; Marinkovic, S.D. The Zeros of Polynomials Orthogonal with Respect to q-Integral on Several Intervals in the Complex Plane. In Proceedings of the Fifth International Conference on Geometry, Integrability and Quantization, Varna, Bulgaria, 5–12 June 2003. [Google Scholar]
- Alp, N.; Sarikaya, M.Z.; Kunt, M.; Iscan, I. q-Hermite Hadamard Inequalities and Quantum Estimates for Midpoint Type Inequalities Via Convex and Quasi-Convex Functions. J. King Saud Univ. Sci. 2018, 30, 193–203. [Google Scholar] [CrossRef]
- Bermudo, S.; Kórus, P.; Valdés, J.N. On q-Hermite–Hadamard Inequalities for General Convex Functions. Acta Math. Hung. 2020, 162, 364–374. [Google Scholar] [CrossRef]
- Alp, N.; Budak, H.; Erden, S.; Sarikaya, M.Z. New Bounds q-Midpoint Type Inequalities for Twice q-Differentiable Convex Functions on Quantum Calculus. Soft Comput. 2022, 26, 10321–10329. [Google Scholar] [CrossRef]
- Tariboon, J.; Ntouyas, S.K. Quantum integral inequalities on finite intervals. J. Inequal. Appl. 2014, 2014, 121. [Google Scholar] [CrossRef]
- Mohammed, P.O. Some integral inequalities of fractional quantum type. Malaya J. Mat. 2016, 4, 93–99. [Google Scholar]
- Noor, M.A.; Noor, K.I.; Awan, M.U. Some quantum estimates for Hermite Hadamard inequalities. Appl. Math. Comput. 2015, 251, 675–679. [Google Scholar] [CrossRef]
- Xu, P.; Butt, S.I.; Ain, Q.U.; Budak, H. New Estimates for Hermite-Hadamard Inequality in Quantum Calculus via (α, m)-Convexity. Symmetry 2022, 14, 1394. [Google Scholar] [CrossRef]
- Alqudah, M.A.; Kashuri, A.; Mohammed, P.O.; Abdeljawad, T.; Raees, M.; Anwar, M.; Hamed, Y.S. Hermite-Hadamard Integral Inequalities on Co-ordinated Convex Functions in Quantum Calculus. Adv. Differ. Equ. 2021, 2021, 264. [Google Scholar] [CrossRef]
- Rashid, S.; Butt, S.I.; Kanwal, S.; Ahmad, H.; Wang, M.K. Quantum integral inequalities with respect to Raina’s function via coordinated generalized-convex functions with applications. J. Funct. Spaces. 2021, 2021, 6631474. [Google Scholar] [CrossRef]
- Ali, M.A.; Alp, N.; Budak, H.; Chu, Y.; Zhang, Z. On Some New Quantum Midpoint Type Inequalities for Twice Quantum Differentiable Convex Functions. Open Math. 2021, 19, 427–439. [Google Scholar] [CrossRef]
- Butt, S.I.; Budak, H.; Nonlaopon, K. New Variants of Quantum Midpoint-Type Inequalities. Symmetry 2022, 14, 2599. [Google Scholar] [CrossRef]
- Budak, H.; Kara, H. On Quantum Hermite-Jensen-Mercer Inequalities. Miskolc Math. Notes, 2020; accepted. [Google Scholar]
- Mosin, B.B.; Saba, M.; Javed, M.Z.; Awan, M.U.; Budak, H.; Nonlaopon, K. A Quantum Calculus View of Hermite-Hadamard-Jensen-Mercer Inequalities with Applications. Symmetry 2022, 14, 1246. [Google Scholar] [CrossRef]
- Bohner, M.; Budak, H.; Kara, H. Post-Quantum Hermite-Jensen-Mercer Inequalities. Rocky Mt. J. Math. 2022; in press. [Google Scholar]
- Butt, S.I.; Budak, H.; Nonlaopon, K. New Quantum Mercer Estimates of Simpson-Newton like Inequalities via Convexity. Symmetry 2022, 14, 1935. [Google Scholar] [CrossRef]
- Siricharuanun, P.; Erden, S.; Ali, M.A.; Budak, H.; Chasreechai, S.; Sitthiwirattham, T. Some New Simpson’s and Newton’s Formulas Type Inequalities for Convex Functions in Quantum Calculus. Mathematics 2021, 9, 1992. [Google Scholar] [CrossRef]
- Sarikaya, M.Z.; Saglam, A.; Yildirim, H. New Inequalities of Hermite-Hadamard Type for Functions Whose Second Derivatives Absolute Values are Convex and Quasi-convex. Int. J. Open Probl. Comput. Sci. Math. 2012, 5. [Google Scholar] [CrossRef]
- Noor, M.A.; Awan, M.U. Some integral inequalities for two kinds of convexities via fractional integrals. Transylv. J. Math. Mech. 2013, 5, 129–136. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Butt, S.I.; Umar, M.; Budak, H. New Study on the Quantum Midpoint-Type Inequalities for Twice q-Differentiable Functions via the Jensen–Mercer Inequality. Symmetry 2023, 15, 1038. https://doi.org/10.3390/sym15051038
Butt SI, Umar M, Budak H. New Study on the Quantum Midpoint-Type Inequalities for Twice q-Differentiable Functions via the Jensen–Mercer Inequality. Symmetry. 2023; 15(5):1038. https://doi.org/10.3390/sym15051038
Chicago/Turabian StyleButt, Saad Ihsan, Muhammad Umar, and Hüseyin Budak. 2023. "New Study on the Quantum Midpoint-Type Inequalities for Twice q-Differentiable Functions via the Jensen–Mercer Inequality" Symmetry 15, no. 5: 1038. https://doi.org/10.3390/sym15051038




