Ray Tracing Simulation of X-ray Microdiffraction Beamline on the Inverse Compton Source
Abstract
:1. Introduction
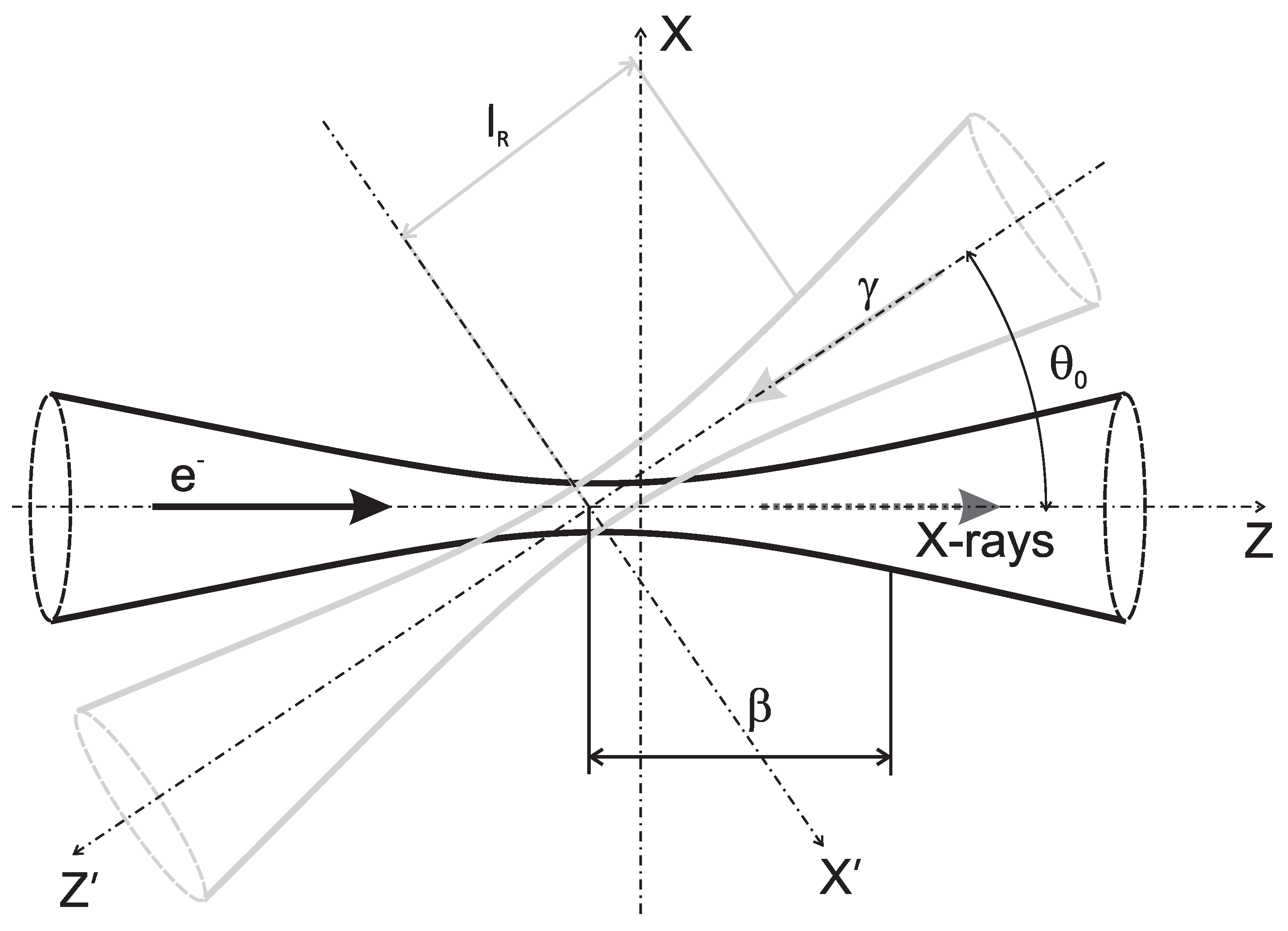
2. Theoretical Basis of ICS Simulation

| Parameter | Value |
|---|---|
| Electron bunch | |
| Electron energy | 45 MeV |
| Bunch charge | 1 nC |
| Energy spread of the electrons | 1% |
| Electron beam emittance | 5 mm·mrad |
| Beta function | 10 mm |
| Electron bunch semi-length | 4 mm |
| Laser pulse | |
| Laser wavelength | 1.06 m |
| Laser pulse energy | 10 mJ |
| Laser pulse repetition frequency (in optical cavity) | 80 MHz |
| Laser pulse semi-length | 4 mm |
| Rayleigh length | 6.8 m |
| Laser-electron collision angle | 2 |
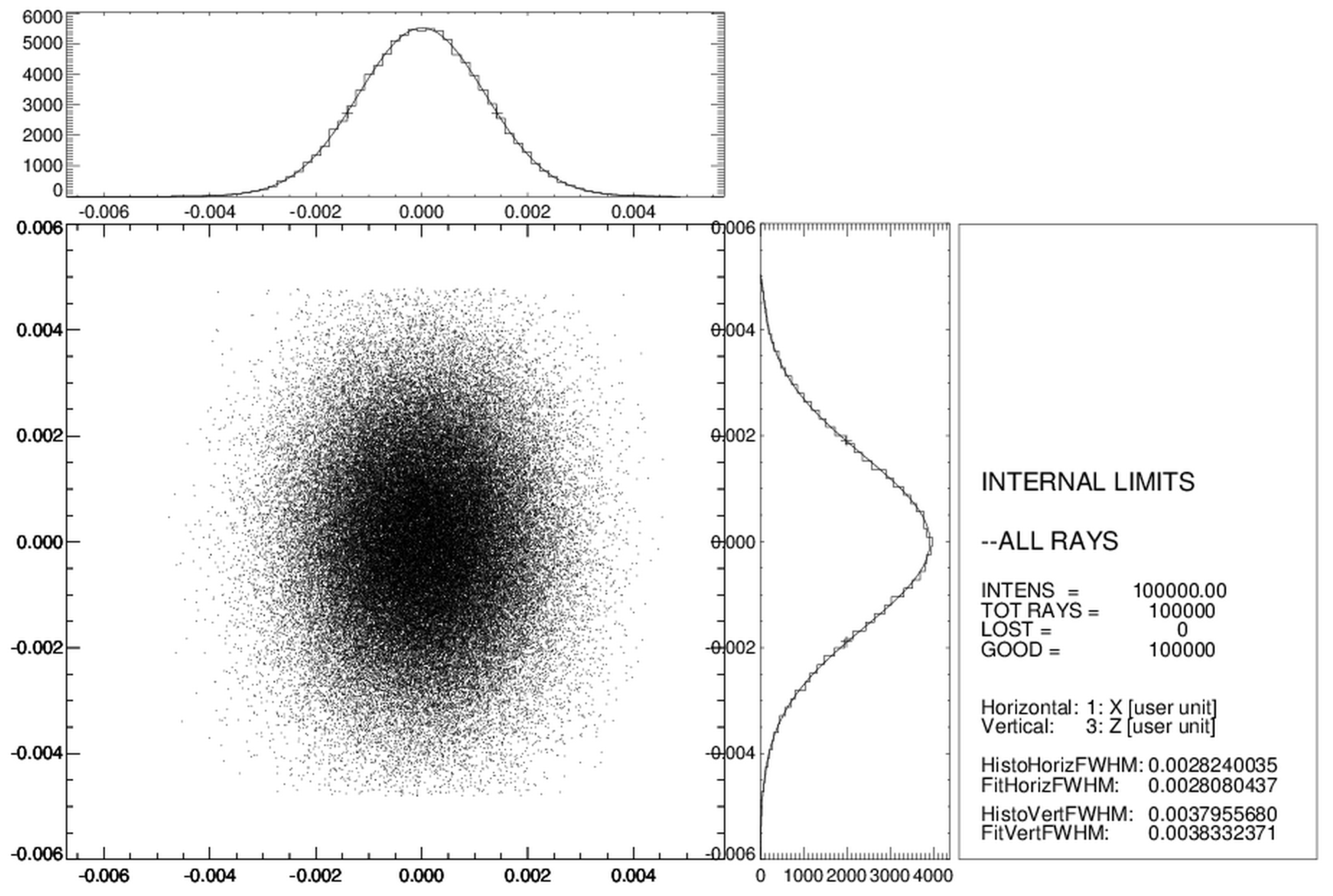
3. X-ray Beamline Design and Simulation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Günther, B.; Gradl, R.; Jud, C.; Eggl, E.; Huang, J.; Kulpe, S.; Achterhold, K.; Gleich, B.; Dierolf, M.; Pfeiffer, F. The versatile X-ray beamline of the Munich Compact Light Source: Design, instrumentation and applications. J. Synchrotron Radiat. 2020, 27, 1395–1414. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Yan, L.; Hua, J.; Du, Q.; Zhang, Z.; Li, R.; Qian, H.; Huang, W.; Chen, H.; Tang, C. Generation of first hard X-ray pulse at Tsinghua Thomson Scattering X-ray Source. Rev. Sci. Instrum. 2013, 84, 053301. [Google Scholar] [CrossRef] [PubMed]
- Bazzani, A.; Cardarelli, P.; Paternò, G.; Placidi, M.; Taibi, A.; Turchetti, G. BoCXS: A compact multidisciplinary X-ray source. Phys. Open 2020, 5, 100036. [Google Scholar] [CrossRef]
- Dupraz, K.; Alkadi, M.; Alves, M.; Amoudry, L.; Auguste, D.; Babigeon, J.L.; Baltazar, M.; Benoit, A.; Bonis, J.; Bonenfant, J.; et al. The ThomX ICS source. Phys. Open 2020, 5, 100051. [Google Scholar] [CrossRef]
- Gibson, D.J.; Albert, F.; Anderson, S.G.; Betts, S.M.; Messerly, M.J.; Phan, H.H.; Semenov, V.A.; Shverdin, M.Y.; Tremaine, A.M.; Hartemann, F.V.; et al. Design and operation of a tunable MeV-level Compton-scattering-based γ-ray source. Phys. Rev. ST Accel. Beams 2010, 13, 070703. [Google Scholar] [CrossRef]
- Drebot, I.; Bacci, A.; Bosotti, A.; Broggi, F.; Canella, F.; Cardarelli, P.; Cialdi, S.; Faillace, L.; Galzerano, G.; Gambaccini, M.; et al. BriXs Ultra High Flux Inverse Compton Source Based on Modified Push-Pull Energy Recovery Linacs. Instruments 2019, 3, 49. [Google Scholar] [CrossRef]
- Huang, Z.; Ruth, R.D. Laser-electron storage ring. Phys. Rev. Lett. 1998, 80, 976. [Google Scholar] [CrossRef]
- Jacquet, M. High intensity compact Compton X-ray sources: Challenges and potential of applications. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2014, 331, 1–5. [Google Scholar] [CrossRef]
- Artyukov, I.; Bessonov, E.; Gorbunkov, M.; Maslova, Y.Y.; Popov, N.; Vinogradov, A. Thomson linac-based X-ray generator: A primer for theory and design. Laser Part. Beams 2016, 34, 637–644. [Google Scholar] [CrossRef]
- Mușat, V.; Latina, A.; D’Auria, G. A High-Energy and High-Intensity Inverse Compton Scattering Source Based on CompactLight Technology. Photonics 2022, 9, 308. [Google Scholar] [CrossRef]
- Hornberger, B.; Kasahara, J.; Ruth, R.; Loewen, R.; Khaydarov, J. Inverse Compton scattering X-ray source for research, industry and medical applications. In Proceedings of the International Conference on X-ray Lasers 2020, Online, 8–10 December 2020; Bleiner, D., Ed.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2021; Volume 11886, p. 1188609. [Google Scholar] [CrossRef]
- Feshchenko, R.; Vinogradov, A.; Artyukov, I. Influence of the electron beam emittance on the polarization of a laser-electron x-ray generator. Phys. Rev. Accel. Beams 2016, 19, 114702. [Google Scholar] [CrossRef]
- Hartemann, F.; Brown, W.; Gibson, D.; Anderson, S.; Tremaine, A.; Springer, P.; Wootton, A.; Hartouni, E.; Barty, C. High-energy scaling of Compton scattering light sources. Phys. Rev. Spec. Top.-Accel. Beams 2005, 8, 100702. [Google Scholar] [CrossRef]
- Landau, L.; Lifchitz, E. Theoretical Physics. Field Theory; Editions Ellipses: Paris, France, 2004. [Google Scholar]
- Brown, W.J.; Hartemann, F.V. Three-dimensional time and frequency-domain theory of femtosecond x-ray pulse generation through Thomson scattering. Phys. Rev. Spec. Top.-Accel. Beams 2004, 7, 060703. [Google Scholar] [CrossRef]
- Sun, C.; Wu, Y.K. Theoretical and simulation studies of characteristics of a Compton light source. Phys. Rev. Spec. Top.-Accel. Beams 2011, 14, 044701. [Google Scholar] [CrossRef]
- Artyukov, I.; Savelév, A.; Shvedunov, V.; Vinogradov, A. Compton X-ray source based on 50-MeV accelerator and its applications. In Proceedings of the LXXII International Conference “NUCLEUS-2022: Fundamental Problems and Applications”, Moscow, Russia, 11–16 July 2022; Stopani, K., Zelenskaya, N., Eds.; Skobeltsyn Institute of Nuclear Physics, Amirit: Saratov, Russia, 2022; pp. 273–274. [Google Scholar]
- Welnak, C.; Chen, G.; Cerrina, F. SHADOW: A synchrotron radiation and X-ray optics simulation tool. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1994, 347, 344–347. [Google Scholar] [CrossRef]
- Lee, H.; Zhang, Z. Applicability of phase ray-tracing method for light scattering from rough surfaces. J. Thermophys. Heat Transf. 2007, 21, 330–336. [Google Scholar] [CrossRef]
- Sanchez del Rio, M.; Canestrari, N.; Jiang, F.; Cerrina, F. SHADOW3: A new version of the synchrotron X-ray optics modelling package. J. Synchrotron Radiat. 2011, 18, 708–716. [Google Scholar] [CrossRef]
- Sanchez del Rio, M.; Dejus, R.J. XOP v2. 4: Recent developments of the X-ray optics software toolkit. Adv. Comput. Methods X-ray Opt. II 2011, 8141, 368–372. [Google Scholar] [CrossRef]
- Mikhailov, I.; Baturin, A.; Kondratenko, V.; Kopilets, I.; Mikhailov, A. Prospects for application of X-ray anomalous transmission effect to monochromatization of broadband spectrum. J. X-ray Sci. Technol. 2017, 25, 25–32. [Google Scholar] [CrossRef]
- Abendroth, J.; McCormick, M.S.; Edwards, T.E.; Staker, B.; Loewen, R.; Gifford, M.; Rifkin, J.; Mayer, C.; Guo, W.; Zhang, Y.; et al. X-ray structure determination of the glycine cleavage system protein H of Mycobacterium tuberculosis using an inverse Compton synchrotron X-ray source. J. Struct. Funct. Genom. 2010, 11, 91–100. [Google Scholar] [CrossRef]
- Gradl, R.; Dierolf, M.; Günther, B.; Hehn, L.; Möller, W.; Kutschke, D.; Yang, L.; Donnelley, M.; Murrie, R.; Erl, A.; et al. In vivo dynamic phase-contrast X-ray imaging using a compact light source. Sci. Rep. 2018, 8, 6788. [Google Scholar] [CrossRef] [PubMed]
- Eggl, E.; Schleede, S.; Bech, M.; Achterhold, K.; Loewen, R.; Ruth, R.D.; Pfeiffer, F. X-ray phase-contrast tomography with a compact laser-driven synchrotron source. Proc. Natl. Acad. Sci. USA 2015, 112, 5567–5572. [Google Scholar] [CrossRef] [PubMed]
- Bessonov, E.G.; Vinogradov, A.V.; Gorbunkov, M.V.; Tur’yanskii, A.G.; Feshchenko, R.M.; Shabalin, Y.V. Laser electron-beam X-ray source for medical applications. Physics-Uspekhi 2003, 46, 872–876. [Google Scholar] [CrossRef]
- Artyukov, I.; Bessonov, E.; Feshchenko, R.; Gorbunkov, M.; Maslova, Y.Y.; Popov, N.; Dyachkov, N.; Postnov, A.; Vinogradov, S.; Vinogradov, A. Design study of Thomson Laser-Electron X-ray Generator (LEX) for Millisecond Angiography. J. Phys. Conf. Ser. 2017, 784, 012002. [Google Scholar] [CrossRef]
- Kulpe, S.; Dierolf, M.; Günther, B.; Busse, M.; Achterhold, K.; Gleich, B.; Herzen, J.; Rummeny, E.; Pfeiffer, F.; Pfeiffer, D. K-edge Subtraction Computed Tomography with a Compact Synchrotron X-ray Source. Sci. Rep. 2019, 9, 1332. [Google Scholar] [CrossRef]
- Huang, J.; Günther, B.; Achterhold, K.; Cui, Y.T.; Gleich, B.; Dierolf, M.; Pfeiffer, F. Energy-Dispersive X-ray Absorption Spectroscopy with an inverse compton Source. Sci. Rep. 2020, 10, 8772. [Google Scholar] [CrossRef]
- Huang, J.; Deng, F.; Günther, B.; Achterhold, K.; Liu, Y.; Jentys, A.; Lercher, J.A.; Dierolf, M.; Pfeiffer, F. Laboratory-scale in situ X-ray absorption spectroscopy of a palladium catalyst on a compact inverse-Compton scattering X-ray beamline. J. Anal. At. Spectrom. 2021, 36, 2649–2659. [Google Scholar] [CrossRef]
- Dombrowsky, A.C.; Burger, K.; Porth, A.K.; Stein, M.; Dierolf, M.; Günther, B.; Achterhold, K.; Gleich, B.; Feuchtinger, A.; Bartzsch, S.; et al. A proof of principle experiment for microbeam radiation therapy at the Munich compact light source. Radiat. Environ. Biophys. 2020, 59, 111–120. [Google Scholar] [CrossRef]
- Polyakov, S.; Artyukov, I.; Blank, V.; Zholudev, S.; Feshchenko, R.; Popov, N.; Yaroslavtsev, A.; Vinogradov, A. Evaluation of laser-electron X-ray source and related optics for x-ray diffractometry and topography. In Proceedings of the X-ray Lasers and Coherent X-ray Sources: Development and Applications, Prague, Czech Republic, 24–26 April 2017; SPIE: Bellingham, WA, USA, 2017; Volume 10243, pp. 124–131. [Google Scholar] [CrossRef]
- Walter, P.; Variola, A.; Zomer, F.; Jaquet, M.; Loulergue, A. A new high quality X-ray source for cultural heritage. Comptes Rendus Phys. 2009, 10, 676–690. [Google Scholar] [CrossRef]
- Gibson, D.J.; Anderson, S.G.; Barty, C.P.; Betts, S.M.; Booth, R.; Brown, W.J.; Crane, J.K.; Cross, R.R.; Fittinghoff, D.N.; Hartemann, F.V.; et al. PLEIADES: A picosecond Compton scattering x-ray source for advanced backlighting and time-resolved material studies. Phys. Plasmas 2004, 11, 2857–2864. [Google Scholar] [CrossRef]
- Hack, S.; Tóth, Z.; Varró, S.; Czirják, A. Isolated attosecond pulses of μ J energy via coherent Thomson-backscattering, driven by a chirped laser pulse. Eur. Phys. J. D 2019, 73, 77. [Google Scholar] [CrossRef]
- Albert, F.; Anderson, S.; Gibson, D.; Marsh, R.; Wu, S.; Siders, C.; Barty, C.; Hartemann, F. Design of narrow-band Compton scattering sources for nuclear resonance fluorescence. Phys. Rev. Spec. Top.-Accel. Beams 2011, 14, 050703. [Google Scholar] [CrossRef]
- Thirolf, P.; Csige, L.; Habs, D.; Günther, M.; Jentschel, M.; Krasznahorkay, A.; Filipescu, D.; Glodariu, T.; Stroe, L.; Tesileanu, O.; et al. Perspectives for photofission studies with highly brilliant, monochromatic γ–ray beams. In Proceedings of the EPJ Web of Conferences, Madrid, Spain, 25–27 June 2012; EDP Sciences: Les Ulis, France, 2012; Volume 38, p. 08001. [Google Scholar] [CrossRef]
- Petrillo, V.; Drebot, I.; Ruijter, M.; Samsam, S.; Bacci, A.; Curatolo, C.; Opromolla, M.; Conti, M.R.; Rossi, A.R.; Serafini, L. State of the Art of High-Flux Compton/Thomson X-rays Sources. Appl. Sci. 2023, 13, 752. [Google Scholar] [CrossRef]

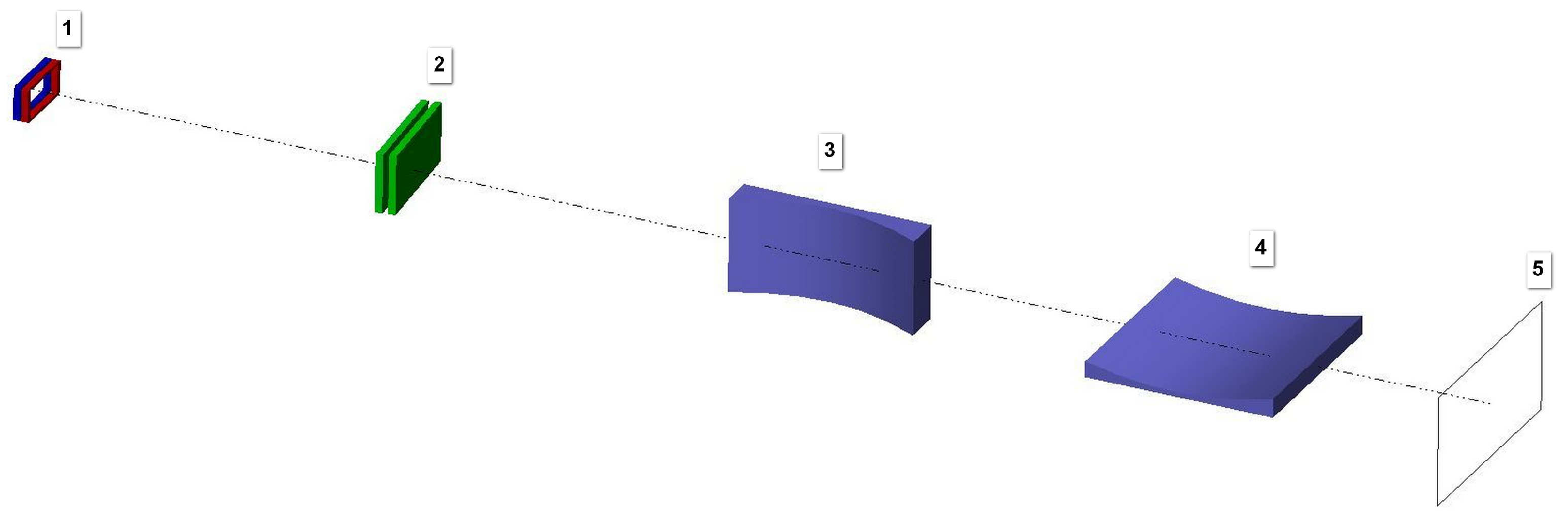


| Mirror 1 | Mirror 2 | |
|---|---|---|
| Shape | elliptical | elliptical |
| Distance from the source to the mirror center, mm | 2610 | 3000 |
| Major semi-axis, mm | 1750 | 1750 |
| Minor semi-axis, mm | 3.04824 | 2.45000 |
| Mirror length, mm | 520 | 260 |
| Demagnification | 2.93 | 6.00 |
| Parameter | Value |
|---|---|
| Horizontal spot size , m | 8.08 |
| Vertical spot size , m | 7.26 |
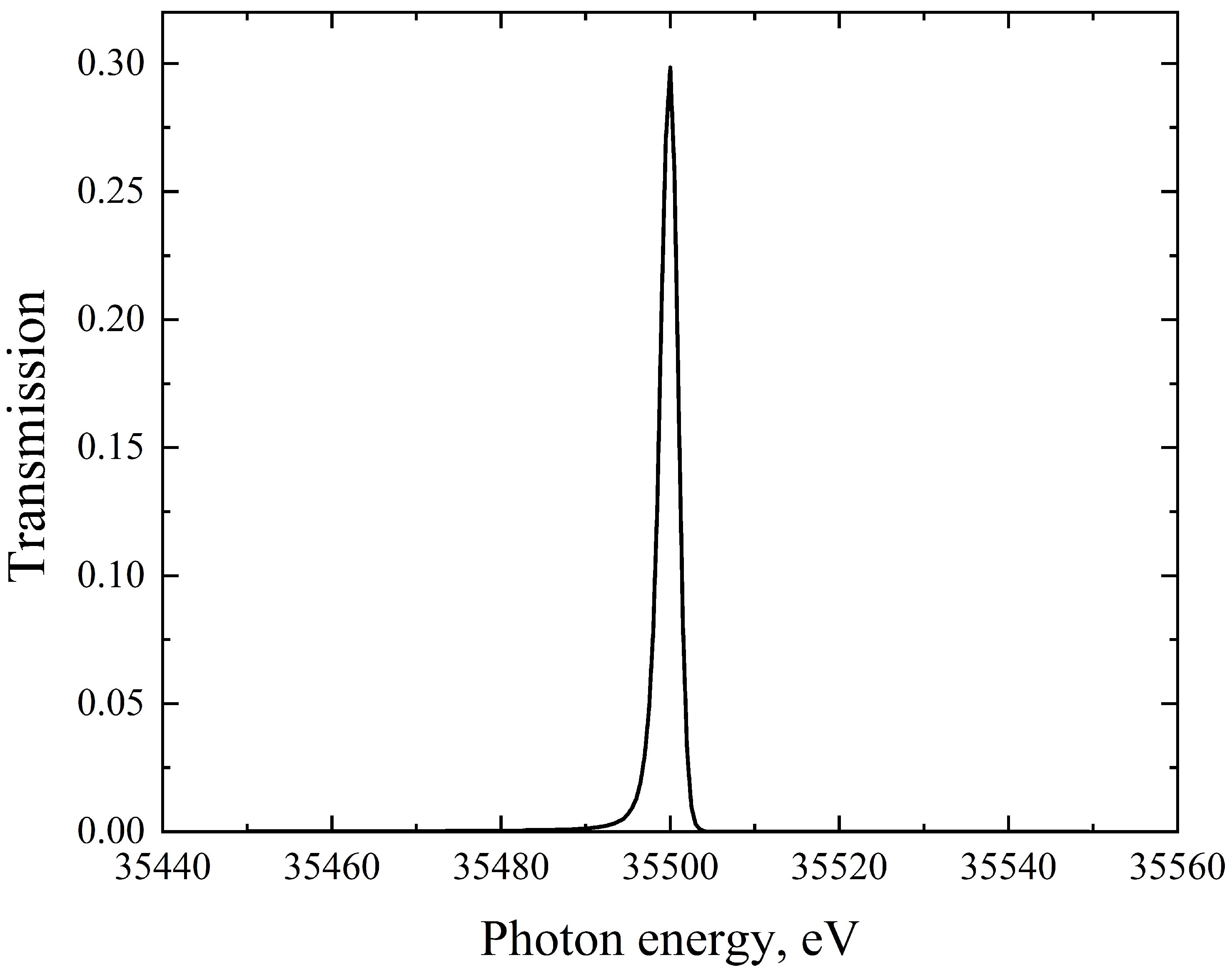
| Spectral width , eV | 46.2 |
| Horizontal angular divergence , mrad | 0.18 |
| Vertical angular divergence , mrad | 0.61 |
| Total beamline throughput | 3.42 |
| Flux in the focal spot at the sample, ph/s | 1.4 |
| Flux density at the sample, ph/s/cm | 2.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vinogradov, A.; Feshchenko, R.; Shvedunov, V.; Artyukov, I. Ray Tracing Simulation of X-ray Microdiffraction Beamline on the Inverse Compton Source. Symmetry 2023, 15, 1068. https://doi.org/10.3390/sym15051068
Vinogradov A, Feshchenko R, Shvedunov V, Artyukov I. Ray Tracing Simulation of X-ray Microdiffraction Beamline on the Inverse Compton Source. Symmetry. 2023; 15(5):1068. https://doi.org/10.3390/sym15051068
Chicago/Turabian StyleVinogradov, Alexander, Ruslan Feshchenko, Vasiliy Shvedunov, and Igor Artyukov. 2023. "Ray Tracing Simulation of X-ray Microdiffraction Beamline on the Inverse Compton Source" Symmetry 15, no. 5: 1068. https://doi.org/10.3390/sym15051068
APA StyleVinogradov, A., Feshchenko, R., Shvedunov, V., & Artyukov, I. (2023). Ray Tracing Simulation of X-ray Microdiffraction Beamline on the Inverse Compton Source. Symmetry, 15(5), 1068. https://doi.org/10.3390/sym15051068








