Capped L_2,p-Norm Metric Based on Robust Twin Support Vector Machine with Welsch Loss

Abstract

A twin bounded support vector machine (TBSVM) is a phenomenon of symmetry that improves the performance of the traditional support vector machine classification algorithm. In this paper, we propose an improved model based on a TBSVM, called a Welsch loss with capped $L_{2,p}$-norm distance metric robust twin bounded support vector machine (WCTBSVM). On the one hand, by introducing the capped $L_{2,p}$-norm metric in the TBSVM, the problem of the non-sparse output of the regularization term is solved; thus, the generalization and robustness of the TBSVM is improved and the principle of minimizing the structural risk is realized. On the other hand, a bounded, smooth, and non-convex Welsch loss function is introduced to reduce the influence of noise, which further improves the classification performance of the TBSVM. We use a half-quadratic programming algorithm to solve the model non-convexity problem caused by Welsch loss. Therefore, the WCTBSVM is more robust and effective in dealing with noise compared to the TBSVM. In addition, to reduce the time complexity and speed up the convergence of the algorithm, we constructed a least squares version of the WCTBSVM, named the fast WCTBSVM (FWCTBSVM). Experimental results on both UCI and artificial datasets show that our model can show better classification performance on classification problems.

1. Introduction

The support vector machine (SVM) [1,2,3,4,5] is designed for the binary classification problem, which is the development basis of other classifiers in machine learning due to its superior performance in text classification tasks. The SVM is widely used in data classification and regression analysis problems, such as artificial intelligence, speech recognition, remote image analysis, financial management, etc. Scene recognition plays a crucial role in supporting cognitive communications of unmanned aerial vehicle (UAV). To leverage scenario-dependent channel characteristics, we propose an air-to-ground (A2G) scenario identification model based on support vector machine (SVM) [6]. SVM is based on the principle of structural risk minimization, which has excellent generalization performance, and the basic idea is to determine the maximum distance between the two types of data. Although a SVM is highly applicable to classification problems, it still faces some challenges in handling its learning tasks. To avoid the occurrence of over-fitting, a SVM is extended to a soft-margin SVM (C-SVM) [7] after introducing relaxation variables. The loss function of the C-SVM is a hinge loss, which is very sensitive to the noise points in the sample, so as to avoid over-fitting. Moreover, the SVM needs to solve a quadratic programming problem (QPP) of complexity $O\left(n^3\right)$ [7] in the process of solving. Therefore, many new programmes have been proposed to speed up the training process of the SVM. For example, how to decompose a large QPP into multiple small QPPs, or how to build other variant models of the new SVM. Among the more popularly accepted is the generalized eigenvalue proximal support vector machine (GEPSVM) [8] and the twin support vector machine (TSVM) [3,9,10,11,12]. The GEPSVM searches for two nonparallel hyperplanes by solving two related generalized eigenvalue problems. The TSVM divides a large QPP into two small QPPs, of which the principle is based on the GEPSVM search for two nonparallel hyperplanes, so that the positive (negative) sample is as close as possible to the positive class (negative class) hyperplane, and as close to the other hyperplane as possible. Therefore, the TSVM runs much faster than the SVM in theory.

In the process of studying the TSVM, some scholars have found that the TSVM needs to solve two QPPs, which is not feasible for large-scale classification. In order to reduce the calculated amount of the TSVM and maintain the advantage, the least squares support vector machine (LSSVM) was first proposed by Suykens et al. [2,13,14]. The LSSVM is one of the important achievements in the field of machine learning in recent years, and its training process follows the principle of risk minimization, which replaces the inequality constraints with equality constraints and solves two sets of linear equations. Based on this, Tomar et al. extended the LSTSVM to a multi-class classification and proposed a multi-class least-squares twin support vector machine (MLSTSVM) [7]. For multiple samples, the MLSTSVM generates multiple hyperplanes, where one plane corresponds to one sample, where the ith sample is as close as possible to the ith hyperplane, while being as far away from the other hyperplane as possible. Xie et al. [15] propose a novel Laplacian Lp norm least squares twin support vector machine (Lap-LpLSTSVM). The experimental results on both synthetic and real-world datasets show that the Lap-LpLSTSVM outperforms other state-of-the-art methods and can also deal with noisy datasets. Ye et al. proposed the information-weighted TWSVM classification method (WLTSVM) [16], which represents the compactness of intra-class samples and the discreteness of inter-class samples by using inter-class graphs. In addition, a new SVM was also proposed by Shao et al. [8], which is a twin bounded support vector machine (TBSVM) [9]. It increases the regularization term containing the 2-norm and achieves the principle of minimizing the structural risk and improves the classification performance of the SVM. The TSVM is calculated faster than the SVM, but the square $L_2$-norm distance used in the TSVM increases the effect of the outliers; thus, affecting the construction of the hyperplane in the presence of noise. To enhance the classification performance of twin support vector machines (TSVMs) on imbalanced datasets, a reduced universum twin support vector machine for class imbalance learning (RUTSVM) has been proposed based on the universum TSVM framework. However, RUTSVM suffers from a key drawback in terms of matrix inverse computation involved in solving its dual problem and finding classifiers. To address this issue, Moosae [17] proposes an improved version of RUTSVM called IRUTSVM. Therefore, on the basis of the TSVM, Wang et al. proposed the term capped $L_1$-norm twin support vector machines (CTSVM) [18,19]; thus, eliminating the effect of partial outliers and increasing the robustness. From here, we see that the $L_1$-norm increases the robustness better than the square $L_2$-norm. However, the classification of the $L_1$-norm distance measures also shows its drawbacks. When the outliers are large, the capped $L_1$-norm measures are neither convex nor smooth, making them difficult to optimize. For the problem of the $L_1$-norm, a robust twin support vector machine based on the $L_{2,p}$-norm (pTSVM) [20,21,22] formula was proposed recently, which better suppresses the effect of outliers than the $L_1$-norm and the square $L_2$-norm.

To further suppress the adverse effects of the outliers, we introduce a bounded, smooth, and non-convex Welsch loss [23,24,25]. The Welsch loss is based on the loss function of the Welsch estimation method, of which the Welsch estimation method is one method in robust estimation. When the data error is normally distributed, it is comparable to the mean square error loss, but the Welsch loss is more robust when the error is a non-normal distribution and the error is caused by outliers. To improve the robustness and generalization performance of the TBSVM, this paper proposes a classifier to increase the terms of the Welsch loss function on the basis of the capped $L_{2,p}$-norm, which is a capped $L_{2,p}$-norm metric based on a robust twin support vector machine with a Welsch loss (WCTBSVM). The WCTBSVM is more robust than the TBSVM, while reducing the effect of outliers and improving the classification performance. Beyond this, the fast WCTBSVM (FWCTBSVM) is proposed based on the idea of least squares; changing the inequality constraint to the equality constraint accelerates the operation of the algorithm.

Combined with the above content, this article carries out the main work and mainly has the following points:

(1) By analyzing the characteristics of both the Welsch loss function and the capped $L_{2,p}$-norm metric distance, a new robust learning algorithm based on a TBSVM is proposed as a WCTBSVM. Without loss of precision, a least squares version of WCTBSVM is constructed, named FWCTBSVM.

(2) The iterative algorithms of WCTBSVM and FWCTBSVM models are given, and their convergence is analyzed according to the characteristics of the models.

(3) Through experiments on UCI datasets and artificial datasets, we found that the WCTBSVM and FWCTBSVM have advantages over several other methods in terms of robustness and feasibility.

(4) To see the advantages of the WRTBSVM and FWRTBSVM more intuitively, we conducted a statistical monitoring analysis to further verify that the classification performance of the WRTBSVM and FWRTBSVM was stronger than that of the TSVM, TBSVM, LSTSVM, and CTSVM.

In Section 2, we introduce some related models, such as the TSVM, TBSVM, CTSVM, LSTSVM, and capped $L_{2,p}$-norm. In Section 3, we integrate the Welsch function into the model, and then solve the model. A large number of data experiments are conducted to test the operation of the model in Section 5. The fifth chapter is a summary of the full text.

2. Related Work

In this paper, we propose two models based on the following relevant content. We first make a simple introduction to four classification models: the twin support vector machine (TSVM), twin bounded support vector machine (TBSVM), capped $L_1$-norm twin support vector machine (CTSVM), and least squares twin support vector machine (LSTSVM), as well as the capped $L_{2,p}$-norm and Welsch loss functions to be introduced in the model of this paper [25].

2.1. TSVM

The TSVM was first proposed by Jayadeva et al. The basic theory is to produce two nonparallel classification planes, and keep each class close to the corresponding one, and far away from the other one. The TSVM differs from the SVM by dividing a convex quadratic programming problem into two convex quadratic programming problems; thus, speeding up the rate of classification identification.

We set up a training dataset ${\zeta }_l=\left\{(x_i,y_i)\right|i=1,2\dots l\}\in {(R^n,Y)}^l$, where $x_i\in R^n$ and $y_i\in Y=\{-1,1\}$ denote the class to which the point ith belongs. Class 1 and class -1 are represented as positive samples and negative samples, respectively. The number of samples in ${\zeta }_l$ containing positive class samples is denoted by $m_1$, and the number of samples containing negative class samples is denoted by $m_2$, where $l=m_1+m_2$. Let $A\in R^{m_1\times n}$ represents all positive class samples, and $B\in R^{m_2\times n}$ represents all negative class samples. Thus, we determine two non-parallel hyperplanes:

$$\begin{array}{c}\hfill f_1\left(x\right)={\omega }_1^{T}x+b_1=0\end{array}$$

(1)

and

$$\begin{array}{c}\hfill f_2\left(x\right)={\omega }_2^{T}x+b_2=0\end{array}$$

(2)

where ${\omega }_1,{\omega }_2\in R^n$ are the normal vector of the hyperplane and $b_1,b_2\in R$ are the offset of the hyperplane.

Subsequently, we can obtain a model of the TSVM:

$$\begin{array}{c}\underset{{\omega }_1,b_1}{min}\frac{1}{2}{\parallel A{\omega }_1+e_1{b}_1\parallel }_2^2+C_1{e}_2^T{\xi }_1\hfill \\ s.t.-(B{\omega }_1+e_2{b}_1)+{\xi }_1\ge e_2,{\xi }_1\ge 0\hfill \end{array}$$

(3)

$$\begin{array}{c}\underset{{\omega }_2,b_2}{min}\frac{1}{2}{\parallel B{\omega }_2+e_2{b}_2\parallel }_2^2+C_2{e}_1^T{\xi }_2\hfill \\ s.t.(A{\omega }_2+e_1{b}_2)+{\xi }_2\ge e_1{\xi }_1\ge 0\hfill \end{array}$$

(4)

where $C_1\ge 0,C_2\ge 0$ are regularization parameters, $e_1$ and $e_2$ are vectors of ones of appropriate dimensions, ${\xi }_1$ and ${\xi }_2$ are the slack vectors.

Introducing the Lagrange multipliers $\alpha$ and $\beta$, let $H=[A,e_1]$ and $Z=[B,e_2]$, and we can get the dual problem:

$$\begin{array}{c}\underset{\alpha }{min}\frac{1}{2}{\alpha }^{T}Z{\left(H^{T}H\right)}^{-1}{Z}^T\alpha -e_2^T\alpha \hfill \\ s.t.0\le \alpha \le C_1{e}_2\hfill \end{array}$$

(5)

$$\begin{array}{c}\underset{\beta }{min}\frac{1}{2}{\beta }^{T}H{\left(Z^{T}Z\right)}^{-1}{H}^T\beta -e_2^T\beta \hfill \\ s.t.0\le \beta \le C_2{e}_1.\hfill \end{array}$$

(6)

Finally, two nonparallel hyperplanes can be obtained by solving the QPPs in formulas (5) and (6)

$${[{\omega }_1,b_1]}^T=-{\left(H^{T}H\right)}^{-1}{Z}^T\alpha ,{[{\omega }_2,b_2]}^T={\left(Z^{T}Z\right)}^{-1}{H}^T\beta .$$

(7)

2.2. TBSVM

To enhance the classification performance of the TSVM, a new TSVM model called a TBSVM was proposed by Shao et al. [8]. The TBSVM is two non-parallel hyperplanes for classification by solving two smaller QPPs. Thus, we can write the TBSVM as:

$$\begin{array}{c}\underset{{\omega }_1,b_1}{min}\frac{1}{2}\parallel A{\omega }_1+e_1{b}_1{\parallel }_2^2+C_1{e}_2^T{\xi }_1+\frac{C_3}{2}(\parallel {\omega }_1{\parallel }_2^2+b_1^2)\hfill \\ s.t.-(B{\omega }_1+e_2{b}_1)+{\xi }_1\ge e_2,{\xi }_1\ge 0\hfill \end{array}$$

(8)

and

$$\begin{array}{c}\underset{{\omega }_2,b_2}{min}\frac{1}{2}\parallel B{\omega }_2+e_2{b}_2{\parallel }_2^2+C_2{e}_1^T{\xi }_2+\frac{C_4}{2}(\parallel {\omega }_2{\parallel }_2^2+b_2^2)\hfill \\ s.t.s.t.(A{\omega }_2+e_1{b}_2)+{\xi }_2\ge e_1,{\xi }_2\ge 0\hfill \end{array}$$

(9)

where ${\xi }_1$ and ${\xi }_2$ are the slack vectors, 0 is a zero vector, $C_1\ge 0,C_2\ge 0,C_3\ge 0$ and $C_4\ge 0$ are the regularization parameters,  $e_1,e_2$ are all unit vectors, A and B are the same as A and B of (3). Based on optimization theory and dual theory, let $H=[A,e_1]$ and $Z=[B,e_2]$. We can then get the dual problems of (8) and (9) as follows:

$$\begin{array}{c}\underset{\alpha }{min}\frac{1}{2}{\alpha }^{T}Z{(H^{T}H+C_{3}I)}^{-1}{Z}^T\alpha -e_2^T\alpha \hfill \\ s.t.0\le \alpha \le C_1{e}_2\hfill \end{array}$$

(10)

and

$$\begin{array}{c}\underset{\beta }{min}\frac{1}{2}{\beta }^{T}H{(Z^{T}Z+C_{4}I)}^{-1}{H}^T\beta -e_2^T\beta \hfill \\ s.t.0\le \beta \le C_2{e}_1\hfill \end{array}$$

(11)

where $\alpha \in R^{m_2}$ and $\beta \in R^{m_1}$ are $Lagrange$ multipliers. Further, we can get the solution problems of (10) and (11) as follows:  

$${[{\omega }_1,b_1]}^T=-{(H^{T}H+C_{3}I)}^{-1}{Z}^T\alpha ,$$

(12)

$${[{\omega }_2,b_2]}^T={(Z^{T}Z+C_{4}I)}^{-1}{H}^T\beta .$$

(13)

2.3. CTSVM

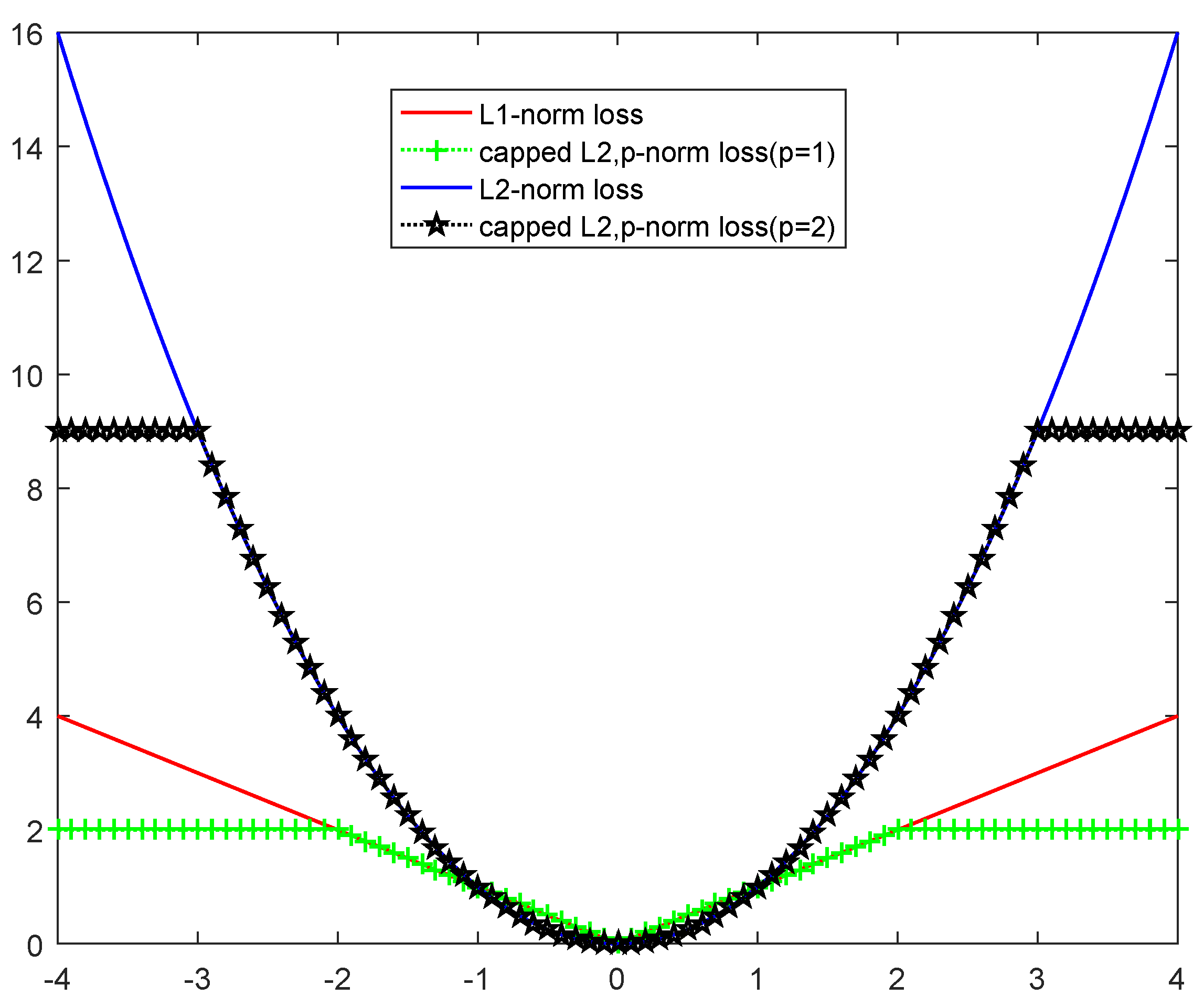
Using the $L_2$-norm in the TSVM increases the effect of the noises without reaching the structure of the optimized classification hyperplanes. Therefore, the capped $L_1$-norm twin support vector machine (CTSVM) is introduced to increase the robustness to the noise, which helps reduce noise during the model training. The capped $L_1$-norm is shown in Figure 1.

The CTSVM classifier is obtained by solving the following problems:

$$\begin{array}{c}\underset{{\omega }_1,b_1}{min}\sum _{i=1}^{m_1}min(\parallel {\omega }_1{x}_i+b_1\parallel ,{\epsilon }_1)+C_1\sum _{i=1}^{m_2}min(\parallel {\xi }_{1,i}{\parallel }_1,{\epsilon }_2)\hfill \\ s.t.-(B{\omega }_1+e_2{b}_1)+{\xi }_1\ge e_2\hfill \end{array}$$

(14)

and

$$\begin{array}{c}\underset{{\omega }_2,b_2}{min}\sum _{i=1}^{m_2}min(\parallel {\omega }_2{x}_i+b_2\parallel ,{\epsilon }_3)+C_2\sum _{i=1}^{m_1}min(\parallel {\xi }_{2,i}{\parallel }_1,{\epsilon }_4)\hfill \\ s.t.(A{\omega }_1+e_1{b}_2)+{\xi }_2\ge e_1\hfill \end{array}$$

(15)

where, $C_1>0$ and $C_2>0$, $e_1\in {\mathbb{R}}^{m_1}$ and $e_2\in {\mathbb{R}}^{m_2}$ are the unit vectors, ${\epsilon }_1,{\epsilon }_2,{\epsilon }_3$, ${\epsilon }_4$ are the thresholding parameters, and ${\xi }_1$ and ${\xi }_2$ are the slack vectors. Here, we use the capped $L_1$-norm to reduce the influence of the outliers. At the capped $L_1$-norm loss function, when the data point is misclassfied, the loss is $\epsilon$.

We can reformulate the problems as the following approximation ones:

$$\begin{array}{c}\underset{{\omega }_1,b_1}{min}\frac{1}{2}{(A{\omega }_1+e_1{b}_1)}^{T}F(A{\omega }_1+e_1{b}_1)+\frac{1}{2{\sigma }^2}{C}_1{\xi }_1^{T}Q{\xi }_1\hfill \\ s.t.-(B{\omega }_1+e_2{b}_1)+{\xi }_1\ge e_2\hfill \end{array}$$

(16)

and

$$\begin{array}{c}\underset{{\omega }_2,b_2}{min}\frac{1}{2}{(A{\omega }_2+e_2{b}_2)}^{T}K(A{\omega }_2+e_2{b}_2)+\frac{1}{2{\sigma }^2}{C}_2{\xi }_2^{T}U{\xi }_2\hfill \\ s.t.(A{\omega }_2+e_1{b}_2)+{\xi }_2\ge e_1\hfill \end{array}$$

(17)

where F, Q, K and U are four diagonal matrices with diagonal elements as:

$$f_i=\left\{\begin{array}{cc}\frac{1}{\mid {\omega }_1{x}_i+b_1\mid },\hfill & \mid {\omega }_1{x}_i+b_1\mid \le {\epsilon }_1.\\ \\ 0,\hfill & other.\end{array}\right.,q_i=\left\{\begin{array}{cc}\frac{1}{\mid {\xi }_{1,i}\mid },\hfill & \mid {\xi }_{1,i}\mid \le {\epsilon }_2.\\ \\ 0,\hfill & other.\end{array}\right.$$

(18)

$$k_i=\left\{\begin{array}{cc}\frac{1}{\mid {\omega }_2{x}_i+b_2\mid },\hfill & \mid {\omega }_2{x}_i+b_2\mid \le {\epsilon }_3.\\ \\ 0,\hfill & other.\end{array}\right.,u_i=\left\{\begin{array}{cc}\frac{1}{\mid {\xi }_{2,i}\mid },\hfill & \mid {\xi }_{2,i}\mid \le {\epsilon }_4.\\ \\ 0,\hfill & other.\end{array}\right.$$

(19)

Based on optimization theory and dual theory, let $H=[A,e_1]$ and $Z=[B,e_2]$. We can then get the dual problems of (16) and (17)

$$\begin{array}{c}\underset{\alpha }{min}\frac{1}{2}{\alpha }^T(Z{\left(H^{T}FH\right)}^{-1}{Z}^T+\left(\frac{1}{C_1}\right)Q^{-1})\alpha -e_2^T\alpha \hfill \\ s.t.0\le \alpha \hfill \end{array}$$

(20)

and

$$\begin{array}{c}\underset{\beta }{min}\frac{1}{2}{\beta }^T(H{\left(Z^{T}KZ\right)}^{-1}{H}^T+\left(\frac{1}{C_2}\right)U^{-1})\beta -e_1^T\beta \hfill \\ s.t.0\le \beta \hfill \end{array}$$

(21)

where $\alpha \in R^{m_2}$ and $\beta \in R^{m_1}$ are $Lagrange$ multipliers.

2.4. LSTSVM

The TSVM has a great advantages over the SVM in the process of classification, but it also expands the influence of noise; thus, increasing the calculation difficulty when processing large amounts of data. However, the least squares twin support vector machine (LSTSVM) can change the inequality constraint into the equation constraint, which can avoid the problems that the TSVM deals with regarding large amounts of data. Therefore, we have the LSTSVM as

$$\begin{array}{c}\underset{{\omega }_1,b_1}{min}\frac{1}{2}{\parallel A{\omega }_1+e_1{b}_1\parallel }_2^2+\frac{C_1}{2}{\xi }_1^T{\xi }_1\hfill \\ s.t.-(B{\omega }_1+e_2{b}_1)+{\xi }_1=e_2\hfill \end{array}$$

(22)

and

$$\begin{array}{c}\underset{{\omega }_2,b_2}{min}\frac{1}{2}{\parallel B{\omega }_2+e_2{b}_2\parallel }_2^2+\frac{C_1}{2}{\xi }_2^T{\xi }_2\hfill \\ s.t.(A{\omega }_2+e_1{b}_2)+{\xi }_2=e_1\hfill \end{array}$$

(23)

where, $C_1>0$ and $C_2>0$ represent regularization parameters, and ${\xi }_1$ and ${\xi }_2$ are slack vectors.

Furthermore, the optimization problems (22) and (23) can be rewritten:

$$\underset{{\omega }_1,b_1}{min}\sum _{i=1}^{m_1}\frac{1}{2}\parallel A{\omega }_1+e_1{b}_1{\parallel }_2^2+\frac{1}{2}{C}_1{\parallel e_2+B{\omega }_1+e_2{b}_1\parallel }_2^2,$$

(24)

and

$$\underset{{\omega }_2,b_2}{min}\sum _{i=1}^{m_2}\frac{1}{2}\parallel B{\omega }_2+e_2{b}_2{\parallel }_2^2+\frac{1}{2}{C}_2{\parallel e_1-A{\omega }_1-e_1{b}_2\parallel }_2^2.$$

(25)

Let $H=[A,e_1]$ and $Z=[B,e_2]$. We take the partial derivative of ${\omega }_1$ and $b_1$, ${\omega }_2$ and $b_2$ to 0 in (24) and (25). Thus, we can get:

$${\left[\begin{array}{cc}{\omega }_1& b_1\end{array}\right]}^T=-{(\frac{1}{C_1}{H}^{T}H+Z^{T}Z)}^{-1}{Z}^T{e}_2$$

(26)

and

$${\left[\begin{array}{cc}{\omega }_2& b_2\end{array}\right]}^T=-{(\frac{1}{C_2}{Z}^{T}Z+H^{T}H)}^{-1}{H}^T{e}_1.$$

(27)

2.5. Capped $L_{2p}$-norm

It is well known that the squared $L_2$-norm distance metric is used in most variant classifiers associated with the TSVM, but this is more sensitive to outliers. Because of the differentiable of the squared $L_2$-norm, the negative effect on the outliers with the square term is added; thus, decreasing the classification performance of the model. However, the $L_{2,p}$-norm inhibits the negative effect of the outliers better than the $L_1$-norm and squared $L_2$-norm, and the $p=1$, $L_{2,p}$-norm becomes the $L_1$-norm. Obviously, by setting an appropriate p, based on the capped $L_{2,p}$-norm, there is more robustness than the capped $L_2$-norm, and these algorithms show that the capped $L_{2,p}$-norm is robust to Gaussian noise.

For any vector, the $a\in R^n$ and $p\in [0,2]$, $L_{2,p}$-norm and capped $L_{2,p}$-norm are defined as:

$$f_1\left(a\right)={\left(\sum _{i=1}^n{a}_i^2\right)}^{\frac{p}{2}},f_2\left(a\right)=min({\left(\sum _{i=1}^n{a}_i^2\right)}^{\frac{p}{2}},\epsilon ),$$

(28)

where $\epsilon \ge 0$ is the thresholding parameter.

From Figure 2 we can find that the capped $L_{2,p}$-norm is more robust than the $L_1$-norm and $L_2$-norm; thus, making the classification performance of the model better.

Because the capped $L_{2,p}$-norm is relatively so well robust, we introduce the capped $L_{2,p}$-norm in the model proposed in this paper and further improve the generalization and robustness of the TBSVM.

2.6. Welsch Regularization

In this paper, we focus on the Welsch loss function. It is a bounded, smooth, and non-convex loss, which is very robust to the noises. It is defined as:

$$\begin{array}{c}\hfill V\left(\xi \right)=\frac{{\sigma }^2}{2}[1-\exp (-\frac{{\xi }^2}{2{\sigma }^2})]\end{array}$$

(29)

where, $\sigma$ is a penalty parameter. Figure 3 shows the Welsch loss function, $V\left(\xi \right)$ under different values of $\sigma$, which changes from 1 to 3 [23,26,27,28,29].

Through Figure 3, we found that the upper bound of the Welsch loss function increases and the convergence speed slows down as $\sigma$ gradually increases. Thus, the impact of noise on the model during the training process is limited. Consequently, the Welsch loss can further enhance the robustness of the model.

3. Main Contributions

To improve the generalization performance of the TBSVM, this paper proposes the WCTBSVM and FWCTBSVM for classification problems.

3.1. WCTBSVM

To suppress the adverse impact caused by the outliers, we propose to incorporate the Welsch loss and capped $L_{2,p}$-norm distance metric twin bounded support vector machines to the framework of the TBSVM, which is represented as:

$$\begin{array}{c}\hfill \begin{array}{cc}& \underset{{\omega }_1,b_1}{min}\sum _{i=1}^{m_1}min(\parallel {\omega }_1{x}_i+b_1{\parallel }_2^p,{\epsilon }_1)+C_1\sum _{i=1}^{m_2}[1-\exp (-\frac{{\xi }_{1,i}^2}{2{\sigma }^2})]+\frac{C_3}{2}(\parallel {\omega }_1{\parallel }_2^2+b_1^2)\hfill \\ & s.t.-(B{\omega }_1+e_2{b}_1)+{\xi }_1\ge e_2\hfill \end{array}\end{array}$$

(30)

and

$$\begin{array}{c}\hfill \begin{array}{cc}& \underset{{\omega }_1,b_1}{min}\sum _{i=1}^{m_2}min(\parallel {\omega }_2{x}_i+b_2{\parallel }_2^p,{\epsilon }_3)+C_2\sum _{i=1}^{m_1}[1-\exp (-\frac{{\xi }_{2,i}^2}{2{\sigma }^2})]+\frac{C_4}{2}(\parallel {\omega }_1{\parallel }_2^2+b_1^2)\hfill \\ & s.t.(A{\omega }_2+e_1{b}_2)+{\xi }_2\ge e_1\hfill \end{array}\end{array}$$

(31)

where, $C_1$, $C_2$, $C_3$, $C_4$ > 0 are regularization parameters, $e_1\in {\mathbb{R}}^{m_1}$ and $e_2\in {\mathbb{R}}^{m_2}$ are the unit vectors. The model is modified on the basis of the TBSVM, where the first term introduces a capped $L_{2,p}$-norm that satisfies the principle of structural risk minimization and improves the generalization performance of the model. The second term introduces the Welsch loss function to reduce the influence of noise. The last term introduces the $L_2$-norm to prevent over-fitting of the model.

Let

$$\left\{\begin{array}{c}R({\omega }_1,b_1)=\sum _{i=1}^{m_1}min(\parallel {\omega }_1{x}_i+b_1{\parallel }_2^p,{\epsilon }_1)+\frac{C_3}{2}(\parallel {\omega }_1{\parallel }_2^2+b_1^2),\hfill \\ \\ Q({\omega }_1,b_1)=C_1\sum _{i=1}^{m_2}\left[1-exp\left(-\frac{{\xi }_{1,i}^2}{2{\sigma }^2}\right)\right].\hfill \end{array}\right.$$

(32)

Further, we can get

$$\overline{Q}({\omega }_1,b_1)=\underset{{\omega }_1,b_1}{max}Q({\omega }_1,b_1),$$

(33)

where $\overline{Q}({\omega }_1,b_1)=C_1{\sum }_{i=1}^{m_2}\left[exp\left(-\frac{{\xi }_{1,i}^2}{2{\sigma }^2}\right)\right]$. To facilitate the following derivations, we then define a convex function $g\left(v\right)=-vlog(-v)+v$, where $v<0$. Based on the conjugate function theory, we have

$$exp\left(-\frac{{\xi }_1^2}{2{\sigma }^2}\right)=\underset{v<0}{sup}\left\{v\frac{{\xi }_1^2}{2{\sigma }^2}-g\left(v\right)\right\},$$

(34)

where

$$v=-exp\left(-\frac{{\xi }_1^2}{2{\sigma }^2}\right).$$

(35)

Thus, we can get

$$\underset{{\omega }_1,b_1,v}{max}M({\omega }_1,b_1,v)=\sum _{i=1}^{m_2}\left(v_i\frac{{\xi }_{1,i}^2}{2{\sigma }^2}-g\left(v_i\right)\right)-R({\omega }_1,b_1).$$

(36)

Use the half-quadratic optimization of (34), suppose that we have $v^s$, where the superscript s denotes the something iteration, so that the v can be written:

$$\underset{v_i^s<0}{max}\sum _{i=1}^{m_2}\left\{v_i^s\frac{{\left({\xi }_1^s\right)}^2}{2{\sigma }^2}-g\left(v_i^s\right)\right\},$$

(37)

$$v_i^s=-exp\left(-\frac{{\left({\xi }_1^s\right)}^2}{2{\sigma }^2}\right).$$

(38)

Further, the optimization problem (30) can be rewritten as:

$$\begin{array}{c}\underset{{\omega }_1,b_1}{min}\sum _{i=1}^{m_1}min(\parallel {\omega }_1{x}_i+b_1{\parallel }_2^p,{\epsilon }_1)+\frac{C_1}{2{\sigma }^2}{\xi }_1^T{\Omega }_1{\xi }_1+\frac{C_3}{2}(\parallel {\omega }_1{\parallel }_2^2+b_1^2),\hfill \\ s.t.-(B{\omega }_1+e_2{b}_1)+{\xi }_1\ge e_2.\hfill \end{array}$$

(39)

In a similar way, the optimization problem (31) can be rewritten as:

$$\begin{array}{c}\underset{{\omega }_2,b_2}{min}\sum _{i=1}^{m_1}min(\parallel {\omega }_2{x}_i+b_2{\parallel }_2^p,{\epsilon }_1)+\frac{C_2}{2{\sigma }^2}{\xi }_2^T{\Omega }_2{\xi }_2+\frac{C_4}{2}(\parallel {\omega }_1{\parallel }_2^2+b_1^2),\hfill \\ s.t.(A{\omega }_1+e_1{b}_2)+{\xi }_2\ge e_1\hfill \end{array}$$

(40)

where the ${\Omega }_j=diag(-v_{j,i}^s,0)$, $j=1,2$.

Theorem 1.

Let $g\left(\theta \right):R^n\to R$ be a continuous non-convex function and suppose $h\left(\theta \right):{\mathbb{R}}^n\to \Xi$ is a map with a range of  Ξ. We assume that there exists a concave function $\overline{g}\left(u\right)$ defined on Ξ, such that $g\left(\theta \right)=g\left(h\right(\theta \left)\right)$ holds. Under the above assumption, the non-convex function $g\left(\theta \right)$ is expressed as:

$$g\left(\theta \right)=\underset{v\in R^n}{inf}[v^{T}h\left(\theta \right)-g^{*\left(v\right)}].$$

(41)

According to concave duality, $g^{*}\left(v\right)$ is the concave dual of $\overline{g}\left(u\right)$ given as

$$g^{*}\left(v\right)=\underset{u\in }{inf}[v^{T}h\left(\theta \right)-g^{*\left(v\right)}].$$

(42)

In addition, the minimum value to the right of (41) is as follows:

$$v^{*}=\frac{\partial \overline{g}\left(\theta \right)}{\partial \theta }{|}_{u=h\left(\theta \right)}.$$

(43)

Based on Theorem 1, we give a concave function $\overline{g}\left(\theta \right):\mathbb{R}\to \mathbb{R}$ such that arbitrary $\theta >0$,

$$\begin{array}{c}\hfill \overline{g}\left(\theta \right)=min({\theta }^{\frac{p}{2}},\epsilon ).\end{array}$$

(44)

Assuming that $h\left(\mu \right)={\mu }^2$, we can get

$$\begin{array}{c}\hfill min(\parallel \omega x_i+b{\parallel }_2^p,\epsilon )=\overline{g}\left(h\left(\mu \right)\right),\end{array}$$

(45)

where $\mu =\parallel \omega x_i{+b\parallel }_2$. Based on (30), (45) can be rewritten as:

$$\begin{array}{c}\underset{{\omega }_1,b_1}{min}\sum _{i=1}^{m_1}\overline{g}(\parallel {\omega }_1{x}_i+b_1{\parallel }_2^2)+\frac{1}{2{\sigma }^2}{C}_1{\xi }_1^T{\Omega }_1{\xi }_1+\frac{C_3}{2}(\parallel {\omega }_1{\parallel }_2^2+b_1^2),\hfill \\ s.t.-(B{\omega }_1+e_2{b}_1)+{\xi }_1\ge e_2.\hfill \end{array}$$

(46)

Similarly, based on (31) and (45), we can get

$$\begin{array}{c}\underset{{\omega }_2,b_2}{min}\sum _{i=1}^{m_2}\overline{g}(\parallel {\omega }_2{x}_i+b_2{\parallel }_2^2)+\frac{1}{2{\sigma }^2}{C}_2{\xi }_1^T{\Omega }_2{\xi }_1+\frac{C_4}{2}(\parallel {\omega }_2{\parallel }_2^2+b_2^2),\hfill \\ s.t.(A{\omega }_2+e_1{b}_2)+{\xi }_2\ge e_1.\hfill \end{array}$$

(47)

Let ${\theta }_1=h\left({\mu }_1\right)={\parallel {\omega }_1{x}_i+b_1\parallel }_2^2$, via Theorem 1, the first term of (30) can be expressed as:

$$min(\parallel {\omega }_1{x}_i+b_1{\parallel }_2^p,{\epsilon }_1)=\overline{g}(\parallel {\omega }_1{x}_i+b_1{\parallel }_2^2)=\underset{f_{ii}\ge 0}{inf}(f_{ii}h\left({\mu }_1\right)-g^{*}\left(f_{ii}\right))=\underset{f_{ii}\ge 0}{inf}(f_{ii}{\theta }_1-g^{*}\left(f_{ii}\right)).$$

(48)

Therefore, the concave dual function of $\overline{g}\left({\theta }_1\right)$ is

$$g^{*}\left(f_{ii}\right)=\underset{{\theta }_1}{inf}[f_{ii}{\theta }_1-\overline{g}\left({\theta }_1\right]=\underset{{\theta }_1}{inf}\left\{\begin{array}{c}{f}_{ii}{\theta }_1-{\theta }_1^{\frac{p}{2}},{\theta }_1^{\frac{p}{2}}<{\epsilon }_1.\hfill \\ f_{ii}{\theta }_1-{\epsilon }_1,{\theta }_1^{\frac{p}{2}}\ge {\epsilon }_1.\hfill \end{array}\right.$$

(49)

By optimizing ${\theta }_1$ for (49), we can get:

$$g^{*}\left(f_{ii}\right)=\left\{\begin{array}{c}{f}_{ii}{\left(\frac{2}{p}{f}_{ii}\right)}^{\frac{2}{p-2}}-{\left(\frac{2}{p}{f}_{ii}\right)}^{\frac{2}{p-2}},{\theta }_1^{\frac{p}{2}}<{\epsilon }_1.\hfill \\ f_{ii}{\epsilon }_1^{\frac{2}{p}}-{\epsilon }_1,{\theta }_1^{\frac{p}{2}}\ge {\epsilon }_1.\hfill \end{array}\right.$$

(50)

Therefore, the objective function (30) can be further written as:

$$\underset{{\omega }_1,b_1}{min}\sum _{i=1}^{m_1}min(\parallel {\omega }_1{x}_i+b_1{\parallel }_2^p,{\epsilon }_1)+\frac{1}{2{\sigma }^2}{C}_1{\xi }_1^T{\Omega }_1{\xi }_1+\frac{C_3}{2}(\parallel {\omega }_1{\parallel }_2^2+b_1^2),$$

$$\iff \underset{{\omega }_1,b_1}{min}\sum _{i=1}^{m_1}\underset{f_{ii}\ge 0}{inf}{L}_i({\omega }_1,b_1,f_{ii},{\epsilon }_1)+\frac{1}{2{\sigma }^2}{C}_1{\xi }_1^T{\Omega }_1{\xi }_1+\frac{C_3}{2}(\parallel {\omega }_1{\parallel }_2^2+b_1^2),$$

(51)

$$\iff \underset{{\omega }_1,b_1,f_{ii}\ge 0}{min}\sum _{i=1}^{m_1}{L}_i({\omega }_1,b_1,f_{ii},{\epsilon }_1)+\frac{1}{2{\sigma }^2}{C}_1{\xi }_1^T{\Omega }_1{\xi }_1+\frac{C_3}{2}(\parallel {\omega }_1{\parallel }_2^2+b_1^2).$$

Finally, the first term in the objective (30) can be rewritten as:

$$L_i({\omega }_1,b_1,f_{ii},{\epsilon }_1)=\left\{\begin{array}{c}{f}_{ii}{\theta }_1-f_{ii}{\left(\frac{2}{p}{f}_{ii}\right)}^{\frac{2}{p-2}}+{\left(\frac{2}{p}{f}_{ii}\right)}^{\frac{2}{p-2}},{\theta }_1^{\frac{p}{2}}<{\epsilon }_1.\hfill \\ f_{ii}{\theta }_1-f_{ii}{\epsilon }_1^{\frac{2}{p}}+{\epsilon }_1,{\theta }_1^{\frac{p}{2}}\ge {\epsilon }_1.\hfill \end{array}\right.$$

(52)

The objective function (52) is solved by learning the optimal classifier via the alternate optimization algorithm. We calculate the gradient of the function $g\left(\theta \right)$ with respect to $\theta$ as follows:

$$\frac{\partial \overline{g}\left(\theta \right)}{\partial \theta }=\left\{\begin{array}{c}\frac{p}{2}{\theta }^{\frac{p}{2}-1},0<\theta <{\epsilon }^{\frac{2}{p}},\hfill \\ 0,\theta >{\epsilon }^{\frac{2}{p}}.\hfill \end{array}\right.$$

(53)

If ${\theta }_1=h\left({\mu }_1\right)={\parallel {\omega }_1{x}_i+b_1\parallel }_2^2$, we fix ${\omega }_1$ and $b_1$, can get:

$$f_{ii}=\frac{\partial \overline{g}\left({\theta }_1\right)}{\partial {\theta }_1}{|}_{{\theta }_1}={\parallel {\omega }_1{x}_i+b_1\parallel }_2^2=\left\{\begin{array}{c}\frac{p}{2}\parallel {\omega }_1{x}_i+b_1{\parallel }_2^{p-2},0<{\parallel {\omega }_1{x}_i+b_1\parallel }_2^p<{\epsilon }_1.\hfill \\ 0,else.\hfill \end{array}\right.$$

(54)

The same as (54), we can get

$$k_{ii}=\frac{\partial \overline{g}\left({\theta }_2\right)}{\partial {\theta }_2}{|}_{{\theta }_2}={\parallel {\omega }_2{x}_i+b_2\parallel }_2^2=\left\{\begin{array}{c}\frac{p}{2}\parallel {\omega }_2{x}_i+b_2{\parallel }_2^{p-2},0<{\parallel {\omega }_2{x}_i+b_2\parallel }_2^p<{\epsilon }_3.\hfill \\ 0,else.\hfill \end{array}\right.$$

(55)

When variables $f_i$ and $k_i$ are fixed, in order to solve the classification model of an unknown quantity the ${\omega }_1$, ${\omega }_2$ and $b_1$, $b_2$, optimization problem formula (30) can be written as:

$$\begin{array}{c}\underset{{\omega }_1,b_1}{min}\sum _{i=1}^{m_1}{f}_{ii}\parallel {\omega }_1{x}_i+b_1{\parallel }_2^2+\frac{1}{2{\sigma }^2}{C}_1{\xi }_1^T{\Omega }_1{\xi }_1+\frac{C_3}{2}(\parallel {\omega }_1{\parallel }_2^2+b_1^2),\hfill \\ s.t.-(B{\omega }_1+e_2{b}_1)+{\xi }_1\ge e_2.\hfill \end{array}$$

(56)

The same as (56), the optimization problem formula (31) can be written as:

$$\begin{array}{c}\underset{{\omega }_2,b_2}{min}\sum _{i=1}^{m_2}{k}_{ii}\parallel {\omega }_2{x}_i+b_2{\parallel }_2^2+\frac{1}{2{\sigma }^2}{C}_2{\xi }_2^T{\Omega }_2{\xi }_2+\frac{C_4}{2}(\parallel {\omega }_2{\parallel }_2^2+b_2^2),\hfill \\ s.t.(A{\omega }_2+e_1{b}_2)+{\xi }_2\ge e_1.\hfill \end{array}$$

(57)

Let $F=diag(f_{11},f_{22},f_{33},\dots ,f_{m_1,m_1})$ is a $m_1\times m_1$ diagonal matrix, $K=diag(k_{11},k_{22},k_{33},\dots ,k_{m_2,m_2})$ is a $m_2\times m_2$ diagonal matrix (30) written as:

$$\begin{array}{c}\underset{{\omega }_1,b_1}{min}\frac{1}{2}{(A{\omega }_1+e_1{b}_1)}^{T}F(A{\omega }_1+e_1{b}_1)+\frac{1}{2{\sigma }^2}{C}_1{\xi }_1^T{\Omega }_1{\xi }_1+\frac{C_3}{2}(\parallel {\omega }_1{\parallel }_2^2+b_1^2),\hfill \\ s.t.-(B{\omega }_1+e_2{b}_1)+{\xi }_1\ge e_2.\hfill \end{array}$$

(58)

Similarly, (31) can be written as:

$$\begin{array}{c}\underset{{\omega }_2,b_2}{min}\frac{1}{2}{(B{\omega }_2+e_2{b}_2)}^{T}K(B{\omega }_2+e_2{b}_2)+\frac{1}{2{\sigma }^2}{C}_1{\xi }_2^T{\Omega }_2{\xi }_2+\frac{C_3}{2}(\parallel {\omega }_2{\parallel }_2^2+b_2^2),\hfill \\ s.t.(B{\omega }_2+e_2{b}_2)+{\xi }_2\ge e_1.\hfill \end{array}$$

(59)

The corresponding Lagrange function of the above optimization problem (58) can be written as:

$$\begin{array}{ccc}\hfill L({\omega }_1,b_1,{\xi }_1,\alpha )& =& \frac{1}{2}{(A{\omega }_1+e_1{b}_1)}^{T}F(A{\omega }_1+e_1{b}_1)+\frac{1}{2{\sigma }^2}{C}_1{\xi }_1^T{\Omega }_1{\xi }_1+\frac{C_3}{2}(\parallel {\omega }_1{\parallel }_2^2+b_1^2)\hfill \\ & -& {\alpha }^T(-(B{\omega }_1+e_2{b}_1)+{\xi }_1-e_2).\hfill \end{array}$$

(60)

where, $\alpha$ is a Lagrange multiplier, derive the Lagrange function about ${\omega }_1$ and $b_1$, and get the following Karush–Kuhn–Tucker conditions

$$\left\{\begin{array}{ccc}\frac{\partial L}{\partial {\omega }_1}=A^{T}F(A{\omega }_1+e_1{b}_1)+B^T\alpha +C_3{\omega }_1=0,\hfill & \hfill \left(i\right)& \\ \frac{\partial L}{\partial b_1}=e_1^{T}F(A{\omega }_1+e_1{b}_1)+e_2^T\alpha +C_3{b}_1=0,\hfill & \hfill \left(ii\right)& \\ \frac{\partial L}{\partial {\xi }_1}=\frac{1}{{\sigma }^2}{C}_1{\Omega }_1{\xi }_1-\alpha =0,\hfill & \hfill \left(iii\right)& \\ {\alpha }^T(B{\omega }_1+e_2{b}_1-{\xi }_1+e_2)=0,\hfill & \hfill \left(iv\right)& \\ \alpha \ge 0.\hfill & \hfill \left(v\right)\end{array}\right.$$

(61)

Combine $\left(i\right)$ and $\left(ii\right)$ to get

$$\left[\begin{array}{c}{A}^T\\ e_1^T\end{array}\right]F\left[\begin{array}{cc}A& e_1\end{array}\right]\left[\begin{array}{c}{\omega }_1\\ b_1\end{array}\right]+\left[\begin{array}{c}{B}^T\\ e_2^T\end{array}\right]\alpha +C_3\left[\begin{array}{c}{\omega }_1\\ b_1\end{array}\right]=0.$$

(62)

Define

$$Z_1=\left[\begin{array}{c}{\omega }_1\\ b_1\end{array}\right],H=\left[\begin{array}{cc}A& e_1\end{array}\right],E=\left[\begin{array}{cc}B& e_2\end{array}\right].$$

(63)

Thus, we can get

$$H^{T}FH{Z}_1+E^T\alpha +C_3{Z}_1=0,Z_1={[{\omega }_1,b_1]}^T=-{(H^{T}FH+C_{3}I)}^{-1}{E}^T\alpha .$$

(64)

At the same time, we can get ${\xi }_1={\sigma }^2{\left(C_1{\Omega }_1\right)}^{-1}\alpha$. Therefore, the Lagrange function can be rewritten as

$$\begin{array}{ccc}\hfill L({\omega }_1,b_1,{\xi }_1,\alpha )& =& \frac{1}{2}{\left(H{Z}_1\right)}^{T}F\left(H{Z}_1\right)+\frac{C_1}{2{\sigma }^2}{\left(\frac{{\sigma }^2}{C_1}{\Omega }_1^{-1}\alpha \right)}^T{\Omega }_1\left(\frac{{\sigma }^2}{C_1}{\Omega }_1^{-1}\alpha \right)\hfill \\ & -& {\alpha }^T(-E{Z}_1+\frac{{\sigma }^2}{C_1}{\Omega }_1^{-1}\alpha -e_2)+\frac{C_3}{2}{Z}_1^T{Z}_1\hfill \\ & =& e_2^T\alpha -\frac{1}{2}{\alpha }^T(E{(H^{T}FH+C_{3}I)}^{-1}{E}^T+\frac{{\sigma }^2}{C_1}{\Omega }_1^{-1})\alpha .\hfill \end{array}$$

Therefore, the dual problem of (58) is as follows:

$$\begin{array}{c}\underset{\alpha }{min}\frac{1}{2}{\alpha }^T(E{(H^{T}FH+C_{3}I)}^{-1}{E}^T+\frac{{\sigma }^2}{C_1}{\Omega }_1^{-1})\alpha -e_2^T\alpha ,\hfill \\ s.t.0\le \alpha \le C_1{e}_2.\hfill \end{array}$$

(65)

Similarly, the dual problem of (59) is as follows:

$$\begin{array}{c}\underset{\beta }{min}\frac{1}{2}{\beta }^T(H{(E^{T}KE+C_{4}I)}^{-1}{H}^T+\frac{{\sigma }^2}{C_2}{\Omega }_2^{-1})\beta -e_1^T\beta ,\hfill \\ s.t.0\le \beta \le C_2{e}_1.\hfill \end{array}$$

(66)

According to the process of the above operation, we give the pseudo-code of the process, as shown in Algorithm 1.

Algorithm 1 Training WCTBSVM.

Input: Training data $A\in {\mathbb{R}}^{m_1\times n}$ and $B\in {\mathbb{R}}^{m_2\times n}$; Parameters $C_i,(i=1,2,3,4)$ and

${\epsilon }_i,(i=1,2,3,4)$.

Output: $Z_1^{*}$ and $Z_2^{*}$;

Process:

1. Initialize $F\in {\mathbb{R}}^{m_1\times m_1}$ and ${\Omega }_1\in {\mathbb{R}}^{m_2\times m_2}$; $K\in {\mathbb{R}}^{m_2\times m_2}$ and ${\Omega }_2\in {\mathbb{R}}^{m_1\times m_1}$;

2. Calculate by the KKT conditions can get $\alpha$ and $\beta$ by (65) and (66);

3. Calculate $Z_1$ and $Z_2$ by

$Z_1=-{(H^{T}FH+C_{3}I)}^{-1}{E}^T\alpha$

and

$Z_2={(E^{T}KE+C_{4}I)}^{-1}{H}^T\beta$

4. Update the matrix separately ${\Omega }_1,{\Omega }_2,F,K$ by (40), (54) and (55).

3.2. FWCTBSVM

To reduce the computational complexity caused by the Welsch loss, we replace the inequality constraints in the WCTBSVM with equality constraints

$$\begin{array}{c}\hfill \begin{array}{cc}& \underset{{\omega }_1,b_1}{min}\sum _{i=1}^{m_1}min(\parallel {\omega }_1{x}_i+b_1{\parallel }_2^p,{\epsilon }_1)+C_1\sum _{i=1}^{m_2}[1-\exp (-\frac{{\xi }_{1,i}^2}{2{\sigma }^2})]+\frac{C_3}{2}(\parallel {\omega }_1{\parallel }_2^2+b_1^2),\hfill \\ & s.t.-(B{\omega }_1+e_2{b}_1)+{\xi }_1=e_2.\hfill \end{array}\end{array}$$

(67)

$$\begin{array}{c}\hfill \begin{array}{cc}& \underset{{\omega }_1,b_1}{min}\sum _{i=1}^{m_2}min(\parallel {\omega }_2{x}_i+b_2{\parallel }_2^p,{\epsilon }_3)+C_2\sum _{i=1}^{m_1}[1-\exp (-\frac{{\xi }_{2,i}^2}{2{\sigma }^2})]+\frac{C_4}{2}(\parallel {\omega }_1{\parallel }_2^2+b_1^2),\hfill \\ & s.t.(A{\omega }_1+e_1{b}_2)+{\xi }_2=e_1.\hfill \end{array}\end{array}$$

(68)

Further, (67) and (68) can be rewritten as:

$$\begin{array}{c}\underset{{\omega }_1,b_1}{min}\sum _{i=1}^{m_1}min(\parallel {\omega }_1{x}_i+b_1{\parallel }_2^p,{\epsilon }_1)+\frac{C_1}{2{\sigma }^2}{\xi }_1^T{\Omega }_1{\xi }_1+\frac{C_3}{2}(\parallel {\omega }_1{\parallel }_2^2+b_1^2),\hfill \\ s.t.-(B{\omega }_1+e_2{b}_1)+{\xi }_1=e_2.\hfill \end{array}$$

(69)

$$\begin{array}{c}\underset{{\omega }_2,b_2}{min}\sum _{i=1}^{m_2}min(\parallel {\omega }_2{x}_i+b_2{\parallel }_2^p,{\epsilon }_1)+\frac{C_2}{2{\sigma }^2}{\xi }_2^T{\Omega }_2{\xi }_2+\frac{C_4}{2}(\parallel {\omega }_1{\parallel }_2^2+b_1^2),\hfill \\ s.t.(A{\omega }_1+e_1{b}_2)+{\xi }_2=e_1.\hfill \end{array}$$

(70)

Replace the equality constraint into the objective function and we have

$$\begin{array}{c}\underset{{\omega }_1,b_1}{min}\sum _{i=1}^{m_1}min(\parallel {\omega }_1{x}_i+b_1{\parallel }_2^p,{\epsilon }_1)+\frac{C_1}{2{\sigma }^2}{\Omega }_1\Vert e_2+(B{\omega }_1+e_2{b}_1){\Vert }_2^2+\frac{C_3}{2}(\parallel {\omega }_1{\parallel }_2^2+b_1^2),\hfill \end{array}$$

(71)

$$\begin{array}{c}\underset{{\omega }_2,b_2}{min}\sum _{i=1}^{m_2}min(\parallel {\omega }_2{x}_i+b_2{\parallel }_2^p,{\epsilon }_1)+\frac{C_2}{2{\sigma }^2}{\Omega }_2\Vert e_1-(A{\omega }_2+e_1{b}_2){\Vert }_2^2+\frac{C_4}{2}(\parallel {\omega }_2{\parallel }_2^2+b_2^2).\hfill \end{array}$$

(72)

Further, we can obtain:

$$\begin{array}{c}\underset{{\omega }_1,b_1}{min}\frac{1}{2}{(A{\omega }_1+e_1{b}_1)}^{T}F(A{\omega }_1+e_1{b}_1)+\frac{1}{2{\sigma }^2}{C}_1{\xi }_1^T{\Omega }_1{\xi }_1+\frac{C_3}{2}(\parallel {\omega }_1{\parallel }_2^2+b_1^2),\hfill \end{array}$$

(73)

$$\begin{array}{c}\underset{{\omega }_2,b_2}{min}\frac{1}{2}{(A{\omega }_2+e_2{b}_2)}^{T}K(A{\omega }_2+e_2{b}_2)+\frac{1}{2{\sigma }^2}{C}_2{\xi }_2^T{\Omega }_2{\xi }_2+\frac{C_4}{2}(\parallel {\omega }_2{\parallel }_2^2+b_2^2).\hfill \end{array}$$

(74)

The derivative of ${\omega }_1$ and $b_1$ in Equation (73) is zero and gives:

$$\begin{array}{c}\hfill A^{T}F(A{\omega }_1+e_1{b}_1)+\frac{C_1}{2{\sigma }^2}{B}^T{\Omega }_1(B{\omega }_1+e_2{b}_1)+\frac{C_3}{2{\sigma }^2}{\omega }_1=0,\end{array}$$

(75)

$$\begin{array}{c}\hfill e^{T}F(A{\omega }_1+e_1{b}_1)+\frac{C_1}{2e^2}{B}^T{\Omega }_1(B{\omega }_1+e_2{b}_1)+\frac{C_3}{2{\sigma }^2}{b}_1=0.\end{array}$$

(76)

Via (75) and (76), we have

$$\frac{2{\sigma }^2}{C_1}\left[\begin{array}{cc}{A}^{T}FA& A^{T}F{e}_1\\ e_1^{T}FA& e_1^{T}F{e}_1\end{array}\right]\left[\begin{array}{c}{\omega }_1\\ b_1\end{array}\right]+\left[\begin{array}{cc}{B}^T{\Omega }_{1}B& B^T{\Omega }_1{e}_2\\ e_2^T{\Omega }_{1}B& e_2^T{\Omega }_1{e}_2\end{array}\right]\left[\begin{array}{c}{\omega }_1\\ b_1\end{array}\right]+\left[\begin{array}{c}{B}^T{\Omega }_1{e}_2\\ e_2^T{\Omega }_1{e}_2\end{array}\right]+\frac{C_3}{C_1}I\left[\begin{array}{c}{\omega }_1\\ b_1\end{array}\right]=0.$$

(77)

Furthermore, via (77) we can get

$$\left[\begin{array}{c}{\omega }_1\\ b_1\end{array}\right]=-{(\left[\begin{array}{cc}\frac{2{\sigma }^2}{C_1}{A}^{T}FA+B^T{\Omega }_{1}B& \frac{2{\sigma }^2}{C_1}{A}^{T}F{e}_1+B^T{\Omega }_1{e}_2\\ \frac{2{\sigma }^2}{C_1}{e}_1^{T}FA+e_2^T{\Omega }_{1}B& \frac{2{\sigma }^2}{C_1}{e}_1^{T}F{e}_1+e_2^T{\Omega }_1{e}_2\end{array}\right]+\frac{C_3}{C_1}I)}^{-1}\left[\begin{array}{c}{B}^T\\ e_2^T\end{array}\right]{\Omega }_1{e}_2.$$

(78)

Let

$$Z_1=\left[\begin{array}{c}{\omega }_1\\ b_1\end{array}\right],H=\left[\begin{array}{cc}A& e_1\end{array}\right],E=\left[\begin{array}{cc}B& e_2\end{array}\right].$$

(79)

Thus, we can get

$$Z_1=-{(\frac{2{\sigma }^2}{C_1}{H}^{T}FH+E^T{\Omega }_{1}E+\frac{C_3}{C_1}I)}^{-1}{E}^T{\Omega }_1{e}_2.$$

(80)

Similarly, the formula (74) for ${\omega }_2$ and $b_2$ is also convex. We calculate the partial derivative order for them, respectively, and the result is 0 . Thus, we have

$$B^{T}K(B{\omega }_2+e_2{b}_2)+C_2{A}^T{\Omega }_2(e_1-A{\omega }_2+e_1{b}_2)+C_4{\omega }_2=0,$$

(81)

$$e_2^{T}K(B{\omega }_2+e_2{b}_2)+C_2{e}_1^T{\Omega }_2(e_1-A{\omega }_2-e_1{b}_2)+C_4{b}_2=0.$$

(82)

Let

$$Z_2=\left[\begin{array}{c}{\omega }_2\\ b_2\end{array}\right],E=\left[\begin{array}{cc}B& e_2\end{array}\right],H=\left[\begin{array}{cc}A& e_1\end{array}\right].$$

(83)

Therefore, we have

$$Z_2={(\frac{2{\sigma }^2}{C_2}{E}^{T}KE+H^T{\Omega }_{2}H+\frac{C_4}{C_2}I)}^{-1}{H}^T{\Omega }_2{e}_1.$$

(84)

According to the process of the above operation, we give the pseudo-code of the process, as shown in Algorithm 2.

Algorithm 2 Training FWCTBSVM.

Input: Training data $A\in {\mathbb{R}}^{m_1\times n}$ and $B\in {\mathbb{R}}^{m_2\times n}$; Parameters $C_i,(i=1,2,3,4)$ and

${\epsilon }_i,(i=1,2,3,4)$.

Output: $Z_1^{*}$ and $Z_2^{*}$;

Process:

1. Initialize $F\in {\mathbb{R}}^{m_1\times m_1}$ and ${\Omega }_1\in {\mathbb{R}}^{m_2\times m_2}$; $K\in {\mathbb{R}}^{m_2\times m_2}$ and ${\Omega }_2\in {\mathbb{R}}^{m_1\times m_1}$;

2. Calculate $\alpha$ and $\beta$;

3. Calculate $Z_1$ and $Z_2$ by

$Z_1=-{(\frac{2{\sigma }^2}{C_1}{H}^{T}FH+E^T{\Omega }_{1}E+\frac{C_3}{C_1}I)}^{-1}{E}^T{\Omega }_1{e}_2$

and

$Z_2={(\frac{2{\sigma }^2}{C_2}{E}^{T}KE+H^T{\Omega }_{2}H+\frac{C_4}{C_2}I)}^{-1}{H}^T{\Omega }_2{e}_1$;

4. Update the matrix separately ${\Omega }_1,{\Omega }_2,F,K$ by (40), (54) and (55).

3.3. Convergence Analysis

Lemma 1.

For $\forall x\ne y\in R^n$, if $f\left(x\right)=x-\frac{x^2}{2y}$, then inequality $f\left(x\right)<f\left(y\right)$ is always established.

Lemma 2.

For any non-zero vectors $\alpha ,\beta$, when $0<p\le 2$, then inequality

$${\parallel \alpha \parallel }_2^p-\frac{p}{2}{\parallel \beta \parallel }_2^{p-2}{\parallel \alpha \parallel }_2^2\le {\parallel \beta \parallel }_2^p-\frac{p}{2}{\parallel \beta \parallel }_2^{p-2}{\parallel \beta \parallel }_2^2$$

(85)

is always established.

Lemma 3.

For any $u\in R,$

(1)

$h\left(u\right)\ge 0,andh\left(0\right)=0,$

(2)

$h\left(u\right)=h(-u),$

(3)

$h^{{}^{\prime }}\left(u\right)\ge 0,anyu\ge 0.$ Then, there exists a convex function $\Psi \left(s\right)$ and $h\left(u\right)={inf}_{s>0}\left[\frac{1}{2}s{u}^2+\Psi \left(s\right)\right]$

Theorem 2.

The objective function value of (30) as $V({\omega }_1,{\xi }_1)$. The sequence $\{V({\omega }_1,{\xi }_1),$$k=1,2,\dots ,\kappa \}$ generated by Algorithm 1 is convergent.

Proof. 

Let

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill V({\omega }_1,{\xi }_1)& =\underset{{\omega }_1,b_1}{min}\sum _{i=1}^{m_1}min(\parallel {\omega }_1{x}_i+b_1{\parallel }_2^p,{\epsilon }_1)+C_1\sum _{i=1}^{m_2}[1-\exp (-\frac{{\xi }_{1,i}^2}{2{\sigma }^2})]+\frac{C_3}{2}(\parallel {\omega }_1{\parallel }_2^2+b_1^2)\hfill \\ & =\underset{z,{\xi }_{1,i}}{min}\sum _{i=1}^{m_1}min\left(\right(\parallel e_{i}z{\parallel }_2^p,{\epsilon }_1)+C_1\sum _{i=1}^{m_2}[1-\exp (-\frac{{\xi }_{1,i}^2}{2{\sigma }^2})]+\frac{C_3}{2}{z}^{T}z\hfill \end{array}\end{array}$$

(86)

where the $e_i=(x_i,1)$ represents the line of E, and $z={({\omega }_1,b_1)}^T$, $\parallel {\omega }_1,b_1{\parallel }_2^p<{\epsilon }_1$ and $C_1{\sum }_{i=1}^{m_2}[1-\exp (-\frac{{\xi }_{1,i}^2}{2{\sigma }^2})<{\epsilon }_2$. Therefore,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill V(z,{\xi }_1)& =\underset{z,{\xi }_{1,i}}{min}\sum _{i=1}^{m_1}min(\parallel e_{i}z\parallel )+C_1\sum _{i=1}^{m_2}min[1-\exp (-\frac{{\xi }_{1,i}^2}{2{\sigma }^2})]+\frac{C_3}{2}{z}^{T}z.\hfill \end{array}\end{array}$$

(87)

Let

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill V_1\left(z\right)& =\underset{z}{min}\sum _{i=1}^{m_1}(\parallel e_{i}z{\parallel }_2^p),\hfill \end{array}\end{array}$$

(88)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill V_2(z,{\xi }_1)& =C_1\sum _{i=1}^{m_2}[1-\exp (-\frac{{\xi }_{1,i}^2}{2{\sigma }^2}))]+\frac{C_3}{2}{z}^{T}z.\hfill \end{array}\end{array}$$

(89)

Assuming that $z^{(k+1)}$ is the solution of the $k+1$ iteration of the Algorithm, then

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill z^{(k+1)}& =min\frac{1}{2}{\left(Ez\right)}^T{F}^{\left(k\right)}\left(Ez\right).\hfill \end{array}\end{array}$$

(90)

So, we can get

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill z^{(k+1)}& =min\frac{1}{2}{\left(E{z}^{(k+1)}\right)}^T{F}^{\left(k\right)}\left(E{z}^{(k+1)}\right).\hfill \end{array}\end{array}$$

(91)

Therefore,

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\left(E{z}^{(k+1}\right)}^T{F}^{\left(k\right)}\left(E{z}^{(k+1)}\right)\le {\left(E{z}^{(k}\right)}^T{F}^{\left(k\right)}\left(E{z}^{\left(k\right)}\right).\end{array}\end{array}$$

(92)

Based on Lemma 2, we can get:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \frac{p}{2}\parallel E{z}^{k+1}{\parallel }_2^2\parallel E{z}^k{\parallel }_2^{p-2}\le \frac{p}{2}\parallel E{z}^k{\parallel }_2^2{\parallel E{z}^k\parallel }_2^{p-2}\end{array}\end{array}$$

(93)

and

$$\begin{array}{c}\hfill \parallel E{z}^{k+1}{\parallel }_2^p-\frac{p}{2}\parallel E{z}^k{\parallel }_2^{p-2}\parallel E{z}^{k+1}{\parallel }_2^2\le \parallel E{z}^k{\parallel }_2^p-\frac{p}{2}\parallel E{z}^k{\parallel }_2^{p-2}{\parallel E{z}^k\parallel }_2^2.\end{array}$$

(94)

Combine (93) and (94), and we have

$$\begin{array}{c}\hfill \parallel E{z}^{k+1}{\parallel }_2^p\le {\parallel E{z}^k\parallel }_2^p.\end{array}$$

(95)

Therefore, $V_1\left(z\right)$ is the convergence.

Next, we discuss the convergence of $V_2(z,{\xi }_1)$. Let the function $h\left(u\right)=1-\exp (-u^2)$, where $u=\frac{{\xi }_1}{\sqrt{2}\sigma }$, and there exists a convex function $\Psi \left(s\right)$ and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill h\left(u\right)=& \underset{s>0}{inf}\left[\frac{1}{2}s{u}^2+\Psi \left(s\right)\right]\hfill \end{array}\end{array}$$

(96)

where we have a minimum solution $\overline{s}$ to make the equation hold:

$$\begin{array}{c}\hfill \begin{array}{cc}& \underset{s>0}{inf}\left[\frac{1}{2}s{u}^2+\Psi \left(s\right)\right]=\frac{1}{2}\overline{s}{u}^2+\Psi \left(\overline{s}\right)\hfill \end{array}\end{array}$$

(97)

where $\overline{s}=2exp(-u^2)$. Further, we get

$$\begin{array}{c}\hfill \begin{array}{cc}& [1-\exp (-\frac{{\xi }_{1,i}^2}{2{\sigma }^2})]=\underset{s>0}{inf}\frac{s_i{\left({\xi }_1\right)}^2}{4{\sigma }^2}+\Psi \left(s_i\right).\hfill \end{array}\end{array}$$

(98)

Therefore, (88) is equivalent to

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill V_2(z,{\xi }_1,s_i)& =C_1\sum _{i=1}^{m_2}\left\{\frac{s_i{\left({\xi }_1\right)}^2}{4{\sigma }^2}+\Psi \left(s_i\right)\right\}+\frac{C_3}{2}{z}^{T}z.\hfill \end{array}\end{array}$$

(99)

From (89), (99) and Lemma 3, we can get $V_2(z,{\xi }_1,s_i)\ge V_2(z,{\xi }_1)\ge 0$. Thus, the sequence is lower bounded. Suppose that $z^k$, ${\xi }^k$ and $s^k$ are obtained after k iterations,

$$\begin{array}{c}\hfill \begin{array}{c}\hfill V_2(z^k,{\xi }^k,s^k)\ge V_2(z^{k+1},{\xi }^k,s^k),\end{array}\end{array}$$

(100)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill V_2(z^{k+1},{\xi }^k,s^k)\ge V_2(z^{k+1},{\xi }^{k+1},s^k),\end{array}\end{array}$$

(101)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill V_2(z^{k+1},{\xi }^{k+1},s^k)\ge V_2(z^{k+1},{\xi }^{k+1},s^{k+1}).\end{array}\end{array}$$

(102)

Concluding (100)–(102), we have

$$\begin{array}{c}\hfill \begin{array}{c}\hfill V_2(z^k,{\xi }^k,s^k)\ge V_2(z^{k+1},{\xi }^{k+1},s^{k+1})\end{array}\end{array}$$

(103)

Therefore, $V_2(z,{\xi }_1)$ is the convergence. Thus, the sequence is the convergence. □

4. Numerical Experiments

In this section, we will conduct data experiments on WCTBSVM and FWCTBSVM to test the classification performance of the two models. Meanwhile, both models were also used for comparison with the TSVM, TBSVM, CTSVM, and LSTSVM, and further verify whether the classification performance of the WCTBSVM and FWCTBSVM is better. After performing the test on the datasets, we performed a statistical monitoring analysis to further study the classification performance of the proposed model [28]. All of the data are obtained from the normalized dataset. All the experiments were implemented in MATLAB R2016a, equipped with an Intel Core i7 processor (3 GHz) and 8 GB of memory on a ASUS personal computer.

4.1. Experimental Setting

How a model of the algorithm reflects its best performance depends on the choice of parameters. Therefore, we use the traditional accuracy index ($ACC$) to measure the performance of these algorithms, defined as follows:

$$\begin{array}{c}\hfill ACC=\frac{TP+TN}{TP+FN+TN+FP},\end{array}$$

(104)

where $TP$ and $TN$ denote true positives and true negatives, $FP$ and $FN$ denote false negatives and false positives, respectively. The higher value of the ACC is, the better the model is. For these, the TSVM parameters ${\epsilon }_i$ set ${10}^{-5}$, and $c_i$ searched from set {${10}^i\mid -5,-4,-3,-2,-,1,0,1,2,3,4,5$}, and the kernel parameters $\sigma$ searched from set $\{{10}^i\mid -4,-3,-2,-,1,0,1,2,3,4\}$. We performed a 10-fold cross-validation on the dataset. The model was trained and tested multiple times using different cut apart training and test datasets; thus, overcoming the randomness of the individual test results.

We classified the 100 artificial data samples, and divided the data samples into two categories, one represented by +, another represented by ∗. Because the outliers can have some impact on the performance of the classification, six outliers were introduced to compare the robustness of the TSVM, TBSVM, CTSVM, LSTSVM, WCTBSVM, and FWCTBSVM. Respectively, the four outliers were classified on average, two positive and two negative, which are shown in Figure 4.

In order to validate the classification performance of the WCTBSVM and FWCTBSVM with the performance of the correlated algorithms, nine sets of datasets from the UCI dataset were selected in

Table 1. Characteristics of UCI Datasets.

Datasets	Samples	Attributes	Datasets	Samples	Attributes
Vote	432	16	Balance	267	4
Cancer	699	9	German	1000	24
WDBC	569	30	hepat	155	19
spectf	267	44	Pima	768	8
Wholesale	440	7

. These nine sets of data (Balance, Australian, Cancer, CMC, German, Pima, QSAR, WDBC, and wholesale) were used to perform the data experiments. Considering that noise is one of the criteria to measure the robustness of the algorithm, we will study it at the noise points. The classification accuracy changes smoothly with increasing noise, indicating that the proposed algorithm has good noise resistance.

4.2. Experimental Results on Artificial Dataset with Gaussian Noise

Through experiments on the nine sets of UCI datasets, we obtain an even better classification performance and robustness of the WCTBSVM and FWCTBSVM. Therefore, in order to further explore the advantages of the WCTBSVM and FWCTBSVM, we will conduct experiments on artificial datasets. All experimental results are presented in Figure 5.

From Figure 5, we can see the accuracy of the six models classified on an artificial dataset that contained Gaussian noise varies from low to high order and performs roughly equally on the UCI dataset. The precision of the six models are, respectively, TSVM, 58.8%; TBSVM, 63.0%; LSTSVM, 61.6%; CTSVM, 77%; WCTBSVM, 81.3%,; FWCTBSVM, 83.6%. From the experimental data, the WCTBSVM and FWCTBSVM still have high accuracy in the data with Gaussian noise. It also further determines the robustness of the negative effect of the $L_{2,p}$-norm distance and the Welsch loss on the Gaussian noise.

4.3. Experimental Results on the Employed Datasets without Gaussian Noise

To further test the classification performance of the model, we will test it experimentally on the UCI dataset. We perform a 10-fold cross validation on the UCI dataset. The dataset is randomly divided into ten subsets, nine of which are used as training sets and the remaining one is reserved as a test set. This process is repeated ten times. We use the average of the ten test results as the performance measure. All experimental results presented in

Table 2. Experimental results on UCI datasets without Gaussian noise.

	TSVM	TBSVM	LSTBSVM	CTSVM	WCTBSVM	FWCTBSVM
Datasets	ACC (%)	ACC (%)	ACC (%)	ACC (%)	ACC (%)	ACC (%)
	Times (s)	Times (s)	Times (s)	Times (s)	Times (s)	Times (s)
Vote	94.53	94.76	94.56	95.00	95.48	95.13
	1.085	1.625	0.125	6.204	3.368	0.062
Balance	92.57	92.57	92.96	92.87	93.21	93.08
	0.9816	0.924	8.020	12.29	3.421	0.065
Cancer	94.21	94.94	95.48	95.75	96.43	95.94
	5.283	2.947	0.116	14.31	1.483	1.127
German	73.80	74.80	74.62	75.50	76.88	76.00
	5.709	8.893	1.018	22.68	8.021	0.159
Wholesale	82.79	83.72	85.35	86.51	88.47	90.93
	1.244	2.421	0.065	5.656	3.076	0.058
WDBC	93.07	93.71	94.68	95.25	95.96	95.07
	0.170	1.831	0.069	7.632	4.880	0.086
hepat	77.33	78.00	80.67	82.00	85.65	84.65
	0.789	1.261	0.063	2.399	1.561	1.012
Pima	75.32	75.71	75.97	75.92	76.38	77.56
	1.854	3.308	0.105	16.17	1.561	0.093
spectf	80.38	80.77	80.81	81.15	81.54	81.79
	0.446	0.573	0.747	2.906	3.632	0.068

are based on optimal parameters and the average classification accuracy is denoted by ‘ACC’.

Based on the performance of the nine UCI data in Table 2 in the six models, in the absence of Gaussian noise their accuracy order from high to low was WCTBSVM, FWCTBSVM, CTSVM, LSTSVM, TBSVM, and TSVM. The accuracy of FWCTBSVM and WCTBSVM is not much different, but FWCTBSVM run even faster. Therefore, on the basis of adding $L_{2,p}$-norm and Welsch loss functions, the classification mechanism of the model will be even better.

4.4. Experimental Results on the UCI Datasets with Gaussian Noise

In the UCI datasets experiment without adding noise, we obtained that the WCTBSVM and FWCTBSVM classify even better compared to the other four models. To further investigate the robustness of the WCTBSVM and FWCTBSVM, the six models will next be tested in the UCI datasets incorporating noise. The noise added is 10% and 30% Gaussian noise.

According to the experimental results in

Table 3. Experimental results of UCI datasets with 10% Gaussian noise.

	TSVM	TBSVM	LSTBSVM	CTSVM	WCTBSVM	FWCTBSVM
Datasets	ACC (%)	ACC (%)	ACC (%)	ACC (%)	ACC (%)	ACC (%)
	Times (s)	Times (s)	Times (s)	Times (s)	Times (s)	Times (s)
Vote	93.33	94.60	94.02	94.62	95.00	94.48
	1.454	2.301	0.255	5.501	5.259	0.067
Balance	90.68	90.99	91.26	91.54	92.51	92.86
	1.086	0.824	7.925	14.32	5.247	0.080
Cancer	93.06	93.71	93.48	94.65	95.43	95.04
	4.356	3.568	0.211	20.16	5.283	0.096
German	71.82	71.30	72.82	73.48	74.88	74.60
	5.194	8.233	2.110	23.15	8.615	0.154
Wholesale	79.77	80.26	82.33	84.94	85.46	85.93
	0.869	1.352	0.103	5.052	4.113	0.062
WDBC	92.57	92.95	93.68	93.25	94.96	94.18
	4.943	3.655	0.069	7.632	4.880	0.081
hepat	76.03	76.81	77.33	78.06	80.65	80.25
	1.241	2.365	3.063	1.617	3.561	0.612
Pima	74.66	74.71	74.85	75.06	76.38	76.06
	14.53	8.674	0.308	21.53	5.561	0.163
spectf	78.15	78.77	79.37	79.77	80.44	79.93
	2.807	1.561	0.563	7.986	3.632	0.052

and

Table 4. Experimental results of UCI datasets with 30% Gaussian noise.

	TSVM	TBSVM	LSTBSVM	CTSVM	WCTBSVM	FWCTBSVM
Datasets	ACC (%)	ACC (%)	ACC (%)	ACC (%)	ACC (%)	ACC (%)
	Times (s)	Times (s)	Times (s)	Times (s)	Times (s)	Times (s)
Vote	91.86	92.05	91.36	93.03	93.35	93.28
	0.239	1.033	0.072	5.932	2.396	0.062
Balance	89.93	90.15	90.56	90.89	91.72	90.56
	0.928	1.824	7.503	15.75	3.457	0.057
Cancer	92.12	92.75	93.33	93.87	94.43	94.04
	7.041	3.448	0.103	23.17	5.732	0.082
German	69.21	70.93	70.49	71.37	72.88	72.60
	2.194	8.655	0.172	24.52	8.365	0.256
Wholesale	76.06	78.59	79.31	80.35	82.86	82.69
	5.413	1.519	0.206	11.052	5.113	0.103
WDBC	91.52	92.11	92.48	92.98	93.88	93.24
	4.568	4.320	0.056	10.52	3.624	0.081
hepat	74.16	74.81	75.33	75.86	76.23	77.03
	1.241	3.465	4.300	1.715	2.034	1.025
Pima	72.43	72.89	73.57	74.06	75.38	74.28
	9.482	7.901	0.112	23.21	4.210	0.395
spectf	77.30	77.77	78.06	78.80	79.68	78.72
	3.087	2.157	0.630	8.426	3.632	0.071

, the classification performance of WCTBSVM and FWCTBSVM is still higher than TSVM, TBSVM, LSTSVM, and CTSVM. It also found that the classification performance of the model is reduced with the continuous noise improvement. In addition, the experimental results of Table 2, Table 3 and Table 4 can find that WCTBSVM and FWCTBSVM are more robust after adding the $L_{2,\mathrm{p}}$-norm and Welsch loss term.

For a more intuitive observation of the accuracy of the WCTBSVM and FWCTBSVM under different noises, we draw visual line plots according to the data of Table 2, Table 3 and Table 4, Cancer, Wholesale, German, spectf, Hepat and Pima to further show that the WCTBSVM and FWCTBSVM are more stable than several other models. It also shows that $L_{2,\mathrm{p}}$-norm and Welsch loss term make the model more stable. In this section, we randomly choose samples and contaminate the features by introducing Gaussian noise, which obeys a normal distribution $N(0,\tau )$. More specifically, for the training dataset X, we replace X with $X+\widehat{X}$, where $\widehat{X}$ is the noise matrix, which obeys a normal distribution with zero mean and variance of $\tau$. We apply three types of experiments on different datasets: noises factors $\tau =0$, $\tau =1$, $\tau =2$, and $\tau =3$. The experimental results are shown in Figure 6.

4.5. Statistical Analysis

After the six models were tested in the UCI datasets and artificial datasets, both the WCTBSVM and FWCTBSVM showed their accuracy. In order to directly see the classification of the six models on the datasets, we used the Friedman test [30,31] to conduct the statistical monitoring analysis. This test method is a convenient and robust test. Therefore, we first calculated the average ranking and accuracy of the six algorithms and the nine datasets, and the results are shown in

Table 5. Average accuracy and ranking of the six algorithm models on the UCI datasets with different noise proportions.

	TSVM	TBSVM	LSTBSVM	CTSVM	WCTBSVM	FWCTBSVM
Avg.ACC 0%	84.89	85.44	86.12	86.66	87.77	87.79
Avg.rank 0%	5.9	4.8	4.0	3.1	1.3	1.6
Avg.ACC 10%	83.34	83.78	84.35	85.04	86.19	85.92
Avg.rank 10%	5.8	4.6	4.1	3.1	1.3	1.8
Avg.ACC 30%	81.62	82.45	82.72	83.47	84.49	84.04
Avg.rank 30%	5.8	4.7	4.3	2.8	1.1	2.1

.

With the data in Table 5, we can calculate the Friedman statistical variables of the dataset containing 0, 10%, and 30% Gaussian kernels. The calculation formula is as follows:

$$\begin{array}{c}{\chi }_F^2=\frac{12N}{k(k+1)}[\sum _i{R}_i^2-\frac{k{(k+1)}^2}{4}]\hfill \end{array}$$

(105)

In this formula, k expresses the number of algorithms, N represents the number of UCI datasets, and $R_i$ shows the average of the dataset in the ith algorithm. In this paper, $k=6$, $N=9$. According to (105), it is obtained that the Friedmann statistical variables for Gaussian kernel datasets at different proportions are, respectively, 36.54, 32.53, and 36.46. Based on the ${\chi }_F^2$-distribution with $(k-1)$ degrees of freedom, we have

$$\begin{array}{c}\hfill F_F=\frac{(N-1){\chi }_F^2}{N(k-1)-{\chi }_F^2}\end{array}$$

(106)

Thus, according to (106), we can obtain the ${\chi }_F^2$-distribution of Gaussian kernels at the three proportions, respectively 34.55, 20.87, 34.15. Where $F_F((k-1),(k-1)(N-1))$ follows the F-distribution, the number of independent variables is $(k-1)$, and the degree of freedom is $(k-1)(N-1)$. Where $\alpha =0.1$, by viewing the F test threshold table we can get $F_{\alpha }=1.997$. Obviously, $F_F>F_{\alpha }$, so we reject the original hypothesis. From Table 5, we can see that the average ranking of the accuracy of WRTBSVM and FWRTBSVM is low compared to the other four models, explaining that the classification performance of these two models is more outstanding.

To further compare the classification performance of the six models, we used the Nemenyi test to test it. When the mean difference between the accuracy of the WCTBSVM and FWCTBSVM is larger, the two models differ significantly. The difference was not obvious otherwise. By checking the post-hoc test table, we can get the $q_{\alpha =0.1}=2.326$. Then, the Critical Difference (CD) is calculated by the following formula:

$$\begin{array}{c}\hfill CD=q_{\alpha =0.1}\sqrt{\frac{k(k+1)}{6N}}=2.3260\times \sqrt{\frac{6\times 7}{6\times 9}}=2.0513\end{array}$$

Based on the CD values, we visualized the data for post-hoc tests, as shown in Figure 7.

From Figure 7, we can find that the WCTBSVM and FWCTBSVM classification performance is indeed better than the other four models. It is also found that the difference between the two models is less than the CD value, so it can be determined that the performance of the two models is not very different. Thus, the WCTBSVM and FWCTBSVM have better classification performance and robustness.

5. Conclusions and Future Directions

Based on the binary classification problem, a new TBSVM model is proposed in this paper as the WCTBSVM, which introduces bounded, smooth, non-convex Welsch loss terms in the TBSVM model and iterative optimization of the relevant model variables using the HQ optimization algorithm to handle the Welsch loss function term. Meanwhile, the capped $L_{2,p}$-norm distance based on the TBSVM and results in the WCTBSVM model are introduced, which make it more generalized and robust than the TBSVM; thus, improving the classification performance of the model. In order to reduce the time complexity and space complexity of the WCTBSVM, we obtained the FWCTBSVM using least squares, which also speeds up the operation efficiency of the model while maintaining the performance advantages of the WCTBSVM.

According to the theoretical basis, we conducted accuracy testing experiments on a UCI dataset and manual dataset and found that the classification performance of the WCTBSVM model is indeed better than the TSVM, TBSVM, LSTSVM, and CTSVM. To further determine the reliability of the WCTBSVM, we also performed statistical test analysis, of which the results still show that the classification performance of the WCTBSVM is more outstanding. Therefore, we can still apply the model to semi-supervised learning in other classification experiments to further study the performance of the model. In future work, how to extend our method to multi-view learning and multi-instance learning are worthy of further study. Certainly, how to develop fast algorithms for our method is also worth studying.