The Existence of Odd Symmetric Periodic Solutions in the Generalized Elliptic Sitnikov
Abstract
:1. Introduction
2. The Generalized Elliptic Sitnikov -Body Problem
- (i)
- ;
- (ii)
- ;
- (iii)
3. The Existence of Odd Periodic Solutions
3.1. Satisfiability of Hypotheses (H1) and (H2)
3.2. Main Results
- (i)
- , , .
- (ii)
- , is nontrivial, and the zeros of are nondegenerate.
- (iii)
- is continuous.
- (1)
- all solutions of are odd -periodic and have zeros in .
- (2)
- and one of the following alternatives holds:
- (2.a)
- ;
- (2.b)
- with .
- (1)
- if , then statement (2.a) of Theorem 2 holds;
- (2)
- if , then and (2.b) of Theorem 2 holds, , where
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sitnikov, K. Existence of oscillatory motions for the three-body problem. Dokl. Akad. Nauk. 1960, 133, 303–306. [Google Scholar]
- Faruque, S. Solution of the Sitnikov problem. Celest. Mech. Dyn. Astr. 2003, 87, 353–369. [Google Scholar] [CrossRef]
- Jiménez-Lara, L.; Escalona-Buendía, A. Symmetries and bifurcations in the Sitnikov problem. Celest. Mech. Dyn. Astr. 2001, 79, 97–117. [Google Scholar] [CrossRef]
- Kumari, R.; Pal, A.; Abouelmagd, E.; Alhowaity, S. Approximation solution of the nonlinear circular Sitnikov restricted four body problem. Symmetry 2021, 13, 1966. [Google Scholar] [CrossRef]
- Liu, J.; Sun, Y. On the Sitnikov problem. Celest. Mech. Dyn. Astr. 1990, 49, 285–302. [Google Scholar] [CrossRef]
- Markellos, V. Bifurcations of straight line oscillations. Astron. Astrophys. 1978, 67, 229–240. [Google Scholar]
- Moser, J. Stable and Random Motion in Dynamical Systems; Princeton University Press: Princeton, NJ, USA, 1973. [Google Scholar]
- Ortega, R.; Rivera, A. Global bifurcations from the center of mass in the Sitnikov problem. Disc. Contin. Dyn. Syst. Ser. B 2010, 14, 719–732. [Google Scholar] [CrossRef]
- Pavanini, G. Sopra una nuova categoria di soluzioni periodiche nel problema dei tre corpi. Ann. Mat. Pur. Appl. 1907, 13, 179–202. [Google Scholar] [CrossRef]
- Ullah, M.; Idrisi, M.; Sharma, B.; Kaur, C. Sitnikov five-body problem with combined effects of radiation pressure and oblateness. New Astron. 2021, 87, 9. [Google Scholar]
- Szebehely, V. Theory of Orbits the Restricted Problem of Three Bodies; Academic Press: New York, NY, USA, 1967. [Google Scholar]
- Wodnar, K. Analytical approximations for Sitnikov’s problem. In From Newton to Chaos; Springer: Boston, MA, USA, 1995; pp. 513–523. [Google Scholar]
- Belbruno, E.; Llibre, J.; Olle, M. On the families of periodic orbits which bifurcate from the circular Sitnikov motions. Celest. Mech. Dyn. Astr. 1994, 60, 99–129. [Google Scholar] [CrossRef]
- Abouelmagd, E.; Guirao, J.; Pal, A. Periodic solution of the nonlinear Sitnikov restricted three body problem. New Astron. 2020, 75, 10. [Google Scholar] [CrossRef]
- Cen, X.; Cheng, X.; Huang, Z.; Zhang, M. On the stability of symmetric periodic orbits of the elliptic Sitnikov problem. SIAM J. Appl. Dyn. Syst. 2020, 19, 1271–1290. [Google Scholar] [CrossRef]
- Corbera, M.; Llibre, J. Periodic orbits of the Sitnikov problem via a Poincaré map. Celest. Mech. Dyn. Astr. 2000, 77, 273–303. [Google Scholar] [CrossRef]
- Corbera, M.; Llibre, J. On symmetric periodic orbits of the elliptic Sitnikov problem via the analytic continuation method. Contem. Math. 2002, 292, 91–128. [Google Scholar]
- Galán, J.; Núnez, D.; Rivera, A.; Riccio, C. Stability and bifurcations of even periodic orbits in the Sitnikov problem. Celest. Mech. Dyn. Astr. 2018, 130, 20. [Google Scholar]
- Llibre, J.; Ortega, R. On the families of periodic orbits of the Sitnikov problem. SIAM J. Appl. Dyn. Syst. 2008, 7, 561–576. [Google Scholar] [CrossRef]
- Ortega, R. Symmetric periodic solutions in the Sitnikov problem. Arch. Math. 2016, 107, 405–412. [Google Scholar] [CrossRef]
- Zhang, M.; Cen, X.; Cheng, X. Linearized stability and instability of nonconstant periodic solutions of Lagrangian equations. Math. Meth. Appl. Sci. 2018, 41, 4853–4866. [Google Scholar] [CrossRef]
- Cen, X.; Liu, C.; Zhang, M. A proof for a stability conjecture on symmetric periodic orbits of the elliptic Sitnikov problem. SIAM J. Appl. Dyn. Syst. 2021, 20, 941–952. [Google Scholar] [CrossRef]
- Bountis, T.; Papadakis, K.E. The stability of vertical motion in the N-body circular Sitnikov problem. Celest. Mech. Dyn. Astr. 2009, 104, 205–225. [Google Scholar] [CrossRef]
- Rivera, A. Periodic solutions in the generalized Sitnikov(N+1)-body problem. SIAM J. Appl. Dyn. Syst. 2013, 12, 1515–1540. [Google Scholar] [CrossRef]
- Misquero, M. Resonance tongues in the linear Sitnikov equation. Celest. Mech. Dyn. Astr. 2018, 130, 25. [Google Scholar] [CrossRef]
- Leray, J.; Schauder, J. Topologie et équations fonctionnelles. Ann. Sci. Ec. Norm. Supérieure 1934, 51, 45–78. [Google Scholar] [CrossRef]
- Byrd, P.; Friedman, M. Handbook of Elliptic Integrals for Engineers and Physicists; Spring: Berlin/Heidelberg, Germany, 1954. [Google Scholar]
- Gastón, B. On the global families of periodic solution of a generalized Sitnikov Problem. Celest. Mech. Dyn. Astr. 2022, 134, 22. [Google Scholar]
- Coddington, E.A.; Levinson, N. Theory of Ordinary Differential Equations; McGraw-Hill Book Company, Inc.: New York, NY, USA; Toronto, ON, Canada; London, UK, 1955. [Google Scholar]
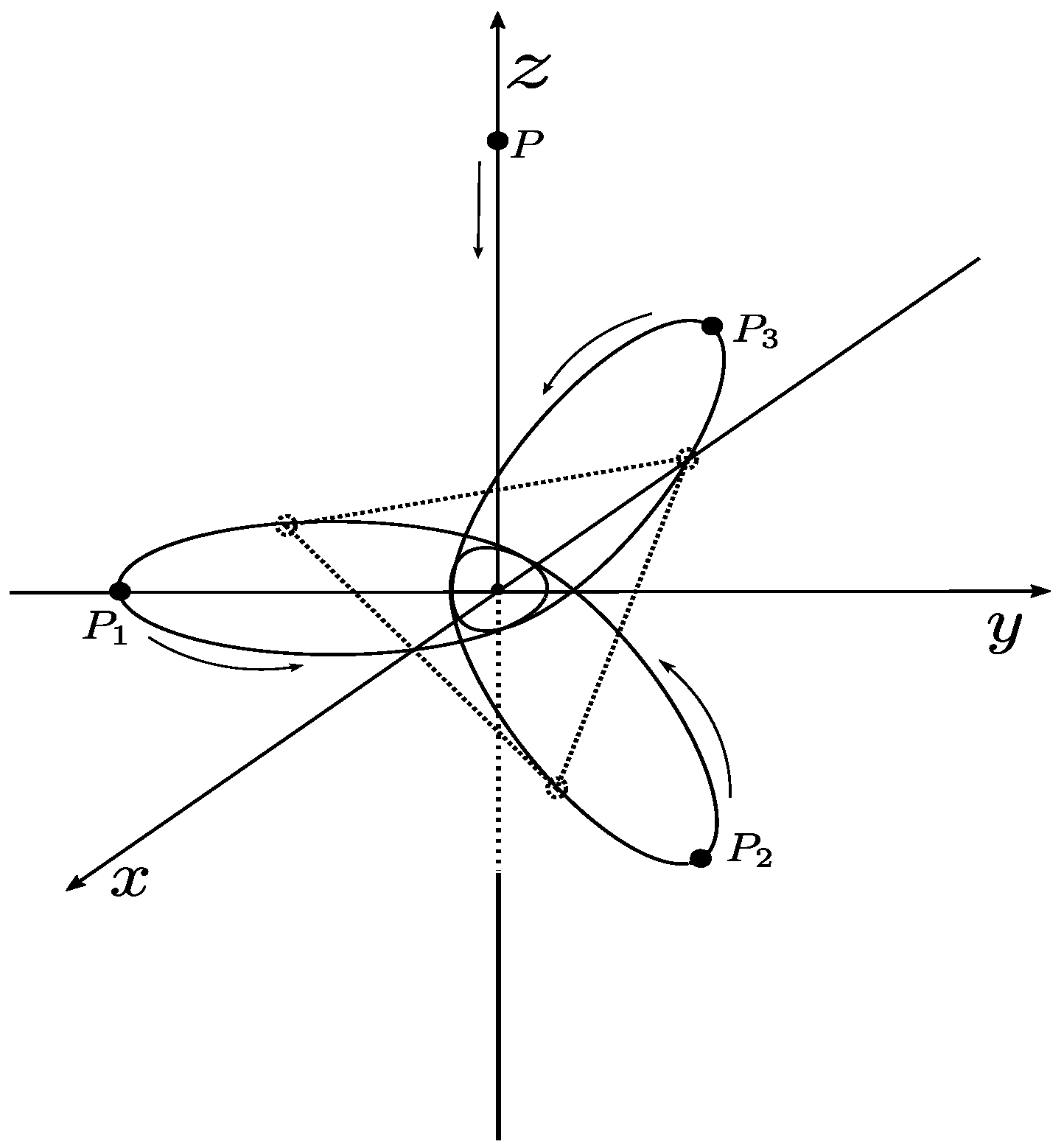
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, X.; Liu, B.
The Existence of Odd Symmetric Periodic Solutions in the Generalized Elliptic Sitnikov
Cheng X, Liu B.
The Existence of Odd Symmetric Periodic Solutions in the Generalized Elliptic Sitnikov
Cheng, Xuhua, and Baoting Liu.
2023. "The Existence of Odd Symmetric Periodic Solutions in the Generalized Elliptic Sitnikov






