Abstract
Computation offloading has received a significant amount of attention in recent years, with many researchers proposing joint offloading decision and resource allocation schemes. However, although existing delay minimization schemes achieve minimum delay costs, they do so at the cost of losing possible further maximization of the number of serviced requests. Furthermore, the asymmetry between uplink and downlink poses challenges to resource allocation in edge computing. This paper addresses this issue by formulating the joint computation offloading and edge resource allocation problem as a mixed-integer nonlinear programming (MINLP) problem in an edge-enabled asymmetrical network. Leveraging the margin between a delay-minimum scheme and a near-deadline scheme, a water pumping and refilling (WPR) algorithm is proposed to maximize the number of accepted requests. The WPR algorithm can function both as a supplementary algorithm to a given offloading scheme and as a standalone algorithm to obtain a resource allocation scheme following a customizable refilling policy. The simulation results demonstrated that the proposed algorithm outperforms delay-minimum schemes in achieving a high acceptance ratio.
1. Introduction
Computation offloading has emerged as a prominent research area in edge computing-enabled systems in recent years [1]. Its fundamental concept involves leveraging the computing resources deployed at the network edge to offer faster and more satisfactory computational services to user devices (UDs) [2,3]. However, the burgeoning number of Internet of Things [4] devices exacerbates the already constrained computing resources of edge nodes. When an asymmetry edge node is overloaded, it is unable to accommodate all the computation offloading requests. Therefore, how to allocate resources to maximize the number of serviced requests in asymmetrical systems, while respecting the given resource limitations, remains a crucial issue.
As computation offloading requests arrive, the BS decides which requests should be accepted and how many resources should be allocated for the accepted requests. Different objectives lead to different resource allocation schemes. The primary objective of current research in computation offloading is to minimize delay or energy consumption [5]. In situations where multiple users demand offloading services, it is common to minimize the weighted sum or the sum of users’ processing delays [6,7]. However, weight setting is typically based on empirical methods, and schemes with different weightings may yield distinct performances. Although designs that minimize delay cost lead to attractive resource allocation schemes, most of their resource allocation results tend to be over-provisioned to some extent. On the other hand, energy consumption minimization schemes, from the perspective of user devices, extend the battery life of UDs and achieve energy efficiency at the system level [8]. However, such schemes may not be optimal from the perspective of network operators (NOs) because they fail to accommodate additional computation offloading requests, thereby reducing the economic revenues of NOs.
Several existing studies propose incentive-driven computation offloading and resource allocation schemes to benefit edge service providers [9]. For example, Yuan et al. [10] aimed to maximize the profits of remote clouds by accepting more requests without causing high bandwidth consumption and energy consumption for task processing. However, such schemes may not be suitable for edge servers with limited resources, particularly when facing excessive terminal requests. Under such circumstances, the edge server may be forced to exhaust its available resources to accommodate end requests, which involves both request acceptance and resource allocation. Therefore, a joint request acceptance and resource allocation scheme with maximized accepted requests is necessary.
Although these designs function well when there are sufficient resources in the serving network, the focus of request acceptance and resource allocation should shift towards utilizing constrained resources to accept as many requests as possible when the resource is insufficient. Considering this, from the user’s perspective, a satisfactory service does not necessarily need have the shortest service delay, as long as a certain level of service agreement [11] is met. Therefore, NOs do not have to distribute the network resource for a system-wide delay minimal objective, which releases the network’s potential to accommodate more requests. In this regard, this paper proposes a joint computation offloading acceptance and edge resource allocation scheme to maximize the number of accepted requests in an edge-enabled asymmetrical network. Additionally, a scalable water pumping and refilling algorithm is proposed to accommodate requests on the basis of the aforementioned delay-minimal schemes. The primary innovations of this paper are summarized as follows:
- A low-complexity water pumping and refilling (WPR) algorithm is proposed to release the untapped potential of the network and accommodate more requests, based on the delay cost minimization scheme. This approach can serve as both a supplementary method and a standalone method when combined with a specific customization strategy.
- The joint computation offloading and edge resource allocation problem is formulated as a mixed integer nonlinear programming problem with the objective of maximizing the number of accepted requests. Resource margins between the delay cost minimization scheme and the desirable quality of service (QoS) scheme are exploited to accommodate more requests.
- We evaluate the performance of the proposed algorithm under various conditions. The simulation results demonstrate that our WPR algorithm outperforms the delay-cost-minimum-based schemes regarding acceptance ratio.
The remainder of this paper is organized as follows. In Section 2, we review related work on computation offloading and resource allocation in edge computing systems. In Section 3, we present the system model and relevant assumptions. The proposed water pumping and refilling algorithm is introduced in Section 4. In Section 5, we analyze and discuss the simulation results. Finally, our paper is concluded in Section 6.
2. Related Work
Among the delay-minimal schemes, Ren et al. [7] proposed a partial offloading model that divides a computational task into two parts and the divided tasks are collaboratively processed by an edge server and a remote cloud. A closed-form task splitting ratio and resource allocation scheme were provided. Similarly, Wang et al. [12] aimed to minimize task duration while meeting energy consumption constraints by allocating bandwidth equally to connected offloading user devices, using the alternating direction method of multipliers (ADMM) algorithm to determine computation node selection and computing resource allocation schemes. Wei et al. [13] selected the joint computation node, decided on the content caching, and determined the resource allocation (including radio bandwidth and computing resources) with a two-hidden-layer deep neural network to minimize end-to-end delay for computation offloading and content delivery services, where the channel state and resource allocation are discretized. Although these schemes have achieved stunning performance, they still fall into the category of delay-minimal schemes, which means resource allocation results could be fine-tuned to accept more requests within a deadline.
Similarly, many research efforts have been made to devise energy cost minimization (ECM) schemes [14,15]. For example, Wang et al. [5] formulated EM and delay cost minimization (DCM) problems for single-user partial computation offloading, using the dynamic voltage scaling technique [16]. They optimized transmission power, computation resource allocation, and offloading ratio and reached the insightful conclusion that if a task has a stringent delay requirement (less than a threshold), it cannot be processed in a partitioned way. In [17], requests from representative locations are grouped, and computation results for requests with duplicated inputs selectively cached. They formulated the cache decision, bandwidth allocation, and computing resource allocation problem as an MINLP problem, aiming to minimize the energy consumption of the base station (BS) and all users. In [18], the deep deterministic policy gradient (DDPG) algorithm is adopted to solve the joint computation node selection and computing resource allocation problem, aiming to minimize system energy consumption. They constructed an SBS–MBS three-layer offloading model for delay-stringent tasks. Apart from the cloud- and edge-enabled processing models, some researchers supplement user devices to enhance performance. For instance, Huang et al. [19] proposed an edge-end cooperation scheme where mobile devices act as computing servers to minimize the energy consumed by the mobile devices. In [20], a three-node computation offloading scenario was studied in which the user device near the access point (AP) is exploited to relay and compute the task of the far user device with the aim of minimizing the energy consumed by the AP in a wireless powered system.
Several studies have investigated resource allocation in computation offloading from different perspectives. In [21], the authors assumed adequate bandwidth between vehicles and the associated MEC server and adopted a Q-value-based deep reinforcement learning method to maximize the acceptance rate in vehicular networks. Zhou and Hu [22] aimed to maximize the ratio of processed bits to the energy consumed by energy-harvesting user devices for non-orthogonal multiple access and time division multiple access systems. Mukherjee et al. [23] focused on maximizing system revenue by analyzing the pricing strategy for offloaded tasks with different time constraints. Yan et al. [24] formulated the DCM and revenue maximization problem as a two-stage game, where computing resources at BS were equally allocated. Wang et al. [25] designed an online auction mechanism to maximize the profit of resource providers in an energy-effective way. Zhou and Zhang [26] proposed compensating tasks with a higher delay-to-deadline ratio to minimize the maximal ratio among users, which was solved using an evolutionary algorithm. Hejja et al. [27] maximized the number of serviced offloading requests under the network function virtualization framework. Finally, Meng et al. [28] developed a task dispatching and scheduling algorithm that focused more on computing node selection and task scheduling to maximize the number of tasks meeting deadline requirements. We summarize part of the studies mentioned above in Table 1.

Table 1.
Summary of the discussed work.
Furthermore, recent research has explored combining deep reinforcement learning with computation offloading to enhance performance [13,17,30,31,32,33]. However, these approaches do not address the problem of maximizing the number of accepted requests among a flood of requests with limited resources in an edge-enabled asymmetrical network. This requires a system of efficient allocation of resources and selection of the appropriate requests while considering their respective delay requirements. This paper proposes a solution to solve this problem, wherein tasks are processed at the edge server, and rejected tasks are considered to be task failures. Notably, our proposed algorithm can function as a supplementary approach and as a standalone approach.
3. System Model
As shown in Figure 1, the system consists of a single BS and M UDs. The BS is equipped with an edge computing server, having a computing power of (in CPU cycles per second). The BS is connected to the edge server via a fiber link [34] to provide computing services for UDs. UDs issue computation offloading requests to the associated BS if local computing resources cannot complete the task within the deadline , and such requests are considered to be timeouts if they are rejected. It is assumed that the computation-intensive tasks arrive at the beginning of a schedule interval [35] and only one task is generated from each UD. Local processing is not considered and requests with no resources allocated are treated as timeouts.
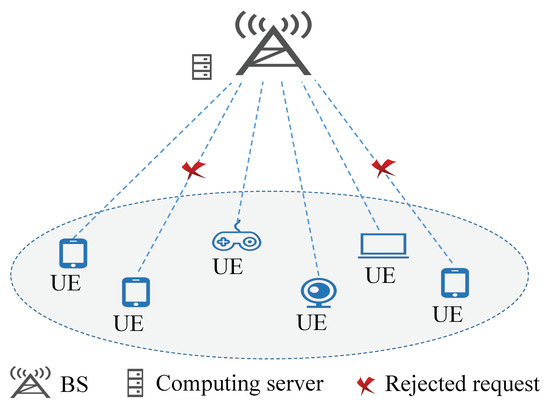
Figure 1.
System model.
There are K kinds of computation applications running in the system. In this paper, it is assumed that the input of computational application k is one of the input files. A computation request of application k is specified by the task input size (in bits), the computation load (the desired computing resource, in CPU cycles), and the task deadline (this can also be a QoS-related delay parameter). Thus, a UD m requesting computation offloading of application k with task input f () can be specified with . indicates the computation task from UD m in the sequel. For simplicity of notations, the parameters of task are written as .
When UDs cannot complete their tasks within the given deadline, they request the associated BS for computation offloading [3]. While some previous research considered local processing power on the UDs, this paper excludes UDs that can process tasks without exceeding the deadline (). As a result, the BS can either accept or decline the computation offloading requests, depending on its processing capabilities. The BS tries to accommodate the requests to the best of its abilities. When task is accepted (i.e., ), the BS ensures that resource allocation meets the delay requirement (or QoS-related delay requirement). If task is denied (i.e., ), the BS incurs a penalty. The BS makes decisions on joint offloading request acceptance and resource allocation with the aim of maximizing the number of accepted requests.
3.1. Transmission Model
The whole system is presumed to function in an orthogonal frequency division multiple access (OFDMA) mode with a bandwidth of B (in hertz). In this way, interference is not considered in our model. Noticing the asymmetry in uplink and downlink, the result download stage is not considered in our model [36]. Wireless access bandwidth is only allocated to accepted requests and the BS assigns a portion bandwidth to UD m to upload the task input file (of size ). Consequently, the maximal upload data rate between UD m and the BS can be expressed as follows:
where is the upload transmission power (usually determined by the association control scheme) of UD m. is the instantaneous channel gain between UD m and the BS. As the transmission may occur over several slots, the averaged channel gain is employed to substitute the instantaneous channel gain [7] across multiple frames (with channel estimation technologies [37]). Supposing request from UD m is accepted, the averaged upload transmission time for UD m to upload its computation task input can be written as:
where is the average of during .
In addition, the allocated access bandwidth of the BS cannot exceed its capacity:
where denotes the set of accepted requests from UDs.
3.2. Computing Model
The heterogeneity in computing resource requirements among accepted requests necessitates efficient allocation of computing resources by the edge server. denotes the set of accepted requests and denotes the set of rejected requests. The BS assigns a fraction of its computing resources to UD m to process the computation task. The resulting computation delay can be written as:
The allocation of computing resources must adhere to its capacity constraint, which can be formally expressed as:
3.3. Problem Formulation
If a request is accepted, the BS ensures that the associated delay constraint is not violated. This requirement can be expressed as:
The main objective is to maximize the number of accommodated requests subject to the constraints imposed by the limited system resources and deadlines, which can be formally expressed as:
is an indicator function and takes value one when and zero otherwise. Constraints and ensure that the bandwidth and computing resources allocated to the accepted requests should not exceed the system’s capacity. Constraint ensures that the delay requirements of the accepted requests are met.
Problem (P1) is known to be intractable, due to the non-smooth and non-convex nature of the objective function. To overcome this challenge, Problem (P1) is transformed into Problem (P2) with the objective of minimizing the total delay cost of all requests. This transformation reduces the search domain of Problem (P1) and enables more efficient solution approaches to solve Problem (P2). Two key observations form the basis of this transformation. First, for an accepted request, the processing delay is always less than the corresponding deadline, while a rejected request receives a relatively large penalty. In this way, the system delay cost can be reduced by accepting more requests. Second, the optimal allocation scheme to Problem (P1) does not necessarily minimize the overall delay cost. Such a scheme could lead to higher delays compared to Problem (P2), which leaves more vacant resources for other requests. Consequently, solutions to Problem (P1) can be obtained by first solving the delay cost minimization (P2) and pushing the resource allocation scheme near to the deadline.
In this paper, rejected requests are treated as timed-out and discarded, incurring penalties. Specifically, the penalty of a timed-out request is denoted as , where is a constant factor for all requests. This penalty factor reflects the severity of a timed-out request in terms of delay cost. To account for these penalties, Problem (P2) is reformulated by adding penalty terms for timed-out requests:
Problem (P2) is a challenging MINLP problem with coupled decision variables. To address this challenge, we follow previous works [38] and Problem (P2) and decompose the problem into two sub-problems: request acceptance and resource allocation. The binary request acceptance problem can be solved with a coordinate descent algorithm [39]. Note that both request acceptance and resource allocation influence the final effect. Specifically, this paper focuses on solving the resource allocation sub-problem to gain insight into Problem (P2).
It can be seen from above that, once is given ( and are determined), Problem (P2.1) can be reformulated as a convex optimization problem [38]. Once an optimal resource allocation scheme is obtained, we readjust the resource allocation result in and try to allocate resources to request in , to accommodate more requests without violating the deadline constraints, and, then, obtain the solutions to the original Problem (P1). This process allows us to iteratively refine our solutions and obtain an optimized allocation of system resources that maximizes the number of accommodated requests within the constraints of the system’s limited resources and deadlines.
4. The Water-Pumping Algorithm
In this section, the classic Lagrange multiplier method and KKT conditions are adopted to derive the solution to Problem (P2.1). Based on this solution, the water pumping and refilling algorithm is proposedto solve the initial asymmetric resource allocation Problem, as stated in Problem (P1).
4.1. The Delay Minimum Solution
By introducing Lagrange multipliers , the Lagrange function of (P2.1) can be formulated as:
Based on Equation (7) and in-depth analysis of Problem (P2.1), using KKT conditions, the following corollaries can be obtained.
Corollary 1.
The necessary condition for an optimal bandwidth and computing resource allocation scheme for is given by:
Proof.
Please see the detailed proof in Appendix A. □
The optimal bandwidth and computing resource allocation scheme for UD m can be obtained from Equation (8). It can be observed that the optimal bandwidth allocation is proportional to , which implies that requests with better channel conditions and larger input data size receive a larger share of the bandwidth allocation. Similarly, requests with higher computation loads are allocated more edge computing resources.
Corollary 2.
The optimal allocation scheme achieves the minimal delay cost for all when the Lagrange multiplier takes the same value (e.g., 0), which can be denoted as:
Proof.
Please see the detailed proof in Appendix B. □
Equation (9) indicates that the delay-minimum resource allocation scheme to Problem (P2.1) in this context leads to the exhaustion of all system resources for accepted requests, without taking into account the possibility of over-provisioning a request, based on its maximum acceptable delay. In general, the ratio of the user’s processing delay to its deadline under the delay-minimum scheme is less than one (), where the processing delay of an accepted request can be represented as:
Upon comparing Equation (8) with Equation (9), it can be observed that the Lagrange multipliers play a crucial role in regulating the allocation of resources, which, in turn, impacts the processing delays of accepted requests. Thus, the proposed WPR algorithm increases the number of accepted requests by reallocating resources (setting ) to extend the processing delays of accepted requests up to their respective deadlines ().
4.2. Water Pumping
It can be inferred from Equation (10) that can be extended to be equal to by adjusting , while keeping (which can be calculated with using Equation (8)) unchanged. This can be denoted as:
Based on this observation, we propose the term “water pumping” to describe the procedure whereby the value of , the water level parameter of an accepted request , is adjusted from its initial value to a new value . To further characterize this process, we define the ratio as . By manipulating the value of , the processing delay is extended to the desired maximal acceptable deadline for request :
Notably, the proposed scheme can be readily extended to a cloud-edge collaboration model [12,40,41]. In this case, the ratio can be redefined as , where denotes the round-trip time between the edge node and the remote cloud server. As we adjust the value of to , the vector shifts to the new value . and shifts to and , accordingly. The decrement of , which is termed the “pumped water”, can be expressed as follows:
4.3. Water Refilling
To accommodate request , the pumped water and should be refilled to ensure that does not violate its deadline constraint. The procedure of setting a feasible for is termed “water refilling”. Successful water refilling involves finding a suitable and setting , within the following constraints:
Here are obtained with according to Equations (A14) and (A15) ( and are obtained with ). The reason for taking the inequality in Equations (15) and (16) is to ensure there is no violation of the resource constraints C1 and C2. Equation (17) guarantees that the allocated resource for meets its deadline requirement. In this regard, compared with Equations (13) and (14), Equations (15) and (16) can be rewritten as:
Furthermore, the value of for the newly accepted request can be decided with the following formula:
Unfortunately, a single trial of “water pumping” may not necessarily result in successful “water refilling”, so situations where multiple trials of “water pumping” are necessary to ensure successful refilling should be considered. Denote () as the current set of “pumped requests”, containing the requests having shrunken (), and ( and ) as the set of “unpumped requests”. According to a predetermined rule, (the pumping policy ), a request can be selected from to perform “water pumping”. Assuming is the chosen request to be “refilled”, based on another predetermined rule, the refilling policy , after several pumping trials, can be determined without violating the following constraints:
Compared with Equations (18) and (19), Equations (21) and (22) can be rewritten as follows:
In this way, the , after multiple pumping trials of can be obtained from:
It should be noted that requests do not violate the deadline requirements after accepting the new request . Equation (11) indicates that the processing time of a pumped request is extended to its deadline. Equations (15) and (21) guarantee that . Similarly, holds. As a result, the processing delay of a pumped request can be reformulated as:
The WPR is all about how to allocate network resources to provide near-to-deadline services for accepted computation offloading requests. The algorithm converges to its final result by continuously pumping and refilling until no request can be successfully added. The whole procedure of the WPR algorithm is summarized in Algorithm 1, and some notations are listed in Table 2.

Table 2.
Summary of notations used in the WPR algorithm.
4.4. Complexity Analysis
The proposed WPR algorithm provides a solution to problem (P1) and offers flexibility in designing service strategies by allowing the choice of requests to shrink during each iteration. It is important to note that the WPR algorithm converges within at most M refilling iterations, provided that the exit condition in Line 14 of Algorithm 1 is not met. Assuming that , the last successful one-to-one pumping and refilling happens at this point in time. After this moment, multiple rounds of pumping are necessary to ensure a successful refilling. Once , no further refilling attempts will succeed, which means the end of the algorithm. Therefore, the total pumping procedure will take iterations. Thus, the time complexity of the WPR algorithm is .
| Algorithm 1: Water Pumping and Refilling |
Input: initial accepted requests set , initial of , pumping policy and refilling policy ; Output: final accepted requests set , final of ;
|
5. Simulation Results and Discussion
In this section, we present results and discussions concerning the edge-enabled asymmetrical network under different parameters.
5.1. Simulation Setting
The system parameters are defined as follows. The bandwidth of the BS is MHz, and the computing capacity of the connected edge server is CPU cycles/second. The channel model utilized in this study was the same as the one presented in [38]. UDs upload task data with a fixed transmission power . The system contains UDs, and it considers only one type of computation application, denoted by . Accordingly, input files are considered, with the input size (in bits) ranging from . Specifically, the input size of with input file f takes the value of following uniform distribution, Zipf distribution [41,42] (skewness factor ) prioritizing small loads and Zipf distribution prioritizing large loads. The computation load () of each task ranges from (in CPU cycles) and computation load of with input file f takes a value of following the same distribution as . and the penalty factor . Unless otherwise specified, the results were obtained based on uniform distribution. In this paper, the default policy selects the request with the highest in to pump first and tries to refill the request with the smallest in . It should be noted that other and can be customized and adopted, such as smallest file size first (SFWPR), and best channel condition first (which is not considered in this paper). The following baseline algorithms were used in this paper:
- Delay cost minimization (DCM): this scheme allocates resources for accepted requests with the aim of minimizing system delay costs. In cases where a request is rejected, the DCM scheme imposes a penalty instead of the processing delay.
- Water pumping and refilling, basing on DCM (WPDCM): this scheme uses results obtained from DCM as the input of WPR and sets each item of to 1.
- Water pumping and refilling (WPR): The initial only includes the request with the smallest which is the refilling policy used by default.
- Smallest input file first water pumping and refilling (SFWPR): using the default policy while refilling requests with the smallest input size. The initial only includes the request with the smallest input size.
5.2. Result Discussion
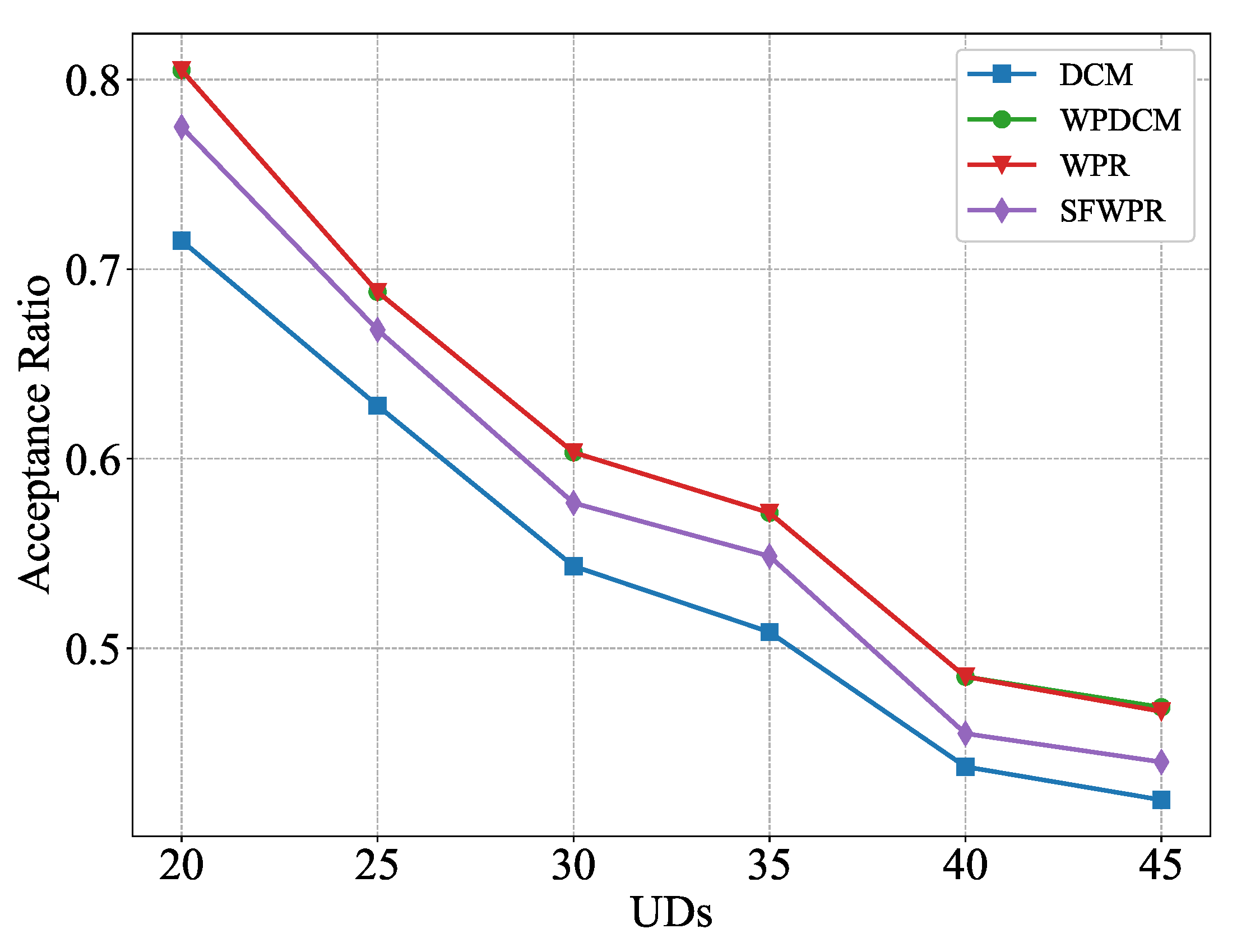
Figure 2 illustrates the relationship between the number of UDs and the acceptance ratio of offloading requests in the system. As the number of UDs requesting computation offloading increased, the acceptance ratio of requests tended to decrease. The reason for this is clear, the limited system resources could not deal with requests beyond the system’s capabilty. The WPR-based algorithms achieved a higher acceptance ratio than the DCM algorithm. The reason for this is that the DCM algorithm prioritized minimization of the sum processing delay of the accepted requests, which came at the expense of reducing the system’s capacity to handle a high volume of user requests. In other words, while minimizing processing delay is a desirable goal to improve system performance, it may result in reduced capacity to handle additional user requests. Moreover, the WPR scheme proposed in this study demonstrated competitive performance, and the highest acceptance ratio among all the schemes considered, including WPDCM. Therefore, the proposed WPR algorithm can be used as a supplementary algorithm to DCM and as an independent algorithm, offering competitive results.
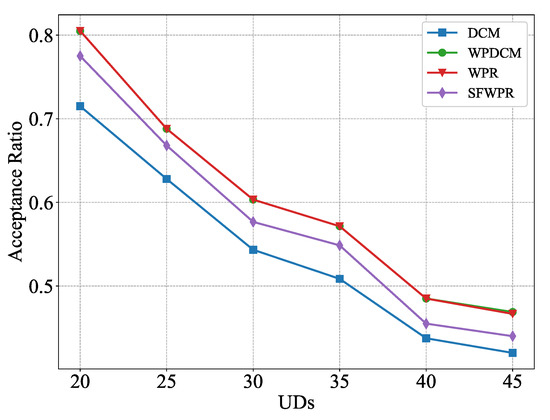
Figure 2.
Acceptance ratio versus UDs.
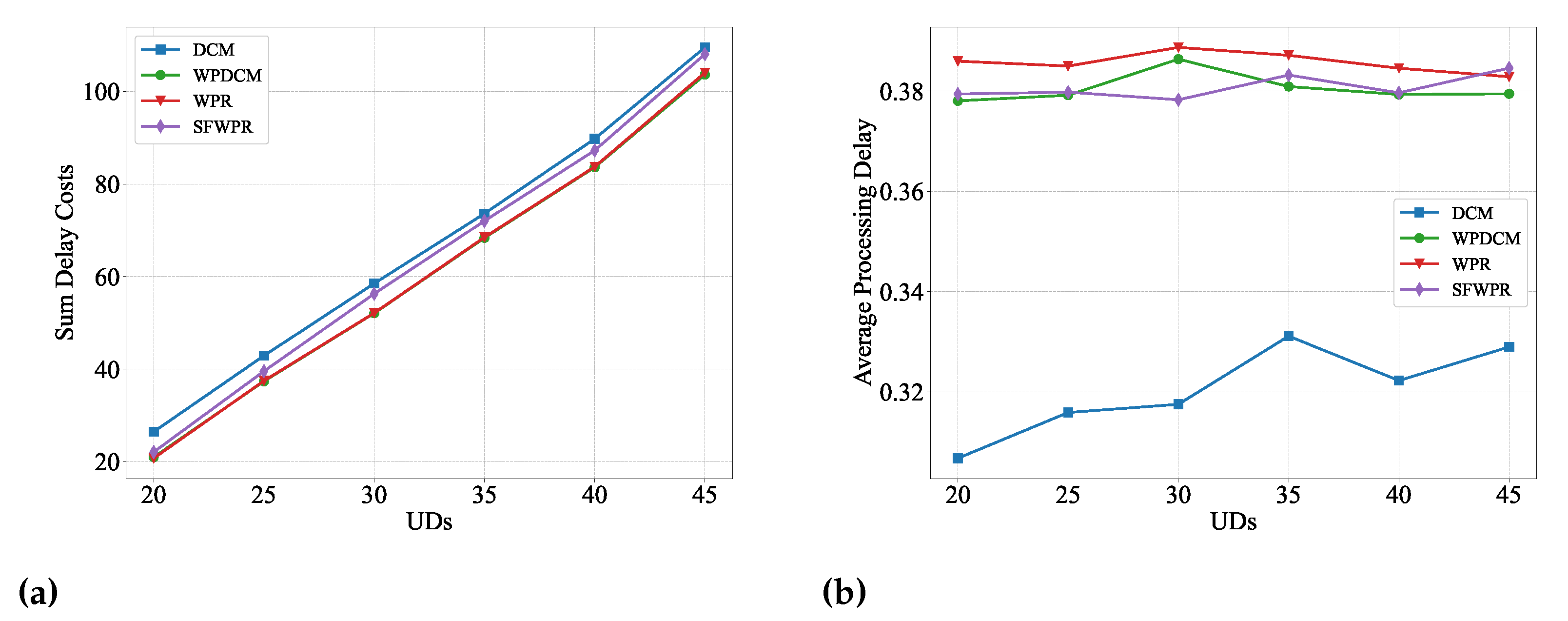
Figure 3a illustrates that the aggregate system delay cost increased proportionally with the number of offloading user devices (UDs). This escalation is primarily attributed to the penalty incurred by rejecting redundant offloading requests that exceed the system’s resource capacity. Notably, the DCM algorithm incurred the highest delay cost, mainly due to its low acceptance ratio. In contrast, Figure 3b illustrates that the WPR-based algorithm achieved a higher acceptance ratio than the DCM algorithm. The DCM algorithm aimed to minimize the processing delay of each accepted request, while the WPR-based algorithm permitted the processing delay of an accepted request to approximate its deadline. This approach left more system resources available to accommodate additional requests.
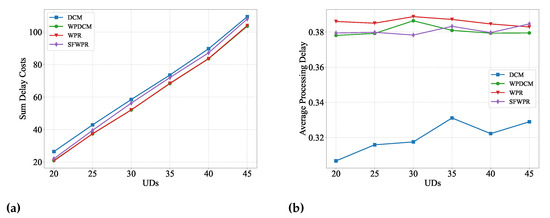
Figure 3.
Delay cost versus UDs: (a) sum delay cost of all UDs; (b) average processing delay for an accepted request.
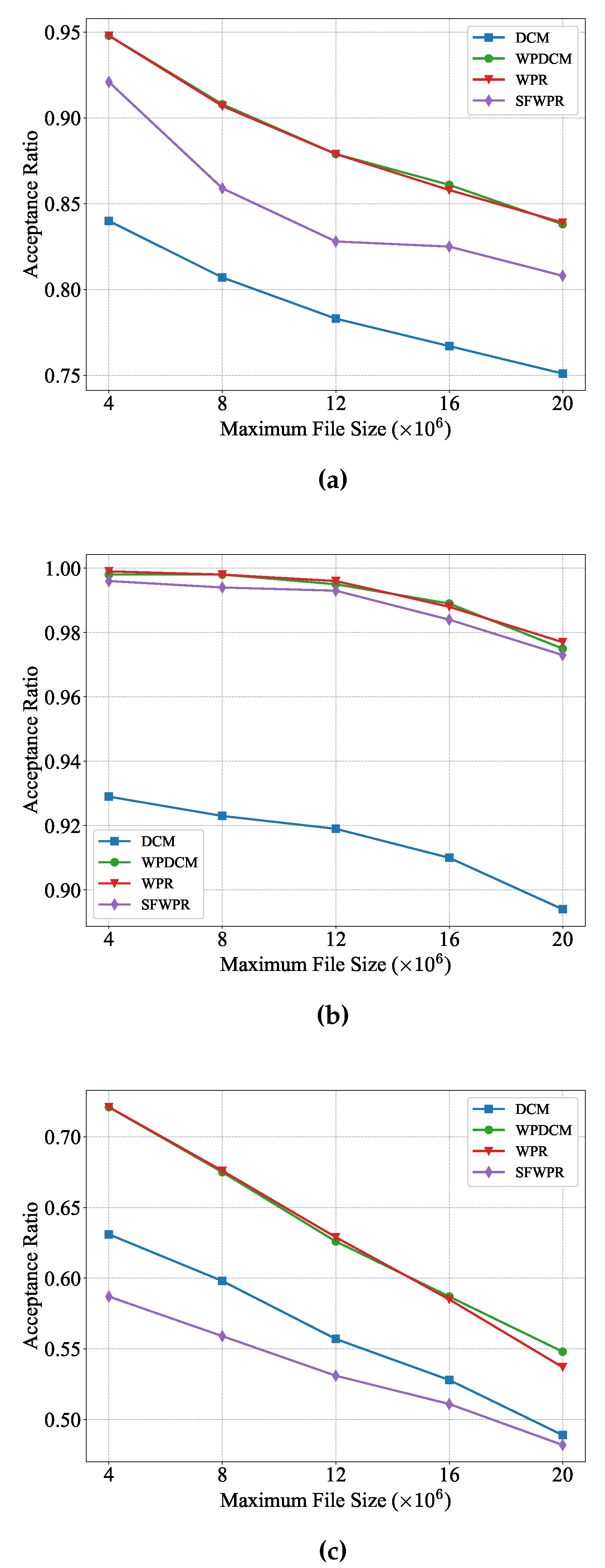
From Figure 4, several conclusions can be drawn. Firstly, it can be observed that all schemes achieved higher acceptance ratios when the input size of the majority of tasks had a small range, as depicted in Figure 4a,b. This is due to the fact that smaller service loads require fewer resources. Secondly, the proposed SFWPR scheme outperforms the DCM scheme in maximizing the acceptance ratio When more tasks carried smaller input sizes. As shown in Figure 4b, the acceptance ratio of SFWPR was higher than that of DCM and was very close to those of WPR and WPDCM. However, it should be noted that SFWPR might not be suitable for scenarios wherein tasks with large input sizes constitute the majority. Lastly, as the input size of tasks increased, the acceptance ratio decreased, due to the increased service load.
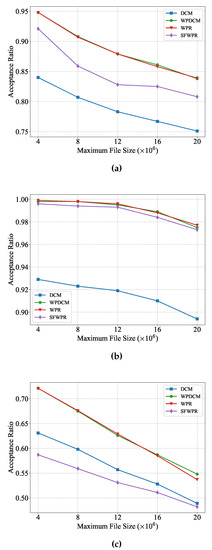
Figure 4.
Acceptance ratio versus maximum file size: (a) uniform distribution; (b) Zipf distribution prioritizing small input files; (c) Zipf distribution prioritizing large input files.
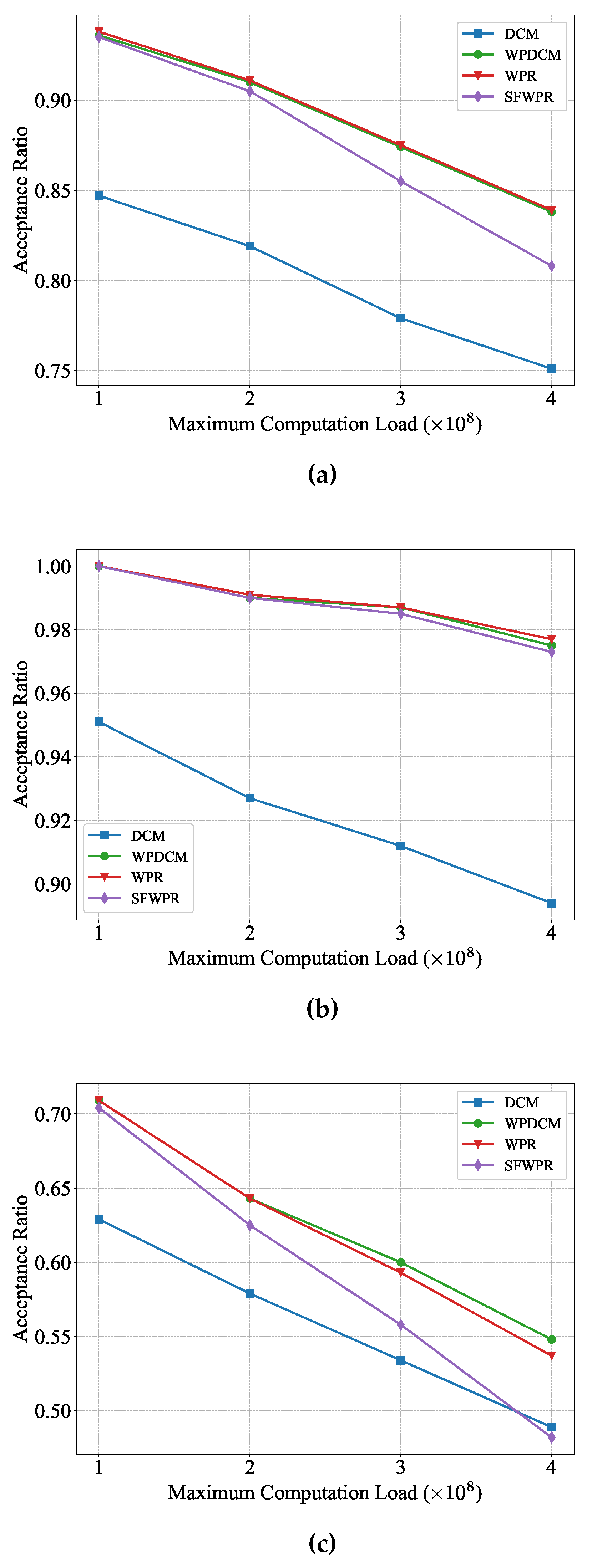
Figure 5 presents the performance of different schemes when the maximum computation load shifted from CPU cycles to CPU cycles. Similar to the observations obtained from Figure 4, it was observed that all schemes achieved higher acceptance ratios when the computation load of tasks varied in a small range. Due to the small range of computation loads, SFWPR outperforms DCM in the uniform distribution (Figure 5a) and the Zipf distribution prioritizing small input files (Figure 5b). However, as the maximum computation load increases, the performance of SFWPR degrades rapidly, and it becomes inferior to DCM in the Zipf distribution prioritizing large input files case (Figure 5c). This is because the minor difference in computation load meant the refilling policy for SFWPR and WPR were approximately the same. Moreover, the evident degradation shown in Figure 5c suggests that SFWPR was sensitive to computing load.
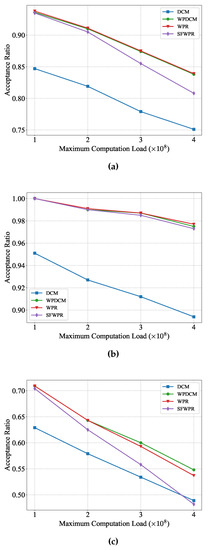
Figure 5.
Acceptance ratio versus maximum computation load: (a) uniform distribution; (b) Zipf distribution prioritizing small input files; (c) Zipf distribution prioritizing large input files.
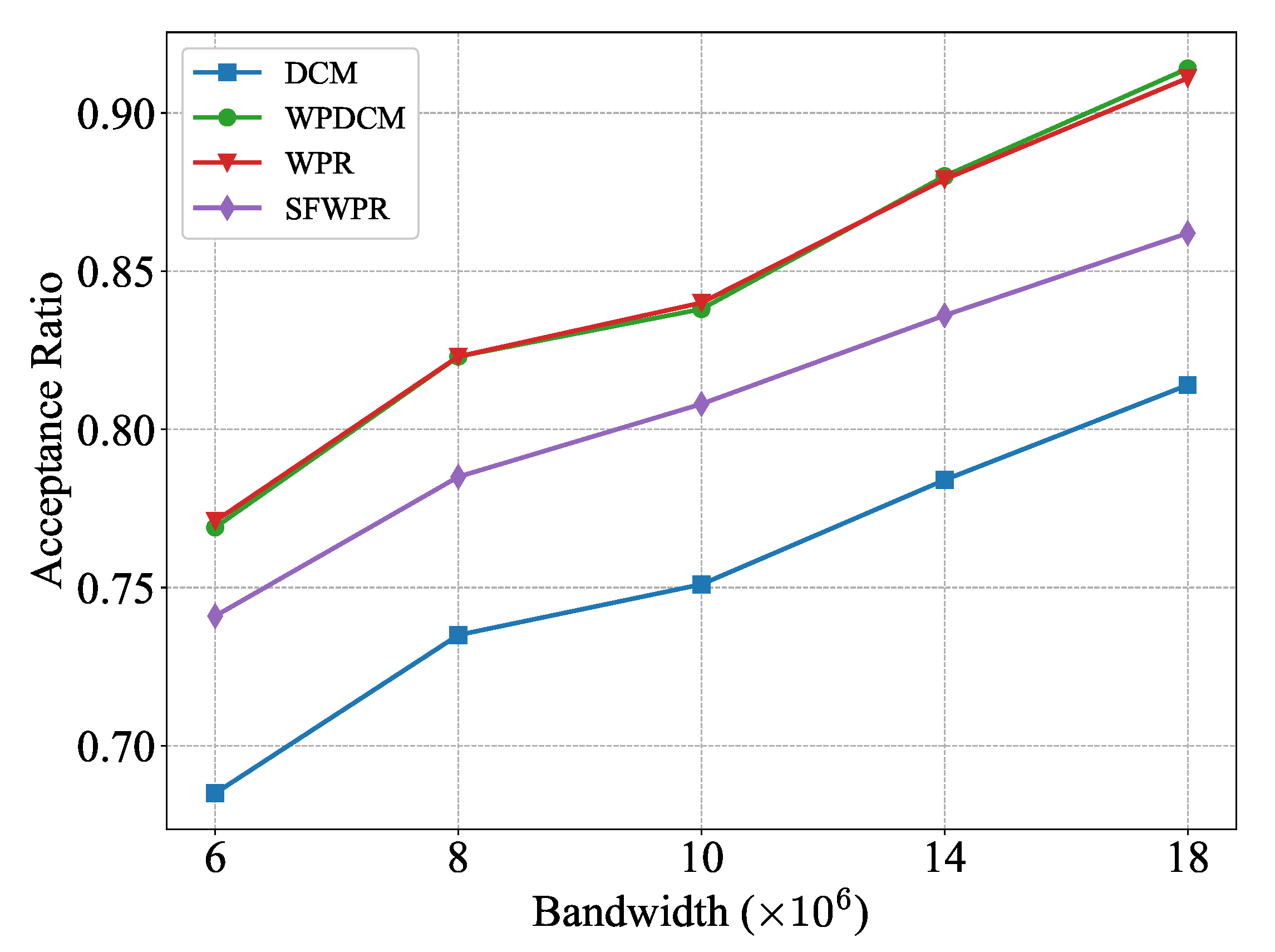
Figure 6 depicts the achieved acceptance ratio of various schemes while varying the system bandwidth from hertz to hertz. It was observed that a larger bandwidth led to a higher acceptance ratio for all schemes. The primary reason for this phenomenon is that the over-provisioned bandwidth reduced the pressure on computing resources. With shorter transmission delay, there is a more considerable margin of compensation for computational delay. As a result, SFWPR outperforms DCM due to the additional supplement of system bandwidth, as compared to the results presented in Figure 2.
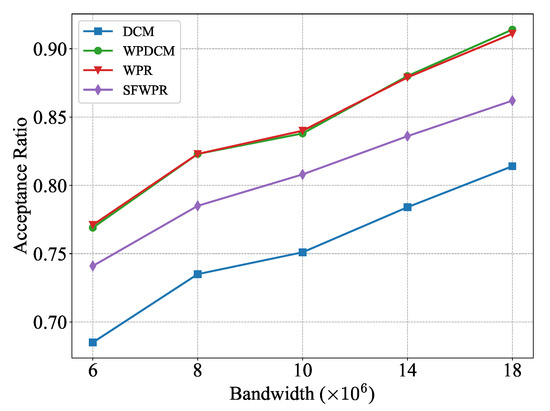
Figure 6.
Acceptance ratio versus system bandwidth.
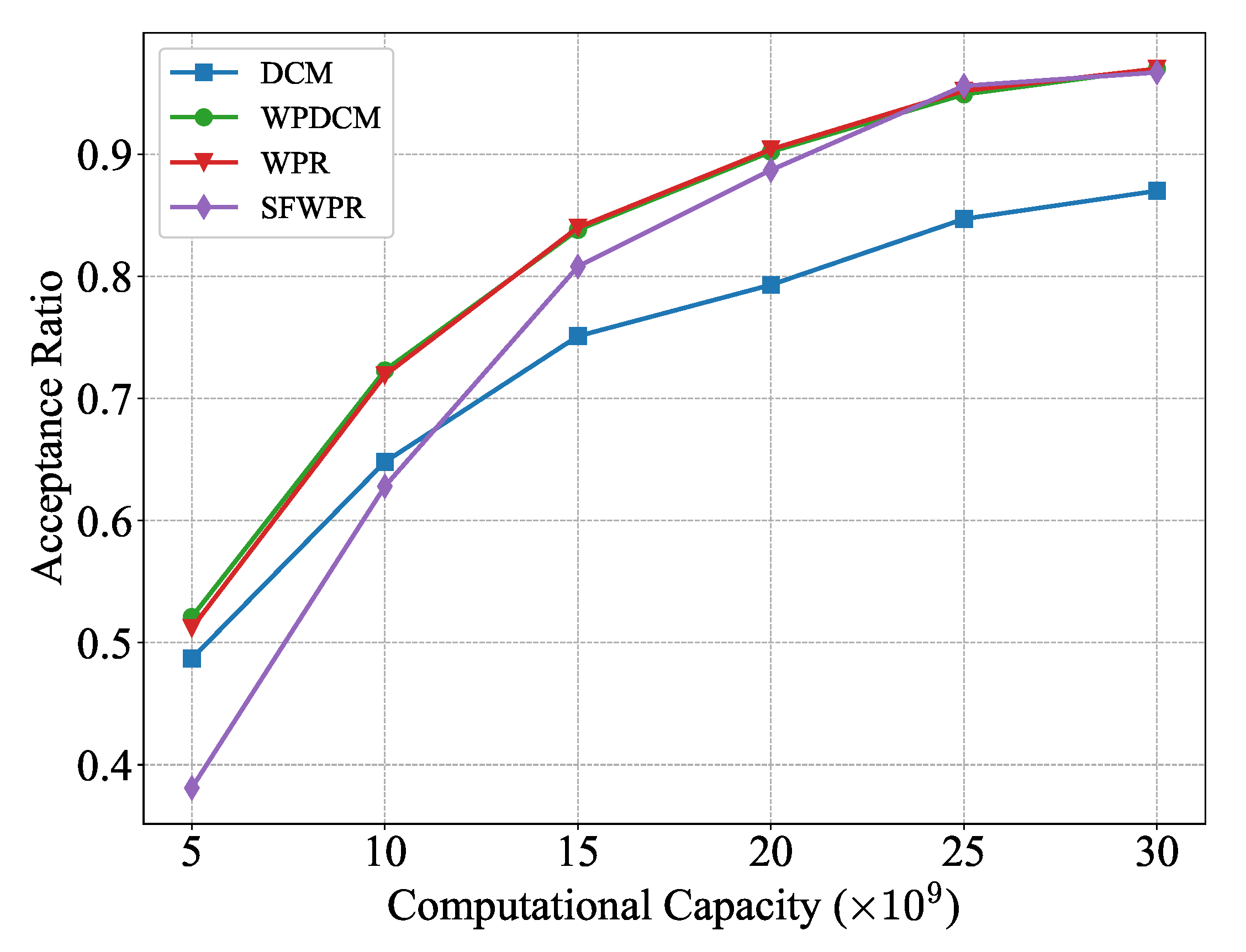
Figure 7 illustrates how the performance of the schemes mentioned above differed as the edge computational capacity increased from CPU cycles per second to CPU cycles per second. It can be concluded that the performance of SFWPR degraded rapidly as the computational capacity became smaller. This is attributed to its refilling policy , which inherently required more computing resources than the WPR scheme. Moreover, the performance gap between the WPR-based schemes (WPDCM, WPR) and DCM widened as the edge computational capacity increased, indicating the superior flexibility of WPR-based schemes in resource allocation.
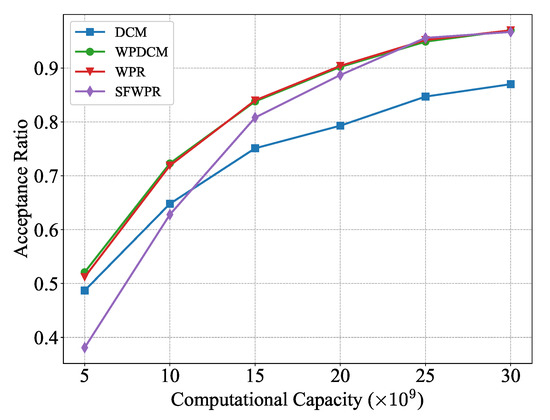
Figure 7.
Acceptance ratio versus edge computational capacity.
6. Conclusions
The current minimum latency scheme is inadequate in fully utilizing resources of the asymmetrical system to provide satisfactory computation offloading service for UDs with a maximum request acceptance ratio. In this paper, we propose a water pumping and refilling algorithm that exploits the margin between the delay-minimum scheme and the near-deadline scheme to achieve the maximal acceptance ratio. We first solve the resource allocation sub-problem of the delay-minimum scheme, which provided inspiration for the design of the water pumping and refilling algorithm. The water pumping algorithm can function not only as a supplementary algorithm to a given scheme, but also as a standalone algorithm to obtain the resource allocation scheme following a customizable refilling policy . The simulation results demonstrated that our proposed algorithm outperforms delay-minimum schemes in achieving a high acceptance ratio.
In the future, we plan to investigate computation offloading and resource allocation schemes under energy consumption constraints. Additionally, we will explore system models with collaborations between multiple base stations.
Author Contributions
Conceptualization, L.D. and Y.L.; methodology, L.D.; software, L.D.; validation, L.D. and W.H.; formal analysis, L.D.; investigation, L.D.; resources, Y.L.; data curation, L.D. and W.H.; writing—original draft preparation, L.D.; writing—review and editing, L.D. and W.H.; visualization, L.D.; supervision, Y.L.; project administration, Y.L.; funding acquisition, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Proof.
The resulting Karush–Kuhn–Tucker (KKT) conditions can be denoted as follows:
With some manipulation to Equations (A1) and (A2), we can obtain the bandwidth and computing resources allocation solution as follows:
With the contradiction technique adopted in Appendix B in [7], we have:
Substituting Equation (A10) and Equation (A11) into Equation (A12) and Equation (A13) respectively, the Lagrange multipliers can be derived as:
Finally, combining Equation (A10) with Equation (A14) and Equation (A11) with Equation (A15), the bandwidth and computing resources allocation scheme to Problem (P2.1) can be denoted as follows:
This ends the proof. □
Appendix B
Proof.
The sum of upload transmission time of UDs in can be written as follows
The first equality comes from Equation (A12) and the inequality comes from Cauchy–Buniakowsky–Schwarz inequality where the equality holds for all UDs in :
where c is a constant. With some manipulation, we have
where the first equality comes from Equation (A10) and the second equality comes from Equation (A16). Thus, to achieve the minimum of Equation (A17), we need to determine the values of to guarantee . An intuitive scheme is to assign with equal values (for example, 1).
Similarly, we can conclude that the sum of edge processing time achieves its minimum if:
where d is a constant. Thus, setting equal value to can obtain the minimum delay cost . Accordingly, the optimal Lagrange multipliers and resource allocation decisions can be denoted as
This ends the proof. □
References
- Dai, Y.; Xu, D.; Maharjan, S.; Zhang, Y. Joint computation offloading and user association in multi-task mobile edge computing. IEEE Trans. Veh. Technol. 2018, 67, 12313–12325. [Google Scholar] [CrossRef]
- Hu, Y.C.; Patel, M.; Sabella, D.; Sprecher, N.; Young, V. Mobile edge computing—A key technology towards 5G. ETSI White Pap. 2015, 11, 1–16. [Google Scholar]
- Lin, L.; Liao, X.; Jin, H.; Li, P. Computation Offloading Toward Edge Computing. Proc. IEEE 2019, 107, 1584–1607. [Google Scholar] [CrossRef]
- Khan, A.A.; Laghari, A.A.; Shaikh, Z.A.; Dacko-Pikiewicz, Z.; Kot, S. Internet of Things (IoT) security with blockchain technology: A state-of-the-art review. IEEE Access 2022, 10, 122679–122695. [Google Scholar] [CrossRef]
- Wang, Y.; Sheng, M.; Wang, X.; Wang, L.; Li, J. Mobile-edge computing: Partial computation offloading using dynamic voltage scaling. IEEE Trans. Commun. 2016, 64, 4268–4282. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, X.; Ning, Z.; Ngai, E.C.H.; Zhou, L.; Wei, J.; Cheng, J.; Hu, B. Energy-latency tradeoff for energy-aware offloading in mobile edge computing networks. IEEE Internet Things J. 2017, 5, 2633–2645. [Google Scholar] [CrossRef]
- Ren, J.; Yu, G.; He, Y.; Li, G.Y. Collaborative cloud and edge computing for latency minimization. IEEE Trans. Veh. Technol. 2019, 68, 5031–5044. [Google Scholar] [CrossRef]
- Mach, P.; Becvar, Z. Mobile edge computing: A survey on architecture and computation offloading. IEEE Commun. Surv. Tutor. 2017, 19, 1628–1656. [Google Scholar] [CrossRef]
- Shakarami, A.; Ghobaei-Arani, M.; Masdari, M.; Hosseinzadeh, M. A survey on the computation offloading approaches in mobile edge/cloud computing environment: A stochastic-based perspective. J. Grid Comput. 2020, 18, 639–671. [Google Scholar] [CrossRef]
- Yuan, H.; Bi, J.; Zhou, M. Geography-aware task scheduling for profit maximization in distributed green data centers. IEEE Trans. Cloud Comput. 2020, 10, 1864–1874. [Google Scholar] [CrossRef]
- Yuan, H.; Zhou, M. Profit-maximized collaborative computation offloading and resource allocation in distributed cloud and edge computing systems. IEEE Trans. Autom. Sci. Eng. 2020, 18, 1277–1287. [Google Scholar] [CrossRef]
- Wang, Y.; Tao, X.; Zhang, X.; Zhang, P.; Hou, Y.T. Cooperative task offloading in three-tier mobile computing networks: An ADMM framework. IEEE Trans. Veh. Technol. 2019, 68, 2763–2776. [Google Scholar] [CrossRef]
- Wei, Y.; Yu, F.R.; Song, M.; Han, Z. Joint optimization of caching, computing, and radio resources for fog-enabled IoT using natural actor–critic deep reinforcement learning. IEEE Internet Things J. 2018, 6, 2061–2073. [Google Scholar] [CrossRef]
- Khan, A.A.; Laghari, A.A.; Shafiq, M.; Awan, S.A.; Gu, Z. Vehicle to Everything (V2X) and Edge Computing: A Secure Lifecycle for UAV-Assisted Vehicle Network and Offloading with Blockchain. Drones 2022, 6, 377. [Google Scholar] [CrossRef]
- Mohajer, A.; Daliri, M.S.; Mirzaei, A.; Ziaeddini, A.; Nabipour, M.; Bavaghar, M. Heterogeneous computational resource allocation for NOMA: Toward green mobile edge-computing systems. IEEE Trans. Serv. Comput. 2022, 16, 1225–1238. [Google Scholar] [CrossRef]
- Zhang, W.; Wen, Y.; Guan, K.; Kilper, D. Energy-Optimal Mobile Cloud Computing under Stochastic Wireless Channel. IEEE Trans. Wirel. Commun. 2013, 12, 4569–4581. [Google Scholar] [CrossRef]
- Chen, J.; Xing, H.; Lin, X.; Nallanathan, A.; Bi, S. Joint Resource Allocation and Cache Placement for Location-Aware Multi-User Mobile-Edge Computing. IEEE Internet Things J. 2022, 9, 25698–25714. [Google Scholar] [CrossRef]
- Dai, Y.; Zhang, K.; Maharjan, S.; Zhang, Y. Edge intelligence for energy-efficient computation offloading and resource allocation in 5G beyond. IEEE Trans. Veh. Technol. 2020, 69, 12175–12186. [Google Scholar] [CrossRef]
- Huang, P.Q.; Wang, Y.; Wang, K.; Liu, Z.Z. A bilevel optimization approach for joint offloading decision and resource allocation in cooperative mobile edge computing. IEEE Trans. Cybern. 2019, 50, 4228–4241. [Google Scholar] [CrossRef]
- Zeng, S.; Huang, X.; Li, D. Joint Communication and Computation Cooperation in Wireless Powered Mobile Edge Computing Networks with NOMA. IEEE Internet Things J. 2023. [Google Scholar] [CrossRef]
- Karimi, E.; Chen, Y.; Akbari, B. Task offloading in vehicular edge computing networks via deep reinforcement learning. Comput. Commun. 2022, 189, 193–204. [Google Scholar] [CrossRef]
- Zhou, F.; Hu, R.Q. Computation efficiency maximization in wireless-powered mobile edge computing networks. IEEE Trans. Wirel. Commun. 2020, 19, 3170–3184. [Google Scholar] [CrossRef]
- Mukherjee, M.; Kumar, V.; Zhang, Q.; Mavromoustakis, C.X.; Matam, R. Optimal Pricing for Offloaded Hard-and Soft-Deadline Tasks in Edge Computing. IEEE Trans. Intell. Transp. Syst. 2021, 23, 9829–9839. [Google Scholar] [CrossRef]
- Yan, J.; Bi, S.; Duan, L.; Zhang, Y.J.A. Pricing-driven service caching and task offloading in mobile edge computing. IEEE Trans. Wirel. Commun. 2021, 20, 4495–4512. [Google Scholar] [CrossRef]
- Wang, Q.; Guo, S.; Liu, J.; Pan, C.; Yang, L. Profit maximization incentive mechanism for resource providers in mobile edge computing. IEEE Trans. Serv. Comput. 2019, 15, 138–149. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, X. Fairness-aware task offloading and resource allocation in cooperative mobile-edge computing. IEEE Internet Things J. 2021, 9, 3812–3824. [Google Scholar] [CrossRef]
- Hejja, K.; Berri, S.; Labiod, H. Network slicing with load-balancing for task offloading in vehicular edge computing. Veh. Commun. 2022, 34, 100419. [Google Scholar] [CrossRef]
- Meng, J.; Tan, H.; Li, X.Y.; Han, Z.; Li, B. Online deadline-aware task dispatching and scheduling in edge computing. IEEE Trans. Parallel Distrib. Syst. 2019, 31, 1270–1286. [Google Scholar] [CrossRef]
- Ren, J.; Yu, G.; Cai, Y.; He, Y. Latency optimization for resource allocation in mobile-edge computation offloading. IEEE Trans. Wirel. Commun. 2018, 17, 5506–5519. [Google Scholar] [CrossRef]
- Bi, S.; Huang, L.; Wang, H.; Zhang, Y.J.A. Lyapunov-guided deep reinforcement learning for stable online computation offloading in mobile-edge computing networks. IEEE Trans. Wirel. Commun. 2021, 20, 7519–7537. [Google Scholar] [CrossRef]
- Qiu, X.; Zhang, W.; Chen, W.; Zheng, Z. Distributed and collective deep reinforcement learning for computation offloading: A practical perspective. IEEE Trans. Parallel Distrib. Syst. 2020, 32, 1085–1101. [Google Scholar] [CrossRef]
- Zhou, H.; Jiang, K.; Liu, X.; Li, X.; Leung, V.C. Deep reinforcement learning for energy-efficient computation offloading in mobile-edge computing. IEEE Internet Things J. 2021, 9, 1517–1530. [Google Scholar] [CrossRef]
- Zhu, X.; Luo, Y.; Liu, A.; Bhuiyan, M.Z.A.; Zhang, S. Multiagent deep reinforcement learning for vehicular computation offloading in IoT. IEEE Internet Things J. 2020, 8, 9763–9773. [Google Scholar] [CrossRef]
- Ndikumana, A.; Tran, N.H.; Ho, T.M.; Han, Z.; Saad, W.; Niyato, D.; Hong, C.S. Joint communication, computation, caching, and control in big data multi-access edge computing. IEEE Trans. Mob. Comput. 2019, 19, 1359–1374. [Google Scholar] [CrossRef]
- Wen, W.; Cui, Y.; Quek, T.Q.; Zheng, F.C.; Jin, S. Joint optimal software caching, computation offloading and communications resource allocation for mobile edge computing. IEEE Trans. Veh. Technol. 2020, 69, 7879–7894. [Google Scholar] [CrossRef]
- Gong, Y.; Yao, H.; Wang, J.; Li, M.; Guo, S. Edge intelligence-driven joint offloading and resource allocation for future 6G industrial internet of things. IEEE Trans. Netw. Sci. Eng. 2022. [Google Scholar] [CrossRef]
- Liu, Y.; Tan, Z.; Hu, H.; Cimini, L.J.; Li, G.Y. Channel estimation for OFDM. IEEE Commun. Surv. Tutor. 2014, 16, 1891–1908. [Google Scholar] [CrossRef]
- Dong, L.; He, W.; Yao, H. Task Offloading and Resource Allocation for Tasks with Varied Requirements in Mobile Edge Computing Networks. Electronics 2023, 12, 366. [Google Scholar] [CrossRef]
- Bi, S.; Zhang, Y.J. Computation rate maximization for wireless powered mobile-edge computing with binary computation offloading. IEEE Trans. Wirel. Commun. 2018, 17, 4177–4190. [Google Scholar] [CrossRef]
- Xu, X.; Li, Y.; Huang, T.; Xue, Y.; Peng, K.; Qi, L.; Dou, W. An energy-aware computation offloading method for smart edge computing in wireless metropolitan area networks. J. Netw. Comput. Appl. 2019, 133, 75–85. [Google Scholar] [CrossRef]
- Fang, C.; Xu, H.; Yang, Y.; Hu, Z.; Tu, S.; Ota, K.; Yang, Z.; Dong, M.; Han, Z.; Yu, F.R.; et al. Deep-reinforcement-learning-based resource allocation for content distribution in fog radio access networks. IEEE Internet Things J. 2022, 9, 16874–16883. [Google Scholar] [CrossRef]
- Fang, C.; Liu, C.; Wang, Z.; Sun, Y.; Ni, W.; Li, P.; Guo, S. Cache-assisted content delivery in wireless networks: A new game theoretic model. IEEE Syst. J. 2020, 15, 2653–2664. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).