An Intelligent Approach to Determine Component Volume Percentages in a Symmetrical Homogeneous Three-Phase Fluid in Scaled Pipe Conditions
Abstract
:1. Introduction
- It shows how to enhance the accuracy of the detection system.
- It is possible to obtain volumetric fraction measurements while a three-phase flow is passing through an oil pipeline in a homogenous flow regime, even in the presence of a scale layer.
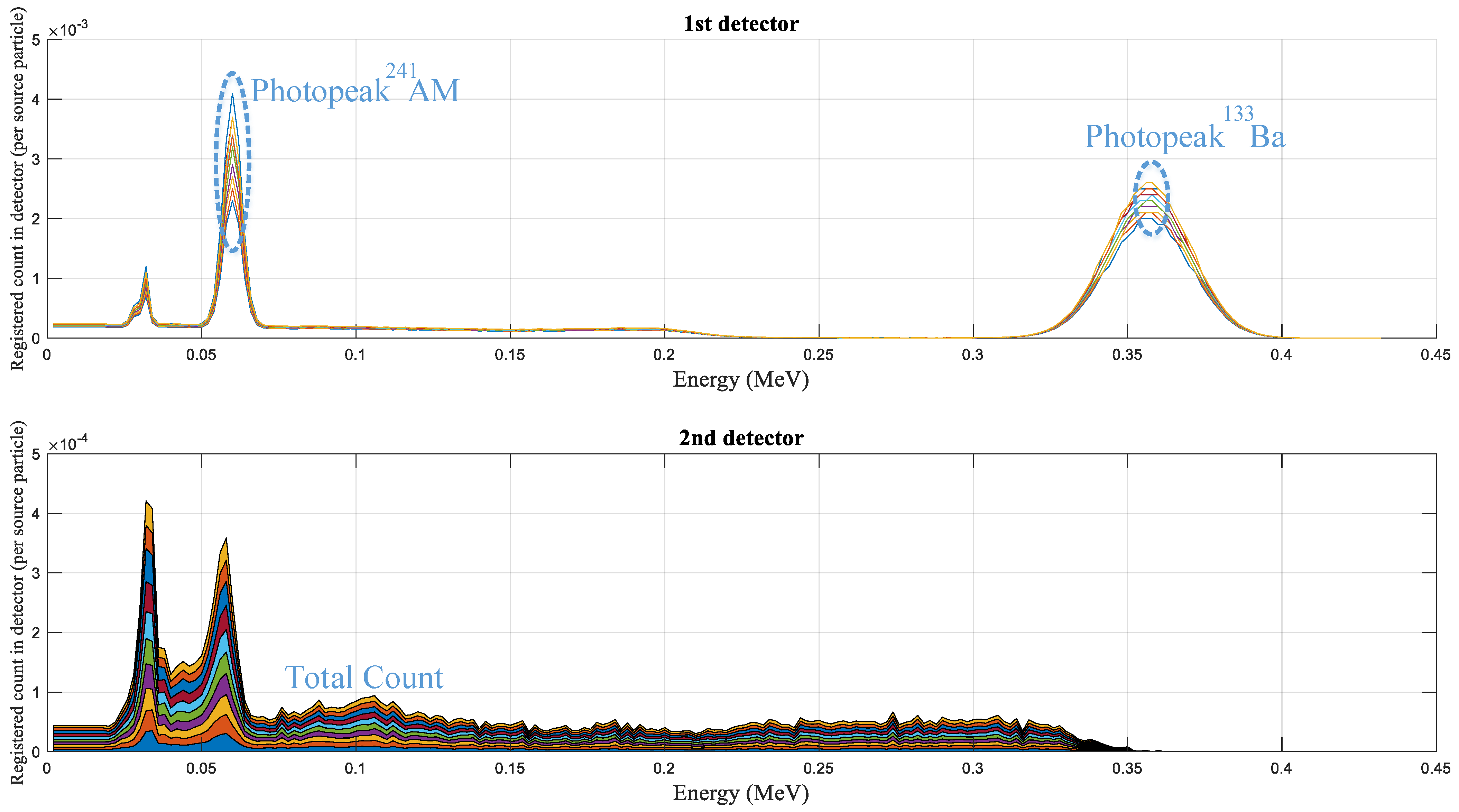
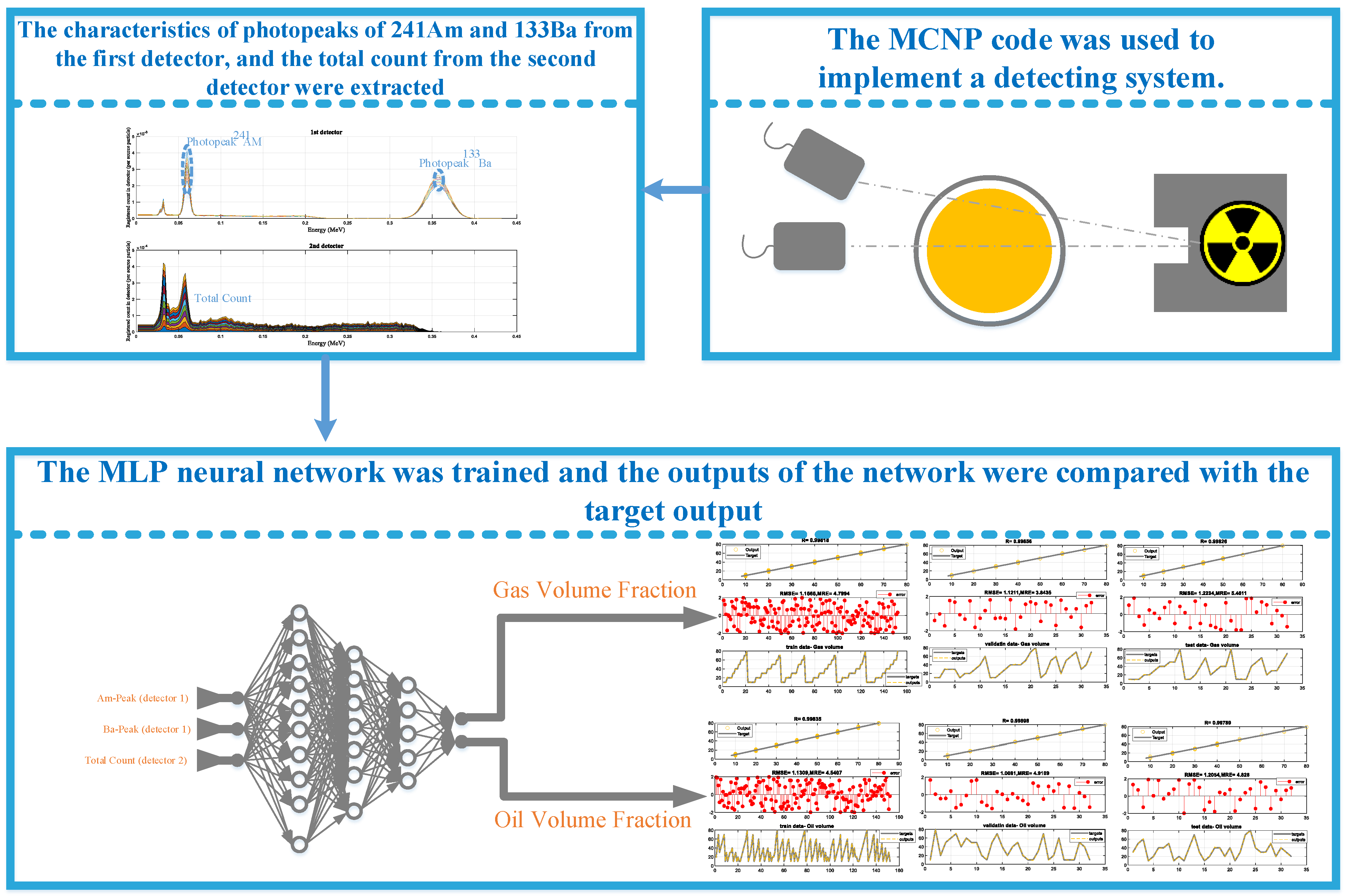
- This study aims to investigate the efficacy of utilising the photopeaks of 241Am and 133Ba in the first detector as well as the total count of the second detector for the purpose of determining volume percentages.
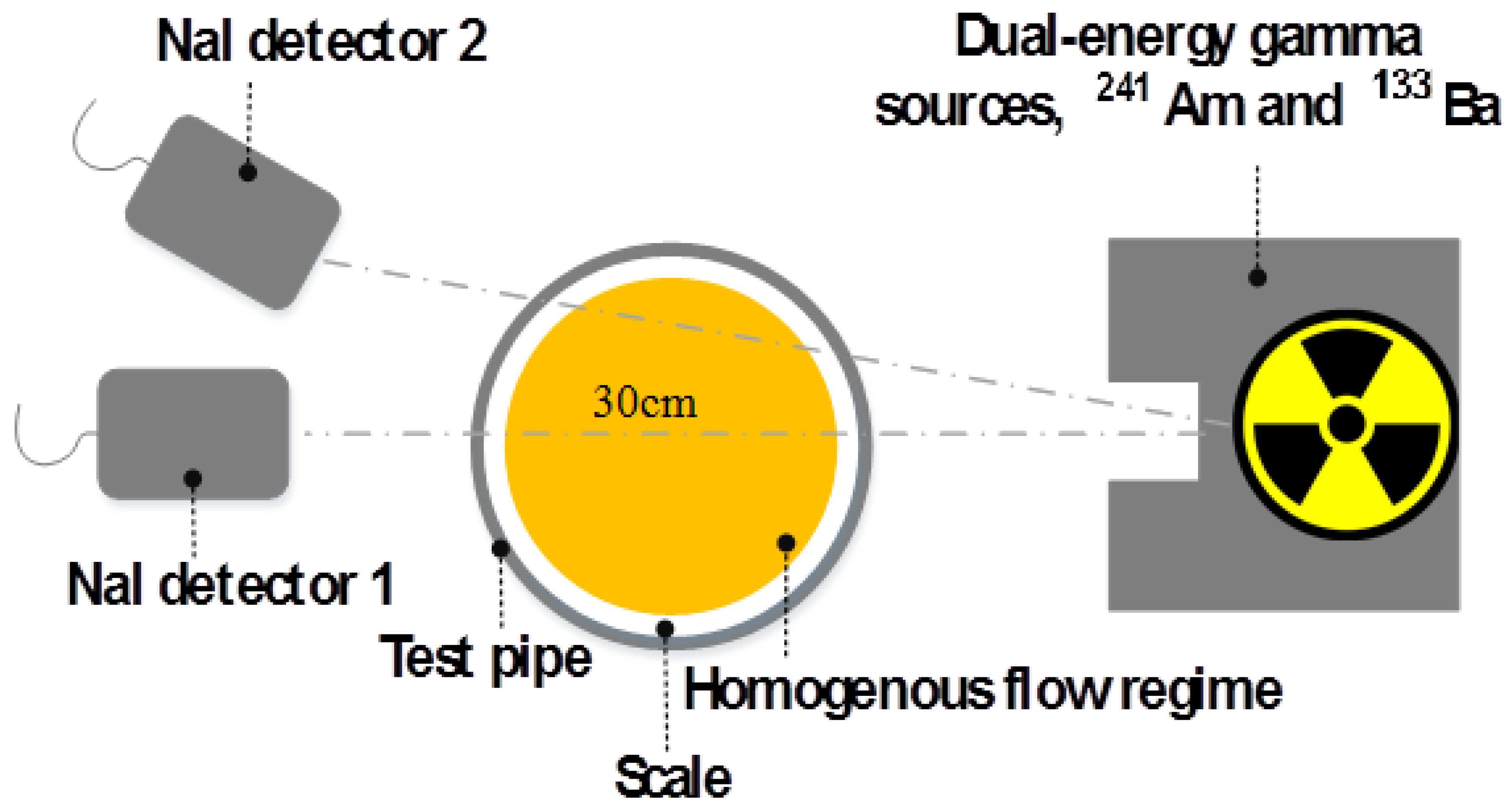
2. Simulation Setup
3. Multilayer Perceptron Neural Network
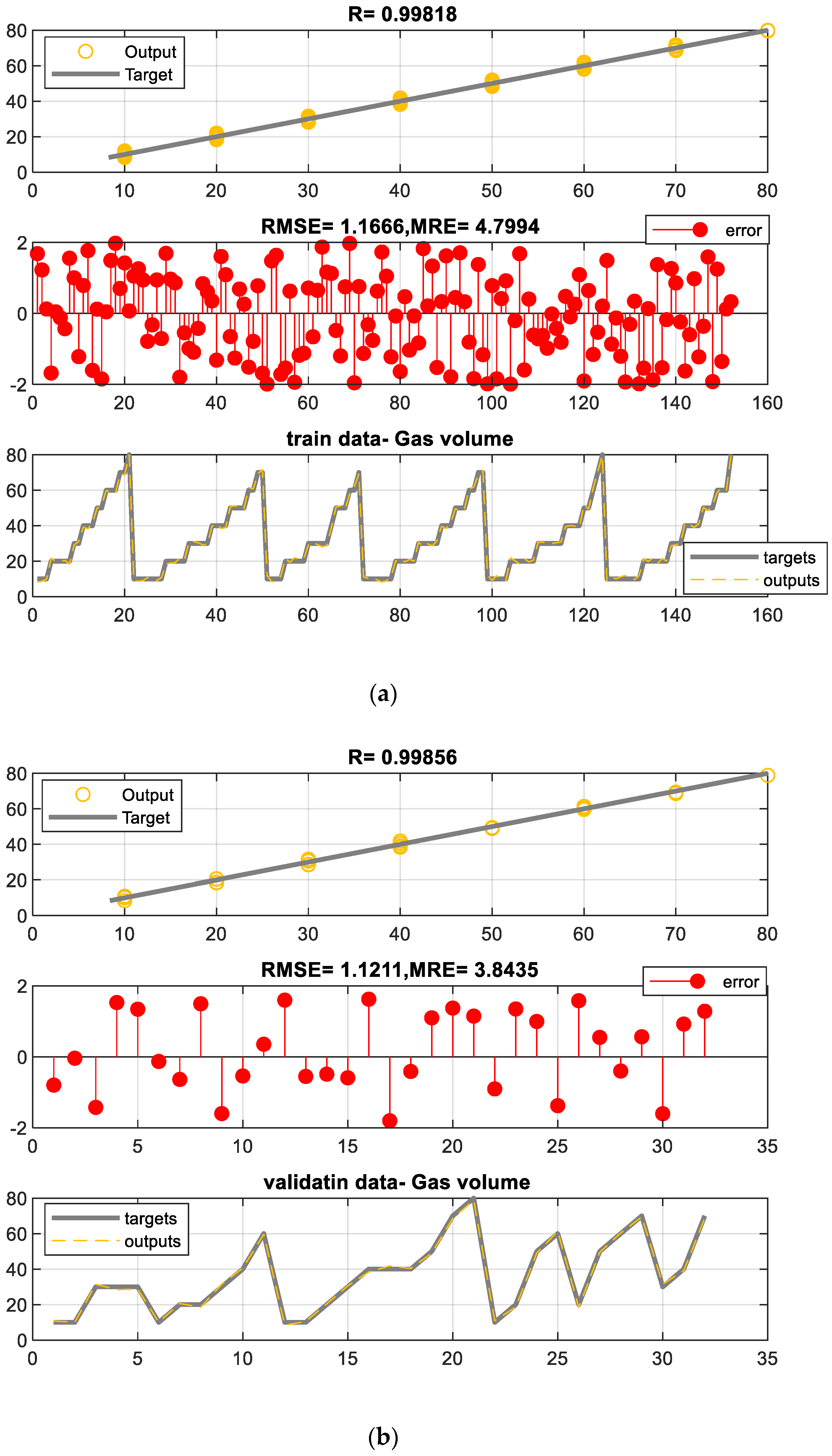
4. Results
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nazemi, E.; Roshani, G.H.; Feghhi, S.A.H.; Setayeshi, S.; Zadeh, E.E.; Fatehi, A. Optimization of a method for identifying the flow regime and measuring void fraction in a broad beam gamma-ray attenuation technique. Int. J. Hydrogen Energy 2016, 41, 7438–7444. [Google Scholar] [CrossRef]
- Roshani, M.; Phan, G.; Roshani, G.H.; Hanus, R.; Nazemi, B.; Corniani, E.; Nazemi, E. Combination of X-ray tube and GMDH neural network as a nondestructive and potential technique for measuring characteristics of gas-oil–water three phase flows. Measurement 2021, 168, 108427. [Google Scholar] [CrossRef]
- Roshani, G.H.; Nazemi, E.; Feghhi, S.A.H. Investigation of using 60Co source and one detector for determining the flow regime and void fraction in gas–liquid two-phase flows. Flow Meas. Instrum. 2016, 50, 73–79. [Google Scholar] [CrossRef]
- Roshani, G.H.; Karami, A.; Nazemi, E. An intelligent integrated approach of Jaya optimization algorithm and neuro-fuzzy network to model the stratified three-phase flow of gas–oil–water. Comput. Appl. Math. 2019, 38, 5. [Google Scholar] [CrossRef]
- Sattari, M.A.; Roshani, G.H.; Hanus, R.; Nazemi, E. Applicability of time-domain feature extraction methods and artificial intelligence in two-phase flow meters based on gamma-ray absorption technique. Measurement 2021, 168, 108474. [Google Scholar] [CrossRef]
- Sattari, M.A.; Roshani, G.H.; Hanus, R. Improving the structure of two-phase flow meter using feature extraction and GMDH neural network. Radiat. Phys. Chem. 2020, 171, 108725. [Google Scholar] [CrossRef]
- Alamoudi, M.; Sattari, M.A.; Balubaid, M.; Eftekhari-Zadeh, E.; Nazemi, E.; Taylan, O.; Kalmoun, E.M. Application of Gamma Attenuation Technique and Artificial Intelligence to Detect Scale Thickness in Pipelines in Which Two-Phase Flows with Different Flow Regimes and Void Fractions Exist. Symmetry 2021, 13, 1198. [Google Scholar] [CrossRef]
- Taylan, O.; Abusurrah, M.; Amiri, S.; Nazemi, E.; Eftekhari-Zadeh, E.; Roshani, G.H. Proposing an Intelligent Dual-Energy Radiation-Based System for Metering Scale Layer Thickness in Oil Pipelines Containing an Annular Regime of Three-Phase Flow. Mathematics 2021, 9, 2391. [Google Scholar] [CrossRef]
- Basahel, A.; Sattari, M.A.; Taylan, O.; Nazemi, E. Application of Feature Extraction and Artificial Intelligence Techniques for Increasing the Accuracy of X-ray Radiation Based Two Phase Flow Meter. Mathematics 2021, 9, 1227. [Google Scholar] [CrossRef]
- Taylan, O.; Sattari, M.A.; Elhachfi Essoussi, I.; Nazemi, E. Frequency Domain Feature Extraction Investigation to Increase the Accuracy of an Intelligent Nondestructive System for Volume Fraction and Regime Determination of Gas-Water-Oil Three-Phase Flows. Mathematics 2021, 9, 2091. [Google Scholar] [CrossRef]
- Roshani, G.H.; Ali, P.J.M.; Mohammed, S.; Hanus, R.; Abdulkareem, L.; Alanezi, A.A.; Kalmoun, E.M. Simulation Study of Utilizing X-ray Tube in Monitoring Systems of Liquid Petroleum Products. Processes 2021, 9, 828. [Google Scholar] [CrossRef]
- Balubaid, M.; Sattari, M.A.; Taylan, O.; Bakhsh, A.A.; Nazemi, E. Applications of Discrete Wavelet Transform for Feature Extraction to Increase the Accuracy of Monitoring Systems of Liquid Petroleum Products. Mathematics 2021, 9, 3215. [Google Scholar] [CrossRef]
- Hosseini, S.; Taylan, O.; Abusurrah, M.; Akilan, T.; Nazemi, E.; Eftekhari-Zadeh, E.; Roshani, G.H. Application of Wavelet Feature Extraction and Artificial Neural Networks for Improving the Performance of Gas–Liquid Two-Phase Flow Meters Used in Oil and Petrochemical Industries. Polymers 2021, 13, 3647. [Google Scholar] [CrossRef] [PubMed]
- Sattari, M.A.; Korani, N.; Hanus, R.; Roshani, G.H.; Nazemi, E. Improving the performance of gamma radiation based two phase flow meters using optimal time characteristics of the detector output signal extraction. J. Nucl. Sci. Technol. (JonSat) 2020, 41, 42–54. [Google Scholar]
- Iliyasu, A.M.; Mayet, A.M.; Hanus, R.; El-Latif, A.A.A.; Salama, A.S. Employing GMDH-Type Neural Network and Signal Frequency Feature Extraction Approaches for Detection of Scale Thickness inside Oil Pipelines. Energies 2022, 15, 4500. [Google Scholar] [CrossRef]
- Mayet, A.M.; Salama, A.S.; Alizadeh, S.M.; Nesic, S.; Guerrero, J.W.G.; Eftekhari-Zadeh, E.; Nazemi, E.; Iliyasu, A.M. Applying Data Mining and Artificial Intelligence Techniques for High Precision Measuring of the Two-Phase Flow’s Characteristics Independent of the Pipe’s Scale Layer. Electronics 2022, 11, 459. [Google Scholar] [CrossRef]
- Pelowitz, D.B. MCNP-X TM User’s Manual; Version 2.5.0; LA-CP-05e0369; Los Alamos National Laboratory: Los Alamos, NM, USA, 2005. [Google Scholar]
- Roshani, S.; Roshani, S. Design of a compact LPF and a miniaturized Wilkinson power divider using aperiodic stubs with harmonic suppression for wireless applications. Wirel. Netw. 2020, 26, 1493–1501. [Google Scholar] [CrossRef]
- Hookari, M.; Roshani, S.; Roshani, S. Design of a low pass filter using rhombus-shaped resonators with an analyticallc equivalent circuit. Turk. J. Electr. Eng. Comput. Sci. 2020, 28, 865–874. [Google Scholar] [CrossRef]
- Roshani, S.; Azizian, J.; Roshani, S.; Jamshidi, M.B.; Parandin, F. Design of a miniaturized branch line microstrip coupler with a simple structure using artificial neural network. Frequenz 2022, 76, 255–263. [Google Scholar] [CrossRef]
- Lalbakhsh, A.; Mohamadpour, G.; Roshani, S.; Ami, M.; Roshani, S.; Sayem, A.S.; Alibakhshikenari, M.; Koziel, S. Design of a Compact Planar Transmission Line for Miniaturized Rat-Race Coupler with Harmonics Suppression; IEEE Access: Piscataway, NJ, USA, 2021; Volume 9, pp. 129207–129217. [Google Scholar]
- Khaleghi, M.; Salimi, J.; Farhangi, V.; Moradi, M.J.; Karakouzian, M. Evaluating the behaviour of centrally perforated unreinforced masonry walls: Applications of numerical analysis, machine learning, and stochastic methods. Ain Shams Eng. J. 2022, 13, 101631. [Google Scholar] [CrossRef]
- Moradi, N.; Tavana, M.H.; Habibi, M.R.; Amiri, M.; Moradi, M.J.; Farhangi, V. Predicting the Compressive Strength of Concrete Containing Binary Supplementary Cementitious Material Using Machine Learning Approach. Materials 2022, 15, 5336. [Google Scholar] [CrossRef] [PubMed]
- Hanus, R.; Zych, M.; Golijanek-Jędrzejczyk, A. Measurements of Dispersed Phase Velocity in Two-Phase Flows in Pipelines Using Gamma-Absorption Technique and Phase of the Cross-Spectral Density Function. Energies 2022, 15, 9526. [Google Scholar] [CrossRef]
- Hanus, R.; Zych, M.; Golijanek-Jędrzejczyk, A. Investigation of liquid–gas flow in a horizontal pipeline using gamma-ray technique and modified cross-correlation. Energies 2022, 15, 5848. [Google Scholar] [CrossRef]
- Mayet, A.; Hussain, M. Amorphous WNx Metal For Accelerometers and Gyroscope. In Proceedings of the MRS Fall Meeting, Boston, MA, USA, 30 November–5 December 2014. [Google Scholar]
- Mayet, A.; Hussain, A.; Hussain, M. Three-terminal nanoelectromechanical switch based on tungsten nitride—An amorphous metallic material. Nanotechnology 2016, 27, 035202. [Google Scholar] [CrossRef]
- Roshani, G.H.; Hanus, R.; Khazaei, A.; Zych, M.; Nazemi, E.; Mosorov, V. Density and velocity determination for single-phase flow based on radiotracer technique and neural networks. Flow Meas. Instrum. 2018, 61, 9–14. [Google Scholar] [CrossRef]
- Roshani, G.H.; Nazemi, E.; Roshani, M.M. Intelligent recognition of gas-oil-water three-phase flow regime and determination of volume fraction using radial basis function. Flow Meas. Instrum. 2017, 54, 39–45. [Google Scholar] [CrossRef]
- Roshani, G.H.; Roshani, S.; Nazemi, E.; Roshani, S. Online measuring density of oil products in annular regime of gas-liquid two phase flows. Measurement 2018, 129, 296–301. [Google Scholar] [CrossRef]
- Nazemi, E.; Feghhi, S.A.H.; Roshani, G.H.; Peyvandi, R.G.; Setayeshi, S. Precise void fraction measurement in two-phase flows independent of the flow regime using gamma-ray attenuation. Nucl. Eng. Technol. 2016, 48, 64–71. [Google Scholar] [CrossRef]
- Roshani, M.; Sattari, M.A.; Ali, P.J.M.; Roshani, G.H.; Nazemi, B.; Corniani, E.; Nazemi, E. Application of GMDH neural network technique to improve measuring precision of a simplified photon attenuation based two-phase flowmeter. Flow Meas. Instrum. 2020, 75, 101804. [Google Scholar] [CrossRef]
- Ahmad, M.; Alfayad, M.; Aftab, S.; Khan, M.; Fatima, A.; Shoaib, B.; Daoud, M.; Sabri, N. Data and Machine Learning Fusion Architecture for Cardiovascular Disease Prediction. Comput. Mater. Contin. 2021, 69, 2717–2731. [Google Scholar] [CrossRef]
- Daoud, M.; Aftab, S.; Ahmad, M.; Khan, M.; Iqbal, A.; Abbas, S.; Iqbal, M.; Ihnaini, B. Machine Learning Empowered Software Defect Prediction System. Intell. Autom. Soft Comput. 2021, 31, 1287–1300. [Google Scholar] [CrossRef]
- Daoud, M.S.; Ayesh, A.; Al-Fayoumi, M.; Hopgood, A.A. Location Prediction Based on a Sector Snapshot for Location-Based Services. J. Netw. Syst. Manag. 2014, 22, 23–49. [Google Scholar] [CrossRef]
- Shehab, M.; Abualigah, L.; Jarrah, M.I.; Alomari, O.A.; Daoud, M.S. (AIAM2019) Artificial Intelligence in Software Engineering and inverse: Review. Int. J. Comput. Integr. Manuf. 2020, 33, 1129–1144. [Google Scholar] [CrossRef]
- Golijanek-Jędrzejczyk, A.; Mrowiec, A.; Kleszcz, S.; Hanus, R.; Zych, M.; Jaszczur, M. A numerical and experimental analysis of multi-hole orifice in turbulent flow. Measurement 2022, 193, 110910. [Google Scholar] [CrossRef]
- Abidi, W.U.; Daoud, M.S.; Ihnaini, B.; Khan, M.A.; Alyas, T.; Fatima, A.; Ahmad, M. Real-Time Shill Bidding Fraud Detection Empowered With Fussed Machine Learning. IEEE Access 2021, 9, 113612–113621. [Google Scholar] [CrossRef]
- Jedkare, E.; Shama, F.; Sattari, M.A. Compact Wilkinson power divider with multi-harmonics suppression. AEU-Int. J. Electron. Commun. 2020, 127, 153436. [Google Scholar] [CrossRef]
- Taylor, J.G. Neural Networks and Their Applications; John Wiley & Sons Ltd.: Brighton, UK, 1996. [Google Scholar]
- Gallant, A.R.; White, H. On learning the derivatives of an unknown mapping with multilayer feedforward networks. Neural Netw. 1992, 5, e129–e138. [Google Scholar] [CrossRef]
- Roshani, M.; Ali, P.J.; Roshani, G.H.; Nazemi, B.; Corniani, E.; Phan, N.H.; Tran, H.N.; Nazemi, E. X-ray tube with artificial neural network model as a promising alternative for radioisotope source in radiation based two phase flowmeters. Appl. Radiat. Isot. 2020, 164, 109255. [Google Scholar] [CrossRef] [PubMed]
- Peyvandi, R.G.; Rad, S.I. Application of artificial neural networks for the prediction of volume fraction using spectra of gamma rays backscattered by three-phase flows. Eur. Phys. J. Plus 2017, 132, 511. [Google Scholar] [CrossRef]
- Roshani Gholam, H.; Nazemi Ehsan Shama Farzin, A.; Mohammad, I.; Salar, M. Designing a simple ra-diometric system to predict void fraction percentage independent of flow pattern using radial basis function. Metrol. Meas. Syst. 2018, 25, 347–358. [Google Scholar]
- Mayet, A.M.; Chen, T.C.; Alizadeh, S.M.; Al-Qahtani, A.A.; Qaisi, R.M.A.; Alhashim, H.H.; Eftekhari-Zadeh, E. Application of Artificial Intelligence for Determining the Volume Percentages of a Stratified Regime’s Three-Phase Flow, Independent of the Oil Pipeline’s Scale Thickness. Processes 2022, 10, 1996. [Google Scholar] [CrossRef]
- Mayet, A.M.; Chen, T.C.; Ahmad, I.; Tag Eldin, E.; Al-Qahtani, A.A.; Narozhnyy, I.M.; Alhashim, H.H. Application of neural network and dual-energy radiation-based detection techniques to measure scale layer thickness in oil pipelines containing a stratified regime of three-phase flow. Mathematics 2022, 10, 3544. [Google Scholar] [CrossRef]
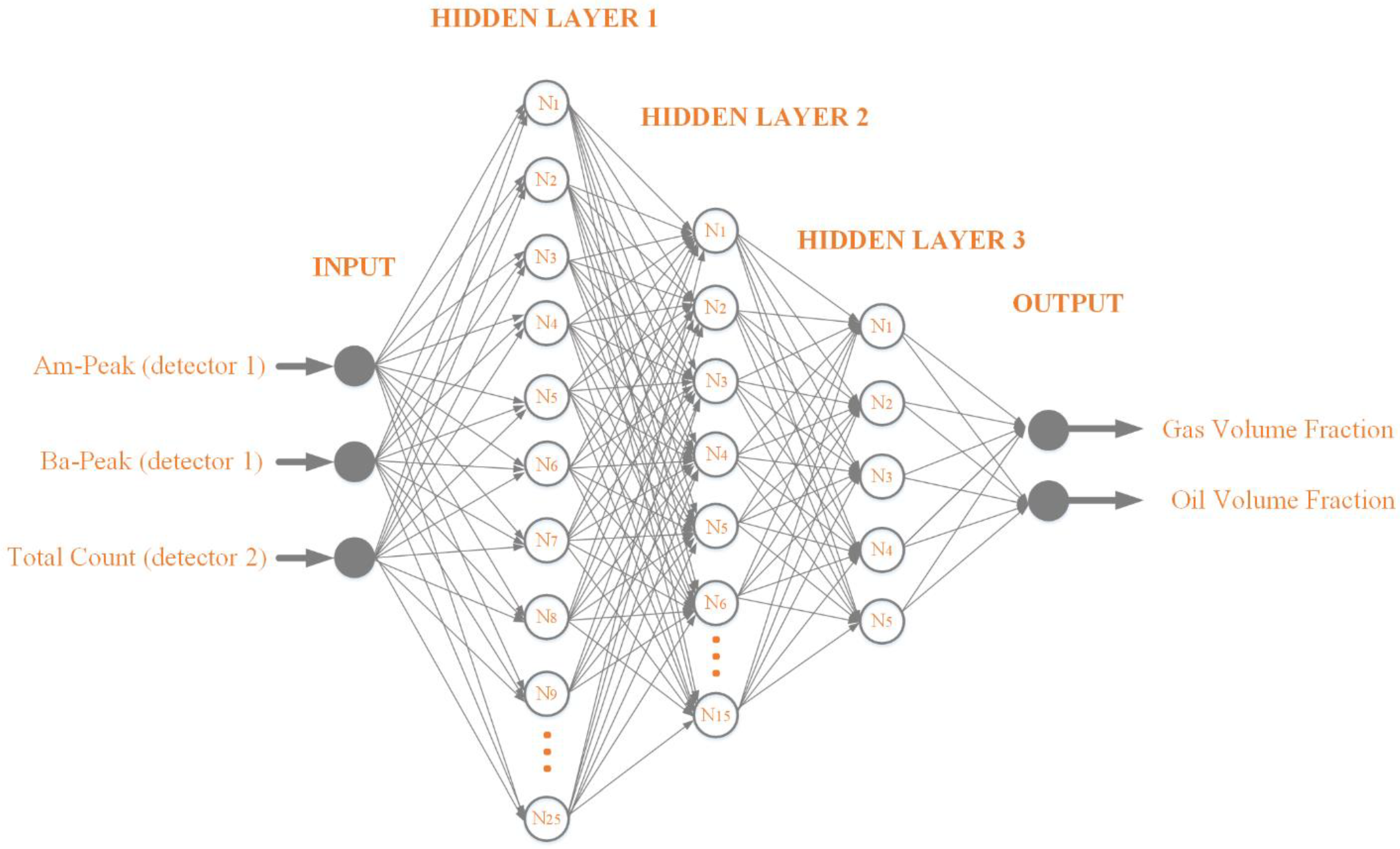
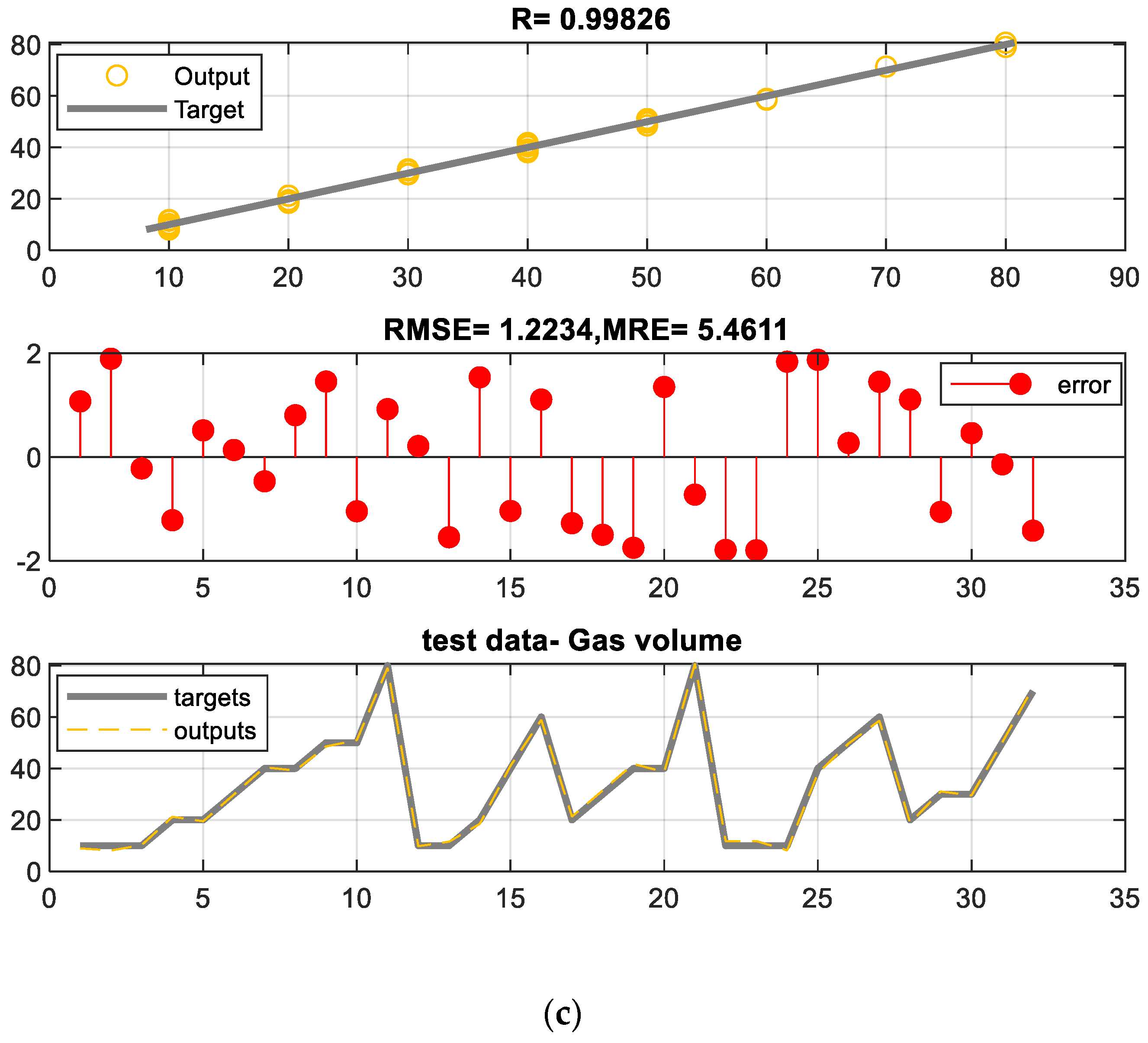
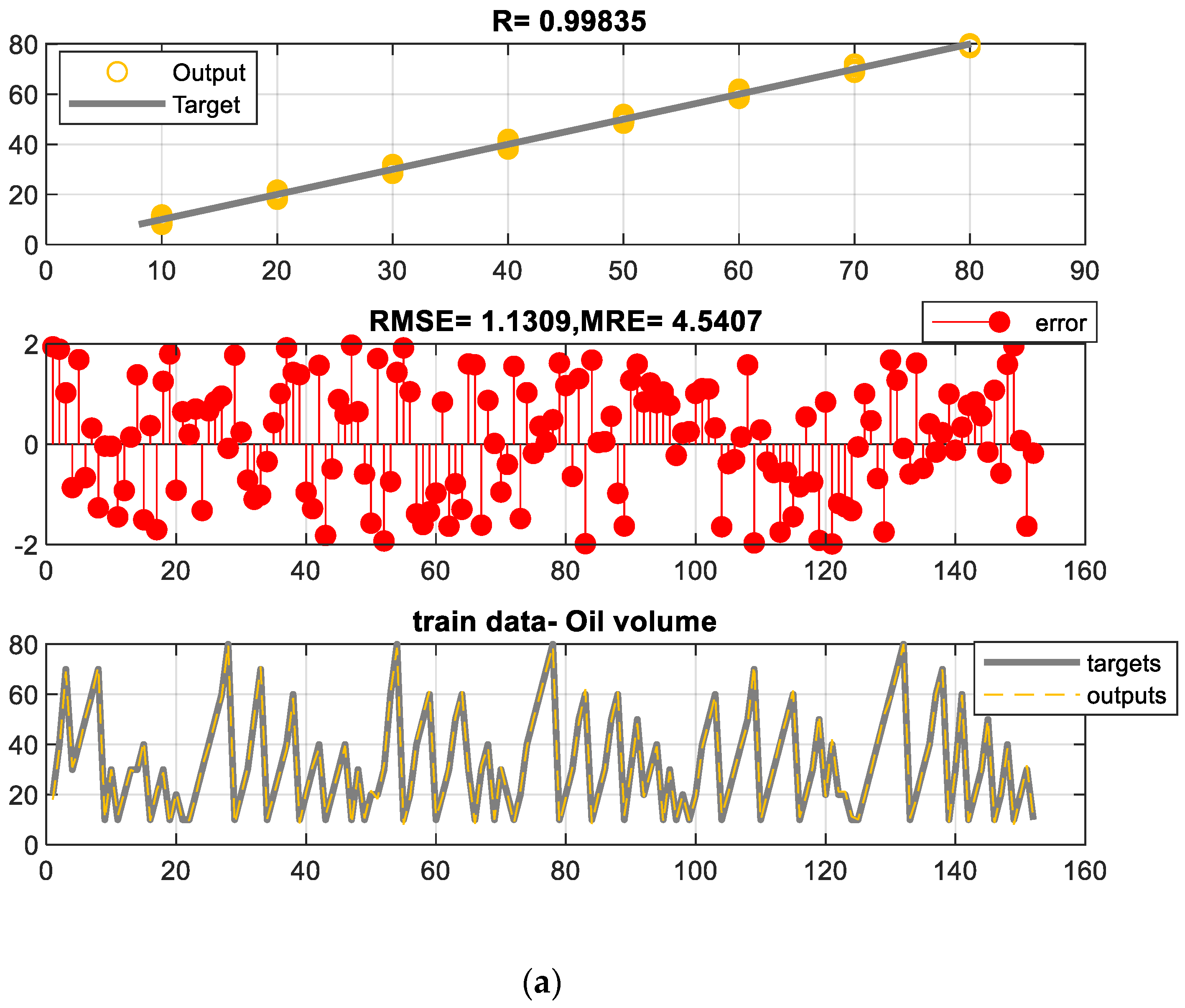
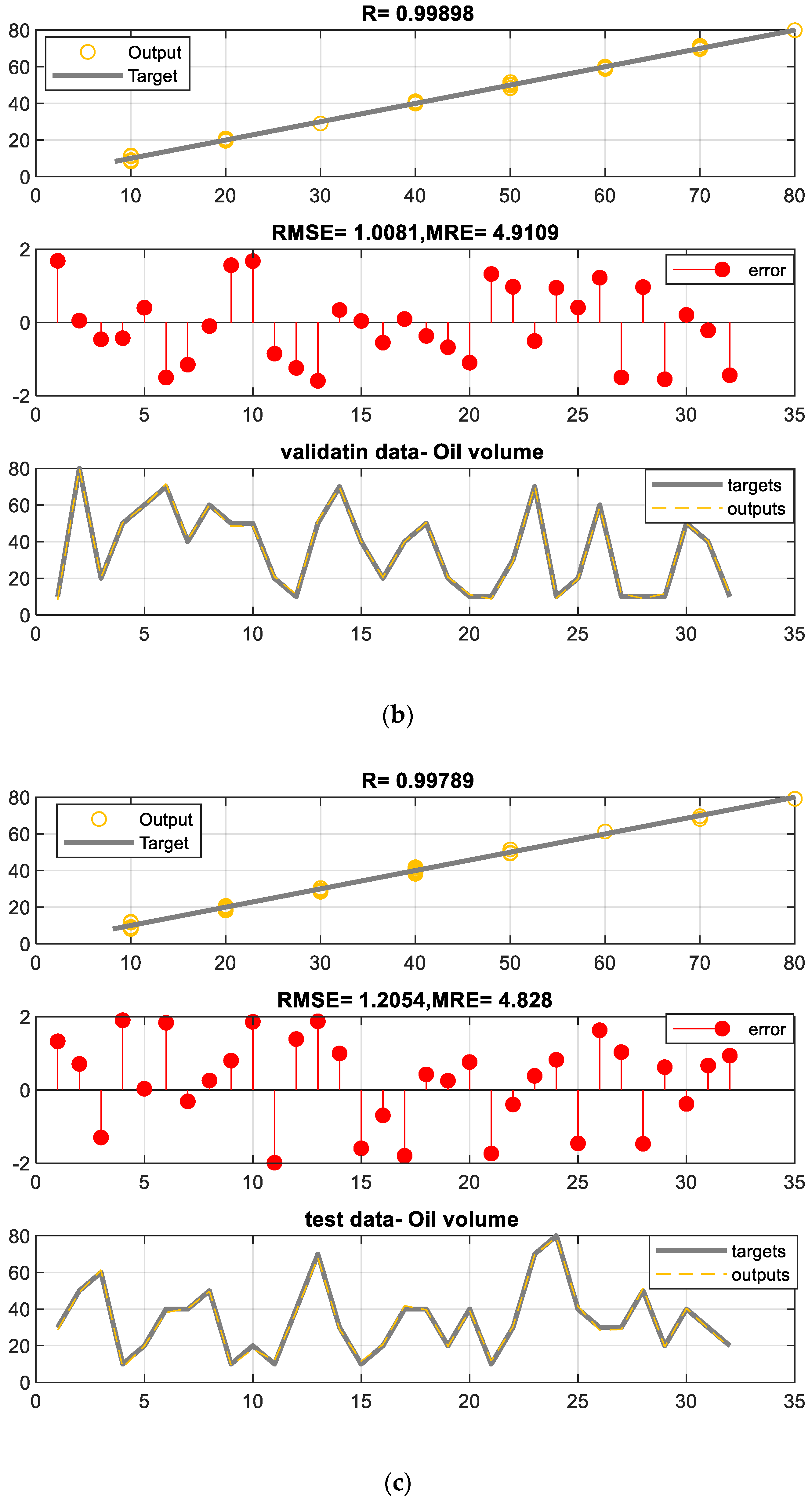
| ANN | MLP | |||||
|---|---|---|---|---|---|---|
| Input layer neurons | 3 | |||||
| Neurons in the 1st hidden layer | 20 | |||||
| Neurons in the 2nd hidden layer | 15 | |||||
| Neurons in the 3rd hidden layer | 5 | |||||
| Neurons in the output layer | 2 | |||||
| Epochs | 480 | |||||
| Activation function | Tansig | |||||
| Output | Gas | Oil | ||||
| RMSE | Train | Validation | Test | Train | Validation | Test |
| 1.16 | 1.12 | 1.22 | 1.13 | 1.00 | 1.20 | |
| MRE% | 4.79 | 3.84 | 5.46 | 4.54 | 4.91 | 4.82 |
| Ref | Type of Neural Network | Extracted Features | Maximum RMSE | Maximum MSE |
|---|---|---|---|---|
| [1] | RBF | No feature extraction | 1.29 | 1.66 |
| [32] | GMDH | No feature extraction | 2.71 | 7.34 |
| [43] | MLP | No feature extraction | 4.13 | 17.05 |
| [44] | MLP | No feature extraction | 1.6 | 2.56 |
| [45] | RBF | Compton continuum and counts under full energy peaks of 1173 and 1333 keV | 6.12 | 37.45 |
| [46] | MLP | No feature extraction | 2.12 | 4.49 |
| [current study] | MLP | Photopeaks of 241Am and 133Ba in the first and total count of second detectors | 1.22 | 1.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mayet, A.M.; Alizadeh, S.M.; Ijyas, V.P.T.; Grimaldo Guerrero, J.W.; Shukla, N.K.; Bhutto, J.K.; Eftekhari-Zadeh, E.; Aiesh Qaisi, R.M. An Intelligent Approach to Determine Component Volume Percentages in a Symmetrical Homogeneous Three-Phase Fluid in Scaled Pipe Conditions. Symmetry 2023, 15, 1131. https://doi.org/10.3390/sym15061131
Mayet AM, Alizadeh SM, Ijyas VPT, Grimaldo Guerrero JW, Shukla NK, Bhutto JK, Eftekhari-Zadeh E, Aiesh Qaisi RM. An Intelligent Approach to Determine Component Volume Percentages in a Symmetrical Homogeneous Three-Phase Fluid in Scaled Pipe Conditions. Symmetry. 2023; 15(6):1131. https://doi.org/10.3390/sym15061131
Chicago/Turabian StyleMayet, Abdulilah Mohammad, Seyed Mehdi Alizadeh, V. P. Thafasal Ijyas, John William Grimaldo Guerrero, Neeraj Kumar Shukla, Javed Khan Bhutto, Ehsan Eftekhari-Zadeh, and Ramy Mohammed Aiesh Qaisi. 2023. "An Intelligent Approach to Determine Component Volume Percentages in a Symmetrical Homogeneous Three-Phase Fluid in Scaled Pipe Conditions" Symmetry 15, no. 6: 1131. https://doi.org/10.3390/sym15061131
APA StyleMayet, A. M., Alizadeh, S. M., Ijyas, V. P. T., Grimaldo Guerrero, J. W., Shukla, N. K., Bhutto, J. K., Eftekhari-Zadeh, E., & Aiesh Qaisi, R. M. (2023). An Intelligent Approach to Determine Component Volume Percentages in a Symmetrical Homogeneous Three-Phase Fluid in Scaled Pipe Conditions. Symmetry, 15(6), 1131. https://doi.org/10.3390/sym15061131












