On Disks Enclosed by Smooth Jordan Curves

Abstract

Given a smooth-plane Jordan curve with bounded absolute curvature $\kappa >0$, we determine equivalence classes of distinctive disks of radius $1/\kappa$ included in both plane regions separated by the curve. The bound on absolute curvature leads to a completely symmetric trajectory behaviour with respect to the curve turning. These lead to a decomposition of the plane into a finite number of maximal regions with respect to set inclusion leading to natural lower bounds for the length an area enclosed by the curve. We present a “half version” of the Pestov–Ionin theorem, and subsequently a generalisation of the classical Blaschke rolling disk theorem. An interesting consequence is that we describe geometric conditions relying exclusively on curvature and independent of any kind of convexity that allows us to give necessary and sufficient conditions for the existence of families of rolling disks for planar domains that are not necessarily convex. We expect this approach would lead to further generalisations as, for example, characterising volumetric objects in closed surfaces as first studied by Lagunov. Although this is a classical problem in differential geometry, recent developments in industrial manufacturing when cutting along some prescribed shapes on prescribed materials have revived the necessity of a deeper understanding on disks enclosed by sufficiently smooth Jordan curves.

1. Introduction

In this article, we prove the existence of distinguished disks enclosed by smooth plane Jordan curves satisfying a bound on the absolute curvature $\kappa >0$. Note that the boundary of a disk corresponds to the epitome of symmetric behaviour since a circle has full rotational symmetry. In consequence, a bound on absolute curvature leads to a completely symmetric trajectory behaviour with respect to the curve turning. These distinguished disks have a radius and quantity proportional to the curvature bound given by $1/\kappa$. The best result known in this direction is the classical inclusion theorem by Pestov and Ionin in the Ref. [1] which was proven in 1959 establishing the existence of a single radius $1/\kappa$ disk in the interior region separated by the curve.

The Blaschke rolling disk theorem is an inclusion principle first proven in 1916 by Blaschke [2]. It states that a convex domain $\mathcal{K}\subset {\mathbb{R}}^2$ whose boundary $\partial \mathcal{K}$ is a curve of class $C^2$ with curvature not exceeding a constant $\kappa >0$ is such that for each point in $\partial \mathcal{K}$ there exists a disk of radius $1/\kappa$ tangent to $\partial \mathcal{K}$ included in the closure of $\mathcal{K}$.

The convexity of $\mathcal{K}$ implies that the curvature of $\partial \mathcal{K}$ is signed. That is, the curvature of $\partial \mathcal{K}$ may be nonnegative or nonpositive, but not both. After dropping the convexity of $\mathcal{K}$, the curvature of $\partial \mathcal{K}$ may change in sign. Accordingly, we assume that the absolute curvature of $\partial \mathcal{K}$ does not exceed $\kappa >0$. Note the Blaschke rolling disk theorem is a local to global result, since a local property as the bound on absolute curvature on $\partial \mathcal{K}$ allows us to conclude a global property of $\mathcal{K}$ as the existence of a radius $1/\kappa$ disk tangent at each point at $\partial \mathcal{K}$ included in the closure of $\mathcal{K}$.

By describing geometric conditions derived from the curvature of $\partial \mathcal{K}$, we find necessary and sufficient conditions for the existence of rolling disks for general domains $\mathcal{K}\subset {\mathbb{R}}^2$. Definition 2 is the key feature to identify the existence of arcs in $\partial \mathcal{K}$ whose end points, called essential and inessential terminals, guarantee the existence of several geometric objects. In particular, the existence of parallel tangents is key to characterising convexity for plane curves.

The Blaschke rolling disk theorem has been extensively studied by researchers of several mathematical communities with different levels of generalisations. We would like to first highlight the monograph by Brooks and Strantzen in which they provide several approaches and setups for the rolling problem [3]. Koutroufiotis generalised the Blaschke rolling theorem for complete curves in ${\mathbb{R}}^2$ and for complete surfaces in ${\mathbb{R}}^3$ [4]. Rauch proved the Blaschke rolling theorem for compact surfaces in ${\mathbb{R}}^n$ [5]. Additionally, Delgado proved a similar result for complete surfaces [6]. For an approach to the rolling problem without assuming smoothness of the boundary, refer to the Refs. [7,8,9]. Karakhanyan studied the problem from the optimal transport theory point of view [10]. A modern insight into the problem is presented by Révész, in which he proposed a discrete version of the problem [11].

Recent developments in industrial manufacturing when cutting along some prescribed shapes on prescribed materials have revived the necessity of a deeper understanding of curves enclosed by smooth Jordan curves [12,13,14,15,16,17,18,19]. The Blaschke rolling theorem for non-convex sets is intimately linked with concepts in mathematical morphology and image processing. For example, in the Ref. [20], Walther presented a geometric characterisation of the Serra regular model in image analysis and mathematical morphology [21].

In Section 2 we introduce one of the main contributions of this paper corresponding to the turning condition Definition 2. This is a local to global principle that is based on data being pair of points that decide on the convexity of the whole loop. From the turning condition we can also infer lower and upper bounds for arcs in a loop. This definition is based on the classification of $\kappa$-constrained curves and summarises several related results [22]. We expect that a version of the turning condition for curves of three-space surfaces would lead to further generalisations, such as, for example, characterising volumetric objects in closed surfaces as first studied by Lagunov [23]. In Section 3 we use all the machinery presented in Section 2 to present the rolling disk decomposition algorithm.

The most relevant contributions of this paper are:

• Theorem 5 which is a “half version” of the Pestov–Ionin theorem [1] in which we prove the existence of a half disk for curves that are not close.
• Theorem 7 where we characterise convexity and non-convexity of a domain $\mathcal{K}\subset {\mathbb{R}}^2$ in terms of the type of terminals its boundary $\partial \mathcal{K}$ admits.
• Theorem 8 gives necessary and sufficient conditions for a planar domain $\mathcal{K}$ to be internally rolling, externally rolling, or both simultaneously.
• In Theorem 10 we provide an algorithm leading to a decomposition of any planar domain into a finite number of maximal rolling regions. As a consequence of Theorem 8, we obtain an updated version for the Blaschke rolling disk theorem.
• The methods here presented allow natural adaptations in higher dimensions.

2. The Turning Condition

We consider a loop $\sigma :S^1\to {\mathbb{R}}^2$ to be the homeomorphic image of the circle. The loops are of class $C^1$, regular, arc length parametrised, traversed clockwise with periods equal to its length. A loop is called $\kappa$-constrained if is of piecewise class $C^2$ and has bounded absolute curvature i.e., $\left|\right|{\sigma }^{\prime \prime }\left|\right|\le \kappa$, when defined, with $r:=1/\kappa >0$ as a constant. Therefore, $\kappa$-constrained loops have, almost everywhere, well-defined curvatures with respect to its arc length parameter. We often refer to a loop instead to a $\kappa$-constrained loop.

We endow the space of $\kappa$-constrained loops with the $C^1$ metric. The ambient space of the loops is the Euclidean plane with the topology induced by the Euclidean metric. The interior, boundary, closure and complement of a set $\mathcal{K}\subset {\mathbb{R}}^2$ are denoted by $int\left(\mathcal{K}\right)$, $\partial \mathcal{K}$, $cl\left(\mathcal{K}\right)$ and ${\mathcal{K}}^c$, respectively. A planar domain is considered to be an open connected set in ${\mathbb{R}}^2$. We regard a loop as either the map $\sigma :S^1\to {\mathbb{R}}^2$ or its image when no confusion arises.

The Jordan curve theorem asserts that the complement of a loop in ${\mathbb{R}}^2$ corresponds to two regions, each of which has a boundary of the loop. One region is a topological disk enclosed by the loop and the other is unbounded [24].

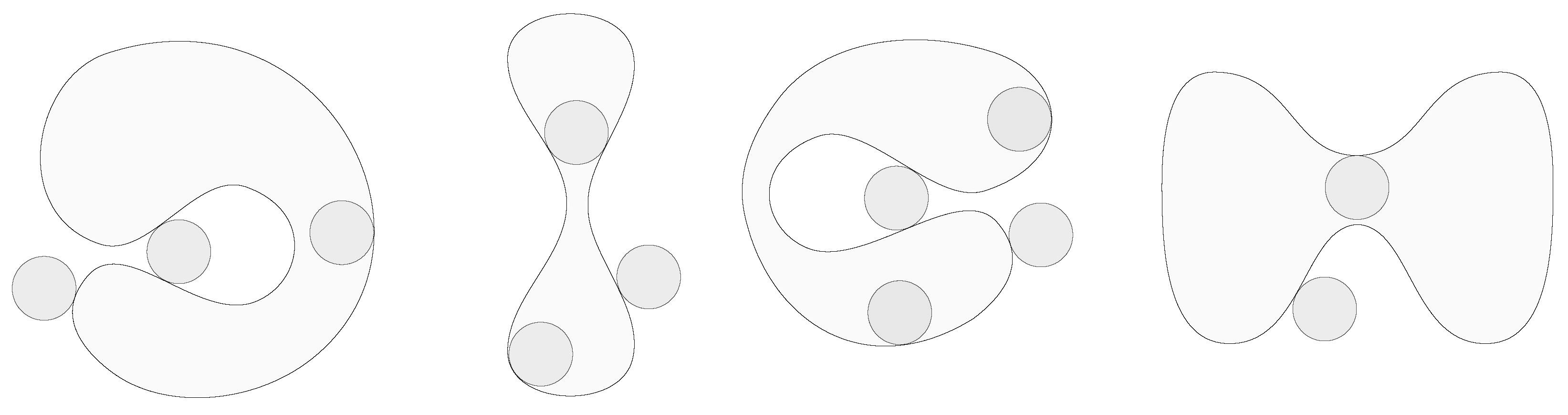
Definition 1.

Let $T\left(t\right)$ and $N\left(t\right)$ be a continuous choice of a tangent and normal line at $\sigma \left(t\right)$, $t\in S^1$. A domain $\mathcal{K}\subset {\mathbb{R}}^2$ is called internally rolling if its boundary $\partial \mathcal{K}=\sigma$ is a κ-constrained loop such that for all $t\in S^1$ there exist a disk $D\left(t\right)$ of radius $r=1/\kappa$ tangent to $T\left(t\right)$ with $D\left(t\right)\subset cl\left(\mathcal{K}\right)$. A domain $\mathcal{K}\subset {\mathbb{R}}^2$ is called externally rolling if its boundary $\partial \mathcal{K}=\sigma$ is a κ-constrained loop such that for all $t\in S^1$ there exist a disk $E\left(t\right)$ of radius $r=1/\kappa$ tangent to $T\left(t\right)$ with $E\left(t\right)\subset cl\left({\mathcal{K}}^c\right)$. A domain $\mathcal{K}\subset {\mathbb{R}}^2$ is called rolling if it is internally and externally rolling, see Figure 1.

Next we observe some simple equivalences of Definition that are worth noticing Definition 1.

Observation 1

(Rolling equivalences). A domain is internal (external) rolling if there is an embedded one-sided internal (external) neighbourhood of radius $2r$ of the loop. A domain is rolling if there is an embedded neighbourhood of radius $2r$ of the loop.

Due to smoothness, a κ-constrained loop admits a pair of points whose chord is perpendicular to the curve, the so-called double critical pair. For $t_1,t_2\in S^1$, we defined the doubly critical self distance of $\partial \mathcal{K}=\sigma$ to be,

$$dcsd\left(\sigma \right)=min\left\{\right||\sigma \left(t_2\right)-\sigma \left(t_1\right)||:(\sigma \left(t_1\right),\sigma \left(t_2\right))is a doubly critical pair\}.$$

We say that $\partial \mathcal{K}$ is rolling if $dcsd\left(\sigma \right)\ge 2r$.

Figure 1. Examples of planar domains and tangent disks of radius $r=1/\kappa$. From left to right. A domain that is internally rolling but not externally rolling. A domain that is externally rolling but not internally rolling. A domain that is neither internal nor externally rolling. A domain that is rolling. Clearly, none of these are convex.

Figure 1. Examples of planar domains and tangent disks of radius $r=1/\kappa$. From left to right. A domain that is internally rolling but not externally rolling. A domain that is externally rolling but not internally rolling. A domain that is neither internal nor externally rolling. A domain that is rolling. Clearly, none of these are convex.

Next we rewrite the well-known Blaschke rolling disk theorem whose proof in its original form can be found in the Ref. [2].

Theorem 1.

A convex domain $\mathcal{K}\subset {\mathbb{R}}^2$ with boundary of class $C^2$ and (signed) curvature not exceeding a positive constant is internally rolling.

The definition below is based on the classification of the homotopy classes of $\kappa$-constrained curves [22]. Therein, curves were used to denominate paths with bounded absolute curvature connecting two points in the plane. In Observation 2 we explain the connections between the results in the Ref. [22] and Definition 2.

Definition 2

(Turning condition). Let $\sigma :S^1\to {\mathbb{R}}^2$ be a κ-constrained loop. Consider $\sigma :[t_1,t_2]\subset S^1\to {\mathbb{R}}^2$. Let $D_1,D_2$ be radius $r=1/\kappa$ disks with $\sigma \left(t_1\right),\sigma \left(t_2\right)\in \partial D_1\cap \partial D_2$. A short curve satisfies:

• $\left|\right|\sigma \left(t_1\right)-\sigma \left(t_2\right)\left|\right|\le 2r$;
• $\sigma \left([t_1,t_2]\right)\subset D_1\cap D_2$.

A long curve satisfies:

• $\left|\right|\sigma \left(t_1\right)-\sigma \left(t_2\right)\left|\right|<2r$;
• $\sigma \left([t_1,t_2]\right)$ has a point in ${(D_1\cap D_2)}^c$.

A curve is called simple if $\left|\right|\sigma \left(t_1\right)-\sigma \left(t_2\right)\left|\right|\ge 2r$. By definition, an arc of a circle of radius r is short, simple but never long. We refer to the points $\sigma \left(t_1\right),\sigma \left(t_2\right)$ as terminals. Note that terminals separate a loop into two complementary curves. Terminals are called essential if both complementary curves are long. Terminals that are not essential are called inessential. A curve is said to be essential or inessential depending on its terminals, see Figure 2.

Figure 2. Left: a $\kappa$-constrained loop with a pair of inessential terminals is decomposed into two curves one long and one short. Short curves are always included in $D_1\cap D_2$. Centre: a $\kappa$-constrained loop with a pair of essential terminals is decomposed into two long curves. Long curves always have a point in ${(D_1\cap D_2)}^c$. Right: a $\kappa$-constrained curve whose terminals are distant apart less or equal to $2r$ cannot make a u-turn while defined in an open band of width $2r$.

Figure 2. Left: a $\kappa$-constrained loop with a pair of inessential terminals is decomposed into two curves one long and one short. Short curves are always included in $D_1\cap D_2$. Centre: a $\kappa$-constrained loop with a pair of essential terminals is decomposed into two long curves. Long curves always have a point in ${(D_1\cap D_2)}^c$. Right: a $\kappa$-constrained curve whose terminals are distant apart less or equal to $2r$ cannot make a u-turn while defined in an open band of width $2r$.

Two $\kappa$-constrained curves with fixed common terminals are said to be $\kappa$-constrained homotopic if, at each stage of the deformation, the intermediate curves are $\kappa$-constrained curves while keeping the terminals fixed. Next, we explain our main results in the Ref. [22] and put Definition 2 into context.

Observation 2.

Let $D_1,D_2$ be radius $r=1/\kappa$ disks. Let $\sigma :[t_1,t_2]\to {\mathbb{R}}^2$ be a κ-constrained curve with (fixed) terminals satisfying $0<\left|\right|\sigma \left(t_1\right)-\sigma \left(t_2\right)\left|\right|<2r$ with $\sigma \left(t_1\right),\sigma \left(t_2\right)\in \partial D_1\cap \partial D_2$. Then, there are exactly two connected components of κ-constrained curves connecting these terminals. One is an isotopy class of short curves. All the curves in this class are embedded and confined to be in $D_1\cap D_2$, see Theorem 4.21 in the Ref. [22]. The curves in $D_1\cap D_2$ are κ-constrained homotopic to the line segment connecting the terminals. The other is a homotopy class of long curves connecting the same terminals. These curves are such that they are κ-constrained homotopic to a curve with a point in ${(D_1\cap D_2)}^c$, see Theorem 4.22 in the Ref. [22]. There are two length-minimiser long curves in this homotopy class. These are the longest arcs in the circles $\partial D_1$ and $\partial D_2$ connecting the terminals.

Accordingly (for fixed terminals), a curve cannot be κ-constrained homotopic to a short and a long curve simultaneously. Therefore a curve cannot be short and long simultaneously.

In addition, if $\left|\right|\sigma \left(t_1\right)-\sigma \left(t_2\right)\left|\right|\ge 2r$, there is a single connected component of simple curves, similarly as for homotopies between continuous plane paths. If $\sigma \left(t_1\right)=\sigma \left(t_2\right)$ there is a single connected component of closed curves allowing a kink. The bound on an absolute curvature as a condition is so rigid that a curve with terminals $\sigma \left(t_1\right),\sigma \left(t_2\right)\in \partial D_1\cap \partial D_2$ being entirely defined in $D_1\cup D_2$ cannot have a point in $int(D_1\cup D_2)\backslash cl(D_1\cap D_2)$.

Observation 3.

A long curve can meander in between its terminals or spiral around them, see Figure 3. If a long curve meanders in between its terminals, we consider the intersection between the long curve and the line connecting its terminals. In this fashion, we split a meandering long curve into several adjacent subcurves. For example, suppose a long curve intersects the line joining the terminals at a point $\sigma \left(t^{*}\right)$ other than its terminals. Then, we split the long curve into the two adjacent long curves $\sigma \left([t_1,t^{*}]\right)$ and $\sigma \left([t^{*},t_2]\right)$, see Figure 3. Note short curves can meander in between terminals but clearly never spiral around them. In addition, a long curve that spirals around its terminals always admits a point $\sigma \left(t^{*}\right)$ in the line connecting its terminals such that $\sigma \left([t_1,t_2]\right)\subset \sigma \left([t_1,t^{*}]\right)$.

Figure 3. A meandering long curve with terminals $\sigma \left(t_1\right),\sigma \left(t_2\right)$ can be decomposed into two adjacent long curves. A long curve that spirals around its terminals is a subcurve of a longer long curve with terminals $\sigma \left(t_1\right),\sigma \left(t^{*}\right)$.

Figure 3. A meandering long curve with terminals $\sigma \left(t_1\right),\sigma \left(t_2\right)$ can be decomposed into two adjacent long curves. A long curve that spirals around its terminals is a subcurve of a longer long curve with terminals $\sigma \left(t_1\right),\sigma \left(t^{*}\right)$.

Definition 3.

A κ-constrained curve $\sigma :I\to {\mathbb{R}}^2$ is called an arc if the region enclosed by its image and the line connecting its terminals $\sigma (\partial I)$ is homeomorphic to a disk. An arc with terminals removed is called "open".

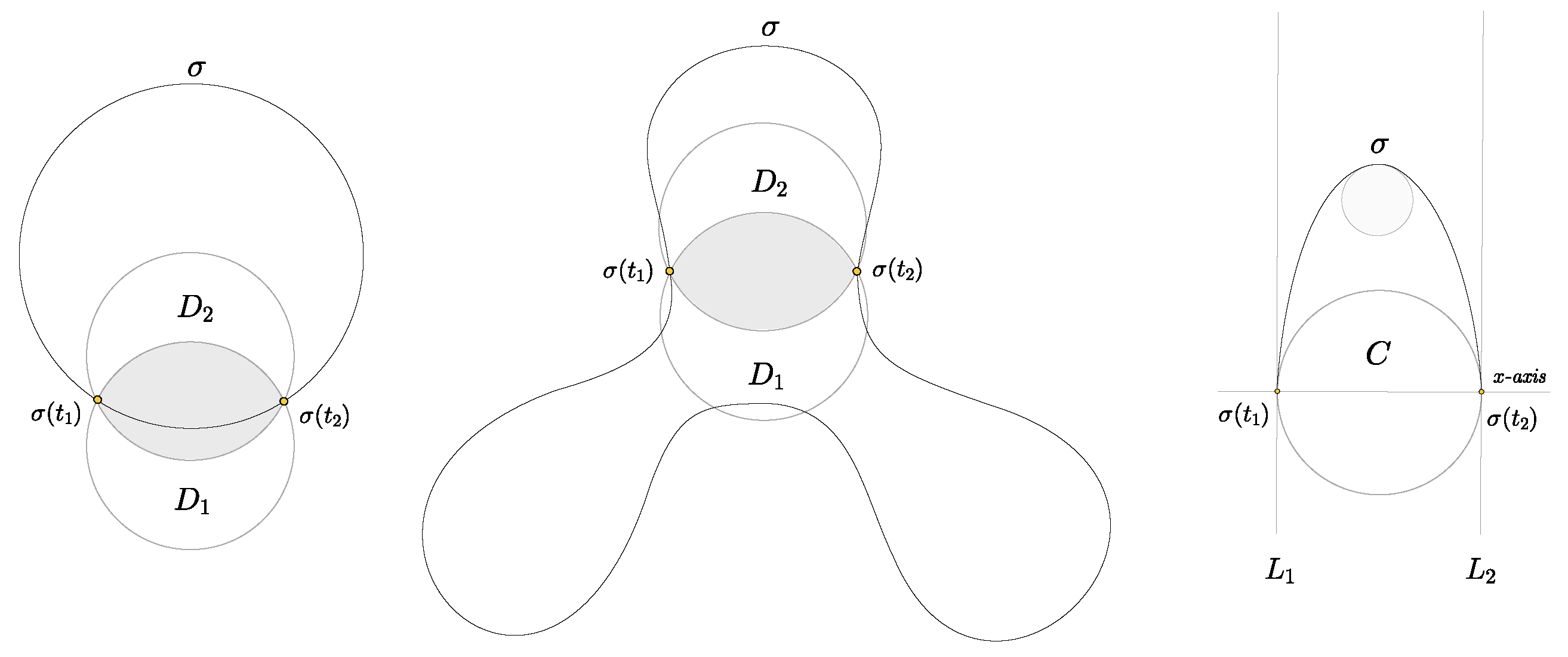
Theorem 2.

A κ-constrained loop admits a long arc.

Proof. 

Every $\kappa$-constrained loop admits a short arc since terminals can be chosen to be arbitrarily close. Consider a short arc $\alpha :[0,s]\to {\mathbb{R}}^2$ in an arc length parametrised loop $\sigma :[0,\ell ]\to {\mathbb{R}}^2$ with $\sigma \left(0\right)=\sigma (\ell )$. Suppose that this loop does not admit a long arc. In this case, the terminals of $\alpha$ split the loop into two complementary short arcs $\alpha :[0,s]\to {\mathbb{R}}^2$, $\beta :[s,\ell ]\to {\mathbb{R}}^2$.

Since $\alpha$ is short, Theorem 4.21 in the Ref. [22] implies that $\alpha \left([0,s]\right)\subset D_1\cap D_2$ where $D_1,D_2$ are the radius r disks with $\alpha \left(0\right),\alpha \left(s\right)\in \partial D_1\cap \partial D_2$, see Figure 4 left. Since $\beta$ is also short, Theorem 4.21 in the Ref. [22] implies that $\beta \left([s,\ell ]\right)\subset D_1\cap D_2$ with $\beta \left(s\right),\beta (\ell )\in \partial D_1\cap \partial D_2$. Let $L_1$ and $L_2$ be the lines tangent to $\partial D_1$ and $\partial D_2$ at $\alpha \left(s\right)=\beta \left(s\right)$ respectively, see Figure 4. These lines divide the plane into four quadrants. Since $\alpha \left([0,s]\right)\subset D_1\cap D_2$, the bound on curvature implies that ${\alpha }^{\prime }\left(s\right)$ can only range in quadrant I. On the other hand, since $\beta \left([s,\ell ]\right)\subset D_1\cap D_2$, we have that ${\beta }^{\prime }\left(s\right)$ can only range in quadrant III. We conclude that ${\alpha }^{\prime }\left(s\right)\ne {\beta }^{\prime }\left(s\right)$ implying that ${\sigma }^{\prime }\left(s\right)$ is not of class $C^1$, contradicting the smoothness of $\sigma$. Therefore, $\beta$ must have a point in ${(D_1\cap D_2)}^c$ concluding that it is a long curve. We conclude the proof by noting that this long curve can be split or completed as in Observation 3 to obtain the desired long arc. □

Figure 4. From left to right. The notation for Theorem 2. A long arc with a distinguished end characterised by $\hat{C}\in \mathcal{S}$ in Theorem 3. An end does not intersect the half disk H supporting its terminals, otherwise it would admit essential terminals. An illustration of a cross-section.

Figure 4. From left to right. The notation for Theorem 2. A long arc with a distinguished end characterised by $\hat{C}\in \mathcal{S}$ in Theorem 3. An end does not intersect the half disk H supporting its terminals, otherwise it would admit essential terminals. An illustration of a cross-section.

Definition 4.

Consider $\sigma :(t_1,t_2)\subset S^1\to {\mathbb{R}}^2$ such that $\sigma \left(t\right),\sigma \left(t^{\prime }\right)$ are not essential terminals for any $t,t^{\prime }\in (t_1,t_2)$. Then $\sigma :[t_1,t_2]\to {\mathbb{R}}^2$ is called an end. An end is called essential if this is a subset of an arc whose terminals are essential. An end that is not essential is called inessential.

Theorem 3.

A long arc admits an end. The terminals of an end are distant and apart by $2r$.

Proof. 

Let $\sigma :[t_1^{*},t_2^{*}]\to {\mathbb{R}}^2$ be a long arc with terminals $\sigma \left(t_1^{*}\right),\sigma \left(t_2^{*}\right)$.

Let $\mathcal{S}$ be the set of radius r circles $C\subset {\mathbb{R}}^2$ such that $\sigma \left(t_1\right),\sigma \left(t_2\right)\in C$ are the terminals of an arc $\sigma :[t_1,t_2]\to {\mathbb{R}}^2$ satisfying:

• $\left|\right|\sigma \left(t_1\right)-\sigma \left(t_2\right)\left|\right|\le 2r$;
• $\sigma \left([t_1,t_2]\right)\subset \sigma \left([t_1^{*},t_2^{*}]\right)$ has a point above C.

It is easy to see that $\mathcal{S}$ is closed and bounded, considered as a subset of the plane consisting of the centres of the circles $C\in \mathcal{S}$. Due to compactness, there exists a circle $\widehat{C}\in \mathcal{S}$ such that $\sigma ({\widehat{t}}_1),\sigma ({\widehat{t}}_2)\in \widehat{C}$ are the terminals of an arc $\sigma :[{\widehat{t}}_1,{\widehat{t}}_2]\to {\mathbb{R}}^2$ having the smallest length amongst all the circles in $\mathcal{S}$, see Figure 4. If $\sigma :({\widehat{t}}_1,{\widehat{t}}_2)\to {\mathbb{R}}^2$ admits essential terminals, then the minimality of the length of $\sigma :[{\widehat{t}}_1,{\widehat{t}}_2]\to {\mathbb{R}}^2$ is contradicted, since the existence of essential terminals in $\sigma :({\widehat{t}}_1,{\widehat{t}}_2)\to {\mathbb{R}}^2$ would imply the existence of a shorter long arc. We conclude that $\sigma :[t_1,t_2]\to {\mathbb{R}}^2$ admits an end.

Suppose that the terminals of an end $\sigma ({\widehat{t}}_1),\sigma ({\widehat{t}}_2)\in \widehat{C}$ satisfy $\left|\right|\sigma ({\widehat{t}}_1)-\sigma ({\widehat{t}}_2)\left|\right|<2r$. Then a small perturbation of $\widehat{C}$ would reduce the length of the end contradicting the minimality of the end. The terminals of an end are antipodes in $\widehat{C}\in \mathcal{S}$, concluding the proof. □

Corollary 1.

A κ-constrained loop admits an end.

Proof. 

By Theorem 2 a $\kappa$-constrained loop admits a long arc. The result follows by Theorem 3. □

Ends are objects that uniquely characterise families of long arcs. Suppose that $\sigma :[{\widehat{t}}_1,{\widehat{t}}_2]\to {\mathbb{R}}^2$ is an end. Then this end may also be the end of the family of long arcs $\sigma :[{\widehat{t}}_1-ϵ,{\widehat{t}}_2+ϵ]\to {\mathbb{R}}^2$ for some $ϵ>0$. In particular, $\sigma ([{\widehat{t}}_1,{\widehat{t}}_2])\subset \sigma ([{\widehat{t}}_1-ϵ,{\widehat{t}}_2+ϵ])$.

The detection of essential terminals implies the existence of a long arc, and therefore the existence of an end. The next result gives to a lower bound for the length of the loop in between essential terminals.

Theorem 4.

A long arc has a length of at least $\pi r$.

Proof. 

By Theorem 3 a long arc admits an end. The result follows after proving that an end has a length of at least $\pi r$. Consider a long arc whose end $\sigma :[0,\ell ]\to {\mathbb{R}}^2$ has been reparametrised by its arc length given by $\sigma \left(t\right)=(-\rho (t)cos\theta (t),\rho (t)sin\theta (t\left)\right)$ with $\rho ,\theta :[0,\ell ]\to {\mathbb{R}}^2$.

By Theorem 3, the terminals of an end satisfy $\left|\right|\sigma \left(0\right)-\sigma (\ell )\left|\right|=2r$. Set a coordinate system in which the x-axis passes through $\sigma \left(0\right)=(-r,0)$ and $\sigma (\ell )=(r,0)$ with the origin being the midpoint between them. We obtain that $\rho \left(0\right)=\rho (\ell )=r$ and $\theta \left(0\right)=0$ and $\theta (\ell )=\pi$. Note that,

$${\int }_0^{\ell }\left|\right|{\sigma }^{\prime }\left(t\right)\left|\right|dt={\int }_0^{\ell }\sqrt{\left|\right|{\rho }^{\prime }\left(t\right){\left|\right|}^2+\rho {\left(t\right)}^2\left|\right|{\theta }^{\prime }\left(t\right){\left|\right|}^2}dt\ge {\int }_0^{\ell }\rho \left(t\right)\left|\right|{\theta }^{\prime }\left(t\right)\left|\right|dt.$$

Let H be the radius r half disk with nonnegative ordinates centred at the origin, see Figure 4. Clearly, the end cannot intersect a point of positive ordinates in $\partial H$ unless the end coincides with the semicircle $\partial H$. If so, $\sigma$ would admit essential terminals and no longer be an end. We conclude that $\rho \left(t\right)\ge r$ for points in the upper half of the plane. Since $\theta (\ell )=\pi$, we have that

$${\int }_0^{\ell }\left|\right|{\sigma }^{\prime }\left(t\right)\left|\right|dt\ge {\int }_0^{\ell }\rho \left(t\right)\left|\right|{\theta }^{\prime }\left(t\right)\left|\right|dt\ge \pi r.$$

□

The next result is an inclusion principle for long $\kappa$-constrained arcs. This can be viewed as a half of the Pestov–Ionin theorem [1].

Theorem 5

(Half disk). The region enclosed by a long arc and the line segment connecting its terminals encloses a half disk of radius r.

Proof. 

By Theorem 3 a long arc admits an end. In the proof of Theorem 4, we determined that the end cannot intersect $\partial H$ in a point other than its terminals unless the end coincides with the semicircle $\partial H$. In addition, the end cannot intersect the points in $\partial H$ of zero ordinates other than its terminals, otherwise essential terminals are obtained, contradicting the definition of end. We conclude that H in Theorem 4 is the desired half disk. □

Corollary 2.

A κ-constrained loop has length at least $2\pi r$.

Proof. 

Suppose the loop admits a pair of essential terminals. Then, we apply Theorem 4 to each of the two long arcs with common essential terminals to conclude that the loop has a length of at least $2\pi r$.

If the loop admits only inessential terminals, the boundary of a radius r disk D tangent to the loop cannot intersect the loop transversally. Otherwise, a pair of essential terminals is obtained. Consider the centre of D to be the origin. We proceed similarly as in Theorem 4. Consider the arc length parametrised loop $\sigma :[0,\ell ]\to {\mathbb{R}}^2$ in polar coordinates $\sigma \left(t\right)=(-\rho (t)cos\theta (t),\rho (t)sin\theta (t\left)\right)$ with $\rho ,\theta :[0,\ell ]\to {\mathbb{R}}^2$. Since D is enclosed by the loop, we have that $\rho \left(t\right)\ge r$. Since $\theta (\ell )=2\pi$, we conclude that

$${\int }_0^{\ell }\left|\right|{\sigma }^{\prime }\left(t\right)\left|\right|dt\ge {\int }_0^{\ell }\rho \left(t\right)\left|\right|{\theta }^{\prime }\left(t\right)\left|\right|dt\ge 2\pi r.$$

□

Theorem 6.

A κ-constrained loop finitely has many essential ends and infinitely has many inessential ends.

Proof. 

A loop admitting no essential terminals has an empty set of essential ends, being finite of cardinality zero.

By Theorem 2 a loop admits a long arc. If the terminals of the long arc are essential, then two long arcs share these terminals. By applying Theorem 3 to both arcs, we establish the existence of distinct ends. By Theorem 4 a long arc has a length of at least $\pi r$. Therefore, there must be a finite number of essential ends. Otherwise, the rectifiability of the loop would be contradicted.

If the long arc obtained by Theorem 2 is inessential, its terminals are also the terminals of a short arc. In addition, every pair of inessential terminals has a unique inessential end. Since loops are parametrised in a continuum, there are infinitely many choices of inessential terminals, concluding the proof. □

Definition 5.

An arc $\sigma :I\to {\mathbb{R}}^2$ has parallel tangents if there exist $t_1,t_2\in I$, with $t_1<t_2$, such that ${\sigma }^{\prime }\left(t_1\right)$ and ${\sigma }^{\prime }\left(t_2\right)$ are parallel and pointing in opposite directions.

Definition 6.

Let $L_1$ and $L_2$ be the lines $x=-r$ and $x=r$, respectively. A line joining two points in $\sigma :[t_1,t_2]\to {\mathbb{R}}^2$ is distant and apart by at least $2r$; one to the left of $L_1$ and the other to the right of $L_2$ is called a cross-section, see Figure 4 on the right.

Next we prove the existence of a cross-section and parallel tangents as in Corollary 3.4 in the Ref. [22], but here using the existence of ends.

Corollary 3.

A long arc has a cross-section, parallel tangents and length of at least $2r$.

Proof. 

By Theorem 3 a long arc admits an end $\sigma :[{\widehat{t}}_1,{\widehat{t}}_2]\to {\mathbb{R}}^2$. Since $\left|\right|\sigma ({\widehat{t}}_1)-\sigma ({\widehat{t}}_2)\left|\right|=2r$, the long arc admits a cross-section. Therefore, the end has a length of at least $2r$, and also the long arc containing it.

According to the proof of Theorem 3 the terminals of an end are antipodes in $\widehat{C}\in \mathcal{S}$ and the end is of minimal length amongst all the choices for terminals in $C\in \mathcal{S}$. Let L be the line joining the terminals and $L_1,L_2$ be the perpendicular lines to L at each terminal. The maximality of $\widehat{C}$ implies that locally, the trajectory of the end after the first terminal must be to the left of $L_1$ (or coincides with $L_1$) and the trajectory of the end before the second terminal must be to the right of $L_2$ (or coincides with $L_2$). Otherwise, we find essential terminals, leading to a contradiction.

If the trajectories coincide with the parallels, then there exist parallel tangents. If none of the trajectories coincides with the parallels, by continuity, the end intersects $L_1$ and $L_2$ at points other than the terminals, see Figure 4 on the right. By the mean value theorem, there exist $t_1,t_2\in [{\widehat{t}}_1,{\widehat{t}}_2]$ such that ${\sigma }^{\prime }\left(t_1\right)$ and ${\sigma }^{\prime }\left(t_2\right)$ are parallel pointing in opposite directions. The case when only one trajectory coincides with a parallel runs similarly. □

Observation 4.

Let $\sigma :S^1\to {\mathbb{R}}^2$ be a κ-constrained loop. In Corollary 2 we proved that length$\left(\sigma \right)\ge 2\pi r$. In Theorem 2 we proved that σ admits a long arc. In Theorem 3 we proved that a long arc admits an end. Ends by definition are proper subsets of long arcs. In Theorem 4 we proved that $length\left(longarc\right)\ge \pi r$. From Corollary 3 we have that a long arc admits a cross-section with $length(cross-section)\ge 2r$. We derive the following:

$$length(\sigma )>length\left(longarc\right)>length\left(end\right)>length(cross-section).$$

The following result establishes that a $\kappa$-constrained curve whose terminals are distant and apart less than $2r$ cannot make a U-turn while defined in the open band of width $2r$ without violating the curvature bound, see Figure 2 on the right.

Lemma 1

(Lemma 3.1 in [22]). A κ-constrained curve $\sigma :[t_1,t_2]\to \mathcal{B}$ where,

$$\mathcal{B}=\{(x,y)\in {\mathbb{R}}^2|-r<x<r,y>0\}$$

cannot satisfy both:

• $\sigma \left(t_1\right),\sigma \left(t_2\right)$ are points on the x-axis;
• If C is a radius r circle with the centre on the nonpositive y-axis and $\sigma \left(t_1\right),\sigma \left(t_2\right)\in C$, then some point in $\sigma \left([t_1,t_2]\right)$ lies above C.

Observation 5.

Lemma 1 remains valid if we consider $\left|\right|\sigma \left(t_1\right)-\sigma \left(t_2\right)\left|\right|=2r$. However, in this case, we must consider $\sigma :(t_1,t_2)\to \mathcal{B}$, see Figure 2 on the right.

The next result provides a characterisation of convexity through curvature. A regular closed plane curve is convex if and only if it is the boundary of a convex set $\mathcal{K}\subset {\mathbb{R}}^2$[24]. Next we assert on the convexity of $\partial \mathcal{K}$ to conclude on the convexity of $\mathcal{K}$.

Theorem 7.

If $\mathcal{K}\subset {\mathbb{R}}^2$ is a domain with boundary $\partial \mathcal{K}=\sigma$ a κ-constrained loop admitting a pair of essential terminals. Then, $\mathcal{K}$ is not convex. If $\mathcal{K}\subset {\mathbb{R}}^2$ is a convex domain with boundary $\partial \mathcal{K}=\sigma$ a κ-constrained loop. Then, $\partial \mathcal{K}=\sigma$ admits only inessential terminals.

Proof. 

Since a regular simple closed convex plane curve always has two and only two parallel tangents to any given direction [25], we contradicted convexity by searching for a third one. We borrowed the notation from Corollary 3.

Consider a long arc with essential terminals. By Corollary 3 this long arc admits two parallel tangents located somewhere at an end whose existence is guaranteed by Theorem 3. Next, we analyse the trajectory for the loop before and after the terminals of the end. Let $\sigma ({\widehat{t}}_1-ϵ)$ and $\sigma ({\widehat{t}}_2+ϵ)$ be points sufficiently close to the terminals of the end, $ϵ>0$, see Figure 5. We have some cases:

• $\sigma ({\widehat{t}}_1-ϵ),\sigma ({\widehat{t}}_2+ϵ)$ lie in between $L_1$ and $L_2$.
• $\sigma ({\widehat{t}}_1-ϵ)$ lies to the right of $L_1$ and $\sigma ({\widehat{t}}_2+ϵ)$ lies to the right of $L_2$.
• $\sigma ({\widehat{t}}_1-ϵ)$ lies to the left of $L_1$ and $\sigma ({\widehat{t}}_2+ϵ)$ lies to the left of $L_2$.
• $\sigma ({\widehat{t}}_1-ϵ)$ lies to the left of $L_1$ and $\sigma ({\widehat{t}}_2+ϵ)$ lies to the right of $L_2$.

Proof of (1). Note these are the terminals of two long arcs, from one of which we already obtained a pair of parallel tangents. By Lemma 1 the second long arc cannot be entirely defined in the open band in between $L_1$ and $L_2$, see Figure 5 on the left. Therefore, the loop must abandon the band and reenter it. Suppose the loop leaves and reenters the band intersecting $L_2$ twice, see the second illustration in Figure 5. By the mean value theorem, there exists another pair of parallel tangents implying that the loop has three parallel tangents, concluding that it cannot be the boundary of a convex set. The case where the loop leaves and reenters the band intersecting $L_1$ twice is analogous. If the loop intersects $L_1$ and $L_2$, we obtain four parallel tangents, so it cannot be the boundary of a convex set, see the third illustration in Figure 5.

The cases (2) and (3) run similarly. The case (4) is illustrated in Figure 5 on the right, and also runs similarly. In general, any possible way of connecting the terminals $\sigma ({\widehat{t}}_1-ϵ),\sigma ({\widehat{t}}_2+ϵ)$ would lead to at least a third parallel tangent, concluding the proof. □

Figure 5. The first three figures illustrate case (1) below. The last figure illustrates case (4).

Figure 5. The first three figures illustrate case (1) below. The last figure illustrates case (4).

Definition 7.

Consider the domain delimited by a long arc and the line segment connecting its terminals. If this is included in the bounded plane region separated by a κ-constrained loop, we call it internal. If this is included in the unbounded region separated by a κ-constrained loop, we call it external. Certain domains are neither internal nor external.

We can easily determine whether domains are internal or external by the means of a parity function counting the number of times a ray based at a point in the domain crosses a the loop.

The next result gives necessary and sufficient conditions for the existence of rolling disks for planes, not necessarily convex domains, whose boundaries are $\kappa$-constrained curves.

Observation 6.

If $\mathcal{K}$ is internally rolling, then $\partial D\left(t\right)\cap \partial \mathcal{K}$ with $D\left(t\right)\subset cl\left(\mathcal{K}\right)$ can only be a singleton, a pair of antipodal points in $D\left(t\right)$, or an arc in $D\left(t\right)$, see Definition 1.

Theorem 8.

Let $\mathcal{K}\subset {\mathbb{R}}^2$ be a domain with boundary $\partial \mathcal{K}=\sigma$ a κ-constrained loop. Then,

1. 

$\mathcal{K}$ is internally rolling if and only if $\partial \mathcal{K}$ does not admit a pair of essential terminals for complementary internal long arcs.

2. 

$\mathcal{K}$ is externally rolling if and only if $\partial \mathcal{K}$ does not admit a pair of essential terminals for complementary external long arcs, one bounded and the other unbounded.

3. 

$\mathcal{K}$ is rolling if and only if $\mathcal{K}$ admits only inessential terminals. Here, $\mathcal{K}$ is not necessarily convex.

Proof. 

(1) Suppose $\mathcal{K}$ is internally rolling. Then, for each $\sigma \left(t\right)\in \partial \mathcal{K}$ there exists a radius r disk $D\left(t\right)\subset cl\left(\mathcal{K}\right)$. Suppose $\partial \mathcal{K}$ admits a pair of essential terminals for complementary internal long arcs. Since the distance between essential terminals is less than $2r$ we have that no disk tangent to an essential terminal can be included in $cl\left(\mathcal{K}\right)$ leading to a contradiction.

Conversely, suppose $\partial \mathcal{K}$ does not admit a pair of essential terminals for complementary internal long arcs. If $\mathcal{K}$ is not internally rolling, then there exists a radius r disk $D\left(t\right)$ tangent to $\partial \mathcal{K}$ at $\sigma \left(t\right)$ such that $\partial D\left(t\right)\cap \partial \mathcal{K}$ has an element different from the ones in Observation 6. Let $\sigma \left(t^{*}\right)$ be such an element. Since $D\left(t\right)$ is tangent at $\sigma \left(t\right)$ Lemma 1 implies that the arc $\sigma :[t,t^{*}]\to {\mathbb{R}}^2$ as a point above $\partial D\left(t\right)$, implying this arc is long, concluding that $\sigma \left(t\right),\sigma \left(t^{*}\right)$ are essential terminals, leading to a contradiction.

Case (2) runs similarly as (1) after replacing the internal with the external. The existence of an unbounded long arc comes from the non-compactness of ${\mathbb{R}}^2$. In Figure 1 on the left we show a non-externally rolling domain admitting a pair of essential terminals, in this case, the line joining the terminals decomposes the plane into one external region homeomorphic to a disk, and one unbounded region. Note that by adding a point at the infinite to ${\mathbb{R}}^2$ the unbounded long arc becomes bounded.

(3) Since $\mathcal{K}$ is rolling if and only if it is internally and externally rolling, the proof follows by combining (1) and (2). Note that sets admitting only inessential terminals are not necessarily convex. □

We present an updated version for the Blaschke rolling disk theorem [2] for $C^1$ and piecewise $C^2$ simple closed curves satisfying a bound on absolute curvature.

Theorem 9.

Suppose that a convex domain $\mathcal{K}\subset {\mathbb{R}}^2$ has boundary $\partial \mathcal{K}=\sigma$ a κ-constrained loop. Then $\mathcal{K}$ is rolling.

Proof. 

By Theorem 7 a convex domain with a boundary with a $\kappa$-constrained loop admits only inessential terminals. The result follows by (3) in Theorem 8. □

3. Rolling Disk Decomposition

In Theorem 8 we established that a domain $\mathcal{K}\subset {\mathbb{R}}^2$ is rolling if and only if $\partial \mathcal{K}$ does not admit essential terminals. Next, we propose a method for obtaining a finite collection of maximal (internal or external) rolling regions for a domain that is not necessarily internally or externally rolling.

Theorem 10.

Suppose a domain $\mathcal{K}\subset {\mathbb{R}}^2$ has boundary $\partial \mathcal{K}=\sigma$ with a κ-constrained loop. Then there exists a decomposition of ${\mathbb{R}}^2\backslash \partial \mathcal{K}$ into a finite number of maximal (internal or external) rolling regions and certain excluded regions.

Proof. 

Suppose $\partial \mathcal{K}=\sigma$ is a loop with only inessential terminals. Then, Theorem 8 implies that $\mathcal{K}$ is rolling. The decomposition of ${\mathbb{R}}^2\backslash \partial \mathcal{K}$ consists exactly of the two planar regions separated by the loop.

Suppose $\partial \mathcal{K}=\sigma$ is a loop admitting a pair of essential terminals.

• Rolling algorithm: We proceed to construct a domain such that for each element on its boundary, there exist disks of radius $r=1/\kappa$ tangent to the boundary included in the domain.
  By the Pestov–Ionin theorem [1] the bounded region delimited by the loop encloses a radius r disk $D_0$ that can be chosen to be tangent to $\partial \mathcal{K}$. With Definition 1 in mind, proceed to roll clockwise $D_0$ until it first intersects the loop at a point other than the tangent point at $\partial \mathcal{K}$. If the first intersecting point is one of the types described in Observation 6, we continue the rolling process until we obtain a pair of essential terminals tangent to the boundary of a rolling disk, see Figure 6. Let $D_1$ be the rolling disk containing such essential terminals on its boundary and let ${\lambda }_1$ be the shortest arc in $\partial D_1$ connecting these terminals. Replace one of the two long arcs by ${\lambda }_1$. The long arc replaced was chosen to be the one having a point to the “above” (to the left) of ${\lambda }_1$, see Lemma 1.
  We continued this rolling and replacing process until cyclically we returned to the starting replacement ${\lambda }_1={\lambda }_{k+1}$. Since each of the detected essential terminals characterise a unique long arc and those loops are rectifiable, the replacing process must be finite. Let ${\mathcal{R}}_1$ be the domain enclosed by the cyclic concatenation of the portions of $\partial \mathcal{K}$ rolled by ${\left\{D_j\right\}}_{j=1}^k$ together with the replacing arcs ${\left\{{\lambda }_j\right\}}_{j=1}^k$, see Figure 6 on the right. Clearly, ${\mathcal{R}}_1$ is maximal with respect to the set inclusion. Note that the piecewise smooth curve traced by the center of the rolling disks uniquely determines ${\mathcal{R}}_1$.
  Figure 6. An example of the rolling algorithm for $k=3$. The grey region depicts ${\mathcal{R}}_1$.

  Figure 6. An example of the rolling algorithm for $k=3$. The grey region depicts ${\mathcal{R}}_1$.
• Necks: In the previous step we exchanged k long arcs by k (replacing) arcs. Now, we concentrate on each of the replaced long arcs. Consider the rolling disk $D_j$ containing the replacing arc ${\lambda }_j$ whose terminals $\sigma \left(t_{1j}\right),\sigma \left(t_{2j}\right)$ are also the (essential) terminals of the replaced long arc.
  By continuously sweeping along the long arc $\sigma :[t_{1j},t_{2j}]\to {\mathbb{R}}^2$ with a family of circles $C\in \mathcal{S}$ (similarly as in Theorem 3), we determine the existence of an end, see Corollary 1. Let $D_j^0$ be a radius r disk tangent to one of the terminals of the end, see Figure 7. The case where $D_j^0$ intersects $\partial \mathcal{K}=\sigma$ transversally is treated in (3). Roll $D_j^0$ towards the line connecting the terminals of the end to obtain a pair of essential terminals. Let $D_j^1$ be the radius r disk containing on its boundary such terminals denoted by $\sigma \left(t_{3j}\right),\sigma \left(t_{4j}\right)$.
  Figure 7. An example of the process described in (2) for $j=2$ according to Figure 6. The coloured "parallel arcs" depict a neck. The loop intersects transversally $\partial D_2^0$ at several points.

  Figure 7. An example of the process described in (2) for $j=2$ according to Figure 6. The coloured "parallel arcs" depict a neck. The loop intersects transversally $\partial D_2^0$ at several points.
  Due to the continuous circle sweeping each of the arcs, $\sigma :[t_{1j},t_{3j}]\to {\mathbb{R}}^2$ and $\sigma :[t_{4j},t_{2j}]\to {\mathbb{R}}^2$ may be short or simple, but never long. Let a neck be conformed by the two "parallel arcs" in a loop obtained as above. In this case, we obtained the neck $\sigma \left([t_{1j},t_{3j}]\right)\cup \sigma \left([t_{4j},t_{2j}]\right)$, see the third illustration in Figure 7. Note that a neck is a set of "parallel essential terminals". The regions enclosed by a neck and their respective replacement arcs are clearly (excluded) not the rolling domain.
• Disk intersections: If $D_j^0$ transversally intersects the loop, then $D_j^0$ encloses a portion on a (excluded) not rolling domain. In this case, we consider pairs of elements in $\partial D_j^0\cap \partial \mathcal{K}$ and apply to them the turning condition in Definition 2 to determine the arc type, see Figure 7 on the right. Select the essential terminals in $\partial D_j^0\cap \partial \mathcal{K}$ and proceed to apply the procedure in (2) to determine their associated necks. Note some excluded regions may have as part of its boundary a replacement arc.
  If $D_j^1$ only intersects the loop according to Observation 6 and at the detected essential terminals, we then apply the rolling algorithm in (1) to obtain another rolling domain.
  By recursively applying this process, we obtained a decomposition of ${\mathbb{R}}^2\backslash \partial \mathcal{K}$ into a finite number of excluded regions and a finite number of rolling regions. It is easy to see that this decomposition is unique and maximal with respect to set inclusion, concluding the proof.

□

4. Conclusions

In conclusion, we have conducted a thorough examination of the relationship between the absolute curvature bound of a smooth plane Jordan curve and the presence of equivalent classes of distinctive disks with a radius of $1/\kappa$. Our results include a “half version” of the Pestov–Ionin theorem and proof of the existence of half disks for curves that are not close. We also established the convexity and non-convexity of a domain based on its boundary terminals. Our analysis provides necessary and sufficient conditions for a planar domain to exhibit internally rolling, externally rolling, or both. Additionally, we have developed an algorithm for dividing a planar domain into a finite number of maximal rolling regions and updated the classical Blaschke rolling disk theorem.