On the Approximation of Fractional-Order Differential Equations Using Laplace Transform and Weeks Method
Abstract
:1. Introduction
2. Preliminaries
- 1.
- The ML function in one parameter is defined as [34]where and η is an arbitrary positive constant. The LT of the ML function in one parameter is given aswhere
- 2.
- The ML function in two parameters is defined as [34]where and η and σ are arbitrary positive constants. The LT of the ML function in two parameter is given aswhere
- 3.
3. Proposed Method
3.1. Time-Fractional Differential Equation
3.2. Weeks Method
Error Analysis
- First is the truncation of the series to N terms;
- Second is the computation of the expansion coefficients numerically;
- Third is the approximation of ILT numerically. This error in (21) reveals itself in the fact that any error in the evaluated coefficients are increased with increasing t when .
| Algorithm 1 Computation of |
| The user needs to provide t, and N, and a rectangle , which likely contains the optimal values of and . The algorithm then works by solving
|
4. Numerical Results and Discussions
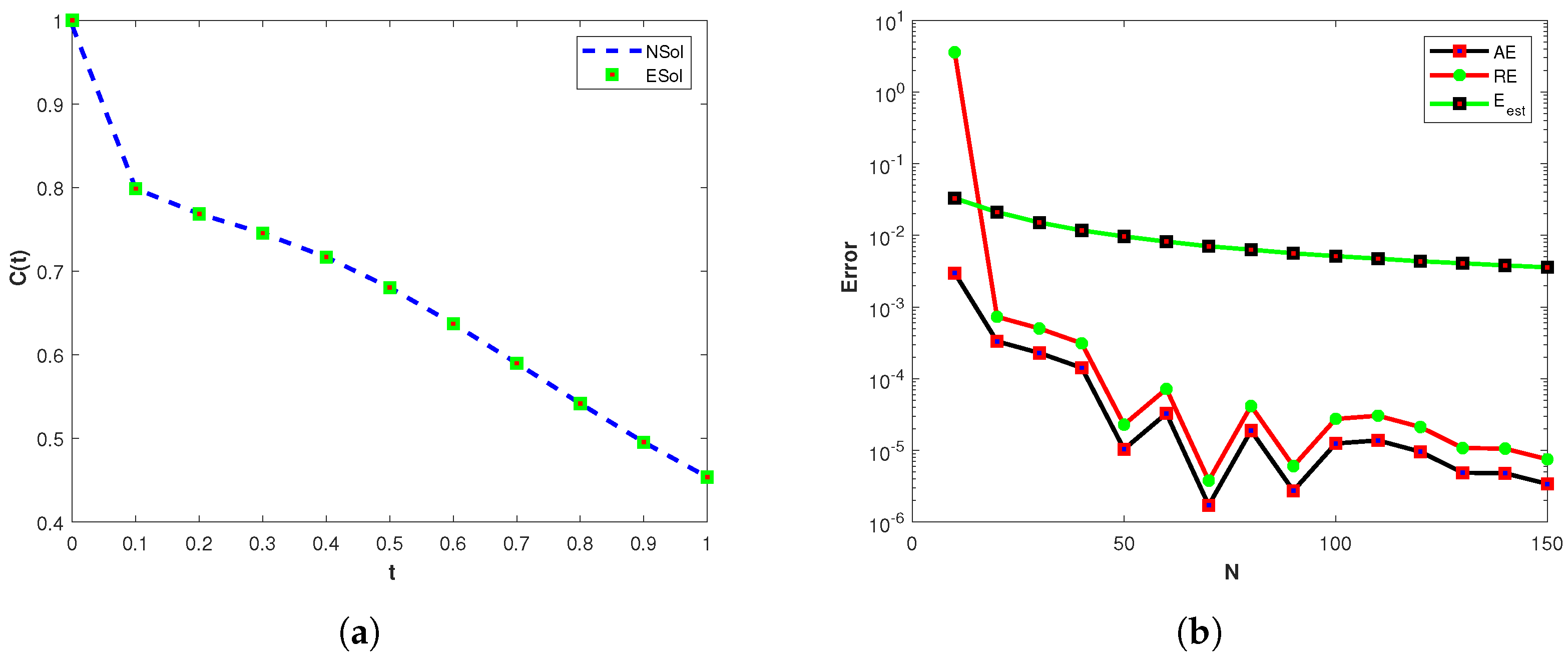
4.1. Example 1
4.2. Example 2
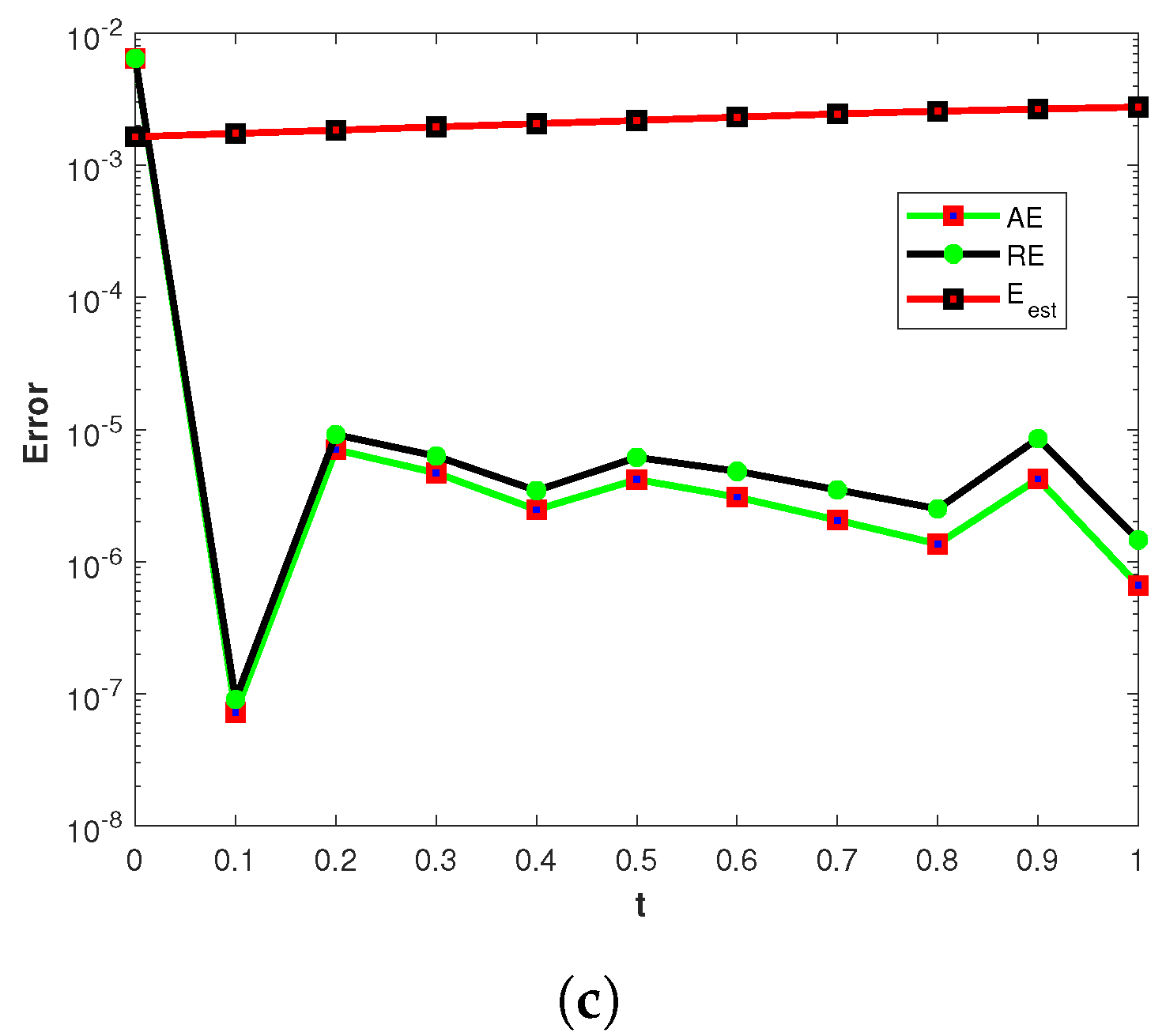
4.3. Example 3
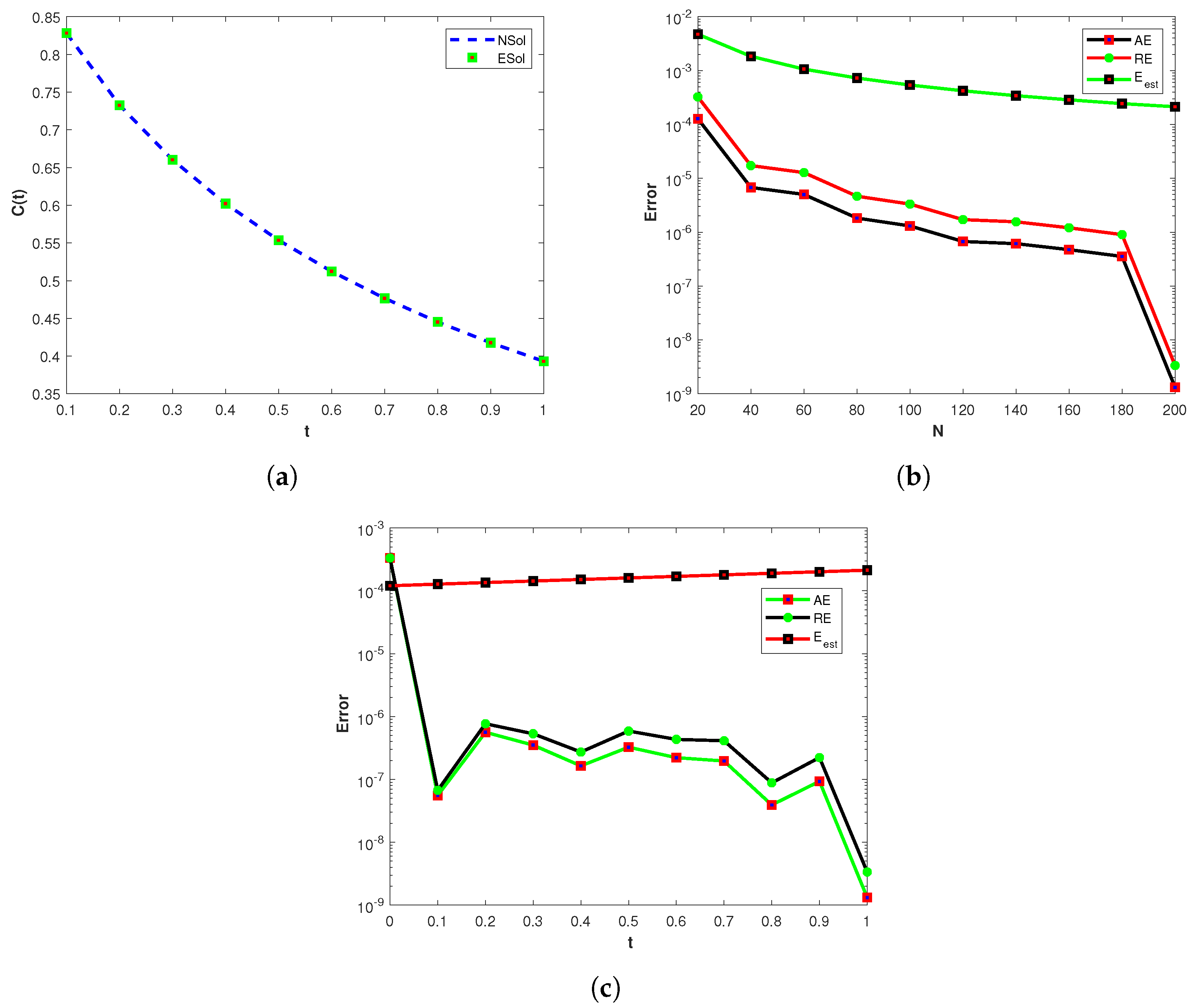
4.4. Example 4
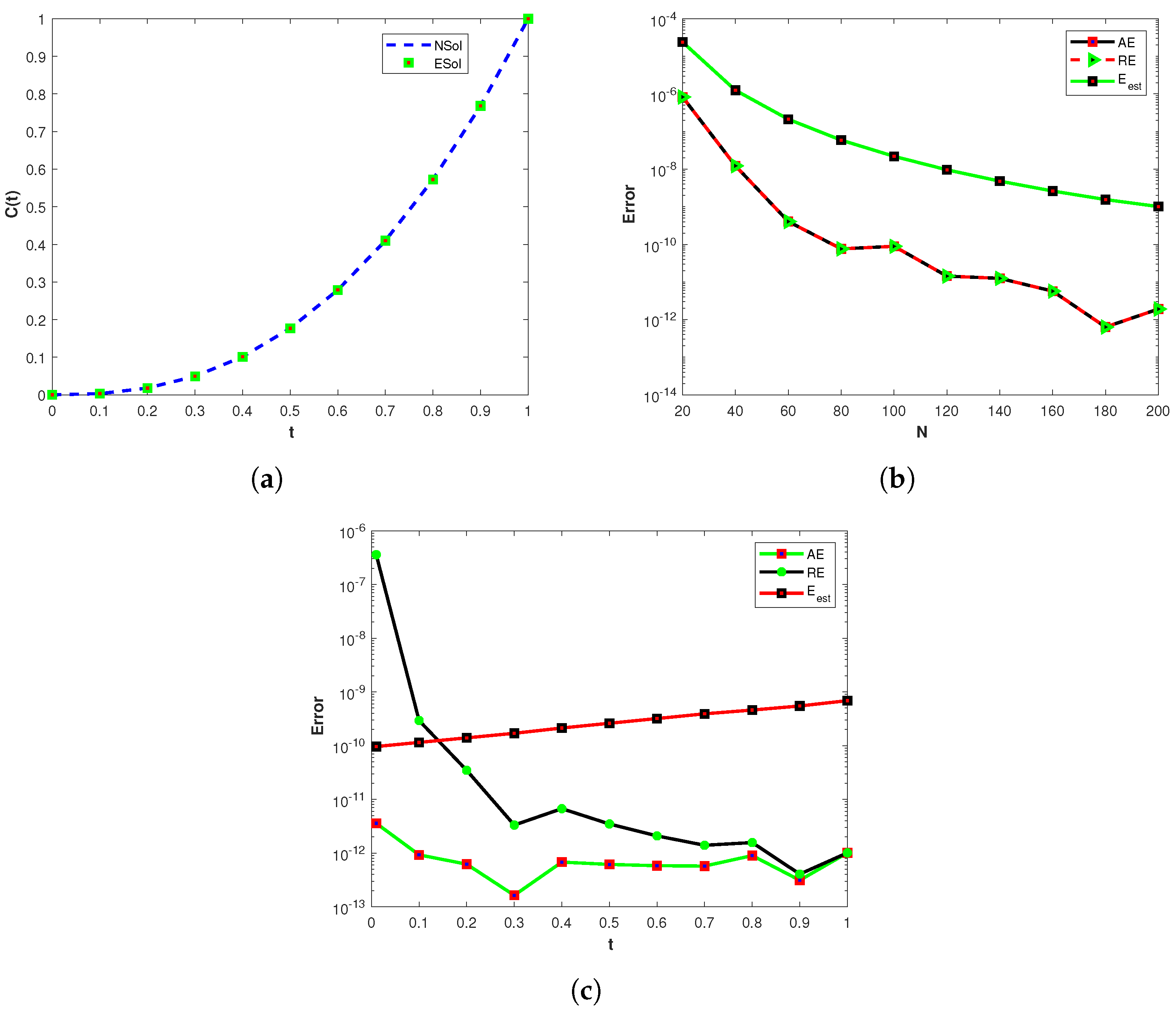
4.5. Example 5
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Oldham, K.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order; Elsevier: Amsterdam, The Netherlands, 1974. [Google Scholar]
- Kamran; Shah, F.A.; Aly, W.H.F.; Aksoy, H.; Alotaibi, F.M.; Mahariq, I. Numerical Inverse Laplace Transform Methods for Advection-Diffusion Problems. Symmetry 2022, 14, 2544. [Google Scholar] [CrossRef]
- Hattaf, K.; Yousfi, N. Global stability for fractional diffusion equations in biological systems. Complexity 2020, 2020, 5476842. [Google Scholar] [CrossRef]
- Shah, K.; Abdeljawad, T. Study of a mathematical model of COVID-19 outbreak using some advanced analysis. Waves Random Complex Media 2022, 33, 1–18. [Google Scholar] [CrossRef]
- Ali, A.; Khalid, S.; Rahmat, G.; Kamran; Ali, G.; Nisar, K.S.; Alshahrani, B. Controllability and Ulam–Hyers stability of fractional order linear systems with variable coefficients. Alex. Eng. J. 2022, 61, 6071–6076. [Google Scholar] [CrossRef]
- Kamran; Asif, M.; Shah, K.; Abdalla, B.; Abdeljawad, T. Numerical solution of Bagley–Torvik equation including Atangana-Baleanu derivative arising in fluid mechanics. Results Phys. 2023, 49, 106468. [Google Scholar] [CrossRef]
- Gambo, Y.Y.; Ameen, R.; Jarad, F.; Abdeljawad, T. Existence and uniqueness of solutions to fractional differential equations in the frame of generalized Caputo fractional derivatives. Adv. Differ. Equ. 2018, 2018, 134. [Google Scholar] [CrossRef] [Green Version]
- Nanware, J.A.; Dhaigude, D.B. Existence and uniqueness of solutions of differential equations of fractional order with integral boundary conditions. J. Nonlinear Sci. Appl. 2014, 7, 246–254. [Google Scholar] [CrossRef] [Green Version]
- Saha, K.K.; Sukavanam, N.; Pan, S. Existence and uniqueness of solutions to fractional differential equations with fractional boundary conditions. Alex. Eng. J. 2023, 72, 147–155. [Google Scholar] [CrossRef]
- Boulares, H.; Ardjouni, A.; Laskri, Y. Existence and uniqueness of solutions to fractional order nonlinear neutral differential equations. Appl. Math. E–Notes 2018, 18, 25–33. [Google Scholar]
- Gill, V.; Modi, K.; Singh, Y. Analytic solutions of fractional differential equation associated with RLC electrical circuit. J. Stat. Manag. Syst. 2018, 21, 575–582. [Google Scholar] [CrossRef]
- Shi, X.C.; Huang, L.L.; Deng, Z.G.; Liu, D. Analytical solutions of fractional differential equations using the convenient adomian series. Abstr. Appl. Anal. 2014, 2014, 284967. [Google Scholar] [CrossRef] [Green Version]
- Attar, M.A.; Roshani, M.; Hosseinzadeh, K.; Ganji, D.D. Analytical solution of fractional differential equations by Akbari–Ganji’s method. Partial. Differ. Equ. Appl. Math. 2022, 6, 100450. [Google Scholar] [CrossRef]
- Jia, H. Analytical Solutions for Fractional Differential Equations Using a General Conformable Multiple Laplace Transform Decomposition Method. Symmetry 2023, 15, 389. [Google Scholar] [CrossRef]
- Ibis, B.; Bayram, M.; Agargun, A.G. Applications of fractional differential transform method to fractional differential-algebraic equations. Eur. J. Pure Appl. Math. 2011, 4, 129–141. [Google Scholar]
- Karaagac, B. New exact solutions for some fractional order differential equations via improved sub-equation method. Discrete Contin. Dyn. Syst. 2019, 12, 447–454. [Google Scholar] [CrossRef] [Green Version]
- Ford, N.J.; Simpson, A.C. The numerical solution of fractional differential equations: Speed versus accuracy. Numer. Algorithms 2001, 26, 333–346. [Google Scholar] [CrossRef]
- Garrappa, R. Numerical solution of fractional differential equations: A survey and a software tutorial. Mathematics 2018, 6, 16. [Google Scholar] [CrossRef] [Green Version]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Li, Y.; Sun, N. Numerical solution of fractional differential equations using the generalized block pulse operational matrix. Comput. Math. Appl. 2011, 62, 1046–1054. [Google Scholar] [CrossRef] [Green Version]
- Uddin, M.; Khan, S.; Kamran. On the numerical solution of fractional order differential equations using transforms and quadrature. TWMS J. Appl. Eng. Math. 2019, 8, 267–274. [Google Scholar]
- Kamran; Ahmad, S.; Shah, K.; Abdeljawad, T.; Abdalla, B. On the Approximation of Fractal-Fractional Differential Equations Using Numerical Inverse Laplace Transform Methods. Comput. Model. Eng. Sci. 2023, 135, 2743–2765. [Google Scholar] [CrossRef]
- Sheng, H.; Li, Y.; Chen, Y. Application of numerical inverse Laplace transform algorithms in fractional calculus. J. Frankl. Inst. 2011, 348, 315–330. [Google Scholar] [CrossRef]
- Crump, K.S. Numerical inversion of Laplace transforms using a Fourier series approximation. J. ACM 1976, 23, 89–96. [Google Scholar] [CrossRef]
- De Hoog, F.R.; Knight, J.H.; Stokes, A.N. An improved method for numerical inversion of Laplace transforms. SIAM J. Sci. Stat. Comput. 1982, 3, 357–366. [Google Scholar] [CrossRef]
- Stehfest, H. Algorithm 368: Numerical inversion of Laplace transforms [D5]. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]
- Talbot, A. Theaccurate numerical inversion of Laplace transforms. IMA J. Appl. Math. 1979, 23, 97–120. [Google Scholar] [CrossRef] [Green Version]
- Davies, B.; Martin, B. Numerical inversion of the Laplace transform: A survey and comparison of methods. J. Comput. Phys. 1979, 33, 1–32. [Google Scholar] [CrossRef]
- Abate, J.; Valkó, P.P. Multi-precision Laplace transform inversion. Int. J. Numer. Methods Eng. 2004, 60, 979–993. [Google Scholar] [CrossRef]
- Weeks, W.T. Numerical inversion of Laplace transforms using Laguerre functions. J. ACM (JACM) 1966, 13, 419–429. [Google Scholar] [CrossRef]
- Abate, J.; Choudhury, G.L.; Whitt, W. On the Laguerre method for numerically inverting Laplace transforms. INFORMS J. Comput. 1996, 8, 413–427. [Google Scholar] [CrossRef] [Green Version]
- Brio, M.; Kano, P.O.; Moloney, J.V. Application of Weeks method for the numerical inversion of the Laplace transform to the matrix exponential. Commun. Math. Sci. 2005, 3, 335–372. [Google Scholar] [CrossRef] [Green Version]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and applications of fractional differential equations. In North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Kilbas, A.A.; Saigo, M.; Saxena, R.K. Generalized Mittag-Leffler function and generalized fractional calculus operators. Integral Transform. Spec. Funct. 2004, 15, 31–49. [Google Scholar] [CrossRef]
- Weideman, J.A.C. Algorithms for parameter selection in the Weeks method for inverting the Laplace transform. SIAM J. Sci. Comput. 1999, 21, 111–128. [Google Scholar] [CrossRef]
- Kumar, P.; Agrawal, O.P. An approximate method for numerical solution of fractional differential equations. Signal Process. 2006, 86, 2602–2610. [Google Scholar] [CrossRef]
- Weilbeer, M. Efficient Numerical Methods for Fractional Differential Equations and Their Analytical Background. Ph.D. Thesis, Technische Universität Braunschweig, Braunschweig, Germany, 2005. [Google Scholar]
- Rani, D.; Mishra, V.; Cattani, C. Numerical inverse Laplace transform for solving a class of fractional differential equations. Symmetry 2019, 11, 530. [Google Scholar] [CrossRef] [Green Version]
- Podlubny, I. Matrix approach to discrete fractional calculus. Fract. Calc. Appl. Anal. 2000, 3, 359–386. [Google Scholar]




| N | ||||
|---|---|---|---|---|
| 20 | 1.8035 | 3.9733 | 2.1213 | |
| 30 | 2.4871 | 5.4792 | 1.5070 | |
| 50 | 8.2630 | 1.8204 | 9.6074 | |
| 80 | 6.0354 | 1.3296 | 6.3258 | |
| 150 | 4.9259 | 1.0852 | 3.5762 | |
| 200 | 4.1822 | 9.2136 | 2.7660 | |
| 250 | 2.4210 | 5.3336 | 2.2599 | |
| 300 | 4.5779 | 1.0085 | 1.9116 | |
| 400 | 5.7410 | 1.2648 | 1.6436 | |
| 800 | 1.8042 | 3.9748 | 9.8380 |
| N | ||||
|---|---|---|---|---|
| 20 | 1.2757 | 3.2451 | 4.7261 | |
| 40 | 6.7695 | 1.7220 | 1.8397 | |
| 60 | 5.0217 | 1.2774 | 1.0649 | |
| 80 | 1.8286 | 4.6516 | 7.2735 | |
| 100 | 1.3060 | 3.3223 | 5.3878 | |
| 120 | 6.7202 | 1.7095 | 4.2151 | |
| 140 | 6.1228 | 1.5575 | 3.4158 | |
| 160 | 4.7414 | 1.2061 | 2.8644 | |
| 180 | 3.5444 | 9.0163 | 2.4342 | |
| 200 | 1.3183 | 3.3536 | 2.1308 | |
| [36] | 6.1390 |
| N | ||||
|---|---|---|---|---|
| 20 | 1.9976 | 4.3539 | 1.4882 | |
| 40 | 4.6340 | 1.0100 | 6.1742 | |
| 60 | 3.5713 | 7.7836 | 3.6354 | |
| 80 | 1.2002 | 2.6159 | 2.4726 | |
| 100 | 4.1455 | 9.0352 | 1.8310 | |
| 120 | 3.3696 | 7.3441 | 1.4324 | |
| 140 | 1.6198 | 3.5304 | 1.1596 | |
| 160 | 1.4706 | 3.2052 | 9.6314 | |
| 180 | 1.1823 | 2.5768 | 8.2130 | |
| 200 | 9.7606 | 2.1273 | 7.0906 |
| N | ||||
|---|---|---|---|---|
| 20 | 8.3012 | 8.3012 | 2.3953 | |
| 40 | 1.2261 | 1.2261 | 1.2510 | |
| 60 | 4.0476 | 4.0476 | 2.1214 | |
| 80 | 7.6084 | 7.6084 | 5.9160 | |
| 100 | 8.8868 | 8.8868 | 2.1932 | |
| 120 | 1.4327 | 1.4327 | 9.6073 | |
| 140 | 1.2495 | 1.2495 | 4.8024 | |
| 160 | 5.7061 | 5.7061 | 2.6232 | |
| 180 | 6.3372 | 6.3372 | 1.5543 | |
| 200 | 1.9100 | 1.9100 | 1.0129 | |
| 220 | 1.0096 | 1.0096 | 6.8743 |
| N | ||||
|---|---|---|---|---|
| 20 | 9.8946 | 1.6140 | 9.8357 | |
| 40 | 2.0725 | 3.3806 | 3.7709 | |
| 60 | 4.7066 | 7.6774 | 2.2084 | |
| 80 | 3.3449 | 5.4562 | 1.7700 | |
| 100 | 2.8179 | 4.5966 | 1.4797 | |
| 120 | 7.9360 | 1.2945 | 1.2782 | |
| 140 | 6.6768 | 1.0891 | 1.1295 | |
| 160 | 1.3086 | 2.1346 | 1.0147 | |
| 180 | 1.6979 | 2.7695 | 9.2328 | |
| 200 | 8.1590 | 1.3309 | 8.4849 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamran; Khan, S.U.; Haque, S.; Mlaiki, N. On the Approximation of Fractional-Order Differential Equations Using Laplace Transform and Weeks Method. Symmetry 2023, 15, 1214. https://doi.org/10.3390/sym15061214
Kamran, Khan SU, Haque S, Mlaiki N. On the Approximation of Fractional-Order Differential Equations Using Laplace Transform and Weeks Method. Symmetry. 2023; 15(6):1214. https://doi.org/10.3390/sym15061214
Chicago/Turabian StyleKamran, Sharif Ullah Khan, Salma Haque, and Nabil Mlaiki. 2023. "On the Approximation of Fractional-Order Differential Equations Using Laplace Transform and Weeks Method" Symmetry 15, no. 6: 1214. https://doi.org/10.3390/sym15061214
APA StyleKamran, Khan, S. U., Haque, S., & Mlaiki, N. (2023). On the Approximation of Fractional-Order Differential Equations Using Laplace Transform and Weeks Method. Symmetry, 15(6), 1214. https://doi.org/10.3390/sym15061214







