Magnetic Dipole Effects on Radiative Flow of Hybrid Nanofluid Past a Shrinking Sheet
Abstract
:1. Introduction
2. Mathematical Formulation
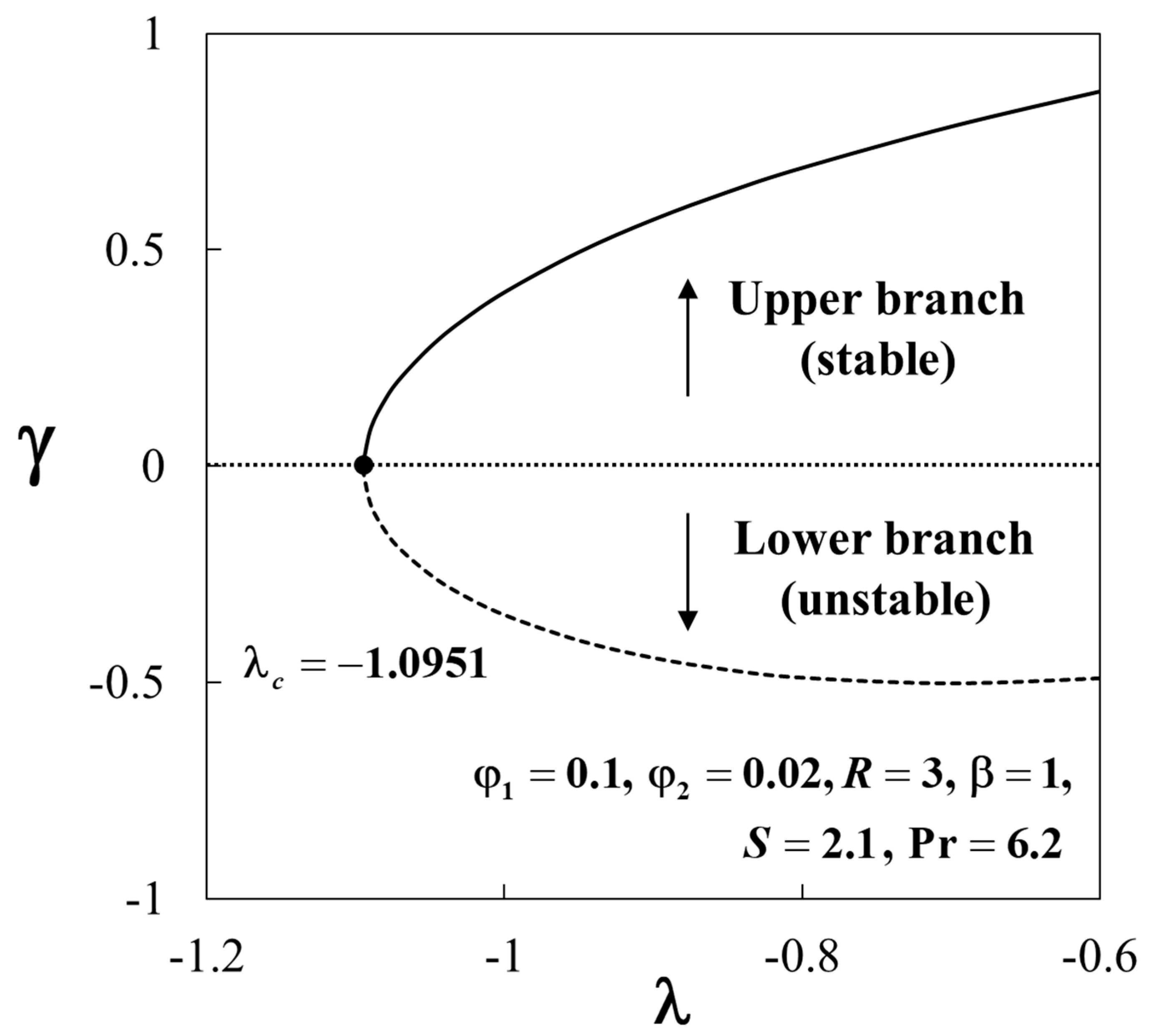
3. Stability Analysis
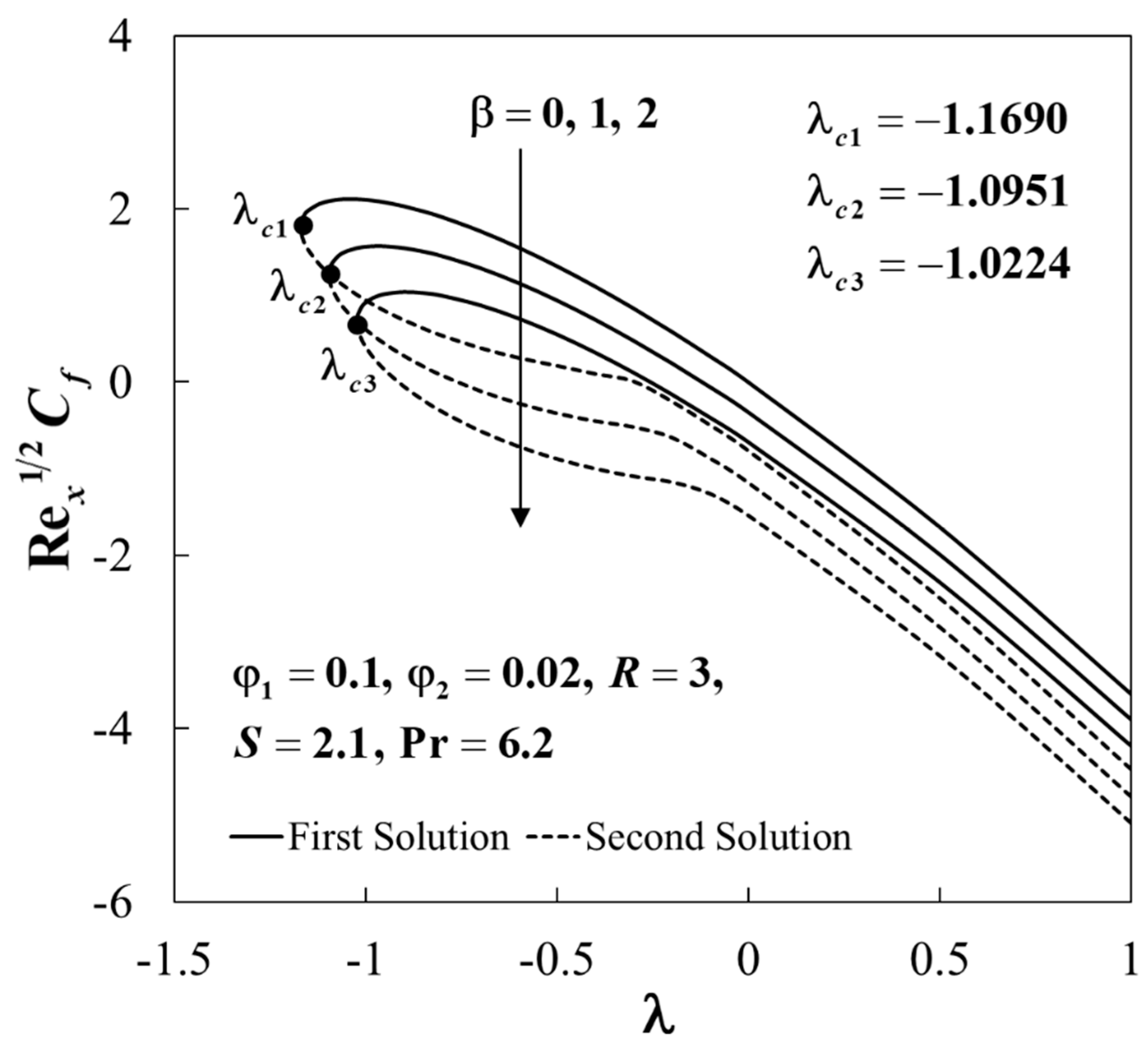
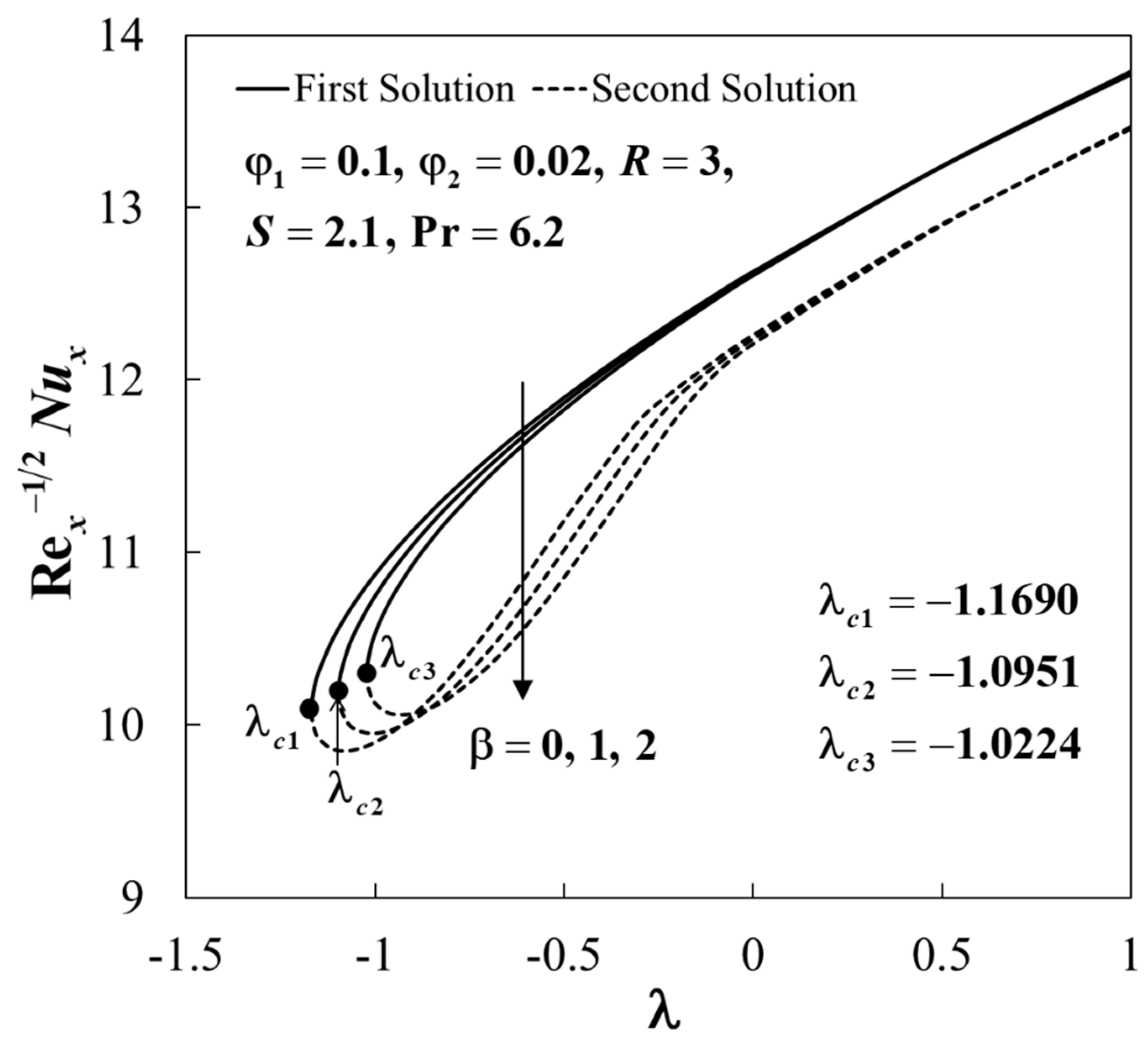
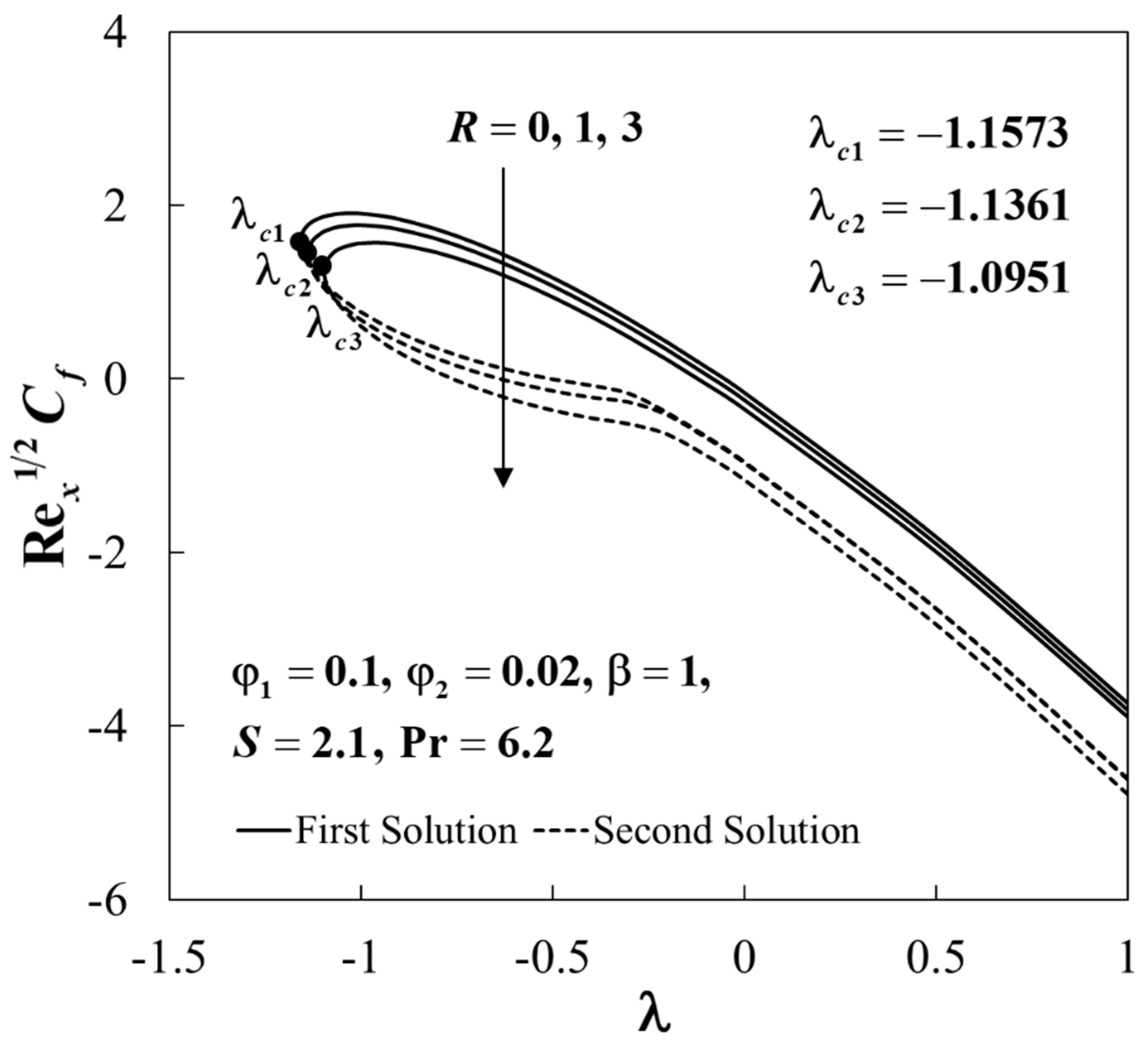
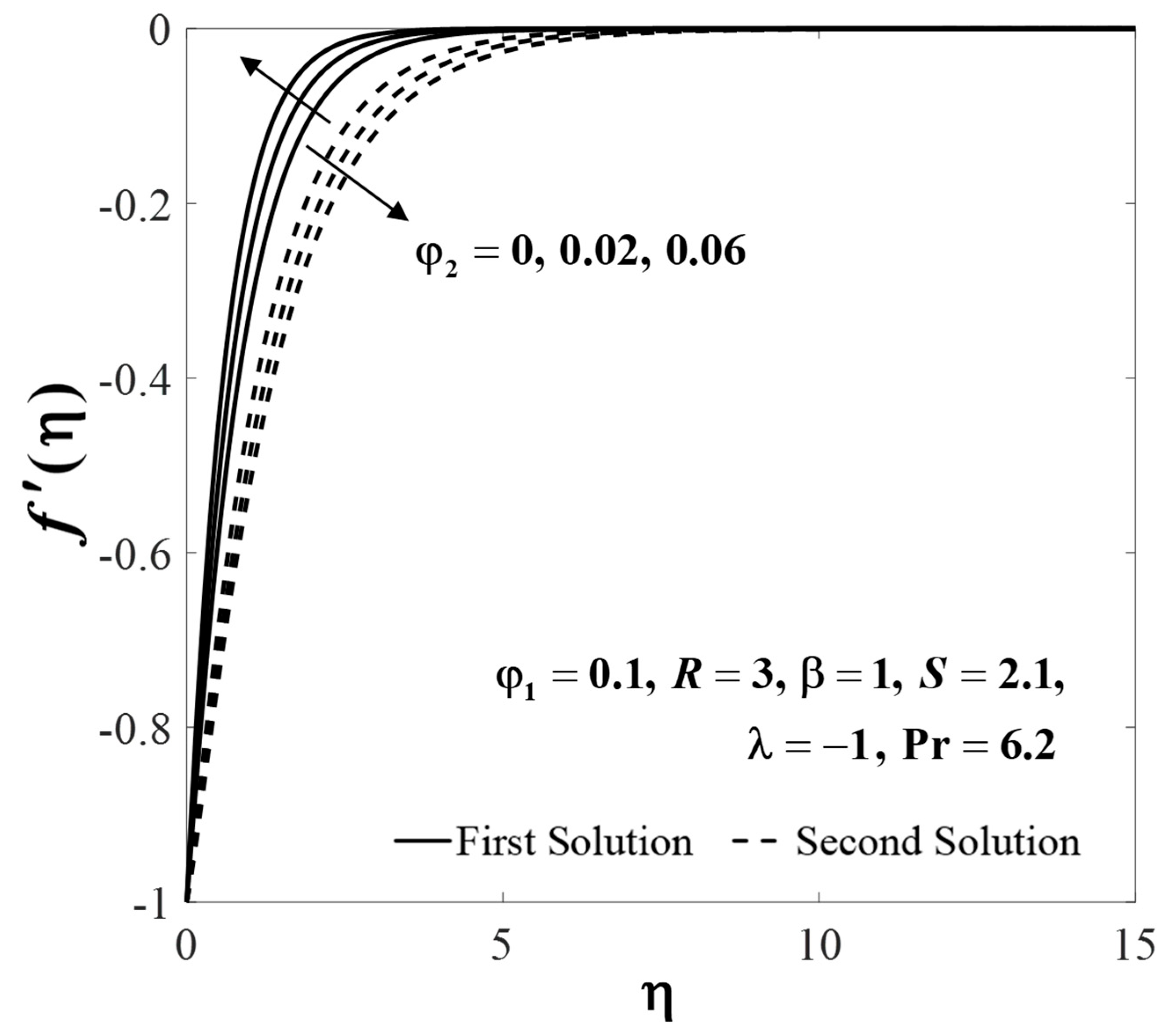
4. Results and Discussion
4.1. Computational Approach
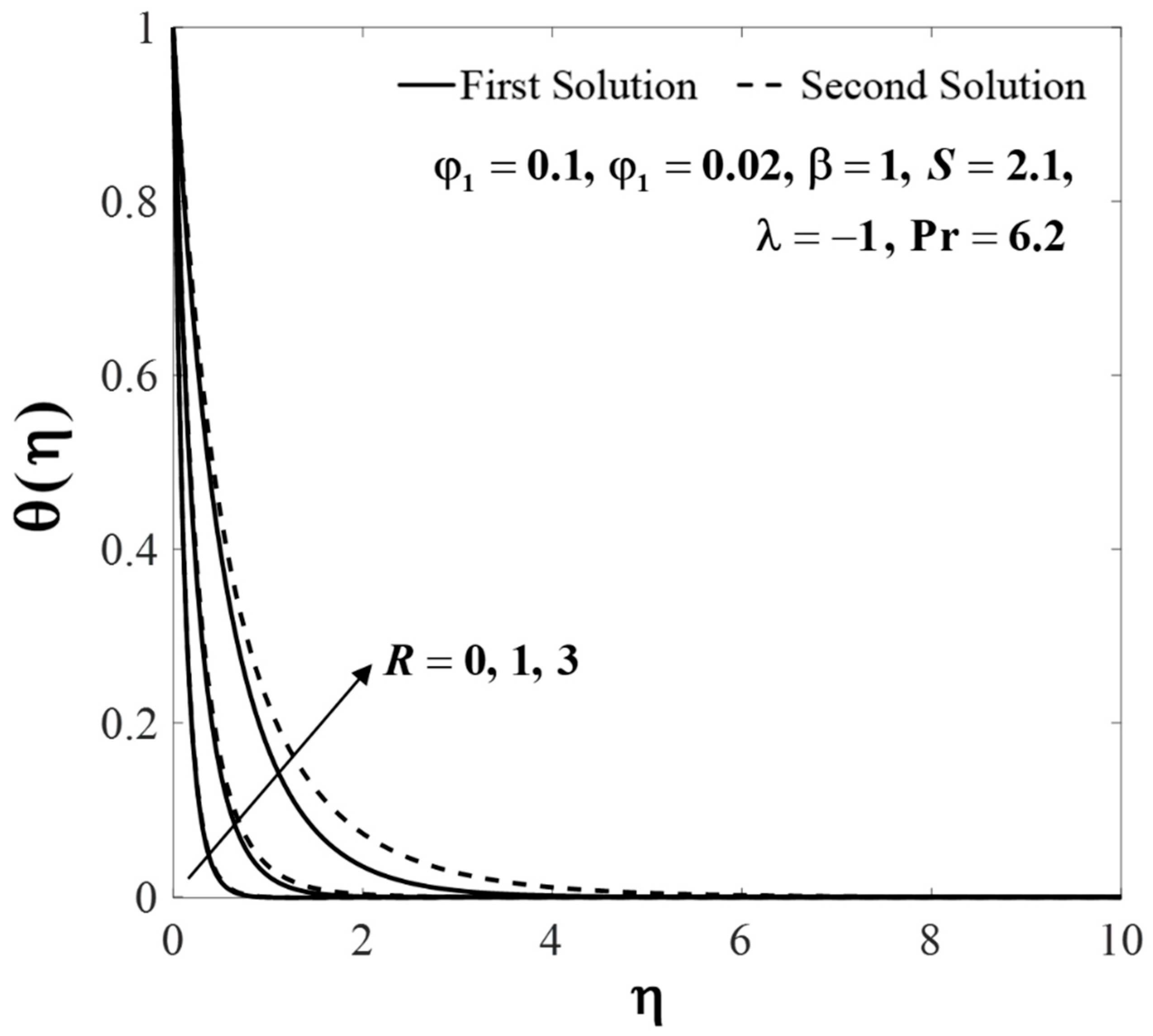
4.2. Results Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| constant | |
| skin friction coefficient | |
| specific heat at constant pressure | |
| heat capacitance of the fluid | |
| distance between origin and center of magnetic dipole | |
| dimensionless stream function | |
| magnetic field | |
| pyromagnetic coefficient | |
| thermal conductivity of the fluid | |
| Rosseland mean absorption coefficient | |
| local Nusselt number | |
| magnetization | |
| Prandtl number | |
| radiative heat flux in y direction | |
| surface heat flux | |
| radiation parameter | |
| local Reynolds number | |
| mass flux parameter | |
| time | |
| fluid temperature | |
| surface temperature | |
| Curie temperature | |
| velocity component in the x- and y-directions | |
| surface velocity | |
| mass flux velocity | |
| Cartesian coordinates | |
| Greek symbols | |
| dimensionless distance | |
| ferrohydrodynamic interaction | |
| eigenvalue | |
| magnetic field strength | |
| dimensionless temperature | |
| dimensionless coordinates | |
| dimensionless temperature | |
| stretching/shrinking parameter | |
| viscous dissipation | |
| magnetic permeability | |
| dynamic viscosity of the fluid | |
| kinematic viscosity of the fluid | |
| density of the fluid | |
| electrical conductivity of the fluid | |
| Stefan–Boltzmann constant | |
| dimensionless time variable | |
| wall shear stress | |
| scalar magnetic potential | |
| nanoparticle volume fractions for Al2O3 (alumina) | |
| nanoparticle volume fractions for Cu (copper) | |
| stream function | |
| Subscripts | |
| base fluid | |
| nanofluid | |
| hybrid nanofluid | |
| solid component for Al2O3 (alumina) | |
| solid component for Cu (copper) | |
| Superscript | |
| differentiation with respect to | |
References
- Choi, S.U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles. In Proceedings of the 1995 ASME International Mechanical Engineering Congress and Exposition, FED 231/MD, San Francisco, CA, USA, 12–17 November 1995. [Google Scholar] [CrossRef] [Green Version]
- Khanafer, K.; Vafai, K.; Lightstone, M. Buoyancy-Driven Heat Transfer Enhancement in a Two-Dimensional Enclosure Utilizing Nanofluids. Int. J. Heat Mass Transf. 2003, 46, 3639–3653. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu-Nada, E. Numerical Study of Natural Convection in Partially Heated Rectangular Enclosures Filled with Nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Das, S.K.; Choi, S.U.S.; Yu, W.; Pradeep, T. Nanofluids: Science and Technology; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008; ISBN 9780470074732. [Google Scholar]
- Minkowycz, W.J.; Sparrow, E.M.; Abraham, J.P. Nanoparticle Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA; Taylor & Fracis Group: New York, NY, USA, 2013; Volume 4, ISBN 9781439861950. [Google Scholar]
- Shenoy, A.; Sheremet, M.; Pop, I. Convective Flow and Heat Transfer from Wavy Surfaces: Viscous Fluids, Porous Media, and Nanofluids; CRC Press: Boca Raton, FL, USA; Taylor and Francis Group: New York, NY, USA, 2016; ISBN 9781498760904. [Google Scholar]
- Nield, D.A.; Bejan, A. Convection in Porous Media, 5th ed.; Springer International Publishing: New York, NY, USA, 2017; ISBN 9781461455400. [Google Scholar]
- Kakaç, S.; Pramuanjaroenkij, A. Review of Convective Heat Transfer Enhancement with Nanofluids. Int. J. Heat Mass Transf. 2009, 52, 3187–3196. [Google Scholar] [CrossRef]
- Manca, O.; Jaluria, Y.; Poulikakos, D. Heat Transfer in Nanofluids. Adv. Mech. Eng. 2010, 2, 380826. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D. Nanofluid Convective Heat Transfer Using Semi Analytical and Numerical Approaches: A Review. J. Taiwan Inst. Chem. Eng. 2016, 65, 43–77. [Google Scholar] [CrossRef]
- Myers, T.G.; Ribera, H.; Cregan, V. Does Mathematics Contribute to the Nanofluid Debate? Int. J. Heat Mass Transf. 2017, 111, 279–288. [Google Scholar] [CrossRef] [Green Version]
- Khanafer, K.; Vafai, K. Applications of Nanofluids in Porous Medium A Critical Review. J. Therm. Anal. Calorim. 2019, 135, 1479–1492. [Google Scholar] [CrossRef]
- Mahian, O.; Kianifar, A.; Kalogirou, S.A.; Pop, I.; Wongwises, S. A Review of the Applications of Nanofluids in Solar Energy. Int. J. Heat Mass Transf. 2013, 57, 582–594. [Google Scholar] [CrossRef]
- Mahian, O.; Kolsi, L.; Amani, M.; Estellé, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Siavashi, M.; Taylor, R.A.; Niazmand, H.; et al. Recent Advances in Modeling and Simulation of Nanofluid Flows—Part I: Fundamentals and Theory. Phys. Rep. 2019, 790, 1–48. [Google Scholar] [CrossRef]
- Mahian, O.; Kolsi, L.; Amani, M.; Estellé, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Taylor, R.A.; Abu-nada, E.; Rashidi, S.; et al. Recent Advances in Modeling and Simulation of Nanofluid Flows—Part II: Applications. Phys. Rep. 2019, 791, 1–59. [Google Scholar] [CrossRef]
- Turcu, R.; Darabont, A.; Nan, A.; Aldea, N.; Macovei, D.; Bica, D.; Vekas, L.; Pana, O.; Soran, M.L.; Koos, A.A.; et al. New Polypyrrole-Multiwall Carbon Nanotubes Hybrid Materials. J. Optoelectron. Adv. Mater. 2006, 8, 643–647. [Google Scholar]
- Jana, S.; Salehi-Khojin, A.; Zhong, W.H. Enhancement of Fluid Thermal Conductivity by the Addition of Single and Hybrid Nano-Additives. Thermochim. Acta 2007, 462, 45–55. [Google Scholar] [CrossRef]
- Sarkar, J.; Ghosh, P.; Adil, A. A Review on Hybrid Nanofluids: Recent Research, Development and Applications. Renew. Sustain. Energy Rev. 2015, 43, 164–177. [Google Scholar] [CrossRef]
- Hemmat Esfe, M.; Alirezaie, A.; Rejvani, M. An Applicable Study on the Thermal Conductivity of SWCNT-MgO Hybrid Nanofluid and Price-Performance Analysis for Energy Management. Appl. Therm. Eng. 2017, 111, 1202–1210. [Google Scholar] [CrossRef]
- Akilu, S.; Sharma, K.V.; Baheta, A.T.; Mamat, R. A Review of Thermophysical Properties of Water Based Composite Nanofluids. Renew. Sustain. Energy Rev. 2016, 66, 654–678. [Google Scholar] [CrossRef] [Green Version]
- Sidik, N.A.C.; Adamu, I.M.; Jamil, M.M.; Kefayati, G.H.R.; Mamat, R.; Najafi, G. Recent Progress on Hybrid Nanofluids in Heat Transfer Applications: A Comprehensive Review. Int. Commun. Heat Mass Transf. 2016, 78, 68–79. [Google Scholar] [CrossRef]
- Sundar, L.S.; Sharma, K.V.; Singh, M.K.; Sousa, A.C.M. Hybrid Nanofluids Preparation, Thermal Properties, Heat Transfer and Friction Factor—A Review. Renew. Sustain. Energy Rev. 2017, 68, 185–198. [Google Scholar] [CrossRef]
- Leong, K.Y.; Ku Ahmad, K.Z.; Ong, H.C.; Ghazali, M.J.; Baharum, A. Synthesis and Thermal Conductivity Characteristic of Hybrid Nanofluids—A Review. Renew. Sustain. Energy Rev. 2017, 75, 868–878. [Google Scholar] [CrossRef]
- Babu, J.A.R.; Kumar, K.K.; Rao, S.S. State-of-Art Review on Hybrid Nanofluids. Renew. Sustain. Energy Rev. 2017, 77, 551–565. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Hybrid Nanofluids for Heat Transfer Applications—A State-of-the-Art Review. Int. J. Heat Mass Transf. 2018, 125, 82–103. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Mirlohi, A.; Alhuyi Nazari, M.; Ghasempour, R. A Review of Thermal Conductivity of Various Nanofluids. J. Mol. Liq. 2018, 265, 181–188. [Google Scholar] [CrossRef]
- Devi, S.P.A.; Devi, S.S.U. Numerical Investigation of Hydromagnetic Hybrid Cu- Al2O3/Water Nanofluid Flow over a Permeable Stretching Sheet with Suction. Int. J. Nonlinear Sci. Numer. Simul. 2016, 17, 249–257. [Google Scholar] [CrossRef]
- Devi, S.S.U.; Devi, S.P.A. Numerical Investigation of Three-Dimensional Hybrid Cu–Al2O3/Water Nanofluid Flow over a Stretching Sheet with Effecting Lorentz Force Subject to Newtonian Heating. Can. J. Phys. 2016, 94, 490–496. [Google Scholar] [CrossRef]
- Suresh, S.; Venkitaraj, K.P.; Selvakumar, P.; Chandrasekar, M. Synthesis of Al2O3-Cu/Water Hybrid Nanofluids Using Two Step Method and Its Thermo Physical Properties. Colloids Surf. A Physicochem. Eng. Asp. 2011, 388, 41–48. [Google Scholar] [CrossRef]
- Hayat, T.; Nadeem, S. Heat Transfer Enhancement with Ag–CuO/Water Hybrid Nanofluid. Results Phys. 2017, 7, 2317–2324. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Unsteady Flow and Heat Transfer Past a Stretching/Shrinking Sheet in a Hybrid Nanofluid. Int. J. Heat Mass Transf. 2019, 136, 288–297. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid Nanofluid Flow on a Shrinking Cylinder with Prescribed Surface Heat Flux. Int. J. Numer. Methods Heat Fluid Flow 2021, 31, 1987–2004. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid Nanofluid Flow over a Permeable Non-Isothermal Shrinking Surface. Mathematics 2021, 9, 538. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Abu Bakar, S.; Ishak, A. Unsteady Stagnation-Point Flow of a Hybrid Nanofluid over a Spinning Disk: Analysis of Dual Solutions. Neural Comput. Appl. 2022, 34, 8193–8210. [Google Scholar] [CrossRef]
- Yasir, M.; Sarfraz, M.; Khan, M.; Alzahrani, A.K.; Ullah, M.Z. Estimation of Dual Branch Solutions for Homann Flow of Hybrid Nanofluid towards Biaxial Shrinking Surface. J. Pet. Sci. Eng. 2022, 218, 110990. [Google Scholar] [CrossRef]
- Hayat, T.; Nadeem, S.; Khan, A.U. Rotating Flow of Ag-CuO/H2O Hybrid Nanofluid with Radiation and Partial Slip Boundary Effects. Eur. Phys. J. E 2018, 41, 75. [Google Scholar] [CrossRef]
- Jamshed, W.; Aziz, A. Cattaneo–Christov Based Study of TiO2–CuO/EG Casson Hybrid Nanofluid Flow over a Stretching Surface with Entropy Generation. Appl. Nanosci. 2018, 8, 685–698. [Google Scholar] [CrossRef]
- Yousefi, M.; Dinarvand, S.; Eftekhari Yazdi, M.; Pop, I. Stagnation-Point Flow of an Aqueous Titania-Copper Hybrid Nanofluid toward a Wavy Cylinder. Int. J. Numer. Methods Heat Fluid Flow 2018, 28, 1716–1735. [Google Scholar] [CrossRef]
- Dinarvand, S. Nodal/Saddle Stagnation-Point Boundary Layer Flow of CuO–Ag/Water Hybrid Nanofluid: A Novel Hybridity Model. Microsyst. Technol. 2019, 25, 2609–2623. [Google Scholar] [CrossRef]
- Subhani, M.; Nadeem, S. Numerical Analysis of Micropolar Hybrid Nanofluid. Appl. Nanosci. 2019, 9, 447–459. [Google Scholar] [CrossRef]
- Aly, E.H.; Pop, I. MHD Flow and Heat Transfer over a Permeable Stretching/Shrinking Sheet in a Hybrid Nanofluid with a Convective Boundary Condition. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 3012–3038. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Waini, I.; Zainal, N.A.; Hamzah, K. Hybrid Nanofluid Flow Past a Shrinking Cylinder with Prescribed Surface Heat Flux. Symmetry 2020, 12, 1493. [Google Scholar] [CrossRef]
- Atashafrooz, M.; Sajjadi, H.; Amiri Delouei, A. Simulation of combined convective-radiative heat transfer of hybrid nanofluid flow inside an open trapezoidal enclosure considering the magnetic force impacts. J. Magn. Magn. Mater. 2023, 567, 170354. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Cimpean, D.S.; Pop, I. Thermogravitational Convection of Hybrid Nanofluid in a Porous Chamber with a Central Heat-Conducting Body. Symmetry 2020, 12, 593. [Google Scholar] [CrossRef] [Green Version]
- Neuringer, J.L. Some Viscous Flows of a Saturated Ferro-Fluid under the Combined Influence of Thermal and Magnetic Field Gradients. Int. J. Non-Linear Mech. 1966, 1, 123–137. [Google Scholar] [CrossRef]
- Andersson, H.I.; Valnes, O.A. Flow of a Heated Ferrofluid over a Stretching Sheet in the Presence of a Magnetic Dipole. Acta Mech. 1998, 128, 39–47. [Google Scholar] [CrossRef]
- Majeed, A.; Zeeshan, A.; Hayat, T. Analysis of Magnetic Properties of Nanoparticles Due to Applied Magnetic Dipole in Aqueous Medium with Momentum Slip Condition. Neural Comput. Appl. 2019, 31, 189–197. [Google Scholar] [CrossRef]
- Muhammad, N.; Nadeem, S. Ferrite Nanoparticles Ni-ZnFe2O4, Mn-ZnFe2O4 and Fe2O4 in the Flow of Ferromagnetic Nanofluid. Eur. Phys. J. Plus 2017, 132. [Google Scholar] [CrossRef]
- Muhammad, N.; Nadeem, S.; Mustafa, M.T. Analysis of Ferrite Nanoparticles in the Flow of Ferromagnetic Nanofluid. PLoS ONE 2018, 13, e0188460. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zeeshan, A.; Majeed, A. Heat Transfer Analysis of Jeffery Fluid Flow over a Stretching Sheet with Suction/Injection and Magnetic Dipole Effect. Alex. Eng. J. 2016, 55, 2171–2181. [Google Scholar] [CrossRef] [Green Version]
- Nadeem, S.; Raishad, I.; Muhammad, N.; Mustafa, M.T. Mathematical Analysis of Ferromagnetic Fluid Embedded in a Porous Medium. Results Phys. 2017, 7, 2361–2368. [Google Scholar] [CrossRef]
- Ijaz, M.; Ayub, M. Simulation of Magnetic Dipole and Dual Stratification in Radiative Flow of Ferromagnetic Maxwell Fluid. Heliyon 2019, 5, e01465. [Google Scholar] [CrossRef] [Green Version]
- Hayat, T.; Ahmad, S.; Khan, M.I.; Alsaedi, A. Simulation of Ferromagnetic Nanomaterial Flow of Maxwell Fluid. Results Phys. 2018, 8, 34–40. [Google Scholar] [CrossRef]
- Hayat, T.; Ahmad, S.; Khan, M.I.; Alsaedi, A. Exploring Magnetic Dipole Contribution on Radiative Flow of Ferromagnetic Williamson Fluid. Results Phys. 2018, 8, 545–551. [Google Scholar] [CrossRef]
- Nadeem, S.; Ullah, N.; Khan, A.U.; Akbar, T. Effect of Homogeneous-Heterogeneous Reactions on Ferrofluid in the Presence of Magnetic Dipole along a Stretching Cylinder. Results Phys. 2017, 7, 3574–3582. [Google Scholar] [CrossRef]
- Muhammad, N.; Nadeem, S.; Haq, R.U. Heat Transport Phenomenon in the Ferromagnetic Fluid over a Stretching Sheet with Thermal Stratification. Results Phys. 2017, 7, 854–861. [Google Scholar] [CrossRef]
- Titus, L.S.R.; Abraham, A. Ferromagnetic Liquid Flow Due to Gravity-Aligned Stretching of an Elastic Sheet. J. Appl. Fluid Mech. 2015, 8, 591–600. [Google Scholar] [CrossRef]
- Zeeshan, A.; Majeed, A.; Ellahi, R. Effect of Magnetic Dipole on Viscous Ferro-Fluid Past a Stretching Surface with Thermal Radiation. J. Mol. Liq. 2016, 215, 549–554. [Google Scholar] [CrossRef]
- Yasmeen, T.; Hayat, T.; Khan, M.I.; Imtiaz, M.; Alsaedi, A. Ferrofluid Flow by a Stretched Surface in the Presence of Magnetic Dipole and Homogeneous-Heterogeneous Reactions. J. Mol. Liq. 2016, 223, 1000–1005. [Google Scholar] [CrossRef]
- Rosseland, S. Astrophysik und Atom-Theoretische Grundlagen; Springer: Berlin/Heidelberg, Germany, 1931; ISBN 9783662245330. [Google Scholar]
- Cortell, R. Heat and Fluid Flow Due to Non-Linearly Stretching Surfaces. Appl. Math. Comput. 2011, 217, 7564–7572. [Google Scholar] [CrossRef] [Green Version]
- Magyari, E.; Pantokratoras, A. Note on the Effect of Thermal Radiation in the Linearized Rosseland Approximation on the Heat Transfer Characteristics of Various Boundary Layer Flows. Int. Commun. Heat Mass Transf. 2011, 38, 554–556. [Google Scholar] [CrossRef]
- Merkin, J.H. On Dual Solutions Occurring in Mixed Convection in a Porous Medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M.J. The Effect of Transpiration on Self-Similar Boundary Layer Flow over Moving Surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed Convection Boundary-Layer Flow near the Stagnation Point on a Vertical Surface in a Porous Medium: Brinkman Model with Slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Shampine, L.F.; Gladwell, I.; Thompson, S. Solving ODEs with MATLAB; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Khan, W.A.; Pop, I. Boundary-Layer Flow of a Nanofluid Past a Stretching Sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Hamad, M.A.A. Analytical Solution of Natural Convection Flow of a Nanofluid over a Linearly Stretching Sheet in the Presence of Magnetic Field. Int. Commun. Heat Mass Transf. 2011, 38, 487–492. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Flow and Heat Transfer along a Permeable Stretching/Shrinking Curved Surface in a Hybrid Nanofluid. Phys. Scr. 2019, 94, 105219. [Google Scholar] [CrossRef]

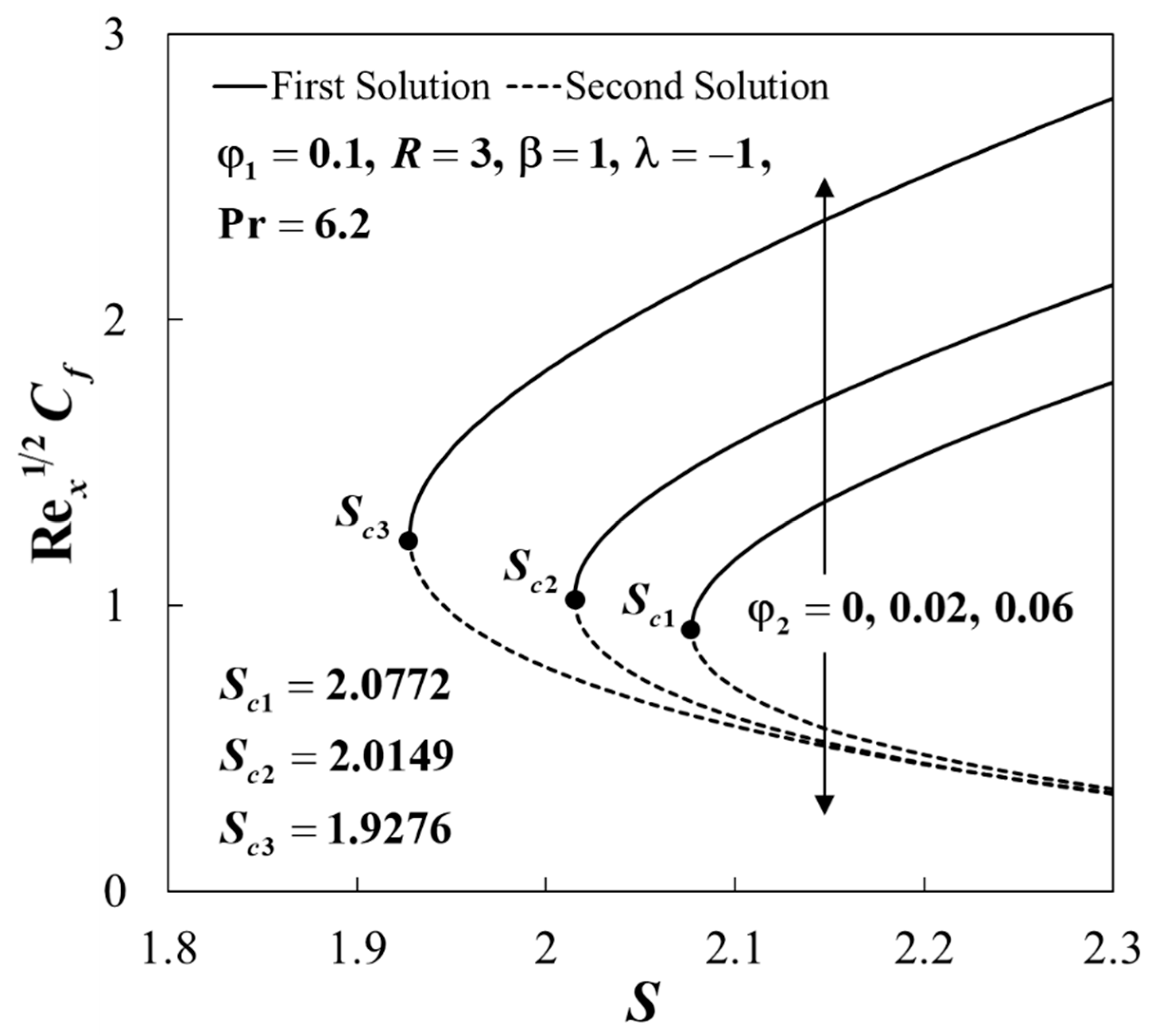
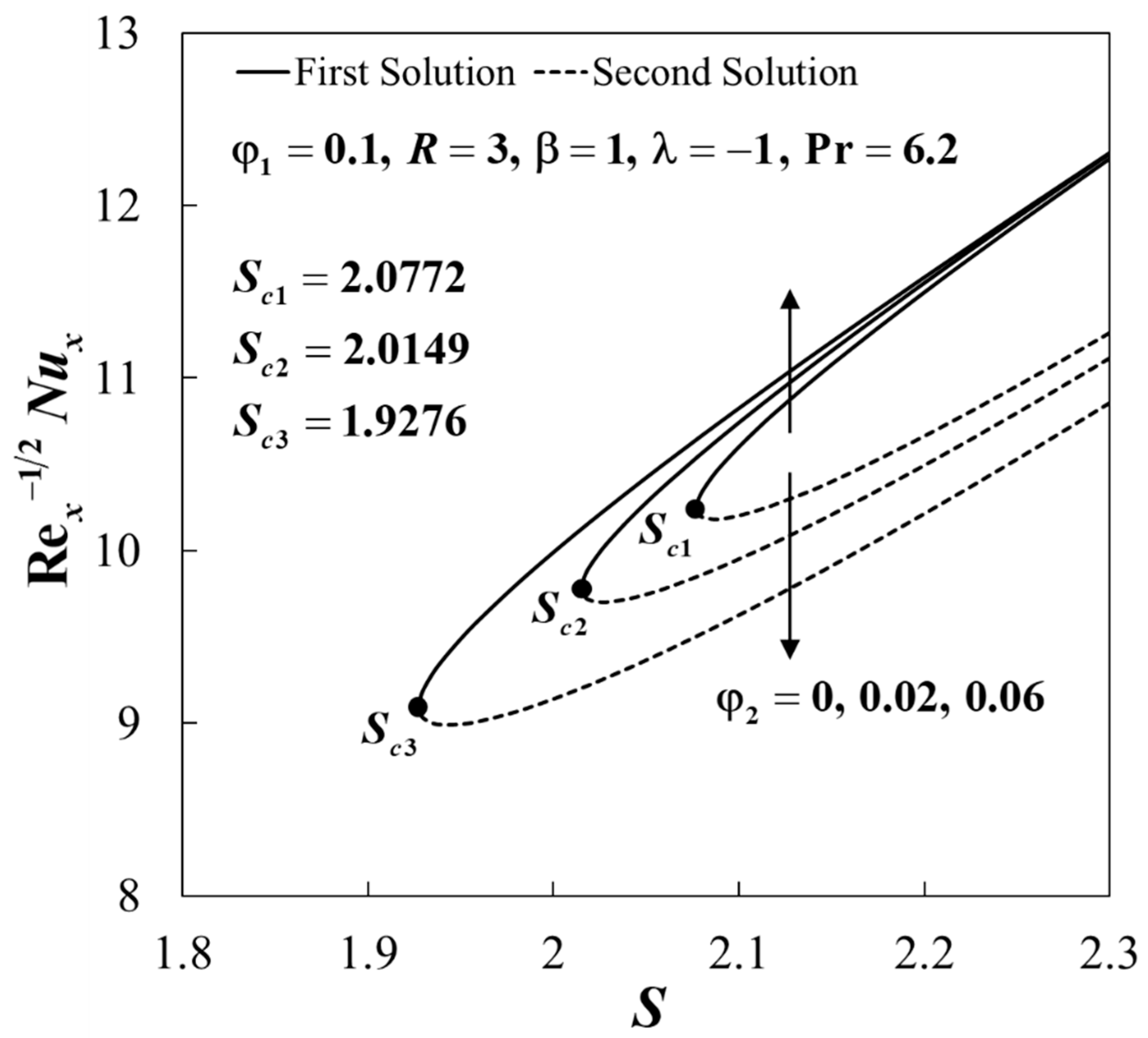
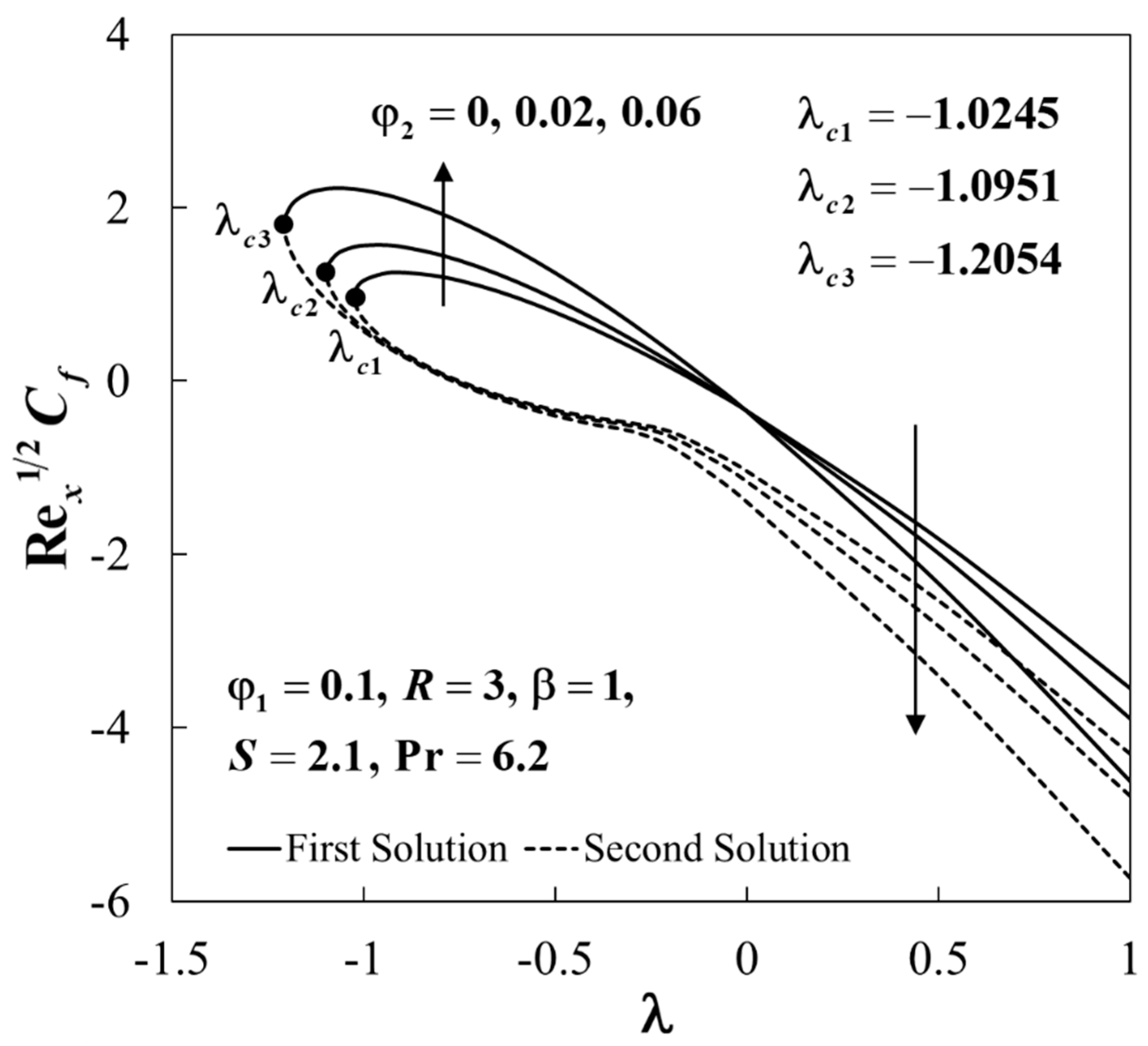
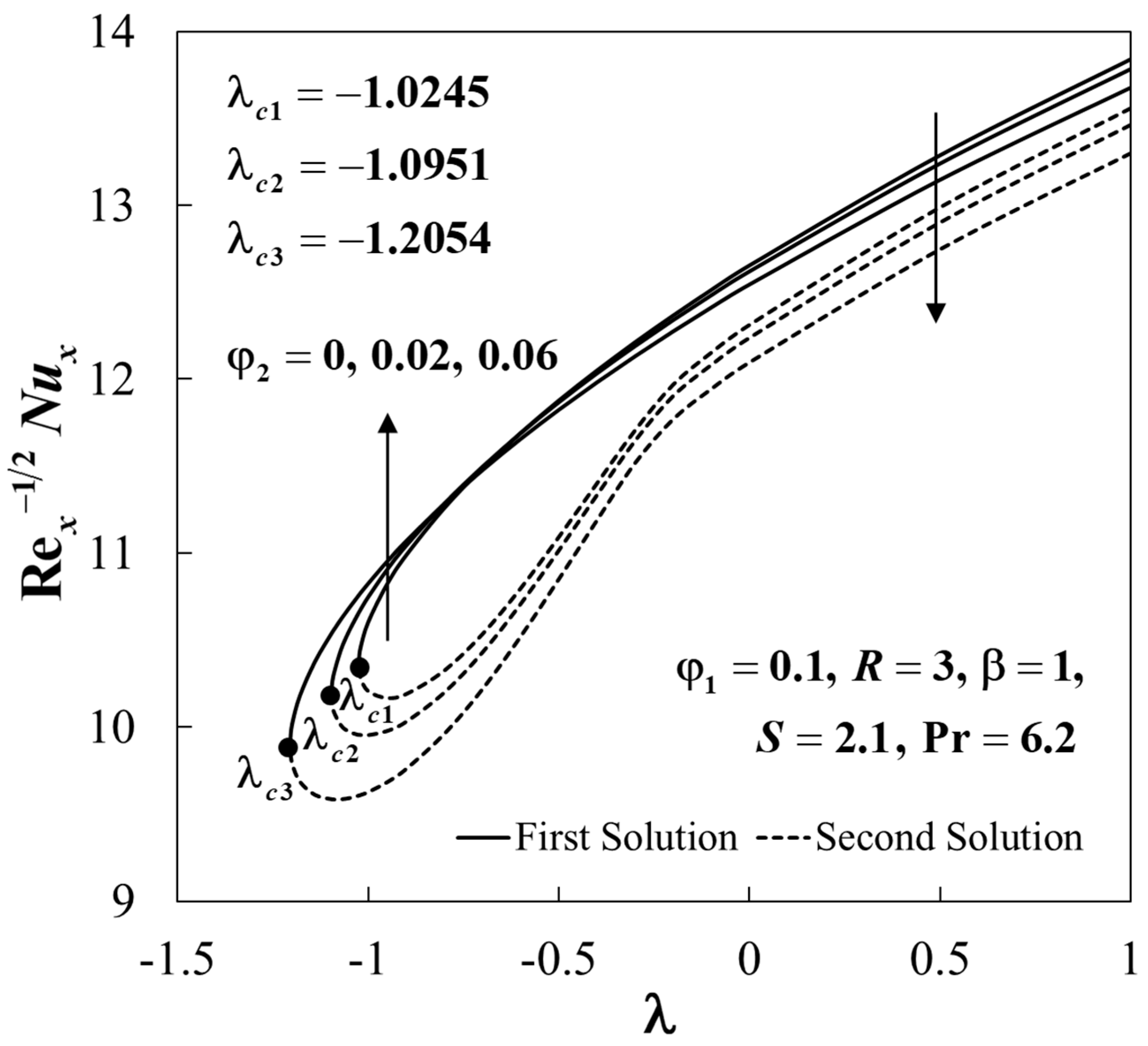

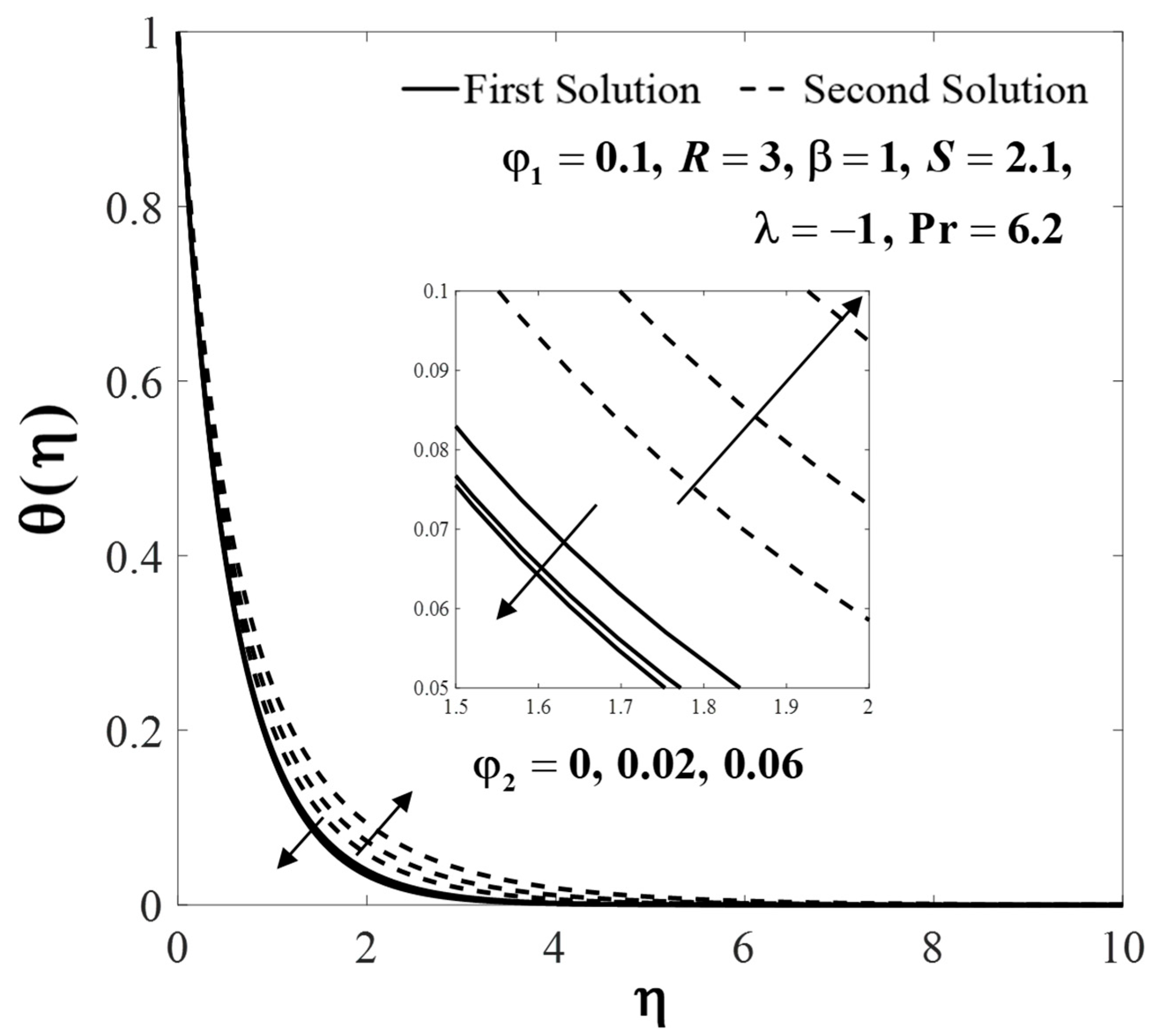
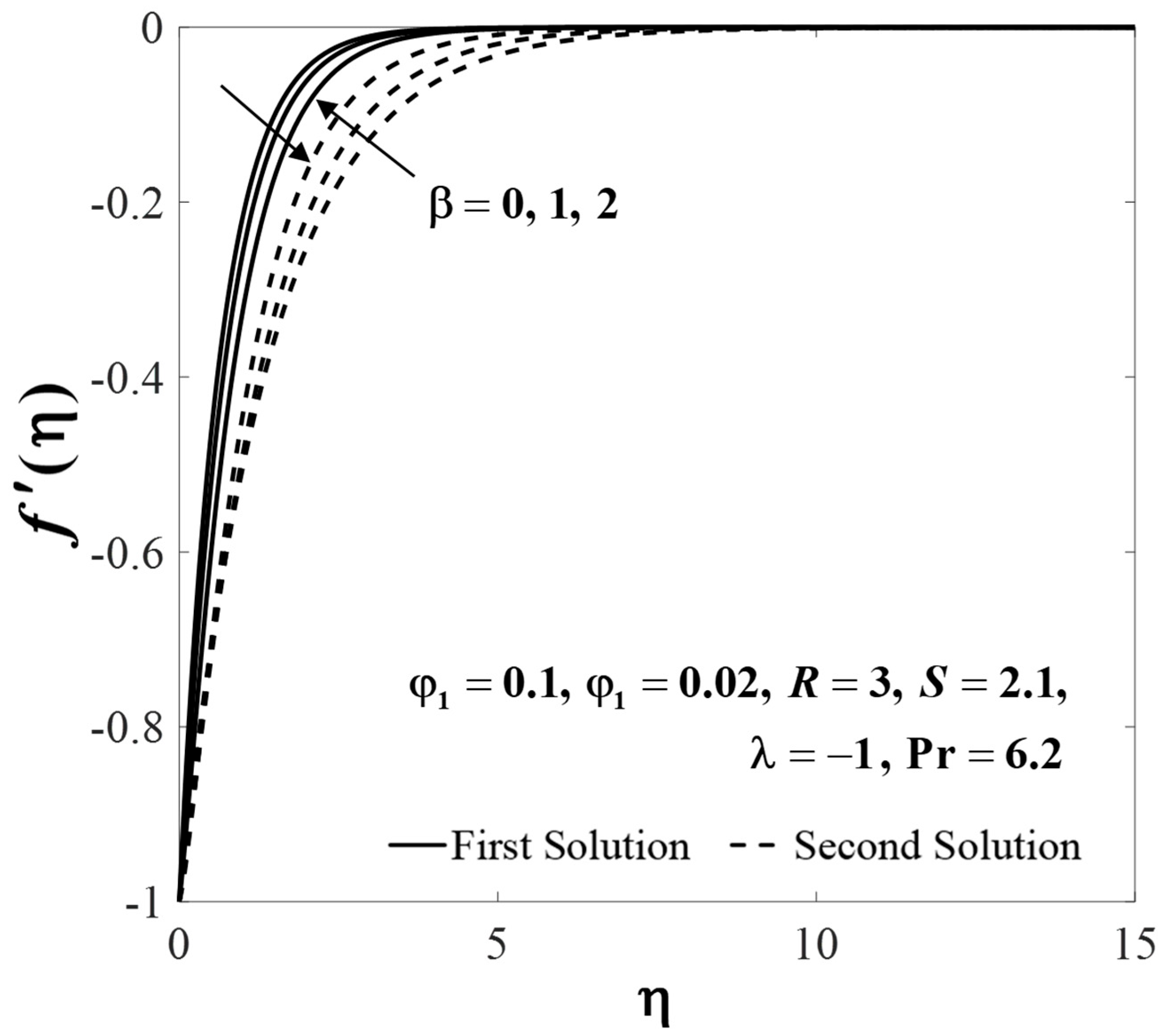
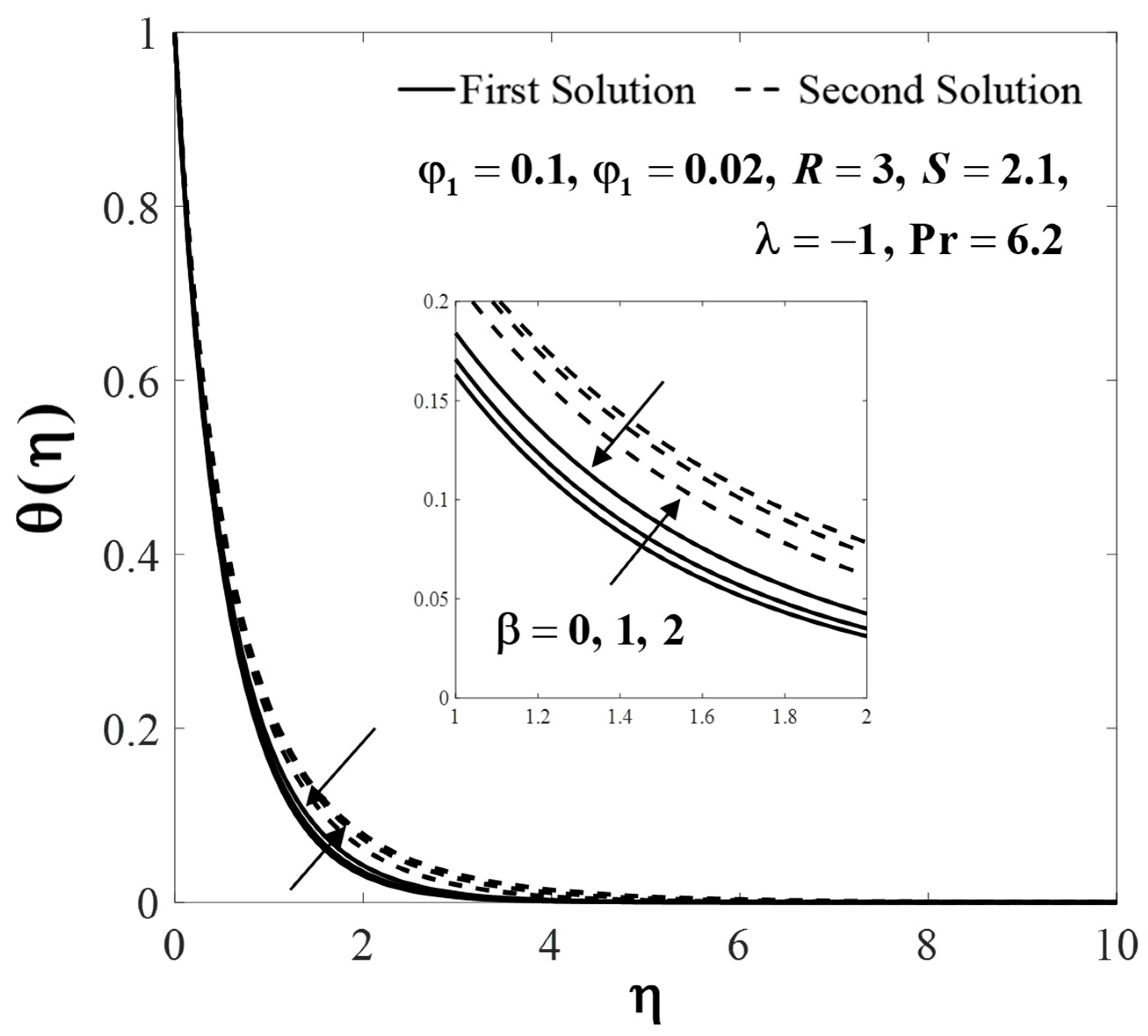
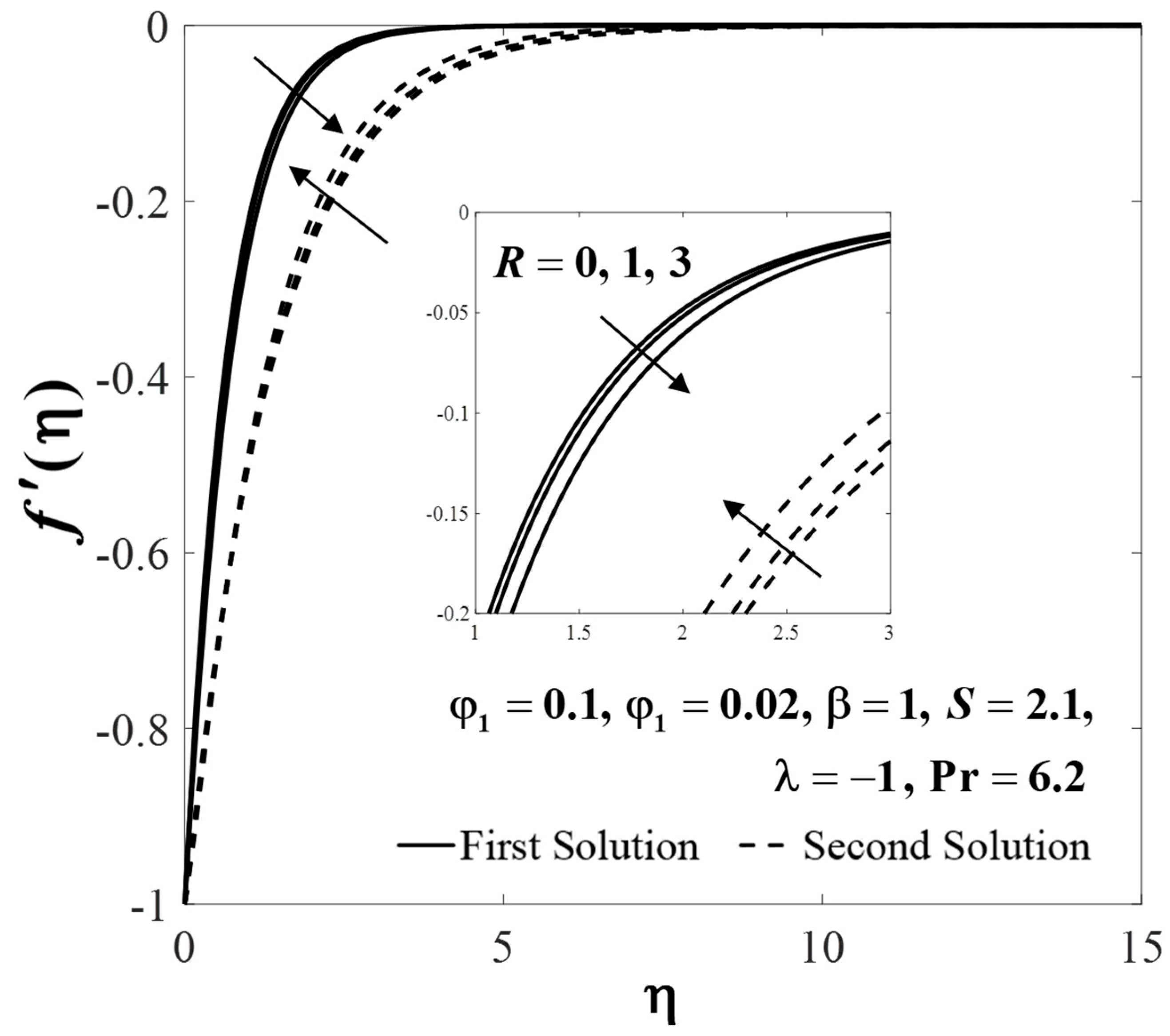
| Thermophysical Properties | Nanofluid | Hybrid Nanofluid |
|---|---|---|
| Dynamic viscosity | ||
| Heat capacity | ||
| Density | ||
| Thermal conductivity | where |
| Thermophysical Properties | Water | ||
|---|---|---|---|
| 400 | 40 | 0.613 | |
| 385 | 765 | 4179 | |
| 8933 | 3970 | 997.1 | |
| Prandtl number, | 6.2 |
| Pr | Devi and Devi [27] | Waini et al. [31] | Khan and Pop [67] | Hamad [68] | Present Results |
|---|---|---|---|---|---|
| 2 | 0.91135 | 0.911353 | 0.9113 | 0.91136 | 0.91136 |
| 6.2 | - | - | - | - | 1.77095 |
| 7 | 1.89540 | 1.895400 | 1.8954 | 1.89540 | 1.89540 |
| 20 | 3.35390 | 3.353902 | 3.3539 | 3.35390 | 3.35390 |
| Waini et al. [69] | Hamad [68] | Present Results | Hamad [68] | Present Results | |
|---|---|---|---|---|---|
| 0.05 | 1.10892 | 1.10892 | 1.10892 | 1.59899 | 1.59899 |
| 0.1 | 1.17475 | 1.17475 | 1.17475 | 1.45207 | 1.45207 |
| 0.15 | 1.20886 | 1.20886 | 1.20886 | 1.32465 | 1.32465 |
| 0.2 | 1.21804 | 1.21804 | 1.21804 | 1.21290 | 1.21290 |
(Nanofluid) | (Hybrid Nanofluid) | |||||
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | −1.00000 | 1.77095 | −1.29975 | 1.96441 |
| 0.02 | 0 | 0 | −1.10419 | 1.80221 | −1.40946 | 2.00140 |
| 0.04 | 0 | 0 | −1.20831 | 1.83408 | −1.52069 | 2.03888 |
| 0.06 | 0 | 0 | −1.31329 | 1.86658 | −1.63408 | 2.07693 |
| 0.02 | 0.5 | 0 | −1.24681 | 1.78936 | −1.56126 | 1.98814 |
| 0.02 | 1 | 0 | −1.39058 | 1.77601 | −1.71411 | 1.97443 |
| 0.02 | 2 | 0 | −1.68191 | 1.74768 | −2.02320 | 1.94549 |
| 0.02 | 3 | 0 | −1.97900 | 1.71678 | −2.33737 | 1.91423 |
| 0.02 | 1 | 0.5 | −1.41962 | 2.16737 | −1.73651 | 2.30785 |
| 0.02 | 1 | 1 | −1.43792 | 2.45694 | −1.75163 | 2.56590 |
| 0.02 | 1 | 2 | −1.46084 | 2.87521 | −1.77150 | 2.95160 |
| 0.02 | 1 | 3 | −1.47519 | 3.17146 | −1.78439 | 3.23279 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Waini, I.; Khashi’ie, N.S.; Zainal, N.A.; Hamzah, K.B.; Kasim, A.R.M.; Ishak, A.; Pop, I. Magnetic Dipole Effects on Radiative Flow of Hybrid Nanofluid Past a Shrinking Sheet. Symmetry 2023, 15, 1318. https://doi.org/10.3390/sym15071318
Waini I, Khashi’ie NS, Zainal NA, Hamzah KB, Kasim ARM, Ishak A, Pop I. Magnetic Dipole Effects on Radiative Flow of Hybrid Nanofluid Past a Shrinking Sheet. Symmetry. 2023; 15(7):1318. https://doi.org/10.3390/sym15071318
Chicago/Turabian StyleWaini, Iskandar, Najiyah Safwa Khashi’ie, Nurul Amira Zainal, Khairum Bin Hamzah, Abdul Rahman Mohd Kasim, Anuar Ishak, and Ioan Pop. 2023. "Magnetic Dipole Effects on Radiative Flow of Hybrid Nanofluid Past a Shrinking Sheet" Symmetry 15, no. 7: 1318. https://doi.org/10.3390/sym15071318
APA StyleWaini, I., Khashi’ie, N. S., Zainal, N. A., Hamzah, K. B., Kasim, A. R. M., Ishak, A., & Pop, I. (2023). Magnetic Dipole Effects on Radiative Flow of Hybrid Nanofluid Past a Shrinking Sheet. Symmetry, 15(7), 1318. https://doi.org/10.3390/sym15071318











