Abstract
This study addresses the nonlinear forced vibration of a functionally graded (FG) nanobeam subjected to mechanical impact and electromagnetic actuation. Two symmetrical actuators were present in the mechanical model, and their mechanical behaviors were analyzed considering the symmetry in actuation. The model considered the longitudinal–transverse vibration of a simple supported Euler–Bernoulli beam, which accounted for von Kármán geometric nonlinearity, including the first-order strain–displacement relationship. The FG nanobeam was made of a mixture of metals and ceramics, while the volume fraction varied in terms of thickness when a power law function was used. The nonlocal Eringen theory of elasticity was used to study the simple supported Euler–Bernoulli nanobeam. The nonlinear governing equations of the FG nanobeam and the associated boundary conditions were gained using Hamilton’s principle. To truncate the system with an infinite degree of freedom, the coupled longitudinal–transverse governing equations were discretized using the Galerkin–Bubnov approach. The resulting nonlinear, ordinary differential equations, which took into account the curvature of the nanobeam, were studied via the Optimal Auxiliary Functions Method (OAFM). For this complex nonlinear problem, an explicit, analytical, approximate solution was proposed near the primary resonance. The simultaneous effects of the following elements were considered in this paper: the presence of a curved nanobeam; the transversal inertia, which is not neglected in this paper; the mechanical impact; and electromagnetic actuation. The present study proposes a highly accurate analytical solution to the abovementioned conditions. Moreover, in these conditions, the study of local stability was developed using two variable expansion methods, the Jacobian matrix and Routh–Hurwitz criteria, and global stability was studied using the Lyapunov function.
1. Introduction
Functionally graded (FG) materials were first introduced by Japanese scientists [1] and represent a new, improved kind of composite material that is fabricated to have spatially varied material properties, providing a nonuniform microstructure. FG materials are generally composed of two different parts, ceramic and metal, and they can improve the properties of thermal barrier systems, as cracking and delamination are reduced by the smooth transition of material properties. These new materials have been employed in many engineering applications in various fields, such as nuclear reactors, the biomedical industry, aerospace structures, chemical plants, the defense industry, electronics, etc.
FG materials have attracted considerable interest from many researchers in structural dynamics and statics, and they have been extensively studied, especially in the last few years. Alimoradzadeh et al. [2] proposed the nonlinear vibration analysis of a simply supported axial FG beam subjected to a moving harmonic load and resting on a Winkler–Pasternak nonlinear elastic foundation using Green’s strain tensor. An approximate analytical solution for forced nonlinear vibration was obtained using the variational iteration method. The nonlinear forced vibration of FG carbon nanotube-reinforced composite beams resting on a nonlinear viscoelastic foundation was considered by Shafiei and Setoodeh [3]. The Eshelby–Mori–Tanaka approach and extended rule of mixtures were used to predict the material’s properties, and the variational iteration method was applied to solve the nonlinear governing equation. A comprehensive study on the size-dependent coupled longitudinal–transverse rotational free vibration behaviors of post-buckled FG micro- and nanobeams based on Mindlin’s strain gradient theory was presented by Ansari et al. [4]. The model incorporated size effects and the first-order, shear, deformable beam, and von Kármán geometric nonlinearity was considered. The governing equations were discretized using generalized differential quadrature, and the shifted Chebyshev–Gauss–Lobatto grid was employed to generate grid points.
Mu and Zhao [5] explored the fundamental frequency of sandwich beams with an FG face sheet and a homogeneous core. The face sheet was composed of a mixture of metal and ceramic, while the homogeneous core was made of foam metal. The transverse normal and shear strains of the core were considered, the classical plate theory was used to analyze the face sheet, and a higher-order theory was proposed to analyze the core of the standard beams. The fundamental frequency was obtained via a theoretical model validated using ABAQUS.
Ebrahimi and Barati [6] investigated the free vibration of size-dependent FG nanobeams with simply supported boundary conditions using Reddy’s third-order beam theory and assuming higher-order longitudinal displacement variations in the beam’s thickness. It should be emphasized that this theory captures both microstructural and shear deformation effects without requiring any shear correction factors. The effect of its small scale was considered based on Eringen’s nonlocal elasticity. Nonlocal governing equations were solved using the Navier method. Furthermore, the third shear deflection beam theory was examined by Gangnian et al. [7] for the nonlinear bending of FG beams, and the differential quadrature method was utilized to obtain numerical results. Reddy et al. [8] studied the classical first-order and third-order shear deformation of FG straight beams, and analytical solutions for bending were determined.
The analytical treatment of the size-dependent nonlinear secondary resonance of FG porous materials subjected to periodical, strong excitations was proposed by Fattahi et al. [9] in the simultaneous presence of nonlocality and strain gradient size dependencies. The mechanical properties of the beam were studied for uniform and different porosity dispersions using the closed-cell Gaussian-random field scheme. An exact solution for the nonlinear static behavior of an FG beam with porosities resting on an elastic foundation was presented by Long et al. [10]. Based on the neutral surface concept, nonlinear governing equations have simple forms which can be directly solved. Wu et al. [11] investigated the nonlinear forced vibration of bidirectional FG porous material beams where the gradient of the material components changed in terms of both their thickness and axial direction. Vibration response curves and bifurcation diagrams were obtained using the pseudo-arclength technique, and it was found that the periodic motion of the beam may undergo cyclic fold bifurcation. Alhaifi et al. [12] explored the deflection of FG-saturated porous rectangular plates subjected to transverse loading. To describe the displacement components of the plate, Biot’s model, which considers the effect of fluids within pores, the first-order shear deformation theory, and the calculus of variation, was applied. The generalized differential quadrature method was used to solve the nonlinear problem. Dang and Nguyen [13] explored the buckling and nonlinear free vibration of an FG porous micro-beam resting on an elastic foundation based on the nonlocal strain gradient theory and the Euler–Bernoulli beam theory. Two porosity distribution models, including even and uneven distributions, were used to consider the porosity effect.
The thermal vibration of FG porous nanocomposite beams reinforced by graphene platelets was analyzed by Yas and Rahimi [14]. The temperature varied linearly across the thickness direction, and the elastic modulus of a nanocomposite was achieved using the Halpin–Tsui micromechanics model. The governing equations were discretized and then solved using the generalized differential quadrature method. Yang et al. [15] investigated the dynamic pull-in instability of an FG carbon nanotube-reinforced nanoactuator’s damping behavior. The material properties of FG nanotubes are temperature-dependent, and the influences of van der Waals and Casimir force were considered. The effect of temperature field on the natural frequencies of FG beams was analyzed by Kashyzadeh and Asfarjani [16] using a finite element model simulated in ANSYS. It was found that the natural frequency of the system was reduced as the temperature increased under all support conditions. The free and forced vibrations of an FG Timoshenko beam in a thermal environment were examined by Nguyen and Bui [17] using a higher-order finite beam and hierarchical functions to interpolate the kinematic variables. The material properties are temperature-dependent, and the temperature is nonlinearly distributed throughout the beam’s thickness. The nonlinear vibration of FG carbon nanotube-reinforced composite beams resting on a nonlinear elastic foundation in a thermal environment was explored by Fan and Huang [18] using the Haar wavelet discretization method. The thickness and temperature were assumed to be FG. Nonlinear governing equations are based on the first-order shear deformation beam theory in combination with von Kármán nonlinearity.
The vibration analysis of a rotary, axially tapered FG Timoshenko nanobeam was performed by Shafiei et al. [19]. This model was studied in a thermal environment using the nonlocal theory. The solution was obtained using the generalized differential quadrature element method. The isogeometric analysis of the free vibration of FG double-tapered Timoshenko beams was performed by Zhou et al. [20] using nonuniform rotational B-spline (NURBS) basis functions, while Sari et al. [21] studied the vibration of an FG, axially double-tapered Euler–Bernoulli beam using the nonlocal elasticity theory. Herein, the Chebyshev spectral collocation method is proposed to transform coupled governing equations of motion into algebraic equations.
A unified solution for the free and transient vibration analysis of an FG piezoelectric curved Timoshenko beam was developed by Su et al. [22]. The study was derived using the variational principle in conjunction with a modified Fourier series, which consists of standard Fourier cosine series and supplementary functions. The finite element method was employed to understand the buckling behavior and bifurcation point of an FG piezoelectric Euler–Bernoulli beam in a thermal environment. Direct and inverse piezoelectric effects were considered, and the buckling of the beam in the sensor state was investigated. Nadirzadeh et al. [23] explored the buckling behavior and bifurcation point of an FG piezoelectric beam using the finite element method. Ma et al. [24] investigated the electromechanical behavior of FG piezoelectric composite beams subjected to an electrical load. Employing the electromechanical coupling theory and load simulation method, the expression of the simulation loading of piezoelectric actuators was obtained. Singh and Kumari [25] explored the two-dimensional piezoelasticity vibration of axially FG beams integrated with piezoelectric layers. The extended Kantorovich method was proposed to reduce governing equations into sets of ordinary differential equations along the axial and thickness directions. Chen et al. [26] studied the mechanical and electrical properties of FG flexo-piezoelectric beams. Deflection and induced electric potentials were given as analytical expressions for the FG cantilever beam. The numerical results show that the flexoelectric effect, piezoelectric effect, and gradient distribution have a considerable influence on the electro-mechanical performance of FG beams. El Khouddar et al. [27] proposed the study of a geometrically, nonlinearly vibrated FG beam reinforced by surface-bounded piezoelectric fibers located on an arbitrary number of supports subjected to excitation forces and thermoelectric changes. Thermal and electrical changes, the volume fraction of structure, the harmonic force, and the number of supports have a great influence on the forced nonlinear dynamic response.
Nazmul et al. [28] obtained an analytical solution for the vibration of bidirectional FG nanobeams. The material characteristics of nanobeams vary along the axial and the thickness directions. Eringen’s nonlocal elasticity theory of was applied to Euler–Bernoulli and Timoshenko beams, and an analytical solution of the governing equations was obtained using the Laplace transform function. Recently, other interesting studies in the field have been reported in [29,30,31,32,33,34,35,36,37,38,39].
The present study is devoted to the nonlinear forced vibration of an FG nanobeam using the nonlocal theory that was subjected to a mechanical impact and symmetrical electromagnetic actuation. Coupled longitudinal–transverse governing equations were discretized using the Galerkin–Bubnov procedure. Nonlinearity is caused by the curvature of the nanobeam and by electromagnetic actuation. Nonlinear ordinary differential equations were solved using the Optimal Auxiliary Functions Method. A very accurate solution was obtained using a moderate number of convergence control parameters. The local stability of equilibrium points was studied using the variable expansion method. For global stability, the Lyapunov function and control law were established. According to the authors’ knowledge, this is the first time that the Lyapunov function of such a dynamic system has been defined to approximate solutions.
2. Derivation of the Governing Equations
2.1. Modeling of the Functionally Nanobeam
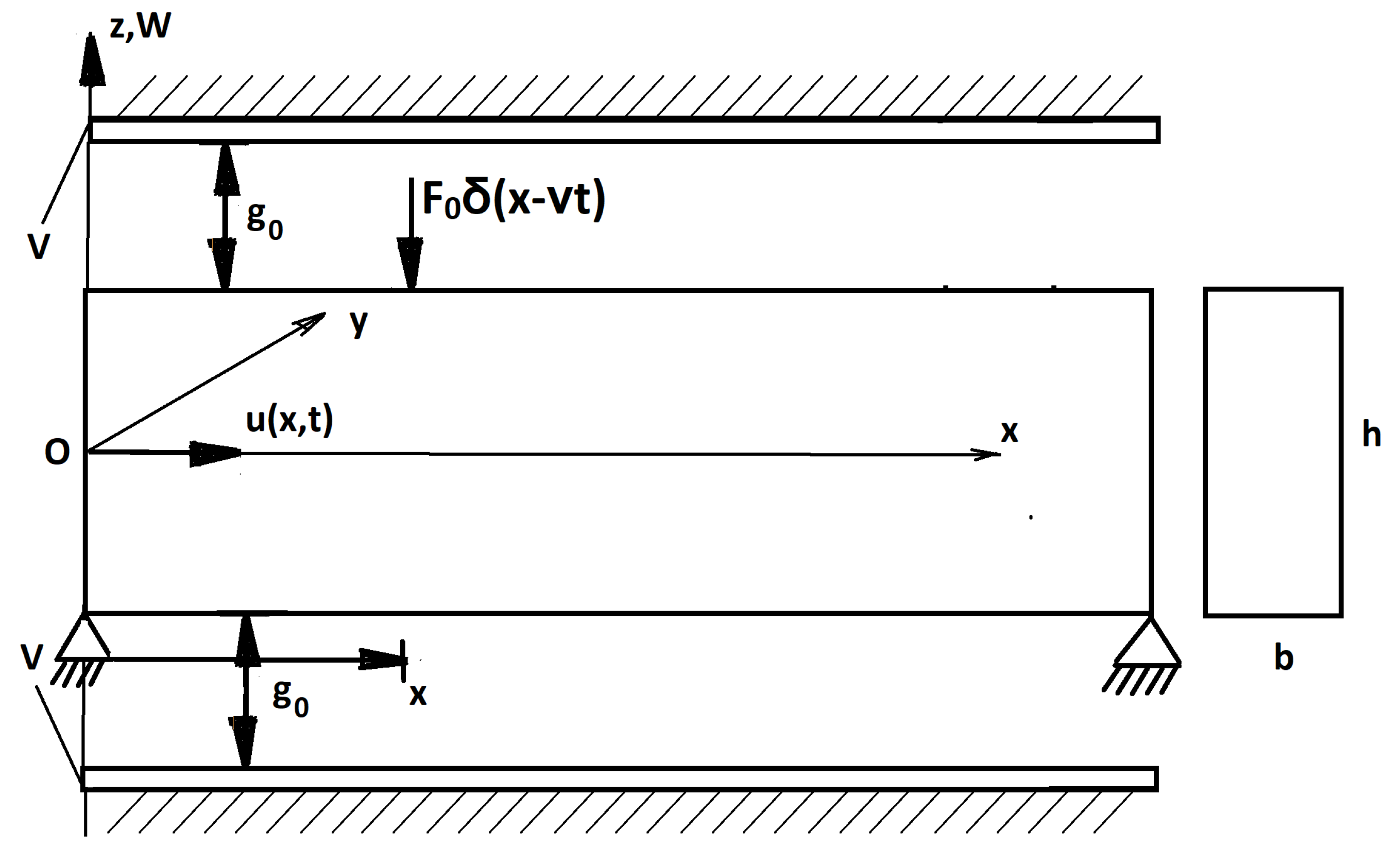
Here, we consider an FG nanobeam of length, L; width, b; and thickness, h, as shown in Figure 1.
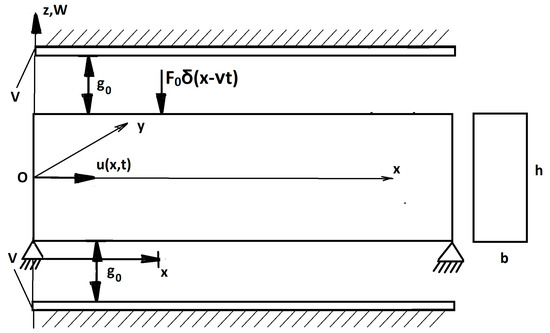
Figure 1.
The model of the FG simply supported nanobeam subjected to mechanical impact and two symmetrical electromagnetic actuators.
The simply supported beam was subjected to a mechanical impact with force, F0, and two symmetrical electromagnetic actuators with the same bias voltage, V.
Coordinates with x, y, and z axes along the length, width, and height directions, respectively, were taken. The material properties of the nanobeam vary as a function of the thickness coordinate. The FG nanobeam was assumed to be composed of a mixture of ceramic (upper surface at z = h/2) and metal (lower surface at z = −h/2). The volume fractions, Vc and Vm, were:
where n is the material power law index, which prescribes the material variation; z is the thickness coordinate from the geometry neutral surface; and the subscript c and m denote ceramic and metal phases, respectively. The effective material properties, P(z), can be stated as:
in which PC and Pm are the properties of materials, and the volume fraction of the materials verify the identity:
Taking into consideration the material properties, Young’s modulus and the mass density can be expressed as:
2.2. Kinematic Relations
Based on the Euler–Bernoulli beam theory, the displacement field of an arbitrary point along the nanobeam along x, y, and z axes can be written as:
where u(x,t) and W(x,t) denote mid-plane stretching and middle surface displacements, respectively, and t represents time.
Nonlinear strain–displacement relationships, including the mid-plane stretching effect, can be estimated using the von Kármán formula in the form:
The main components of the symmetrical section of stress tensor are given by:
where λ(z) and μ(z) are Lame parameters.
The strain energy of the nanostructure can be written as:
where σij represents the nonlocal stress tensor.
In accordance with Eringen assumptions, the nonlocal stress constitutive equation is [40]:
in which is the Laplacian operator, and is a scalable length parameter. The nonlocal parameter, τ, represents the significance of the inter-atomic long-range force, which considers the influence of small scales on the response of nanostructures, including mode shapes, boundary conditions, chirality, and the essence of motion. Eringen considers τ = (π − 4)1/2/2π ≈ 0.21. This parameter was experimentally obtained for various materials, for example, τ < 4 (nm)2 for a single-walled carbon nanotube. In general, it is assumed that τ is in the range 0–8 (nm)2.
For a material in one dimension, the constitutive relation of the nonlocal theory can be expressed as [6]:
where σ and ε are the nonlocal stress and strain, respectively, and E is the Young’s modulus.
2.3. The Governing Equation for FG Nanobeam
For the Euler–Bernoulli nanobeam structure, we have:
The strain energy (8) stored in an FG nanobeam obtained using the nonclassical continuum theory became:
where
in which
and in Expression (14), we considered the curvature of the nanobeam.
The last term in Equation (14), which defines the curvature of the nanobeam, can be rewritten as:
The work conducted due to the mechanical impact and by the electromagnetic actuator is given by:
The kinetic energy of the nanobeam is:
where A denotes the cross-sectional area of the nanobeam, and inertia terms are defined as:
After some mathematical manipulations, from Equation (19), one can obtain:
The Hamilton’s principle states that:
By substituting Equations (12), (17), and (18) into (20), the following equations are obtained:
Now, from Equations (13) and (22), we observed that:
By inserting Equation (24) into Equation (22), one can obtain:
By inserting Equation (24) into (23), it follows that:
From Equations (14) and (26), it follows that:
By substituting Equations (24) and (27) into Equation (23), one retrieves:
where the external moving transverse load with speed, v, can be considered a mechanical impact under the action of the Dirac delta function:
Nanobeam vibration depends on the action of the DC voltage source, such that electromagnetic actuation can be considered as:
in which C0 is the capacitance of the actuator, g0 is the gap width, and V is the voltage. Expression (30) can be simplified as:
The maximum error between the two functions from Equation (31):
is ε = 3.3·10−6, and therefore, F2 is a very good approximation for function F1.
For convenience, the following dimensionless variable were adopted:
where λ0, μ0, and ρ0 are the classical Lame constants and mass density for a homogeneous nanobeam made of metal.
The nonlocal nonlinear governing equations of an FG nanobeam in dimensionless terms of transverse and longitudinal displacements can be derived from Equations (25), (28), (29), (31), and (33) by omitting the bar:
Using the Galerkin–Bubnov procedure, the solutions of Equations (34) and (35) can be expressed in a discretized form. For this purpose, it was assumed that u(x,t) and W(x,t) can be written as follows:
where the expressions X(x) and Y(x) are analytical forms corresponding to the boundary conditions.
It is worth mentioning that the considered governing equations are slightly different from Equation (46) in paper [38] and from Equation (28) in paper [39] because the studied problems are slightly different. The transversal inertia, , is not neglected in the present paper: , where the term cannot be always neglected. However, can be neglected if .
After the substitution of Equation (36) into Equations (34) and (35), multiplying Equation (34) by X(x) and Equation (35) by Y(x) and integrating the domain [0,1], and using the expression:
one can obtain the following nonlinear differential equations:
where the dot denotes the derivative with respect to the dimensionless term, t, and the coefficients that appear in Equations (38) and (39). These are given in the Appendix A.
In the case of the simply supported beam, the boundary conditions are [9]:
such that Equations (38) and (39) can be rewritten as:
where, for Equations (41) and (42), we took into consideration that from Equation (40), one can obtain . It is worth mentioning that the proposed solution procedure can be applied to any other boundary conditions without difficulty.
The initial conditions for Equations (41) and (42) are:
The solution of Equations (41) and (43) may be written as:
3. Solution Procedure
In this section, we will remark on how we found approximate analytical solutions to Equations (42) and (43) using the OAFM [41,42,43,44,45]. With the help of the following transformation:
where Ω is the unknown frequency of the system, Equations (42) and (43) can be rewritten as:
Following this, we considered the nonlinear problem near the primary resonance:
The linear and nonlinear operators corresponding to Equation (46) are, respectively:
where prime denotes differentiation with respect to τ.
According to [41,42,43,44,45], the approximate solution for Equation (46) can be written as:
The initial approximation, from the last expression is defined as solution of the linear equation:
which can be rewritten in the form:
whose solution is:
Inserting Equation (52) into the second expression of Equation (48), it was found that:
where
The first approximation,, from Equation (49) was determined from the linear equation:
As we mentioned in [41,42,43,44,45], the expression from the right side of Equation (55) is not unique. Also, we can choose any of the following forms of the equation for the first approximation:
or
or
and so on. In these last equations, Ci, i = 1, 2, … are unknown parameters.
Considering only Equation (55), this can be rewritten as:
By avoiding the secular term in Equation (59), we can find the frequency of the system:
The solution of Equation (59) becomes:
The approximate solution of Equations (42) and (43) can be obtained from Equations (45), (49), (53), and (61):
where Ω is given by Equation (6).
The values of the convergence control parameters, Ci, i = 1, 2, 3, 4, can be optimally determined using the least square method, Ritz method, collocation method, Galerkin method, and so on.
To prove the efficiency of our procedure, we considered the case from the data presented in Appendix A: B = 1, ω = 0.812, ω2 = 0.811, a2 = 0.051, a3 = 0.31, a5 = 1.77, f0 = 0.03. Using the collocation approach, the optimal values of the convergence control parameters and frequency were found to be C1 = −0.02618575067906715; C2 = 0.0004574655408149; C3 = −0.9299640963105; and C4 = −0.001457943137, Ω = 1.389.
The approximate solution (62) became:
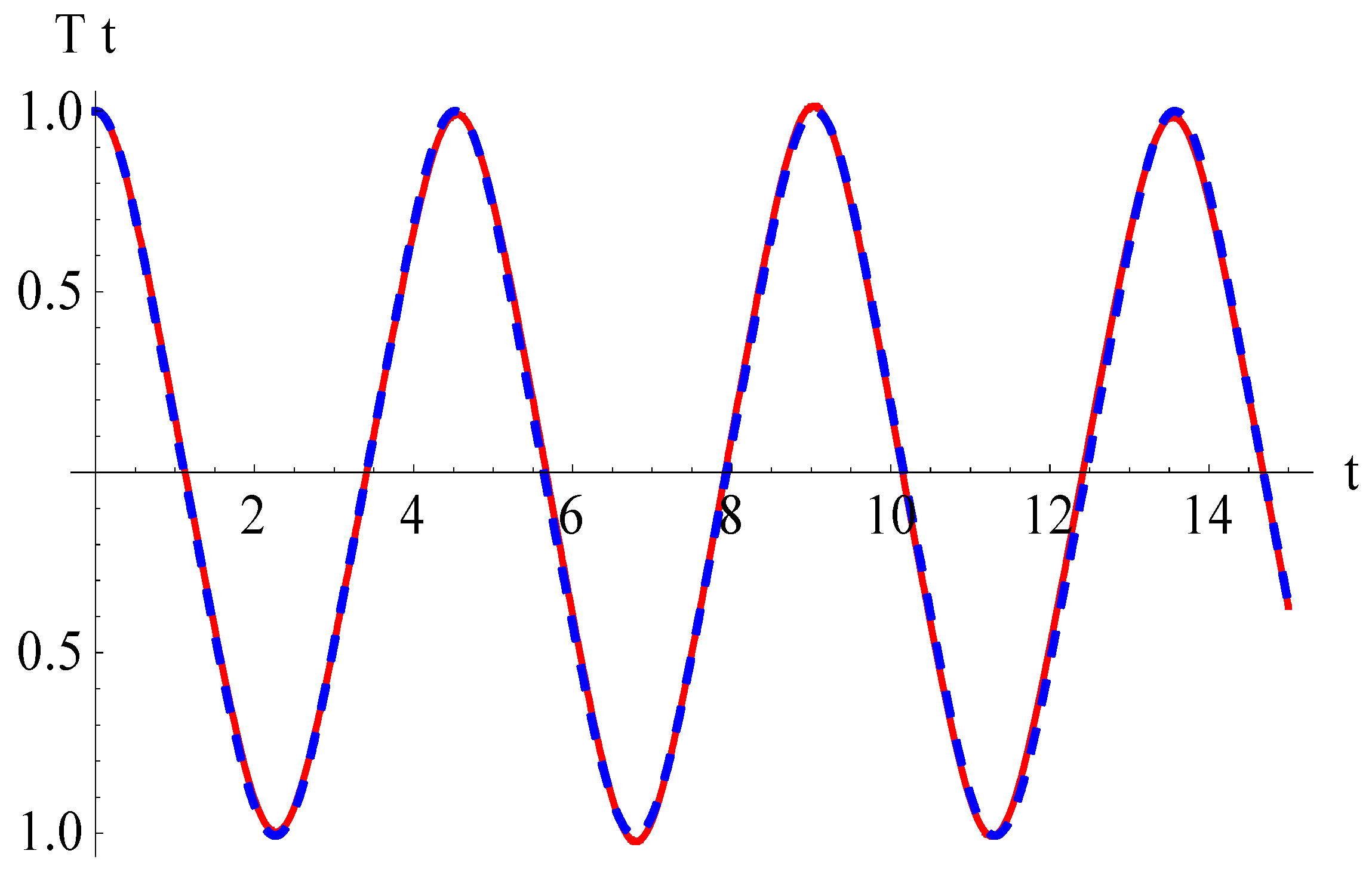
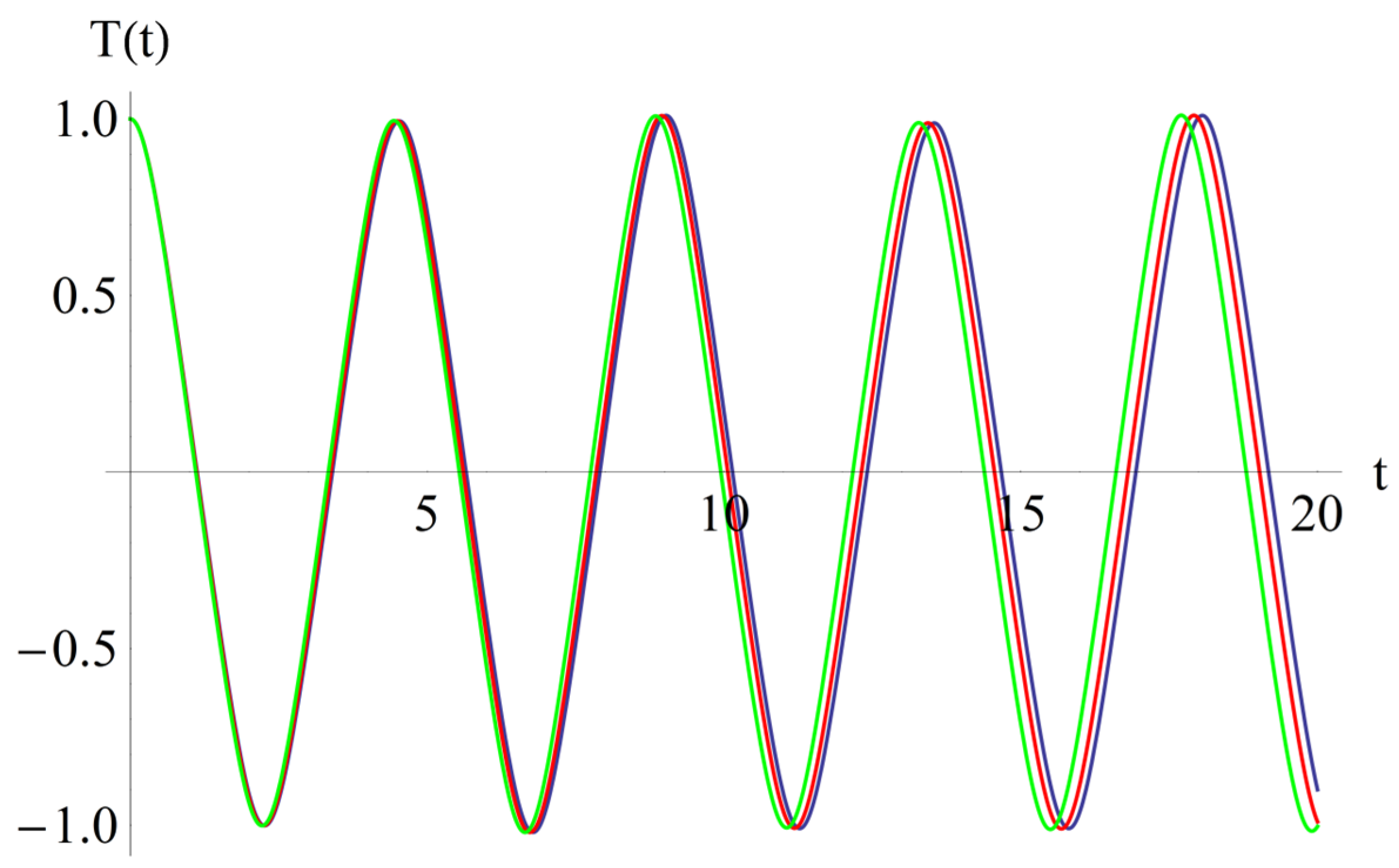
To validate the obtained results derived from using the OAFM, we created Figure 2, which compares the analytical approximate solution (63) and numerical integration results obtained using a fourth-order Runge–Kutta approach.
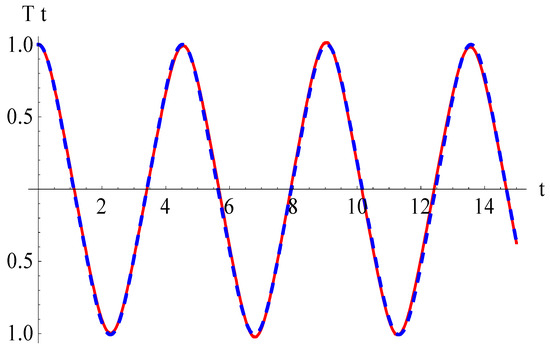
Figure 2.
Comparison between analytical solution (63) and numerical integration results for Equations (42) and (43): ______ numerical solution; _ _ _ _ _ analytical solution.
It is easy to observe that the approximate solution for the FG nanobeam obtained using the OAFM is nearly identical to the numerical integration results, which proves the efficiency of our technique.
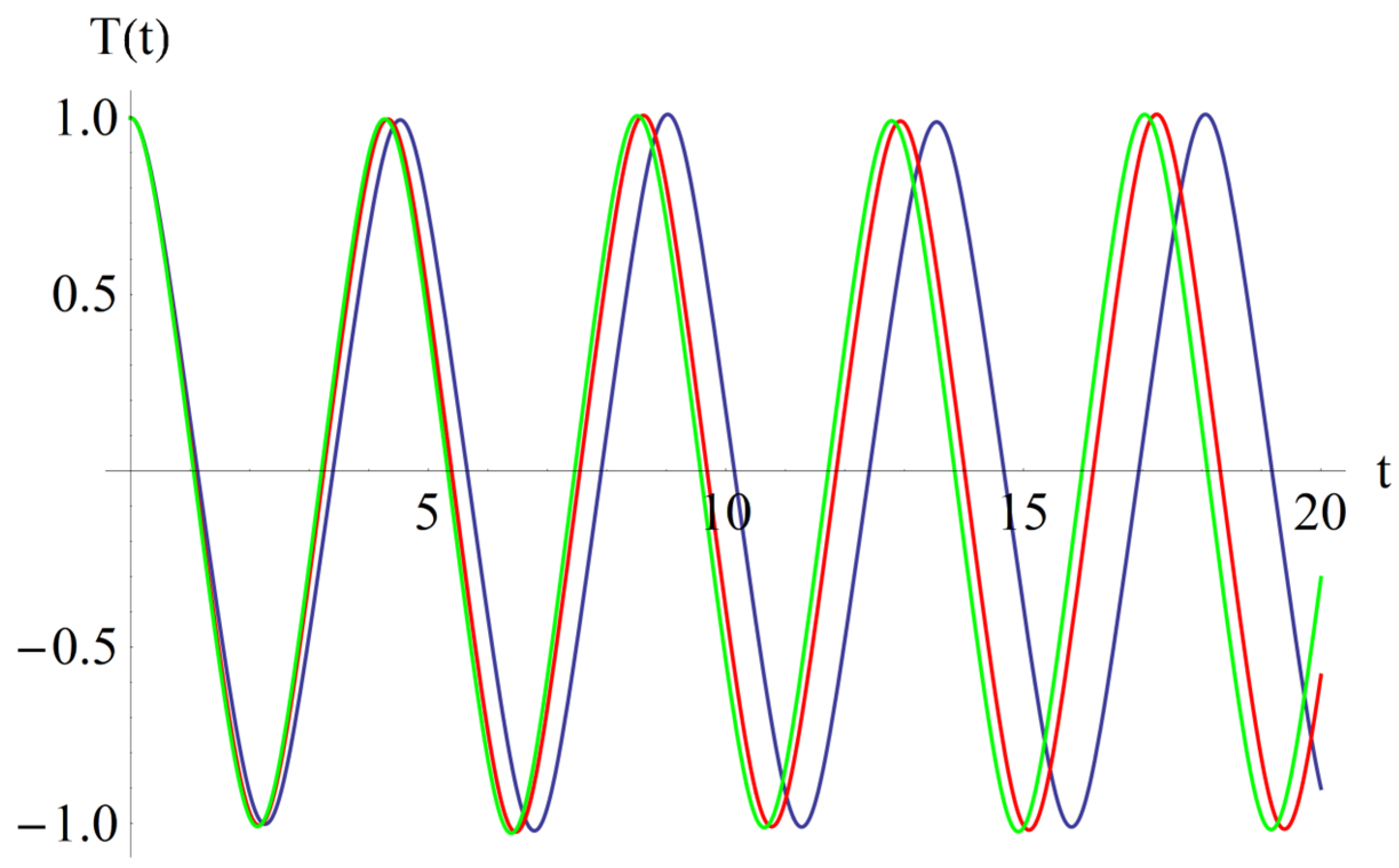
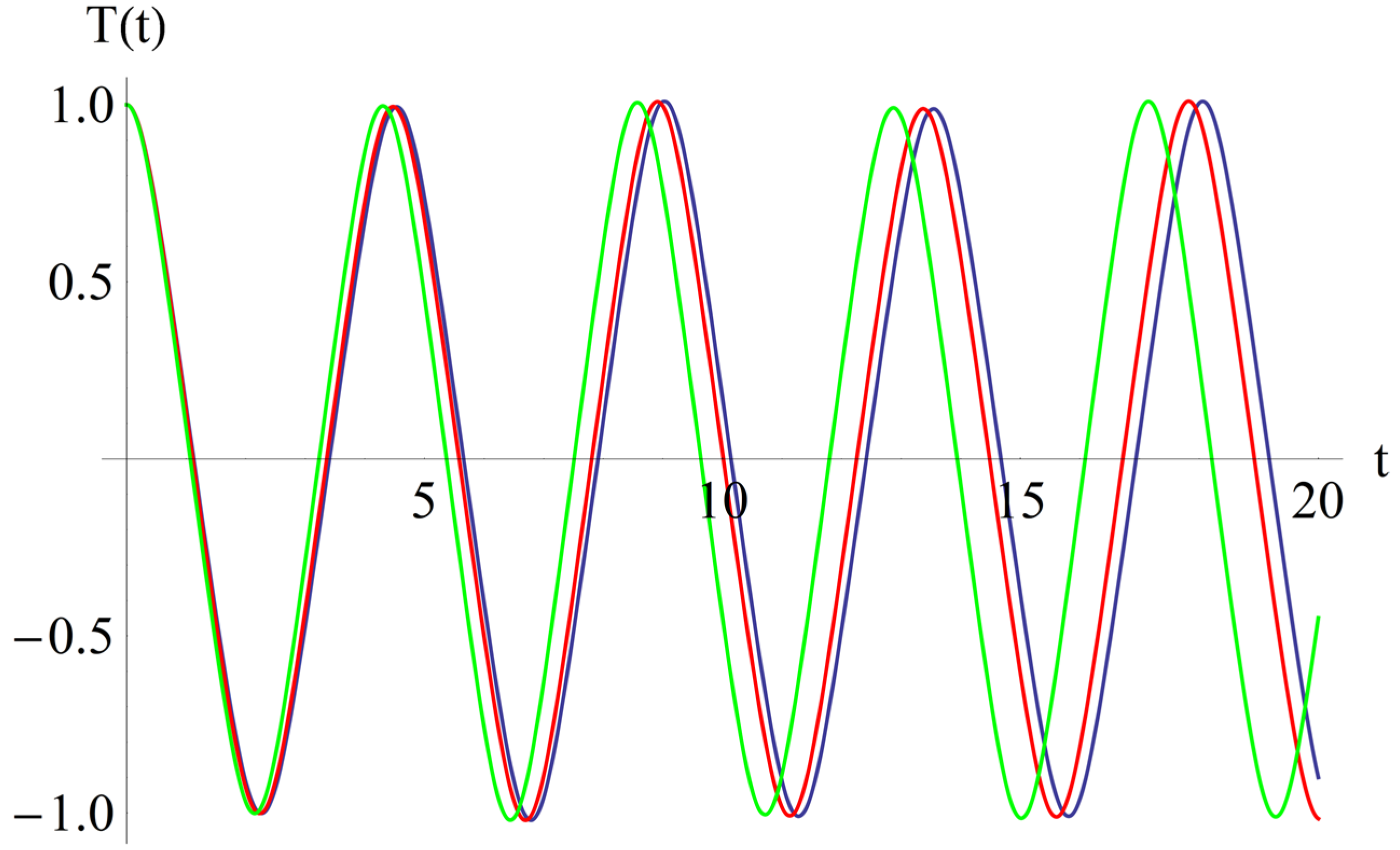
In Figure 3, Figure 4, Figure 5 and Figure 6, we present the effects of the coefficients, α1, α2, β1, and β2, respectively, in the solution of Equation (42).
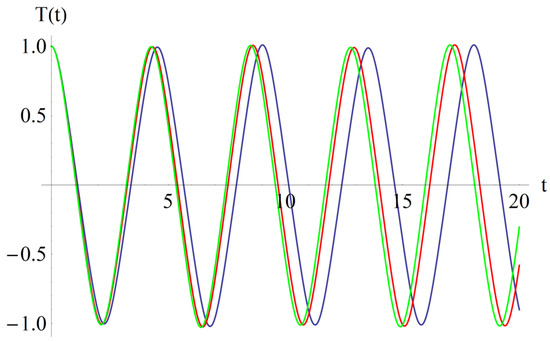
Figure 3.
The effect of the coefficient, α1: α1 = 0.1 (blue); α1 = 0.3 (red); α1 = 0.5 (green).
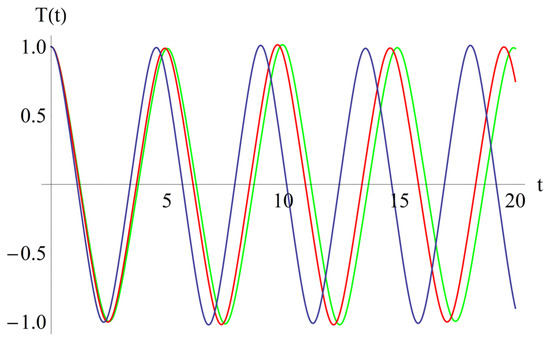
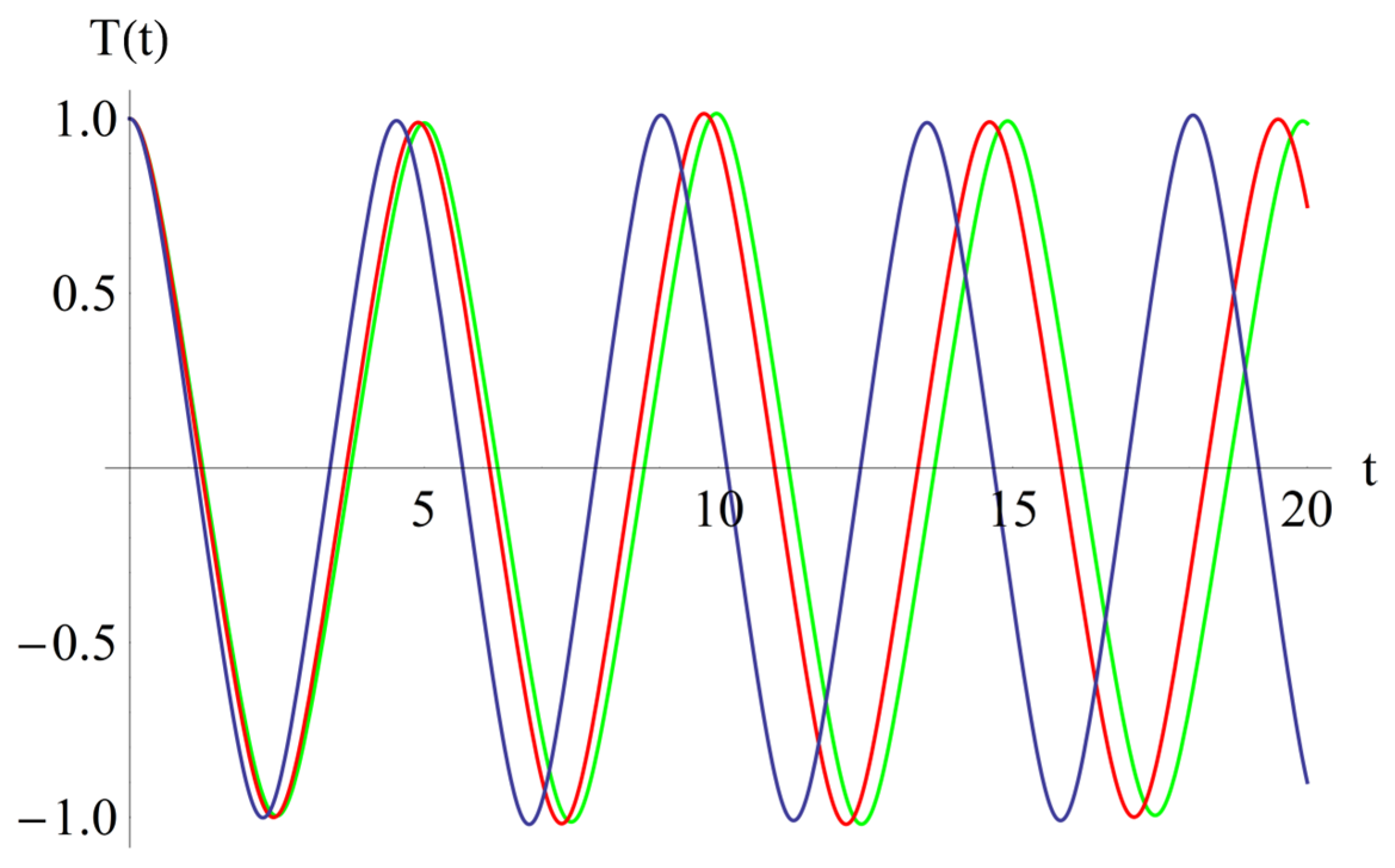
Figure 4.
The effect of the coefficient, α2: α2 = 0.001 (blue); α2 = 0.002 (red); α2 = 0.003 (green).
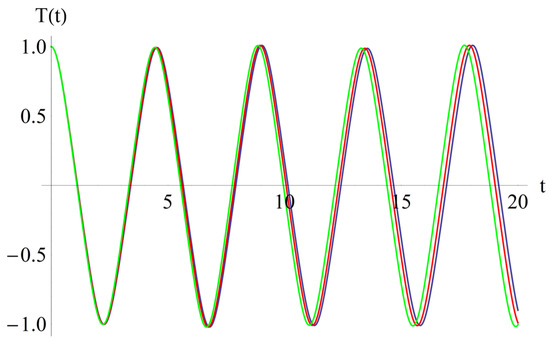
Figure 5.
The effect of the coefficient, β1: β1 = 0.4 (blue); β1 = 0.5 (red); β1 = 0.6 (green).
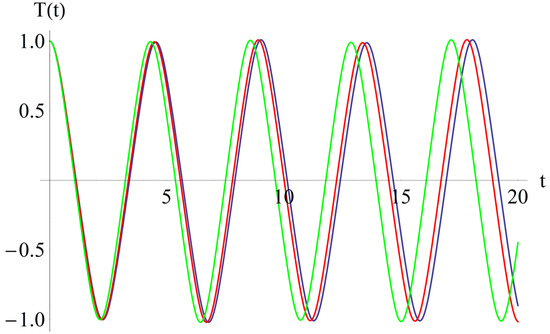
Figure 6.
The effect of the coefficient, β2: β2 = 0.2 (blue); β2 = 0.1 (red); β2 = 0.05 (green).
From Figure 3, we deduced that if α1 increases, then the abscissa of the intersection point of T(t) with the horizontal axis decreases. Also, from Figure 3, one can conclude that if α1 increases, then the frequency increases, while the effect of the parameter, α2, is inverse in Figure 4. From Figure 5, it follows that if β1 increases, then the above-mentioned abscissa decreases, and from Figure 6, it follows that the effect of β2 is inverse to the effect of β1. If β1 increases, then the frequency increases.
4. Stability of the Steady–State Motion for the FG Nanobeam
The approach applied in this section was used to distinguish between two-time scales by associating a separate independent variable with each one. We reconsidered the primary resonance for Equation (42): ω = ω2 + σε, ω = πv, with σ being a detuning parameter and ε being a small parameter. We use notation ξ, which represents stretched time, ωt, and notation, η, which represents slow time, εt (two-variable expansion method [46]):
To substitute these transformations into Equation (42), we need expressions:
By expanding the power series and inserting Equation (65) into (42), one obtains the following partial differential equation:
By neglecting the terms of 0(ε2) after collecting terms, one can obtain:
The general solution to the linear differential Equation (67) is:
For a nonresonant term in Equation (68), the coefficients of sin ξ and cos ξ need to vanish, such that we have the following slow flow formula:
The equilibrium points of the slow flow Equations (70) and (71) correspond to the periodic motion of Equation (42). To determine them, we determined:
From Equations (70)–(72), equilibrium points (Ae and Be) can be obtained from the algebraic equations:
Only the following case is possible:
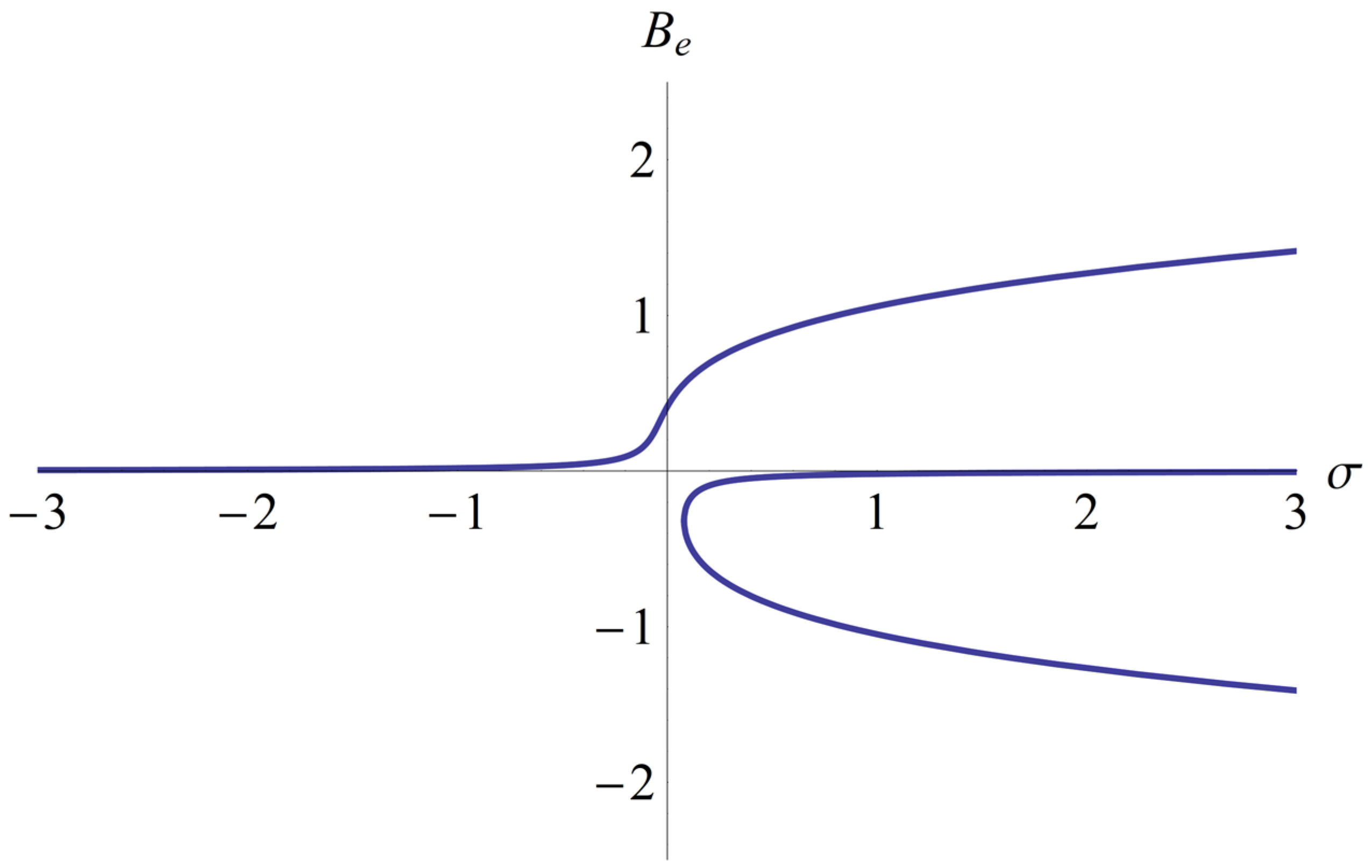
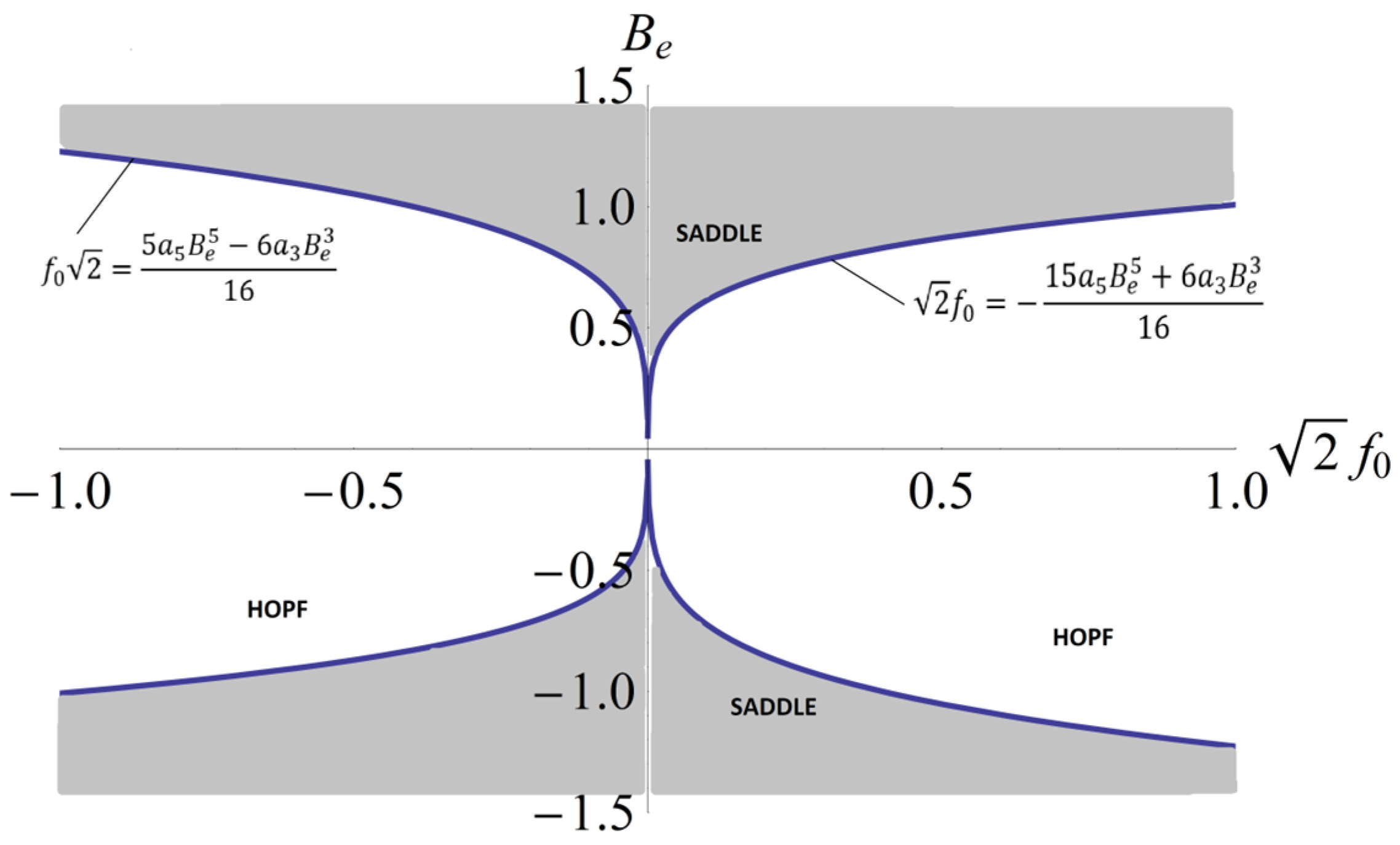
For the data presented in Section 3 (ω2 = 0.811; a3 = 0.31; a5 = 1.77; f0 = 0.0212131) in Figure 7, equilibrium points Be are depicted in respect to parameter σ.
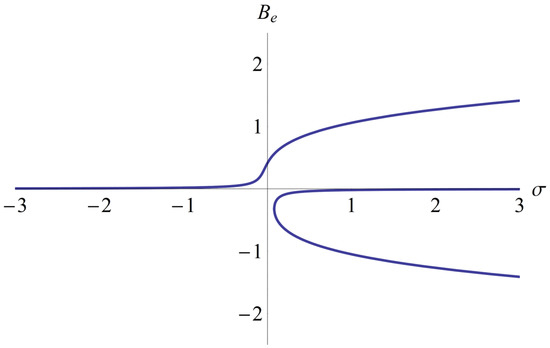
Figure 7.
The equilibrium points Be in respect to σ for a3 = 0.3; a5 = 1.77; ω2 = 0.811; f0 = 0.0212131.
It was observed that there are one or three equilibrium points. More precisely, for σ < 0, there is a unique equilibrium point, and for σ ≥ 0, there are three equilibrium points.
The stability of steady-state motion is determined using eigenvalues of the Jacobian matrix obtained from Equations (70) and (71) (the Routh–Hurwitz criterion):
where
After some manipulations, from Equations (70), (71), and (77), the coefficient ai, has the forms:
The eigenvalues of the Jacobian matrix were obtained using the characteristic equation:
where Iz is the unity matrix of the second order, and λ is the eigenvalue of the Jacobian matrix.
Considering Expression (77), the characteristic Equation (79) becomes:
where the trace of the Jacobian matrix is given by:
and the determinant of J is:
In this way, the characteristic equation can be rewritten as:
Using the second side of Equation (75), one obtains:
Such that Equation (82) can be rewritten as:
We have the following possible cases.
Case 4.1: If
then one or two eigenvalues are equal to zero; thus, there is no motion.
Case 4.2.a: If a5 > 0 and
then λ1 = −λ2 is real. The points move toward the equilibrium in one situation, but away from the equilibrium point in the other. This is called a saddle.
Case 4.2.b: If a5 > 0, but
then there is a pair of eigenvalues that are purely imaginary, and the signs of their imaginary parts must be opposite. The resulting motion involves points around an ellipse; this means that there is no net motion towards or away from the equilibrium (centers) of Hopf bifurcation.
Case 4.3.a: If a5 < 0 and
then similar to Case 4.2.a, λ1 and λ2 are real with opposite signs.
Case 4.3.b: If a5 < 0 and
then, this situation is similar to Case 4.2.b.
5. Numerical Examples
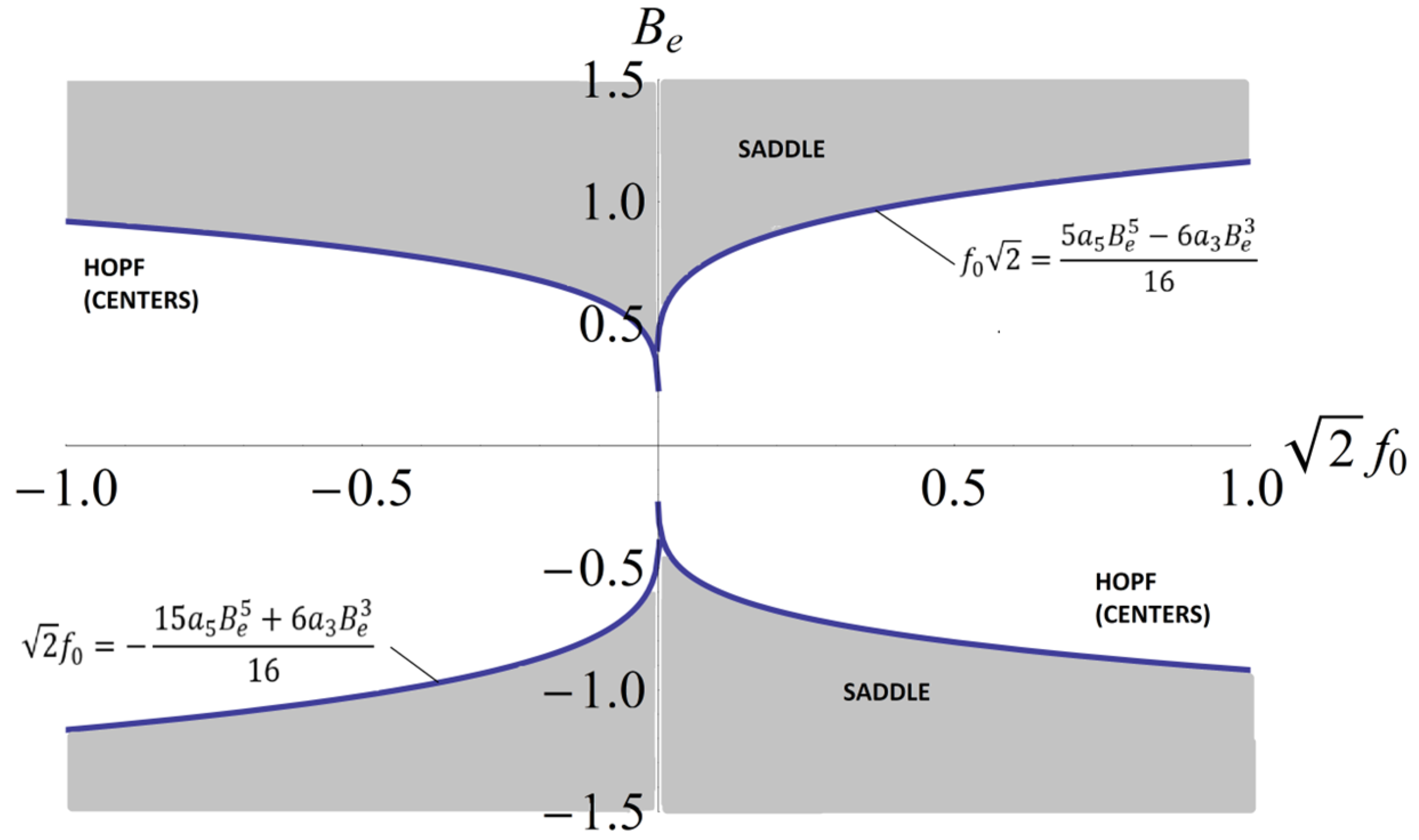
For a3 = 0.31 and a5 = 1.77, local stability is depicted in Figure 8, and for a3 = 0.31 and a5 = −0.9, local stability is depicted in Figure 9.
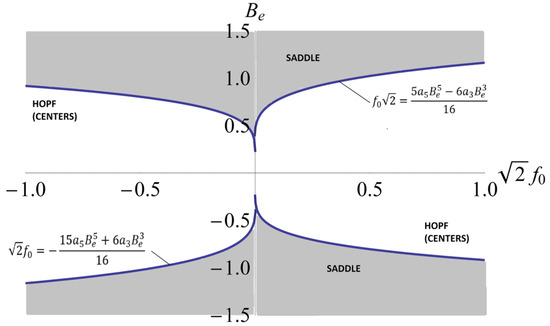
Figure 8.
Local stability for the cases a3 = 0.31 and a5 = 1.77.
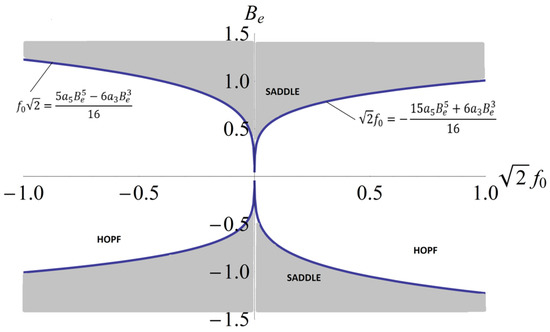
Figure 9.
Local stability for the cases a3 = 0.31 and a5 = −0.9.
6. Global Stability by the Lyapunov Function
The governing equation of the FG nanobeam dynamics of a mechanical impact and electromagnetic actuation can be written by adding the control input, U, as:
We defined the tracking errors, E1 and E2, as:
where is the approximate analytical solution of Equation (42) above, which was obtained using the OAFM, θ is a positive parameter, which is defined later, and U is the control.
If , , , and are defined as estimated parameters, then the estimations of errors of these parameters are defined as [47]:
The following Lyapunov function form was used:
where λi, i = 1, 2, …, 7 are any positive parameters. The time derivative of the Lyapunov function can be written, considering Equations (92)–(94) in the following form:
The input control is defined using Equation (95) in the following form:
such that Equation (95) can be rewritten as:
After some simple manipulations, the last equation can be rewritten as:
The estimate parameters , , , and from the last equation are defined as:
or considering Equation (92):
Equation (97) becomes:
A positive parameter is defined as:
from which it is clear that dV/dt < 0.
Using the Lyapunov function and La Salle’s invariance principle, the system studied in the present work is globally asymptotically stable because function V is a positive definite function and dV/dt is negative definite function.
7. Conclusions
The present study is devoted to the longitudinal–transverse vibration of an FG using von Kármán geometric nonlinearity, the nonlocal Eringen theory of elasticity, and a first-order, shear, deformable beam. The Euler–Bernoulli nanobeam was subjected to mechanical impact using the Dirac delta function and to electromagnetic actuation. Coupled longitudinal–transverse governing equations were discretized using the classical Galerkin–Bubnov procedure.
The resulting nonlinear differential equation contains a term dependent on the curvature of the nanobeam and was solved near the primary resonance using the OAFM. The proper procedure leads to a very accurate solution after the first iteration for a complex problem. The main novelties of our technique are the presence of some auxiliary functions and convergence control parameters and the original construction of the initial and first iterations. It should be emphasized that any nonlinear differential equations of practical interest were reduced to two linear differential equations. To the best of the authors’ knowledge, no papers in the literature have investigated or reported the effects of the simultaneous actions of the following elements considered in the present paper—the presence of a curved nanobeam, the transversal inertia, which is not neglected in our paper, the mechanical impact, and electromagnetic actuation—and this encapsulates the main novelty of this paper. Practical applications of the present work may be identified in the fields of aerospace structures, nuclear reactors, the biomedical industry, chemical plants, optical semiconductors, the defense industry, and electronics.
Our original technique is a powerful tool that can be used to solve a nonlinear problem without the presence of any small parameters in the governing equation or in the boundary conditions. The best quality of our procedure is the existence of so-called “auxiliary functions”. These functions were gained from two sources, more precisely, from the initial approximation and from the term defined through the corresponding nonlinear operator calculated for the initial approximation. The presence of some convergence control parameters assures the rapid convergence of approximate solutions after the first iteration. The convergence control parameters were evaluated using rigorous mathematical procedures. We have great freedom to select both auxiliary functions and the number of convergence control parameters. Our technique has proved to be very accurate, simple, and easy to implement for any complicated nonlinear problems.
The local stability of an FG nanobeam was studied using Routh–Hurwitz criteria and eigenvalues of the Jacobian matrix. The local stability depends on the nature of the solutions of the characteristic equation and on the signs of the eigenvalues, which leads to the study of borderline cases.
Global stability was analyzed using Lyapunov’s direct method and La Salle’s invariance principle. We pointed out that the Lyapunov function depends on the approximate solution obtained using the OAFM. To the best of our knowledge, a highly accurate approximate solution was employed for the first time in the construction of the Lyapunov function. Also, the control variable of Pontryagin’s principle was applied.
The effects of some physical parameters have been highlighted.
Author Contributions
Conceptualization, V.M. and N.H.; methodology, V.M. and N.H.; software, B.M. and N.H.; validation, V.M., B.M. and N.H.; formal analysis, V.M.; investigation, V.M., N.H.; resources, N.H.; data curation, B.M. and N.H.; writing—original draft preparation, V.M. and N.H.; writing—review and editing, V.M. and N.H.; visualization, B.M. and N.H.; supervision, N.H.; project administration, N.H.; funding acquisition, N.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The prime denotes the derivative with respect to x.
References
- Miyamoto, Y.; Kaysser, W.A.; Rabin, B.H.; Kawasaki, A.; Ford, R.G. Functionally Graded Materials; Springer: New York, NY, USA, 1999. [Google Scholar]
- Alimoradzadeh, M.; Salemi, M.; Esfarjani, S.M. Nonlinear dynamic response of an axially functionally graded (AFG) beam resting on nonlinear elastic foundation subjected to moving load. Nonlinear Eng. 2019, 8, 250–260. [Google Scholar] [CrossRef]
- Shafiei, H.; Setoodei, A.R. An analytical study on the nonlinear forced vibration of functionally graded carbon nanotube-reinforced composite beams on nonlinear viscoelastic foundation. Arch. Mech. 2020, 72, 81–107. [Google Scholar]
- Ansari, R.; Gholami, R.; Shojaei, M.F.; Mohammadi, V.; Darabi, M.A. Coupled longitudinal-transverse-rotational free vibration of post-buckled functionally graded first-order shear deformable micro- and nano-beams on the Mindlin’s strain gradient theory. Appl. Math. Model. 2016, 40, 9872–9891. [Google Scholar] [CrossRef]
- Mu, L.; Zhao, G. Fundamental frequency analysis of sandwich beams functionally graded face and metallic foam core. Shock Vibr. 2016, 2016, 3287645. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R. A nonlocal higher-order shear deformation beam theory for vibration analysis of size-dependent functionally graded nanobeams. Arab. J. Sci. Eng. 2016, 41, 1679–1690. [Google Scholar] [CrossRef]
- Gangnian, X.; Lian, M.; Youzni, W.; Quan, Y.; Weijie, Y. Differential quadrature method of nonlinear bending of functionally graded beam. Mater. Sci. Eng. 2008, 307, 012058. [Google Scholar] [CrossRef]
- Reddy, J.N.; Ruoco, E.; Loya, J.A.; Neves, A.M.A. Theories and analysis of functionally graded beams. Appl. Sci. 2021, 11, 7159. [Google Scholar] [CrossRef]
- Fattani, A.M.; Sahmani, S.; Ahmed, N.A. Nonlocal strain gradient beam model for nonlinear secondary resonance analysis of functionally graded porous micro/nano-beams under periodic hard excitations. Mech. Based Des. Struct. Mach. 2019, 48, 1–30. [Google Scholar]
- Long, N.V.; Nguyen, V.L.; Tran, M.T.; Thai, D.K. Exact solution for nonlinear static behaviors of functionally graded beams with porosities resting on elastic foundation using neutral surface concept. J Mech. Eng. Sci. 2022, 236, 481–495. [Google Scholar] [CrossRef]
- Wu, J.; Chen, L.; We, R.; Chen, X. Nonlinear forced vibration of bidirectional functionally graded porous material beam. Shock Vibr. 2021, 2021, 6675125. [Google Scholar] [CrossRef]
- Alhaifi, K.; Arshid, E.; Khorshidvand, A.R. Large deflection analysis of functionally graded saturated porous rectangular plates on nonlinear elastic foundation via GDQM. Steel Comp. Struct. 2021, 39, 795–809. [Google Scholar]
- Dang, V.H.; Nguyen, T.H. Buckling and nonlinear vibration of functionally graded porous microbeam resting on elastic foundation. Mech. Adv. Compos. Struct. 2022, 9, 75–88. [Google Scholar]
- Yas, M.H.; Rahimi, S. Thermal vibration of functionally graded porous nanocomposite beams reinforced with graphene platelets. Appl. Math. Mech. 2020, 41, 1209–1226. [Google Scholar] [CrossRef]
- Yang, W.D.; Yang, F.P.; Wang, X. Coupling influences of nonlocal stress and strain gradient on dynamic pull-in of functionally graded nanotubes reinforced nano-actuator with damping effects. Sens. Actuators A Phys. 2016, 248, 101021. [Google Scholar] [CrossRef]
- Kashyzadeh, K.R.; Asfarjani, A.A. Finite element study in the vibration of functionally graded beam with different temperature conditions. Adv. Mater. 2016, 5, 57–65. [Google Scholar] [CrossRef]
- Nguyen, D.K.; Bui, V.T. Dynamic analysis of functionally graded Timoshenko beams in thermal environment using a higher-order hierarchical beam element. Math. Probl. Eng. 2017, 2017, 7025750. [Google Scholar] [CrossRef]
- Fan, J.; Huang, J. Haar wavelet method for nonlinear vibration of functionally graded CHT-reinforced composite beams resting on nonlinear elastic foundations in thermal environment. Shock Vibr. 2018, 2018, 9597541. [Google Scholar]
- Shafiei, N.; Hamisi, M.; Ghadiri, M. Vibration analysis of rotary tapered axially functionally graded Timoshenko nanobeams in thermal environment. J. Solid Mech. 2020, 12, 16–32. [Google Scholar]
- Zhou, Z.; Chen, M.; Jia, W. Free vibration analysis of axially functionally graded double-tapered Timoshenko beam by NURBS approach. In Proceedings of the 30th International Ocean and Polar Engineering Conference, Shanghai, China, 11–16 October 2020. [Google Scholar]
- Sari, M.S.; Al-Kouz, W.G.; Atieh, A.M. Transverse vibration of functionally graded tapered double nanobeams resting on elastic foundation. Appl. Sci. 2020, 10, 493. [Google Scholar] [CrossRef]
- Su, Z.; Jin, G.; Ye, T. Vibration analysis and transient response of a functionally graded piezoelectric curved beam with boundary conditions. Smart Mater. Struct. 2016, 25, 065003. [Google Scholar] [CrossRef]
- Nasirzadeh, R.; Benjat, B.; Kharazi, M. Finite element study on thermal buckling of functionally graded piezoelectric beams considering inverse effects. J. Theor. Appl. Mech. 2018, 56, 1097–1108. [Google Scholar] [CrossRef]
- Ma, X.; Wang, S.; Zhou, B.; Xue, S. Study of the electromechanical behavior of functionally graded piezoelectric composite beams. J. Mech. 2020, 36, 841–848. [Google Scholar] [CrossRef]
- Singh, A.; Kumari, P. Two-dimensional free vibration analysis of axially functionally graded beams integrated with piezoelectric layers: A piezoelectric approach. Int. J. Appl. Mech. 2020, 12, 2050037. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, M.; Su, Y.; Zhou, Z. Coupling analysis of flexoelectric effect of functionally graded piezoelectric cantilever nanobeams. Micromachines 2021, 12, 595. [Google Scholar] [CrossRef]
- El Knoudoar, Y.; Adri, A.; Oufassafte, O.; Rifai, S.; Benamar, R. Nonlinear forced vibration analysis of piezoelectric functionally graded beams in thermal environment. Int. J. Eng. 2021, 34, 2587–2597. [Google Scholar]
- Nazmul, I.M.; Nahed, S.; Indromil, D. Analytical solutions for vibration of bi-directional functionally graded nonlocal nanobeams. Results Eng. 2023, 2023, 101046. [Google Scholar]
- Fang, L.; Yin, B.; Zhang, X.; Yang, B. Size-dependent vibration of functionally graded rotating nanobeams with different boundary conditions based on nonlocal elasticity theory. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 236, 2756–2774. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Marin, M.; Askar, S.S. Analysis of the magneto-thermoelastic vibrations of rotating Euler–Bernoulli nanobeams using the nonlocal elasticity model. Bound. Value Probl. 2023, 2023, 21. [Google Scholar] [CrossRef]
- Lal, R.; Dangi, C. Thermomechanical vibration of bi-directional functionally graded non-uniform Timoshenko nanobeam using nonlocal elasticity theory. Compos. Part B Eng. 2019, 172, 724–742. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, C.; Yu, Y. A boundary knot method for 3D time harmonic elastic wave problems. Appl. Math. Lett. 2020, 104, 106210. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, C.; Chen, Z.; Lim, C.W. Relaxation and mixed mode oscillations in a shape memory alloy oscillator driven by parametric and external excitations. Chaos Solitons Fractals 2020, 140, 110145. [Google Scholar] [CrossRef]
- Chen, D.; Wang, B.; Chen, Z.; Yu, Y. Parametrically excited vibrations in a nonlinear damped triple-well oscillator with resonant frequency. J. Vibr. Eng. Techn. 2022, 10, 781–788. [Google Scholar] [CrossRef]
- Malikan, M.; Wiczenbach, T.; Eremeyev, V.A. Thermal buckling of functionally graded piezomagnetic micro- and nanobeams presenting the flexomagnetic effect. Contin. Mech. Thermodyn. 2022, 34, 1051–1066. [Google Scholar] [CrossRef]
- Jalaei, M.H.; Thai, H.T.; Civalek, O. On viscoelastic transient response of magnetically imperfect functionally graded nanobeams. Int. J. Eng. Sci. 2022, 172, 103629. [Google Scholar] [CrossRef]
- Al-Zahrani, M.A.; Asiri, S.A.; Ahmed, K.I.; Eltaher, M.A. Free vibration analysis of 2D functionally graded strip beam using finite element method. J. Appl. Comput. Mech. 2022, 8, 1422–1430. [Google Scholar]
- Malikan, M.; Eremeyev, V.A. On time-dependent nonlinear dynamic response of micro-elastic solids. Int. J. Eng. Sci. 2023, 182, 103793. [Google Scholar] [CrossRef]
- Civalek, O.; Uzun, B.; Yaylı, M.O. On nonlinear stability analysis of saturated embedded porous nanobeams. Int. J. Eng. Sci. 2023, 190, 103898. [Google Scholar] [CrossRef]
- Lim, C.W.; Zhang, G.; Reddy, J.N. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J. Mech. Phys. Solids 2015, 78, 298–313. [Google Scholar] [CrossRef]
- Herisanu, N.; Marinca, V. An efficient analytical approach to investigate the dynamics of a misaligned multirotor system. Mathematics 2020, 8, 1083. [Google Scholar] [CrossRef]
- Marinca, V.; Herisanu, N.; Marinca, B. Optimal Auxiliary Functions Method for Nonlinear Dynamical Systems; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Herisanu, N.; Marinca, V. An effective analytical approach to nonlinear free vibration of elastically actuated microtubes. Meccanica 2021, 56, 812–823. [Google Scholar] [CrossRef]
- Marinca, B.; Marinca, V.; Bogdan, C. Dynamical SEIR epidemic model by Optimal Auxiliary Functions Method. Chaos Solitons Fractals 2021, 147, 110949. [Google Scholar] [CrossRef] [PubMed]
- Herisanu, N.; Marinca, B.; Marinca, V. Nonlinear vibration of double-walled carbon nanotubes subjected to mechanical impact and embedded on Winkler-Pasternak foundation. Materials 2022, 15, 8599. [Google Scholar] [CrossRef] [PubMed]
- Rand, R. Lectures Notes on Nonlinear Vibrations; Version 45; Cornell University: Ithaca, NY, USA, 2003. [Google Scholar]
- Luo, S.; Ma, H.; Li, F.; Ouakad, N.M. Dynamical analysis and chaos control of MEMS resonator by using the analog circuit. Nonl. Dyn. 2022, 108, 1–16. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).