Assessing Asymmetrical Rates in Multivariate Phylogenetic Trait Evolution: An Extension of Statistical Models for Heterogeneous Rate Estimation
Abstract
:1. Introduction
2. Method
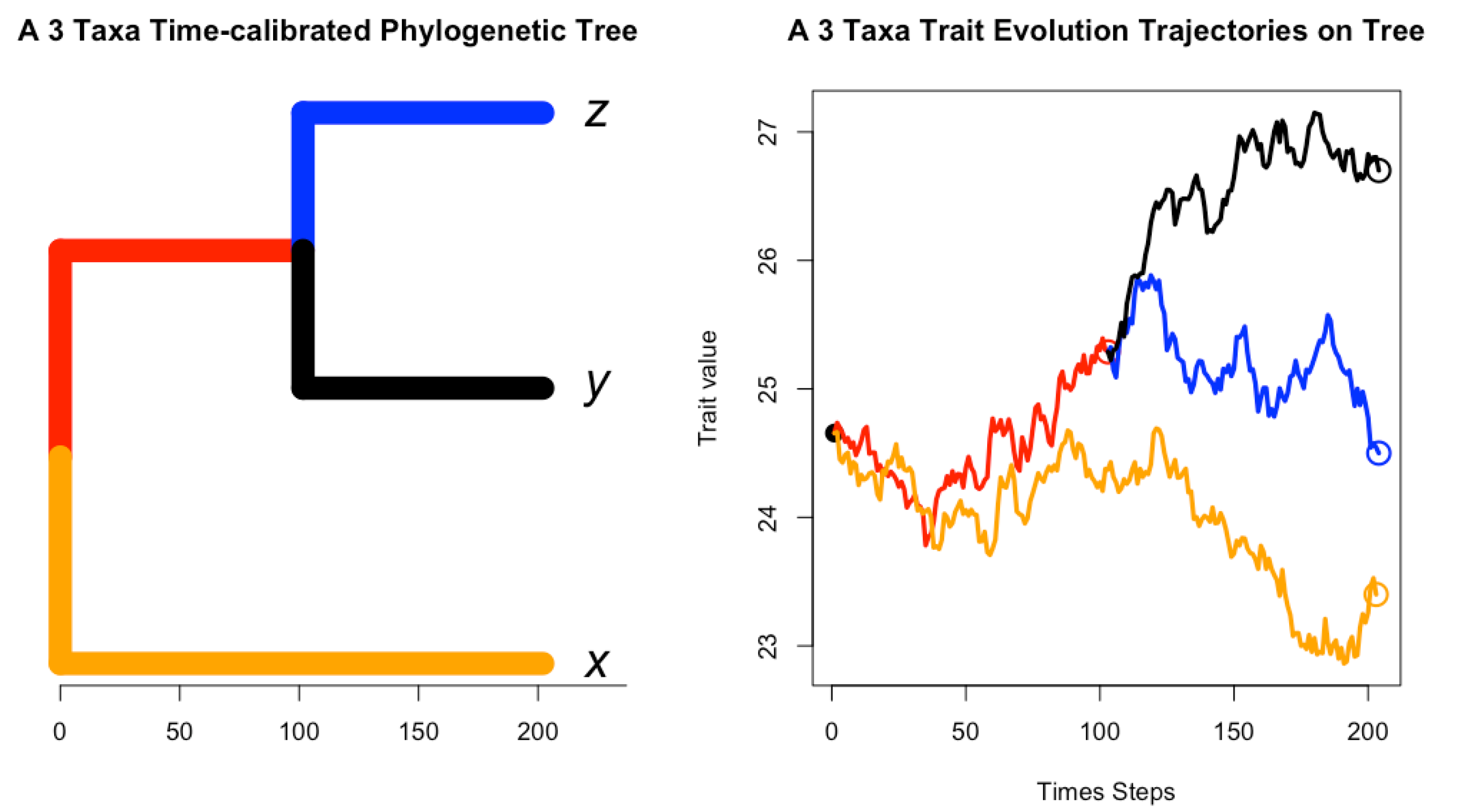
2.1. Gaussian Process for Trait Evolution along Tree
2.2. Statistical Model for Multiple Traits Evolution
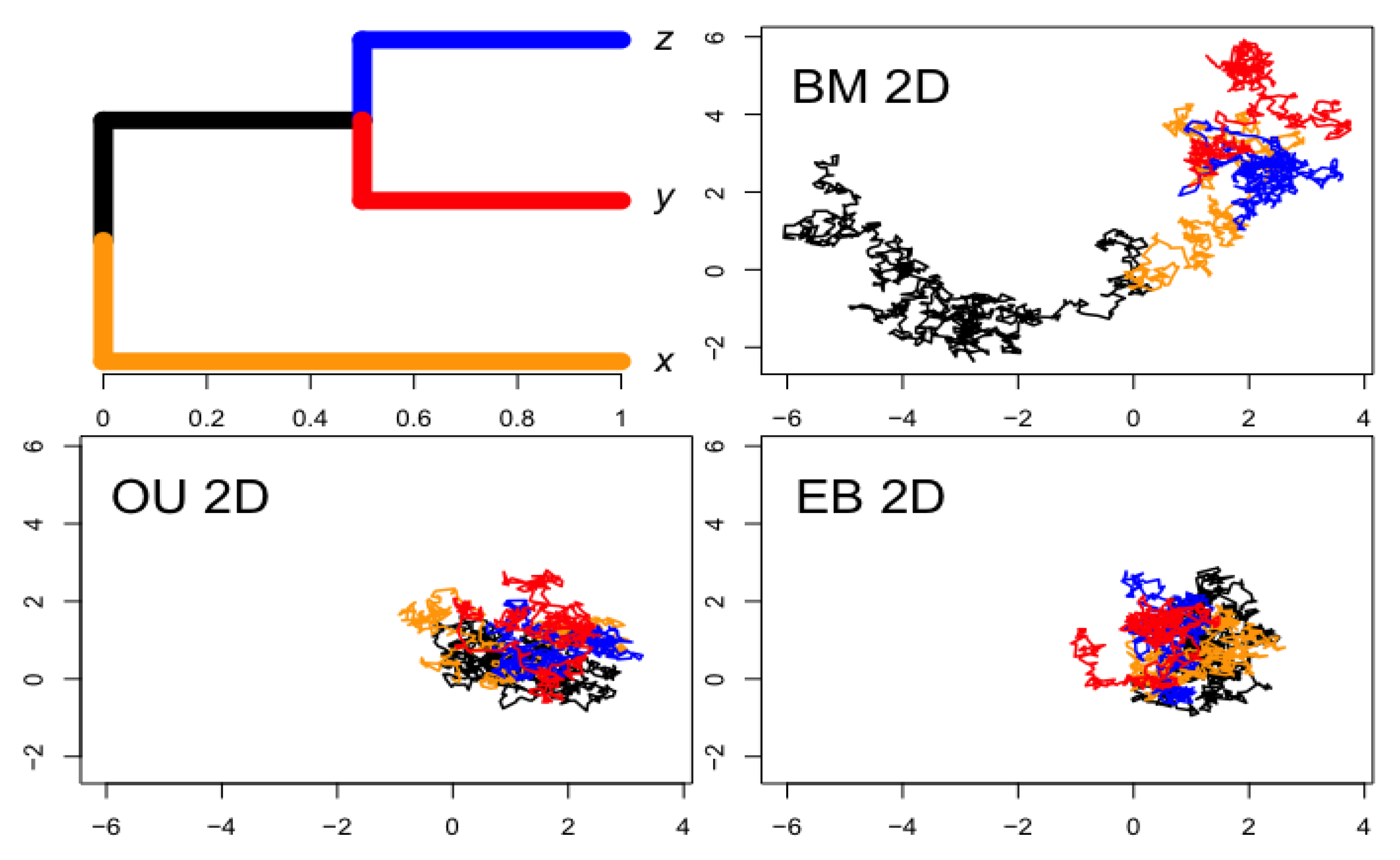
2.2.1. Multivariate Brownian Motion Model
2.2.2. Multivariate Ornstein–Uhlenbeck Model
2.2.3. Multivariate Early Burst Model
2.2.4. Multivariate Phylogenetic Mixed Model
3. Parameter Estimation and Testing
3.1. Estimation of the Rate Matrix and Compute the Likelihood
3.2. Compare the Fit of Models
4. Results
4.1. Simulation: Power Analysis
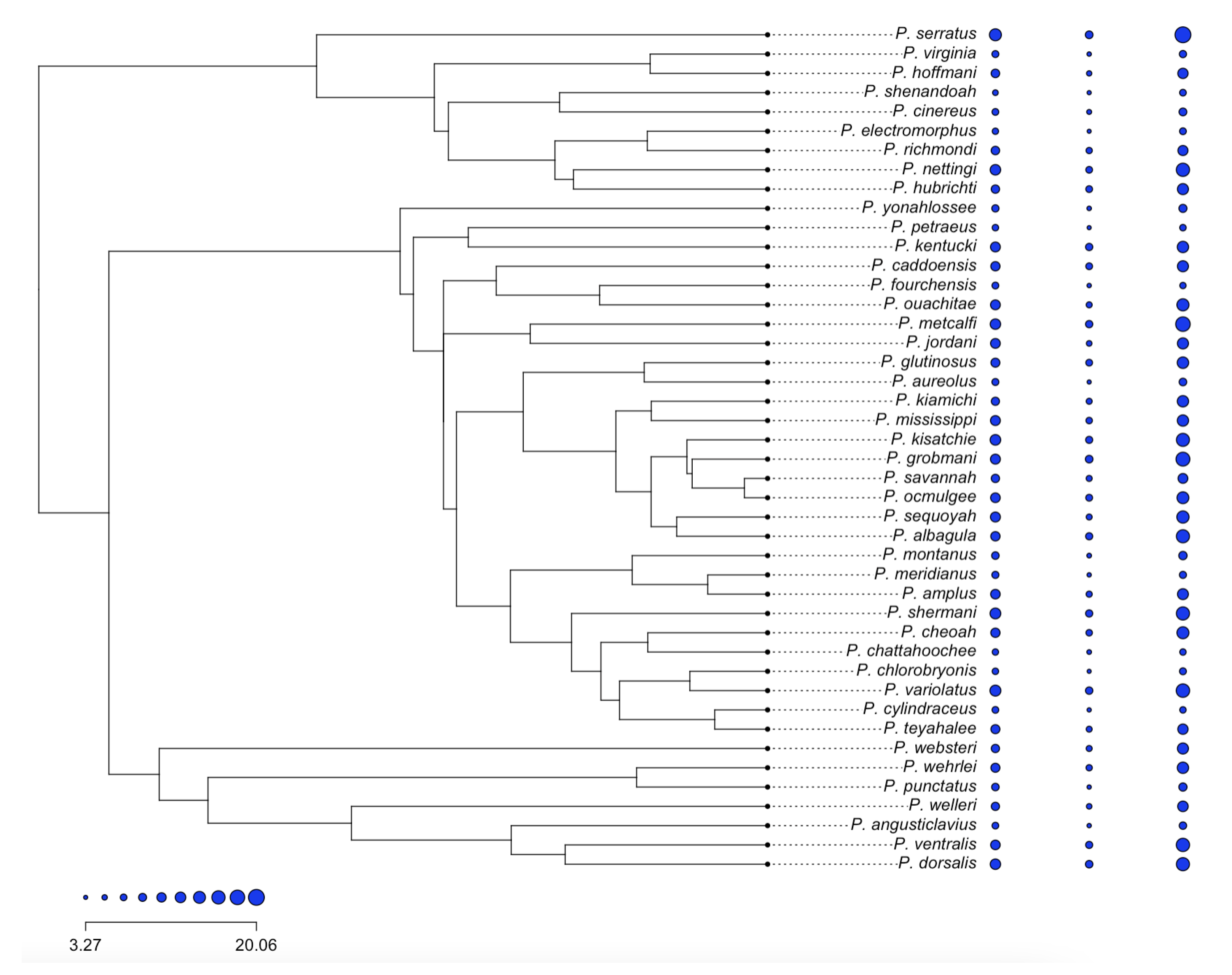
4.2. Empirical Study: Heterogeneous Rate of Evolution of the Salamander
- (i)
- Head length: An increase in a creature’s head (and thereby, jaw) length is anticipated to enhance its biting strength and its proficiency in prey capture.
- (ii)
- Forelimb length: A longer forelimb is projected to augment the creature’s perceived body size during aggressive displays, possibly offering a competitive edge.
- (iii)
- Body width: Currently, there is no substantiated evidence indicating any impact of a creature’s body width on competitive behavior.
4.2.1. Head Length vs. Body Width
4.2.2. Forelimb Length vs. Body Width
4.3. Accessing Adequacy of Models via Many Empirical Datasets
5. Discussion
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Code and Scripts
- Figure 1: https://tonyjhwueng.info/phymvrates/onetreetraj.html (accessed on 10 July 2023)
- Figure 2: https://tonyjhwueng.info/phymvrates/2dbmou.html (accessed on 10 July 2023)
- Figure 3: https://tonyjhwueng.info/phymvrates/powerplot.html (accessed on 10 July 2023)
- a.
- BM: Power analysis for Brownian motion model https://tonyjhwueng.info/phymvrates/simsBM.html (accessed on 10 July 2023)
- b.
- OU: Power analysis for Ornstein–Uhlenbeck model https://tonyjhwueng.info/phymvrates/simsOU.html (accessed on 10 July 2023)
- c.
- EB: Power analysis for early burst model https://tonyjhwueng.info/phymvrates/simsEB.html (accessed on 10 July 2023)
- d.
- PMM: Power analysis for phylogenetic mixed model https://tonyjhwueng.info/phymvrates/simsPMM.html (accessed on 10 July 2023)
- Figure 4: https://tonyjhwueng.info/phymvrates/phyratepic.html (accessed on 10 July 2023)
- Figure 5: https://tonyjhwueng.info/phymvrates/adequacy.html (accessed on 10 July 2023)
- Models code
- d.
- BM: Section 2.2.1: Multivariate Brownian motion model https://tonyjhwueng.info/phymvrates/ComparingBM.html (accessed on 10 July 2023)
- e.
- OU: Section 2.2.2: Multivariate Ornstein–Uhlenbeck model https://tonyjhwueng.info/phymvrates/ComparingOU.html (accessed on 10 July 2023)
- f.
- EB: Section 2.2.3: Multivariate early burst model https://tonyjhwueng.info/phymvrates/ComparingEB.html (accessed on 10 July 2023)
- g.
- PMM: Section 2.2.4: Mixed multivariate phylogenetic model https://tonyjhwueng.info/phymvrates/ComparingPMM.html (accessed on 10 July 2023)
Appendix A.2. Proof of Lemma
Appendix A.2.1. Covariance for EB Model
Appendix A.2.2. Simplification of Covariance Matrix in PMM Model
- (i)
- Some useful operations for the tensor product of two matrices , and .
- (ii)
- Given and with . If and and , where is a diagonal matrix of eigenvalues of a square matrix , then . In particular, if and , then .
- (iii)
- Woodbury matrix identity gives where , , and . Set , .
- Claim 1:
- Proof:
- Let , by (iii) .
- Claim 2:
- where is a diagonal matrix composed of the eigenvalues of .
- Proof:
- First, let the eigen decomposition and such that . Let such that . Let such that . Then by (ii) . Hence .
Appendix A.3. Trait Dataset
| No. | Scientific Name | Common Name |
|---|---|---|
| 1 | Plethodon Dorsalis (https://en.wikipedia.org/wiki/Plethodon_dorsalis (accessed on 10 July 2023)) | Northern Zigzag Salamander |
| 2 | Plethodon Ventralis (https://en.wikipedia.org/wiki/Plethodon_ventralis (accessed on 10 July 2023)) | Southern Zigzag Salamander |
| 3 | Plethodon Angusticlavius (https://en.wikipedia.org/wiki/Plethodon_angusticlavius (accessed on 10 July 2023)) | Ozark Zigzag Salamander |
| 4 | Plethodon Welleri (https://en.wikipedia.org/wiki/Plethodon_welleri (accessed on 10 July 2023)) | Weller’s Salamander |
| 5 | Plethodon Punctatus (https://en.wikipedia.org/wiki/Plethodon_punctatus (accessed on 10 July 2023)) | Cow Knob Salamander |
| 6 | Plethodon Wehrlei (https://en.wikipedia.org/wiki/Plethodon_wehrlei (accessed on 10 July 2023)) | Wehrle’s Salamander |
| 7 | Plethodon Websteri (https://en.wikipedia.org/wiki/Plethodon_websteri (accessed on 10 July 2023)) | Webster’s Salamander |
| 8 | Plethodon Teyahalee (https://en.wikipedia.org/wiki/Plethodon_teyahalee (accessed on 10 July 2023)) | Southern Appalachian Salamander |
| 9 | Plethodon Cylindraceus (https://en.wikipedia.org/wiki/Plethodon_cylindraceus (accessed on 10 July 2023)) | White-spotted Slimy Salamander |
| 10 | Plethodon Variolatus (https://en.wikipedia.org/wiki/Plethodon_variolatus (accessed on 10 July 2023)) | South Carolina Slimy Salamander |
| 11 | Plethodon Chlorobryonis (https://en.wikipedia.org/wiki/Plethodon_chlorobryonis (accessed on 10 July 2023)) | Atlantic Coast Slimy Salamander |
| 12 | Plethodon Chattahoochee (https://en.wikipedia.org/wiki/Plethodon_chattahoochee (accessed on 10 July 2023)) | Chattahoochee Slimy Salamander |
| 13 | Plethodon Cheoah (https://en.wikipedia.org/wiki/Plethodon_cheoah (accessed on 10 July 2023)) | Cheoah Bald Salamander |
| 14 | Plethodon Shermani (https://en.wikipedia.org/wiki/Plethodon_shermani (accessed on 10 July 2023)) | Red-legged Salamander |
| 15 | Plethodon Amplus (https://en.wikipedia.org/wiki/Plethodon_amplus (accessed on 10 July 2023)) | Blue Ridge Gray-cheeked Salamander |
| 16 | Plethodon Meridianus (https://en.wikipedia.org/wiki/Plethodon_meridianus (accessed on 10 July 2023)) | South Mountain Gray-cheeked Salamander |
| 17 | Plethodon Montanus (https://en.wikipedia.org/wiki/Plethodon_montanus (accessed on 10 July 2023)) | Northern Gray-cheeked Salamander |
| 18 | Plethodon Albagula (https://en.wikipedia.org/wiki/Plethodon_albagula (accessed on 10 July 2023)) | Western Slimy Salamander |
| 19 | Plethodon Sequoyah (https://en.wikipedia.org/wiki/Plethodon_sequoyah (accessed on 10 July 2023)) | Sequoyah Slimy Salamander |
| 20 | Plethodon Ocmulgee (https://en.wikipedia.org/wiki/Plethodon_ocmulgee (accessed on 10 July 2023)) | Ocmulgee Slimy Salamander |
| 21 | Plethodon Savannah (https://en.wikipedia.org/wiki/Plethodon_savannah (accessed on 10 July 2023)) | Savannah Slimy Salamander |
| 22 | Plethodon Grobmani (https://en.wikipedia.org/wiki/Plethodon_grobmani (accessed on 10 July 2023)) | Western Slimy Salamander |
| 23 | Plethodon Kisatchie (https://en.wikipedia.org/wiki/Plethodon_kisatchie (accessed on 10 July 2023)) | Louisiana Slimy Salamander |
| 24 | Plethodon Mississippi (https://en.wikipedia.org/wiki/Plethodon_mississippi (accessed on 10 July 2023)) | Mississippi Slimy Salamander |
| 25 | Plethodon Kiamichi (https://en.wikipedia.org/wiki/Plethodon_kiamichi (accessed on 10 July 2023)) | Kiamichi Slimy Salamander |
| 26 | Plethodon Aureolus (https://en.wikipedia.org/wiki/Plethodon_aureolus (accessed on 10 July 2023)) | Tellico Salamander |
| 27 | Plethodon Glutinosus (https://en.wikipedia.org/wiki/Plethodon_glutinosus (accessed on 10 July 2023)) | Northern Slimy Salamander |
| 28 | Plethodon Jordani (https://en.wikipedia.org/wiki/Plethodon_jordani (accessed on 10 July 2023)) | Red-cheeked Salamander |
| 29 | Plethodon Metcalfi (https://en.wikipedia.org/wiki/Plethodon_metcalfi (accessed on 10 July 2023)) | Southern Gray-cheeked Salamander |
| 30 | Plethodon Ouachitae (https://en.wikipedia.org/wiki/Plethodon_ouachitae (accessed on 10 July 2023)) | Rich Mountain Salamander |
| 31 | Plethodon Fourchensis (https://en.wikipedia.org/wiki/Plethodon_fourchensis (accessed on 10 July 2023)) | Fourche Mountain Salamander |
| 32 | Plethodon Caddoensis (https://en.wikipedia.org/wiki/Plethodon_caddoensis (accessed on 10 July 2023)) | Caddo Mountain Salamander |
| 33 | Plethodon Kentucki (https://en.wikipedia.org/wiki/Cumberland_Plateau_salamander (accessed on 10 July 2023)) | Cumberland Plateau salamander |
| 34 | Plethodon Petraeus (https://en.wikipedia.org/wiki/Pigeon_Mountain_salamander (accessed on 10 July 2023)) | Pigeon Mountain salamander |
| 35 | Plethodon Yonahlossee (https://en.wikipedia.org/wiki/Yonahlossee_salamander (accessed on 10 July 2023)) | Yonahlossee salamander |
| 36 | Plethodon Hubrichti (https://en.wikipedia.org/wiki/Peaks_of_Otter_salamander (accessed on 10 July 2023)) | Peaks of Otter salamander |
| 37 | Plethodon Nettingi (https://en.wikipedia.org/wiki/Cheat_Mountain_salamander (accessed on 10 July 2023)) | Cheat Mountain salamander |
| 38 | Plethodon Richmondi (https://en.wikipedia.org/wiki/Ravine_salamander (accessed on 10 July 2023)) | Ravine salamander |
| 39 | Plethodon Electromorphus (https://en.wikipedia.org/wiki/Northern_ravine_salamander (accessed on 10 July 2023)) | Northern ravine salamander |
| 40 | Plethodon Cinereus (https://en.wikipedia.org/wiki/Red-backed_salamander (accessed on 10 July 2023)) | Red-backed salamander |
| 41 | Plethodon Shenandoah (https://en.wikipedia.org/wiki/Shenandoah_salamander (accessed on 10 July 2023)) | Shenandoah salamander |
| 42 | Plethodon Hoffmani (https://en.wikipedia.org/wiki/Valley_and_ridge_salamander (accessed on 10 July 2023)) | Valley and ridge salamander |
| 43 | Plethodon Virginia (https://en.wikipedia.org/wiki/Shenandoah_Mountain_salamander (accessed on 10 July 2023)) | Shenandoah Mountain salamander |
| 44 | Plethodon Serratus (https://en.wikipedia.org/wiki/Southern_red-backed_salamander (accessed on 10 July 2023)) | Southern red-backed salamander |
References
- Walsh, B.; Lynch, M. Evolution and Selection of Quantitative Traits; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Shankar, A.; Cisneros, I.N.; Thompson, S.; Graham, C.H.; Powers, D.R. A heterothermic spectrum in hummingbirds. J. Exp. Biol. 2022, 225, jeb243208. [Google Scholar] [CrossRef] [PubMed]
- Rico-Guevara, A.; Hurme, K.J.; Rubega, M.A.; Cuban, D. Nectar feeding beyond the tongue: Hummingbirds drink using phase-shifted bill opening, flexible tongue flaps and wringing at the tips. J. Exp. Biol. 2023, 226, jeb245074. [Google Scholar] [CrossRef] [PubMed]
- Piper, R. Extraordinary Animals: An Encyclopedia of Curious and Unusual Animals; Greenwood Press: London, UK, 2007; Volume 125. [Google Scholar]
- Stebbins, R.C.; Cohen, N.W. A Natural History of Amphibians; Princeton University Press: Princeton, NJ, USA, 1997. [Google Scholar]
- Adams, D.C. Comparing evolutionary rates for different phenotypic traits on a phylogeny using likelihood. Syst. Biol. 2013, 62, 181–192. [Google Scholar] [CrossRef] [PubMed]
- Beaulieu, J.M.; Leitch, I.J.; Patel, S.; Pendharkar, A.; Knight, C.A. Genome size is a strong predictor of cell size and stomatal density in angiosperms. New Phytol. 2008, 179, 975–986. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beaulieu, J.M.; Jhwueng, D.C.; Boettiger, C.; O’Meara, B.C. Modeling stabilizing selection: Expanding the Ornstein–Uhlenbeck model of adaptive evolution. Evol. Int. J. Org. Evol. 2012, 66, 2369–2383. [Google Scholar] [CrossRef]
- Revell, L.J.; González-Valenzuela, L.E.; Alfonso, A.; Castellanos-García, L.A.; Guarnizo, C.E.; Crawford, A.J. Comparing evolutionary rates between trees, clades and traits. Methods Ecol. Evol. 2018, 9, 994–1005. [Google Scholar] [CrossRef]
- O’Meara, B.C.; Ané, C.; Sanderson, M.J.; Wainwright, P.C. Testing for different rates of continuous trait evolution using likelihood. Evolution 2006, 60, 922–933. [Google Scholar]
- Adams, D.C.; Felice, R.N. Assessing trait covariation and morphological integration on phylogenies using evolutionary covariance matrices. PLoS ONE 2014, 9, e94335. [Google Scholar] [CrossRef] [Green Version]
- Hansen, T.F. Stabilizing selection and the comparative analysis of adaptation. Evolution 1997, 51, 1341–1351. [Google Scholar] [CrossRef]
- Bartoszek, K.; Pienaar, J.; Mostad, P.; Andersson, S.; Hansen, T.F. A phylogenetic comparative method for studying multivariate adaptation. J. Theor. Biol. 2012, 314, 204–215. [Google Scholar] [CrossRef]
- Harmon, L. Phylogenetic Comparative Methods: Learning from Trees; CreateSpace Independent Publishing Platform: Scotts Valley, CA, USA, 2018. [Google Scholar]
- Housworth, E.A.; Martins, E.P.; Lynch, M. The phylogenetic mixed model. Am. Nat. 2004, 163, 84–96. [Google Scholar] [CrossRef] [Green Version]
- Nelson, E. Dynamical Theories of Brownian Motion; Princeton University Press: Princeton, NJ, USA, 2020; Volume 101. [Google Scholar]
- Gramacy, R.B. Surrogates: Gaussian Process Modeling, Design, and Optimization for the Applied Sciences; Chapman and Hall/CRC: Boca Raton, FL, USA, 2020. [Google Scholar]
- Jhwueng, D.C.; O’Meara, B.C. On the Matrix Condition of Phylogenetic Tree. Evol. Bioinform. 2020, 16, 1176934320901721. [Google Scholar] [CrossRef]
- Hsu, M.H. Studying Rate of Evolution in Multi Dimensional Trait Space. Master’s Thesis, Feng-Chia University, Taichung, Taiwan, 2022. [Google Scholar]
- Adams, D.C.; Collyer, M.L. Multivariate phylogenetic comparative methods: Evaluations, comparisons, and recommendations. Syst. Biol. 2018, 67, 14–31. [Google Scholar] [CrossRef]
- Hassler, G.; Tolkoff, M.R.; Allen, W.L.; Ho, L.S.T.; Lemey, P.; Suchard, M.A. Inferring phenotypic trait evolution on large trees with many incomplete measurements. J. Am. Stat. Assoc. 2020, 117, 678–692. [Google Scholar] [CrossRef]
- Butler, M.A.; King, A.A. Phylogenetic comparative analysis: A modeling approach for adaptive evolution. Am. Nat. 2004, 164, 683–695. [Google Scholar] [CrossRef]
- Blomberg, S.P.; Garland, T., Jr.; Ives, A.R. Testing for phylogenetic signal in comparative data: Behavioral traits are more labile. Evolution 2003, 57, 717–745. [Google Scholar]
- Jhwueng, D. Some Problems in Phylogenetic Comparative Method. Ph.D. Thesis, Indiana University Bloomington, Bloomington, IN, USA, 2010. [Google Scholar]
- Puttick, M. Mixed evidence for early bursts of morphological evolution in extant clades. J. Evol. Biol. 2018, 31, 502–515. [Google Scholar] [CrossRef] [Green Version]
- Grant, P.R. Ecology and Evolution of Darwin’s Finches; Princeton Science Library Edition; Princeton University Press: Princeton, NJ, USA, 2017. [Google Scholar]
- Burns, K.J.; Hackett, S.J.; Klein, N.K. Phylogenetic relationships and morphological diversity in Darwin’s finches and their relatives. Evolution 2002, 56, 1240–1252. [Google Scholar]
- Paradis, E. Analysis of Phylogenetics and Evolution with R; Springer Science & Business Media: New York, NY, USA, 2011. [Google Scholar]
- R Core Team. R: 4.2.3 A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Anderson, D.; Burnham, K. Model Selection and Multi-Model Inference, 2nd ed.; Springer: New York, NY, USA, 2004; Volume 63, p. 10. [Google Scholar]
- Grafen, A. The phylogenetic regression. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1989, 326, 119–157. [Google Scholar]
- Popescu, A.A.; Huber, K.T.; Paradis, E. ape 3.0: New tools for distance-based phylogenetics and evolutionary analysis in R. Bioinformatics 2012, 28, 1536–1537. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.; Stecher, G.; Suleski, M.; Hedges, S.B. TimeTree: A resource for timelines, timetrees, and divergence times. Mol. Biol. Evol. 2017, 34, 1812–1819. [Google Scholar] [CrossRef] [PubMed]
- Adams, D.C.; Berns, C.M.; Kozak, K.H.; Wiens, J.J. Are rates of species diversification correlated with rates of morphological evolution? Proc. R. Soc. B Biol. Sci. 2009, 276, 2729–2738. [Google Scholar] [CrossRef] [PubMed]
- Adams, D.C. Quantifying and comparing phylogenetic evolutionary rates for shape and other high-dimensional phenotypic data. Syst. Biol. 2014, 63, 166–177. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beaulieu, J.M.; O’Meara, B.C. Detecting hidden diversification shifts in models of trait-dependent speciation and extinction. Syst. Biol. 2016, 65, 583–601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stern, D.B.; Breinholt, J.; Pedraza-Lara, C.; López-Mejía, M.; Owen, C.L.; Bracken-Grissom, H.; Fetzner, J.W., Jr.; Crandall, K.A. Phylogenetic evidence from freshwater crayfishes that cave adaptation is not an evolutionary dead-end. Evolution 2017, 71, 2522–2532. [Google Scholar] [CrossRef] [Green Version]
- Melville, J.; Swain, R. Evolutionary correlations between escape behaviour and performance ability in eight species of snow skinks (Niveoscincus: Lygosominae) from Tasmania. J. Zool. 2003, 261, 79–89. [Google Scholar] [CrossRef]
- Moreeteau, B.; Gibert, P.; Pétavy, G.; Morteau, J.C.; Huey, R.; David, J. Morphometrical evolution in a Drosophila clade: The Drosophila obscura group. J. Zool. Syst. Evol. Res. 2003, 41, 64–71. [Google Scholar] [CrossRef] [Green Version]
- Bonine, K.E.; Gleeson, T.T.; Garland, T., Jr. Muscle fiber-type variation in lizards (Squamata) and phylogenetic reconstruction of hypothesized ancestral states. J. Exp. Biol. 2005, 208, 4529–4547. [Google Scholar] [CrossRef] [Green Version]
- Vanhooydonck, B.; Van Damme, R.; Aerts, P. Variation in speed, gait characteristics and microhabitat use in lacertid lizards. J. Exp. Biol. 2002, 205, 1037–1046. [Google Scholar] [CrossRef]
- Tubaro, P.L.; Lijtmaer, D.A.; Palacios, M.G.; Kopuchian, C. Adaptive modification of tail structure in relation to body mass and buckling in woodcreepers. Condor 2002, 104, 281–296. [Google Scholar] [CrossRef]
- Sanchez, J.A.; Lasker, H.R. Patterns of morphological integration in marine modular organisms: Supra-module organization in branching octocoral colonies. Proc. R. Soc. Lond. Ser. B Biol. Sci. 2003, 270, 2039–2044. [Google Scholar] [CrossRef]
- Aguirre, L.F.; Herrel, A.; Van Damme, R.; Matthysen, E. Ecomorphological analysis of trophic niche partitioning in a tropical savannah bat community. Proc. R. Soc. Lond. Ser. B Biol. Sci. 2002, 269, 1271–1278. [Google Scholar] [CrossRef]
- Rice, A.; Mayrose, I. Model adequacy tests for probabilistic models of chromosome-number evolution. New Phytol. 2021, 229, 3602–3613. [Google Scholar] [CrossRef]
- Tung Ho, L.s.; Ané, C. A linear-time algorithm for Gaussian and non-Gaussian trait evolution models. Syst. Biol. 2014, 63, 397–408. [Google Scholar] [CrossRef]
- Baken, E.K.; Mellenthin, L.E.; Adams, D.C. Is salamander arboreality limited by broad-scale climatic conditions? PLoS ONE 2021, 16, e0255393. [Google Scholar] [CrossRef]
- Juarez, B.H.; Adams, D.C. Evolutionary allometry of sexual dimorphism of jumping performance in anurans. Evol. Ecol. 2022, 36, 717–733. [Google Scholar] [CrossRef]
- Juarez, B.H.; Moen, D.S.; Adams, D.C. Ecology, sexual dimorphism, and jumping evolution in anurans. J. Evol. Biol. 2023, 36, 829–841. [Google Scholar] [CrossRef]
- Higham, N.J. Accuracy and Stability of Numerical Algorithms; SIAM: Philadelphia, PA, USA, 2002. [Google Scholar]
- AmphibiaWeb. 2023. Available online: https://amphibiaweb.org/ (accessed on 10 July 2023).


| BM | OU | PMM | EB | |
|---|---|---|---|---|
| Obs () | 0.23, 0.13 | 0.23, 0.13 | 0.22, 0.13 | 0.23, 0.12 |
| Con () | 1.02, 0.13 | 1.02, 0.16 | 1.02, 0.13 | 1.02, 0.13 |
| −126.85 | −126.39 | −126.82 | −126.86 | |
| −188.32 | −185.95 | −187.82 | −188.32 | |
| 122.94 | 119.11 | 121.99 | 122.91 | |
| p-value | 1.44 × | 9.90 × | 2.32 × | 1.46 × |
| 261.70 | 264.79 | 265.65 | 265.72 | |
| 382.63 | 381.90 | 385.64 | 386.63 |
| BM | OU | PMM | EB | |
|---|---|---|---|---|
| Obs () | (0.12, 0.20) | (0.13, 0.21) | (0.13, 0.20) | (0.12, 0.20) |
| Con () | (1.04, 0.20) | (1.05, 0.24) | (1.04, 0.21) | (1.01, 0.11) |
| −134.21 | −133.53 | −134.25 | −142.98 | |
| −193.43 | -191.40 | −192.87 | −193.97 | |
| 118.43 | 115.75 | 117.24 | 101.99 | |
| p-value | 1.40 × | 5.40 × | 2.54 × | 5.57 × |
| 276.43 | 279.05 | 280.50 | 297.95 | |
| 392.85 | 392.80 | 395.74 | 397.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jhwueng, D.-C. Assessing Asymmetrical Rates in Multivariate Phylogenetic Trait Evolution: An Extension of Statistical Models for Heterogeneous Rate Estimation. Symmetry 2023, 15, 1445. https://doi.org/10.3390/sym15071445
Jhwueng D-C. Assessing Asymmetrical Rates in Multivariate Phylogenetic Trait Evolution: An Extension of Statistical Models for Heterogeneous Rate Estimation. Symmetry. 2023; 15(7):1445. https://doi.org/10.3390/sym15071445
Chicago/Turabian StyleJhwueng, Dwueng-Chwuan. 2023. "Assessing Asymmetrical Rates in Multivariate Phylogenetic Trait Evolution: An Extension of Statistical Models for Heterogeneous Rate Estimation" Symmetry 15, no. 7: 1445. https://doi.org/10.3390/sym15071445
APA StyleJhwueng, D.-C. (2023). Assessing Asymmetrical Rates in Multivariate Phylogenetic Trait Evolution: An Extension of Statistical Models for Heterogeneous Rate Estimation. Symmetry, 15(7), 1445. https://doi.org/10.3390/sym15071445








