Nucleon-Pair Shell Model within a Symmetry Broken Basis
Abstract
:1. Introduction
2. The Model
2.1. NPSM Framework
2.2. Symmetry Broken Basis
2.2.1. Axially-Deformed Basis
2.2.2. Triaxially-Deformed Basis
3. Numerical Results
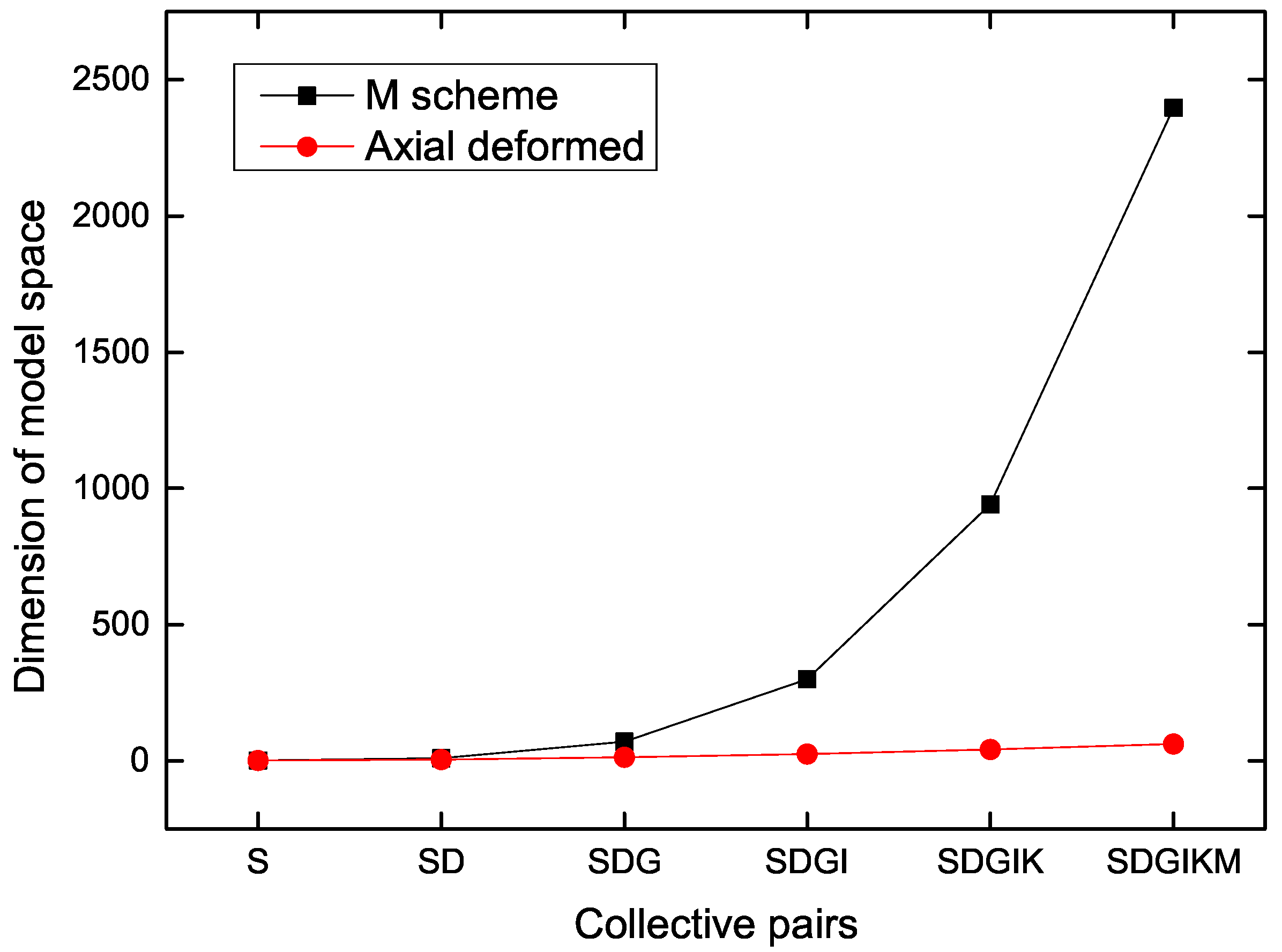
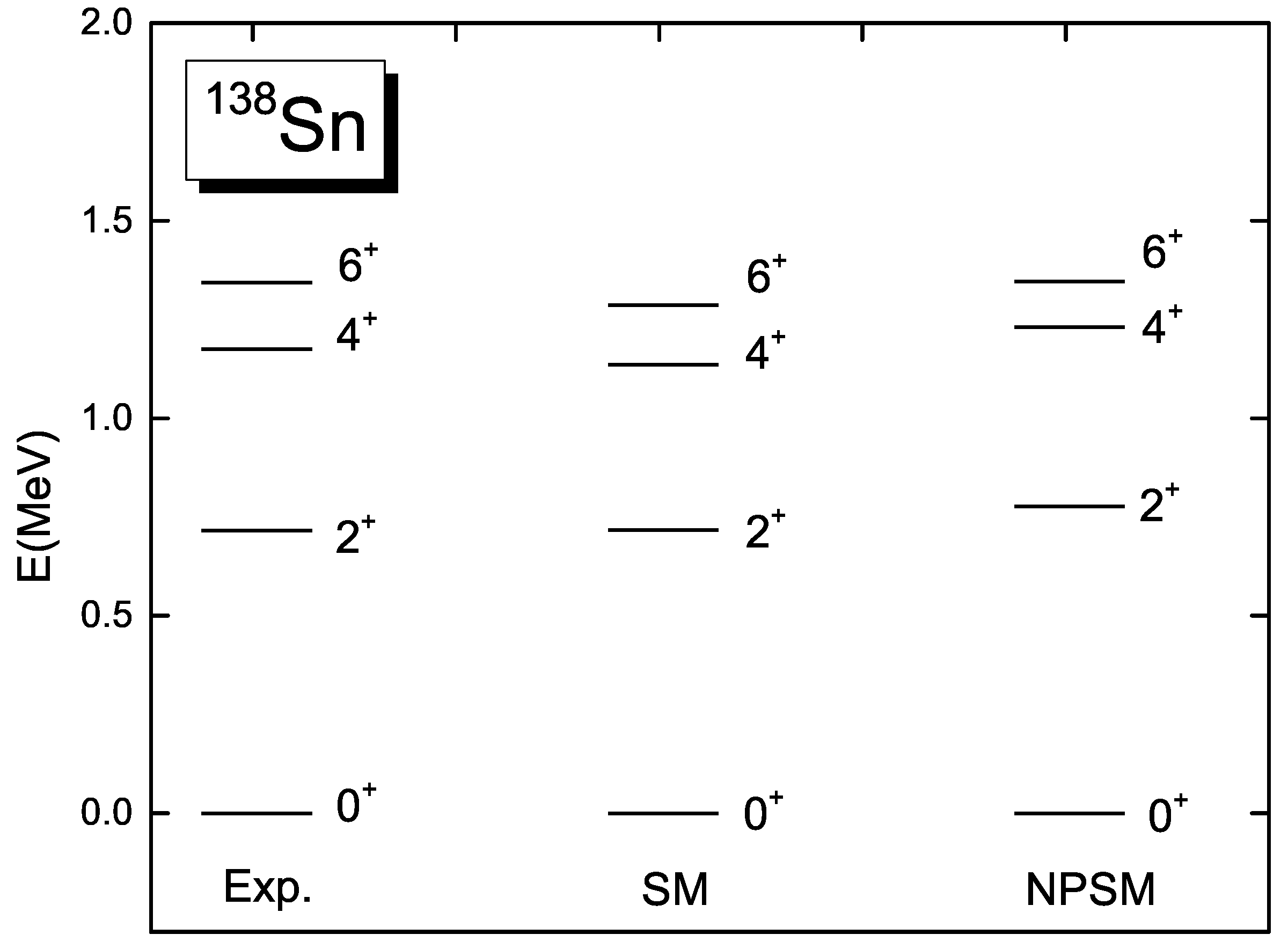
3.1. Axially-Deformed Basis
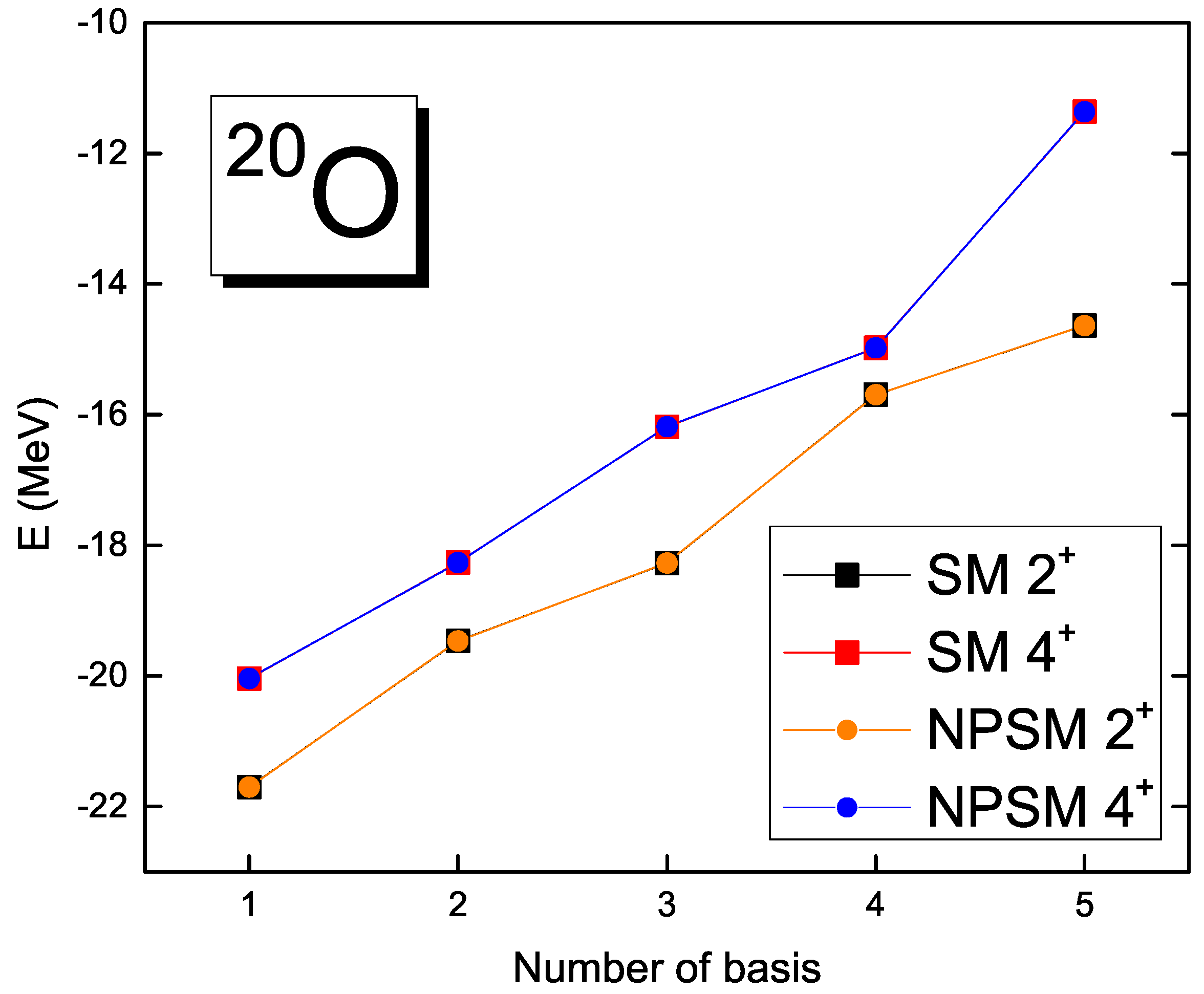
3.2. Triaxially-Deformed Basis
4. Summary and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Carlson, J.; Schiavilla, R. Structure and dynamics of few-nucleon systems. Rev. Mod. Phys. 1998, 70, 743. [Google Scholar]
- Pieper, S.C.; Wiringa, R.B. Quantum Monte Carlo Calculations of Light Nuclei. Annu. Rev. Nucl. Part. Sci. 2001, 51, 53. [Google Scholar] [CrossRef]
- Barrett, B.R.; Navratil, P.; Vary, J.P. Ab initio no core shell model. Prog. Part. Nucl. Phys. 2012, 69, 1022919. [Google Scholar]
- Dytrych, T.; Launey, K.D.; Draayer, J.P.; Maris, P.; Vary, J.P.; Saule, E.; Catalyurek, U.; Sosonkina, M.; Langr, D.; Caprio, M.A. Collective Modes in Light Nuclei from First Principles. Phys. Rev. Lett. 2013, 111, 252501. [Google Scholar] [CrossRef] [PubMed]
- Hagen, G.; Papenbrock, T.; Hjorth-Jensen, M.; Dean, D.J. Coupled-cluster computations of atomic nuclei. Rep. Prog. Phys. 2014, 77, 096302. [Google Scholar] [CrossRef]
- Gregorio, G.D.; Knapp, F.; Iudice, N.L.; Vesely, P. Odd nuclei spectroscopy within a self-consistent multiphonon approach. J. Phys. Conf. Ser. 2018, 866, 012007. [Google Scholar] [CrossRef]
- Vesely, P.; Gregorio, G.D.; Knapp, F.; Iudice, N.L. A center of mass free equation of motion method and its application to 4He. J. Phys. Conf. Ser. 2023, 2453, 012008. [Google Scholar] [CrossRef]
- Rowe, D.J. Equations-of-Motion Method and the Extended Shell Model. Rev. Mod. Phys. 1968, 40, 153. [Google Scholar] [CrossRef]
- Bender, M.; Heenen, P.-H.; Reinhard, P.-G. Self-consistent mean-field models for nuclear structure. Rev. Mod. Phys. 2003, 75, 121. [Google Scholar]
- Roth, R. Importance truncation for large-scale configuration interaction approaches. Phys. Rev. C 2009, 79, 064324. [Google Scholar] [CrossRef]
- Bertulani, C. Nuclear Physics in a Nutshell; Princeton University Press: Princeton, NJ, USA, 2007; p. 119. [Google Scholar]
- Talmi, I.; Barrett, B. Simple Models of Complex Nuclei: The Shell Model and Interacting Boson Model. Phys. Today 1994, 47, 102. [Google Scholar] [CrossRef]
- Lawson, R.D. Theory of the Nuclear Shell Model; Oxford University Press: New York, NY, USA, 1980. [Google Scholar]
- Otsuka, T.; Honma, M.; Mizusaki, T.; Shimizu, N.; Utsuno, Y. New-generation Monte Carlo shell model for the K computer era. Prog. Part. Nucl. Phys. 2001, 47, 319. [Google Scholar] [CrossRef]
- Caurier, E.; Martinez-Pinedo, G.; Nowacki, F.; Poves, A.; Zuker, A.P. The shell model as a unified view of nuclear structure. Rev. Mod. Phys. 2005, 77, 427. [Google Scholar] [CrossRef]
- Koonin, S.E.; Dean, D.J.; Langanke, K. Shell model Monte Carlo methods. Phys. Rep. 1996, 278, 1–77. [Google Scholar] [CrossRef]
- Iachello, F.; Talmi, I. Shell-model foundations of the interacting boson model. Rev. Mod. Phys. 1987, 59, 339. [Google Scholar] [CrossRef]
- Ring, P.; Schuck, P.; Strayer, M.R. The Nuclear Many-Body Problem; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Gunye, M.R.; Warke, C.S. Strayer, The Nuclear Many-Body Problem. Phys. Rev. 1967, 456, 1087. [Google Scholar] [CrossRef]
- Rodríguez, T.R.; Egido, J.L.; Robledo, L.M.; Rodríguez-Guzmán, R. Quality of the restricted variation after projection method with angular momentum projection. Phys. Rev. C 2005, 71, 044313. [Google Scholar] [CrossRef]
- Hara, K.; Hayashi, A.; Ring, P. Exact angular momentum projection of cranked Hartree-Fock-Bogoliubov wave functions. Nucl. Phys. A 1982, 385, 14. [Google Scholar] [CrossRef]
- Enami, K.; Tanabe, K.; Yoshinaga, N. Microscopic description of high-spin states: Quantum-number projections of the cranked Hartree-Fock-Bogoliubov self-consistent solution. Phys. Rev. C 1999, 59, 135. [Google Scholar] [CrossRef]
- Sheikh, J.A.; Ring, P. Symmetry-projected Hartree–Fock–Bogoliubov equations. Nucl. Phys. A 2000, 665, 71. [Google Scholar] [CrossRef]
- Yao, J.M.; Meng, J.; Ring, P.; Arteaga, D.P. Three-dimensional angular momentum projection in relativistic mean-field theory. Phys. Rev. C 2009, 79, 044312. [Google Scholar] [CrossRef]
- Honma, M.; Mizusaki, T.; Otsuka, T. Nuclear Shell Model by the Quantum Monte Carlo Diagonalization Method. Phys. Rev. Lett. 1996, 77, 3315. [Google Scholar] [CrossRef]
- Abe, T.; Maris, P.; Otsuka, T.; Shimizu, N.; Tsunoda, Y.; Utsuno, Y.; Vary, J.P.; Yoshida, T. Recent development of Monte Carlo shell model and its application to no-core calculations. J. Phys. Conf. Ser. 2013, 454, 012066. [Google Scholar] [CrossRef]
- Hara, K.; Sun, Y. Projected Shell Model and High-Spin Spectroscopy. Int. J. Mod. Phys. E 1995, 4, 637. [Google Scholar] [CrossRef]
- Sun, Y.; Hara, K. Fortran code of the Projected Shell Model: Feasible shell model calculations for heavy nuclei. Comput. Phys. Commun. 1997, 104, 245. [Google Scholar] [CrossRef]
- Sheikh, J.A.; Hara, K. Triaxial Projected Shell Model Approach. Phys. Rev. Lett. 1999, 82, 3968. [Google Scholar] [CrossRef]
- Gao, Z.-C.; Horoi, M. Angular momentum projected configuration interaction with realistic Hamiltonians. Phys. Rev. C 2009, 79, 014311. [Google Scholar] [CrossRef]
- Rodríguez-Guzmán, R.; Egido, J.L.; Robledo, L.M. Quadrupole collectivity in N = 28 nuclei with the angular momentum projected generator coordinate method. Phys. Rev. C 2002, 65, 024304. [Google Scholar] [CrossRef]
- Yao, J.M.; Meng, J.; Ring, P.; Vretenar, D. Configuration mixing of angular-momentum-projected triaxial relativistic mean-field wave functions. Phys. Rev. C 2010, 81, 044311. [Google Scholar] [CrossRef]
- Chen, J.-Q. The Wick theorem for coupled fermion clusters. Nucl. Phys. A 1993, 562, 218. [Google Scholar] [CrossRef]
- Chen, J.Y.; Chen, B.Q.; Klein, A. Factorization of commutators: The Wick theorem for coupled operators. Nucl. Phys. A 1993, 554, 61. [Google Scholar]
- Chen, J.-Q. Nucleon-pair shell model: Formalism and special cases. Nucl. Phys. A 1997, 626, 686. [Google Scholar] [CrossRef]
- Iachello, F. The Interacting Boson Model; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Luo, Y.-A.; Chen, J.-Q.; Draayer, J. Nucleon-pair shell model calculations of the even–even Xe and Ba nuclei. Nucl. Phys. A 2000, 669, 101. [Google Scholar] [CrossRef]
- Zhao, Y.M.; Yoshinaga, N.; Yamaji, S.; Arima, A. Validity of the SD-pair truncation of the shell model. Phys. Rev. C 2000, 62, 014316. [Google Scholar] [CrossRef]
- Zhao, Y.; Arima, A. A collective pair-condensed configuration variational method for pairwise approximation calculations. Phys. Rep. 2014, 545, 4. [Google Scholar]
- He, B.C.; Li, L.; Luo, Y.A.; Zhang, Y.; Pan, F.; Draayer, J.P. Nucleon pair shell model in M scheme. Phys. Rev. C 2020, 102, 024304. [Google Scholar] [CrossRef]
- Lei, Y.; Lu, Y.; Zhao, Y.M. Nucleon-pair approximation with uncoupled representation. Chin. Phys. C 2021, 45, 054103. [Google Scholar] [CrossRef]
- Fu, G.J.; Lei, Y.; Zhao, Y.M.; Pittel, S.; Arima, A. Nucleon-pair approximation of the shell model with isospin symmetry. Phys. Rev. C 2013, 87, 044310. [Google Scholar] [CrossRef]
- Fu, G.J.; Shen, J.J.; Zhao, Y.M.; Arima, A. Spin-aligned isoscalar pair correlation in 96Cd, 94Ag, and 92Pd. Phys. Rev. C 2013, 87, 044310. [Google Scholar] [CrossRef]
- Cheng, Y.Y.; Zhao, Y.M.; Arima, A. Nucleon-pair approximation with particle-hole excitations. Phys. Rev. C 2018, 97, 024303. [Google Scholar] [CrossRef]
- Meng, X.-f.; Wang, F.-r.; Luo, Y.-a.; Pan, F.; Draayer, J.P. SD-pair shell model study for 126Xe and 128Ba. Phys. Rev. C 2008, 77, 047304. [Google Scholar] [CrossRef]
- Wang, J.-Q.; Gao, Z.-C.; Ma, Y.-J.; Chen, Y.S. New algorithm in the variation after projection calculations for non-yrast nuclear states. Phys. Rev. C 2018, 98, 021301. [Google Scholar] [CrossRef]
- Suhonen, J. From Nucleons to Nucleus; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Andreozzi, F.; Coraggio, L.; Covello, A.; Gargano, A.; Kuo, T.T.S.; Porrino, A. Structure of neutron-rich nuclei around 132Sn. Phys. Rev. C 1997, 56, R16. [Google Scholar] [CrossRef]
- Machleidt, R. High-precision, charge-dependent Bonn nucleon-nucleon potential. Phys. Rev. C 2001, 63, 024001. [Google Scholar] [CrossRef]
- Bogner, S.; Kuo, T.T.S.; Coraggio, L.; Covello, A.; Itaco, N. Low momentum nucleon-nucleon potential and shell model effective interactions. Phys. Rev. C 2002, 65, 051301. [Google Scholar] [CrossRef]
- Hjorth-Jensen, M.; Kuo, T.T.; Osnes, E. Realistic effective interactions for nuclear systems. Phy. Rep. 1995, 261, 125. [Google Scholar] [CrossRef]
- Coraggio, L.; Covello, A.; Gargano, A.; Itaco, N.; Kuo, T. Shell-model calculations and realistic effective interactions. Prog. Part. Nucl. Phys. 2009, 62, 135. [Google Scholar] [CrossRef]
- Coraggio, L.; Covello, A.; Gargano, A.; Itaco, N.; Kuo, T. Effective shell-model hamiltonians from realistic nucleon–nucleon potentials within a perturbative approach. Ann. Phys. 2012, 327, 2125. [Google Scholar] [CrossRef]
- Shimizu, N.; Mizusaki, T.; Utsuno, Y.; Tsunoda, Y. Thick-restart block Lanczos method for large-scale shell-model calculations. Comput. Phys. Commun. 2019, 344, 372. [Google Scholar] [CrossRef]
- Simpson, G.S.; Gey, G.; Jungclaus, A.; Taprogge, J.; Nishimura, S.; Sieja, K.; Doornenbal, P.; Lorusso, G.; Söderström, P.-A.; Sumikama, T.; et al. Yrast 6+ Seniority Isomers of 136,138Sn. Phys. Rev. Lett. 2014, 113, 132502. [Google Scholar] [CrossRef]
- Brown, B.A.; Richter, W.A. New “USD” Hamiltonians for the sd shell. Phys. Rev. C 2006, 74, 034315. [Google Scholar] [CrossRef]
- Tilley, D.; Cheves, C.; Kelley, J.; Raman, S.; Weller, H. Energy levels of light nuclei, A = 20. Nucl. Phys. A 1998, 636, 249. [Google Scholar] [CrossRef]

| v(n, l, j) | ||||||
|---|---|---|---|---|---|---|
| −2.45 | −1.60 | −0.89 | −0.80 | −0.45 | 0.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, B.; Zhang, S.; Zhang, Y.; Li, L.; Luo, Y.; Pan, F.; Draayer, J.P. Nucleon-Pair Shell Model within a Symmetry Broken Basis. Symmetry 2023, 15, 1653. https://doi.org/10.3390/sym15091653
He B, Zhang S, Zhang Y, Li L, Luo Y, Pan F, Draayer JP. Nucleon-Pair Shell Model within a Symmetry Broken Basis. Symmetry. 2023; 15(9):1653. https://doi.org/10.3390/sym15091653
Chicago/Turabian StyleHe, Bingcheng, Siyao Zhang, Yu Zhang, Lei Li, Yanan Luo, Feng Pan, and Jerry P. Draayer. 2023. "Nucleon-Pair Shell Model within a Symmetry Broken Basis" Symmetry 15, no. 9: 1653. https://doi.org/10.3390/sym15091653
APA StyleHe, B., Zhang, S., Zhang, Y., Li, L., Luo, Y., Pan, F., & Draayer, J. P. (2023). Nucleon-Pair Shell Model within a Symmetry Broken Basis. Symmetry, 15(9), 1653. https://doi.org/10.3390/sym15091653





