Numerical Analysis of Nonlinear Coupled Schrödinger–KdV System with Fractional Derivative
Abstract
:1. Introduction
2. Preliminaries
- 1.
- 2.
- 3.
3. General Procedure of the Proposed Methods
3.1. LRPSM Procedure
- and for each
- .
3.2. NIM Procedure
4. Numerical Problem
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yavuz, M.; Sulaiman, T.A.; Yusuf, A.; Abdeljawad, T. The Schrodinger-KdV equation of fractional order with Mittag-Leffler nonsingular kernel. Alex. Eng. J. 2021, 60, 2715–2724. [Google Scholar] [CrossRef]
- Alshammari, S.; Al-Sawalha, M.M. Approximate analytical methods for a fractional-order nonlinear system of Jaulent-Miodek equation with energy-dependent Schrodinger potential. Fractal Fract. 2023, 7, 140. [Google Scholar] [CrossRef]
- Al-Sawalha, M.M.; Ababneh, O.Y.; Nonlaopon, K. Numerical analysis of fractional-order Whitham-Broer-Kaup equations with non-singular kernel operators. AIMS Math. 2023, 8, 308–2336. [Google Scholar] [CrossRef]
- Botmart, T.; Alotaibi, B.M.; El-Sherif, L.S.; El-Tantawy, S.A. A Reliable Way to Deal with the Coupled Fractional Korteweg-De Vries Equations within the Caputo Operator. Symmetry 2022, 14, 2452. [Google Scholar] [CrossRef]
- Alderremy, A.A.; Aly, S.; Fayyaz, R.; Khan, A.; Shah, R.; Wyal, N. The analysis of fractional-order nonlinear systems of third order KdV and Burgers equations via a novel transform. Complexity 2022, 2022, 4935809. [Google Scholar] [CrossRef]
- Yasmin, H.; Aljahdaly, N.H.; Saeed, A.M. Investigating Families of Soliton Solutions for the Complex Structured Coupled Fractional Biswas-Arshed Model in Birefringent Fibers Using a Novel Analytical Technique. Fractal Fract. 2023, 7, 491. [Google Scholar] [CrossRef]
- Yasmin, H.; Aljahdaly, N.H.; Saeed, A.M.; Shah, R. Investigating Symmetric Soliton Solutions for the Fractional Coupled Konno-Onno System Using Improved Versions of a Novel Analytical Technique. Mathematics 2023, 11, 2686. [Google Scholar] [CrossRef]
- Lyu, W.; Wang, Z. Global classical solutions for a class of reaction-diffusion system with density-suppressed motility. Electron. Res. Arch. 2022, 30, 995–1015. [Google Scholar] [CrossRef]
- He, H.M.; Peng, J.G.; Li, H.Y. Iterative approximation of fixed point problems and variational inequality problems on Hadamard manifolds. UPB Bull. Ser. A 2022, 84, 25–36. [Google Scholar]
- He, H.; Peng, J.; Li, H. Implicit viscosity iterative algorithm for nonexpansive mapping on Hadamard manifolds. Fixed Point Theory 2023, 24, 213–220. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, Z.; Yuan, X.; Wang, Y.; Shen, X. L2-Gain Adaptive Robust Control for Hybrid Energy Storage System in Electric Vehicles. IEEE Trans. Power Electron. 2021, 36, 7319–7332. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, Y.; Zhang, W. A Composite Adaptive Fault-Tolerant Attitude Control for a Quadrotor UAV with Multiple Uncertainties. J. Syst. Sci. Complex. 2022, 35, 81–104. [Google Scholar] [CrossRef]
- Li, Q.; Lin, H.; Tan, X.; Du, S. H ∞ Consensus for Multiagent-Based Supply Chain Systems Under Switching Topology and Uncertain Demands. IEEE Trans. Syst. Man, Cybern. Syst. 2020, 50, 4905–4918. [Google Scholar] [CrossRef]
- Mi, C.; Huang, S.; Zhang, Y.; Zhang, Z.; Postolache, O. Design and Implementation of 3-D Measurement Method for Container Handling Target. J. Mar. Sci. Eng. 2022, 10, 1961. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhang, Y.; Kaku, I.; Kang, R.; Pan, X. Electric vehicle routing problem: A systematic review and a new comprehensive model with nonlinear energy recharging and consumption. Renew. Sustain. Energy Rev. 2021, 151, 111567. [Google Scholar] [CrossRef]
- Guo, C.; Hu, J. Fixed-Time Stabilization of High-Order Uncertain Nonlinear Systems: Output Feedback Control Design and Settling Time Analysis. J. Syst. Sci. Complex. 2023, 36, 1351–1372. [Google Scholar] [CrossRef]
- Guo, C.; Hu, J.; Hao, J.; Celikovsky, S.; Hu, X. Fixed-time safe tracking control of uncertain high-order nonlinear pure-feedback systems via unified transformation functions. Kybernetika 2023, 59, 342–364. [Google Scholar] [CrossRef]
- Lee, Y.Y.; Tang, T.K.; Phuah, E.T.; Lai, O.M. Recent Advances in Edible Fats and Oils Technology: Processing, Health Implications, Economic and Environmental Impact; Springer: Singapore, 2022. [Google Scholar]
- Zhang, T.; Li, Y. Global exponential stability of discrete-time almost automorphic Caputo-Fabrizio BAM fuzzy neural networks via exponential Euler technique. Knowl.-Based Syst. 2022, 246, 108675. [Google Scholar] [CrossRef]
- Shafee, A.; Alkhezi, Y. Efficient Solution of Fractional System Partial Differential Equations Using Laplace Residual Power Series Method. Fractal Fract. 2023, 7, 429. [Google Scholar] [CrossRef]
- Mainardi, F.; Luchko, Y.; Pagnini, G. The fundamental solution of the space-time fractional diffusion equation. arXiv 2007, arXiv:cond-mat/0702419. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Alshehry, A.S.; Yasmin, H.; Ghani, F.; Shah, R.; Nonlaopon, K. Comparative Analysis of Advection-Dispersion Equations with Atangana-Baleanu Fractional Derivative. Symmetry 2023, 15, 819. [Google Scholar] [CrossRef]
- Tarasov, V.E. On history of mathematical economics: Application of fractional calculus. Mathematics 2019, 7, 509. [Google Scholar] [CrossRef]
- Yasmin, H.; Alshehry, A.S.; Saeed, A.M.; Nonlaopon, K. Application of the q-Homotopy Analysis Transform Method to Fractional-Order Kolmogorov and Rosenau-Hyman Models within the Atangana-Baleanu Operator. Symmetry 2023, 15, 671. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Bronski, J.C.; Carr, L.D.; Deconinck, B.; Kutz, J.N. Bose-Einstein condensates in standing waves: The cubic nonlinear Schrodinger equation with a periodic potential. Phys. Rev. Lett. 2001, 86, 1402. [Google Scholar] [CrossRef] [PubMed]
- Trombettoni, A.; Smerzi, A. Discrete solitons and breathers with dilute Bose-Einstein condensates. Phys. Lett. 2001, 86, 2353. [Google Scholar] [CrossRef]
- Triki, H.; Biswas, A. Dark solitons for a generalized nonlinear Schrodinger equation with parabolic law and dual-power law nonlinearities. Math. Methods Appl. Sci. 2011, 34, 958–962. [Google Scholar] [CrossRef]
- Zhang, L.H.; Si, J.G. New soliton and periodic solutions of (1+ 2)-dimensional nonlinear Schrodinger equation with dual-power law nonlinearity. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 2747–2754. [Google Scholar] [CrossRef]
- Nore, C.; Brachet, M.; Fauve, S. Numerical study of hydrodynamics using the nonlinear Schrodinger equation. Phys. D Nonlinear Phenom. 1993, 65, 154–162. [Google Scholar] [CrossRef]
- Burqan, A.; El-Ajou, A.; Saadeh, R.; Al-Smadi, M. A new efficient technique using Laplace transforms and smooth expansions to construct a series solution to the time-fractional Navier-Stokes equations. AlexandriaEng. J. 2022, 61, 1069–1077. [Google Scholar] [CrossRef]
- Khater, M.M.; Attia, R.A.; Lu, D. Numerical solutions of nonlinear fractional Wu-Zhang system for water surface versus three approximate schemes. J. Ocean Eng. Sci. 2019, 4, 144–148. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.; Magesh, N.; Nandeppanavar, M.; Christopher, A.J. Numerical simulation for fractional Jaulent-Miodek equation associated with energy-dependent Schrodinger potential using two novel techniques. Waves Random Complex Media 2021, 31, 1141–1162. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Baleanu, D.; Rathore, S. On the local fractional wave equation in fractal strings. Math. Methods Appl. Sci. 2019, 42, 1588–1595. [Google Scholar] [CrossRef]
- El-Ajou, A. Adapting the Laplace transform to create solitary solutions for the nonlinear time-fractional dispersive PDEs via a new approach. Eur. Phys. J. Plus 2021, 136, 229. [Google Scholar] [CrossRef]
- El-Ajou, A.; Al-Smadi, M.; Moaath, N.O.; Momani, S.; Hadid, S. Smooth expansion to solve high-order linear conformable fractional PDEs via residual power series method: Applications to physical and engineering equations. Ain Shams Eng. J. 2020, 11, 1243–1254. [Google Scholar] [CrossRef]
- El-Ajou, A.; Moaath, N.O.; Al-Zhour, Z.; Momani, S. A class of linear non-homogenous higher order matrix fractional differential equations: Analytical solutions and new technique. Fract. Calc. Appl. Anal. 2020, 23, 356–377. [Google Scholar] [CrossRef]
- Aljahdaly, N.H.; Akgul, A.; Shah, R.; Mahariq, I.; Kafle, J. A comparative analysis of the fractional-order coupled Korteweg-De Vries equations with the Mittag-Leffler law. J. Math. 2022, 2022, 8876149. [Google Scholar] [CrossRef]
- El-Ajou, A.; Al-Zhour, Z.; Oqielat, M.; Momani, S.; Hayat, T. Series solutions of nonlinear conformable fractional KdV-Burgers equation with some applications. Eur. Phys. J. Plus 2019, 134, 402. [Google Scholar] [CrossRef]
- Moaath, N.O.; El-Ajou, A.; Al-Zhour, Z.; Alkhasawneh, R.; Alrabaiah, H. Series solutions for nonlinear time-fractional Schrodinger equations: Comparisons between conformable and Caputo derivatives. Alex. Eng. J. 2020, 59, 2101–2114. [Google Scholar]
- Benchohra, M.; Cabada, A.; Seba, D. An existence result for nonlinear fractional differential equations on Banach spaces. Bound. Value Probl. 2009, 2009, 628916. [Google Scholar] [CrossRef]
- Areshi, M.; Khan, A.; Shah, R.; Nonlaopon, K. Analytical investigation of fractional-order Newell-Whitehead-Segel equations via a novel transform. Aims Math. 2022, 7, 6936–6958. [Google Scholar] [CrossRef]
- Arqub, O.A.; El-Ajou, A.; Momani, S. Constructing and predicting solitary pattern solutions for nonlinear time-fractional dispersive partial differential equations. J. Comput. Phys. 2015, 293, 385–399. [Google Scholar] [CrossRef]
- Li, C.; Qian, D.; Chen, Y. On Riemann-Liouville and caputo derivatives. Discret. Dyn. Nat. Society 2011, 2011, 562494. [Google Scholar] [CrossRef]
- Kexue, L.; Jigen, P. Laplace transform and fractional differential equations. Appl. Math. Lett. 2011, 24, 2019–2023. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V.; Jafari, H. An iterative method for solving nonlinear functional equations. J. Ofmath. Anal. Appl. 2006, 316, 753–763. [Google Scholar] [CrossRef]
- Hemeda, A. New iterative method: Application to nth-order integro-differential equations. Int. Forum 2012, 7, 2317–2332. [Google Scholar]
- Momani, S. An explicit and numerical solutions of the fractional KdV equation. Math. Comput. Simul. 2005, 70, 110–118. [Google Scholar] [CrossRef]
- Shah, R.; Hyder, A.A.; Iqbal, N.; Botmart, T. Fractional view evaluation system of Schrodinger-KdV equation by a comparative analysis. AIMS Math. 2022, 7, 19846–19864. [Google Scholar] [CrossRef]

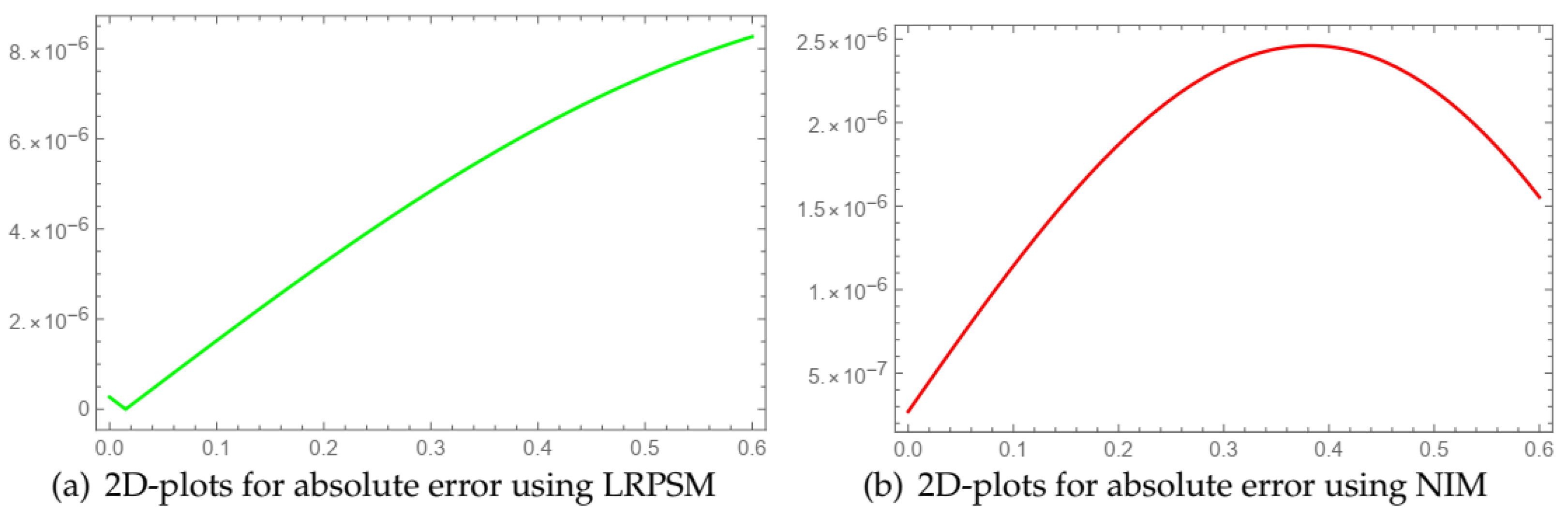
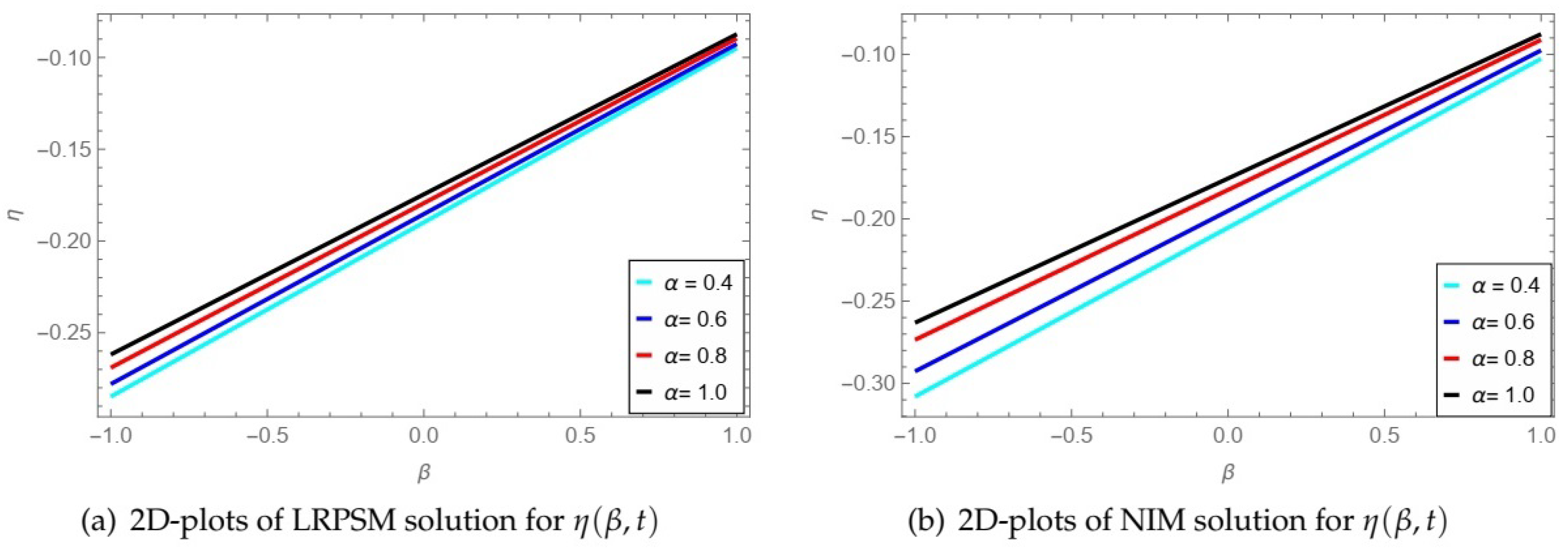
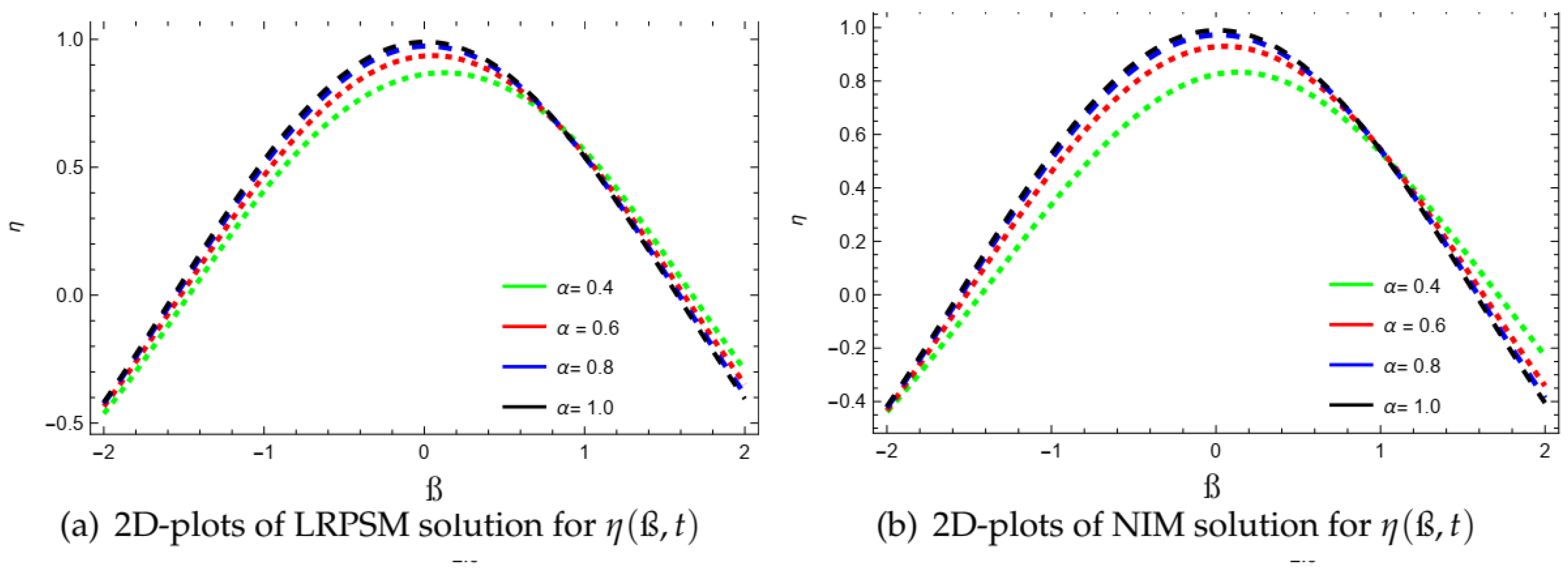
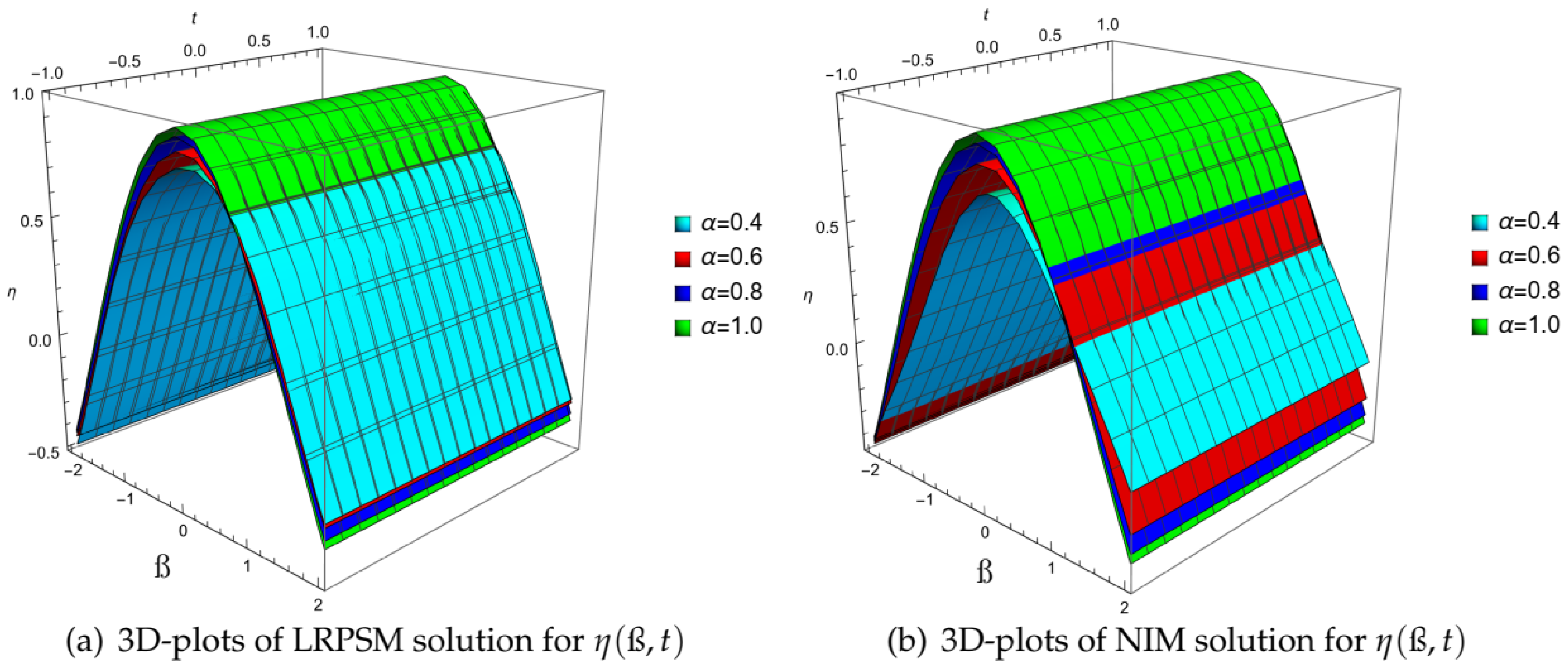
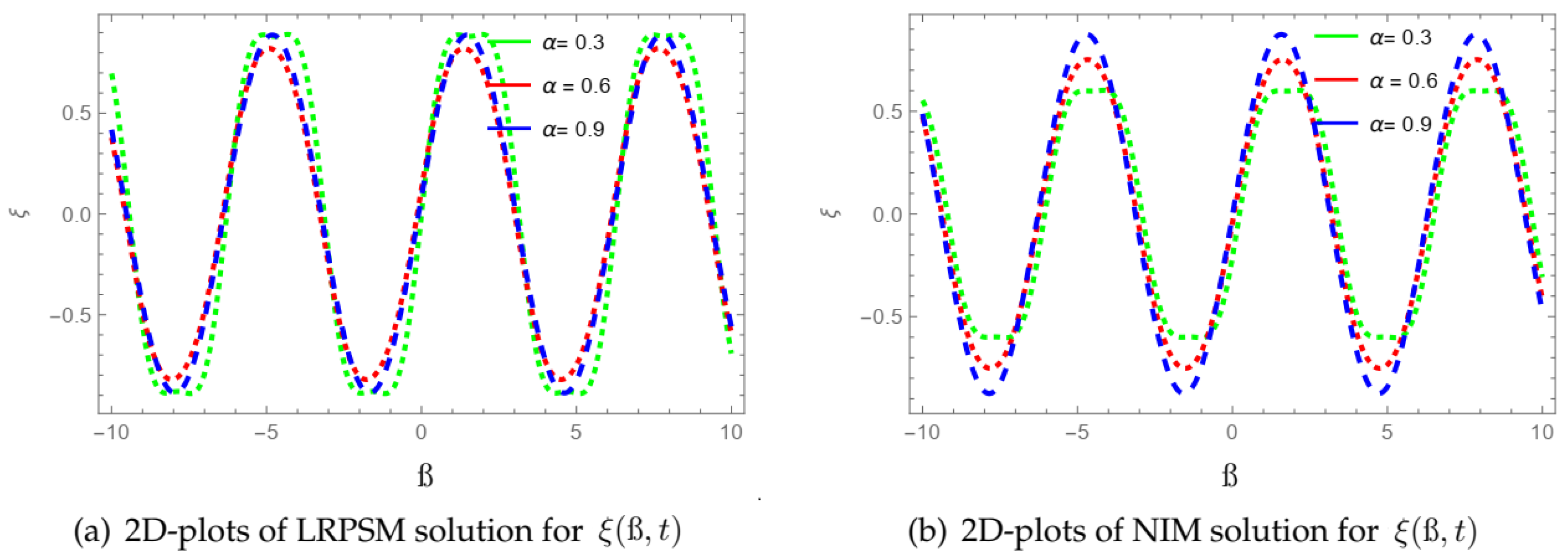
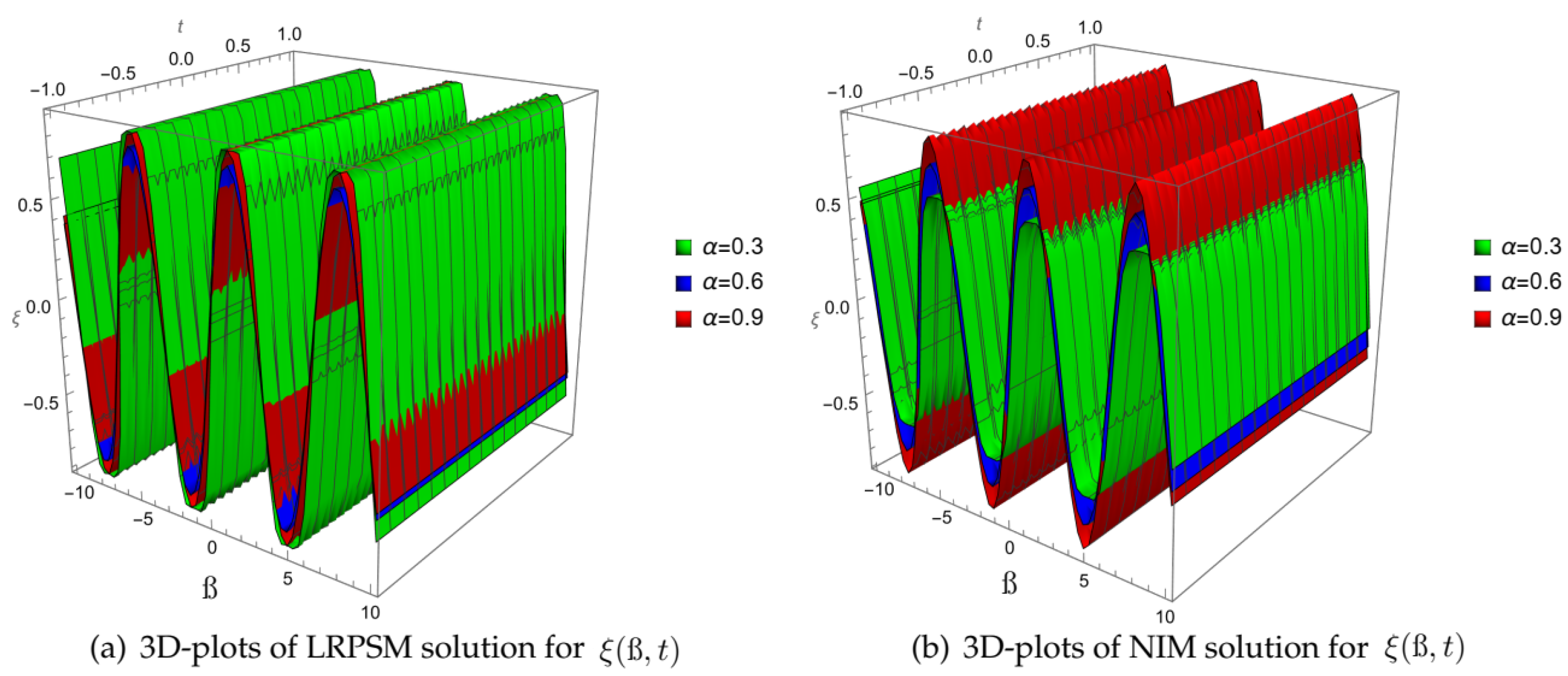
| ß | ||||
|---|---|---|---|---|
| 0.1 | 0.49885 | 0.49885 | 5.24347 | 2.65047 |
| 0.2 | 0.495229 | 0.495229 | 1.03199 | 4.84593 |
| 0.3 | 0.489206 | 0.489206 | 1.4969 | 6.29355 |
| 0.4 | 0.480899 | 0.480899 | 1.90139 | 6.74469 |
| 0.5 | 0.470466 | 0.470466 | 2.23189 | 6.07651 |
| 0.6 | 0.4581 00 | 0.458100 | 2.47961 | 4.30081 |
| 0.7 | 0.444021 | 0.444021 | 0.64079 | 1.55325 |
| 0.8 | 0.428469 | 0.428469 | 2.71647 | 1.93312 |
| 0.9 | 0.411693 | 0.411693 | 2.71195 | 5.86445 |
| 1 | 0.39395 | 0.39395 | 2.6359 | 9.92581 |
| ß | ||||||
|---|---|---|---|---|---|---|
| 0.1 | 0.434414 | 0.440173 | 0.475125 | 0.476806 | 0.492521 | 0.492951 |
| 0.2 | 0.442031 | 0.453097 | 0.481234 | 0.484463 | 0.496035 | 0.49686 |
| 0.3 | 0.448889 | 0.464403 | 0.485383 | 0.489911 | 0.497171 | 0.498328 |
| 0.4 | 0.455015 | 0.473809 | 0.487534 | 0.493019 | 0.495917 | 0.49732 |
| 0.5 | 0.460346 | 0.481064 | 0.487657 | 0.493704 | 0.492302 | 0.493848 |
| 0.6 | 0.46473 | 0.48596 | 0.485733 | 0.49193 | 0.486393 | 0.487977 |
| 0.7 | 0.467943 | 0.488344 | 0.48176 | 0.487715 | 0.478294 | 0.479817 |
| 0.8 | 0.469719 | 0.488128 | 0.475755 | 0.481128 | 0.468146 | 0.46952 |
| 0.9 | 0.469782 | 0.48529 | 0.467762 | 0.472288 | 0.456117 | 0.457274 |
| 1 | 0.467887 | 0.479877 | 0.457859 | 0.461359 | 0.442404 | 0.443299 |
| ß | ||||||
|---|---|---|---|---|---|---|
| 0.1 | −0.189874 | −0.176482 | −0.172736 | −0.169667 | −0.165132 | −0.164485 |
| 0.2 | −0.17988 | −0.167194 | −0.163645 | −0.160737 | −0.15644 | −0.155828 |
| 0.3 | −0.169887 | −0.157905 | −0.154553 | −0.151807 | −0.147749 | −0.14717 |
| 0.4 | −0.159894 | −0.148617 | −0.145462 | −0.142877 | −0.139058 | −0.138513 |
| 0.5 | −0.1499 | −0.139328 | −0.136371 | −0.133948 | −0.130367 | −0.129856 |
| 0.6 | −0.139907 | −0.13004 | −0.127279 | −0.125018 | −0.121676 | −0.121199 |
| 0.7 | −0.129914 | −0.120751 | −0.118188 | −0.116088 | −0.112985 | −0.112542 |
| 0.8 | −0.11992 | −0.111463 | −0.109096 | −0.107158 | −0.104294 | −0.103885 |
| 0.9 | −0.109927 | −0.102174 | −0.100005 | −0.0982282 | −0.0956025 | −0.0952279 |
| 1 | −0.0999335 | −0.0928855 | −0.0909137 | −0.0892983 | −0.0869114 | −0.0865708 |
| ß | NIM | LRPSM | Exact | NIM Error | LRPSM Error | HPSTM Error [50] |
|---|---|---|---|---|---|---|
| 0 | 0.991481 | 0.991556 | 0.999998 | 0.00851667 | 0.0084413 | 0.0084617 |
| 0.2 | 0.972981 | 0.97305 | 0.979642 | 0.00666104 | 0.00659231 | 0.00669431 |
| 0.4 | 0.915696 | 0.915755 | 0.920231 | 0.00453561 | 0.0044759 | 0.0045769 |
| 0.6 | 0.821906 | 0.821955 | 0.824134 | 0.00222747 | 0.00217903 | 0.00237503 |
| 0.8 | 0.695349 | 0.695384 | 0.695181 | 0.00016832 | 0.00020345 | 0.00021345 |
| 1 | 0.541067 | 0.541087 | 0.538513 | 0.00255363 | 0.00257369 | 0.00267168 |
| 1.2 | 0.365208 | 0.365212 | 0.360376 | 0.00483206 | 0.0048358 | 0.0039348 |
| 1.4 | 0.174786 | 0.174773 | 0.167873 | 0.00691323 | 0.0069001 | 0.0069231 |
| 1.6 | −0.0226073 | -0.022637 | −0.0313235 | 0.00871626 | 0.00868658 | 0.00967657 |
| ß | NIM | LRPSM | Exact | NIM Error | LRPSM Error | HPSTM Error [50] |
|---|---|---|---|---|---|---|
| 0 | −0.0000270 | 0.0063208 | 0.002125 | 0.002152 | 0.004195 | 0.006295 |
| 0.2 | 0.196972 | 0.2032 | 0.200752 | 0.00377968 | 0.00244894 | 0.00256804 |
| 0.4 | 0.386115 | 0.391976 | 0.391375 | 0.0052597 | 0.00060127 | 0.00070134 |
| 0.6 | 0.55986 | 0.565119 | 0.566395 | 0.0065352 | 0.00127557 | 0.00138435 |
| 0.8 | 0.711279 | 0.715728 | 0.718835 | 0.00755558 | 0.00310701 | 0.00321702 |
| 1 | 0.834339 | 0.837799 | 0.842617 | 0.00827852 | 0.00481835 | 0.00471935 |
| 1.2 | 0.924135 | 0.926469 | 0.932807 | 0.00867223 | 0.00633839 | 0.00643939 |
| 1.4 | 0.977091 | 0.978205 | 0.985809 | 0.00871776 | 0.00760327 | 0.00780727 |
| 1.6 | 0.991098 | 0.990949 | 0.999509 | 0.00841091 | 0.00856015 | 0.00957010 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alzahrani, A.B.M. Numerical Analysis of Nonlinear Coupled Schrödinger–KdV System with Fractional Derivative. Symmetry 2023, 15, 1666. https://doi.org/10.3390/sym15091666
Alzahrani ABM. Numerical Analysis of Nonlinear Coupled Schrödinger–KdV System with Fractional Derivative. Symmetry. 2023; 15(9):1666. https://doi.org/10.3390/sym15091666
Chicago/Turabian StyleAlzahrani, Abdulrahman B. M. 2023. "Numerical Analysis of Nonlinear Coupled Schrödinger–KdV System with Fractional Derivative" Symmetry 15, no. 9: 1666. https://doi.org/10.3390/sym15091666
APA StyleAlzahrani, A. B. M. (2023). Numerical Analysis of Nonlinear Coupled Schrödinger–KdV System with Fractional Derivative. Symmetry, 15(9), 1666. https://doi.org/10.3390/sym15091666





