The Onset of Darcy–Brinkman Convection in a Porous Layer with Mutual Impact of Thermal Non-Equilibrium and Non-Uniform Temperature Gradients

Abstract

The two-field thermal conditions of local thermal nonequilibrium (LTNE) were used to investigate linear stability of thermal convection in a liquid-saturated, porous layer via the extended Brinkman–Darcy model for different non-uniform basic thermal gradients. The critical values were numerically computed by the Galerkin method for rigid isothermal boundaries. The impact of LTNE and different forms of non-uniform basic temperature gradients on the onset of porous convection was examined. The porosity modified conductivity ratio has no influence on system stability at a small inter-phase heat transport coefficient limit. However, for higher values of the inter-phase heat transport coefficient, an increase in the porosity modified conductivity ratio hastens the onset of convection. An increase in the Darcy number delays the convective motions. The results for different basic temperature profiles are symmetric qualitatively. In addition, the possibility of control of convection by a basic temperature profile was studied in detail.

1. Introduction

Rayleigh–Bénard convection, also known as natural convection or thermal convection, is the study of convection heat transport in permeable media induced by density variations. Over the last few decades, many authors have studied this because it has many different applications in both science and engineering. Nield and Bejan [1] adequately documented the expanding volume of work encompassing different features of the problem. The assumption that the liquid and permeable media phases are in local thermal equilibrium (LTE) provides the foundation for the exploration of convective flow in porous media. However, LTNE does occur when the fluid and permeable medium phases have different volume-average temperatures. In physical science, symmetry is a significant notion, and its modern implementation to comprehend non-equilibrium behavior is yielding profound insights and innovative outcomes. The first study of LTNE effects on convective motions in permeable media using the Darcy equation was performed by Banu and Rees [2]. Postelnicu [3], Postelnicu and Rees [4], and Malashetty et al. [5] used the Brinkman equation to study the LTNE impact on permeable convective flow. Straughan [6] discussed the nonlinear stability in porous convection using the LTNE model. Further research on the impacts of LTNE on permeable convection has been conducted throughout the last few decades [7,8,9,10,11,12,13,14,15,16,17,18]. The study of heat transfer and convective fluid flows through a porous medium has been the primary objective of the investigators’ work [19,20], with particular attention being paid to symmetry principles that emerged from the collective research. Under circumstances where the Reynolds number is high, the symmetry fails. However, numerous scholars have looked into the practical implications of these issues based on different dynamics. Recently, Suma et al. [21] discussed the effect of anisotropy on convective flows under the LTNE regime for asymmetric thermal boundaries. Capone and Gianfrani [22] explored the impact of the second sound effect on LTNE anisotropic porous convective motions.

The flow of fluids with a non-uniform thermal gradient occurs in natural and industrial systems when fluid temperature varies unevenly. This temperature change affects fluid behavior, creating intriguing and complicated flow patterns. Such fluxes are studied in fluid dynamics and heat transfer, which affect meteorology and engineering. In many practical circumstances, nonlinear temperature gradient scenarios are preferred over uniform profile cases. Nield [23] discussed the impact of thermal gradient on system stability. The study of thermal porous convection with different forms of inhomogeneous temperature gradient for adiabatic boundaries was considered by Rudraiah et al. [24]. The Brinkman model was utilized by Vasseur and Robillard [25] to discuss the thermal distribution influence on the stability of the system. In an asymmetric geometry of porous matrix, Degan and Vasseur [26] studied the inhomogeneous thermal gradient impact on thermal convection. The influence of an inhomogeneous thermal profile on a micropolar liquid was carried out by Idris et al. [27]. Shivakumara et al. [28] and Lee et al. [29] revised the impact of both LTNE and nonlinear thermal profiles on the beginning of convection in isotropic permeable media. The thermal gradient effect on the threshold of dual diffusive convection in a permeable media was conferred by Hamid et al. [30].

The occurrence of a non-uniform temperature gradient due to differential heating with depth is prevalent in geophysical and engineering applications. As a result, understanding the influence of a non-uniform basic temperature gradient on the onset of porous convection under the LTNE regime is of practical importance and no attention has been given to assessing the combined effects of LTNE and non-uniform basic temperature gradients on the criterion for the onset of porous convection, despite its importance in understanding convective motions encountered in many scientific and technological problems. The aim of this paper was to use the LTNE model to determine the impact of several non-uniform basic temperature gradients on the beginning of convection in a liquid-saturated porous media. Such a study helps in understanding the control of convection. The discussion considers four different types of fundamental temperature profiles: (i) linear thermal profile (M1), (ii) inverted parabolic thermal profile (M2), (iii) cubic-1 thermal profile (M3), and (iv) cubic-2 thermal profile (M4). The porous layer’s bounding surfaces are considered to be rigid isothermal, and the resulting eigenvalue is solved numerically using the Galerkin method, while a detailed parametric study on the criterion for the onset of convection effects is presented graphically.

2. Mathematical Formulation

A fluid-saturated, porous layer with rigid horizontal boundaries at $z=0$ and $d$ is considered (see Figure 1). The lower surface is maintained at a constant temperature $T_l$, and the upper surface is maintained at $T_u$ (<$T_l$). A Cartesian coordinate system is selected for the gravitational field, with the origin at the lower end of the permeable layer and the $z$-axis vertically upward. For the temperature equation, a two-field thermal condition describing liquid and solid phases separately is used. The basic state is quiescent and is perturbed infinitesimal disturbances. The governing linear perturbation equations in the non-dimensional form may then be demonstrated by applying the techniques described in Shivakumara et al. [28] and Lee et al. [29].

$$\left[Da \left(D^2-a^2\right)-1\right]\left(D^2-a^2\right)W=R{a}^2\mathsf{\Theta }$$

(1)

$$\left(D^2-a^2\right)\mathsf{\Theta }+H\left(\mathsf{\Phi }-\mathsf{\Theta }\right)=-f(z)W$$

(2)

$$\left(D^2-a^2\right)\mathsf{\Phi }+\gamma H\left(\mathsf{\Theta }-\mathsf{\Phi }\right)=0$$

(3)

In the above equations, $\mathsf{\Theta }(z)$ is the amplitude of perturbed fluid temperature, $\gamma =\epsilon k_f/\left(1-\epsilon \right) k_s$ is the porosity modified conductivity ratio, $a=\sqrt{l^2+m^2}$ is the overall horizontal wave number, $D=d/dz$ is the differential operator, $H=h{d}^2/\epsilon k_f$ is the coefficient of inter-phase heat transport, $W(z)$ is the amplitude of perturbed vertical velocity, $Da={\tilde{\mu }}_{f}K/{\mu }_f{d}^2$ is the Darcy number, $\mathsf{\Phi }(z)$ is the amplitude of perturbed solid temperature, $R=\beta gKd\Delta T/\epsilon \nu {\kappa }_f$ is the Darcy–Rayleigh number and $f(z)$ is a dimensionless basic thermal gradient. Following Idris et al. [27], $f(z)$ is taken in the following form:

$$f(z)=b_1+2b_2(z-1)+3b_3{(z-1)}^2$$

(4)

where $b_1$, $b_2$, and $b_3$ are constants. We note that the case where $b_1=1$, $b_2=0$, and $b_3=0$ corresponds to classical linear basic state thermal profile distribution and the corresponding problem was discussed by Postelnicu [3] and Malashetty et al. [5].

The upper and lower bounding surfaces of the permeable layer are assumed to be rigid with fixed temperatures for both liquid and solid phases at the boundaries. Consequently, the boundary constraints are as follows:

$$W=DW=\mathsf{\Theta }=\mathsf{\Phi }=0 \mathrm{at}z=0,1.$$

(5)

3. Numerical Solution

An eigenvalue problem (EVP) is formed from the Equations (1)–(3) and the boundary conditions (5). Below are the different sorts of basic thermal profiles that are to be discussed:

Model (i): Linear thermal profile (M1)

$$f\left(z\right)=1$$

(6)

which corresponds when $b_1=1$ and $b_2=0=b_3$.

Model (ii): Inverted parabolic thermal profile (M2)

$$f\left(z\right) = 2\left(1-z\right)$$

(7)

which corresponds when $b_1=0=b_3$ and $b_2=-1$.

Model (iii): Cubic-1 thermal profile (M3)

$$f\left(z\right) = 3{(z-1)}^2$$

(8)

which corresponds when $b_1=0=b_2$ and $b_3=1$.

Model (iv): Cubic-2 thermal profile (M4)

$$f\left(z\right) =0.6+1.02{(z-1)}^2$$

(9)

which corresponds when $b_1=0.6$, $b_2=0$ and $b_3=0.34$.

To solve the EVP for various kinds of $f\left(z\right)$, the Galerkin technique is found to be more appropriate. Consequently, $W(z)$, $\mathsf{\Theta }(z)$, and $\mathsf{\Phi }(z)$ are expanded as follows:

$$W={\displaystyle \sum _{i=1}^n{A}_i W_i(z)},\mathsf{\Theta }(z)={\displaystyle \sum _{i=1}^n{B}_i{\mathsf{\Theta }}_i(z)},\mathsf{\Phi }(z)= {\displaystyle \sum _{i=1}^n{C}_i{\mathsf{\Phi }}_i(z)}$$

(10)

where $A_i$, $B_i$, and $C_i$ are unknown coefficients. The base functions $W_i(z)$, ${\mathsf{\Theta }}_i(z)$, and ${\mathsf{\Phi }}_i(z)$ are assumed in the following form:

$$W_i=(z^4-2z^3+z^2) T_{i-1}^{*}, {\mathsf{\Theta }}_i=z(z-1)T_{i-1}^{*}={\mathsf{\Phi }}_i$$

(11)

where $T_i^{*}$s are the modified Chebyshev polynomials, such that $W_i, {\mathsf{\Theta }}_i$, and ${\mathsf{\Phi }}_i$ satisfy the boundary constraints. Equation (11) is substituted in Equations (1)–(3) and the resulting equations are multiplied respectively, by $W_j(z)$, ${\mathsf{\Theta }}_j(z)$, and ${\mathsf{\Phi }}_j(z)$, integrated by parts with respect to z between z = 0 and 1, We obtain the following system of algebraic equations by utilizing the boundary conditions:

$$A_{ji}{A}_i+B_{ji}{B}_i=0$$

(12)

$$C_{ji}{A}_i+D_{ji}{B}_i+E_{ji}{C}_i=0$$

(13)

$$F_{ji}{B}_i+G_{ji}{C}_i=0$$

(14)

The coefficients $A_{ji} \mathrm{to} G_{ji}$ involve the inner products of the base functions and are given by the following:

$$\begin{array}{l}{A}_{ji}=Da<D^2{W}_j{D}^2{W}_i>+(2 a^2 Da+1)<D{W}_{j}D{W}_i>+a^2(a^{2}Da+1)<W_j{W}_i>\\ B_{ji}=-a^{2}R < W_j{\mathsf{\Theta }}_i> \\ C_{ji}=-<f(z){\mathsf{\Theta }}_j{W}_i>\\ D_{ji}=<D{\mathsf{\Theta }}_{j}D{\mathsf{\Theta }}_i>+(a^2+H)<{\mathsf{\Theta }}_j{\mathsf{\Theta }}_i>\\ E_{ji}=-H<{\mathsf{\Theta }}_j{\mathsf{\Phi }}_i>\\ F_{ji}=-\gamma H<{\mathsf{\Phi }}_j{\mathsf{\Theta }}_i>\\ G_{ji}=<D{\mathsf{\Phi }}_{j}D{\mathsf{\Phi }}_i>+(a^2+\gamma H) <{\mathsf{\Phi }}_j{\mathsf{\Phi }}_i>\end{array}$$

(15)

where the inner product is defined as $<\cdots > = {\displaystyle \underset{0}{\overset{1}{\int }}(\cdots ) dz.}$

The $R_c$ (critical Rayleigh number) is found by numerically solving the characteristic equation given by Equations (12)–(14) corresponding to Model (i)–(iv) basic temperature profiles as a wave number $a$ function for diverse $\gamma$, $Da$, and $H$ values. When all physical parameters are fixed, the Newton–Raphson method is utilized to derive the Rayleigh number as a function of wave number, and the bisection method is built in to discover the key stability parameters to the appropriate degree of accuracy. It should be noted that the results are converged by employing six terms in the series expansion.

4. Results and Discussion

On the criteria for the onset of porous convection, the impact of LTNE and the non-uniform thermal gradient arising from transitory heating are presented. Due to its many applications, including building insulation, solar collectors, cooling of radioactive waste containers, nuclear engineering, geothermal energy, fire control, and compact heat exchangers, the phenomenon of natural convection through porous materials has gained attention. The Galerkin technique is applied to solve the resulting EVP. The curves for neutral stability in the $(R,a)$-plane are demonstrated graphically in Figure 2 and Figure 3 for various basic thermal profiles and for range values of $Da$, $H$, and $\gamma$. We see that the stability curves have a single minimum with these figures. The area above each curve denotes an unstable state, whereas the region below each curve denotes a stable state. The neutral curves for various basic temperature profiles and two values of $\gamma$ (= 0.5 and 2) with $Da=0.01$ and $H=100$ are presented in Figure 2a. For an increasing $\gamma$, the minimum Rayleigh number declines; it signifies that the result of $\gamma$ is destabilizing the system. The system stability for model M4 is the most stable followed by model M3, model M1, and the least stable for model M2 when $\gamma =0.5$, while for $\gamma =2$, the least stable on the onset of convection for model M4. The same trend is noticed for the considered types of temperature profiles M1, M2, and M3 as observed in $\gamma =0.5$. Figure 2b shows the findings for the same parametric settings as Figure 2a, but with a different value of $Da=0.1$. Figure 2b displays the same kind of behavior as Figure 2a. Here, the result of growing $Da$ is to delay the convective motions.

Figure 3a,b shows the result of growing $H$ is to increase the $R$ value and increase the stability region. The neutral curves for the model M4 are the most stabilizing followed by model M3, model M1, and least stable for model M2 when $H=50$. For $H=10$, model M3 has a more stabilizing effect when compared to model M4 at the lower value of the wave number, while the opposite trend is noticed at the higher values of the wave number followed by M1 and least stable for model M2. From these Figures, it is noted that there is no substantial impact on the system for the models M1 and M2 at lower wave numbers.

The behavior of $R_c$ and $a_c$ as function of $H$ for different basic temperature profiles and for dual values of $\gamma$ (= 0.5, 10) is computed numerically and the outcomes are summarized in Figure 4 and Figure 5 at $Da=0.01$ and $Da=0.1$, respectively. In Figure 4a and Figure 5a, it is observed that the impact of $\gamma$ on the system stability is destabilizing, while the increase in $H$ is to stabilize the system. We note that $R_c$ increases monotonically with $H$ for diverse basic thermal profiles. It is found that $R_c$ is independent of $\gamma$ at lower $H$ and is leftover independent of $H$ for $\gamma >10$. This is due to the small $H$ and higher $\gamma$; there is no substantial heat transport among the liquid and solid phases, and so the criterion for the system’s stability is unaffected by the solid phase’s characteristics for all of the temperature distributions considered. Further, the deviation in $R_c$ between the models M1 and M2 is observed to be not so significant as compared to the models M3 and M4. The work therefore demonstrates the ability of efficiently managing (suppressing or enhancing) porous convection in a liquid saturated permeable layer by the appropriate choice of various fundamental thermal profiles. The values of $R_c$ are higher for model M4 and least for model M2 when $\gamma =0.5$, while the system is more stable for model M3 and least stable for model M2 for $\gamma =10$. The performance of $a_c$ as function of $H$ for diverse basic temperature profiles and for two values of $\gamma$ (=0.5, 10) is shown in the Figure 4b and Figure 5b at $Da=0.01$ and $Da=0.1$, respectively. The values of $a_c$ are leftover constant at the higher and lower $H$ values and they display a non-monotonic behavior for different basic temperature profiles as well as for various $\gamma$ at intermediate $H$ except for the model M4 at $\gamma =0.5$. The values of $a_c$ are unbounded growth for the model M4 at $\gamma =0.5$ for $Da=0.01$ and $0.1$. The critical wave numbers remain almost independent of $H$ for $\gamma >10$. Upsurge in $\gamma$ is to diminution the $a_c$ and the consequence is to upsurge the convection cell size for all the models considered. Increase in $Da$ is to diminish the convection cell size. Here, it is disclosed that $a_c$ is advanced for model M3 followed by M2, then model M4, and least for model M1.

5. Conclusions

Linear stability of thermal convection in a permeable layer via the LTNE regime was explored and various forms of basic temperature profiles were taken into account in this study. The subsequent EVP was solved by means of the Galerkin scheme for rigid isothermal boundaries. The results of this study can be summarized as follows:

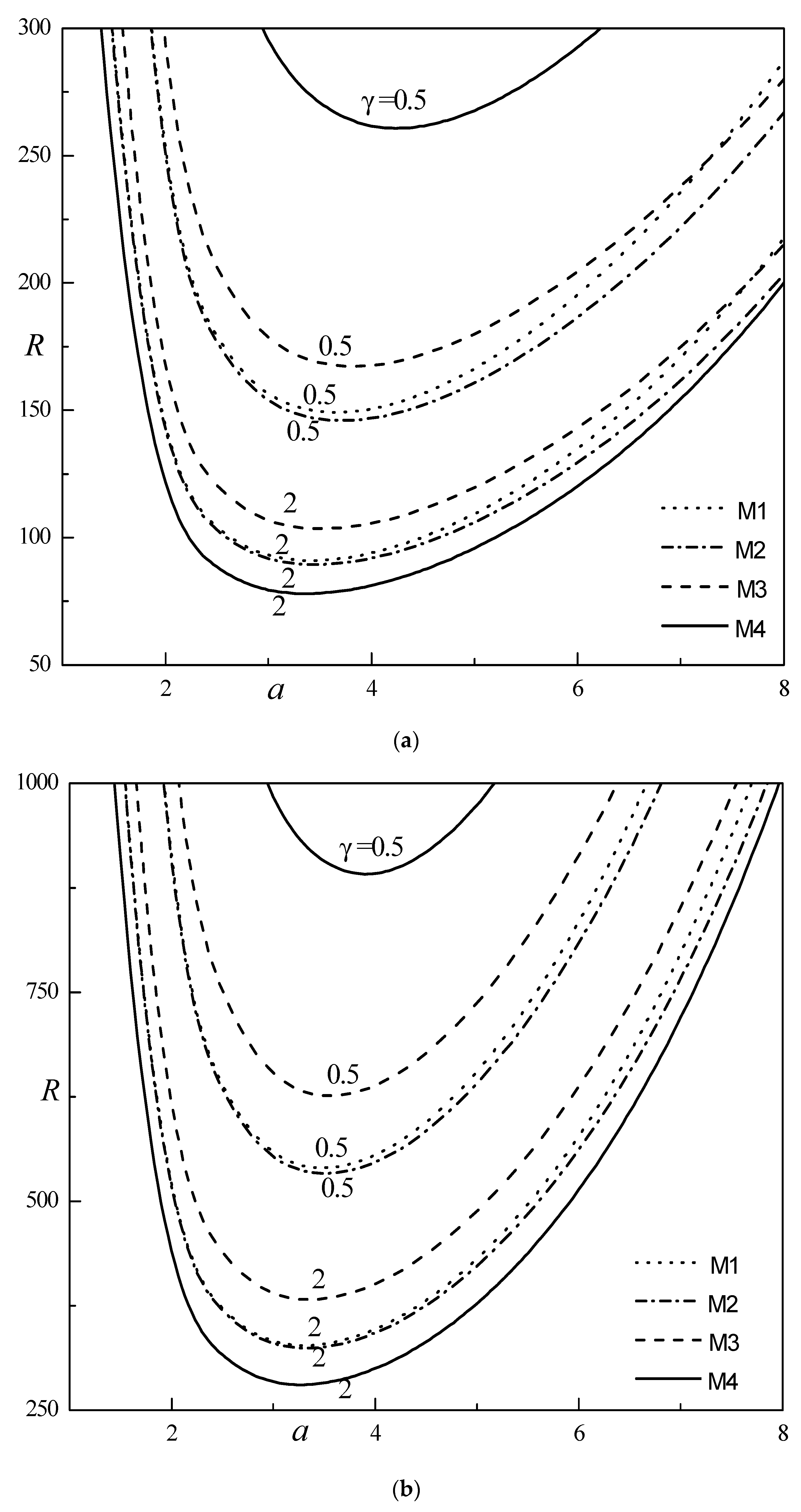
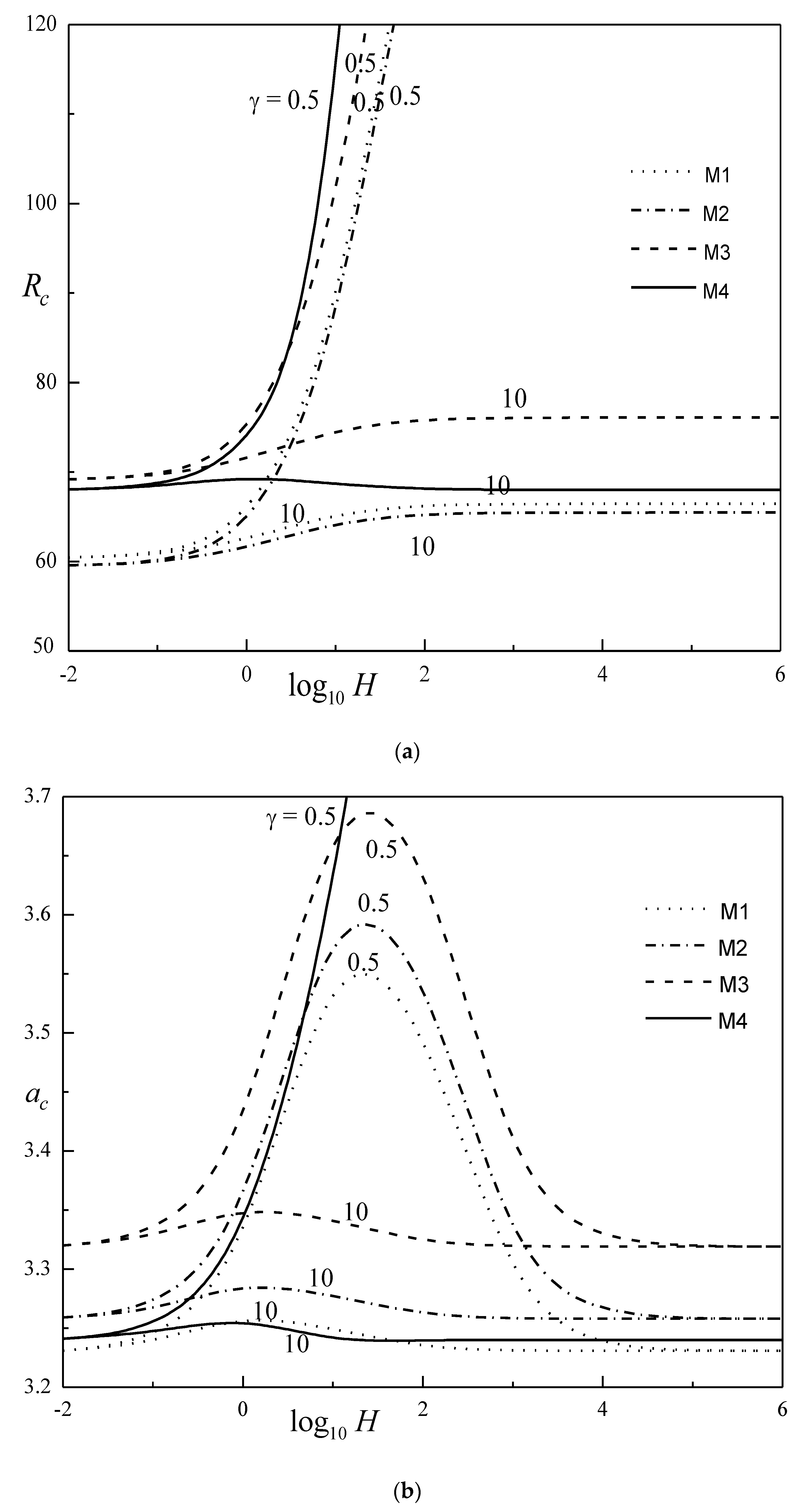
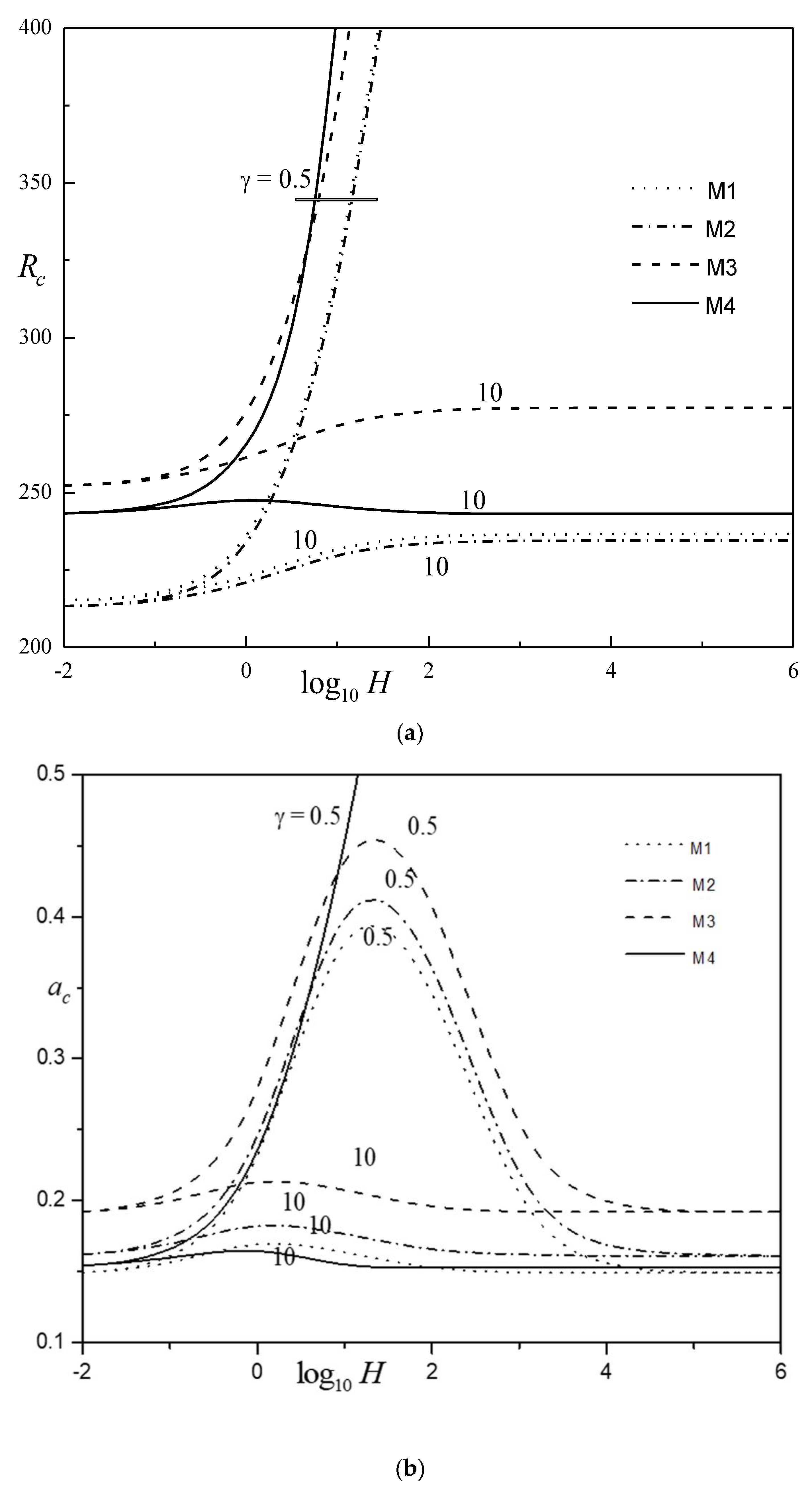
• The system was found to be more stable for model M4 (Cubic-2 temperature profile) when compared to non-uniform temperature profiles. In particular, model M2 hastens the onset of convection.
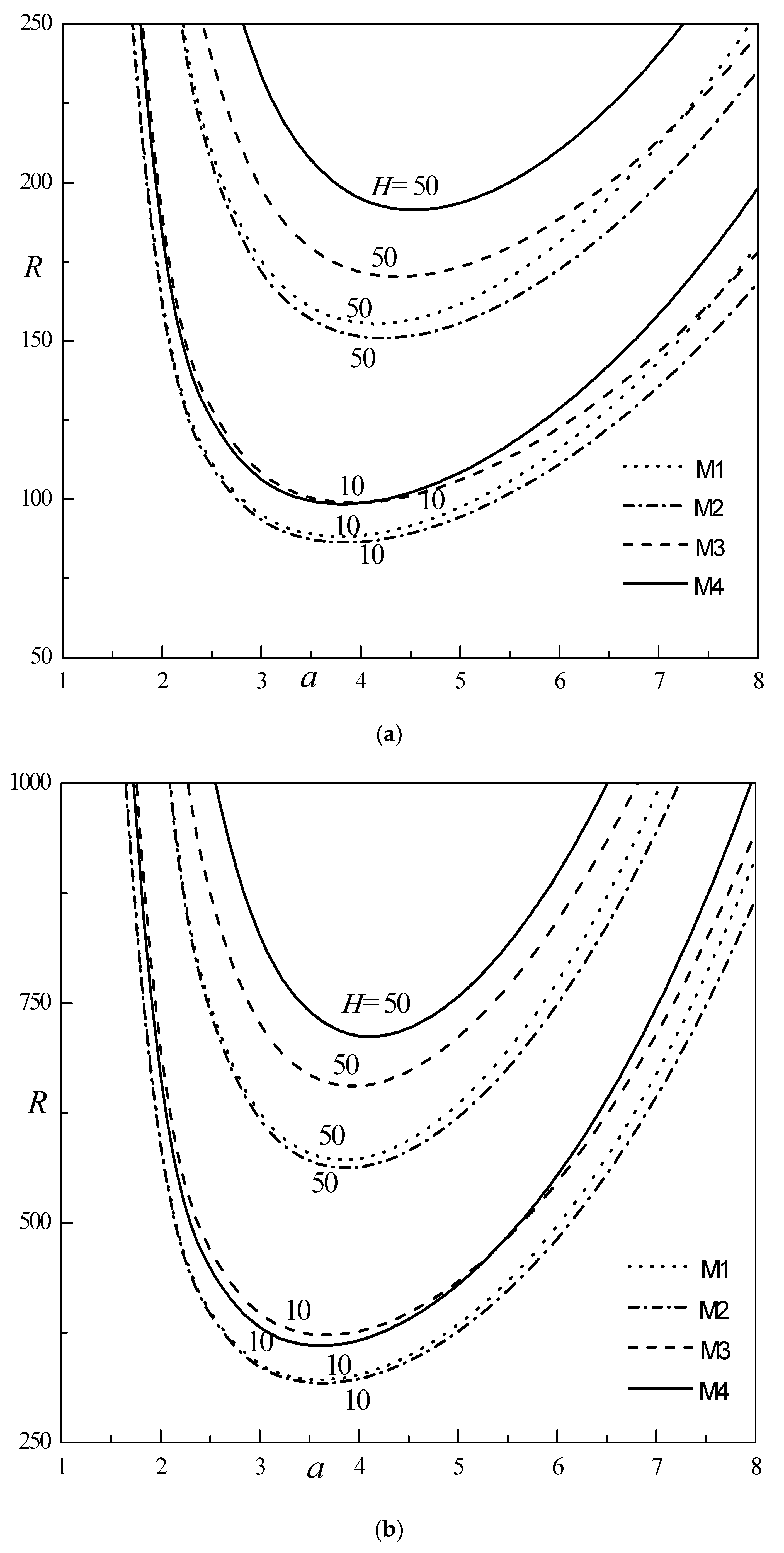
• The porosity modified conductivity ratio $\gamma$ has no impact on the system stability at the small-$H$ limit for all the temperature profiles considered, while for higher $H$ values, an increase in $\gamma$ hastens the onset of convection.
• The system is found to be stable with increase in $H$ and $Da$ for all the temperature profiles considered. The values of $R_c$ remain almost independent of $H$ at large $\gamma \ge 10$. The values of $a_c$ attain the maximum for diverse values of $\gamma$ at intermediate $H$ and remain constant at small and higher $H$ values.
• The rise in $\gamma$ causes upsurge of the convection size, while increasing $Da$ diminishes the convection cell size for all models considered.
• The $a_c$ is higher for model (M3) (Cubic-1 temperature profile) and least for model (M1) (linear temperature profile). The values of $a_c$ are unbounded growth for model (M4) at lower $\gamma$.
• The results for various basic temperature profiles are asymmetric quantitatively, and more importantly, they give an idea about the possibility of controlling convection using an appropriate choice for the basic temperature profile.