1. Introduction
Various areas of knowledge can use modeling involving one or more response variables of interest, i.e., two or more attributes to be modeled. If these attributes are not independent and a practical explanation exists for this situation, multivariate statistical models should be used with the objective of explaining and capturing the correlation of these variables.
For this purpose, joint continuous distributions are commonly used. The bivariate normal and t-Student distributions are most often used, although they can be highly restrictive. Besides this, employing them implies a linear relationship and elliptical structure of the variables. These premises do not always hold.
The modeling of multivariate data based on copula functions is an interesting alternative to overcome these drawbacks. According to Nelsen (1986) [
1], copulas provide a way to relate functions of multivariate distributions based on their marginal distribution functions. The main advantages from a statistical standpoint using this method are:
For constructing joint distributions, copulas allow each of them to be modeled individually by a different marginal distribution, thus enabling more flexible associations by fitting different marginal distributions;
Employment of copulas is a useful approach to model and understand the phenomenon of dependence, i.e., the dependence between these variables can assume diverse structures, including nonlinear ones, according to the type of copula utilized;
The marginal distributions should not depend on the association of the variables under analysis;
A copula is invariant from continuous transformations of the marginals.
Various bivariate distributions have been proposed based on copula functions such as the Weibull bivariate derived from the Farlie–Gumbel–Morgenstern (FGM) copula functions, Ali–Mikhail–Haq (AMH), Gumbel–Hougaard, Gumbel–Barnett [
2], generalized bivariate Rayleigh using the Clayton copula (El-Sherpieny and Almetwally [
3]), bivariate Fréchet based on the FGM or AMH copulas [
4], and generalized inverted Kumaraswamy using the Marshal–Olkin method [
5]. Samanthi and Sepanski [
6] defined families from four bivariate copulas using the Kumaraswamy distribution, the bivariate exponentiated half logistic based on the Marshall–Olkin class [
7], and the bivariate Lindley distribution via the FGM copula [
8]. Here, we focus on Archimedean copulas, which have closed-form expressions as an important characteristic, since they can be easily constructed starting from specific generator functions. Further, they are highly flexible, permitting the modeling of various forms of dependence, including asymmetry and extreme dependence. Due to the ease of their construction, these copulas have a large number of applications in various areas of knowledge, such as finance ([
3,
9,
10]), health ([
11,
12]), hydrology ([
13,
14,
15]), and survival analysis ([
16,
17,
18]). Detailed studies of these families and their applications can be found in Nelsen (2007).
In many practical situations, the response variable presents an asymmetric and/or bimodal behavior. The motivation for this work comes from an experiment carried out at the Plekhanov Russian University of Economics that evaluated the growth of oak leaf lettuce (Lactuca sativa var. crispa). The histograms of the response variables fresh weight (grams) (
) and plant height (cm) (
) measured in the experiment are reported in
Figure 1a,b. It is noted that they present bimodal behavior and positive asymmetries. In addition, the scatter plot between them (
Figure 1c) indicates that they present a strong and positive correlation.
Although a wide range of flexible bivariate distributions can be found in the literature, we note a scarcity of bimodal bivariate distributions. For this purpose, we use the
exponentiated odd log-logistic-G (EOLL-G) family (Alizadeh et al., 2020) [
19]), whose densities have great flexibility in modeling data, such as bimodality and/or positive or negative asymmetry. The Clayton and Frank copulas are adopted, so the new models are called the BCEOLL-G and BFEOLL-G families, respectively. We consider these copulas because they are suitable to model data with positive correlation (Naifar, 2011) [
9] according to the dataset in
Figure 1c.
This paper is structured as follows:
Section 2 provides a summary of copula functions.
Section 3 proposes the bivariate Clayton and Frank copulas generated from the EOLL-G family.
Section 4 introduces the Frank and Clayton copulas generated from the EOLL Normal distribution.
Section 5 formulates the bivariate bimodal regression with copulas and presents inferential issues.
Section 6 performs some simulations for different scenarios.
Section 7 illustrates the new methodology for lettuce plants from an experimental trial.
Section 8 concludes the article.
2. Archimedean Copulas
According to [
20], copulas can be described as functions that link univariate marginal distributions, or alternatively, functions with a multivariate distribution whose marginals are uniform in the interval
. The name and theory of copulas are based on the theorem of Sklar [
21]. This important theorem pertaining to the copula method, which guarantees the mentioned relations, is described below. The proof can be found in [
22].
Sklar’s Theorem: Let
be a random vector with marginal cumulative distribution functions (cdfs)
, and let
be their joint cdfs. Define
. Then, there is a copula function
such that
By differentiating (
1), the joint probability density function (pdf) follows as
where
is the marginal pdf of
and
is the copula density by taking the derivative of the copula function. For independent marginals,
and
, and then
, which means the independence of the random variables.
Henceforth, we consider the bivariate case for the data introduced in
Section 1.
Archimedean copulas are constructed by a strictly decreasing continuous generating function
, where
and
. Thus, the distribution function of a two-dimensional Archimedean copula can be expressed as
where
is the control parameter of the degree of dependency. The lower and upper tail dependence measures for a bivariate copula
C are defined in Joe (1993) [
23] (if the limits exist) as
For the Archimedean copula, these limits hold
Here, we employ the most cited bivariate Archimedean copulas (Clayton, 1978 [
24]; Frank, 1979 [
25]) for constructing new bivariate response regression models.
2.1. Clayton Copula
The Clayton copula [
24] has generating function
and distribution and density functions given by
and
respectively, where
. In this case, there is independence between the two variables when
tends to zero. As
and
, it follows from Equation (
3)
and
2.2. Frank Copula
The Frank copula [
25] has generating function
and distribution and density functions given by
and
respectively, where
. If
tends to zero, the two variables can be independent, and if
tends to infinity the two variables are correlated. As
and
, it follows from Equation (
3) using L’Hôpital rule
and
3. A Bivariate EOLL-G Family Based on Clayton and Frank Copulas
For any baseline cdf
depending on a parameter vector
, Alizadeh et al. (2020) [
19] defined the cdf of the exponentiated odd log-logistic (“EOLL-G”) family (for
) by
where
,
and
are two extra shape parameters.
The pdf associated to Equation (
8) becomes
where
.
From now on, let
be a random variable with pdf (
9). Let
X have cdf
such that
(for
) are finite. Some properties of
Y are reported below:
- (a)
The positive moments of
Y, i.e.,
,
, are finite when
(see
Appendix A.1).
- (b)
The variable
Y admits the stochastic representation:
, where
S has the Dagum distribution with shape parameters
and
, and unit scale, and
denotes the inverse function of
(see
Appendix A.2).
- (c)
The positive moments of the standardization version of
Y, say
, are finite if
(see
Appendix A.3).
Definition 1. Let be an independent copy of , i.e., is independent of and both have the same joint cdf . Following Koshevoy (1997) [26], the distance-Gini mean difference for F iswhere denotes the Euclidean distance in . - (d)
The distance-Gini mean difference
corresponding to the joint cdf
F in (
1), where
,
, is finite when
and
X have moments of order greater than one (see
Appendix A.4).
- (e)
If
, then
where
is the quantile function (qf) of G.
The EOLL-G family includes as special cases: the OLL-G class for
(Gleaton and Lynch, 2006 [
27]), and the exponentiated (Exp-G) class (Mudholkar et al., 1996 [
28]) for
. Clearly, Equation (
9) becomes the baseline G when
.
Thus, we consider the following marginal distributions
where
and
are parameter vectors of the baseline G, and
,
,
and
are positive shape parameters.
3.1. BCEOLL-G Model
By inserting (
8) and (
9) in Equations (
1), (
2), (
4) and (
5), the bivariate joint BCEOLL-G cdf reduces to
The corresponding joint pdf has the form
where (for
)
3.2. BFEOLL-G Model
Similarly, the joint cdf of the bivariate BFEOLL-G model can be expressed as
The corresponding joint BFEOLL-G pdf becomes
The BCEOLL-G and BFEOLL-G models include three special cases:
The bivariate Clayton Exponentiated (Exp)-G and Frank Exp-G classes when ;
The bivariate Clayton odd log-logistic (OLL)-G and Frank OLL-G classes when .
The bivariate Clayton and Frank baseline models when .
We can generate many bivariate models from Equations (
14) and (
16) by choosing different parent distributions.
3.3. Copula Dependence Measures
Pearson correlation is one of the most widely used measures, but it cannot be used in cases where the joint distributions are not normally distributed, and also cannot capture nonlinear relations between the variables.
We study the association of the variables by means of copulas using nonparametric concordance measures for the ranks of the variables, thus enabling coping with data not normally distributed and allowing nonlinear relations between the variables. A concordance measure can be defined as follows: let and be two observations of the bivariate random variable . Concordance exists when , while discordance exists when .
The Kendall () and Spearman () correlations are concordance measures adopted in this methodology and their expressions derived from the copula dependence parameters are given below:
Clayton copula: . The expression for is very complicated.
Frank copula: and , where is the kth order Debye function (for ).
4. BCEOLL Normal and BFEOLL Normal Models
Here, we discuss special cases of the BCEOLL-G and BFEOLL-G models. The density functions (
14) and (
16) will be most tractable when the cdf
has a simple analytic expression.
It is known that the data of many experiments follow a normal distribution. So, we present special models considering the normal baseline (
)
where
and
are the cdf and pdf of the standard normal, respectively,
,
is a location and
is a scale (for
). Hereafter, let
be a random variable.
If the marginals follow the EOLLN distribution, the joint cdf is determined by inserting (
17) in Equations (
14) and (
16). So, the joint pdfs of the BCEOLL Normal (BCEOLLN) and BFEOLL Normal (BFEOLLN) models are
and
respectively, where (for
)
Figure 2 and
Figure 3 report the joint densities, their contour plots, and bivariate cdfs for the Clayton and Frank copulas. The presence of bimodality is noted by the joint density. In the contour plots, we clearly find different association structures.
5. Bivariate Regression Models
Let be a bivariate random sample from the BCEOLLN and BEOLLN models, and , where and (for and ).
Considering a sample
, a systematic component can be defined as
where
is the explanatory variable vector of dimension
(for
and
), and
is the vector of unknown parameters.
Considering
n independent observations
(for
), the model defined by (
20) and the joint pdf given in Equations (
18) and (
19). Further, let
,
, and
.
If , , (for ), the total log-likelihood functions for have the forms below:
For copulas, the estimation of the parameters is usually conducted in two stages to create bivariate response models. In the first stage, the events are considered independent and the parameters are estimated marginally. The estimates are then used in the second stage, where the association parameter is estimated. This approach is coherent when the focus of the study is to estimate the association parameter . If the coefficients of the regression are the focus, this marginal two-stage approach does not add any additional information compared to the use of independent models. Then, it is best to conduct a joint estimation of the regression coefficients and .
The maximum likelihood estimate (MLE)
can be calculated by maximizing (
21) and (
22). We use the simplex method of Nelder and Mead (1965) [
29] implemented in the
optim function in the
R software [
30]. This method is a robust and direct search method, which uses only function values, i.e., it does not use gradient information. It compares the function values at the vertices of a general simplex, then replaces the vertex with the highest value by another point. The simplex adapts itself to the local landscape, and contracts on to the final minimum. Initial values for
,
and
are taken from the fits of the sub-models with
and
. It proves to be effective, computationally compact and provides the Hessian matrix, necessary for inference. See [
29] for details. The asymptotic normal distribution of
can be considered for inference, tests, and confidence intervals.
6. Simulation Study
A Monte Carlo simulation study examines the accuracy of the estimates in the bivariate EOLLN regression model. We use the Multivariate Copula Description (
MvCD) from the
copula package [
31] in
R. The
MvCD function generates the required univariate marginals according to the supplied association parameter using the inverse transformation method.
We consider the sample sizes
,
replications and a covariate
related to
and
by the identity link functions
and
, respectively. Further, we take
,
and
. Then, let
(for
), the quantile function (qf) has the form
where
,
, is the normal qf, namely
and
is the inverse error function.
The true parameter values are: , and .
The average estimates (AEs), biases, and mean squared errors (MSEs) are given by
where
.
For each of the Clayton and Frank copulas and sample size, the calculations follow the Algorithm 1.
| Algorithm 1: |
![Symmetry 15 01778 i001]() |
For both copulas, the biases and MSEs in
Table 1 and
Table 2 decrease when
n grows. So, the consistency of the estimators holds. The empirical coverage probabilities (CPs) in
Table 3 show that their values converge to the 95% nominal level.
7. Application to Lettuce Leaf Data
This dataset refers to the effect of the foliar application of different concentrations of silicon dioxide and organosilicon compounds on the growth and biochemical contents of Lactuca sativa var. crispa grown in phytotron conditions. The experiment was carried out on 12 March 2020, in the Department of Goods Commodity and Expertise of Goods Products in Moscow, Russian Federation. More details of the experiment are described in [
32]. Here, we check the response variables fresh weight (grams) (
) and plant height (cm) (
) together in order to verify the existing correlation between them. We also present a regression model relating these covariates with the following treatments:
The levels of gradual concentrations of amorphous silicon dioxide (AS) and 1-ethoxysilatrane (ES) solutions are: AS1 (50 mg·L), AS2 (100 mg·L), AS3 (200 mg·L), AS4 (300 mg·L), and ES1 (5 × 10 mL·L), ES2 (10 mL·L), ES3 (5 × 10 mL·L) and ES4 (10 mL·L). These variables are defined by dummy variables as follows:
Hence, the systematic component has the form (for
and
):
7.1. Descriptive Analysis
First, we present a descriptive analysis of the dataset.
Table 4 indicates positive asymmetry and kurtosis for both response variables.
Figure 1a,b displays the histograms of these variables, thus indicating bimodal behavior for both. Pearson’s coefficient is
, which is a strong positive correlation, as can be noted in
Figure 1.
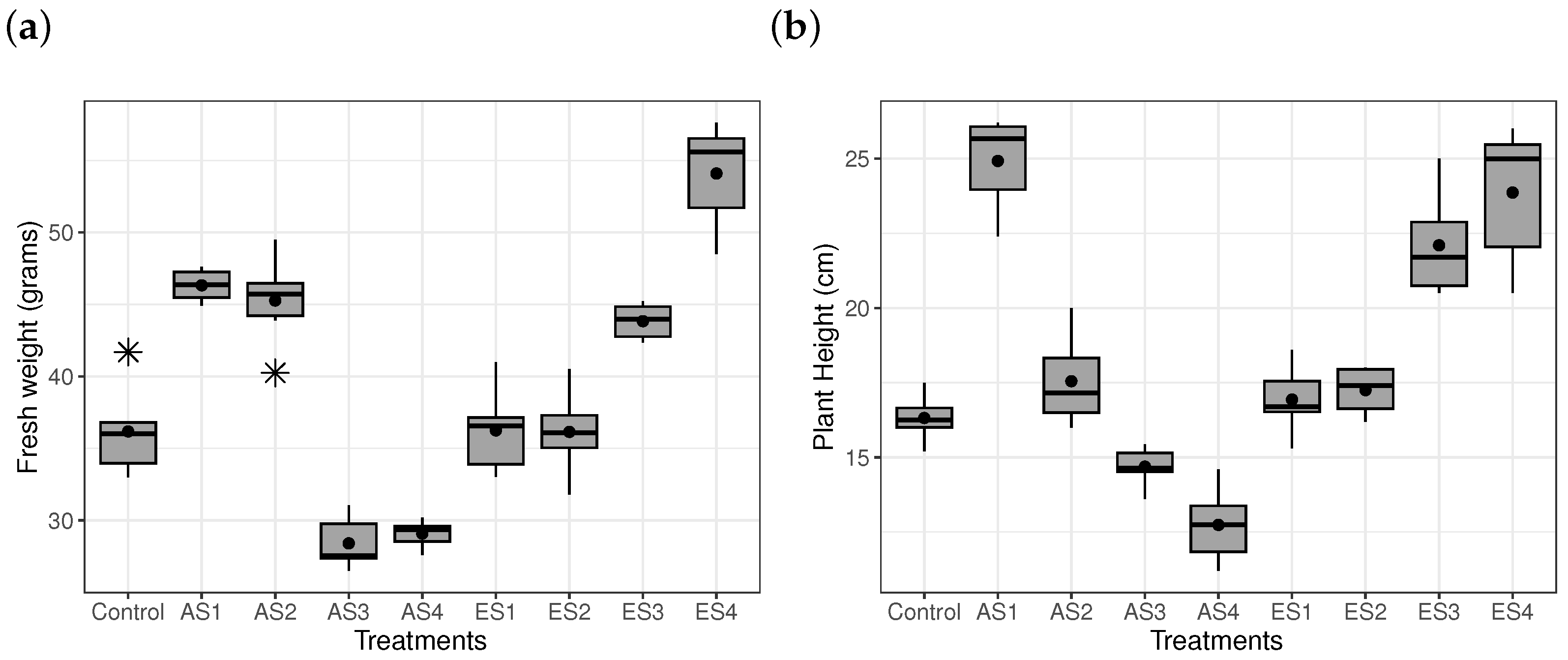
Figure 4 provides the boxplots for different experimental treatments.
7.2. Univarite Marginal Analysis
Univariate analysis of the response variables is conducted under the EOLLN distribution and its special cases: OLLN, Exp-N, and Normal. The Akaike information criterion (AIC) and Global Deviance (GD) in
Table 5 reveal that the OLLN model is more adequate for
(fresh weight) and the EOLLN model for
(plant height).
Figure 5a and
Figure 6a report the histograms with estimated densities, and
Figure 5b and
Figure 6b their empirical and estimated cumulative distributions, thus supporting the findings in
Table 5.
7.3. Bivariate Analysis and Regression Model
Next, we carry out a joint analysis of the response variables from the current sixteen models for the Clayton and Frank copulas.
Table 6 reveals that the bivariate (OLLN × EOLLN) regression model with Clayton and Frank copulas is the most suitable model to explain the response variables (
), thus agreeing with the univariate analysis.
Additionally, we provide the values of the copula dependence parameter (
), Kendall’s correlation (
), and Spearman correlation (
). For both models and the two copulas, these values indicate that the variables have strong positive dependence, thus confirming the required dependence structure.
Table 7 provides the estimated quantities for the best bivariate regression model.
We can conclude the following facts:
Finally,
Figure 7 displays the plots of the observed and predicted values and corresponding CIs, thus supporting that the best bivariate regression model is a good predictor for the current data.
8. Conclusions
This article proposed a new bivariate family based on Archimedean copulas. Motivated by an experiment that evaluated the growth of oak lettuce plants, which presented the variables fresh mass and height with bimodal behavior, we used the exponentiated odd log-logistic family, whose densities can model different types of data, including bimodality. Furthermore, these variables showed a strong positive correlation and the Clayton and Frank copulas were suitable for studying data with a positive correlation.
We presented some mathematical properties of the new family and a simulation study showed the consistency of the maximum likelihood estimators. We considered two categorical explanatory variables (each one with four treatments) to explain two response variables: fresh weight and plant height. Some important results were obtained from the application: (i) For both variables, the same treatments were significant or not; (ii) Two treatments had negative effects on the two variables and two other treatments had the greatest effects on the variables, i.e., with these treatments greater fresh mass and greater plant height were obtained. The bivariate regression model proved to be adequate for predicting fresh weight and plant height values of oak lettuce under the effect of different treatments. The choice of these copulas proved to be adequate due to the positive dependence structure between the variables. Other baseline distributions can be used as well as applications in other areas of knowledge.
Author Contributions
Conceptualization, G.M.R., E.M.M.O., G.M.C. and R.V.; methodology, G.M.R., E.M.M.O., G.M.C. and R.V.; software, G.M.R., E.M.M.O., G.M.C. and R.V.; validation, G.M.R., E.M.M.O., G.M.C. and R.V.; formal analysis, G.M.R., E.M.M.O., G.M.C. and R.V.; investigation, G.M.R., E.M.M.O., G.M.C. and R.V.; data curation, G.M.R., E.M.M.O., G.M.C. and R.V.; writing—original draft preparation, G.M.R., E.M.M.O., G.M.C. and R.V.; writing—review and editing, G.M.R., E.M.M.O., G.M.C. and R.V.; visualization, G.M.R., E.M.M.O., G.M.C. and R.V.; supervision, G.M.R., E.M.M.O., G.M.C. and R.V. All authors have read and agreed to the current version of the manuscript.
Funding
This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior-Brasil (CAPES) and Conselho Nacional de Desenvolvimento Cientifico e Tecnológico (CNPq).
Informed Consent Statement
Not applicable.
Data Availability Statement
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Some Properties Related to the EOLL-G Model
Appendix A.1. Real Moments
Let
. We obtain sufficient conditions that guarantee the existence of the real moments of
Y. By using the well-known formula (for the moments of positive random variables)
it is clear that
if and only if
for some
so that
. We now verify the finiteness of
I. In fact, let
S be a Dagum random variable with shapes
and
, and unit scale, say
. Since
the integral
I becomes
By applying Markov’s inequality, the inequality holds
If
is a cdf,
for
. Let
X have cdf
. So, the integral in (
A3) can be expressed as
where it is used Equation (
A1). We obtain
As
for
leads to the condition
, we have
.
Hence, under conditions and , we have .
Appendix A.2. Stochastic Representation
We can write from (
A2),
Finally, it is evident that
provides a stochastic representation for
.
Appendix A.3. Standardized Moments
Under the previous conditions,
Appendix A.1 guarantees the existence of moments of positive order of
Y, and then the existence of mean and variance. Let
and
, and let
be the standardized version of
Y.
By using the triangle inequality and the
inequality
,
, where
and
, we have
since
. As the function
is increasing for all
and
, we have from the previous inequality
where in the last inequality again we use the
inequality, and
and
are the norms in
of
Z and
Y, respectively.
Appendix A.1 leads to
,
and
, and then
from the above inequality.
Appendix A.4. The Multivariate Distance-Gini Mean Difference
Let
be an independent copy of
, where
follows the joint cdf
as given in (
1), and
,
. The distance-Gini mean difference for
F is defined as in (
10) (see Koshevoy 1997 [
26]).
Since
, where
is the Manhattan norm, it is clear that
As
is an independent copy of
, we have that
is idenpendent of
and both have the same univariate distribution
, with variance denoted by
. By using the following inequality (see Item (5) of reference Vila et al., 2023 [
33]), if
Z is the standardized version of
, then
we have from (
A4)
Hence, under conditions , and , we obtain .
References
- Nelsen, R.B. Properties of a one-parameter family of bivariate distributions with specified marginals. Commun. Stat.-Theory Methods 1986, 15, 3277–3285. [Google Scholar] [CrossRef]
- Quiroz-Flores, A. Testing copula functions as a method to derive bivariate Weibull distributions. In Proceedings of the APSA Annual Meeting & Exhibition, Toronto, ON, Canada, 3–6 September 2009. [Google Scholar]
- El-Sherpieny, E.S.; Almetwally, E.M. Bivariate generalized rayleigh distribution based on Clayton Copula. In Proceedings of the 54rd Annual Conference on Statistics, Computer Science and Operation Research, Cairo, Egypt, 9–11 December 2019; pp. 1–19. [Google Scholar]
- Almetwally, E.M.; Muhammed, H.Z. On a Bivariate Frechet Distribution. J. Stat. Appl. Probab. 2020, 9, 1–21. [Google Scholar]
- Muhammed, H.Z. On a bivariate generalized inverted Kumaraswamy distribution. Phys. A Stat. Mech. Its Appl. 2020, 553, 124281. [Google Scholar] [CrossRef]
- Samanthi, R.G.M.; Sepanski, J. On bivariate Kumaraswamy-distorted copulas. Commun. Stat.-Theory Methods 2022, 51, 2477–2495. [Google Scholar] [CrossRef]
- Alotaibi, R.M.; Rezk, H.R.; Ghosh, I.; Dey, S. Bivariate exponentiated half logistic distribution: Properties and application. Commun. Stat.-Theory Methods 2021, 50, 6099–6121. [Google Scholar] [CrossRef]
- Vaidyanathan, V.S.; Sharon Varghese, A. Morgenstern type bivariate Lindley distribution. Stat. Optim. Inf. Comput. 2016, 4, 132–146. [Google Scholar] [CrossRef]
- Naifar, N. Modelling dependence structure with Archimedean copulas and applications to the iTraxx CDS index. J. Comput. Appl. Math. 2011, 235, 2459–2466. [Google Scholar] [CrossRef]
- Yang, L.; Cai, X.J.; Li, M.; Hamori, S. Modeling dependence structures among international stock markets: Evidence from hierarchical Archimedean copulas. Econ. Model. 2015, 51, 308–314. [Google Scholar] [CrossRef]
- Novianti, P.; Kartiko, S.H.; Rosadi, D. Application of Clayton Copula to identify dependency structure of COVID-19 outbreak and average temperature in Jakarta Indonesia. J. Phys. Conf. Ser. 2021, 1, 012154. [Google Scholar] [CrossRef]
- Li, H.; Lu, Y. Modeling cause-of-death mortality using hierarchical Archimedean copula. Scand. Actuar. J. 2019, 3, 247–272. [Google Scholar] [CrossRef]
- Janga Reddy, M.; Ganguli, P. Risk assessment of hydroclimatic variability on groundwater levels in the Manjara basin aquifer in India using Archimedean copulas. J. Hydrol. Eng. 2012, 17, 1345–1357. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Bivariate rainfall frequency distributions using Archimedean copulas. J. Hydrol. 2007, 332, 93–109. [Google Scholar] [CrossRef]
- Tsakiris, G.; Kordalis, N.; Tigkas, D.; Tsakiris, V.; Vangelis, H. Analysing drought severity and areal extent by 2D Archimedean copulas. Water Resour. Manag. 2016, 30, 5723–5735. [Google Scholar] [CrossRef]
- He, W.; Lawless, J.F. Bivariate location–scale models for regression analysis, with applications to lifetime data. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2005, 67, 63–78. [Google Scholar] [CrossRef]
- Wienke, A.; Locatelli, I.; Yashin, A.I. The modelling of a cure fraction in bivariate time-to-event data. Austrian J. Stat. 2006, 35, 67–76. [Google Scholar] [CrossRef]
- Fachini, J.B.; Ortega, E.M.; Cordeiro, G.M. A bivariate regression model with cure fraction. J. Stat. Comput. Simul. 2014, 84, 1580–1595. [Google Scholar] [CrossRef]
- Alizadeh, M.; Tahmasebi, S.; Haghbin, H. The exponentiated odd log-logistic family of distributions: Properties and applications. J. Stat. Model. Theory Appl. 2020, 1, 29–52. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Sklar, M. Fonctions de répartition à n dimensions et leurs marges. Ann. de L’ISUP 1959, 8, 229–231. [Google Scholar]
- Sklar, A. Random variables, joint distribution functions, and copulas. Kybernetika 1973, 9, 449–460. [Google Scholar]
- Joe, H. Multivariate dependence measures and data analysis. Comput. Statist. Data Anal. 1993, 16, 279–297. [Google Scholar] [CrossRef]
- Clayton, D.G. A model for association in bivariate life tables and its applications in epidemiological studies of familial tendency in chronic disease incidence. Biometrika 1978, 65, 141–151. [Google Scholar] [CrossRef]
- Frank, M.J. On the simultaneous associativity of F(x,y) and x + y − F(x,y). Aequationes Math. 1979, 19, 194–226. [Google Scholar] [CrossRef]
- Koshevoy, G.A. Multivariate Gini Indices. J. Multivar. Anal. 1997, 60, 252–276. [Google Scholar] [CrossRef]
- Gleaton, J.U.; Lynch, J.D. Properties of generalized log-logistic families of lifetime distributions. J. Probab. Stat. Sci. 2006, 4, 51–64. [Google Scholar]
- Mudholkar, G.S.; Srivastava, D.K.; Kollia, G.D. A generalization of the Weibull distribution with application to the analysis of survival data. J. Am. Stat. Assoc. 1996, 91, 1575–1583. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Kojadinovic, I.; Yan, J. Modeling multivariate distributions with continuous margins using the copula R package. J. Stat. Softw. 2010, 34, 1–20. [Google Scholar] [CrossRef]
- Othman, A.J.; Eliseeva, L.G.; Ibragimova, N.A.; Zelenkov, V.N.; Latushkin, V.V.; Nicheva, D.V. Dataset on the effect of foliar application of different concentrations of silicon dioxide and organosilicon compounds on the growth and biochemical contents of oak leaf lettuce (Lactuca sativa var. crispa) grown in phytotron conditions. Data Brief 2021, 38, 107328. [Google Scholar] [CrossRef] [PubMed]
- Vila, R.; Balakrishnan, N.; Saulo, H. An Upper Bound and a Characterization for Gini’s Mean Difference Based on Correlated Random Variables. Preprint. 2023. Available online: https://arxiv.org/pdf/2301.07229.pdf (accessed on 15 July 2023).
Figure 1.
(a) Histogram of fresh weight, (b) Histogram of plant height, and (c) Scatter plot between fresh weight and plant height.
Figure 1.
(a) Histogram of fresh weight, (b) Histogram of plant height, and (c) Scatter plot between fresh weight and plant height.
Figure 2.
BCEOLLN copula for ), ) and : (a) Bivariate pdf, (b) Contour plots of the pdf and (c) Bivariate cdf.
Figure 2.
BCEOLLN copula for ), ) and : (a) Bivariate pdf, (b) Contour plots of the pdf and (c) Bivariate cdf.
Figure 3.
BFEOLLN copula for ), ) and : (a) Bivariate pdf, (b) Contour plots of the pdf and (c) Bivariate cdf.
Figure 3.
BFEOLLN copula for ), ) and : (a) Bivariate pdf, (b) Contour plots of the pdf and (c) Bivariate cdf.
Figure 4.
(a) Boxplots of fresh weight () and (b) Boxplots of plant height ().
Figure 4.
(a) Boxplots of fresh weight () and (b) Boxplots of plant height ().
Figure 5.
(a) Estimated densities and (b) Estimated cumulative functions and empirical cdf for the fresh weight.
Figure 5.
(a) Estimated densities and (b) Estimated cumulative functions and empirical cdf for the fresh weight.
Figure 6.
(a) Estimated densities and (b) Estimated cumulative functions and empirical cdf for the plant height.
Figure 6.
(a) Estimated densities and (b) Estimated cumulative functions and empirical cdf for the plant height.
Figure 7.
(a) Observed values (black) and predicted values (red) with CIs of the Clayton OLLN EOLLN regression model for fresh weight and (b) Observed values (black) and predicted values (red) with CIs of the Frank OLLN EOLLN regression for plant height.
Figure 7.
(a) Observed values (black) and predicted values (red) with CIs of the Clayton OLLN EOLLN regression model for fresh weight and (b) Observed values (black) and predicted values (red) with CIs of the Frank OLLN EOLLN regression for plant height.
Table 1.
Simulation findings from the fitted bivariate Clayton EOLLN regression model.
Table 1.
Simulation findings from the fitted bivariate Clayton EOLLN regression model.
| True Value | | | | | | |
| AEs | Biases | MSEs | AEs | Biases | MSEs |
| 1.50 | 1.4840 | −0.0160 | 0.1436 | 1.4949 | −0.0051 | 0.0787 |
| 1.32 | 1.3206 | 0.0006 | 0.0523 | 1.3190 | −0.0010 | 0.0244 |
| 1.50 | 1.5448 | 0.0448 | 0.0755 | 1.5383 | 0.0383 | 0.0405 |
| 1.10 | 1.1799 | 0.0799 | 0.0816 | 1.1577 | 0.0577 | 0.0450 |
| 1.40 | 1.4555 | 0.0555 | 0.0892 | 1.4233 | 0.0233 | 0.0453 |
| 1.60 | 1.5966 | −0.0034 | 0.0056 | 1.5986 | −0.0014 | 0.0024 |
| 2.30 | 2.3003 | 0.0003 | 0.0017 | 2.2991 | −0.0009 | 0.0008 |
| 0.60 | 0.6135 | 0.0135 | 0.0484 | 0.6132 | 0.0132 | 0.0224 |
| 1.80 | 1.8481 | 0.0481 | 0.0487 | 1.8314 | 0.0314 | 0.0216 |
| 1.90 | 1.9731 | 0.0731 | 0.0956 | 1.9396 | 0.0396 | 0.0408 |
| 5.00 | 5.2268 | 0.2268 | 0.1417 | 5.1446 | 0.1446 | 0.0601 |
| True Value | | | | | | |
| AEs | Biases | MSEs | AEs | Biases | MSEs |
| 1.50 | 1.4949 | −0.0051 | 0.0437 | 1.5049 | 0.0049 | 0.0164 |
| 1.32 | 1.3172 | −0.0028 | 0.0122 | 1.3219 | 0.0019 | 0.0049 |
| 1.50 | 1.5336 | 0.0336 | 0.0247 | 1.5185 | 0.0185 | 0.0108 |
| 1.10 | 1.1440 | 0.0440 | 0.0272 | 1.1253 | 0.0253 | 0.0112 |
| 1.40 | 1.4147 | 0.0147 | 0.0214 | 1.3992 | −0.0008 | 0.0074 |
| 1.60 | 1.5985 | −0.0015 | 0.0010 | 1.5993 | −0.0007 | 0.0003 |
| 2.30 | 2.2996 | −0.0004 | 0.0004 | 2.3003 | 0.0003 | 0.0002 |
| 0.60 | 0.6149 | 0.0149 | 0.0100 | 0.6089 | 0.0089 | 0.0048 |
| 1.80 | 1.8244 | 0.0244 | 0.0093 | 1.8135 | 0.0135 | 0.0045 |
| 1.90 | 1.9215 | 0.0215 | 0.0174 | 1.9078 | 0.0078 | 0.0057 |
| 5.00 | 5.0736 | 0.0736 | 0.0223 | 5.0178 | 0.0178 | 0.0060 |
Table 2.
Simulation findings from the fitted bivariate Frank EOLLN regression model.
Table 2.
Simulation findings from the fitted bivariate Frank EOLLN regression model.
| True Value | | | | | | |
| AEs | Biases | MSEs | AEs | Biases | MSEs |
| 1.50 | 1.3278 | −0.1722 | 0.5729 | 1.3552 | −0.1448 | 0.3244 |
| 1.32 | 1.3110 | −0.0090 | 0.0905 | 1.3250 | 0.0050 | 0.0432 |
| 1.50 | 1.5802 | 0.0802 | 0.0891 | 1.5753 | 0.0753 | 0.0686 |
| 1.10 | 1.2140 | 0.1140 | 0.1023 | 1.1875 | 0.0875 | 0.0734 |
| 1.40 | 1.6102 | 0.2102 | 0.4140 | 1.5419 | 0.1419 | 0.2325 |
| 1.60 | 1.5604 | −0.0396 | 0.0195 | 1.5730 | −0.0270 | 0.0114 |
| 2.30 | 2.2977 | −0.0023 | 0.0037 | 2.3015 | 0.0015 | 0.0017 |
| 0.60 | 0.6307 | 0.0307 | 0.0566 | 0.6419 | 0.0419 | 0.0446 |
| 1.80 | 1.8510 | 0.0510 | 0.0667 | 1.8546 | 0.0546 | 0.0483 |
| 1.90 | 2.1430 | 0.2430 | 0.3737 | 2.0495 | 0.1495 | 0.2159 |
| 5.00 | 5.1239 | 0.1239 | 0.3300 | 5.0954 | 0.0954 | 0.2026 |
| True Value | | | | | | |
| AEs | Biases | MSEs | AEs | Biases | MSEs |
| 1.50 | 1.4714 | −0.0286 | 0.1427 | 1.4853 | −0.0147 | 0.0666 |
| 1.32 | 1.3145 | −0.0055 | 0.0225 | 1.3264 | 0.0064 | 0.0086 |
| 1.50 | 1.5681 | 0.0681 | 0.0390 | 1.5407 | 0.0407 | 0.0189 |
| 1.10 | 1.1789 | 0.0789 | 0.0414 | 1.1461 | 0.0461 | 0.0210 |
| 1.40 | 1.4391 | 0.0391 | 0.0999 | 1.4102 | 0.0102 | 0.0421 |
| 1.60 | 1.5801 | −0.0199 | 0.0052 | 1.5862 | −0.0138 | 0.0024 |
| 2.30 | 2.2990 | −0.0010 | 0.0008 | 2.3008 | 0.0008 | 0.0003 |
| 0.60 | 0.6271 | 0.0271 | 0.0217 | 0.6278 | 0.0278 | 0.0100 |
| 1.80 | 1.8334 | 0.0334 | 0.0225 | 1.8289 | 0.0289 | 0.0094 |
| 1.90 | 2.0108 | 0.1108 | 0.0961 | 1.9652 | 0.0652 | 0.0465 |
| 5.00 | 5.0431 | 0.0431 | 0.0856 | 5.0227 | 0.0227 | 0.0428 |
Table 3.
CPs for the fitted bivariate Clayton and Frank EOLLN regression models.
Table 3.
CPs for the fitted bivariate Clayton and Frank EOLLN regression models.
| Clayton | | | | | | | | | | |
| n | | | | | | | | | | | |
| 50 | 0.995 | 0.971 | 0.999 | 0.996 | 0.997 | 0.999 | 0.972 | 1.000 | 1.000 | 0.999 | 0.961 |
| 100 | 0.996 | 0.972 | 0.998 | 0.997 | 0.998 | 1.000 | 0.974 | 1.000 | 1.000 | 1.000 | 0.962 |
| 200 | 0.999 | 0.958 | 0.999 | 0.999 | 1.000 | 0.999 | 0.965 | 1.000 | 0.999 | 1.000 | 0.968 |
| 500 | 0.999 | 0.962 | 0.999 | 0.999 | 1.000 | 1.000 | 0.964 | 1.000 | 1.000 | 1.000 | 0.948 |
| Frank | | | | | | | | | | |
| n | | | | | | | | | | | |
| 50 | 0.983 | 0.956 | 1.000 | 0.998 | 0.986 | 0.988 | 0.937 | 1.000 | 1.000 | 0.988 | 0.950 |
| 100 | 0.993 | 0.961 | 0.999 | 1.000 | 0.992 | 0.989 | 0.944 | 1.000 | 0.999 | 0.990 | 0.951 |
| 200 | 0.990 | 0.956 | 0.999 | 0.998 | 0.991 | 0.996 | 0.956 | 1.000 | 1.000 | 0.997 | 0.962 |
| 500 | 0.995 | 0.955 | 0.999 | 0.999 | 0.995 | 0.998 | 0.946 | 1.000 | 1.000 | 0.997 | 0.953 |
Table 4.
Descriptive analysis of fresh weight () and plant height () variables.
Table 4.
Descriptive analysis of fresh weight () and plant height () variables.
| Variable | Mean | Median | s.d. | Min. | Max | Skewness | VC | Kurtosis |
|---|
| 39.511 | 38.925 | 8.406 | 26.500 | 57.610 | 0.268 | 21.274 | 2.208 |
| 18.485 | 17.250 | 4.197 | 11.200 | 26.200 | 0.476 | 22.707 | 2.174 |
Table 5.
Adequacy measures of the univariate models for each response variable.
Table 5.
Adequacy measures of the univariate models for each response variable.
| Model | Fresh Weight | Plant Height |
|---|
| AIC | GD | AIC | GD |
|---|
| EOLLN | 385.98 | 377.98 | 300.80 | 292.80 |
| OLLN | 384.05 | 378.05 | 305.51 | 299.51 |
| Exp-N | 387.40 | 381.40 | 309.57 | 303.57 |
| Normal | 386.16 | 382.16 | 311.16 | 307.16 |
Table 6.
AIC, GD, copula dependence parameter (), Kendall correlation () and Spearman correlation () for sixteen bivariate models fitted to lettuce data.
Table 6.
AIC, GD, copula dependence parameter (), Kendall correlation () and Spearman correlation () for sixteen bivariate models fitted to lettuce data.
| Model for () | Clayton | Frank |
|---|
| AIC | GD | | | | AIC | GD | | | |
|---|
| EOLLN × EOLLN | 623.18 | 605.18 | 2.81 | 0.58 | 0.77 | 615.95 | 597.95 | 10.16 | 0.67 | 0.86 |
| EOLLN × OLLN | 634.02 | 618.02 | 2.27 | 0.53 | 0.72 | 627.92 | 611.92 | 9.67 | 0.66 | 0.85 |
| EOLLN × Exp-N | 629.52 | 613.52 | 3.38 | 0.63 | 0.81 | 628.37 | 612.37 | 8.60 | 0.62 | 0.82 |
| EOLLN × Normal | 625.02 | 611.02 | 3.58 | 0.64 | 0.83 | 630.43 | 616.43 | 10.23 | 0.67 | 0.87 |
| OLLN × EOLLN | 620.25 | 604.25 | 2.93 | 0.59 | 0.78 | 612.78 | 596.78 | 10.79 | 0.69 | 0.88 |
| OLLN × OLLN | 632.00 | 618.00 | 2.31 | 0.54 | 0.72 | 626.71 | 612.71 | 9.47 | 0.65 | 0.85 |
| OLLN × Exp-N | 628.19 | 614.19 | 3.36 | 0.63 | 0.81 | 623.88 | 609.88 | 10.25 | 0.67 | 0.87 |
| OLLN × Normal | 624.47 | 612.47 | 3.82 | 0.66 | 0.84 | 628.43 | 616.43 | 10.36 | 0.68 | 0.87 |
| Exp-N × EOLLN | 622.61 | 606.61 | 2.92 | 0.59 | 0.78 | 616.98 | 600.98 | 10.03 | 0.67 | 0.86 |
| Exp-N × OLLN | 631.90 | 617.90 | 2.87 | 0.59 | 0.78 | 632.15 | 618.15 | 9.11 | 0.64 | 0.84 |
| Exp-N × Exp-N | 632.43 | 618.43 | 3.47 | 0.63 | 0.82 | 636.22 | 622.22 | 10.85 | 0.69 | 0.88 |
| Exp-N × Normal | 626.75 | 614.75 | 3.33 | 0.62 | 0.81 | 632.04 | 620.04 | 9.80 | 0.66 | 0.86 |
| Normal × EOLLN | 620.62 | 606.62 | 3.00 | 0.60 | 0.79 | 615.77 | 601.77 | 10.30 | 0.67 | 0.87 |
| Normal × OLLN | 633.50 | 621.50 | 2.29 | 0.53 | 0.72 | 630.58 | 618.58 | 9.15 | 0.64 | 0.84 |
| Normal × Exp-N | 629.29 | 617.29 | 3.05 | 0.60 | 0.79 | 624.74 | 612.74 | 10.16 | 0.67 | 0.86 |
| Normal × Normal | 624.54 | 614.54 | 3.35 | 0.63 | 0.81 | 630.37 | 620.37 | 9.99 | 0.67 | 0.86 |
Table 7.
Estimated quantities for the best bivariate regression model fitted to lettuce data.
Table 7.
Estimated quantities for the best bivariate regression model fitted to lettuce data.
| MLEs | CIs | SEs | p-Values |
|---|
| 35.8036 | [33.7814, 37.8257] | 1.0086 | <0.001 |
| 10.8022 | [8.1460, 13.4583] | 1.3248 | <0.001 |
| 9.9009 | [7.1183, 12.6833] | 1.3879 | <0.001 |
| −7.6892 | [−10.3286, −5.0497] | 1.3165 | <0.001 |
| −6.7391 | [−9.2985, −4.1795] | 1.2766 | <0.001 |
| 0.6059 | [−2.1540, 3.3658] | 1.3766 | 0.3308 |
| −0.1776 | [−3.0838, 2.7287] | 1.4496 | 0.4515 |
| 8.4060 | [5.3443, 11.4675] | 1.5271 | <0.001 |
| 18.6657 | [15.5123, 21.8191] | 1.5729 | <0.001 |
| 1.8421 | [−4.0207, 7.7049] | 2.9243 | |
| 1.0892 | [−4.9764, 7.1548] | 3.0255 | |
| 17.0122 | [15.8189, 18.2056] | 0.5952 | <0.001 |
| 9.4337 | [8.1786, 10.6887] | 0.6259 | <0.001 |
| 1.6790 | [0.0778, 3.2802] | 0.7986 | 0.0201 |
| −1.6034 | [−2.7452, −0.4617] | 0.5694 | 0.0034 |
| −3.2964 | [−4.6713, −1.9214] | 0.6857 | <0.001 |
| 0.9021 | [−0.4202, 2.2245] | 0.6595 | 0.0885 |
| 1.0147 | [−0.2440, 2.2736] | 0.6279 | 0.0559 |
| 6.3580 | [4.5401, 8.1759] | 0.9067 | <0.001 |
| 8.3849 | [7.0828, 9.6870] | 0.6494 | <0.001 |
| 0.7811 | [−1.6658, 3.2282] | 1.2205 | |
| 1.1064 | [−1.0946, 3.3074] | 1.0978 | |
| −1.0721 | [−2.6434, 0.4992] | 0.7837 | |
| 3.3776 | [1.1464,5.6086] | 1.1129 | |
| =0.339, = 0.492 | | AIC: 456.7843 GD: 408.7843 |
Table 8.
Comparisons between treatments according to the best bivariate regression model.
Table 8.
Comparisons between treatments according to the best bivariate regression model.
| Hypotheses | Fresh Weight | Plant Height |
|---|
| MLEs | SEs | p-Values | MLEs | SEs | p-Values |
|---|
| AS1 - Control | 10.802 | 1.325 | 0.000 | 9.434 | 0.626 | 0.000 |
| AS2 - Control | 9.901 | 1.388 | 0.000 | 1.679 | 0.799 | 0.020 |
| AS3 - Control | −7.689 | 1.317 | 0.000 | −1.603 | 0.569 | 0.003 |
| AS4 - Control | −6.739 | 1.277 | 0.000 | −3.296 | 0.686 | 0.000 |
| ES1 - Control | 0.606 | 1.377 | 0.331 | 0.902 | 0.660 | 0.088 |
| ES2 - Control | −0.178 | 1.450 | 0.452 | 1.015 | 0.628 | 0.056 |
| ES3 - Control | 8.406 | 1.527 | 0.000 | 6.358 | 0.907 | 0.000 |
| ES4 - Control | 18.666 | 1.573 | 0.000 | 8.385 | 0.649 | 0.000 |
| AS1 - ES4 | −8.160 | 2.453 | 0.001 | 0.959 | 0.745 | 0.102 |
| AS2 - ES4 | −9.017 | 2.097 | 0.000 | −6.829 | 0.902 | 0.000 |
| AS3 - ES4 | −26.352 | 2.667 | 0.000 | −9.975 | 0.754 | 0.000 |
| AS4 - ES4 | −25.410 | 2.495 | 0.000 | −11.658 | 0.855 | 0.000 |
| ES1 - ES4 | −18.376 | 2.642 | 0.000 | −7.505 | 0.843 | 0.000 |
| ES2 - ES4 | −18.741 | 2.638 | 0.000 | −7.312 | 0.810 | 0.000 |
| ES3 - ES4 | −10.192 | 2.853 | 0.000 | −1.956 | 1.061 | 0.035 |
| AS1 - ES3 | 2.663 | 1.581 | 0.049 | 3.120 | 1.159 | 0.005 |
| AS2 - ES3 | 1.935 | 1.436 | 0.092 | −4.597 | 0.859 | 0.000 |
| AS3 - ES3 | −15.784 | 1.599 | 0.000 | −7.802 | 1.088 | 0.000 |
| AS4 - ES3 | −14.686 | 1.417 | 0.000 | −9.550 | 0.922 | 0.000 |
| ES1 - ES3 | −7.468 | 1.504 | 0.000 | −5.323 | 0.892 | 0.000 |
| ES2 - ES3 | −8.035 | 1.667 | 0.000 | −5.143 | 1.033 | 0.000 |
| AS1 - ES2 | 10.396 | 1.446 | 0.000 | 8.377 | 0.678 | 0.000 |
| AS2 - ES2 | 9.707 | 1.464 | 0.000 | 0.689 | 0.841 | 0.208 |
| AS3 - ES2 | −7.959 | 1.399 | 0.000 | −2.592 | 0.636 | 0.000 |
| AS4 - ES2 | −6.875 | 1.367 | 0.000 | −4.295 | 0.713 | 0.000 |
| ES1 - ES2 | 0.255 | 1.492 | 0.432 | −0.120 | 0.701 | 0.432 |
| AS1 - ES1 | 10.414 | 1.358 | 0.000 | 8.562 | 0.788 | 0.000 |
| AS2 - ES1 | 9.640 | 1.339 | 0.000 | 0.918 | 0.764 | 0.117 |
| AS3 -
ES1 | −7.931 | 1.363 | 0.000 | −2.409 | 0.718 | 0.001 |
| AS4 - ES1 | −7.025 | 1.243 | 0.000 | −4.117 | 0.694 | 0.000 |
| AS1 - AS4 | 17.472 | 1.218 | 0.000 | 12.768 | 0.794 | 0.000 |
| AS2 - AS4 | 16.701 | 1.129 | 0.000 | 4.995 | 0.781 | 0.000 |
| AS3 - AS4 | −1.036 | 1.191 | 0.194 | 1.715 | 0.715 | 0.010 |
| AS1 - AS3 | 18.338 | 1.252 | 0.000 | 10.951 | 0.591 | 0.000 |
| AS2 - AS3 | 17.712 | 1.303 | 0.000 | 3.355 | 0.875 | 0.000 |
| AS1 - AS2 | 1.090 | 1.315 | 0.205 | 7.782 | 0.977 | 0.000 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).