The Geodetic Number for the Unit Graphs Associated with Rings of Order P and P2
Abstract
:1. Introduction
2. Preliminaries
3. The Unit Graph Associated with Rings of Order p
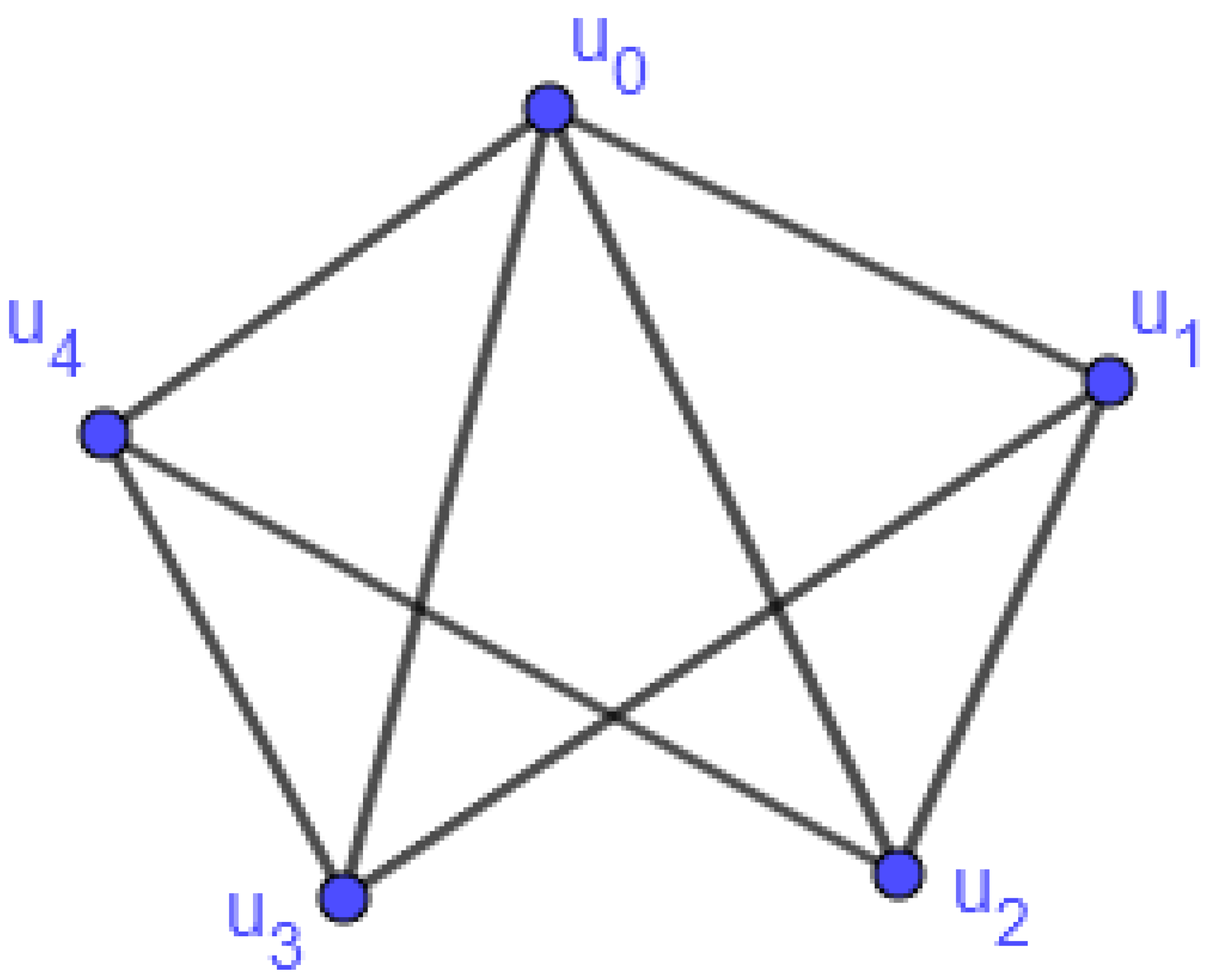
The Geodetic Number for the Unit Graph
4. The Unit Graph Associated with Rings of Order p2
- 1.
- If R is any one of , then it has a unity of or , respectively. Furthermore, since is a field, it has a unity of 1.
- 2.
- If , then for each for some . So, if , then , which contradicts the assumption that R has an order . Furthermore, if , the multiplication is trivial. Hence, the rings and do not contain a unity element.
- 3.
- If then Hence, there is no Similarly, if , it is clear that it does not have a unity element.
- 4.
- If , assume , in which . Then, and and hence, , a contradiction. Thus, R does not have a unity element in this case. Similarly, it can be shown that the ring does not have a unity element.
- 5.
- If , we have and . Thus, . Hence, there is no
4.1. The Geodetic Number for the Unit Graphs Associated with the Rings and
4.1.1. The Unit Graph over the Ring
4.1.2. The Unit Graph over the Ring
4.2. The Geodetic Number for the Unit Graphs Associated with the Rings and
4.2.1. The Geodetic Number for the Unit Graph
4.2.2. The Geodetic Number for the Unit Graph
- Suppose . Then, and If , consider the geodesic . If , consider the geodesic .
- Suppose . If , consider the geodesic . If , then and and so . Thus, we consider as the geodesic.
- Suppose that , where Thus, and with andIf and then and and so, If thenNow, assume that Then, we have the following cases:Case 1: If then, and Let , in which . Then,Case 2: If and let such that Then, and and therefore,
- Suppose that for some Then, and with andIf and then and with and by assumption. Therefore,while, if thenNow, assume that with Then, and and so, for some . Then, If with and let Then, and and therefore,
- Suppose that for some Then, and with and,Assume that with Since then If then and with and hence, .If assume that and Then, for all . Otherwise, assume that and . In this case, we have for some
- Suppose that for some Then, and with and,Assume that Then, and with and If and then If then and and therefore, for all If then and and therefore,If then and or for some . Then, and therefore, for all
- Assume that for some . Since we have Thus, , where a path exists in and is defined by
- Assume that for some . Then, and hence , where there is a path in defined by
- Assume that for some . Then, and hence , where there is a path in :
- Assume that for some . Then, and hence , where a path in is defined by
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Beck, I. Coloring of commutative rings. J. Algebra 1988, 116, 208–226. [Google Scholar] [CrossRef]
- Anderson, D.; Livingston, P.S. The zero-divisor graph of a commutative ring. J. Algebra 1999, 217, 434–447. [Google Scholar] [CrossRef]
- Anderson, D.F.; Badawi, A. The total graph of a commutative ring. J. Algebra 2008, 320, 2706–2719. [Google Scholar] [CrossRef]
- Grimaldi, R.P. Graphs from rings. In Proceedings of the Twentieth Southeastern Conference on Combinatorics, Graph Theory, and Computing, Boca Raton, FL, USA, 20–24 February 1989; Taylor and Francis: Abingdon, UK, 1990; pp. 95–103. [Google Scholar]
- Ashrafi, N.; Maimani, H.R.; Pournaki, M.R.; Yassemi, S. Unit graphs associated with rings. Commun. Algebra 2010, 38, 2851–2871. [Google Scholar] [CrossRef]
- Afkhami, M.; Khosh-Ahang, F. Unit graphs of rings of polynomials and power series. Arab. J. Math. 2013, 2, 233–246. [Google Scholar] [CrossRef]
- Anderson, D.D.; Naseer, M. Beck’s coloring of a commutative ring. J. Algebra 1993, 159, 500–514. [Google Scholar] [CrossRef]
- Su, H.; Zhou, Y. On the girth of the unit graph of a ring. J. Algebra Appl. 2014, 13, 1350082. [Google Scholar] [CrossRef]
- Harary, F.; Loikakis, E.; Tsouros, C. The geodetic number of a graph. Math. Comput. Model. 1993, 17, 89–95. [Google Scholar] [CrossRef]
- Harary, F.; Nieminen, J. Convexity in graphs. J. Differ. Geom. 1981, 16, 185–190. [Google Scholar] [CrossRef]
- Chartrand, G.; Harary, F.; Zhang, P. Geodetic sets in graphs. Discuss. Math. Graph Theory 2000, 20, 129–138. [Google Scholar] [CrossRef]
- Ahangar, H.A.; Samodivkin, V. The total geodetic number of a graph. Util. Math. 2016, 100, 253–268. [Google Scholar]
- Bermudo, S.; Rodriguez-Velazquez, J.A.; Sigarreta, J.M.; Yero, I. On geodetic and k-geodetic sets in graphs. Ars Comb. Waterloo Winn. 2010, 96, 469–478. [Google Scholar]
- Brešar, B.; Kovše, M.; Tepeh, A. Geodetic Sets in Graphs. Struct. Anal. Complex Netw. 2010, 20, 197–218. [Google Scholar]
- Dourado, M.C.; Protti, F.; Rautenbach, D.; Szwarcfiter, J. Some remarks on the geodetic number of agraph. Discret. Math. 2010, 310, 832–837. [Google Scholar] [CrossRef]
- Ekim, T.; Erey, A.; Heggernes, P.; Hof, P.; Meister, D. Computing minimum geodetic sets of proper interval graphs. Lect. Notes Comput. Sci. 2012, 7256, 279–290. [Google Scholar]
- Ge, H.; Wang, Z.; Zou, J. Strong geodetic number in some networks. J. Math. Res. 2019, 11, 20–29. [Google Scholar] [CrossRef]
- Gledel, V.; Irsic, V. Strong geodetic number of complete bipartite graphs, crown graphs and hypercubes. Bull. Malays. Sci. Soc. 2019, 43, 2757–2767. [Google Scholar] [CrossRef]
- Anderson, D.D.; Winders, M. Idealization of a module. J. Commut. Algebra 2009, 1, 3–56. [Google Scholar] [CrossRef]
- Waterhouse, W.C. Rings with cyclic additive group. Am. Math. Mon. 1964, 71, 449–450. [Google Scholar]
- Fine, B. Classification of finite rings of order p2. Math. Mag. 1993, 66, 248–252. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelkarim, H.A. The Geodetic Number for the Unit Graphs Associated with Rings of Order P and P2. Symmetry 2023, 15, 1799. https://doi.org/10.3390/sym15091799
Abdelkarim HA. The Geodetic Number for the Unit Graphs Associated with Rings of Order P and P2. Symmetry. 2023; 15(9):1799. https://doi.org/10.3390/sym15091799
Chicago/Turabian StyleAbdelkarim, Heba Adel. 2023. "The Geodetic Number for the Unit Graphs Associated with Rings of Order P and P2" Symmetry 15, no. 9: 1799. https://doi.org/10.3390/sym15091799



