Time–Energy Uncertainty Relation in Nonrelativistic Quantum Mechanics
Abstract
:1. Introduction
2. Mandelstam–Tamm Uncertainty Relation
3. Conservation of Total Energy and Its Quantum Statistics
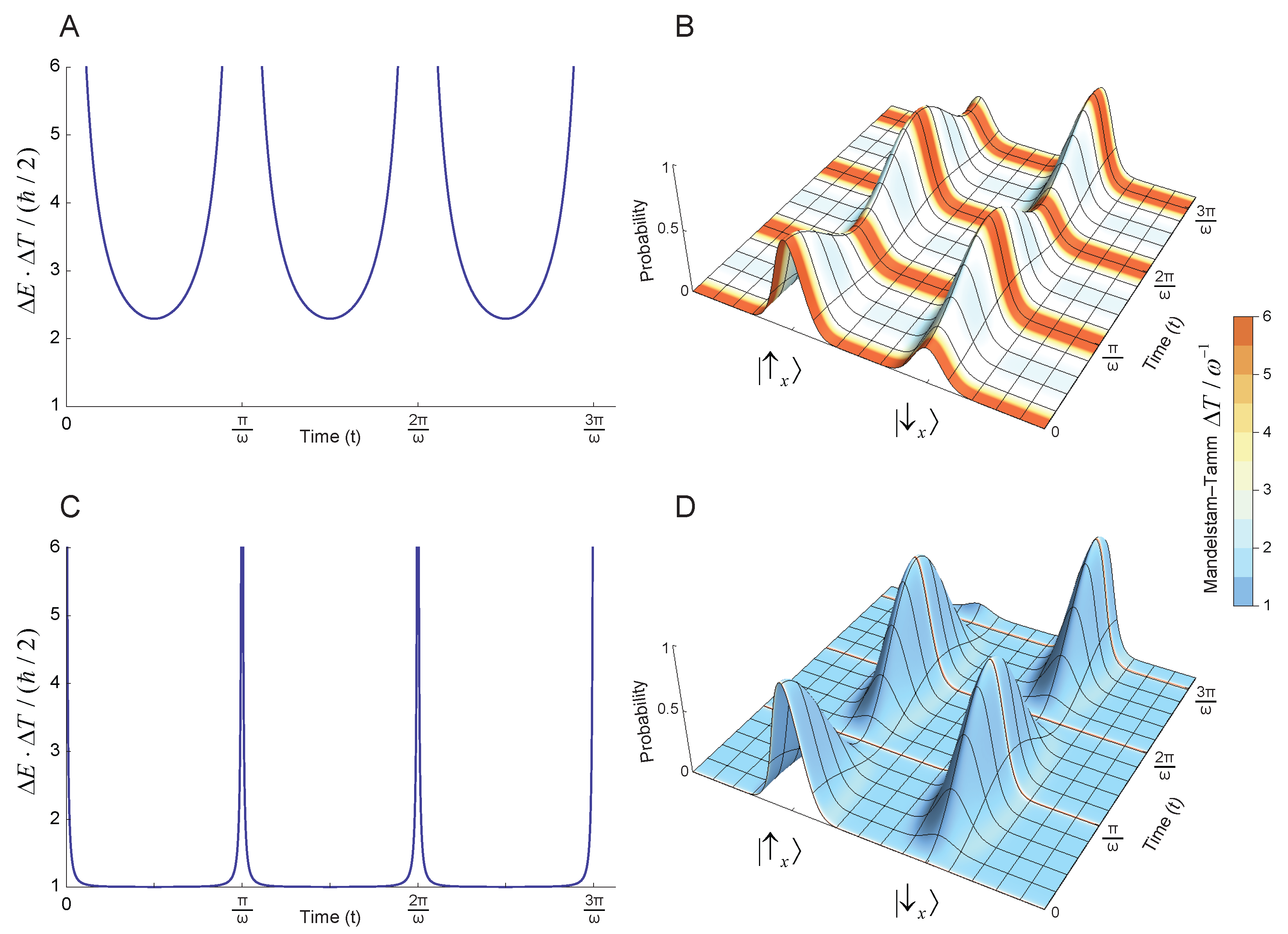
4. Minimal Quantum Toy Model
4.1. Quantum Dynamics of Energy States
4.2. Quantum Dynamics of Eigenstates of the Clock Observable
4.3. Physical Meaning of Mandelstam–Tamm “Time Uncertainty”
4.4. Clock Engineering with the Einstein–Planck Relation
5. Margolus–Levitin Quantum Speed Limit
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Quantum Statistics
Appendix B. Generalized Ehrenfest Theorem
Appendix C. Robertson–Schrödinger Uncertainty Relation
References
- Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 1927, 43, 172–198. [Google Scholar] [CrossRef]
- Heisenberg, W. The physical content of quantum kinematics and mechanics. In Quantum Theory and Measurement; Wheeler, J.A., Zurek, W.H., Eds.; Princeton University Press: Princeton, NJ, USA, 1983; pp. 62–84. [Google Scholar]
- Bohr, N. The quantum postulate and the recent development of atomic theory. Nature 1928, 121, 580–590. [Google Scholar] [CrossRef]
- Einstein, A.; Tolman, R.C.; Podolsky, B. Knowledge of past and future in quantum mechanics. Phys. Rev. 1931, 37, 780–781. [Google Scholar] [CrossRef]
- Born, M.; Jordan, P. Elementare Quantenmechanik: Zweiter Band der Vorlesungen über Atommechanik; Springer: Berlin/Heidelberg, Germany, 1930. [Google Scholar] [CrossRef]
- Bohr, N. Discussion with Einstein on epistemological problems in atomic physics. In Quantum Theory and Measurement; Wheeler, J.A., Zurek, W.H., Eds.; Princeton Series in Physics; Princeton University Press: Princeton, NJ, USA, 1983; pp. 9–49. [Google Scholar]
- Bohr, N. Discussion with Einstein on epistemological problems in atomic physics. In Niels Bohr Collected Works; Kalckar, J., Ed.; Elsevier: Amsterdam, The Netherlands, 1996; Volume 7, pp. 339–381. [Google Scholar] [CrossRef]
- Schrödinger, E. An undulatory theory of the mechanics of atoms and molecules. Phys. Rev. 1926, 28, 1049–1070. [Google Scholar] [CrossRef]
- Schrödinger, E. Collected Papers on Wave Mechanics; Blackie & Son: London, UK, 1928. [Google Scholar]
- Dirac, P.A.M. The Principles of Quantum Mechanics, 4th ed.; Oxford University Press: Oxford, UK, 1967. [Google Scholar]
- Pauli, W. Die allgemeinen Prinzipien der Wellenmechanik. In Quantentheorie; Bethe, H., Hund, F., Mott, N.F., Pauli, W., Rubinowicz, A., Wentzel, G., Smekal, A., Eds.; Handbuch der Physik; Springer: Berlin/Heidelberg, Germany, 1933; pp. 83–272. [Google Scholar] [CrossRef]
- Pauli, W. General Principles of Quantum Mechanics; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar] [CrossRef]
- Ehrenfest, P. Bemerkung über die angenäherte Gültigkeit der klassischen Mechanik innerhalb der Quantenmechanik. Z. Phys. 1927, 45, 455–457. [Google Scholar] [CrossRef]
- Robertson, H.P. The uncertainty principle. Phys. Rev. 1929, 34, 163–164. [Google Scholar] [CrossRef]
- Schrödinger, E. Zum Heisenbergschen Unschärfeprinzip. Sitzungsberichte Preuss. Akad. Wiss. Phys. Math. Kl. 1930, 14, 296–303. [Google Scholar]
- Busch, P. The time–energy uncertainty relation. In Time in Quantum Mechanics; Muga, J.G., Mayato, R.S., Egusquiza, I.L., Eds.; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2002; Volume 72, pp. 69–98. [Google Scholar] [CrossRef]
- Deffner, S.; Campbell, S. Quantum speed limits: From Heisenberg’s uncertainty principle to optimal quantum control. J. Phys. A Math. Theor. 2017, 50, 453001. [Google Scholar] [CrossRef]
- Mandelstam, L.I.; Tamm, I.Y. The uncertainty relation between energy and time in non-relativistic quantum mechanics. J. Phys. 1945, 9, 249–254. [Google Scholar] [CrossRef]
- Margolus, N.; Levitin, L.B. The maximum speed of dynamical evolution. Phys. D Nonlinear Phenom. 1998, 120, 188–195. [Google Scholar] [CrossRef]
- Bhaumik, M.L. The enigmas of fluctuations of the universal quantum fields. Quanta 2023, 12, 190–201. [Google Scholar] [CrossRef]
- Uhlmann, A. An energy dispersion estimate. Phys. Lett. A 1992, 161, 329–331. [Google Scholar] [CrossRef]
- Hörnedal, N.; Allan, D.; Sönnerborn, O. Extensions of the Mandelstam–Tamm quantum speed limit to systems in mixed states. New J. Phys. 2022, 24, 055004. [Google Scholar] [CrossRef]
- Bagchi, S.; Thakuria, D.; Pati, A.K. Stronger quantum speed limit for mixed quantum states. Entropy 2023, 25, 1046. [Google Scholar] [CrossRef]
- Baumgratz, T.; Cramer, M.; Plenio, M.B. Quantifying coherence. Phys. Rev. Lett. 2014, 113, 140401. [Google Scholar] [CrossRef] [PubMed]
- Qureshi, T. Coherence, interference and visibility. Quanta 2019, 8, 24–35. [Google Scholar] [CrossRef]
- Qureshi, T. Predictability, distinguishability and entanglement. Opt. Lett. 2021, 46, 492–495. [Google Scholar] [CrossRef] [PubMed]
- Peled, B.Y.; Te’eni, A.; Georgiev, D.; Cohen, E.; Carmi, A. Double slit with an Einstein–Podolsky–Rosen pair. Appl. Sci. 2020, 10, 792. [Google Scholar] [CrossRef]
- Georgiev, D.D. Quantum information in neural systems. Symmetry 2021, 13, 773. [Google Scholar] [CrossRef]
- Griffiths, D.J.; Schroeter, D.F. Introduction to Quantum Mechanics, 3rd ed.; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar] [CrossRef]
- Campbell, J.E. On a law of combination of operators (second paper). Proc. Lond. Math. Soc. 1897, 29, 14–32. [Google Scholar] [CrossRef]
- Baker, H.F. Alternants and continuous groups. Proc. Lond. Math. Soc. 1905, 2, 24–47. [Google Scholar] [CrossRef]
- Hausdorff, F. Die symbolische Exponentialformel in der Gruppentheorie. Berichte Über Die Verhandlungen Königlich Sächsischen Ges. Wiss. Leipz. Math. Phys. Kl. 1906, 58, 19–48. [Google Scholar]
- Dynkin, E.B. Calculation of the coefficients in the Campbell–Hausdorff formula. Dokl. Akad. Nauk SSSR 1947, 57, 323–326. [Google Scholar]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum limits to dynamical evolution. Phys. Rev. A 2003, 67, 052109. [Google Scholar] [CrossRef]
- Levitin, L.B.; Toffoli, T. Fundamental limit on the rate of quantum dynamics: The unified bound is tight. Phys. Rev. Lett. 2009, 103, 160502. [Google Scholar] [CrossRef]
- Georgiev, D.D.; Gudder, S.P. Sensitivity of entanglement measures in bipartite pure quantum states. Mod. Phys. Lett. B 2022, 36, 2250101. [Google Scholar] [CrossRef]
- Georgiev, D.D.; Glazebrook, J.F. On the quantum dynamics of Davydov solitons in protein α-helices. Phys. A Stat. Mech. Its Appl. 2019, 517, 257–269. [Google Scholar] [CrossRef]
- Davidson, E.R. On derivations of the uncertainty principle. J. Chem. Phys. 1965, 42, 1461–1462. [Google Scholar] [CrossRef]
- Nityananda, R. Schrödinger’s uncertainty principle? Resonance 1999, 4, 24–26. [Google Scholar] [CrossRef]
- Luo, S.; Zhang, Z. An informational characterization of Schrödinger’s uncertainty relations. J. Stat. Phys. 2004, 114, 1557–1576. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Georgiev, D.D. Time–Energy Uncertainty Relation in Nonrelativistic Quantum Mechanics. Symmetry 2024, 16, 100. https://doi.org/10.3390/sym16010100
Georgiev DD. Time–Energy Uncertainty Relation in Nonrelativistic Quantum Mechanics. Symmetry. 2024; 16(1):100. https://doi.org/10.3390/sym16010100
Chicago/Turabian StyleGeorgiev, Danko D. 2024. "Time–Energy Uncertainty Relation in Nonrelativistic Quantum Mechanics" Symmetry 16, no. 1: 100. https://doi.org/10.3390/sym16010100





