Symmetry-Breaking-Induced Internal Mixing Enhancement of Droplet Collision

Abstract

Binary droplet collision is a basic fluid phenomenon for many spray processes in nature and industry involving lots of discrete droplets. It exists an inherent mirror symmetry between two colliding droplets. For specific cases of the collision between two identical droplets, the head-on collision and the off-center collision, respectively, show the axisymmetric and rotational symmetry characteristics, which is useful for the simplification of droplet collision modeling. However, for more general cases of the collision between two droplets involving the disparities of size ratio, surface tension, viscosity, and self-spin motions, the axisymmetric and rotational symmetry droplet deformation and inner flow tend to be broken, leading to many distinct phenomena that cannot occur for the collision between two identical droplets owing to the mirror symmetry. This review focused on interpreting the asymmetric droplet deformation and the collision-induced internal mixing that was affected by those symmetry breaking factors, such as size ratio effects, Marangoni Effects, non-Newtonian effects, and droplet self-spin motion. It helps to understand the droplet internal mixing for hypergolic propellants in the rocket engineering and microscale droplet reactors in the biological engineering, and the modeling of droplet collision in real combustion spray processes.

1. Introduction

The coalescence and fragmentation of water droplets in the cloud account for the mechanism of raindrop formation [1,2,3]. The collision dynamics of fuel droplets [4,5,6,7,8], such as bouncing, coalescence, and separation, are significant to the secondary atomization of the jet breakup [9,10,11] or two impinging jets [12,13,14,15] and subsequent spray combustion. For the above two representative spray processes, the binary droplet collision [4,5,16,17,18,19,20,21,22,23,24,25,26] occurs mostly frequently, whereas the collision between three or more droplets [27] simultaneously is a rare event owing to the fast droplet collision process with the time scale in the order of O(1) ms. There are a series of excellent review papers [28,29,30,31] on these droplet collision problems.

For the modeling of droplet collision [1,19,26,32,33,34,35,36,37,38] in real impinging jets (or spray combustion), a simple physical model should be started from a specific case of the collision between two identical droplets. An arbitrary three-dimensional (3D) collision between two droplets in the laboratory coordinate can be transferred to a binary droplet collision in their mass center coordinate [39,40,41,42,43,44], so there always exists a symmetry plane, as the x-z plane shown in Figure 1, separating the deformed droplet into two parts that being mirror symmetry. The symmetry plane is constituted by the mass center connection line and the direction of relative velocity, indicating that the movement of droplet mass centers is limited on the symmetry plane. For the head-on collision shown in Figure 1a, the droplet deformation is axisymmetric by the x-axis, mirror symmetry by the y-z plane, and also rotational symmetry by the y-axis. For the off-center collision shown in Figure 1b, only the rotational symmetry exists. The symmetric characteristics between the binary droplet collision can significantly simplify the modeling of droplet deformation and inner flow field.

However, the mirror symmetry of the collision between two identical droplets predominantly suppresses the internal mixing [45,46,47,48,49] among the merged droplet, where the internal mixing is significant to microscale droplet reactors in the biological engineering [50,51] and the hypergolic ignition of reactive propellants [48,52,53,54,55,56,57,58] in the rocket propulsion system. For example, the collision between a fuel droplet of N, N, N’, N’-tetramethylethylenediamine (TMEDA) and an oxidizer droplet of white fuming nitric acid (WFNA) [48,57,58,59], the droplet internal mixing and liquid reaction time is about 20 ms, and the ignition delay time is about 30 ms. Although the ignition process of hypergolic propellants is very short, the entire process of the collision between two reactive droplets can be phenomenologically divided into five distinct stages [58,59], namely droplet coalescence and deformation, droplet heating and low vaporization, rapid vaporization, ignition and flame propagation, and combustion and flame extinction. The previous studies [48,57,58,59] have demonstrated that droplet coalescence involving different internal mixing and heat transfer patterns is significant for the hypergolic ignition between two reactive droplets. An effective method to improving the internal mixing is breaking the mirror symmetry of the droplet collision, for example, using two droplets with different diameter sizes, surface tensions, viscosities, and self-spin motions. The symmetry breaking collision leads to many distinct phenomena that cannot occur for the collision between two identical droplets owing to the mirror symmetry.

In this mini-review, we first introduce the symmetric droplet collision outcomes (bouncing, coalescence, and separation) for the collision between two identical droplets; second, the symmetry-preserving methods are introduced to numerically study the binary droplet collision; finally, the effects of several symmetry breaking factors on droplet collision outcomes and internal mixing are summarized, which is significant for understanding the internal mixing for the hypergolic propellants and modeling the droplet collision in real combustion spray processes.

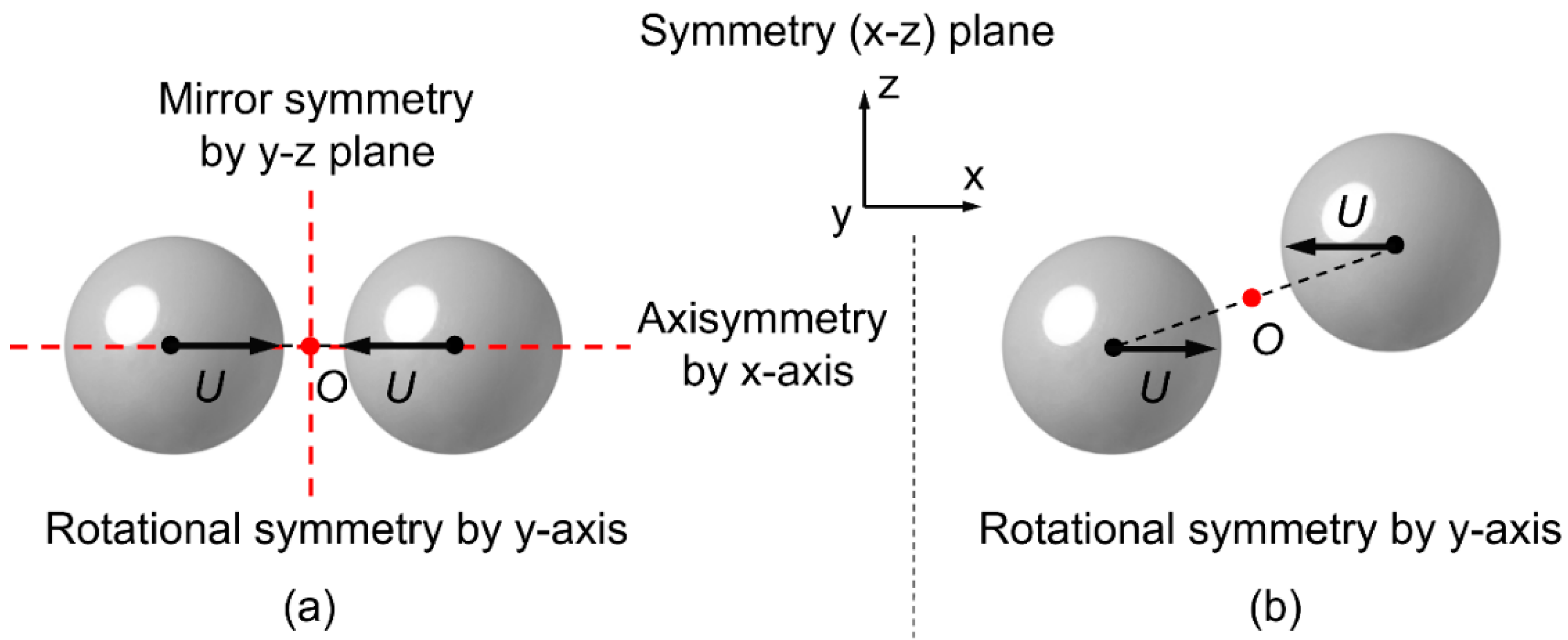
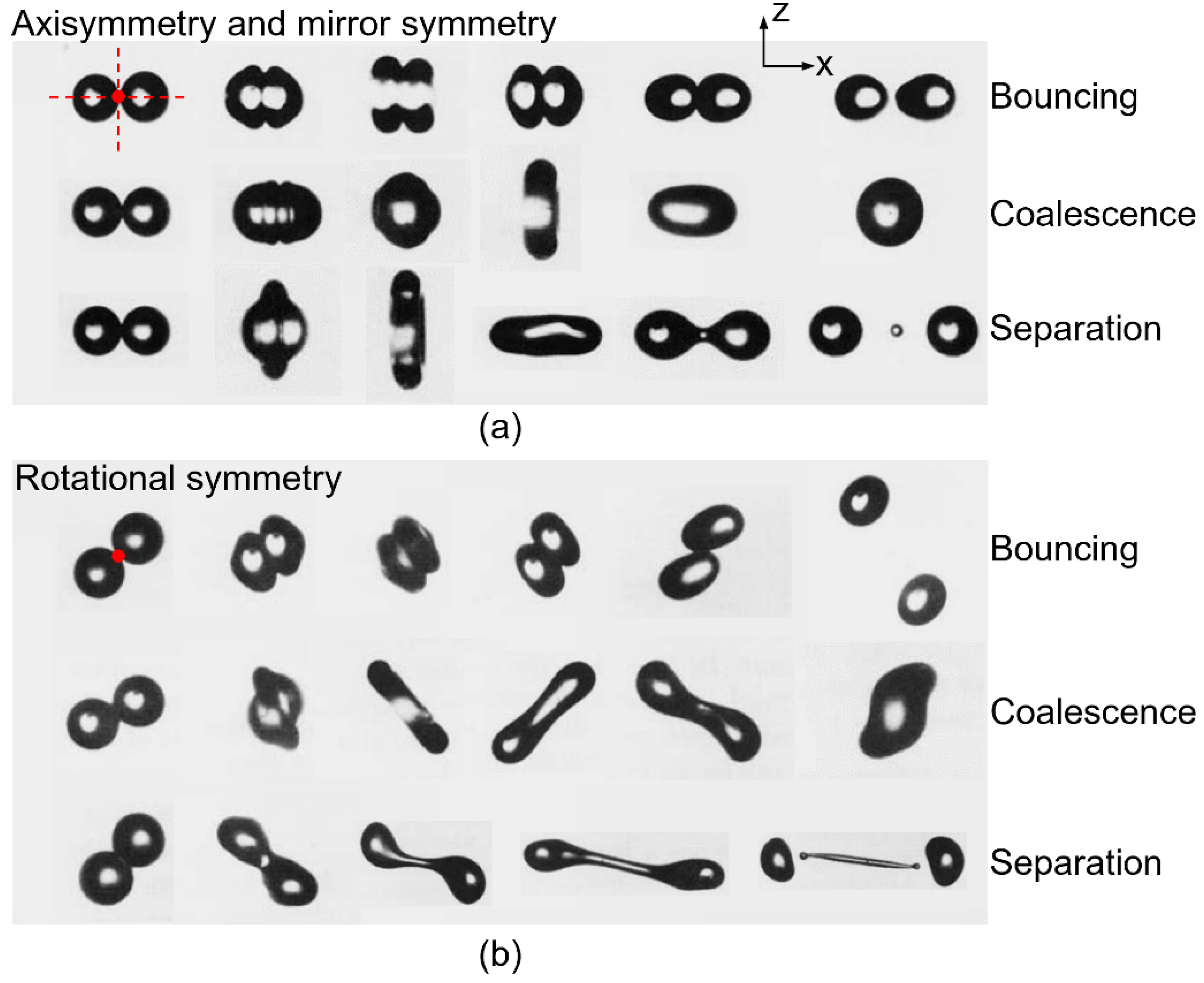
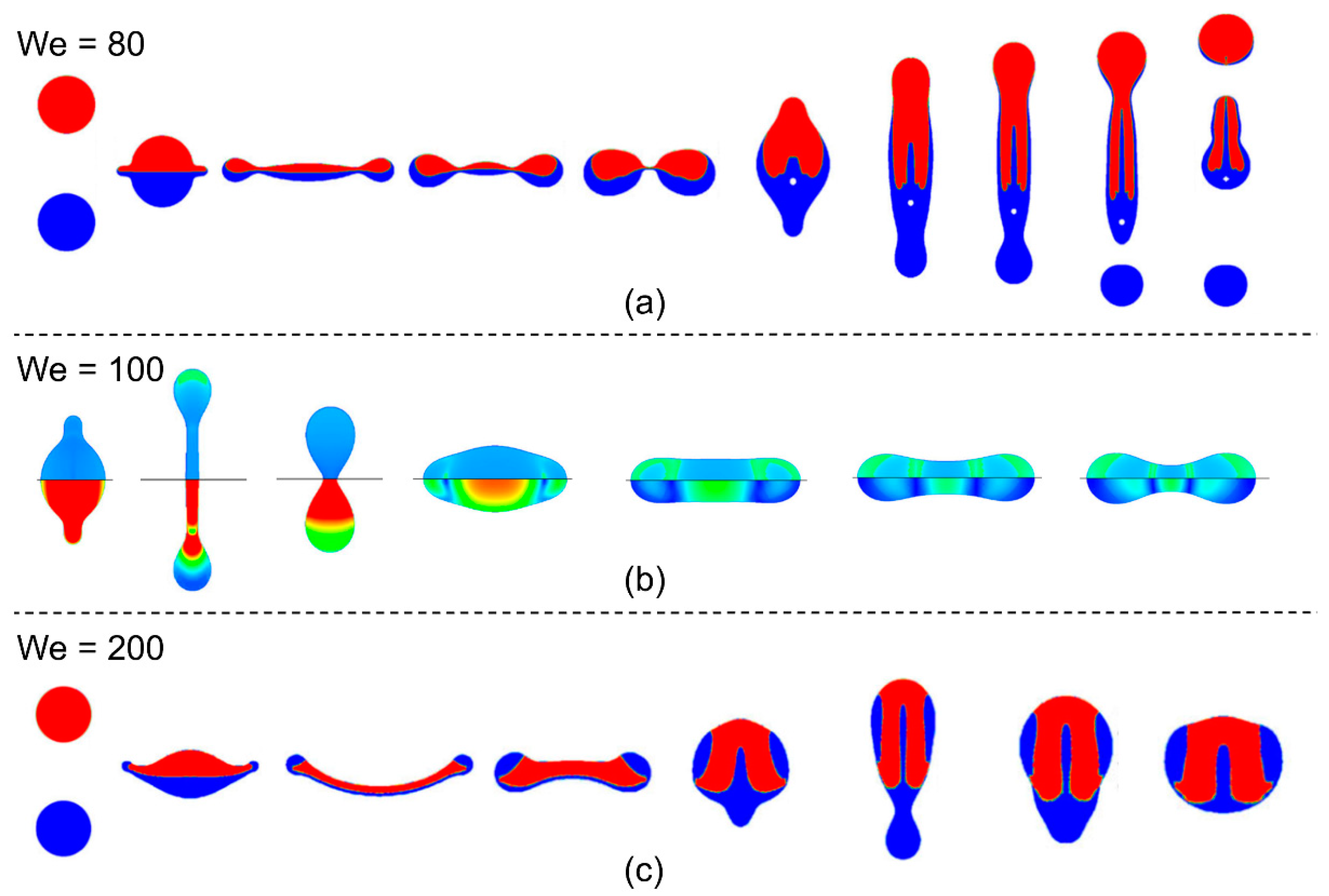
2. Symmetric Collision between Two Identical Droplets

A large number of experimental studies on the binary droplet collision have been reported in the literature [4,5,18,19,20,23,24,25,26,28,29,34,60]. In the context of raindrop formation [1,2,3,61,62], the earlier studies were focused on the collision between two identical water droplets in atmosphere air. Ashgriz and Poo [18] observed three collision outcomes: droplet permanent coalescence at small impact inertia and either reflexive separation (at small B) or stretching separation (at large B) at large impact inertia, where B is the impact parameter characterizing the deviation of the trajectory of droplets from that of the head-on collision, with B = 0 denoting head-on collision and 0 < B < 1 off-center collision. Then, Qian and Law [5] studied the droplet collision at different environment pressures (0.6~12 atm.) and observed the bouncing phenomenon of water droplets at an elevated pressure. Their results show that increasing gas pressure promotes bouncing while decreasing pressure promotes coalescence. The regime boundaries between different collision outcomes is significantly affected by the properties of the ambient gas, such as the gas pressure [4,5], gas molecular weight and viscosity [63], and gas molecular structures [4,5].

As the experimental images shown in Figure 2, it is observed that the axisymmetry and mirror symmetry for the head-on collision and the rotational symmetry for the off-center collision for all the three distinct collision outcomes. The symmetric droplet deformation and the transition between different collision outcomes [19,26,33], such as coalescence, bouncing, separation, are benefits to the modeling simplification that serves for the Lagrangian simulations of sprays [64,65], for example, the classical O’Rourke model [37] and latter improved models [16,19,32] by considering more complex but complete collision outcomes. Specifically, Rabe et al. [23] defined a symmetric Weber number (the ratio of the kinetic energy to the surface energy) to describe the droplet coalescence and separation and found that the critical symmetric Weber number is of the order of unity that being independent of the droplet size ratio, which consolidates the understanding of the droplet separation accounting for the competition between surface tension and inertial effects.

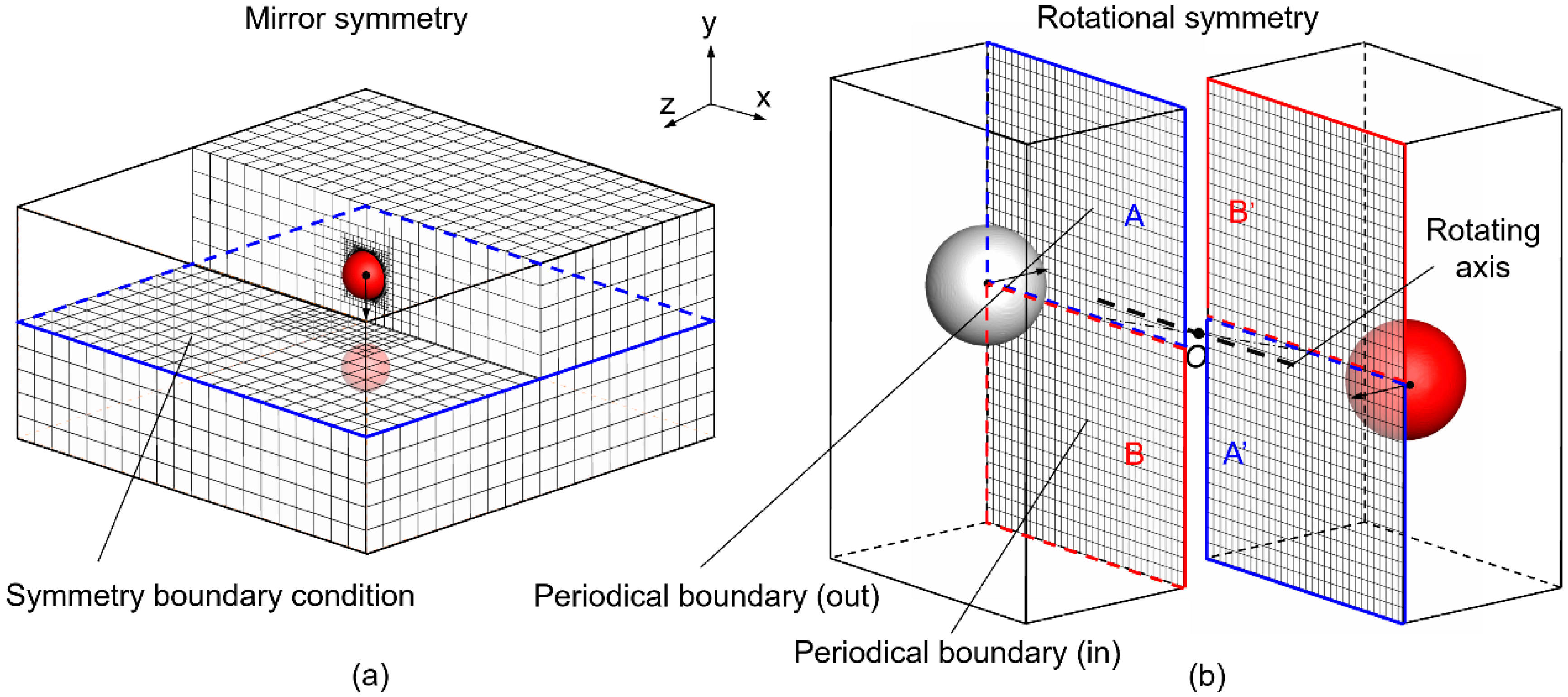
3. Symmetry-Preserving Methods for Binary Droplet Collision

Apart from the experimental observations of droplet collision outcomes, the numerical simulations on the post collision characteristics or the internal mixing [45,46,47,48,49,66,67] and internal flow are significant to the droplet collision model. For the experimental images shown in Figure 2, it is seen slight asymmetric droplet deformation although the collision between two identical droplets should be mirror symmetry or rotational symmetry. This is probably caused by the experimental errors of the slight environment gas disturbances, droplet oscillations, or droplets of unequal sizes. These experimental errors can be easily avoided by the numerical simulation. However, the asymmetric droplet deformation and droplet separation are still observed in previous numerical simulations [13,40,41,44,49,59,68], which is probably attributed to the numerical perturbations that accumulated and amplified with the development of instabilities. Thus, the symmetry-preserving method [69,70] can be applied to the binary droplet collision to ensure the symmetric droplet deformation and internal flow upon the collision between two identical droplets.

In the present problem of the binary droplet collision, the symmetry-preserving method can be achieved by simplifying the numerical settings as follows. For the head-on collision between two identical droplets of mirror symmetry shown in Figure 3a, only half of the full computational domain is required with the collision plane assigned as the symmetry boundary condition [39,47,49,71]. Similarly, for the off-center droplet collision of rotational symmetry shown in Figure 3b, half of the full computational domain is needed and the contact boundary should be divided into two parts with an inlet periodical boundary [72,73,74] and an outlet periodical boundary, respectively, which means the plane A in Figure 3b will be perfectly matched to plane B by rotating 180 degrees based on the rotating axis. The proposed symmetry-preserving method with the numerical simplification for the binary droplet collision can ensure the symmetric droplet deformation and improve the computational efficiency owing to the reduced computational domain. However, it is only valid for the collision between two identical droplets with either mirror symmetry or rotational symmetry, whereas the full computational domain is required for the collision between two different droplets.

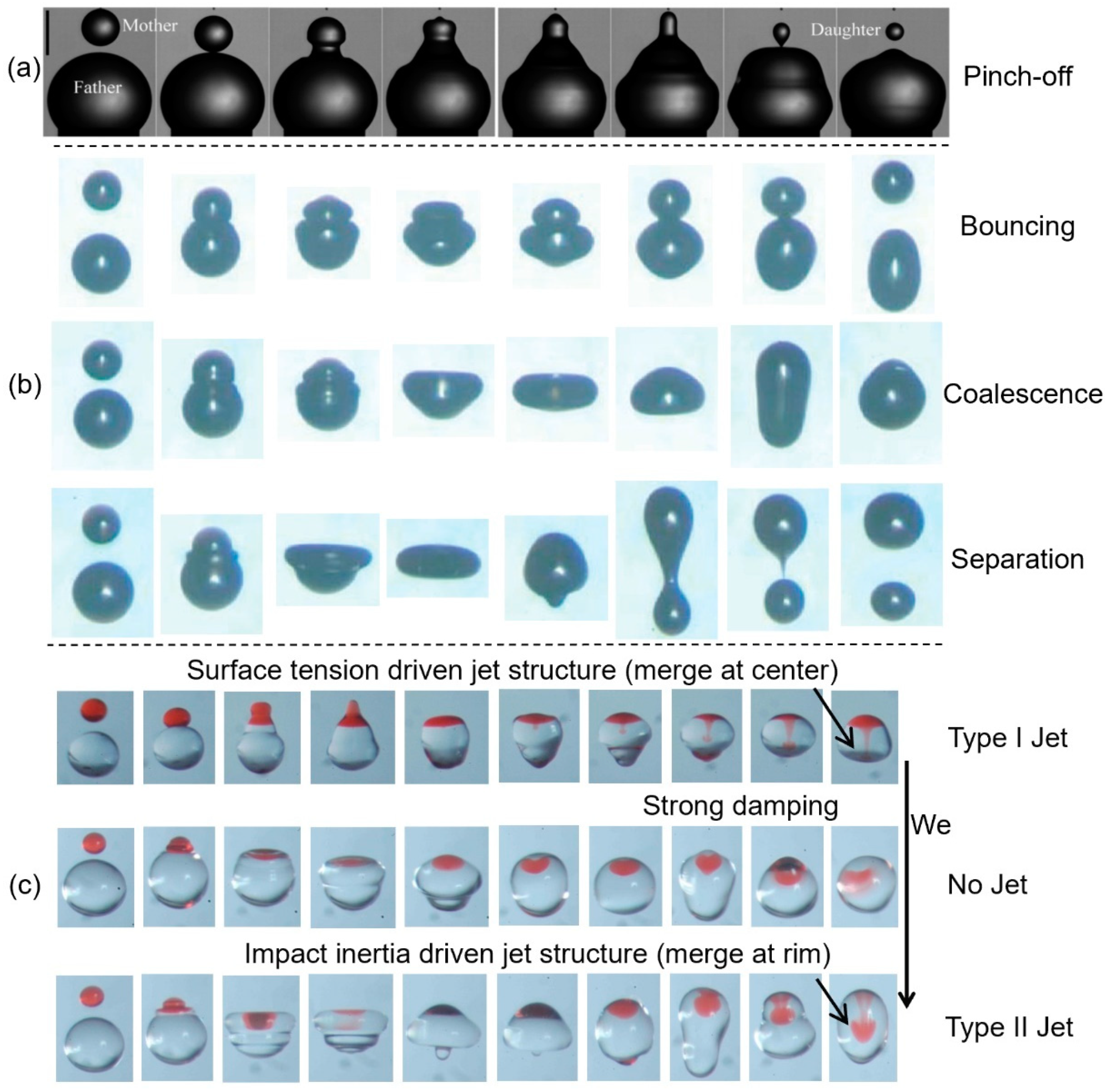
4. Symmetry Breaking between Two Droplets of Unequal Sizes

Collision between two identical droplets is a rare case, whereas the collision between two droplets of unequal sizes occurs more frequently in realistic situations. The mirror symmetry of droplet deformation is then broken showing some distinct phenomena. For example, Figure 4a shows the coalescence process between two initially stationary droplets of unequal sizes [75]. The small droplet starts to merge into the large droplet by forming a prominent capillary wave on the interface. During the droplet merging process, the wave converges at the top forming a cylindrical protrusion, and then the formed bulge would be pinched off by the interface capillary wave to generate a smaller daughter droplet. Zhang et al. [75] experimentally determined a regime boundary Δ-Oh that above the critical Δ occurs the pinch-off and otherwise the droplet coalescence, in which the Oh measures the relative importance of the liquid viscous stress compared to the capillary pressure. The critical Δ for pinch-off regime increases monotonically with Oh owing to the enhanced viscous dissipation.

Although droplet coalescence is promoted with increasing Δ [18,19,23,61,62], it still leads to droplet bouncing and separation. Tang et al. [24] studied the head-on droplet collision of different fluids (water, decane, and tetradecane with different Oh) in the We-Δ parameter space, and the droplet deformation is axisymmetric although the mirror symmetry has been broken, as the experimental images shown in Figure 4b. Their results showed that the critical We of the transition from bouncing to coalescence is slightly influenced by Δ, whereas the critical We of the transition from coalescence to separation increases significantly with increasing Δ. This can be understood by the energy budget analysis [4,5,24] that the symmetry breaking of droplets of unequal sizes tends to form an asymmetric internal flow and enhanced viscous dissipation so as to suppress the separation with increasing the size ratio.

For the complex internal flow induced by the coalescence of droplets of unequal sizes, an interesting phenomenon of internal jet-like mixing is observed. For the head-on droplet collision, Tang et al. [49] reported a non-monotonic variation of internal jet-like mixing (mushroom-like jet structure) by increasing the impact inertia (We). More specifically, as shown in Figure 4c, the mushroom-like jet structure (type I) emerges at small We, however, such a jet structure disappears as increasing We, and another mushroom-like jet structure (type II) reemerges with further increasing We while it shows different appearances. It is explained that the type I jet at small We is driven by surface tension force with droplets merging at center that close to the axis; then the jet structure disappears at large We owing to the suppressed concentration of mass momentum (strong damping) along the central line with droplets merging at a significantly flattened surface. The type II jet at higher We is driven by the impact inertia that strong droplet stretching in the direction of impact carries the spreading out mass of the small droplet into the large droplet to form a centrally hollow jet and thereby different from the type I jet.

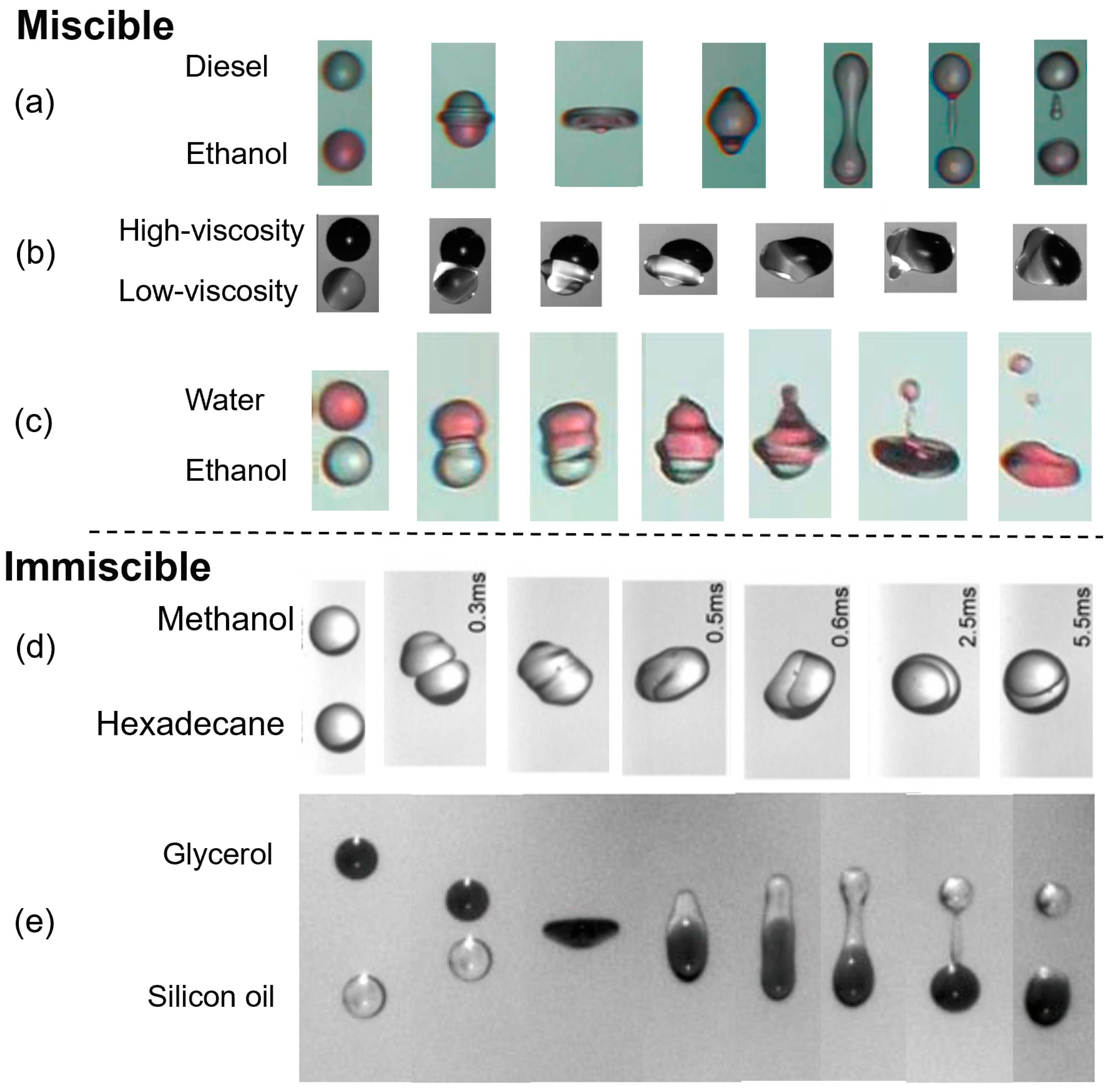
5. Collision between Two Different Droplets

The macroscopic collision outcomes [76,77,78,79,80,81,82,83] between two droplets of different fluids, such as bouncing, coalescence, and separation, are not essentially different from that of the collision between two identical droplets, and thereby showing the similar regime nomogram in We-B parameter space [76,77,78] although the regime boundaries vary with the liquid properties and collision parameters. Generally, the collisions between droplets of different fluids can be divided into two main types, namely the miscible droplet collision and immiscible droplet collision.

Figure 5a–c shows the collision between two different miscible droplets of equal size. Chen [76] compared the collision between diesel–diesel droplets and diesel–ethanol droplets, as shown in Figure 5a, and found nearly the same droplet deformation and reflexive separation. This is because diesel and ethanol droplets have similar surface tension and density although the viscosity of diesel is approximately twice to that of ethanol. Focke et al. [83] studied the collision between two miscible droplets with the same surface tension and density but a sufficiently large viscosity disparity (2.6 mPas vs. 60 mPas), as shown in Figure 5b, and found that viscosity difference can delay the droplet initial coalescence, and the droplet with low viscosity moves faster and slightly overlays the interface of the droplet with high viscosity. However, it is observed substantially asymmetric deformation during the collision between water and ethanol droplets [78], as shown in Figure 5c, with ejecting satellite droplets. This is attributed to the Marangoni flow induced by the surface tension difference ($7.29\times {10}^{-2} \mathrm{N}/\mathrm{m}$ for water and $2.23\times {10}^{-2} \mathrm{N}/\mathrm{m}$ for ethanol). The Marangoni stress drives the mass of ethanol droplet (small surface tension) diffusing along the interface of water droplet (large surface tension) and thereby the induced ring-like Marangoni flow along the interface converges to one point on the symmetry axis to eject satellite droplets. The mechanism of Marangoni-flow-induced partial coalescence [84,85,86,87] was explained by some numerical studies.

Figure 5d,e shows experimental images of the collision between two immiscible droplets, there always exist a free interface between different phases and a moving three-phase contact line. A clear separating interface [88] can be observed between different droplets in Figure 5d owing to the immiscibility, and it is seen an entrapped bubble as illustrated by the small black dot. As shown in Figure 5e, the symmetry of droplet coalescence process has been broken with the silicon oil droplet (small surface tension) overlaying [79] along the interface of glycerol droplet (large surface tension) and showing the “crossing separation” [79]. For the termed “overlaying coalescence”, the droplet encapsulating phenomenon is similar to a “Janus droplet” [89] when the droplet with small surface tension overlays partially on the droplet with large surface tension. The detailed mechanism occurring such rich phenomena for the collision between two immiscible droplets has not been sufficiently understood, which is probably correlated to the time scale of overlaying process and droplet deformation process.

6. Internal Mixing Enhancement by Non-Newtonian Effects

Generally, majority of the fluids in the engineering applications somehow reflect the non-Newtonian flow characteristics that the apparent viscosity is a function of the local shear rate. The most common shear-thinning (shear-thickening) liquids are that whose viscosity decreases (increases) with increasing local shear rate. The experimental studies of the collision between two non-Newtonian droplets are scarce in the literature [29], which is probably attributed to the practical difficulties in generating spatially and temporally stable non-Newtonian droplet usually with very large viscosity.

To analyze the microscopic internal flow of the binary collision between non-Newtonian droplets, several numerical studies [60,67,90,91,92] have been conducted recently. Specifically, Sun et al. [67] numerically studied the binary collision between different non-Newtonian droplets of equal size with non-vanishing We. Figure 6a shows the collision between two droplets with different shear-thinning effects, which indicates that the disparity of shear-thinning effects can enhance the droplet deformation at small We so that easily to separate the merged droplets into several small droplets. In addition, the separated droplets are still mixed with masses from two initial droplets, even though the separation was not desired for the internal mass interminglement. Figure 6b shows the collision between two identical shear-thickening droplets. The droplet deformation was significantly suppressed, owing to the increased viscosity so that the droplet separation cannot occur even at a large We. Figure 6c shows the collision between one shear-thinning droplet and one shear-thickening droplet. It is seen that the “internal mixing” can be promoted by shear-thinning effects and droplet separation can be suppressed by shear-thickening effects so that to allow sufficient mixing, which is a promising concept for the fluid-phase fuel-oxidizer hypergolic ignition system in the rocket engine.

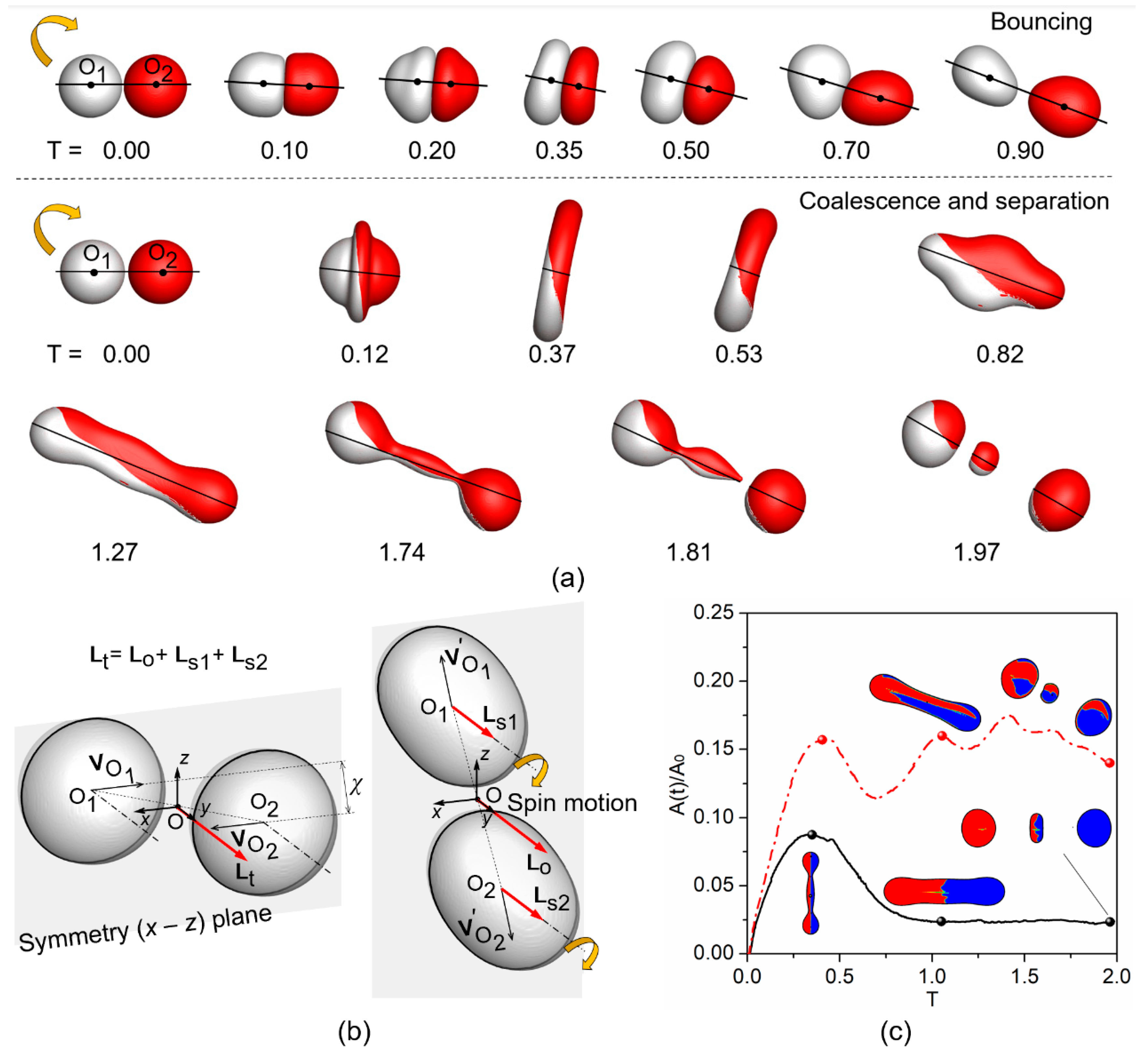
7. Spin Effects on Droplet Collision and Internal Mixing

In the literatures, almost all studies on droplet collision were focused on initially non-spinning droplets. In practical situations of dense sprays, the dispersed droplets usually have spinning motions and are highly likely to collide with each other. The spinning motion can be created either from the preceding off-center collisions (owing to the nonzero total angular momentum) or the non-axisymmetric breakup of impinging jets. Bradley and Stow [17] showed the experimental images of droplet spin after coalescence and measured the angle of rotation as a function of time and impact parameter. However, the droplet spinning motion before the collision was neglected in the previous experimental studies, probably because it is technically challenging to generate stable spinning droplet and quantitatively characterize the spin velocity.

He and Zhang [43,44,68] numerically simulated relevant canonical phenomena, such as coalescence, bouncing, and separation between spinning droplets, as shown in Figure 7a. The head-on collision between two spinning droplets shows the off-center effects with asymmetric droplet deformation because of the conversion of the spin angular momentum into the orbital angular momentum. Figure 7b shows the general schematic of an off-center droplet collision. There always exists a symmetry (x–z) plane. The angular momentum ${\mathbf{L}}_{\mathrm{o}}$ is the orbital angular momentum with respect to the y-axis, ${\mathbf{L}}_{\mathrm{s}}$ for each liquid droplet is the spin angular momentum with respect to the spinning axis across its mass center, and ${\mathbf{L}}_{\mathrm{t}}$ is the total angular momentum of the droplet collision system. The interchange between orbital and spin angular momentums during the collision process is of significance because it can influence the post-collision velocities of bouncing droplets. For the head-on coalescence between a spinning droplet and a non-spinning droplet of equal size [68], as shown in Figure 7c, the spinning motion can promote the mass interminglement of droplets because the locally nonuniform mass exchange occurs at the early collision stage by non-axisymmetric flow and is further stretched along the filament at later collision stages.

8. Conclusions

Binary droplet collision is the most fundamental study to understand the complicated and practical spray processes. The mirror symmetry and rotational symmetry of the collision between two identical droplets is useful to simplify the droplet collision modeling in the Lagrangian simulation of sprays. The asymmetric droplet deformation upon the collision between two droplets with different size ratios, surface tensions, viscosities, and self-spin motions leads to many distinct phenomena, such as the internal mixing, Marangoni flow, non-Newtonian flow, and spinning droplet separation, which are significant to the hypergolic propellants in rocket engineering and the microscale droplet reactor in biological engineering.

The representative phenomena of size ratio effects, Marangoni Effects, non-Newtonian effects, and droplet self-spin motion are certainly distinctive because they are independently attributed to different controlling parameters which are equally significant to the droplet collision. To summarize the collective effects of different phenomena, the symmetry-breaking-induced internal mixing by different parameters is thereby discussed in the present paper. The Marangoni Effects, non-Newtonian effects, and droplet self-spin motion are, respectively, correlated to the surface tension force, viscous force, and inertia force, with all these forces play synergistic and competitive effects to influence the droplet collision and internal mixing. Comparing different effects, the Marangoni Effects owing to the gradient of surface tension along the free interface tend to enhance the internal mixing most substantially at small impact inertia, whereas the non-Newtonian effects become increasingly critical at large impact inertia because the viscosity of shear thinning fluid decreases substantially with increasing the inertia stress. In other words, the symmetry-breaking by the Marangoni flow occurs mainly from the droplet surface into the inner droplet, whereas the non-Newtonian effects break the symmetry from the inner droplet to the surface. Both symmetry-breaking flows are significant to the ignition of hypergolic droplets because the internal mixing and inner liquid phase reaction heat the droplets to the boiling temperature and interface reaction promotes the droplet vaporization for the gaseous ignition and combustion.

The binary droplet collision model varying with different parameters for the Euler-Lagrangian simulation is another division of the droplet collision study, which can also show the collective effects of the different phenomena but is beyond the scope of the present review. Droplet collision in gaseous environment is a multi-scale problem. The droplet diameter is sub-millimeter scale, and the gas film thickness can be as small as 10 nanometers. Apart from the macroscopic droplet collision outcomes, such as coalescence, bouncing, and separation, the microscopic dynamics upon the droplet collision is also of interests, for example, the rarefied flow effect and van der Waals force among the gas film, the entrapped small bubbles by the interface merging, that merits comprehensive studies. The collision between water-in-diesel emulsion droplets is a representative example that involves both the macroscopic collision of diesel droplets in continuous phase and the microscopic collision (interaction) of water droplets in disperse phase. The additive of surfactant into liquid droplet generating Marangoni flows has been adopted extensively in the real industrial applications. The emulsified fuel with water is benefit for the pre-vaporization (micro-explosion) that results in severe disruptive burning arising from dilution effects in both the gas- and liquid-phase reactions and those from the secondary atomization effects of the primary emulsified fuel spray.

The experimental method is a most direct way to study binary droplet collision. However, the experimental technics are still challenging for the microscopic flow field visualization and analysis and merits further developments. In addition, the highly efficient numerical methods are always desired on the prediction of droplet coalescence and bouncing from the first principle, which is of great significance to understand the fundamental physics of binary droplet collision.