Effect of Calcium and Fullerene Symmetry Spatial Minimization on Angiogenesis

Abstract

The topological partition theory states that icosahedral group affine extensions (fullerenes symmetry) are the most effective way to energetically optimize the surface covering. In recent decades, potential applications of fullerene symmetry have emerged in the major fields of biology, like enzyme inhibition and antiviral therapy. This research suggests a novel perspective to interpret the underlying spatial organization of cell populations in tissues from the polyhedral graph theory. We adopted this theoretical framework to study HUVEC cell in vitro angiogenesis assays on Matrigel. This work underscores the importance of extracellular ${\mathrm{C}\mathrm{a}}^{2+}$ gradients, both from conditioned BJ and pretreated HUVEC cells, in angiogenesis fullerene-rule spatial minimization.

1. Introduction

Neovascularization is the process of forming new microvascular networks. In vivo, this process primarily occurs through angiogenesis. The distribution of blood vessels in angiogenesis is heterogeneous but not at all random; at the microscopic level, it exhibits a fractal structure with branching tubes becoming smaller and smaller from a tube of centimeters in diameter to the limit of the size of a red blood cell. The basic structure is similar in different scales, including cm, mm, or micrometers, and it is repeated in a simple and organized way [1]. The investigation of angiogenic geometric patterns remains an unresolved and open question. Although studying this process from a biochemical perspective is a question of great importance, here we focus on the architectonic and geometric principles underlying the network formation.

There is a wide range of normal processes in which angiogenesis is involved. Angiogenic processes occur from the first moments of an embryo’s life. The formation of the placenta requires active vascular proliferation, and during embryonic development, the continuous growth of the vascular bed implies not only the elongation of the blood vessels but also a complex process of remodeling [2,3].

Vascular proliferation is a necessary process for normal tissue growth. In adults, however, angiogenesis occurs infrequently and is seen almost exclusively during wound and fracture repair (the female reproductive system is an exceptional case). These periods of normal angiogenic activity are relatively brief and highly regulated [4]. On the contrary, angiogenesis in pathological conditions (tumors, chronic inflammatory responses, keloid formation, ocular neovascularization, and psoriasis) evades control mechanisms and leads to the formation of an abnormal vascular network, which frequently aggravates the evolution of the clinical picture [5]. Vascularization in a tumor not only facilitates its development but also accelerates the spread of cells to distant areas (metastasis). The formation of an angiogenic network involves endothelial cell directional migration as one of the initial events [6].

Epithelial cells have the remarkable ability to adopt a variety of shapes, modifying their curvature to adopt a shape that maximizes their packing stability [7]. Identifying the signals responsible for cell migration, especially those that depend on mechanical forces and on principles of space minimization, is important not only to understand the formation of embryos and organs but also to identify the necessary targets to fight against uncontrolled cell migration processes [8].

Although, at first, it was thought that angiogenesis only involved the action of soluble factors released from endothelial cells, subsequent work demonstrated that tumor angiogenesis is also mediated by soluble factors released from neoplastic cells [9]. Soluble factors released from fibroblasts have been shown to have angiogenic activity. When endothelial cells are incubated with conditioned media from fibroblasts, tumor cells, or immune system cells, their migration capacity is increased [10,11].

Different studies have explored how the extracellular matrix (ECM) influences the kinetics of cellular spreading and the spatiotemporal evolution of the angiogenesis network [12]. Although the basement membrane of endothelial cells has a complex composition with variations in different organs, which explains the diversity of immunological reactions, their main components are collagen glycoproteins (collagen type IV and V), non-collagen glycoproteins (laminin and fibronectin) and proteoglycans (heparan sulfate) [13,14]. Endothelial cell migration is probably not due to a chemotactic response but rather a haptotactic response to laminin levels [15,16,17].

Today, it is known that multiple factors are involved in the neovascularization process, which acts at different levels and triggers proliferation, migration, differentiation, and the autocrine regulation of blood vessels. Whatever the triggering stimulus for the angiogenic process, stromal cells and ECM actively participate in the development of the vascular response [18].

Calcium is a highly versatile, non-metabolizable secondary messenger within the cell that plays a role in numerous signaling pathways, and it holds significant importance in controlling numerous cellular and physiological processes in both excitable and non-excitable cells, with a highly variable time scale [19,20]. The intracellular calcium concentration is attributed to both the transport from the extracellular environment and from internal calcium stores, primarily the endoplasmic reticulum [21].

In recent years, it has become evident that the mitochondria play a crucial function, both in the regulation of ${\mathrm{C}\mathrm{a}}^{2+}$ signals in general and in the control of capacitive calcium entry and the release of intracellular calcium stores in particular [22]. Mitochondrial calcium plays a dual role in both cell survival and cell death due to the fact that an excessive accumulation of ${\mathrm{C}\mathrm{a}}^{2+}$ in the mitochondria induces the enhanced generation of reactive oxygen species (ROS), the release of cytochrome C, and the alteration of the activity of the mitochondrial permeability transition pore [23], which can lead to apoptosis and necrosis [24].

The ${\mathrm{C}\mathrm{a}}^{2+}$ concentration appears at the epicenter of proliferation, death, and morphological cell regulatory processes [25,26]. Intracellular ${\mathrm{C}\mathrm{a}}^{2+}$ levels also play an important role in embryogenesis, tissue regeneration, and numerous pathological states. Cancer, psoriasis, and rheumatoid arthritis have been associated with elevated serum ${\mathrm{C}\mathrm{a}}^{2+}$ levels [27,28]. The altered expression of certain types of calcium channels and pumps could be a notable characteristic of some types of cancer. One well-known case is that of TRPM8, whose function is associated with tumor proliferation, migration, and invasiveness [29].

These network patterns are related to proper cell spatial organization; that is, endothelial cells need to acquire positional information. Morphogens act as positional signals that control cell location in the network, activating different spatial interrelated responses. Angiogenesis considered a geometric structure question, may be related to the so-called Kelvin or isoperimetric problem. Currently, it not only refers to the classic question of finding the set with the smallest perimeter on a surface among all those that enclose a predetermined amount of area but also encompasses various problems, always with the idea of minimizing a perimeter function under certain restrictions on the area. In this way, multiple isoperimetric problems can be presented, in which several values for the area configuration of curves with the shortest possible length are considered. Another isoperimetric problem related to the previous one is the problem of isoperimetric partitions. In this case, the problem consists of dividing a surface into regions of a predetermined area using the shortest possible length [30].

The isoperimetric regions constitute the global minima of the perimeter function. To find these regions, it is convenient to introduce the weaker concept of stable regions or minimal surfaces, which correspond to the relative minima (the second order) of the perimeter for variations preserving the enclosed area. In this way, we consider that the stable regions are local solutions to the isoperimetric problem. This concept of minimal surfaces involves resistance properties and the construction of an economy linked to their geometric structures. Classical solutions to minimization problems in the Calculus of Variations have received great interest in recent years due to their multiple applications in various physical and biological phenomena, such as the shape that a cellular tissue adopts and the behavior of a membrane separating two fluids [31].

Systems have a natural tendency to minimize their interface areas because the intermolecular forces on the phase boundary act inwardly on average [32]. In other words, surface molecules have a higher energy since they experience less attraction, so the system tends to minimize their surface to obey the principle of minimum energy [33].

From the geometry of polyhedra and polyhedral structures, the endothelial cells are structural units, and the polygons are the smallest functional equivalent construction units of the network [34]. These cells are not distributed randomly but adhere to form polygons since they maximize the molecular interactions that stabilize the network [35].

In some cancer cell types, vascularization grows very rapidly while economizing on the available resources of the involved cell metabolic machinery. Bauer et al. analyzed the migration speeds in angiogenesis and showed that the mean rate of expansion for recently generated vascular sprouts on Matrigel was 14 μm/hour and ranged from 5 to 27 μm/hour [36]. These newly formed blood vessels support tumor progression, so determining the minimal spatial partitioning of vascular endothelial cells is essential to determine the areas of greater accessibility for the supply of nutrients and oxygen to the tumor [37,38].

In the mathematical field of graph theory, the fullerene is a polyhedral graph with 12 pentagons and a variable number of hexagons satisfying the following relationships: $p=12$; $n=2·(h+10)$ and $h=\frac{n}{2}-10$, where $p$ is the number of pentagons, $h$ is the number of hexagons and $n$ is the number of polyhedron vertices. Fullerenes have special characteristics related to the minimization of resources when applied in architectural design. The stability of fullerenes is mainly related to the pentagon and hexagon configuration in the global structure. The best-known fullerene is the truncated icosahedron, formed by 12 pentagons and 20 hexagons [39].

In the chemistry field, fullerenes are pure carbon molecules and, together with graphite and diamond, constitute the three allotropic forms of carbon; in the laboratory, the most abundant fullerene molecule is $C_{60}$ (which geometrically corresponds to the truncated icosahedron polyhedron graph) [40]. Their study represented a great advance in the field of chemistry and later in other fields such as nanotechnology, biology, and medicine. Prior to the discovery of fullerenes, Jones suggested in 1966 the possibility of forming large hollow carbon cage structures [41]. Shortly after, Osawa proposed the $C_{60}$ molecule in 1970 [42]. Fullerenes were discovered, finally, in 1985 by Kroto et al. during experiments to reproduce the chemistry of red giant star atmospheres [43]. From now on, we use the nomenclature $F_n$ (where $n$ is the number of vertices) when referring to geometric fullerenes and $C_n$ when referring to the allotropic forms of carbon (Figure 1).

Although the existence and regularity of results in the graph theory can considerably reduce the set of curve configurations to be examined in an isoperimetric problem, this set is still very large. This is the main difficulty when dealing with this kind of problem. The regions determined by the configurations do not need, in principle, to be convex, so each one could be made up of several components. Furthermore, the complementary region to the global region determined by any configuration, including the exterior region, could also be non-convex, presenting some bounded component. These two statements make the set of possible configurations too large to consider. Intuitively, it is to be expected that any minimizing configuration includes only convex regions, but, unfortunately, the argument that allows us to affirm this in general has not been found so far [44].

The local solution to an isoperimetric problem is based on the classification of the surface regions that determine the isoperimetric regions. Thus, the spatial minimization angiogenesis question becomes an isoperimetric partition problem in the sphere surface, which is the area where the angiogenic networks extend in an in vitro culture of HUVEC cells on Matrigel. Below, we present several results that provide us with the stability criteria for certain sets with a constant geodesic curvature.

Cox et al. [45] solved the Kelvin problem for the sphere surface particular case in 2003. Their main achievement was to obtain a limit on the number of convex components for minimizing configurations, which allowed them to classify all the possible solutions. From the Geometric Component Analysis (GCA) methodology, considering the number of sides and their arrangement in the configuration and using some variational arguments, they managed to rule out all possibilities except fullerenes, thus concluding that this was the solution to the general problem. In other words, Cox et al. presented fullerenes as the best polyhedral approximation of the sphere surface.

How is cell spatial partitioning resolved? Mathematically, the discrete spatial units of the polyhedral structure are the polygons. Starting from these geometric units, the network’s final polyhedral structure can be obtained [46,47]. In the case where stability is achieved with a large number of structure units, the use of the graph theory can better model the polyhedral structure and clarify the involved chemical and physical variables [48]. Our main objective is to geometrically characterize the tumor differentiation dynamics in angiogenic networks under the hypothesis that the morphological landscape of endothelial cell networks reveals fullerene symmetry in space partitioning. In addition, we study the role of ${\mathrm{C}\mathrm{a}}^{2+}$ ions in morphogenetic mechanisms that increase this innate space minimization (Figure 2).

2. Experimental Section

2.1. Synthesis of ${Ca}^{2+}$ Nanoparticles (ACP-NP)

A 0.5 M (NH₄)₂HPO₄ (Panreac, Barcelona, Spain, purity ≥ 99.0%) solution in milli-Q water was adjusted to pH 11 using a 30%-w/v ammonia solution (Sigma-Aldrich, St. Louis, MO, USA) and prepared (solution 1). Next, a 0.5 M Ca(NO₃)₂ (Panreac, Barcelona, Spain, purity ≥ 99.0%) solution in ethanol (Scharlab, Barcelona, Spain, purity ≥ 99.5%) was prepared (solution 2). Then, 15 mL of solution 1 was added to 25 mL of solution 2 (rate of 2 mL/min or less) to reach a Ca/P ratio of 1.67. The sample was allowed to react for 1 h 30 min while maintaining constant stirring and temperature (25 °C). The crystals were aged in the reaction medium at 37 °C for 24 h, separated by centrifugation and washed twice, the first time with milli-Q water and the second with a 60/40 (v/v) mixture of ethanol/water, and placed in the freeze dryer. Finally, the crystalline mass was sonicated for complete deglomeration and filtered (0.2 μm), obtaining the working NPs.

2.2. Nanoparticle Characterization

X-ray diffraction. The wide-angle X-ray diffraction (WAXD) measurements of the powdered samples were conducted using a Bruker D8 Advance dual-circle diffractometer with ${\mathrm{C}\mathrm{u}\mathrm{K}}_{\mathsf{\alpha }}$ radiation. The diffraction patterns were recorded at room temperature in the angle range with a 2° (2$\theta$) −80° (2$\theta$) and 0.02° degree step and a recording time ranging from 2 to 8 s for each step. The model was equipped with a primary monochromator for the ${\mathrm{C}\mathrm{u}\mathrm{K}}_{\mathsf{\alpha }}$ wavelength and an ultra-fast X’Celerator detector. The PeakFit v4 program was used for the design and modeling of diffraction profiles.

The diffracted intensity is a result of the size and orientation of the crystals, the degree of crystallinity in the sample, the intensity of the X-ray beam from the source, the slit width for the scattered rays, and the allowed axial divergence. The average size of the crystallite grains present in the sample ($L$) was determined using the Scherrer equation [49]:

$$L=\frac{k\lambda }{w\mathrm{c}\mathrm{o}\mathrm{s}\mathsf{\theta }}$$

(1)

where $k$ is the shape factor of the crystal, with a value of 0.94, $\lambda$ is the wavelength of the used radiation ($\lambda$ $=$ 0.1542 nm), $\mathsf{\theta }$ is the angular position of the peak of maximum diffraction intensity, and $w$ is the full width at the half maximum of the diffraction peak (expressed in radians).

The crystallinity of the sample (${\chi }_c$) was calculated using the following equation [50]:

$${\chi }_c=1-\frac{{\mathrm{I}}_1}{{\mathrm{I}}_2}$$

(2)

where ${\mathrm{I}}_1$ is the intensity of the minimum peak and ${\mathrm{I}}_2$ is the maximum intensity of the crystalline peak, respectively.

Characterizing the morphology of nanoparticles. Scanning electron microscopy (SEM) allows the characterization of organic and inorganic materials through a topographical or compositional contrast. The samples were analyzed using a Focused Ion Beam Zeiss Neon40 microscope operating at 5 kV. The sample preparation for this method involves placing drops of the liquid sample on silicon disks, followed by drying in an oven. Subsequently, the samples were coated with a carbon film to prevent electric charging problems. Additionally, X-ray fluorescence analysis was performed to check if there was a deposition of precipitated calcium salts.

Zeta potential. Zeta potential measurements were performed on a Malvern Zetasizer Nano-ZS (Malvern Instruments Ltd., Worcestershire, UK). Samples were re-suspended in ultrapure milli-Q water (Millipore, Burlington, VT, USA) at 0.5 mg/mL and conducted in a capillary cell (DTS0012). The suspension of particles were small enough to remain suspended, resulting in a charge on the surface of these particles that was counteracted by an electrical potential in the solution itself. Dynamic light scattering (DLS) is based on determining the distribution of the velocities of particles dispersed in a medium undergoing Brownian motion. This technique allows particle suspensions to work in the range of one nanometer to one micron.

2.3. Stimulation of BJ Cells with ${Ca}^{2+}$ Nanoparticles (ACP-NPs)

BJ cells (fibroblast cells from the normal foreskin of a human neonatal male) were purchased from ATCC (CRL-2522, Manassas, VA, USA). Minimum Essential Medium with Earle’s salts (MEM), Ca²⁺ free MEM, FBS, pen/strep, and the L-glutamine solution purchased from Gibco (Waltham, MA, USA). The characteristics of the media used in the tested cultures are listed in

Table 1. Characteristics of formulated BJ culture media.

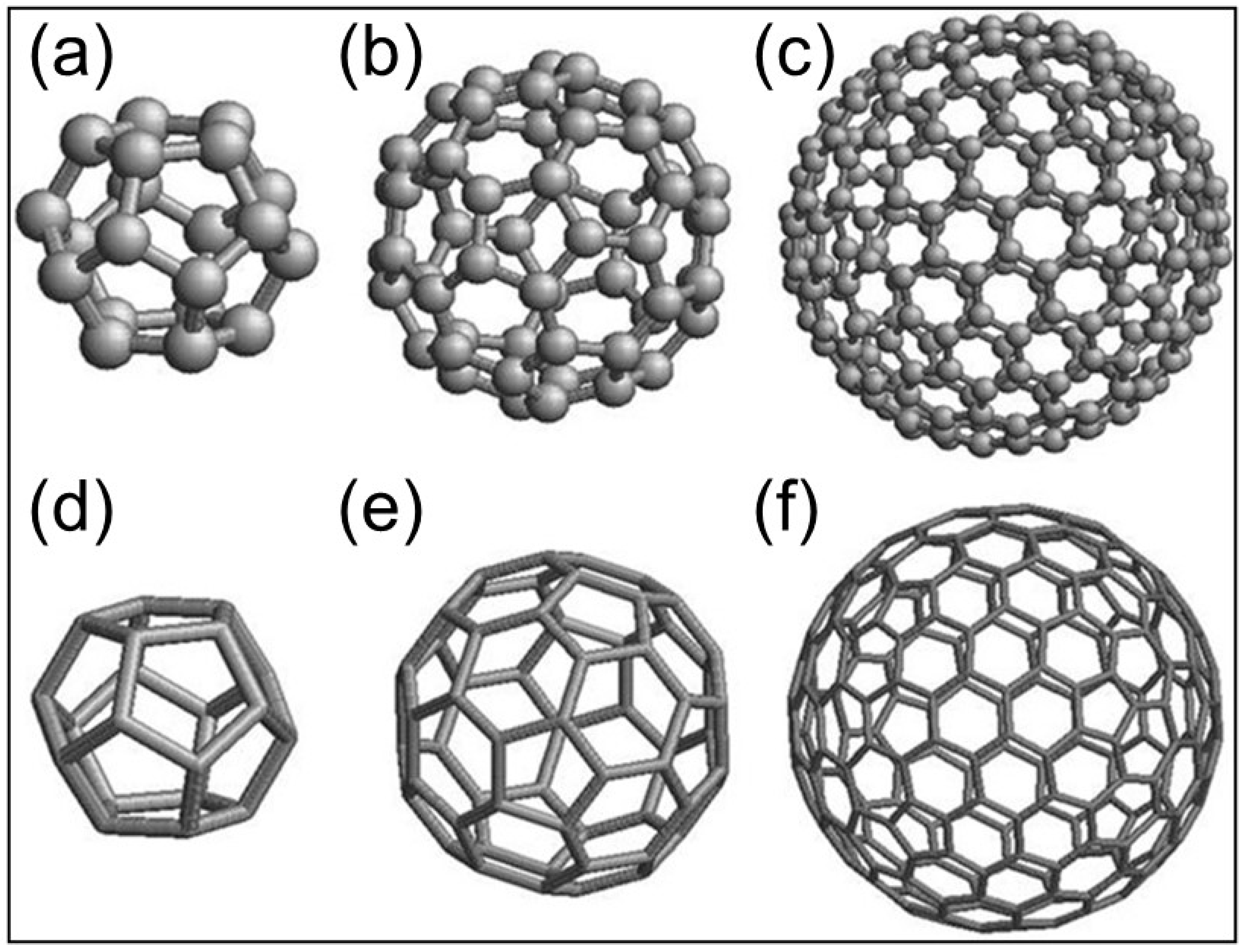
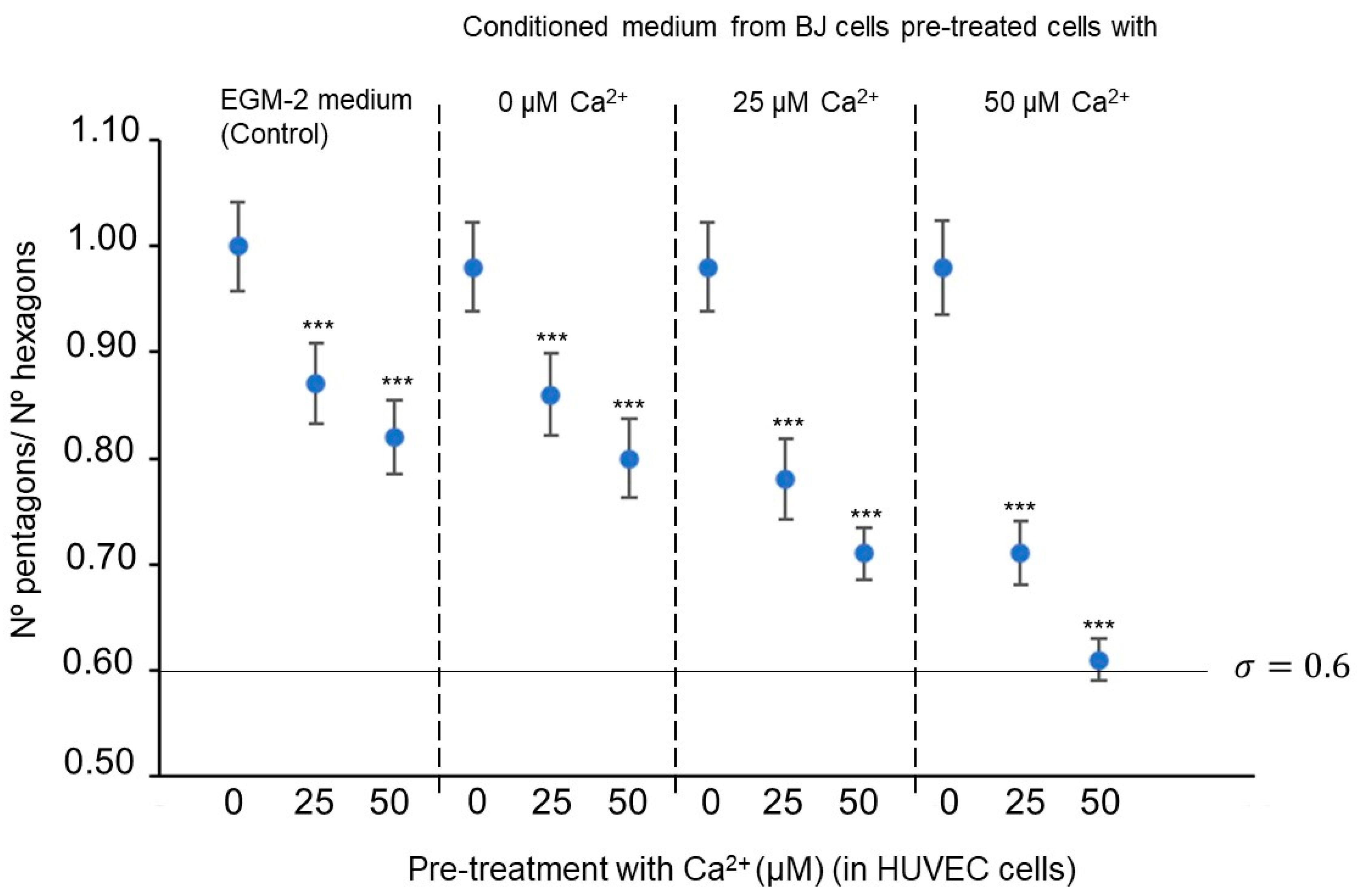
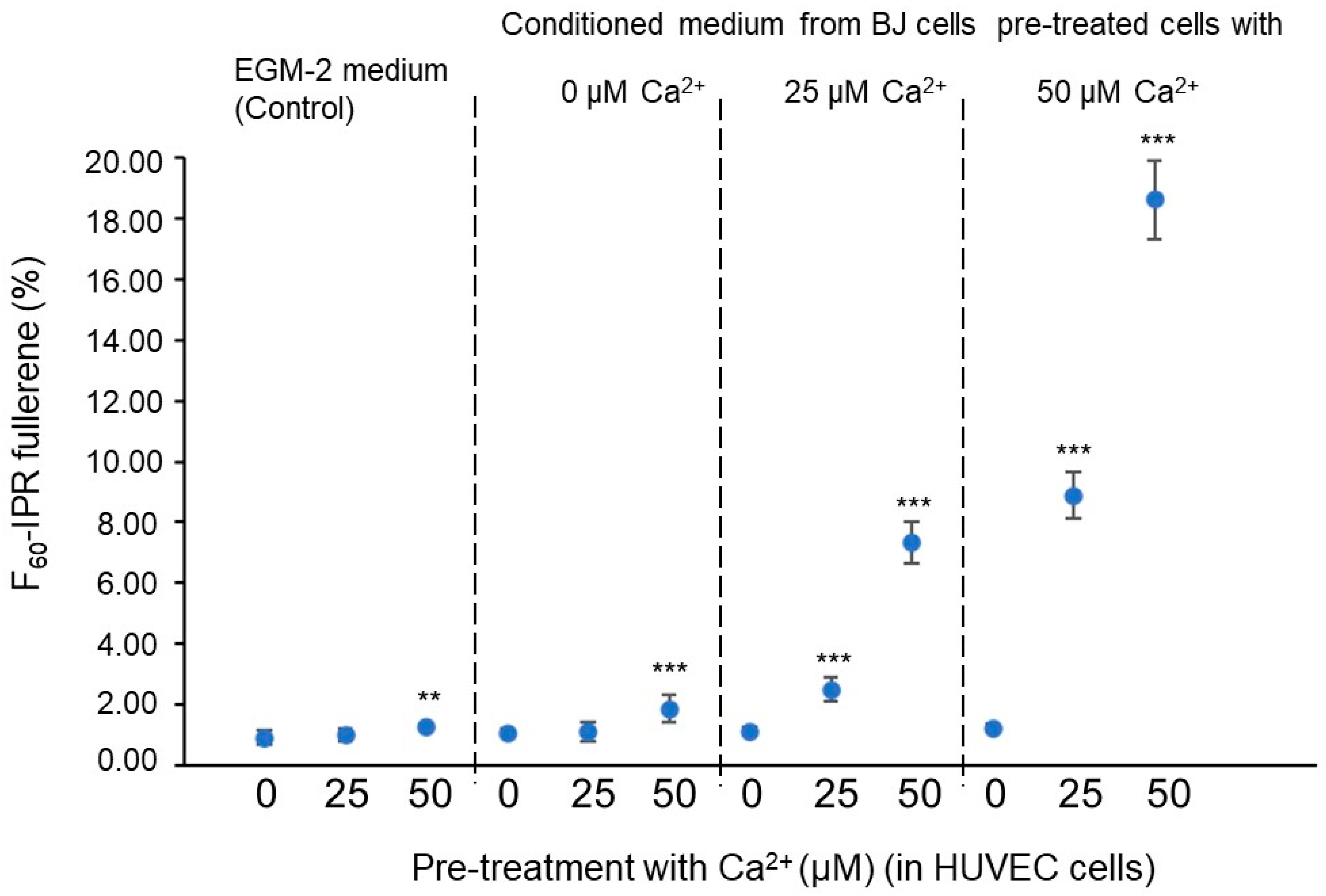
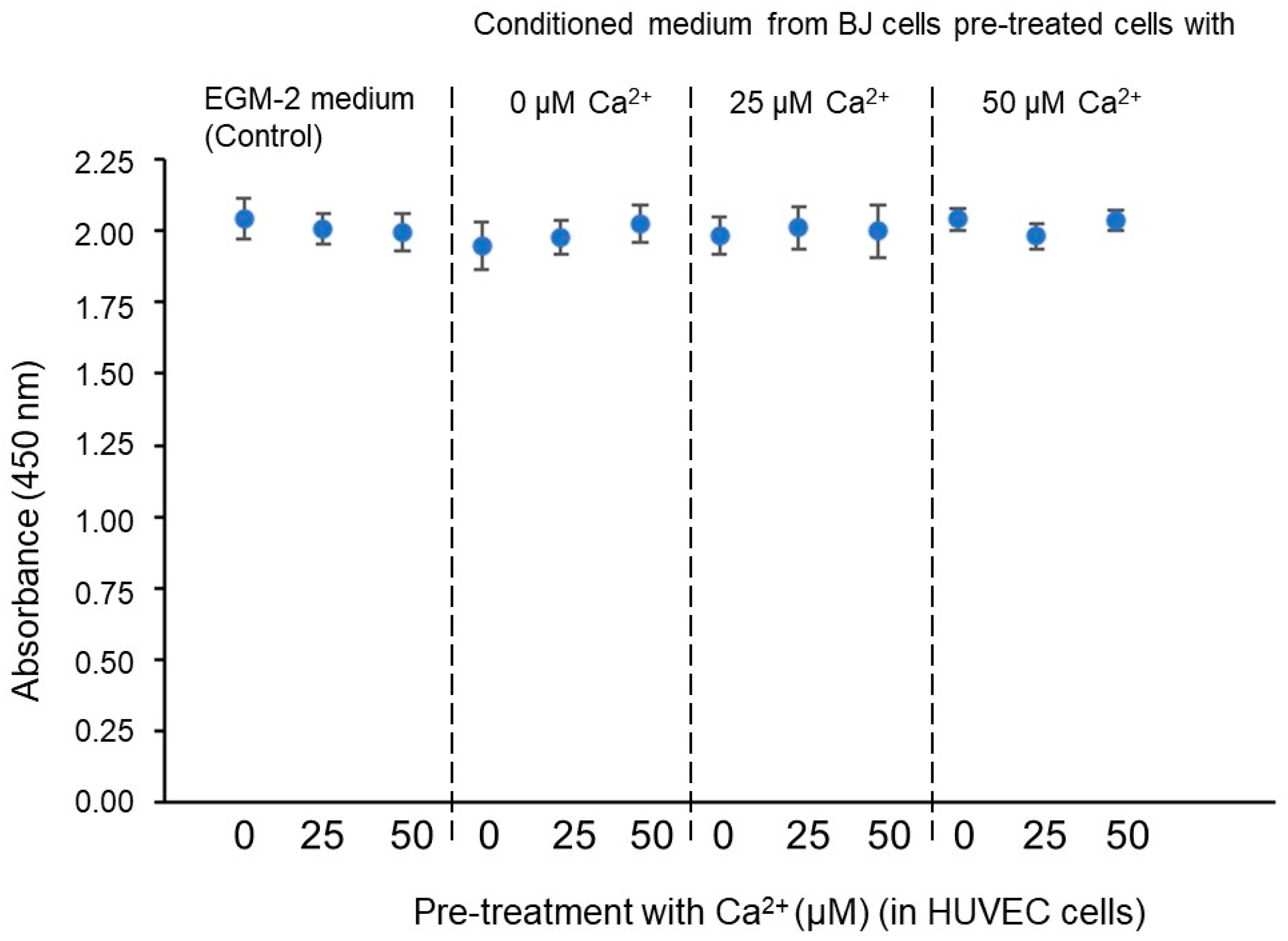
Abbreviature	Composition
BJ-medium 1	MEM basal medium + 1 % pen/strep + 2 mM L-glutamine + 10 %-v/v FBS
BJ-medium 2	MEM basal medium (without calcium) + 1 % pen/strep + 2 mM L-glutamine + 10 %-v/v FBS
BJ-medium 3	MEM basal medium (without calcium) + 1 % pen/strep + 2 mM L-glutamine + 10 %-v/v FBS. Then, calcium phosphate NPs, with diameter < 200 nm were mixed with the medium until final concentration of Ca2+ equivalent to 25 μM.
BJ-medium 4	MEM basal medium (without calcium) + 1 % pen/strep + 2 mM L-glutamine + 10%-v/v FBS. Then, calcium phosphate NPs, with diameter < 200 nm were mixed with the medium until final concentration of Ca2+ equivalent to 50 μM.
BJ-medium 5	MEM basal medium (without calcium), used as a washing culture medium.
BJ-medium 6	Conditioned BJ-medium 2 obtained from 48 h exposition to sensitized BJ cell clone cultures and chelated with 0.5 mM EGTA.
BJ-medium 7	Conditioned BJ-medium 3 obtained from 48 h exposition to sensitized BJ cell clone cultures and chelated with 0.5 mM EGTA.
BJ-medium 8	Conditioned BJ-medium 4 obtained from 48 h exposition to sensitized BJ cell clone cultures and chelated with 0.5 mM EGTA.

. First, we removed the BJ cells’ frozen vial from liquid ${\mathrm{N}}_2$ storage (passage 4), then diluted the thawed cells slowly before seeding them, using the pre-warmed BJ-medium 1 (see Table 1). The cells were cultured in a T25-flask at 37 °C with 5% ${\mathrm{C}\mathrm{O}}_2,$ 95% air and humid atmosphere at 5.000 cells/${\mathrm{c}\mathrm{m}}^2$. Cells nearing 90% confluence in the culture were detached using 0.05% trypsin/EDTA. We repeated this process to ensure two optimal subcultures before obtaining sensitized BJ cell clones. Then, we cultured 3 T75-flasks at 5.000 cells/${\mathrm{c}\mathrm{m}}^2$ using the prewarmed BJ-medium 1 (see Table 1); this medium contains calcium to allow cell adhesion. After 12 h, the culture medium was removed, and cells were washed with BJ-medium 5 (see Table 1) to remove residual ${\mathrm{C}\mathrm{a}}^{2+}$. Then, 1 T75-flask BJ cell was cultured with BJ-medium 2; 1 T75-flask BJ cells were cultured with BJ-medium 3; and 1 T75-flask BJ cells were cultured with BJ-medium 4. This growing trypsinization-seeding process was repeated twice, so we obtained three different sensitized BJ cell clones (passage 8) exposed to different culture media conditions for two subcultures. Finally, we separately collected the media from the three different T75-flasks—named BJ-medium 6, BJ-medium 7, and BJ-medium 8—respectively (see Table 1), inhibited the ${\mathrm{C}\mathrm{a}}^{2+}$ using 0.5 mM EGTA as the chelating agent and stored the media at $-20$ °C. EGTA-AM was purchased from Molecular Probes (Eugene, OR, USA).

2.4. Stimulation of HUVEC Cells with ${Ca}^{2+}$ Nanoparticles (ACP-NPs)

HUVEC (Human Umbilical Vein Endothelial Cell) cells were used as a model of human endothelium and purchased from ATCC (CC-2517, Manassas, USA). Minimum Essential Medium with Earle’s salts (MEM), Ca²⁺ free MEM, FBS, pen/strep). The EGM-2 Bulletkit medium (with and without Ca²⁺) and Endothelial Basal Medium (EBM) (with and without Ca²⁺) were purchased from Lonza (Basel, Switzerland). The characteristics of the media used in the tested cultures are listed in

Table 2. Characteristics of formulated HUVEC culture media.

Abbreviature	Composition
HUVEC-medium 1	EGM-2 Bulletkit medium.
HUVEC-medium 2	EGM-2 Bulletkit medium (without calcium).
HUVEC-medium 3	EGM-2 Bulletkit medium (without calcium). Then, Ca2+ concentration in the culture media was adjusted to 25 μM adding calcium nanoparticles.
HUVEC-medium 4	EGM-2 Bulletkit medium (without calcium). Then, Ca2+ concentration in the culture media was adjusted to 50 μM adding calcium nanoparticles.
HUVEC-medium 5	EGM-2 Bulletkit medium (without calcium). Then, Ca2+ concentration in the culture media was adjusted to 100 μM adding calcium nanoparticles.
HUVEC-medium 6	Endothelial Basal Medium (EBM) without Ca2+.
HUVEC-medium 7	Endothelial Basal Medium (EBM) with Ca2+.

. First, we removed the HUVEC cells’ frozen vial from the liquid ${\mathrm{N}}_2$ storage (passage 4), then diluted the thawed cells slowly before seeding them, using a pre-warmed HUVEC-medium 1 (see Table 2). The cells were cultured in the T25-flask at 37 °C with 5% ${\mathrm{C}\mathrm{O}}_2,$ 95% air and humid atmosphere at 10.000 cells/${\mathrm{c}\mathrm{m}}^2$. The T25-flask for HUVEC cell cultures was previously coated with a 0.1% (w/v) gelatin solution (10 μL solution/${\mathrm{c}\mathrm{m}}^2),$ drying at least 2 h before introducing the cells and medium, and the gelatin solution was purchased from Merck (G1393, Darmstadt, Germany). Cells nearing 90% confluence in the culture were detached using 0.05% trypsin/EDTA. We repeated this process to ensure two optimal subcultures before obtaining sensitized HUVEC cell clones. Then, we cultured 12 T25-flasks at 10.000 cells/${\mathrm{c}\mathrm{m}}^2$ using the prewarmed HUVEC-medium 1 (see Table 2); this medium contains calcium to allow cell adhesion. After 12 h, the culture medium was removed, and cells were washed with the HUVEC-medium 6 (see Table 2) to remove residual ${\mathrm{C}\mathrm{a}}^{2+}$. Then, the 12 T75-flask HUVEC cells were cultured with the media conditions listed in

Table 3. Pre-treatment culture conditions to obtain HUVEC cells and sensitized clones.

Abbreviature	Composition (v/v)
1	HUVEC-medium 2.
2	HUVEC-medium 3.
3	HUVEC-medium 4.
4	HUVEC-medium 2 + BJ-medium 6 (1/1).
5	HUVEC-medium 2 + BJ-medium 7 (1/1).
6	HUVEC-medium 2 + BJ-medium 8 (1/1).
7	HUVEC-medium 4 + BJ-medium 6 (1/1 to adjust the final Ca2+ concentration to 25 μM).
8	HUVEC-medium 4 + BJ-medium 7 (1/1 to adjust the final Ca2+ concentration to 25 μM).
9	HUVEC-medium 4 + BJ-medium 8 (1/1 to adjust the final Ca2+ concentration to 25 μM).
10	HUVEC-medium 5 + BJ-medium 6 (1/1 to adjust the final Ca2+ concentration to 50 μM).
11	HUVEC-medium 5 + BJ-medium 7 (1/1 to adjust the final Ca2+ concentration to 50 μM).
12	HUVEC-medium 5 + BJ-medium 8 (1/1 to adjust the final Ca2+ concentration to 50 μM).

. This growing trypsinization-seeding process was repeated twice, so we obtained 12 different sensitized HUVEC cell clones (passage 8) exposed to different culture media conditions for two subcultures, and we used these clones in the tube-like formation and proliferation assays.

2.5. HUVEC Cells Tube-like Formation Assay

The Matrigel substrate (Becton Dickinson, Franklin Lakes, USA) was used as a basement membrane model for the vessel formation of endothelial cells. To allow polymerization, the plate was incubated at 37 °C and 5% ${\mathrm{C}\mathrm{O}}_2$ for 30 min [51]. HUVEC cells obtained from the 12 different culture conditions described in the previous section were seeded at a density of 5.000 cells/well in 24-well plates coated with a thin gel of 10 mg/mL of Matrigel as a matrix and were maintained with HUVEC-medium 7 supplemented with 20 ng/mL of bFGF (ThermoFischer, Waltham, MA, USA) and 1%-w/v of BSA (Sigma-Aldrich, St. Louis, MO, USA). The cells were cultured and analyzed for 10 days to allow their adhesion to the plate and migration. After network vascular quantification, the cell proliferation BrdU method was used (Amersham Biosciences, Buckinghamshire, UK) [52]; this is an immunocytochemistry technique based on the incorporation of bromodeoxyuridine. An incubation with BrdU was carried out for 48 h, and then the plates were read at 450 nm in an ELISA colorimeter (ThermoFischer, Waltham, MA, USA).

2.6. Optical Microscopic Images

Using the LX AF6000 microscope and the Leica Application Suite software version 5.1.0 (Leica), cells were imaged at regular intervals over an extended period of time. Care was taken to ensure that no air bubbles were present in the Matrigel or the media, as this interfered with the analysis. Images were captured with 10×, 20×, or 40× objectives (Leica, HC PL FLUOTAR, dry immersion lens, aperture 0.15, working distance 12,000) positioned in the center of the well and imaged every 10 min. Images were exported with Fiji/ImageJ. To reduce the noise, image processing was applied for the collected original images using ImageJ image processing software (Version 1.50i; NIH) as follows. The images were subsequently processed with filters (a 3D maximum filter, a 3D Gaussian low-pass filter, a 2D FFT band-pass filter, and a 3D Gaussian low-pass filter). The images were then converted into binary images so that the cell area was white and all other areas were black.

2.7. Digital Image Processing and Three-Dimensional Reconstruction of Angiogenic Networks

Using the bshow program from the Bsoft software package version 2.1.4. [53], the blur in each image was calculated, and an initial manual classification of the images was made (Figure 3). Then, the determination and correction of the contrast transfer function (CFT) were carried out with the ctffind3 and the bctf programs from the Bsoft package (version 2.1.4), respectively. The network selection was performed manually with the tools of the Xmipp package (version 3.22) [54]. Multireference alignment techniques in real space and three-dimensional reconstruction with rear projection were used to process the images obtained, implemented in the Spider (version 6.0) [55] and Xmipp (version 3.22) [56] software packages, with the imposition of icosahedral symmetry.

2.8. Statistical Data Analysis

Nine replicates in each of the twelve pre-treatment cultures were performed to obtain HUVEC cell-sensitized clone conditions (see Table 3), corresponding to three different wells in three different plates (24-well plate). Statistical analysis was performed using the OriginPro v10 software package. Data collected from several different experiments are expressed as the mean ± standard error of the mean (SEM). The Shapiro–Wilk (SW) test was used to confirm normality, while the Bartlett test was used to confirm homogeneity. One-way analysis of variance (ANOVA) was used for comparing means and assessing group differences. Tukey’s test was used in the case of normal distributions, and the Kruskal–Wallis test, followed by Dunett’s multiple comparison test was used for the rest of the cases. All variables with a p < 0.05 were considered statistically significant. The following symbols were used to designate levels of significance: *, **, ***, significant at p < 0.05, 0.01, or 0.001, respectively (no symbol was placed when there were no significant differences compared to the control). The control group corresponds to condition 1 of Table 3.

3. Results

The intracellular levels of calcium ion (${\mathrm{C}\mathrm{a}}^{2+}$) are generally maintained as extremely low, as calcium often forms insoluble complexes with phosphorylated and carboxylated compounds. Typically, cytosolic ${\mathrm{C}\mathrm{a}}^{2+}$ concentrations are around 50–100 nm [57]. In response to stimuli, calcium is released from the external medium or internal reserves to increase the calcium intracellular concentration. In a previous work [58], we analyzed the cell internalization of extracellular ${\mathrm{C}\mathrm{a}}^{2+}$ (${\mathrm{C}\mathrm{a}}^{2+}$-free, NPs < 200 nm and NPs > 200 nm) both in HUVEC and BJ cells. Through ${\mathrm{C}\mathrm{a}}^{2+}$ imaging using Fura-2, we showed that usual extracellular ${\mathrm{C}\mathrm{a}}^{2+}$-free 2–3 mM and extracellular ${\mathrm{C}\mathrm{a}}^{2+}$-NPs (<200 nm) 25–50 μM provoke a similar intracellular between 50 and 100 nM after 24 h. This size in the NPs (<200 nm) led the endocytosis pathways and the composition to provoke a high and sustained calcium intracellular concentration.

The structural and morphological characterization of a nanoparticle is a crucial factor in understanding its properties, not only physically but also chemically. The morphology of the NPs was analyzed using scanning electron microscopy (SEM). Figure 4 shows the micrograph of the calcium phosphate NP used in this study. As we can observe, the NPs form clusters of around 30 nm, which, in turn, create long extensions of several hundred nanometers. These clusters are composed of nanocrystals with an approximate size of 10 nm.

The structure and size of the crystalline domains of the NPs were determined using X-ray diffraction. The diffraction data were analyzed using a general convolution process, allowing any combination of appropriate functions to be employed in modeling the diffractogram. The average dimensions of NP pseudo-spheres and the crystallinity and crystallite size determined for NP samples are listed in

Table 4. Physical parameters as determined using Laser Velocimetry, SEM and X-ray diffraction for ACP-NPs.

	ACP-NPs
Zeta potential (mV) Average radius (R) and length (ℓ) of the observed nanostructures	−2.5 $\pm$ 0.2 R $=$ 2.6 ± 0.2 nm
Cristallinity (see Equation (1))	${\chi }_c$ = 3 ± 1%
Crystallite size (see Equation (2))	L = 6 ± 1 nm

.

The zeta potential of NPs is useful for characterizing their surface electric charge. Understanding this parameter provides a value for the electrokinetic potential of NPs, and it depends on their composition and the dispersing medium. This information is of great interest when studying filtration behavior, sedimentation, and interactions with biological membranes. The zeta potential value is also included in Table 4.

Cell proliferation assays varying the cell seeding density (cells/mm²) and posterior analysis were carried out based on the proliferation and migration experiments performed by Gamba et al. [59,60]. The following behaviors were observed under a critical threshold of $n_c~$50 cells/mm²: on day 1, the formation of capillary-like structures was almost non-existent; on day 4, the formation of aggregates and the network was limited almost exclusively to that indicated in the image (Figure 5a); on day 7, although the aggregates were still visible, the contact region between the aggregates and network was not always evident; and on day 10, the network became progressively disjointed, eventually forming separate, unconnected structures. Conversely, at cell densities surpassing 200 cells/mm² (Figure 5c), the sides of the polygons forming the network increased their thickness to incorporate the increasing number of cells. For an even higher value of $n_c~$300 cells/mm² (Figure 5d), the culture reached confluence, and the network practically disappeared. However, in cultures that started with a seeding density of $n_c~$150 cells/mm², it was observed that on day 1, the cells were rearranged into a capillary-like appearance structure, similar to that described in the literature for endothelial cell cultures with Matrigel [61]. On day 4, the formation of defined aggregates was observed, and the network was even more evident than in the case of cultures that started with a lower number of cells at the same time of culture (Figure 5b). So, we chose this cell seeding density ($n_c~$150 cells/mm²) and day 4 after seeding for the subsequent vascular network characterization.

Firstly, we studied the interaction between fibroblastic and endothelial cells when exposed to extracellular calcium. Specifically, conditioned media from BJ fibroblast cells, sensitized or pre-treated with extracellular ${\mathrm{C}\mathrm{a}}^{2+}$ (at a concentration equivalent to 0, 25, and 50 µM of ${\mathrm{C}\mathrm{a}}^{2+}$), were obtained. The tube-like formation for HUVEC endothelial cells is evaluated in Figure 6. The tube-like length significantly increased as the ${\mathrm{C}\mathrm{a}}^{2+}$ concentration in the pretreated HUVEC cell medium increased. However, at the same ${\mathrm{C}\mathrm{a}}^{2+}$ concentration in the pretreated HUVEC cells, this length was independent of the ${\mathrm{C}\mathrm{a}}^{2+}$ concentration in the conditioned media from BJ cell subcultures. Dai et al. [62] analyzed angiogenic Matrigel tube formation HUVEC cultures combining quantitative angiogenic biology and kinetic imaging models on a microfluidic device. Their results demonstrated that the average tube height was 150 μm with a 12% coefficient variation.

Hexagons are joined together to form flat (two-dimensional) structures, such as graphene or tubular structures and nanotubes. To achieve the spherical (three-dimensional) shape typical of fullerenes, it is necessary to introduce curvature with the pentagons, thus generating additional stress. The surface is formed by fullerene structures that have five alternating hexagons adjacent to one pentagon. In 1987, Kroto suggested that having pentagons sharing bonds increases the stress in the fullerene [63]. He explained that the lower the tension generated by the pentagons, the greater the fullerene stability. Thus, the isolated pentagon rule (IPR) discriminates against the presence of adjacent pentagons since it greatly destabilizes the fullerene. According to the IPR, the $\sigma$ value (the ratio between the number of pentagons and hexagons) is the best criterion for the stability of fullerenes. The most stable fullerenes are those that do not have adjacent pentagons; that is, hexagons encircle each of the 12 pentagons (i.e., $\sigma =\frac{12}{20}=0.6$) [64,65].

Each $F_n$ fullerene family contains as many different fullerenes as different pentagon and hexagon arrangements. The fullerene family with the lowest number of vertices that presents an IPR-type structure is $F_{60}$ [66]; it contains 1812 different fullerenes, and only the truncated icosahedron has an IPR-type structure. The next family with this feature is $F_{70}$ which has 8149 different fullerenes and also a single IPR-type structure fullerene [67]. Within $F_{60}$ and $F_{70}$ fullerene family types, the most topologically stable fullerene is the $F_{60}$-IPR (the truncated icosahedron) [68]. Thus, an alternative criterion for the quantification of angiogenesis spatial minimization is the determination of the fullerene $F_{60}$-IPR percentage [69].

Figure 7 and Figure 8 suggest that the extracellular ${\mathrm{C}\mathrm{a}}^{2+}$ concentration in culture media, both from conditioned BJ and pretreated HUVEC cells, affects the spatial minimization characteristics of HUVEC cell angiogenic networks. Concretely, it is indicated that the ${\mathrm{C}\mathrm{a}}^{2+}$ concentration increase in the pre-treated BJ cells stimulates fullerene symmetry vascularization in the pretreated HUVEC cells with ${\mathrm{C}\mathrm{a}}^{2+}$ exposure (25 and 50 µM) but not in HUVEC cells without ${\mathrm{C}\mathrm{a}}^{2+}$ exposure (0 µM). The $\sigma$ value of HUVEC cell-mixed subcultures, with ${\mathrm{C}\mathrm{a}}^{2+}$ at 50 µM in HUVEC cultures and ${\mathrm{C}\mathrm{a}}^{2+}$ at 50 µM in BJ cultures, is significantly closer to the optimal $\sigma$ fullerene value—0.6—(Figure 7), and the $F_{60}$-IPR percentages of the HUVEC cells mixed subcultures, with ${\mathrm{C}\mathrm{a}}^{2+}$ at 25 or 50 µM in HUVEC cultures and ${\mathrm{C}\mathrm{a}}^{2+}$ at 25 or 50 µM in BJ cultures, significantly higher (Figure 8) than the values in the control conditions.

Our methodology involves identifying an appropriate global polyhedron structure to describe the geometry of the network, which includes associated subpolyhedron structures [70]. However, it is possible to associate many complex subpolyhedral structures within the global structure. For example, each subset of the angiogenic lattice determines a subset of vertices and edges that define a subpolyhedron [71]. On the other hand, some cycles generated by alternating sequences of vertices and edges that end at the initial sequence vertex can be associated with the faces of dimension two. Faces can also be associated using other criteria; for example, vertices of the same angiogenic network subset that are close to each other and coplanar can be considered to determine a convex polygon. Similarly, there are parts of a global structure that, in turn, can be associated with a subpolyhedron [72]. On many occasions, the corresponding global polyhedral structure is immersed in Euclidean space, which allows, by studying the symmetry groups, to classify the subpolyhedron types. From this invariant algebraic analysis, it can be established that, in the case of $F_{60}$-IPR fullerene, the subpolyhedron structure is very simple in the sense that it consists of a unique subpolyhedron type that is the truncated icosahedron, which reduces the topological analysis of the global problem [73].

After the results shown in Figure 6, Figure 7 and Figure 8, a new question arises: is the fullerene spatial partition associated $\sigma$ value ($\sigma$ = 0.6) and the $F_{60}$-IPR percentage increase due to an increase in proliferation or to a greater efficiency in the space partitioning? In order to answer this question, all the previous conditions were tested in HUVEC cell cultures at a density of 150 cells/mm² on Matrigel; once the vascular network was formed (on day 4), proliferation assays were performed based on the incorporation of BrdU and the subsequent reading with ELISA. As expected, in a basement membrane with such a high concentration of growth factors as Matrigel, the cells begin to differentiate almost immediately after seeding and barely divide. In any case, we verified that there were no significant differences in proliferation in any of the conditions tested. As can be seen in Figure 9, the ${\mathrm{C}\mathrm{a}}^{2+}$ concentration in the conditioned BJ cell medium or the ${\mathrm{C}\mathrm{a}}^{2+}$ concentration in the pretreatment of HUVEC cells does not affect the HUVEC cell proliferation on Matrigel assays. So, we can conclude that both the $\sigma$ value optimization and the $F_{60}$-IPR percentage increase are not due to a proliferation increase or a total length increase but to a fullerene rule spatial minimization cell program in the angiogenic network distribution.

The question of whether the angiogenic cell migration is spatially homogenous and isotropic on the microscopic scale is of fundamental importance to biology but has not yet been answered decisively. Collective cell migration promotes directional migration towards or against a stimulus or signal. If the signal is spatially homogeneous (isotropic), the migration is random (random migration), while if it is spatially localized (anisotropic), the migration can be directed (directional migration) [74]. Directed migration is induced via asymmetric signals in the external environment, like an external chemical stimulus, an electric field, an extracellular topology, or a predetermined mechanical orientation [75].

The self-organization of angiogenic structures in the presence of chemical gradients is highly sensitive to the diffusive transport characteristics and the chemical kinetics. These reaction–diffusion systems belong to the field of nonlinear dynamics. The most studied systems in nonlinear chemistry, BZ (Belousov–Zhabotinsky) and CDIMA (Chlorine Dioxide–Malonic Acid) are characterized by chemical reactions at a microscopic level and diffusion at the mesoscopic level based on the Brownian motion of chemical species within a reaction space [76].

The emergence of Turing patterns occurs when spatial differential diffusion appears [77]. The effect of a chemical reaction in a Turing structure, in most cases, is pattern removal, resulting in periodic or chaotic global oscillations. However, it may also be that the pattern is not eliminated, resulting in an oscillating Turing structure. Finally, it is also possible that the system produces spatiotemporal chaos in the form of competition between an incipient Turing pattern and a background chaotic oscillation that constantly eliminates the pattern. On the mathematical modeling of angiogenesis as a reaction–diffusion process, it can be shown that angiogenesis is included in this last dynamic system regime [78].

4. Conclusions

Our paper presents an alternative approach to tackle the problem of analyzing the hallmarks of cancer involving complex spatiotemporal dynamics. In fact, this geometric proposal could actually serve as a pathway to achieve other goals, such as understanding the universal mechanisms of cancer transformation. By recognizing the phenomenon of spatial orientation in tumor cells, we can progress even further in the search for new mechanisms to improve patient survival. Blocking molecules from spatial orientation can provide us with an unexplored direction for antitumor therapy.

The introduction of the phenomenon of spatial orientation in cells is proposed as the basis of the cellular communication process in short-range biochemical signaling processes. The aim of this work is to provide a coherent understanding of the geometry of cancer, clarifying intercellular geometric communication systems and connecting them with important intracellular signal mechanisms. Communication networks are modeled using graph structures with guaranteed delivery in wireless geometric networks. Although approaches based on random messaging systems are interesting, we propose an approach based on assimilating the spatial orientation mechanisms including non-random localization algorithms.

Pattern vessel formation can be viewed as the spatial organization of vascular endothelial cell differentiation. How a group of mesoscopic numbers (hundred-to-thousands) of cells self-organizes remains incompletely understood. Historically, angiogenesis spatial model studies have focused on physiological mechanisms regulating this process. So, mechanical and chemical models of angiogenesis have been critically reviewed with the goal of understanding endogenous chemotaxis. On the contrary, we focus on the geometry of the patterns, providing a bridge from the second messenger biochemical theory to graph theory models.

We calculate several parameters, such as the number of pentagons and hexagons in the vascular network, the $\sigma$ number, and the $F_{60}$-IPR fullerene percentage due to the application of the isolated pentagon rule (IPR). The major prediction of our model is that the $\sigma$ and $F_{60}$-IPR percentage parameters have a greater effect than proliferation or the network total length increase on promoting angiogenesis spatial minimization. Geometric disfunction in minimal vasculature space partition provokes non-optimal $\sigma$ values (the presence of many triangles and quadrilaterals instead of pentagons at low $\sigma$ values and an increasing number of pentagons at high $\sigma$ values) or low $F_{60}$-IPR percentage values. So, our model predicts that altering $\sigma$ and $F_{60}$-IPR percentage values might also be an effective strategy to create non-functional network patterns. Also, our measurements predict that the extracellular ${\mathrm{C}\mathrm{a}}^{2+}$ concentration can trigger geometric behavior modifications in angiogenic patterns and concretely in spatial minimization related to the Kelvin problem.

Although the efficacy of antiangiogenic therapies depends on the biological profile of the tumor, this geometric approach could lead to an effective therapy for many types of tumors. At this point, a simple way to state the problem could be as follows: do endothelial cells ‘learn’ to self-organize in angiogenesis networks ‘thanks to lessons in Geometry’? If this is so, a possible antiangiogenic therapy could involve drugs that modify the soluble factors concentration from any of the tumor stromal cells that alter the spatial orientation of the endothelial cells in the angiogenic network formation.