Sensitive Data Privacy Protection of Carrier in Intelligent Logistics System
Abstract
1. Introduction
- 1.
- A local differential privacy protection algorithm -L_LDP (-Logistic Local Differential Privacy, -L_LDP) for the carrier’s multidimensional numerical sensitive data in the logistics process is proposed. First, a personalized local differential privacy budget method is used to introduce a carrier user’s personalized privacy budget, which ensures that each carrier can modify the privacy protection budget of sensitive data according to individual or carrier company requirements. Then, the data are normalized to [−1, 1] using each attribute data security domain value, introducing [0,1] uniform random variables, and designing the multidimensional data personalized perturbation mechanism algorithm L-PM on segmented perturbation mechanism PM. Then, the carrier’s multidimensional numerical data are perturbed using the L-PM algorithm.
- 2.
- The local differential privacy protection algorithm -LT_LDP (-Logistic Trajectory Location Differential Privacy, -LT_LDP) for the location-based data of carriers is put forward. First, the location region is matrix partitioned and quadtree indexed, and the location data are indexed according to the quadtree to obtain the geographic location code (including area code and inner code) where it is located. Then, this paper adopts a personalized local differential privacy budget method, which introduces a personalized privacy budget for carrier users and ensures that each carrier can modify the privacy protection budget of sensitive data according to personal or company requirements. Then, the geographic location coding vector is normalized to , and a certain probabilistic Bernoulli variable is introduced, which is determined by the privacy budget and the specific geographic location coding vector value, to realize the personalized random response algorithm L-RR for location trajectory data. Finally, the L-RR algorithm is used to realize the perturbation of geographic location coding data.
- 3.
- In this paper, the privacy of the -L_LDP algorithm and the -LT_LDP algorithm are analyzed and proved. In addition to that, simulation experiments are conducted to verify the usability of the algorithms. The evaluation criteria in the experiments are the standard mean square error (MSE), mean absolute percentage error (MAPE), and root mean square error (RMSE). The experimental datasets include: the simulation dataset, which is the GAUSS dataset and UNIFORM dataset; the multidimensional numerical real dataset, which comprises the BR dataset and MX dataset; and the real trajectory (location) dataset, which comprises the GPS data of more than 14,000 cabs selected from 3 August 2014 to 30 August 2014, in Chengdu city. Among them, the -L_LDP algorithm is experimentally compared with three existing algorithms, and the -LT_LDP algorithm is experimentally compared with two existing algorithms for implementation. The experimental results show that the data processed by the scheme in this paper have higher usability under the same privacy budget. The privacy protection scheme proposed in this paper not only ensures the privacy protection of the carrier logistics process but also meets the personalized privacy needs of carrier users, which will help the intelligent logistics platform provide a better and more stable logistics services.
2. Related Work
3. Preliminaries
3.1. Differential Privacy
3.1.1. Definition of Differential Privacy
3.1.2. Noise Mechanisms
3.2. Local Differential Privacy
3.2.1. Definition of Local Differential Privacy
3.2.2. Randomized Response Mechanism
3.3. Location and Trajectory Privacy
4. Local Differential Privacy Protection Solutions for Carrier Sensitive Data
4.1. Scenario and Problem Description
4.2. Local Differential Privacy Preservation Algorithm for Carrier Multidimensional Numerical Data -L_LDP
4.2.1. The General Idea of -L_LDP
4.2.2. Perturbation Algorithm L-PM
| Algorithm 1 Algorithm L-PM |
Input:; Output:
|
4.2.3. Local Differential Privacy Protection Algorithm -L_LDP
| Algorithm 2 Algorithm -L_LDP |
Input:; Output:
|
4.3. Local Differential Privacy Protection Model for Location Data of Carriers
4.3.1. The General Idea of -LT_LDP
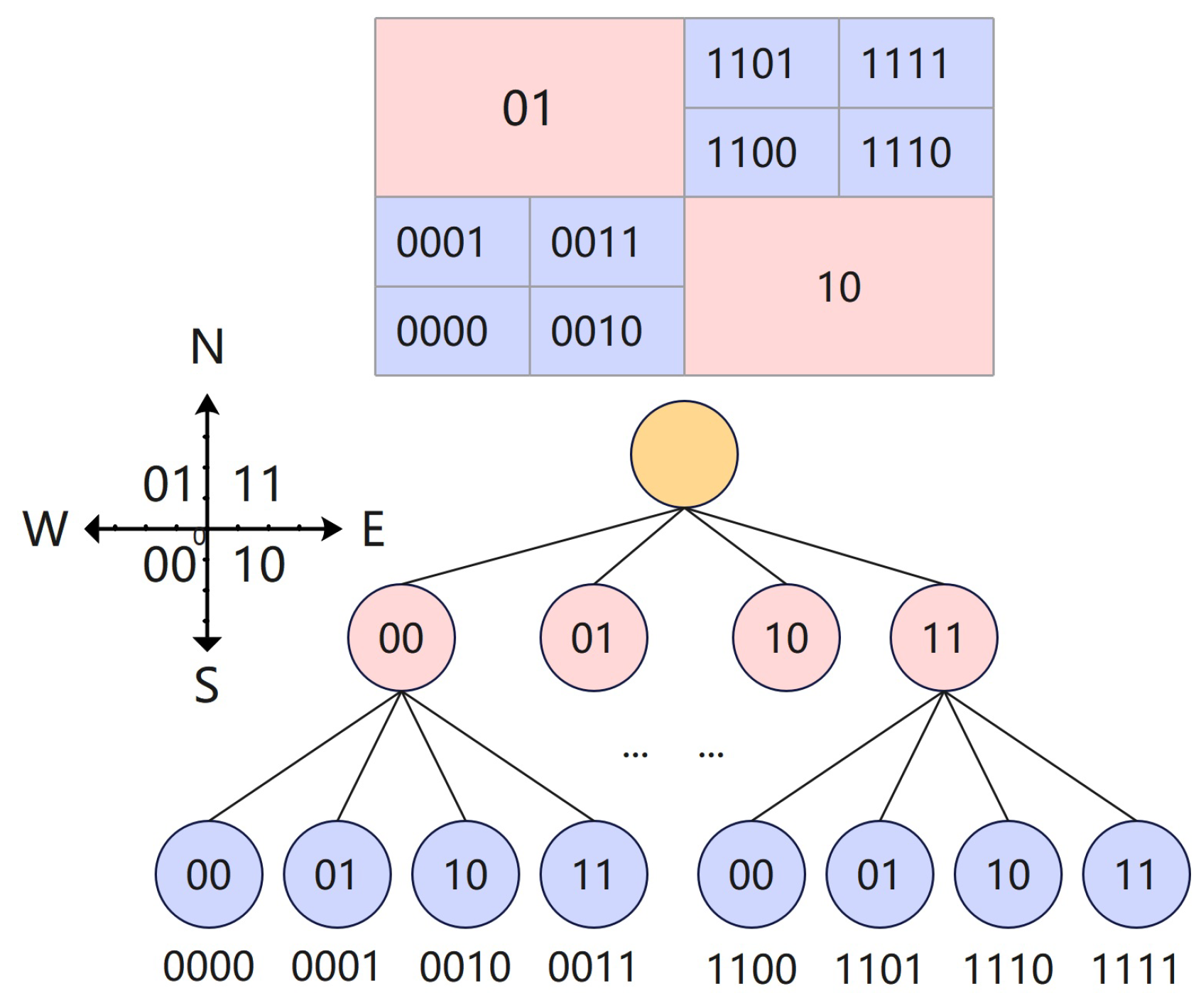
4.3.2. Quadtree Index Construction Method for Location Data
4.3.3. Perturbation Algorithm L-RR
| Algorithm 3 Algorithm L-RR |
Input: B, ; Output: S;
|
4.3.4. Local Differential Privacy Protection Algorithm -LT_LDP
| Algorithm 4 Algorithm -LT_LDP |
Input:; Output: H, S;
|
4.4. Model Algorithmic Analysis
5. Experimental Results and Analysis
5.1. Experimental Environment
5.2. Experimental Analysis of -L_LDP Algorithms
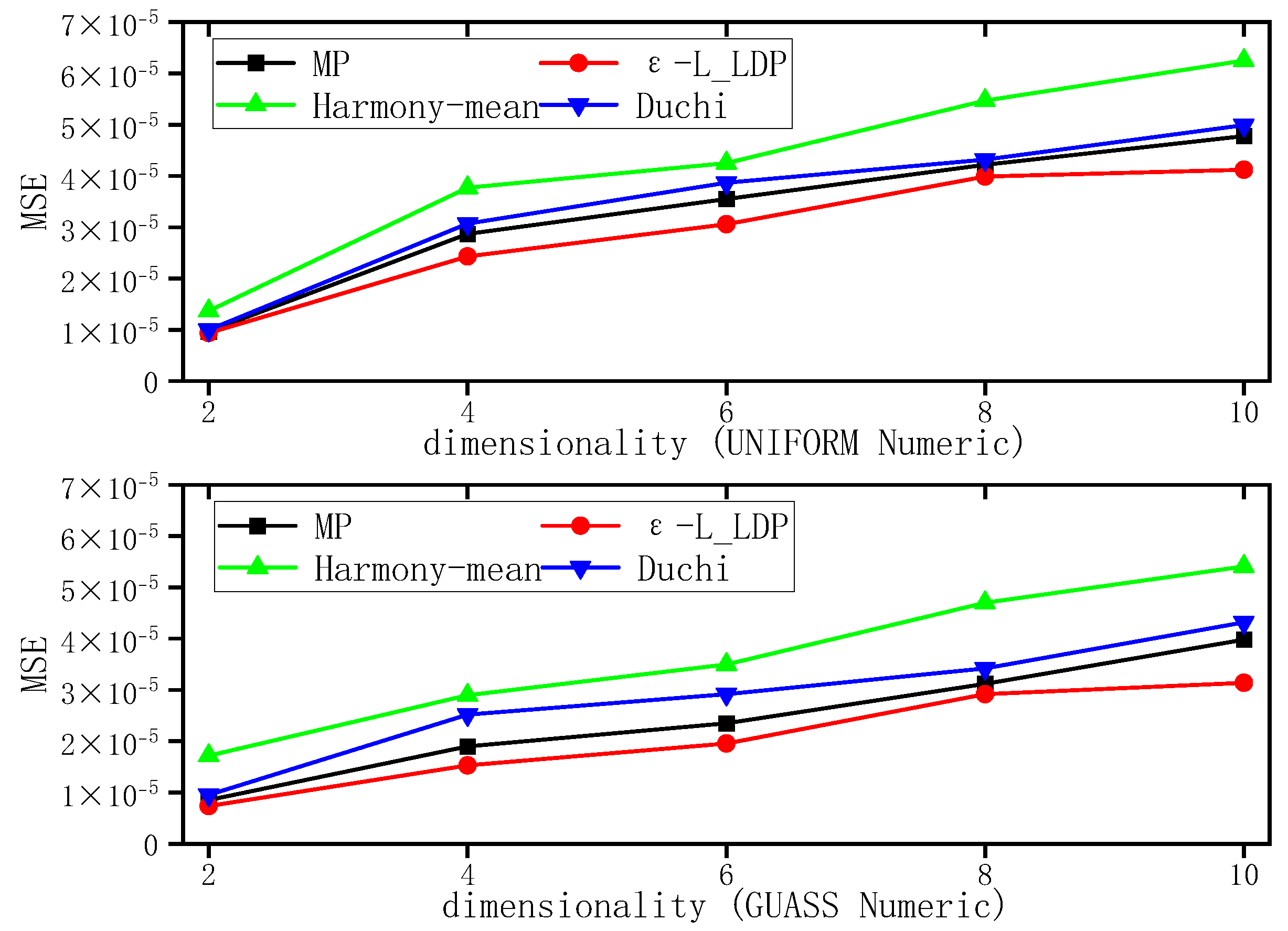
5.2.1. The Impact of the Number of Attributes on Usability
5.2.2. The Impact of Privacy Budgets on Usability
5.3. Experimental Analysis of -LT_LDP Algorithms
5.3.1. The Performance of the Trajectory Proportion Estimation
5.3.2. The Performance of the Location Proportion Estimation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Humayun, M.; Jhanjhi, N.Z.; Hamid, B.; Ahmed, G. Emerging smart logistics and transportation using IoT and blockchain. IEEE Internet Things Mag. 2020, 3, 58–62. [Google Scholar] [CrossRef]
- Ding, Y.; Jin, M.; Li, S.; Feng, D. Smart logistics based on the internet of things technology: An overview. Int. J. Logist. Res. Appl. 2021, 24, 323–345. [Google Scholar] [CrossRef]
- Song, Y.; Yu, F.R.; Zhou, L.; Yang, X.; He, Z. Applications of the Internet of Things (IoT) in smart logistics: A comprehensive survey. IEEE Internet Things J. 2020, 8, 4250–4274. [Google Scholar] [CrossRef]
- Speranza, M.G. Trends in transportation and logistics. Eur. J. Oper. Res. 2018, 264, 830–836. [Google Scholar] [CrossRef]
- Belli, L.; Cilfone, A.; Davoli, L.; Ferrari, G.; Adorni, P.; Di Nocera, F.; Dall’Olio, A.; Pellegrini, C.; Mordacci, M.; Bertolotti, E. IoT-enabled smart sustainable cities: Challenges and approaches. Smart Cities 2020, 3, 1039–1071. [Google Scholar] [CrossRef]
- Liu, W.; Long, S.; Liang, Y.; Wang, J.; Wei, S. The influence of leadership and smart level on the strategy choice of the smart logistics platform: A perspective of collaborative innovation participation. Ann. Oper. Res. 2021, 324, 893–935. [Google Scholar] [CrossRef]
- Yang, M.; Mahmood, M.; Zhou, X.; Shafaq, S.; Zahid, L. Design and implementation of cloud platform for intelligent logistics in the trend of intellectualization. China Commun. 2017, 14, 180–191. [Google Scholar] [CrossRef]
- Mathew, E. Swarm intelligence for intelligent transport systems: Opportunities and challenges. In Swarm Intelligence for Resource Management in Internet of Things; Elsevier: Amsterdam, The Netherlands, 2020; pp. 131–145. [Google Scholar]
- Liu, S.; Wang, J. A security-enhanced express delivery system based on NFC. In Proceedings of the 2016 13th IEEE International Conference on Solid-State and Integrated Circuit Technology (ICSICT), Hangzhou, China, 25–28 October 2016; pp. 1534–1536. [Google Scholar]
- Lin, X.; Jing, P.; Yu, C.; Feng, X. TPLI: A traceable privacy-preserving logistics information scheme via blockchain. In Proceedings of the 2021 International Conference on Networking and Network Applications (NaNA), Lijiang, China, 29 October–1 November 2021; pp. 345–350. [Google Scholar]
- Waters, D. Supply Chain Risk Management: Vulnerability and Resilience in Logistics; Kogan Page Publishers: London, UK, 2011. [Google Scholar]
- Sativell, T.; Sabar, R. The threat of high value cargo faced by logistics companies. In Proceedings of the Simposium Pengurusan Teknologi, Operasi & Logistik (SIPTIK III), Changlun, Malaysia, 11–12 December 2012. [Google Scholar]
- NBC. UPS Driver Kidnapped, Packages Stolen in Brazen Atlanta Heist. Available online: https://www.nbcnews.com (accessed on 29 December 2021).
- Feng, C.; Tan, L.; Xiao, H.; Yu, K.; Qi, X.; Wen, Z.; Jiang, Y. PDKSAP: Perfected double-key stealth address protocol without temporary key leakage in blockchain. In Proceedings of the 2020 IEEE/CIC International Conference on Communications in China (ICCC Workshops), Xiamen, China, 28–30 July 2020; pp. 151–155. [Google Scholar]
- Yang, C.; Tan, L.; Shi, N.; Xu, B.; Cao, Y.; Yu, K. AuthPrivacyChain: A blockchain-based access control framework with privacy protection in cloud. IEEE Access 2020, 8, 70604–70615. [Google Scholar] [CrossRef]
- Tan, L.; Shi, N.; Yang, C.; Yu, K. A blockchain-based access control framework for cyber-physical-social system big data. IEEE Access 2020, 8, 77215–77226. [Google Scholar] [CrossRef]
- Tan, L.; Shi, N.; Yu, K.; Aloqaily, M.; Jararweh, Y. A blockchain-empowered access control framework for smart devices in green internet of things. ACM Trans. Internet Technol. (TOIT) 2021, 21, 1–20. [Google Scholar] [CrossRef]
- Liu, X.; Hu, B.; Zhou, Q.; Liu, J. A Logistics Privacy Protection System Based on Cloud Computing. In Frontier Computing: Theory, Technologies and Applications FC 2016 5; Springer: Singapore, 2018; pp. 455–461. [Google Scholar]
- Léauté, T.; Faltings, B. Coordinating logistics operations with privacy guarantees. In Proceedings of the Twenty-Second International Joint Conference on Artificial Intelligence (IJCAI’11), Barcelona, Spain, 16–22 July 2011; pp. 2482–2487. [Google Scholar]
- Xu, F.J.; Tong, F.C.; Tan, C.J. Auto-ID enabled tracking and tracing data sharing over dynamic B2B and B2G relationships. In Proceedings of the 2011 IEEE International Conference on RFID-Technologies and Applications, Sitges, Spain, 15–16 September 2011; pp. 394–401. [Google Scholar]
- Gao, Q.; Zhang, J.; Ma, J.; Yang, C.; Guo, J.; Miao, Y. LIP-PA: A logistics information privacy protection scheme with position and attribute-based access control on mobile devices. Wirel. Commun. Mob. Comput. 2018, 2018, 9436120. [Google Scholar] [CrossRef]
- Qian, W.E.I.; Xing-Yi, L.I. Express information protection application based on K-anonymity. Appl. Res. Comput./Jisuanji Yingyong Yanjiu 2014, 31, 555–567. [Google Scholar]
- Qi, H.; Chenjie, D.; Yingbiao, Y.; Lei, L. A new express management system based on encrypted QR code. In Proceedings of the 2015 8th International Conference on Intelligent Computation Technology and Automation (ICICTA), Nanchang, China, 14–15 June 2015; pp. 53–56. [Google Scholar]
- Zhang, X.; Li, H.; Yang, Y.; Sun, G.; Chen, G. LIPPS: Logistics information privacy protection system based on encrypted QR code. In Proceedings of the 2016 IEEE Trustcom/BigDataSE/ISPA, Tianjin, China, 23–26 August 2016; pp. 996–1000. [Google Scholar]
- Yan, W.; Yao, Y.; Zhang, W.M. Privacy-preserving scheme for logistics systems based on 2D code and information hiding. Chin. J. Netw. Inf. Secur. 2017, 3, 22–28. [Google Scholar]
- Pournader, M.; Shi, Y.; Seuring, S.; Koh, S.L. Blockchain applications in supply chains, transport and logistics: A systematic review of the literature. Int. J. Prod. Res. 2020, 58, 2063–2081. [Google Scholar] [CrossRef]
- Tijan, E.; Aksentijević, S.; Ivanić, K.; Jardas, M. Blockchain technology implementation in logistics. Sustainability 2019, 11, 1185. [Google Scholar] [CrossRef]
- Rožman, N.; Corn, M.; Požrl, T.; Diaci, J. Distributed logistics platform based on Blockchain and IoT. Procedia CIRP 2019, 81, 826–831. [Google Scholar] [CrossRef]
- Yi, H. A secure logistics model based on blockchain. Enterp. Inf. Syst. 2021, 15, 1002–1018. [Google Scholar] [CrossRef]
- Duan, H.; Yang, J.; Yang, H. A Blockchain-Based Privacy Protection Application for Logistics Big Data. J. Cases Inf. Technol. (JCIT) 2022, 24, 1–12. [Google Scholar] [CrossRef]
- Li, H.; Han, D.; Tang, M. A privacy-preserving storage scheme for logistics data with assistance of blockchain. IEEE Internet Things J. 2021, 9, 4704–4720. [Google Scholar] [CrossRef]
- Zhou, S.; Li, F.; Tao, Y.-F.; Xiao, X.-K. Privacy preservation in database applications: A survey. Chin. J. Comput. 2009, 32, 847–861. [Google Scholar] [CrossRef]
- Sweeney, L. k-anonymity: A model for protecting privacy. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2002, 10, 557–570. [Google Scholar] [CrossRef]
- Machanavajjhala, A.; Kifer, D.; Gehrke, J.; Venkitasubramaniam, M. l-diversity: Privacy beyond k-anonymity. ACM Trans. Knowl. Discov. Data (TKDD) 2007, 1, 3-es. [Google Scholar] [CrossRef]
- Li, N.; Li, T.; Venkatasubramanian, S. t-closeness: Privacy beyond k-anonymity and l-diversity. In Proceedings of the IEEE 23rd International Conference on Data Engineering, Istanbul, Turkey, 17–20 April 2007; pp. 106–115. [Google Scholar]
- Wong, R.C.W.; Li, J.; Fu, A.W.C.; Wang, K. (α, k)-anonymity: An enhanced k-anonymity model for privacy preserving data publishing. In Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Philadelphia, PA, USA, 20–23 August 2006; pp. 754–759. [Google Scholar]
- Ganta, S.R.; Kasiviswanathan, S.P.; Smith, A. Composition attacks and auxiliary information in data privacy. In Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Las Vegas, NV, USA, 24–27 August 2008; pp. 265–273. [Google Scholar]
- Wong, R.C.W.; Fu, A.W.C.; Wang, K.; Yu, P.S.; Pei, J. Can the utility of anonymized data be used for privacy breaches? ACM Trans. Knowl. Discov. Data (TKDD) 2011, 5, 1–24. [Google Scholar] [CrossRef]
- Dwork, C. Differential privacy: A survey of results. In Proceedings of the International Conference on Theory and Applications of Models of Computation, Xi’an, China, 25–29 April 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–19. [Google Scholar]
- Dwork, C.; Lei, J. Differential privacy and robust statistics. In Proceedings of the Forty-First Annual ACM Symposium on Theory of Computing, Bethesda, MD, USA, 31 May–2 June 2009; pp. 371–380. [Google Scholar]
- Dwork, C.; McSherry, F.; Nissim, K.; Smith, A. Calibrating noise to sensitivity in private data analysis. In Theory of Cryptography: Third Theory of Cryptography Conference, TCC 2006, New York, NY, USA, 4–7 March 2006; Proceedings 3; Springer: Berlin/Heidelberg, Germany, 2006; pp. 265–284. [Google Scholar]
- McSherry, F.; Talwar, K. Mechanism design via differential privacy. In Proceedings of the 48th Annual IEEE Symposium on Foundations of Computer Science (FOCS’07), Providence, RI, USA, 20–23 October 2007; pp. 94–103. [Google Scholar]
- Dwork, C.; Naor, M.; Pitassi, T.; Rothblum, G.N.; Yekhanin, S. Pan-Private Streaming Algorithms. In Proceedings of the Innovations in Computer Science—ICS 2010, Beijing, China, 5–7 January 2010; pp. 66–80. [Google Scholar]
- Duchi, J.C.; Jordan, M.I.; Wainwright, M.J. Local privacy and statistical minimax rates. In Proceedings of the 2013 IEEE 54th Annual Symposium on Foundations of Computer Science, Berkeley, CA, USA, 26–29 October 2013; pp. 429–438. [Google Scholar]
- Ye, Q.; Meng, X.; Zhu, M.; Huo, Z. Survey on local differential privacy. J. Softw. 2018, 29, 1981–2005. [Google Scholar]
- Chen, R.; Li, H.; Qin, A.K.; Kasiviswanathan, S.P.; Jin, H. Private spatial data aggregation in the local setting. In Proceedings of the 2016 IEEE 32nd International Conference on Data Engineering (ICDE), Helsinki, Finland, 16–20 May 2016; pp. 289–300. [Google Scholar]
- McSherry, F.D. Privacy integrated queries: An extensible platform for privacy-preserving data analysis. In Proceedings of the 2009 ACM SIGMOD International Conference on Management of Data, Providence, RI, USA, 29 June–2 July 2009; pp. 19–30. [Google Scholar]
- Warner, S.L. Randomized response: A survey technique for eliminating evasive answer bias. J. Am. Stat. Assoc. 1965, 60, 63–69. [Google Scholar] [CrossRef] [PubMed]
- Fanti, G.; Pihur, V.; Erlingsson, Ú. Building a RAPPOR with the unknown: Privacy-preserving learning of associations and data dictionaries. arXiv 2015, arXiv:1503.01214. [Google Scholar] [CrossRef]
- Erlingsson, Ú.; Pihur, V.; Korolova, A. Rappor: Randomized aggregatable privacy-preserving ordinal response. In Proceedings of the 2014 ACM SIGSAC Conference on Computer and Communications Security, Scottsdale, AZ, USA, 3–7 November 2014; pp. 1054–1067. [Google Scholar]
- Bassily, R.; Smith, A. Local, private, efficient protocols for succinct histogram. In Proceedings of the Forty-Seventh Annual ACM Symposium on Theory of Computing, Portland, OR, USA, 14–17 June 2015; pp. 127–135. [Google Scholar]
- Kairouz, P.; Oh, S.; Viswanath, P. Extremal mechanisms for local differential privacy. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; Volume 27. [Google Scholar]
- Duchi, J.C.; Jordan, M.I.; Wainwright, M.J. Local privacy, data processing inequalities, and statistical minimax rates. arXiv 2013, arXiv:1302.3203. [Google Scholar]
- Duchi, J.C.; Jordan, M.I.; Wainwright, M.J. Privacy aware learning. J. ACM (JACM) 2014, 61, 1–57. [Google Scholar] [CrossRef]
- Nguyên, T.T.; Xiao, X.; Yang, Y.; Hui, S.C.; Shin, H.; Shin, J. Collecting and analyzing data from smart device users with local differential privacy. arXiv 2016, arXiv:1606.05053. [Google Scholar]
- Andrés, M.E.; Bordenabe, N.E.; Chatzikokolakis, K.; Palamidessi, C. Geo-indistinguishability: Differential privacy for location-based systems. In Proceedings of the 2013 ACM SIGSAC Conference on Computer & Communications Security, Berlin, Germany, 4–8 November 201 3; pp. 901–914.
- Duchi, J.C.; Jordan, M.I.; Wainwright, M.J. Minimax optimal procedures for locally private estimation. J. Am. Stat. Assoc. 2018, 113, 182–201. [Google Scholar] [CrossRef]
- Wang, N.; Xiao, X.; Yang, Y.; Zhao, J.; Hui, S.C.; Shin, H.; Shin, J.; Yu, G. Collecting and analyzing multidimensional data with local differential privacy. In Proceedings of the 2019 IEEE 35th International Conference on Data Engineering (ICDE), Macao, 8–11 April 2019; pp. 638–649. [Google Scholar]
- Qardaji, W.; Yang, W.; Li, N. Differentially private grids for geospatial data. In Proceedings of the 2013 IEEE 29th International Conference on Data Engineering (ICDE), Brisbane, QLD, Australia, 8–12 April 2013; pp. 757–768. [Google Scholar]
- Bentley, J.L. Multidimensional binary search trees used for associative searching. Commun. ACM 1975, 18, 509–517. [Google Scholar] [CrossRef]
- Samet, H. The quadtree and related hierarchical data structure. ACM Comput. Surv. (CSUR) 1984, 16, 187–260. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, R.; Wu, D.; Wang, H.; Song, H.; Ma, X. Local trajectory privacy protection in 5G enabled industrial intelligent logistics. IEEE Trans. Ind. Inform. 2021, 18, 2868–2876. [Google Scholar] [CrossRef]
- Integrated Public Use Micro-Samples, “IPUMS”. UPS Driver Kidnapped, Packages Stolen in Brazen Atlanta Heist. Available online: https://www.ipums.org (accessed on 10 October 2021).
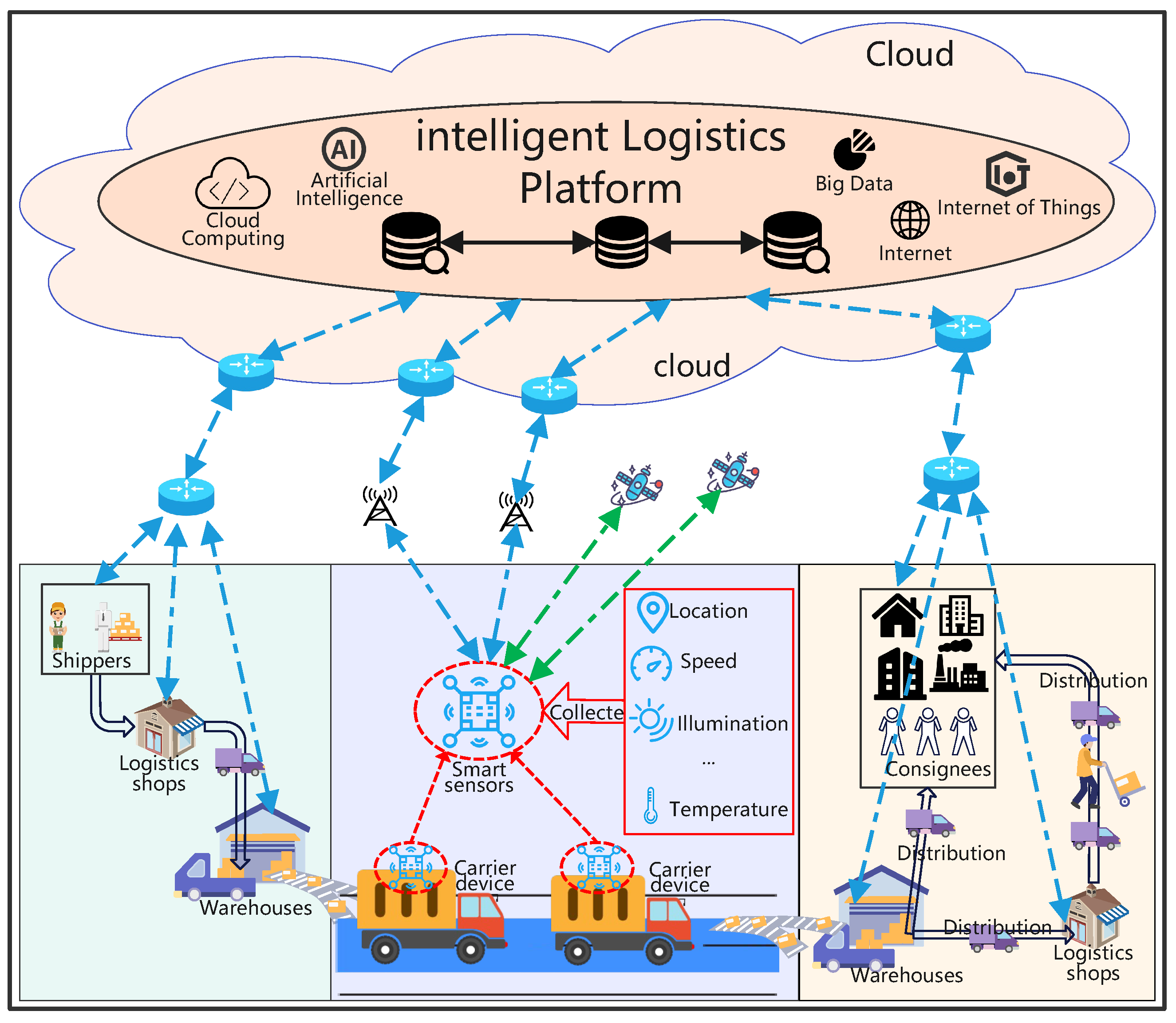






| Researches | Shippers | Consignees | Carriers | Characteristics |
|---|---|---|---|---|
| Paper [15] | ✓ | ✓ | ✕ | Optimizing logistics costs with the use of artificial intelligence and encryption technology to protect users’ private information. |
| Paper [16] | ✓ | ✓ | ✕ | Update and clear tracking and tracing data associated with a given job or partnership under a predefined partnership. |
| Paper [17] | ✓ | ✓ | ✕ | Attribute-based encryption and location-based key exchange for mobile device access control. |
| Paper [18] | ✓ | ✕ | ✕ | The k-anonymity model protects the logistic information, but the consignee’s information is still printed on the logistic face-sheet. |
| Paper [19] | ✓ | ✓ | ✕ | Privacy protection for e-logistics sheets within the logistics system using QR code technology and encryption. |
| Papers [20,21] | ✓ | ✓ | ✕ | The use of QR code technology to solve the problem of privacy leakage caused by the explicit printing of paper logistics sheets. |
| Papers [23,27] | ✓ | ✓ | ✕ | Ensure the security and privacy of logistics data with the decentralized and distributed storage features of blockchain. |
| Papers [24,25] | ✓ | ✓ | ✕ | Ensure the security and privacy of logistics data using the trustworthiness, tamper-evident, and anonymity of blockchain. |
| Paper [26] | ✓ | ✓ | ✕ | The combination of blockchain and anonymous authentication enables users to control and manage access to private data. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, Z.; Tan, L.; Yi, J.; Fu, L.; Zhang, Z.; Tan, X.; Xie, J.; She, K.; Yang, P.; Wu, W.; et al. Sensitive Data Privacy Protection of Carrier in Intelligent Logistics System. Symmetry 2024, 16, 68. https://doi.org/10.3390/sym16010068
Yao Z, Tan L, Yi J, Fu L, Zhang Z, Tan X, Xie J, She K, Yang P, Wu W, et al. Sensitive Data Privacy Protection of Carrier in Intelligent Logistics System. Symmetry. 2024; 16(1):68. https://doi.org/10.3390/sym16010068
Chicago/Turabian StyleYao, Zhengyi, Liang Tan, Junhao Yi, Luxia Fu, Zhuang Zhang, Xinghong Tan, Jingxue Xie, Kun She, Peng Yang, Wanjing Wu, and et al. 2024. "Sensitive Data Privacy Protection of Carrier in Intelligent Logistics System" Symmetry 16, no. 1: 68. https://doi.org/10.3390/sym16010068
APA StyleYao, Z., Tan, L., Yi, J., Fu, L., Zhang, Z., Tan, X., Xie, J., She, K., Yang, P., Wu, W., Ye, D., & Yu, Z. (2024). Sensitive Data Privacy Protection of Carrier in Intelligent Logistics System. Symmetry, 16(1), 68. https://doi.org/10.3390/sym16010068







