Vacuum Currents for a Scalar Field in Models with Compact Dimensions
Abstract
1. Introduction
2. General Formalism
3. Locally Minkowski Spacetime with Toral Dimensions
4. Current Density in Locally dS Spacetime with Compact Dimensions
4.1. Hadamard Function
4.2. Vacuum Current
5. AdS Spacetime with Compact Dimensions
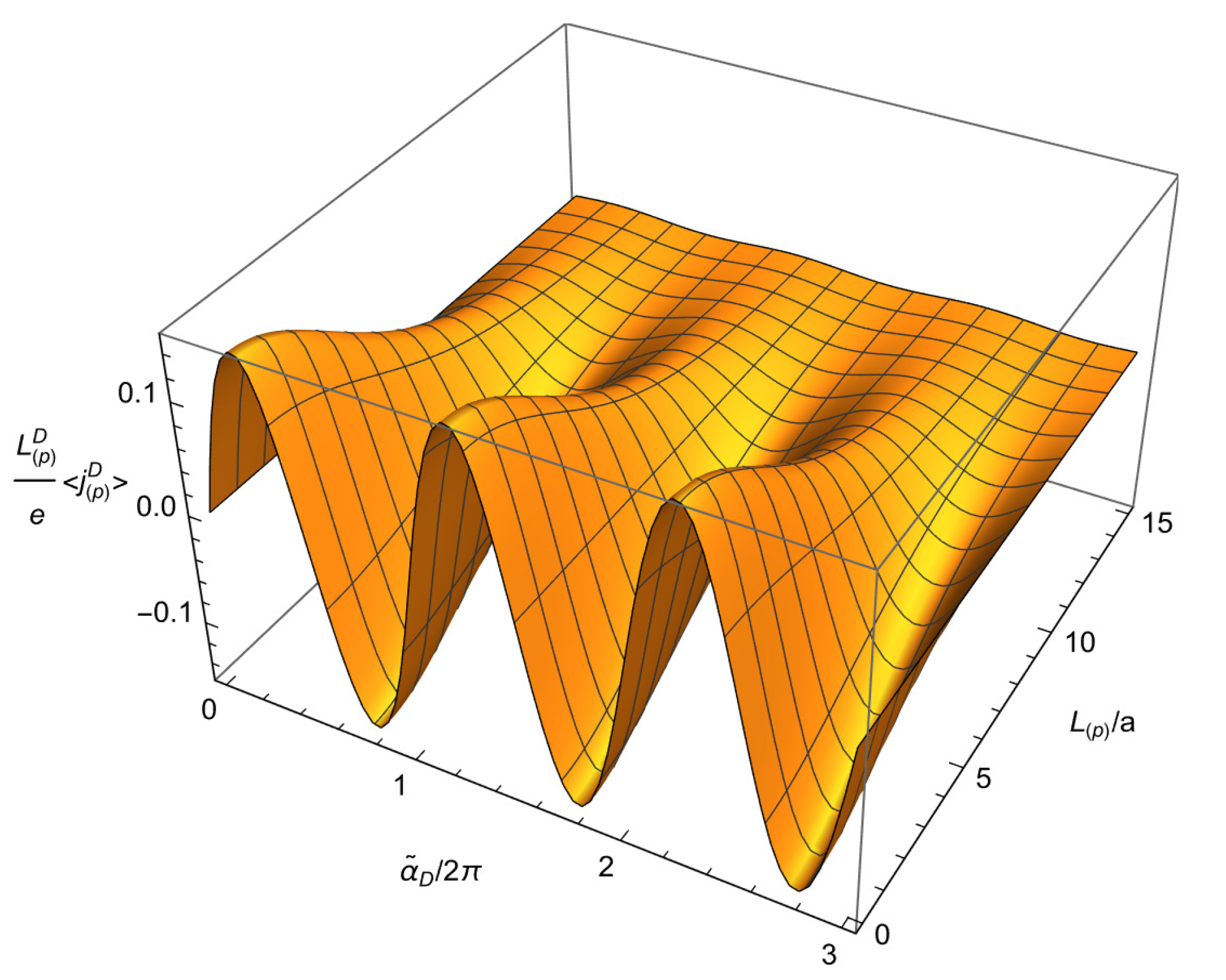
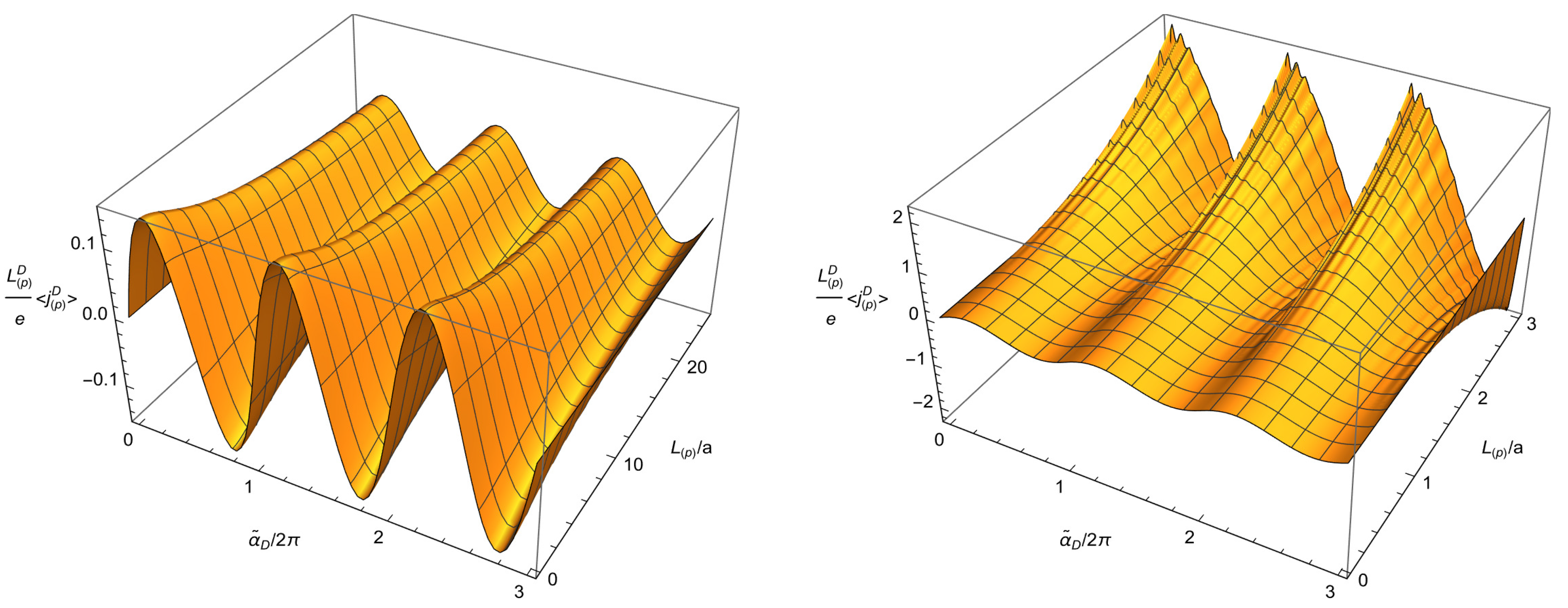
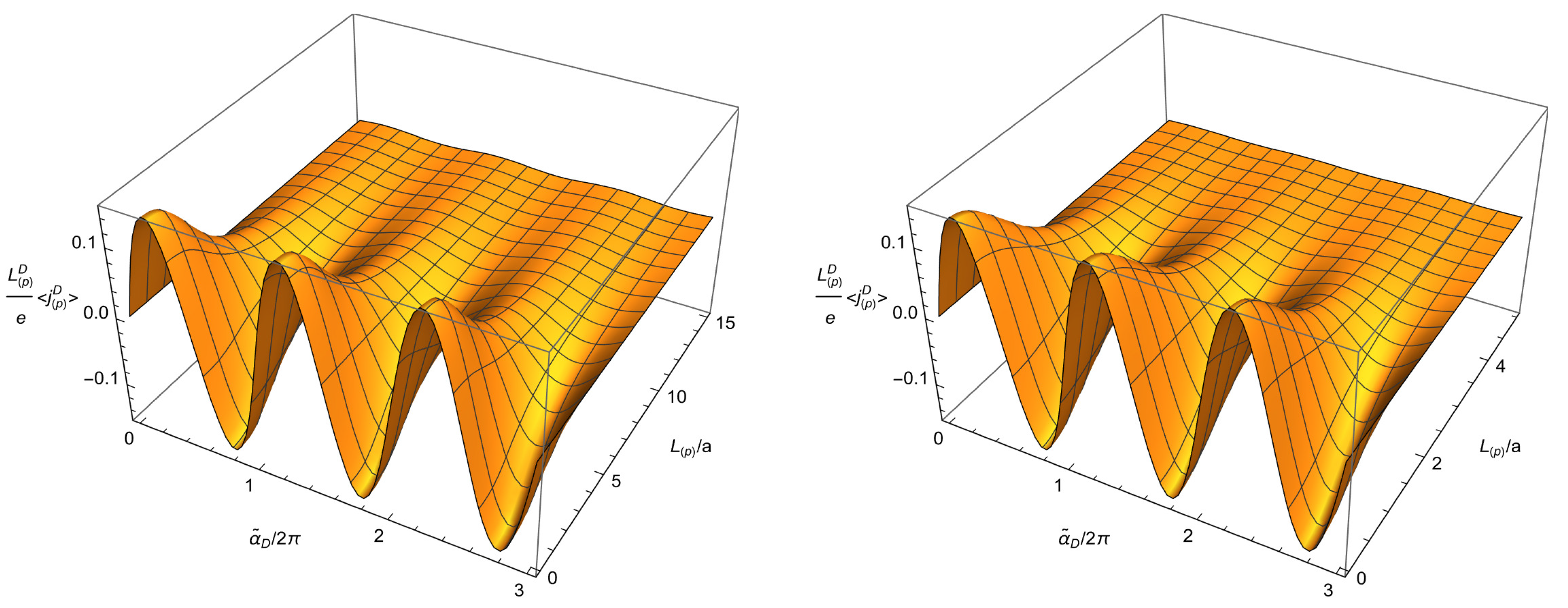
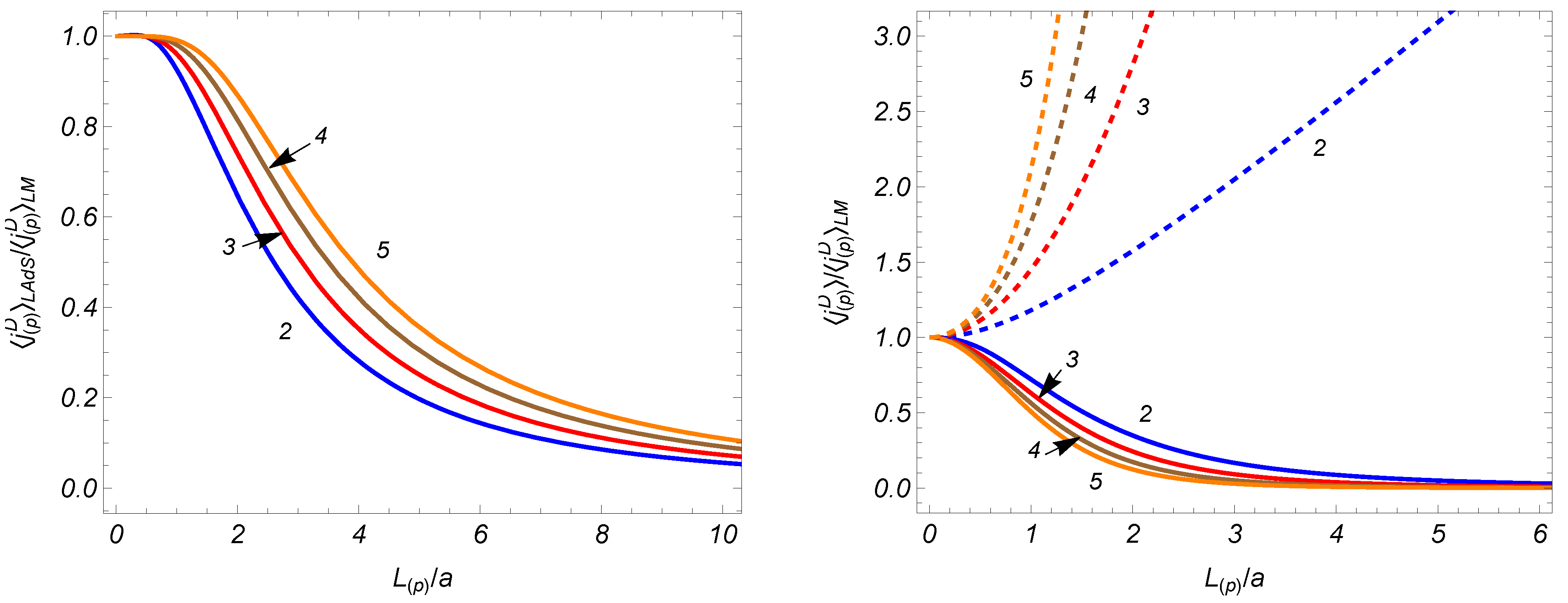
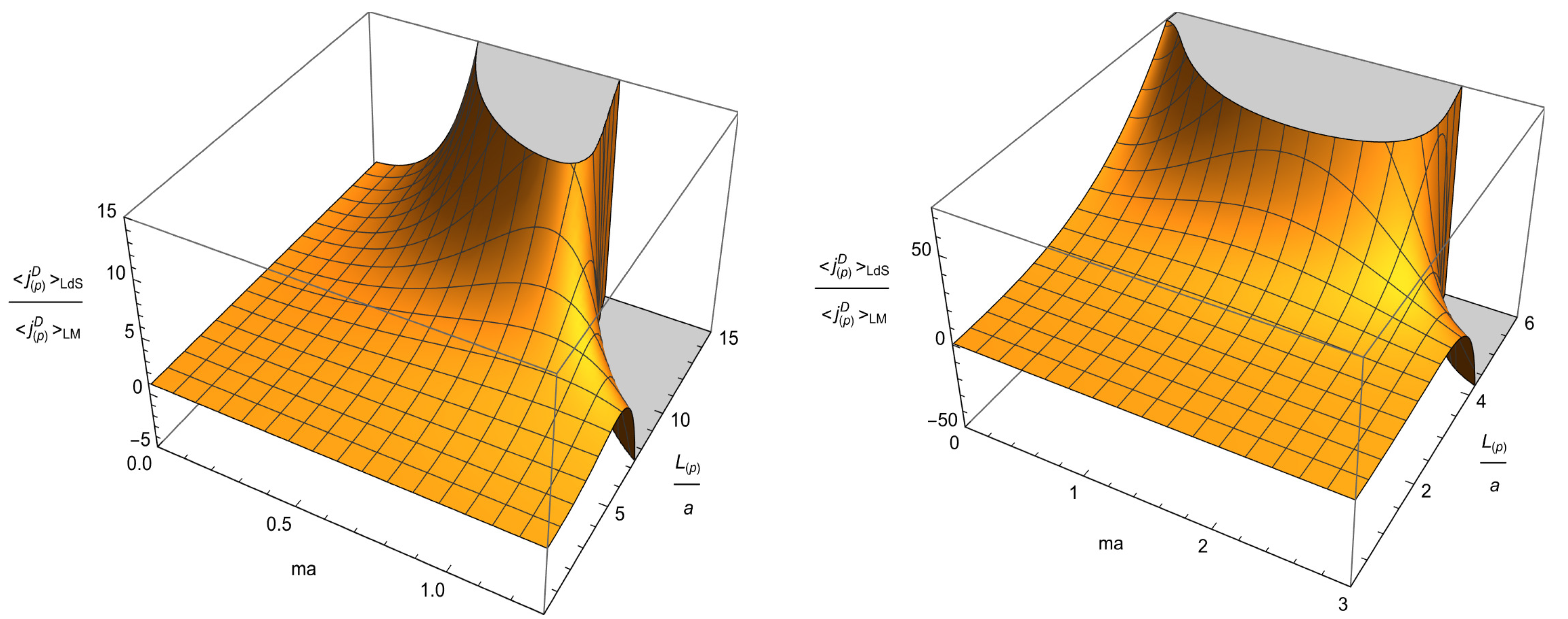
6. Features of the Current Density
6.1. General Features
6.2. Conformal Coupling and Minkowskian Limit
6.3. Large and Small Proper Lengths of Compact Dimensions
6.4. Fermionic Currents
7. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Properties of the Functions in the Expressions for the Currents
References
- Ford, L.H.; Yoshimura, T. Mass generation by self-interaction in non-Minkowskian spacetimes. Phys. Lett. A 1979, 70, 89–91. [Google Scholar] [CrossRef]
- Scherk, J.; Schwarz, J.H. How to get masses from extra dimensions. Nucl. Phys. B 1979, 153, 61–68. [Google Scholar] [CrossRef]
- Ford, L.H. Instabilities in interacting quantum field theories in non-Minkowskian spacetimes. Phys. Rev. D 1980, 22, 3003–3011. [Google Scholar] [CrossRef]
- Toms, D.J. Casimir effect and topological mass. Phys. Rev. D 1980, 21, 928–932. [Google Scholar] [CrossRef]
- Toms, D.J. Symmetry breaking and mass generation by space-time topology. Phys. Rev. D 1980, 21, 2805–2817. [Google Scholar] [CrossRef]
- Odintsov, S.D. Effective action in multidimensional gauged supergravities and spontaneous compactification. Sov. J. Nucl. Phys. 1988, 48, 729–733. [Google Scholar]
- Hosotani, Y. Dynamics of non-integrable phases and gauge symmetry breaking. Ann. Phys. 1989, 190, 233–253. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Odintsov, S.D. Spontaneous supersymmetry breaking and effective action in supersymmetrical Kaluza-Klein theories and strings. Int. J. Mod. Phys. A 1989, 4, 4337–4351. [Google Scholar] [CrossRef]
- Quiros, M. New ideas in symmetry breaking. arXiv 2003, arXiv:hep-ph/0302189. [Google Scholar]
- Mostepanenko, V.M.; Trunov, N.N. The Casimir Effect and Its Applications; Clarendon Press: Oxford, NY, USA, 1997. [Google Scholar]
- Milton, K.A. The Casimir Effect: Physical Manifestation of Zero-Point Energy; World Scientific: Singapore, 2002. [Google Scholar]
- Bordag, M.; Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Advances in the Casimir Effect; Oxford University Press: New York, NY, USA, 2009. [Google Scholar]
- Milonni, P.; Roberts, D.; da Rosa, F. Lecture Notes in Physics. In Casimir Physics; Dalvit, D., Ed.; Springer: Berlin, Germany, 2011; Volume 834. [Google Scholar]
- Elizalde, E.; Odintsov, S.D.; Romeo, A.; Bytsenko, A.A.; Zerbini, S. Zeta Regularization Techniques with Applications; World Scientific: Singapore, 1994. [Google Scholar]
- Candelas, P.; Weinberg, S. Calculation of gauge couplings and compact circumferences from self-consistent dimensional reduction. Nucl. Phys. B 1984, 237, 397–441. [Google Scholar] [CrossRef]
- Bezerra de Mello, E.R.; Saharian, A.A. Finite temperature current densities and Bose–Einstein condensation in topologically nontrivial spaces. Phys. Rev. D 2013, 87, 045015. [Google Scholar] [CrossRef]
- Bellucci, S.; Saharian, A.A.; Bardeghyan, V.M. Induced fermionic current in toroidally compactified spacetimes with applications to cylindrical and toroidal nanotubes. Phys. Rev. D 2010, 82, 065011. [Google Scholar] [CrossRef]
- Gusynin, V.P.; Sharapov, S.G.; Carbotte, J.P. AC conductivity of graphene: From tight-binding model to 2+1-dimensional quantum electrodynamics. Int. J. Mod. Phys. B 2007, 21, 4611–4658. [Google Scholar] [CrossRef]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Bellucci, S.; Saharian, A.A.; Saharyan, N.A. Casimir effect for scalar current densities in topologically nontrivial spaces. Eur. Phys. J. C 2015, 75, 378. [Google Scholar] [CrossRef]
- Bellucci, S.; Saharian, A.A. Fermionic current from topology and boundaries with applications to higher-dimensional models and nanophysics. Phys. Rev. D 2013, 87, 025005. [Google Scholar] [CrossRef]
- Bellucci, S.; Saharian, A.A.; Nersisyan, H.A. Scalar and fermionic vacuum currents in de Sitter spacetime with compact dimensions. Phys. Rev. D 2013, 88, 024028. [Google Scholar] [CrossRef]
- Bezerra de Mello, E.R.; Saharian, A.A.; Vardanyan, V. Induced vacuum currents in anti-de Sitter space with toral dimensions. Phys. Lett. B 2015, 741, 155–162. [Google Scholar] [CrossRef]
- Bellucci, S.; Saharian, A.A.; Vardanyan, V. Fermionic currents in AdS spacetime with compact dimensions. Phys. Rev. D 2017, 96, 065025. [Google Scholar] [CrossRef]
- Bellucci, S.; Saharian, A.A.; Vardanyan, V. Vacuum currents in braneworlds on AdS bulk with compact dimensions. JHEP 2015, 11, 092. [Google Scholar] [CrossRef]
- Bellucci, S.; Saharian, A.A.; Vardanyan, V. Hadamard function and the vacuum currents in braneworlds with compact dimensions: Two-branes geometry. Phys. Rev. D 2016, 93, 084011. [Google Scholar] [CrossRef]
- Bellucci, S.; Saharian, A.A.; Simonyan, D.H.; Vardanyan, V.V. Fermionic currents in topologically nontrivial braneworlds. Phys. Rev. D 2018, 98, 085020. [Google Scholar] [CrossRef]
- Bellucci, S.; Saharian, A.A.; Sargsyan, H.G.; Vardanyan, V.V. Fermionic vacuum currents in topologically nontrivial braneworlds: Two-brane geometry. Phys. Rev. D 2020, 101, 045020. [Google Scholar] [CrossRef]
- Büttiker, M.; Imry, Y.; Landauer, R. Josephson behavior in small normal one-dimensional rings. Phys. Lett. A 1983, 96, 365–367. [Google Scholar] [CrossRef]
- Cheung, H.-F.; Gefen, Y.; Riedel, E.K.; Shih, W.-H. Persistent currents in small one-dimensional metal rings. Phys. Rev. B 1988, 37, 6050–6062. [Google Scholar] [CrossRef]
- Cheung, H.-F.; Riedel, E.K.; Gefen, Y. Persistent currents in mesoscopic rings and cylinders. Phys. Rev. Lett. 1989, 62, 587–590. [Google Scholar] [CrossRef] [PubMed]
- Altshuler, B.L.; Gefen, Y.; Imry, Y. Persistent differences between canonical and grand canonical averages in mesoscopic ensembles: Large paramagnetic orbital susceptibilities. Phys. Rev. Lett. 1991, 66, 88–91. [Google Scholar] [CrossRef] [PubMed]
- von Oppen, F.; Riedel, E.K. Average persistent current in a mesoscopic ring. Phys. Rev. Lett. 1991, 66, 84–87. [Google Scholar] [CrossRef]
- Abraham, M.; Berkovits, R. Persistent currents in an interacting 1D disordered ring: Manifestations of the Mott-Hubbard transition. Phys. Rev. Lett. 1993, 70, 1509–1512. [Google Scholar] [CrossRef]
- Recher, P.; Trauzettel, B.; Rycerz, A.; Blanter, Y.M.; Beenakker, C.W.J.; Morpurgo, A.F. Aharonov–Bohm effect and broken valley degeneracy in graphene rings. Phys. Rev. B 2007, 76, 235404. [Google Scholar] [CrossRef]
- Imry, Y. Introduction to Mesoscopic Physics; Oxford University Press: New York, NY, USA, 2008. [Google Scholar]
- Akkermans, E.; Montambaux, G. Mesoscopic Physics of Electrons and Photons; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Michetti, P.; Recher, P. Bound states and persistent currents in topological insulator rings. Phys. Rev. B 2011, 83, 125420. [Google Scholar] [CrossRef]
- Huang, B.-L.; Chang, M.-C.; Mou, C.-Y. Persistent currents in a graphene ring with armchair edges. J. Phys. Condens. Matter 2012, 24, 245304. [Google Scholar] [CrossRef] [PubMed]
- Sticlet, D.; Dóra, B.; Cayssol, J. Persistent currents in Dirac fermion rings. Phys. Rev. B 2013, 88, 205401. [Google Scholar] [CrossRef]
- Ghosh, S.; Saha, A. Persistent current of relativistic electrons on a Dirac ring in presence of impurities. Eur. Phys. J. B 2014, 87, 167. [Google Scholar] [CrossRef][Green Version]
- Bolivar, N.; Medina, E.; Berche, B. Persistent charge and spin currents in the long-wavelength regime for graphene rings. Phys. Rev. B 2014, 89, 125413. [Google Scholar] [CrossRef]
- Ying, L.; Lai, Y.-C. Robustness of persistent currents in two-dimensional Dirac systems with disorder. Phys. Rev. B 2017, 96, 165407. [Google Scholar] [CrossRef]
- Amico, L.; Birkl, G.; Boshier, M.; Kwek, L.-C. Focus on atomtronics-enabled quantum technologies. New J. Phys. 2017, 19, 020201. [Google Scholar] [CrossRef]
- Fomin, V.M. (Ed.) Physics of Quantum Rings; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar]
- Jurkowski, P.; Szafran, B. Persistent currents in topological and trivial confinement in silicene. Phys. Rev. B 2020, 101, 075408. [Google Scholar] [CrossRef]
- Yerin, Y.; Gusynin, V.P.; Sharapov, S.G.; Varlamov, A.A. Genesis and fading away of persistent currents in a Corbino disk geometry. Phys. Rev. B 2021, 104, 075415. [Google Scholar] [CrossRef]
- Tengstrand, M.N.; Boholm, D.; Sachdeva, R.; Bengtsson, J.; Reimann, S.M. Persistent currents in toroidal dipolar supersolids. Phys. Rev. B 2021, 103, 013313. [Google Scholar] [CrossRef]
- Amico, L.; Anderson, D.; Boshier, M.; Brantut, J.-P.; Kwek, L.-C.; Minguzzi, A.; von Klitzing, W. Colloquium: Atomtronic circuits: From many-body physics to quantum technologies. Rev. Mod. Phys. 2022, 94, 041001. [Google Scholar] [CrossRef]
- Chetcuti, W.J.; Haug, T.; Kwek, L.-C.; Amico, L. Persistent current of SU(N) fermions. SciPost Phys. 2022, 12, 033. [Google Scholar] [CrossRef]
- Lévy, L.P.; Dolan, G.; Dunsmuir, J.; Bouchiat, H. Magnetization of mesoscopic copper rings: Evidence for persistent currents. Phys. Rev. Lett. 1990, 64, 2074. [Google Scholar] [CrossRef] [PubMed]
- Chandrasekhar, V.; Webb, R.A.; Brady, M.J.; Ketchen, M.B.; Gallagher, W.J.; Kleinsasser, A. Magnetic response of a single, isolated gold loop. Phys. Rev. Lett. 1991, 67, 3578–3581. [Google Scholar] [CrossRef] [PubMed]
- Mailly, D.; Chapelier, C.; Benoit, A. Experimental observation of persistent currents in a GaAs-AlGaAs single loop. Phys. Rev. Lett. 1993, 70, 2020–2023. [Google Scholar] [CrossRef] [PubMed]
- Kleemans, N.A.J.M.; Bominaar-Silkens, I.M.A.; Fomin, V.M.; Gladilin, V.N.; Granados, D.; Taboada, A.G.; García, J.M.; Offermans, P.; Zeitler, U.; Christianen, P.C.M.; et al. Oscillatory persistent currents in self-assembled quantum rings. Phys. Rev. Lett. 2007, 99, 146808. [Google Scholar] [CrossRef] [PubMed]
- Bleszynski-Jayich, A.C.; Shanks, W.E.; Peaudecerf, B.; Ginossar, E.; von Oppen, F.; Glazman, L.; Harris, J.G.E. Persistent currents in normal metal rings. Science 2009, 326, 272. [Google Scholar] [CrossRef]
- Bluhm, H.; Koshnick, N.C.; Bert, J.A.; Huber, M.E.; Moler, K.A. Persistent currents in normal metal rings. Phys. Rev. Lett. 2009, 102, 136802. [Google Scholar] [CrossRef]
- Souche, G.M.; Huillery, J.; Pothier, H.; Gandit, P.; Mars, J.I.; Skipetrov, S.E.; Bourgeois, O. Searching for thermal signatures of persistent currents in normal-metal rings. Phys. Rev. B 2013, 87, 115120. [Google Scholar] [CrossRef]
- Cai, Y.; Allman, D.G.; Sabharwal, P.; Wright, K.C. Persistent currents in rings of ultracold fermionic atoms. Phys. Rev. Lett. 2022, 128, 150401. [Google Scholar] [CrossRef]
- Pace, G.D.; Xhani, K.; Falconi, A.M.; Fedrizzi, M.; Grani, N.; Rajkov, D.H.; Inguscio, M.; Scazza, F.; Kwon, W.J.; Roati, G. Imprinting persistent currents in tunable fermionic rings. Phys. Rev. X 2022, 12, 041037. [Google Scholar]
- Hooft, G.T. A property of electric and magnetic flux in non-Abelian gauge theories. Nucl. Phys. 1979, B153, 141–160. [Google Scholar] [CrossRef]
- González-Arroyo, A. Yang–Mills fields on the 4-dimensional torus. Part I: Classical theory. arXiv 1998, arXiv:hep-th/9807108. [Google Scholar]
- Anber, M.M.; Poppitz, E. Nonperturbative effects in the Standard Model with gauged 1-form symmetry. JHEP 2021, 12, 055. [Google Scholar] [CrossRef]
- Elizalde, E. Spectrum of the Casimir effect on a torus. Z. Phys. C 1989, 44, 471–478. [Google Scholar] [CrossRef]
- Tanaka, T.; Hiscock, W.A. Massive scalar field in multiply connected flat spacetimes. Phys. Rev. D 1995, 52, 4503–4511. [Google Scholar] [CrossRef]
- Kleinert, H.; Zhuk, A. The Casimir effect at nonzero temperatures in a Universe with topology S1 × S1 × S1. Theor. Math. Phys. 1996, 108, 1236–1248. [Google Scholar] [CrossRef]
- Hofmann, R.; Kanti, P.; Pospelov, M. (De)stabilization of an extra dimension due to a Casimir force. Phys. Rev. D 2001, 63, 124020. [Google Scholar] [CrossRef]
- Ahmadi, N.; Nouri-Zonoz, M. Massive spinor fields in flat spacetimes with nontrivial topology. Phys. Rev. D 2005, 71, 104012. [Google Scholar] [CrossRef]
- Elizalde, E. Uses of zeta regularization in QFT with boundary conditions: A cosmo-topological Casimir effect. J. Phys. A 2006, 39, 6299–6307. [Google Scholar] [CrossRef]
- Elizalde, E.; Odintsov, S.D.; Saharian, A.A. Repulsive Casimir effect from extra dimensions and Robin boundary conditions: From branes to pistons. Phys. Rev. D 2009, 79, 065023. [Google Scholar] [CrossRef]
- Bellucci, S.; Saharian, A.A. Fermionic Casimir densities in toroidally compactified spacetimes with applications to nanotubes. Phys. Rev. D 2009, 79, 085019. [Google Scholar] [CrossRef]
- Asorey, M.; Cavero-Peláez, I.; Muñoz-Castañeda, M. Vacuum Energy and the Topology of the Universe. In Cosmology, Quantum Vacuum and Zeta Functions; Odintsov, S.D., Sáez-Gómes, D., Xambó-Descamps, S., Eds.; Springer: Berlin, Germany, 2011; pp. 35–44. [Google Scholar]
- Oikonomou, V.K. Shape of compact toroidal dimensions and Casimir effect on spacetime. Commun. Theor. Phys. 2011, 55, 101–110. [Google Scholar] [CrossRef]
- Fornal, B.; Wise, M.B. Standard model with compactified spatial dimensions. JHEP 2011, 7, 086. [Google Scholar] [CrossRef]
- Abreu, L.M.; Linhares, C.A.; Malbouisson, A.P.C.; Malbouisson, J.M.C. Magnetic effects on spontaneous symmetry breaking/restoration in a toroidal topology. Phys. Rev. D 2013, 88, 107701. [Google Scholar] [CrossRef]
- Cao, C.J.; van Caspel, M.; Zhitnitsky, A.R. Topological Casimir effect in Maxwell electrodynamics on a compact manifold. Phys. Rev. D 2013, 87, 105012. [Google Scholar] [CrossRef]
- Khanna, F.C.; Malbouisson, A.P.C.; Malbouisson, J.M.C.; Santana, A.E. Quantum field theory on toroidal topology: Algebraic structure and applications. Phys. Rep. 2014, 539, 135–224. [Google Scholar] [CrossRef]
- Moreira, R.P.M.; Petronilo, G.X.A.; Santana, A.E.; Amorim, R.G.G.; Belich, H. CPT-even electrodynamics in a multidimensional torus: Casimir effect at finite temperature. Eur. Phys. J. C 2022, 82, 999. [Google Scholar] [CrossRef]
- Haridev, S.R.; Samantray, P. Revisiting vacuum energy in compact spacetimes. Phys. Lett. B 2022, 835, 137489. [Google Scholar] [CrossRef]
- Bellucci, S.; Bezerra de Mello, E.R.; Saharian, A.A. Finite temperature fermionic condensate and currents in topologically nontrivial spaces. Phys. Rev. D 2014, 89, 085002. [Google Scholar] [CrossRef]
- Bezerra de Mello, E.R.; Saharian, A.A. Fermionic vacuum polarization by a composite topological defect in higher-dimensional space-time. Phys. Rev. D 2008, 78, 045021. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. (Eds.) Handbook of Mathematical Functions; Dover: New York, NY, USA, 1972. [Google Scholar]
- Kirsten, K. Spectral Functions in Mathematics and Physics; Chapman and Hall/CRC: Boca Raton, FL, USA, 2002. [Google Scholar]
- Elizalde, E. Ten Physical Applications of Spectral Zeta Functions; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Elizalde, E. Multidimensional extension of the generalized Chowla-Selberg formula. Commun. Math. Phys. 1998, 198, 83–95. [Google Scholar] [CrossRef]
- Griffiths, J.B.; Podolský, J. Exact Space-Times in Einstein’s General Relativity; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Bunch, T.S.; Davies, P.C.W. Quantum field theory in de Sitter space: Renormalization by point-splitting. Proc. R. Soc. Lond. Ser. A 1978, 360, 117–134. [Google Scholar]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series; Gordon and Breach: New York, NY, USA, 1986; Volume 2. [Google Scholar]
- Aharony, O.; Gubser, S.S.; Maldacena, J.; Ooguri, H.; Oz, Y. Large N field theories, string theory and gravity. Phys. Rep. 2000, 323, 183–386. [Google Scholar] [CrossRef]
- Năstase, H. Introduction to AdS/CFT Correspondence; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Ammon, M.; Erdmenger, J. Gauge/Gravity Duality: Foundations and Applications; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Natsuume, M. AdS/CFT Duality User Guide; Lecture Notes in Physics; Springer: Tokyo, Japan, 2015; Volume 903. [Google Scholar]
- Maartens, R.; Koyama, K. Brane-world gravity. Living Rev. Relativ. 2010, 13, 5. [Google Scholar] [CrossRef]
- Breitenlohner, P.; Freedman, D.Z. Positive energy in anti-de Sitter backgrounds and gauged extended supergravity. Phys. Lett. B 1982, 115, 197–201. [Google Scholar] [CrossRef]
- Breitenlohner, P.; Freedman, D.Z. Stability in gauged extended supergravity. Ann. Phys. 1982, 144, 249–281. [Google Scholar] [CrossRef]
- Mezincescu, L.; Townsend, P.K. Stability at a local maximum in higher dimensional anti-de Sitter space and applications to supergravity. Ann. Phys. 1985, 160, 406–419. [Google Scholar] [CrossRef]
- Ishibashi, A.; Wald, R.M. Dynamics in non-globally-hyperbolic static spacetimes: II. General analysis of prescriptions for dynamics. Class. Quantum Gravity 2003, 20, 3815–3826. [Google Scholar] [CrossRef]
- Ishibashi, A.; Wald, R.M. Dynamics in non-globally-hyperbolic static spacetimes: III. Anti-de Sitter spacetime. Class. Quantum Gravity 2004, 21, 2981–3013. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Olver, F.W. NIST Handbook of Mathematical Functions; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Dunster, T.M. Bessel functions of purely imaginary order, with an application to second-order linear differential equations having a large parameter. SIAM J. Math. Anal. 1990, 21, 995–1018. [Google Scholar] [CrossRef]
- Milton, K.A.; Wagner, J.; Kirsten, K. Casimir effect for a semitransparent wedge and an annular piston. Phys. Rev. D 2009, 80, 125028. [Google Scholar] [CrossRef]
- Kandus, A.; Kunze, K.E.; Tsagas, C.G. Primordial magnetogenesis. Phys. Rep. 2011, 505, 1–58. [Google Scholar] [CrossRef]
- Campanelli, L. Origin of cosmic magnetic fields. Phys. Rev. Lett. 2013, 111, 061301. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saharian, A.A. Vacuum Currents for a Scalar Field in Models with Compact Dimensions. Symmetry 2024, 16, 92. https://doi.org/10.3390/sym16010092
Saharian AA. Vacuum Currents for a Scalar Field in Models with Compact Dimensions. Symmetry. 2024; 16(1):92. https://doi.org/10.3390/sym16010092
Chicago/Turabian StyleSaharian, Aram A. 2024. "Vacuum Currents for a Scalar Field in Models with Compact Dimensions" Symmetry 16, no. 1: 92. https://doi.org/10.3390/sym16010092
APA StyleSaharian, A. A. (2024). Vacuum Currents for a Scalar Field in Models with Compact Dimensions. Symmetry, 16(1), 92. https://doi.org/10.3390/sym16010092






