Upper Bounds of the Third Hankel Determinant for Bi-Univalent Functions in Crescent-Shaped Domains
Abstract
1. Introduction
- (1)
- ;
- (2)
- is univalent with ;
- (3)
- is starlike with respect to ;
- (4)
- is symmetric about a real axis.
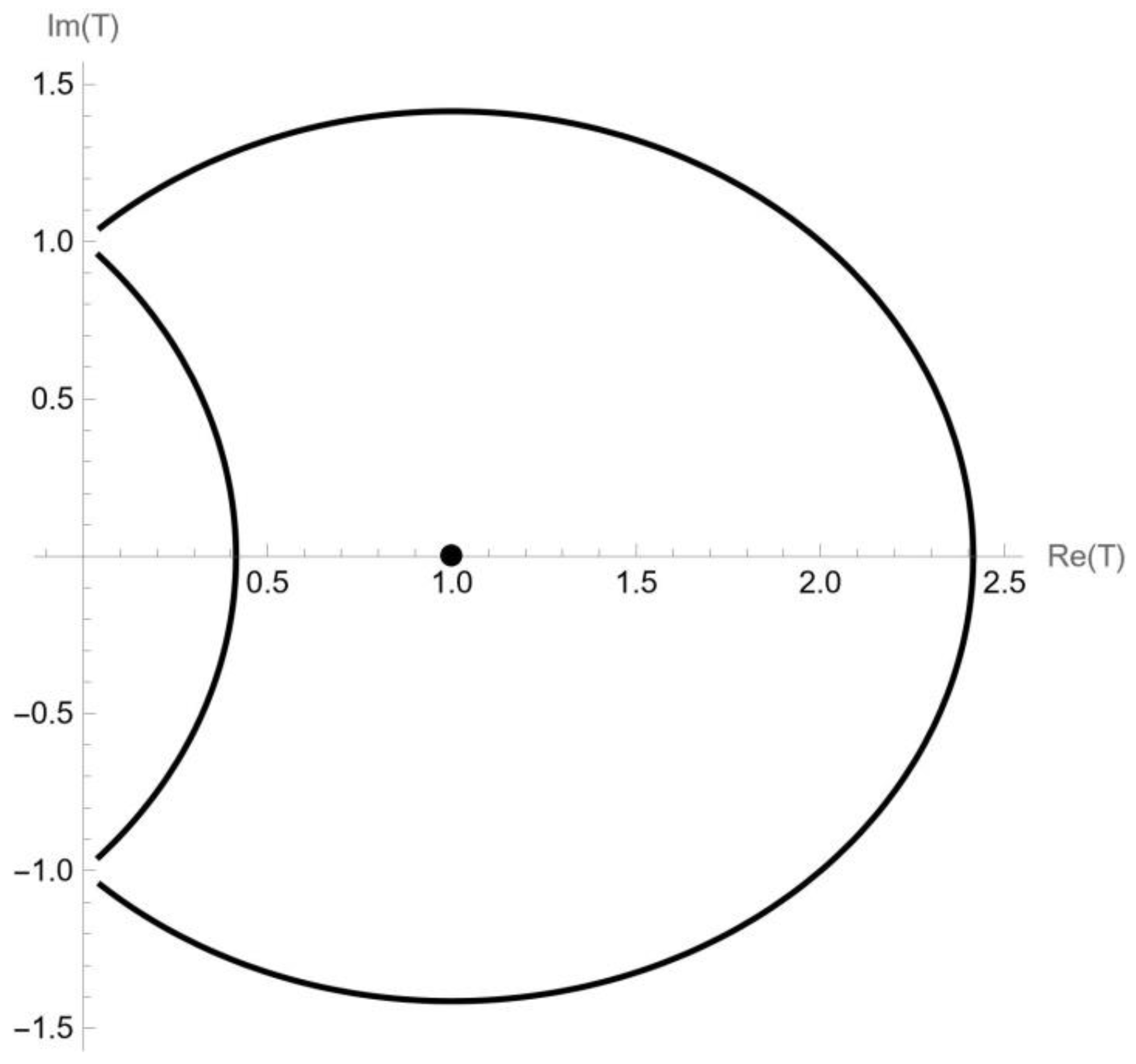
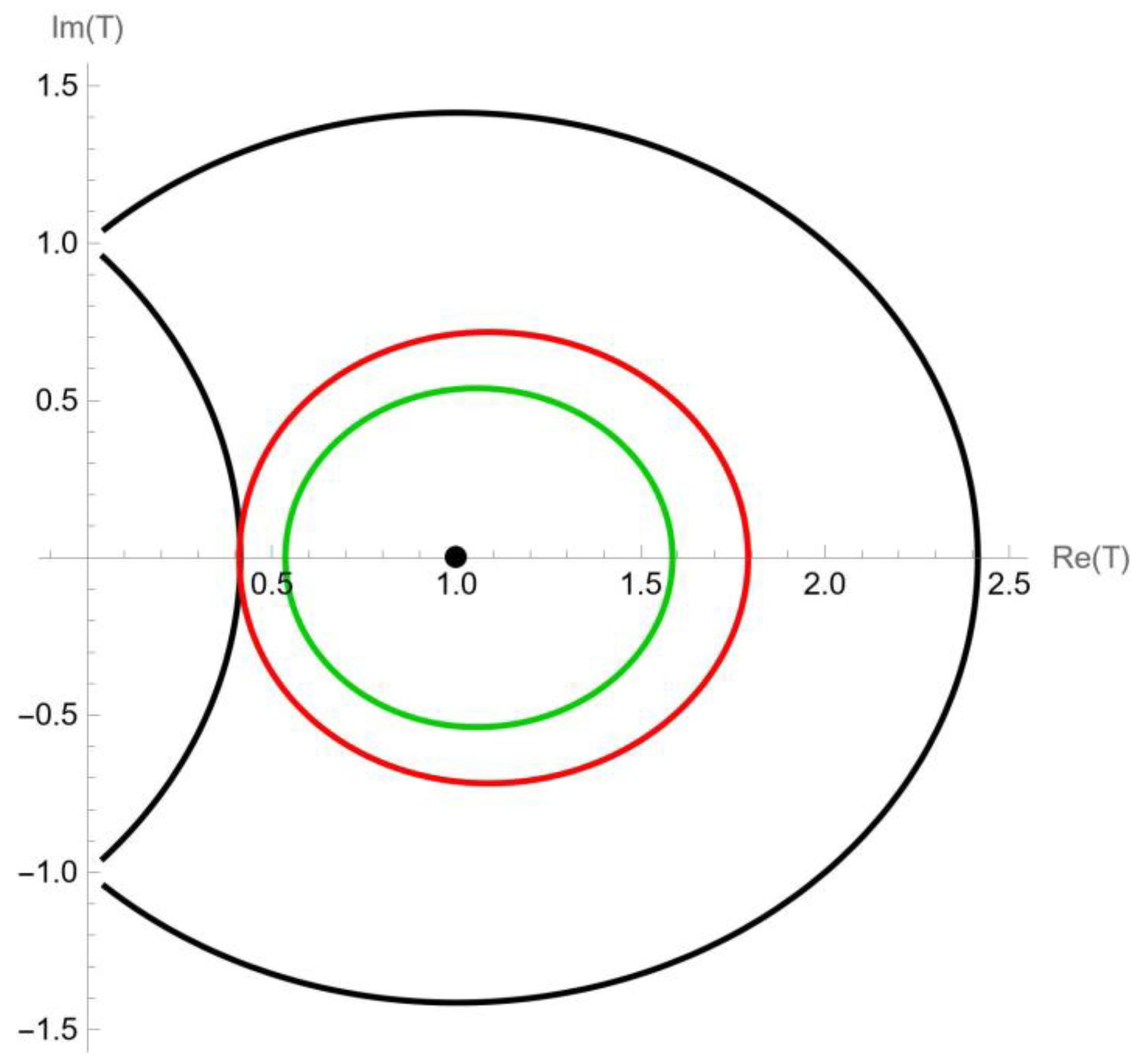
2. About
- (1)
- If , then (7) and (8) are reduced as follows:
- (2)
- If , then (7) and (8) are reduced as follows:
3. Hankel Estimates of
- Case 1: Assume that . In this case, for , and any fixed with , it is clear thati.e., is an increasing function. Hence, for fixed , the maximum of occurs at and
- Case 2: , because , , where , and it is evident that and . Thus, the maximum of occurs at and , and we obtainso, from the cases of , we obtain
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Brannan, D.A.; Taha, T.S. On some classes of bi-univalent functions. Studia Univ. Babes-Bolyai Math. 1986, 31, 70–77. [Google Scholar]
- Taha, T.S. Topics in Univalent Function Theory. Ph.D. Thesis, University of London, London, UK, 1981. [Google Scholar]
- Brannan, D.A.; Clunie, J.G. Aspects of Contemporary Complex Analysis. In Proceedings of the NATO Advanced Study Institute held at the University of Durham, Durham, UK, 1–20 July 1979; Academic Press: New York, NY, USA; London, UK, 1980. [Google Scholar]
- Lewin, M. On a coefficient problem for bi-univalent functions. Proc. Am. Math. Soc. 1967, 18, 63–68. [Google Scholar] [CrossRef]
- Netanyahu, E. The minimal distance of the image boundary from the origin and the second coefficient of a univalent function in |z| < 1. Arch. Ration. Mech. Anal. 1969, 32, 100–112. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Mishra, A.K.; Gochhayat, P. Certain subclasses of analytic and bi-univalent functions. Appl. Math. Lett. 2010, 23, 1188–1192. [Google Scholar] [CrossRef]
- Xu, Q.-H.; Gui, Y.-C.; Srivastava, H.M. Coefficient estimates for a certain subclass of analytic and bi-univalent functions. Appl. Math. Lett. 2012, 25, 990–994. [Google Scholar] [CrossRef]
- Xu, Q.-H.; Xiao, H.-G.; Srivastava, H.M. A certain general subclass of analytic and bi-univalent functions and associated coefficient estimate problems. Appl. Math. Comput. 2012, 218, 11461–11465. [Google Scholar] [CrossRef]
- Shakir, Q.A.; Atshan, W.G. On third Hankel determinant for certain subclass of bi-univalent functions. Symmetry 2024, 16, 239. [Google Scholar] [CrossRef]
- Sakar, F.M.; Aydoğan, S.M. Inequalities of bi-starlike functions involving Sigmoid function and Bernoulli Lemniscate by subordination. Int. J. Open Problems Compt. Math. 2023, 16, 71–82. [Google Scholar]
- Swamy, S.R.; Breaz, D.; Venugopal, K.; Kempegowda, M.P.; Cotîrla, L.-I.; Rapeanu, E. Initial Coefficient Bounds Analysis for Novel Subclasses of Bi-Univalent Functions Linked with Lucas-Balancing Polynomials. Mathematics 2024, 12, 1325. [Google Scholar] [CrossRef]
- Srivastava, H.M.; El-Deeb, S.M.; Breaz, D.; Cotîrla, L.-I.; Salagean, G.S. Bi-Concave Functions Connected with the Combination of the Binomial Series and the Confluent Hypergeometric Function. Symmetry 2024, 16, 226. [Google Scholar] [CrossRef]
- Ma, W.; Minda, D. A unified treatment of some special classes of functions. In Proceedings of the Conference on Complex Analysis, Tianjin, China, 19–23 June 1992; Conference Proceedings and Lecture Notes in Analysis. Li, Z., Ren, F., Yang, L., Zhang, S., Eds.; International Press: Cambridge, MA, USA, 1994; Volume I, pp. 157–169. [Google Scholar]
- Ravichandran, V.; Kumar, S.S. Argument estimate for starlike functions of reciprocal order. Southeast Asian Bull. Math. 2011, 35, 837–843. [Google Scholar]
- Raina, R.K.; Sokół, J. Some properties related to a certain class of starlike functions. C. R. Math. Acad. Sci. Paris 2015, 353, 973–978. [Google Scholar] [CrossRef]
- Gandhi, S.; Ravichandran, V. Starlike functions associated with a lune. Asian Eur. J. Math. 2017, 10, 1750064. [Google Scholar] [CrossRef]
- Raina, R.K.; Sharma, P.; Sokól, J. Certain classes of analytic functions related to the crescent-shaped regions. J. Contemp. Math. Anal. 2018, 53, 355–362. [Google Scholar] [CrossRef]
- Sharma, P.; Raina, R.K.; Sokól, J. Certain Ma–Minda type classes of analytic functions associated with the crescent-shaped region. Anal. Math. Phys. 2019, 9, 1887–1903. [Google Scholar] [CrossRef]
- Noonan, J.W.; Thomas, D.K. On the second Hankel determinant of areally mean p-valent functions. Trans. Am. Math. Soc. 1076, 223, 337–346. [Google Scholar] [CrossRef]
- Fekete, M.; Szegö, G. Eine Bemerkung über ungerade schlichte Funktionen. J. Lond. Math. Soc. 1933, 8, 85–89. [Google Scholar] [CrossRef]
- Koepf, W. On the Fekete-Szego problem for close-to-convex functions. Proc. Am. Math. Soc. 1987, 101, 89–95. [Google Scholar]
- Koepf, W. On the Fekete-Szego problem for close-to-convex functions II. Arch. Math. 1987, 49, 420–433. [Google Scholar] [CrossRef]
- Altınkaya, S.; Yalçin, S. Second hankel determinant for a general subclass of bi-univalent functions. TWMS J. Pure Appl. Math. 2016, 7, 98–104. [Google Scholar]
- Cağlar, M.; Deniz, E.; Srivastava, H.M. Second Hankel determinant for certain subclasses of bi-univalent functions. Turk. J. Math. 2017, 41, 694–706. [Google Scholar] [CrossRef]
- Deniz, E.; Cağlar, M.; Orhan, H. Second Hankel determinant for bi-starlike and bi-convex functions of order β. Appl. Math. Comput. 2015, 271, 301–307. [Google Scholar]
- Motamednezhad, A.; Bulboaca, T.; Adegani, E.A.; Dibagar, N. Second Hankel determinant for a subclass of analytic bi-univalent functions defined by subordination. Turk. J. Math. 2018, 42, 2798–2808. [Google Scholar] [CrossRef]
- Mustafa, N.; Murugusundaramoorthy, G.; Janani, T. Second Hankel determinant for a certain subclass of bi-univalent functions. Mediterr. J. Math. 2018, 15, 119. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Altınkaya, S.; Yalçin, S. Hankel determinant for a subclass of bi-univalent functions defined by using a symmetric q-derivative operator. Filomat 2018, 32, 503–516. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Murugusundaramoorthy, G.; Bulboaca, T. The second Hankel determinant for subclasses of Bi-univalent functions associated with a nephroid domain. Rev. Real Acad. Cienc. Exactas Físicas Naturales. Ser. A. Matemáticas 2022, 116, 145. [Google Scholar] [CrossRef]
- Zaprawa, P. On the Fekete-Szego problem for classes of bi-univalent functions. Bull. Belg. Math. Soc.-Simon Stevin 2014, 21, 169–178. [Google Scholar] [CrossRef]
- Altınkaya, S.; Yalçin, S. Third Hankel determinant for Bazilevic functions. Adv. Math. 2016, 5, 91–96. [Google Scholar]
- Kowalczyk, B.; Lecko, A.; Sim, Y.J. The sharp bound for the Hankel determinant of the third kind for convex functions. Bull. Aust. Math. Soc. 2018, 97, 435–445. [Google Scholar] [CrossRef]
- Shanmugam, G.; Stephen, B.A.; Babalola, K.O. Third Hankel determinant for alpha-starlike functions. Gulf J. Math. 2014, 2, 107–113. [Google Scholar] [CrossRef]
- Shi, L.; Srivastava, H.M.; Arif, M.; Hussain, S.; Khan, H. An investigation of the third Hankel determinant problem for certain subfamilies of univalent functions involving the exponential function. Symmetry 2019, 11, 598. [Google Scholar] [CrossRef]
- Zaprawa, P. Third Hankel determinants for subclasses of univalent functions. Mediterr. J. Math. 2017, 14, 19. [Google Scholar] [CrossRef]
- Duren, P.L. Univalent Functions, In Grundlehren der Mathematischen Wissenschaften, Band 259; Springer: New York, NY, USA; Berlin/Heidelberg, Germany; Tokyo, Japan, 1983. [Google Scholar]
- Grenander, U.; Szegö, G. Toeplitz Forms and Their Applications, California Monographs in Mathematical Sciences; University of California Press: Berkeley, CA, USA, 1958. [Google Scholar]
- Tayyah, A.S.; Atshan, W.G. New Results on r,k,µ-Riemann–Liouville Fractional Operators in Complex Domain with Applications. Fractal Fract. 2024, 8, 165. [Google Scholar] [CrossRef]
- Aldawish, I.; Ibrahim, R.W. Studies on a new K-symbol analytic functions generated by a modified K-symbol Riemann-Liouville fractional calculus. MethodsX 2023, 11, 102398. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shakir, Q.A.; Tayyah, A.S.; Breaz, D.; Cotîrlă, L.-I.; Rapeanu, E.; Sakar, F.M. Upper Bounds of the Third Hankel Determinant for Bi-Univalent Functions in Crescent-Shaped Domains. Symmetry 2024, 16, 1281. https://doi.org/10.3390/sym16101281
Shakir QA, Tayyah AS, Breaz D, Cotîrlă L-I, Rapeanu E, Sakar FM. Upper Bounds of the Third Hankel Determinant for Bi-Univalent Functions in Crescent-Shaped Domains. Symmetry. 2024; 16(10):1281. https://doi.org/10.3390/sym16101281
Chicago/Turabian StyleShakir, Qasim Ali, Adel Salim Tayyah, Daniel Breaz, Luminita-Ioana Cotîrlă, Eleonora Rapeanu, and Fethiye Müge Sakar. 2024. "Upper Bounds of the Third Hankel Determinant for Bi-Univalent Functions in Crescent-Shaped Domains" Symmetry 16, no. 10: 1281. https://doi.org/10.3390/sym16101281
APA StyleShakir, Q. A., Tayyah, A. S., Breaz, D., Cotîrlă, L.-I., Rapeanu, E., & Sakar, F. M. (2024). Upper Bounds of the Third Hankel Determinant for Bi-Univalent Functions in Crescent-Shaped Domains. Symmetry, 16(10), 1281. https://doi.org/10.3390/sym16101281









