On a Symmetry-Based Structural Deterministic Fractal Fractional Order Mathematical Model to Investigate Conjunctivitis Adenovirus Disease
Abstract
:1. Introduction
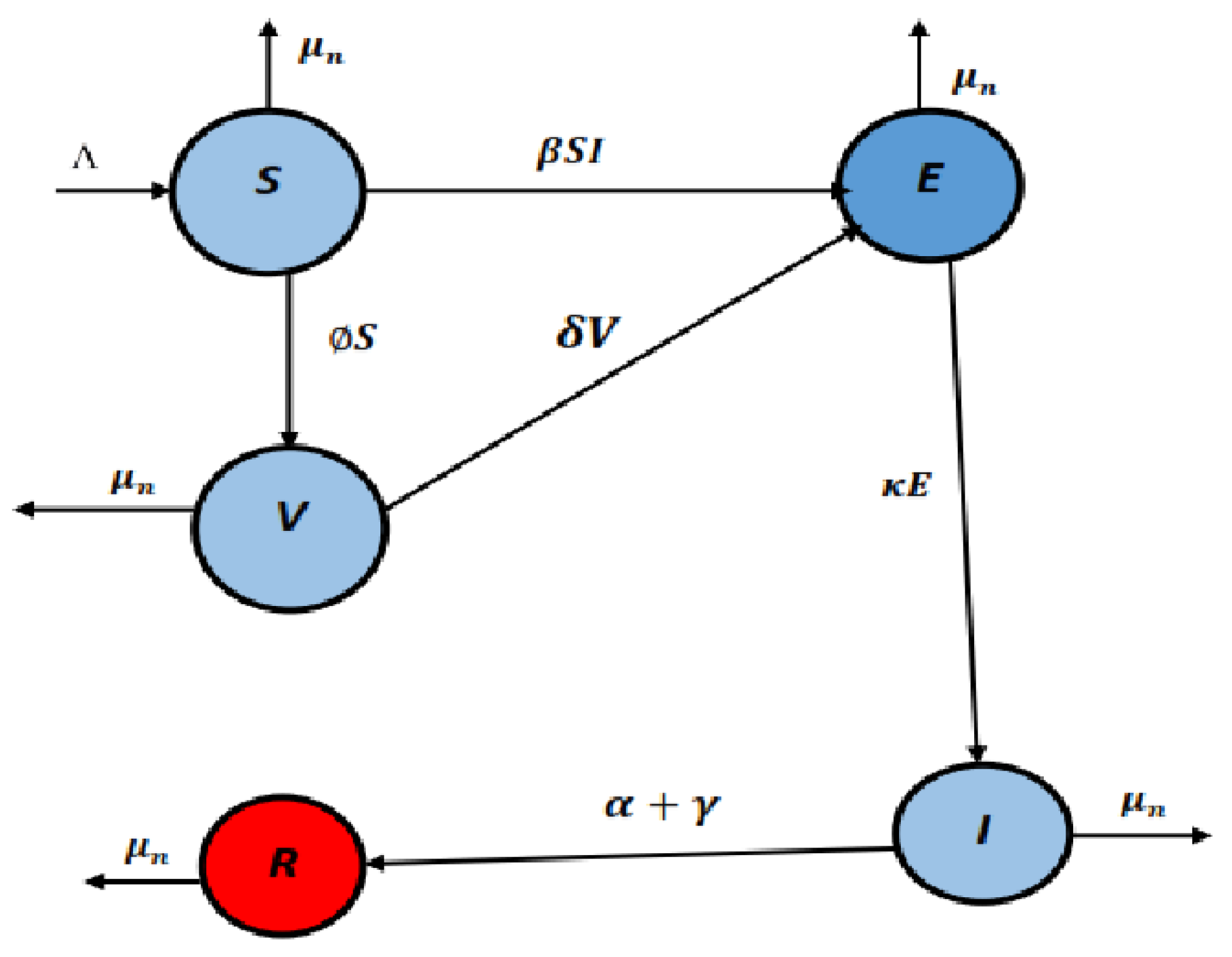
2. Formulation of the Model
3. Basic Results and Tools
4. Some Basic Results
4.1. Positivity and Boundedness
4.2. Equilibrium Points and Reproduction Number
- if , then is globally asymptotically stable.
- where , for , while is an M-matrix, and is the feasible region.
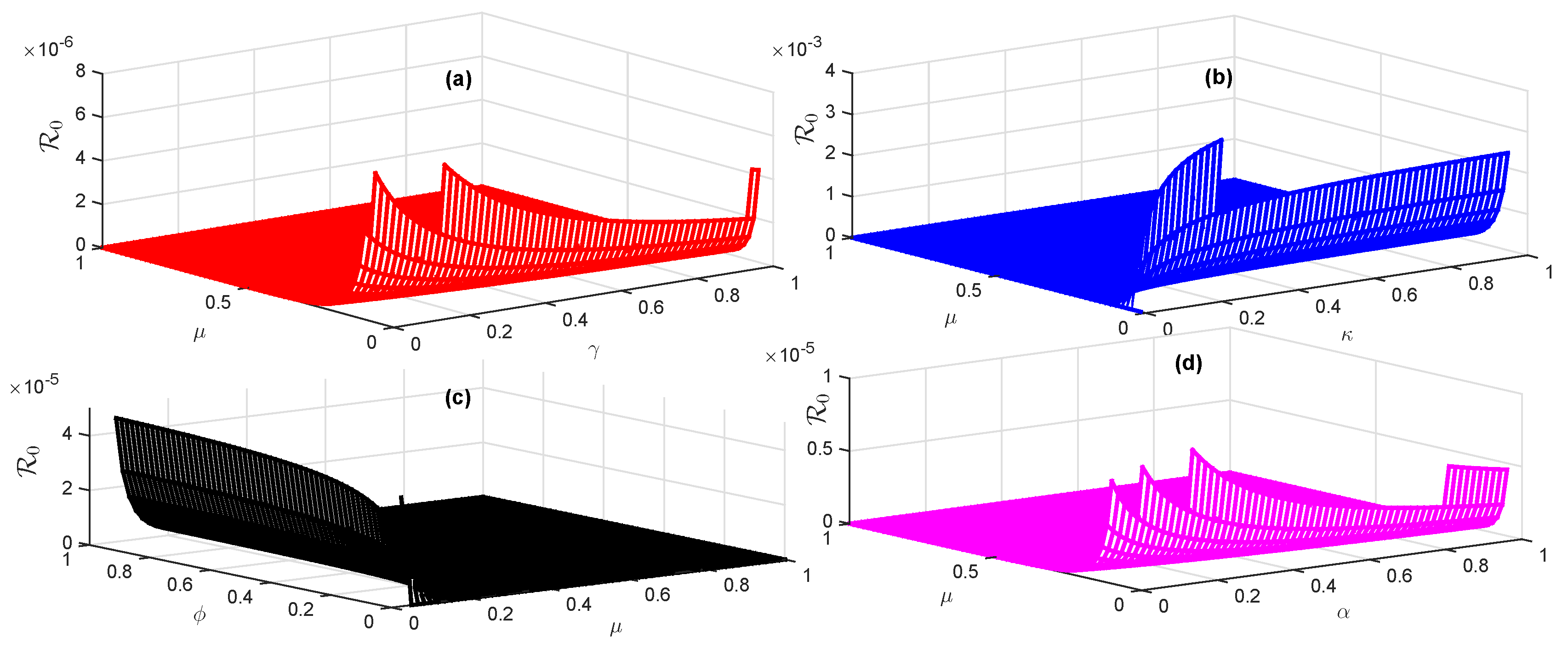
4.3. Sensitivity Analysis
- Linearizing the considered model.
- Latin hypercube sampling method.
- Direct differentiation method.
5. Existence Theory
- (P1)
- Let, there exist two positive constants , such that
- (P2)
- Let there exist a positive constant, such that
5.1. Ulam–Hyers Stability
5.2. Ulam–Hyer’s Stability
5.3. Generalized-Ulam–Hyers Stability
5.4. Ulam–Hyers–Rassias Stability
5.5. Generalized-Ulam–Hyers–Rassias Stability
- (I)
- (II)
- (I)
- (II)
5.6. Computational Scheme
| Algorithm 1: Algorithm for Computation. |
close all; Step 1: tmax = 830; h = 0.1; t(1) = 0; nstep = tmax/h; t = 0:h:t max; N = ceil(tmax/h); Step 2: Parameters values; Step 3: Assign Fractional orders sigma; Step 4: Assign Fractal orders xi; Step 5: Initial conditions Step 6: for n = 1:N−1 i = 2:n; t(i + 1) = t(i) + h; end |
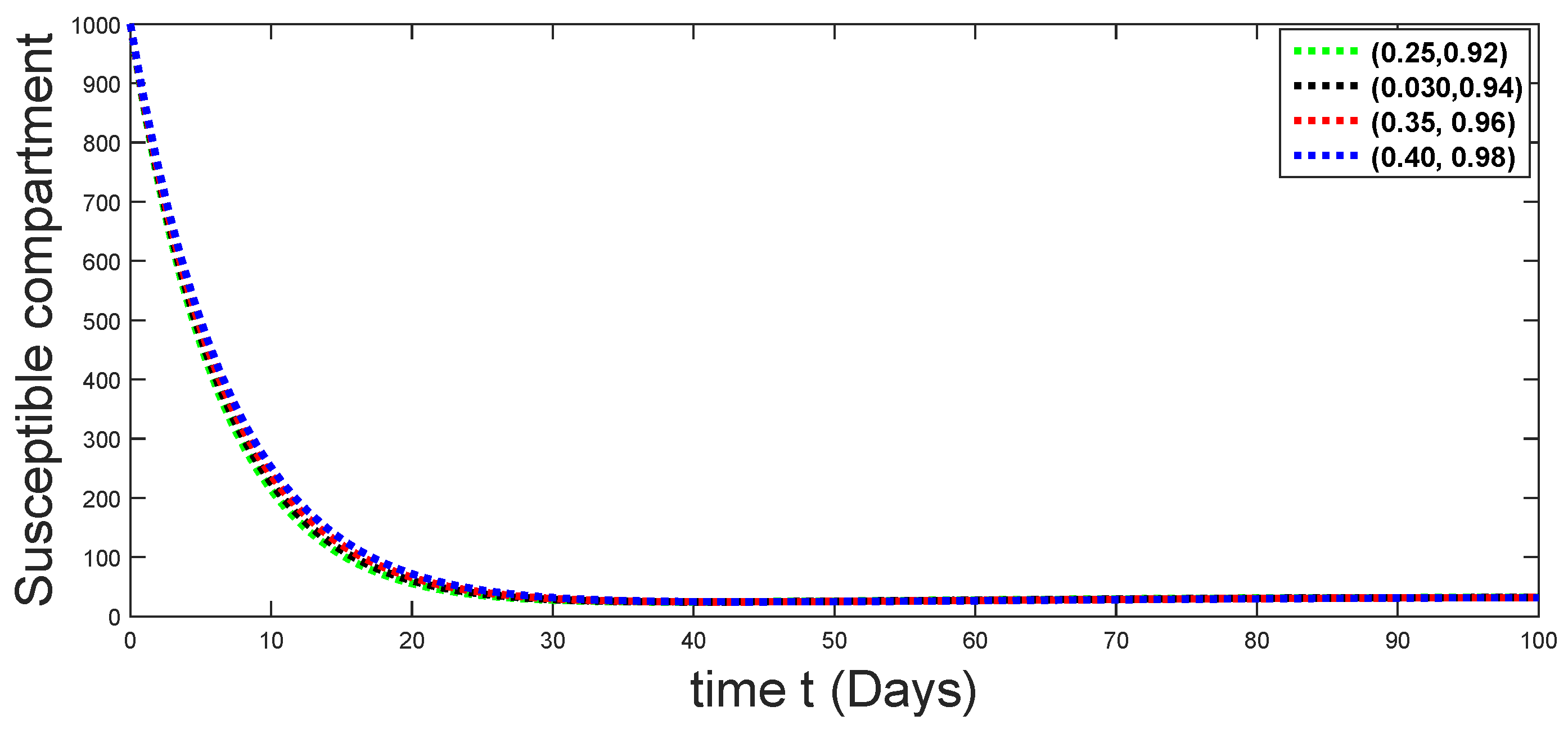
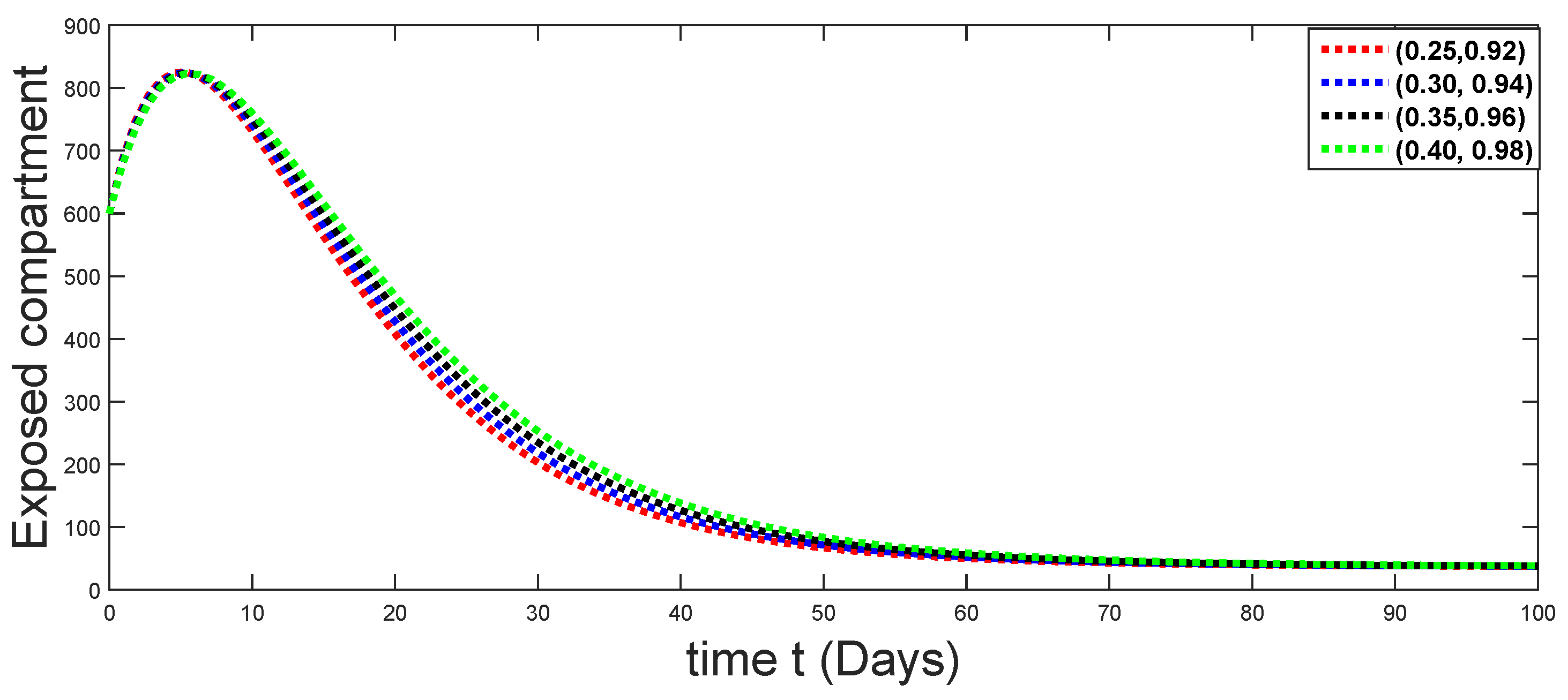
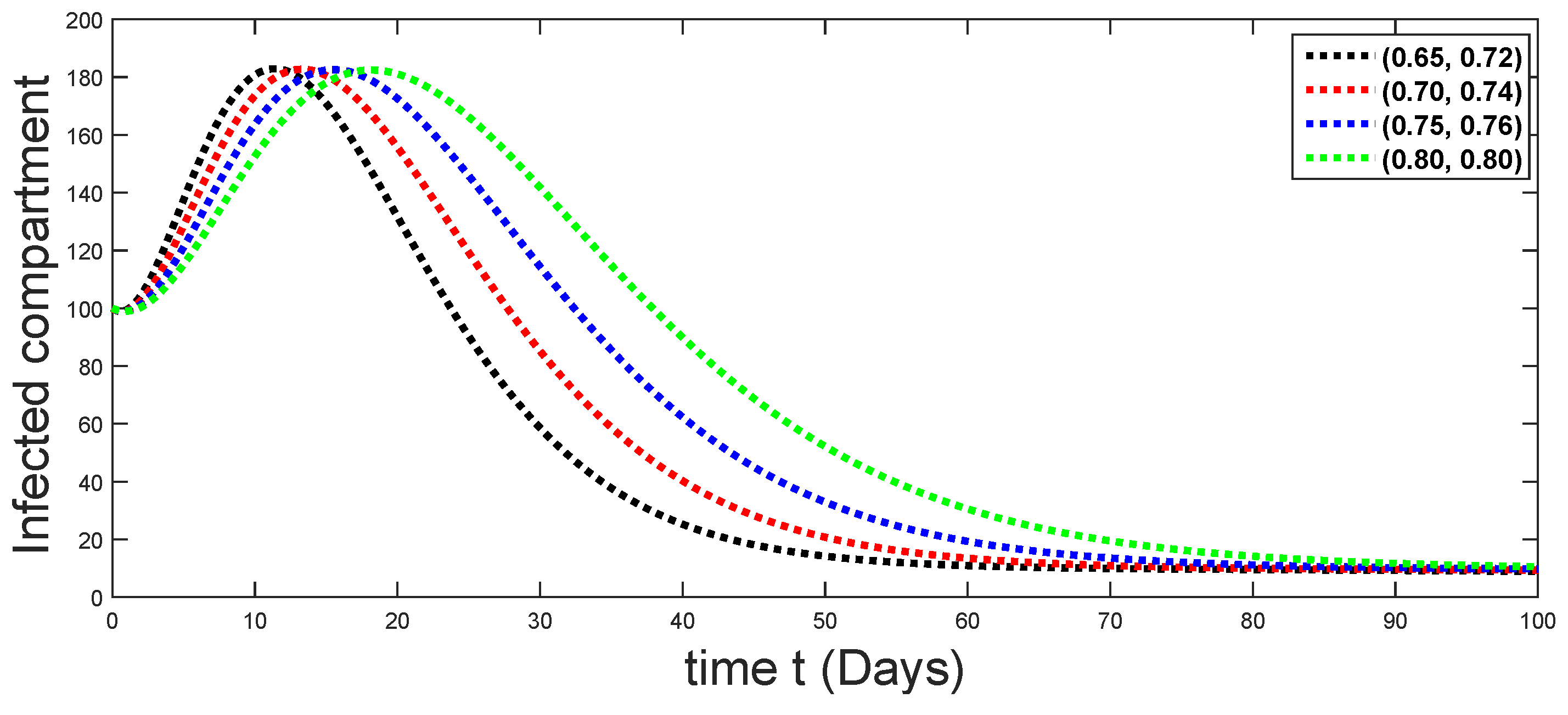
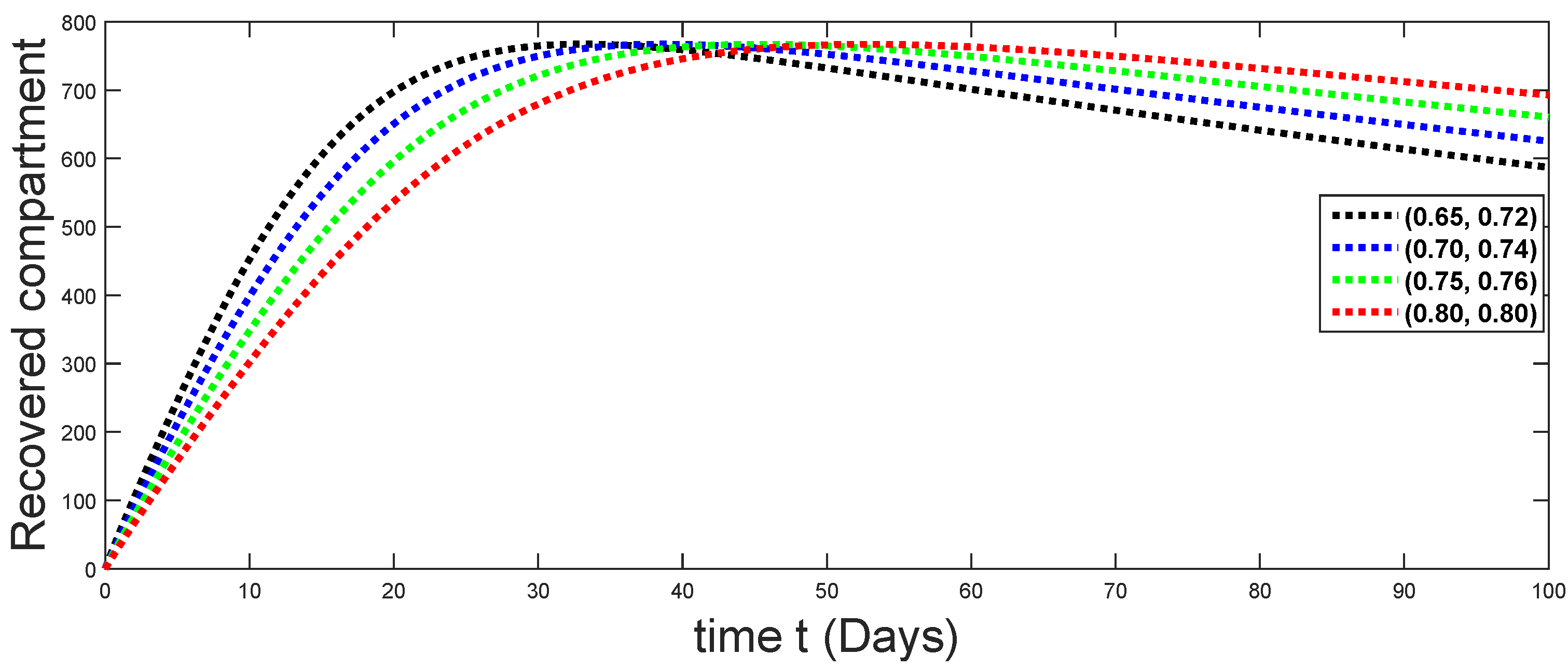
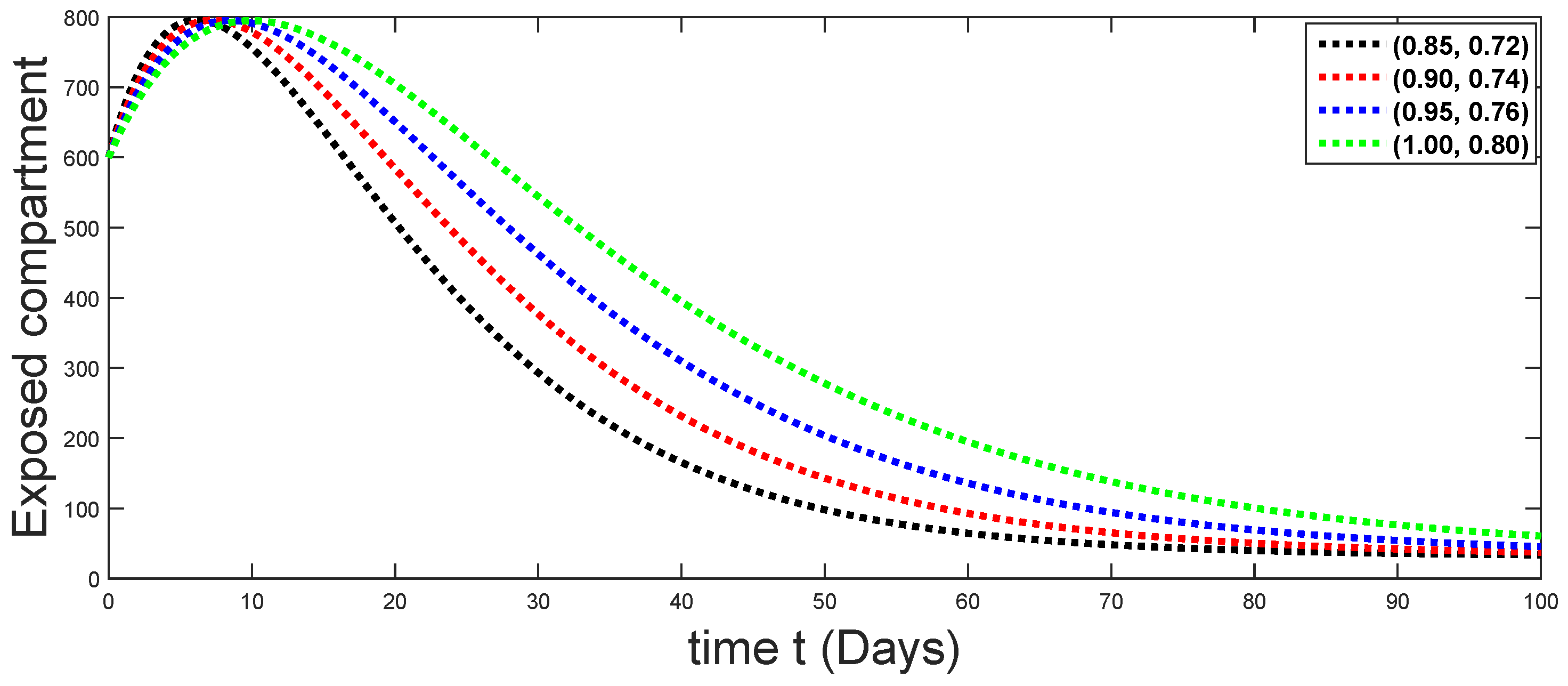
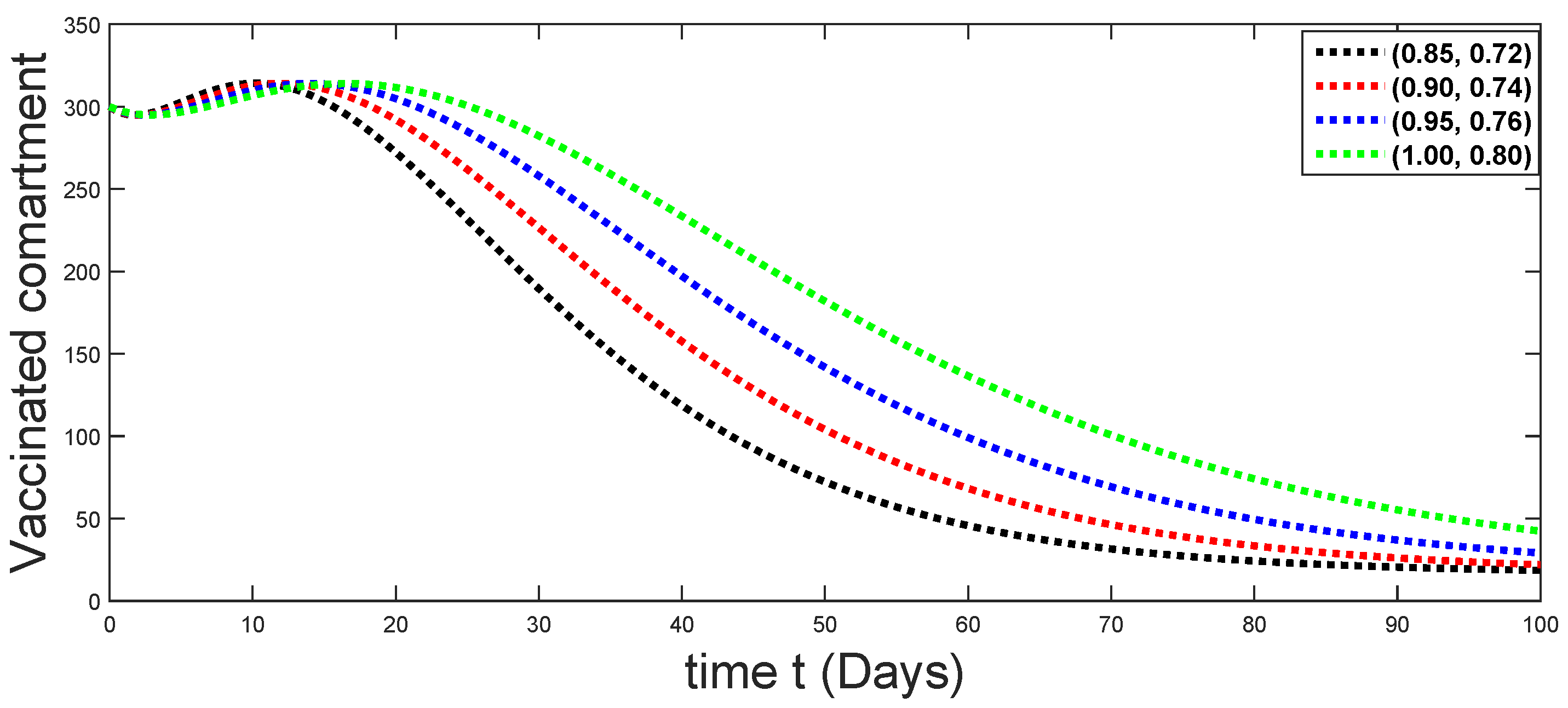
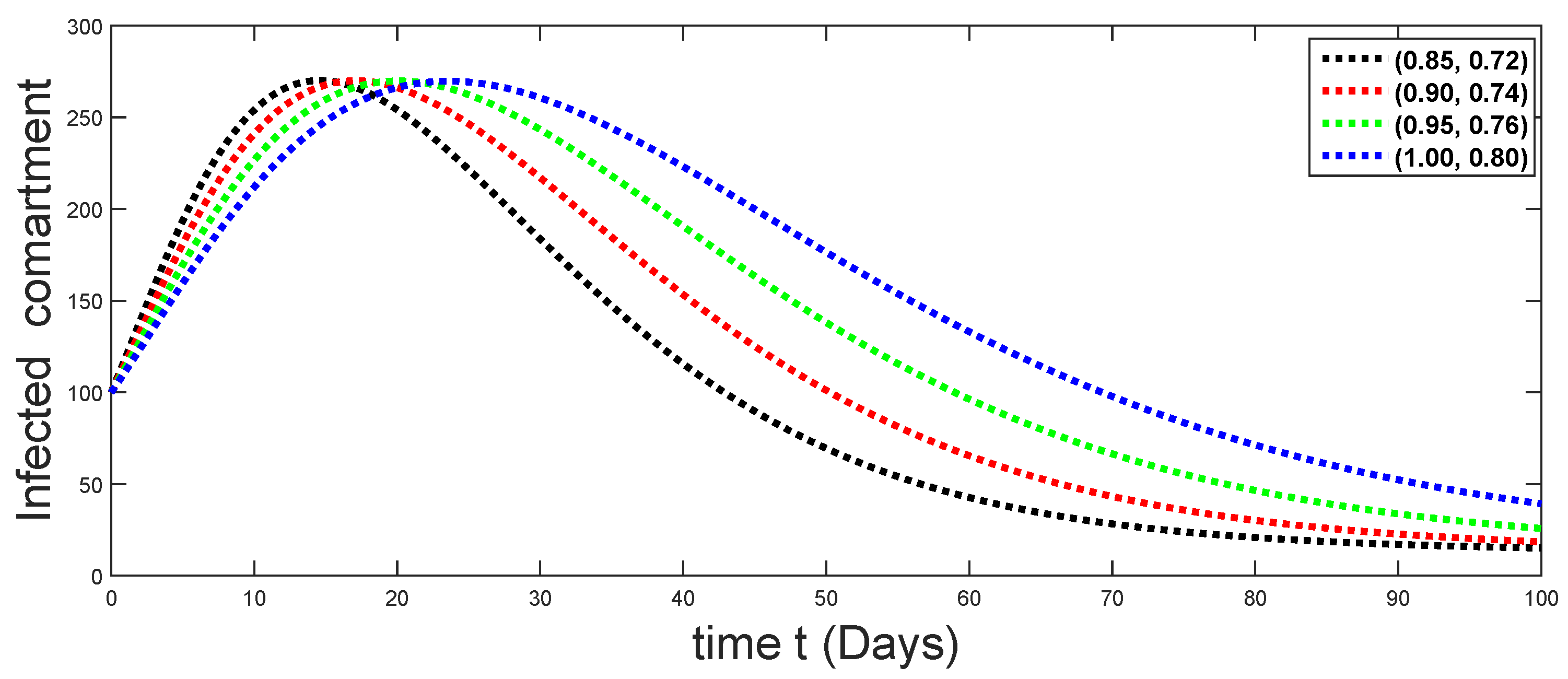
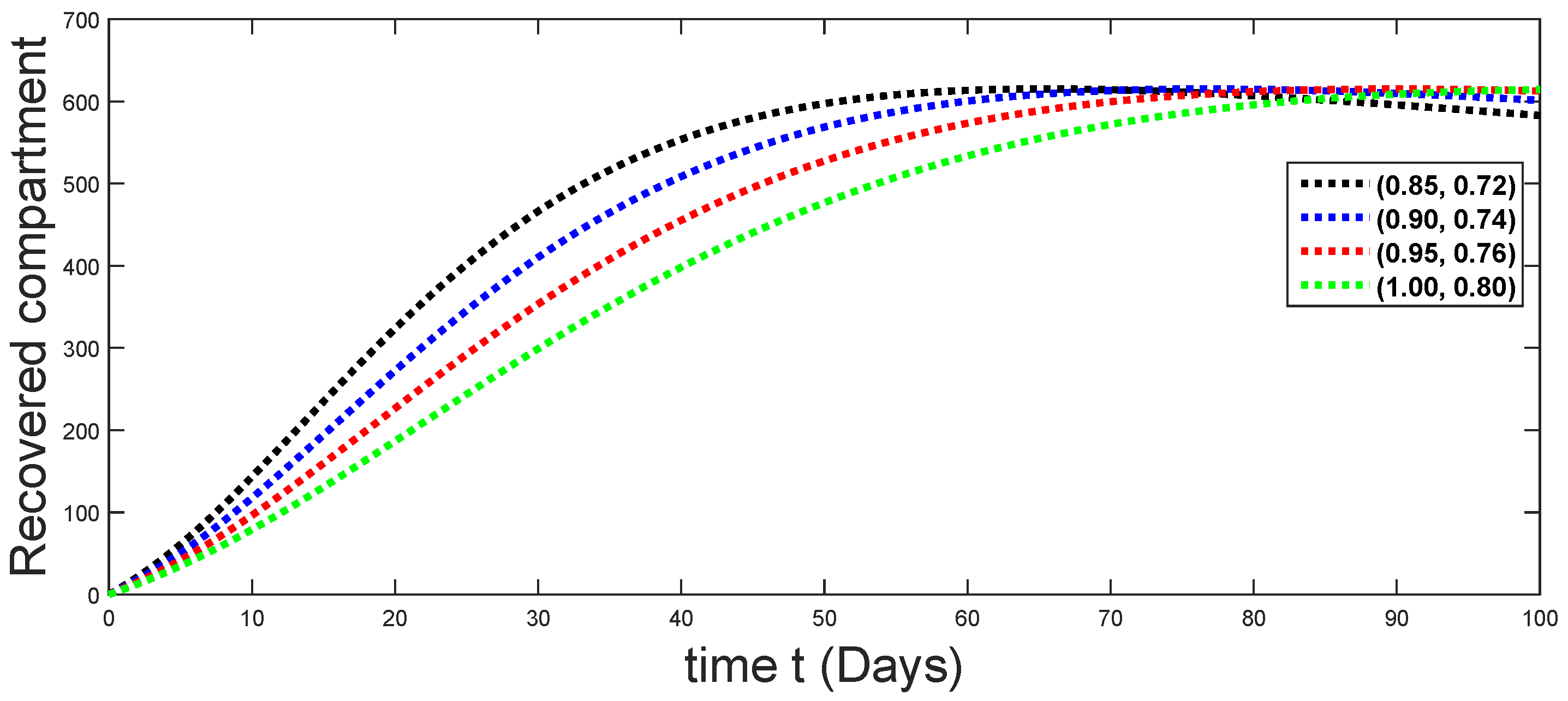
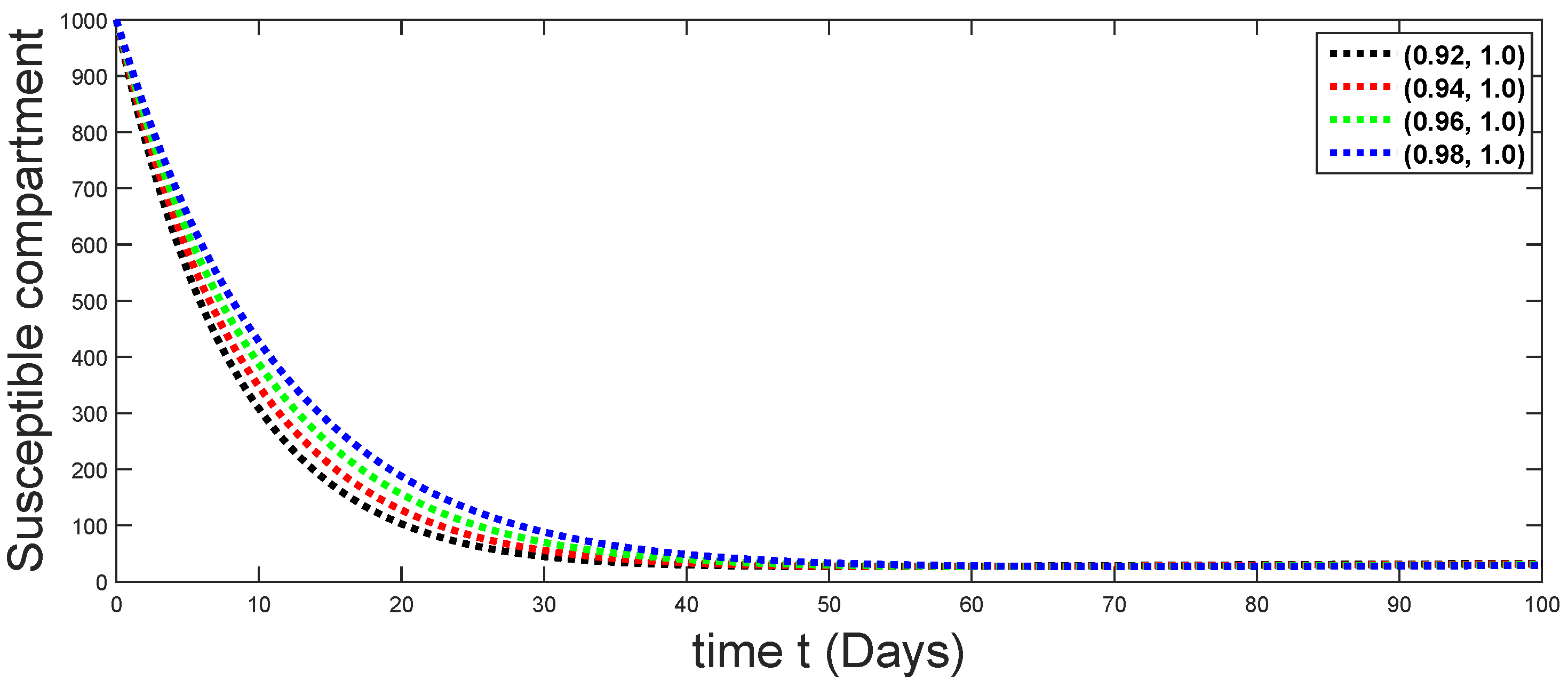
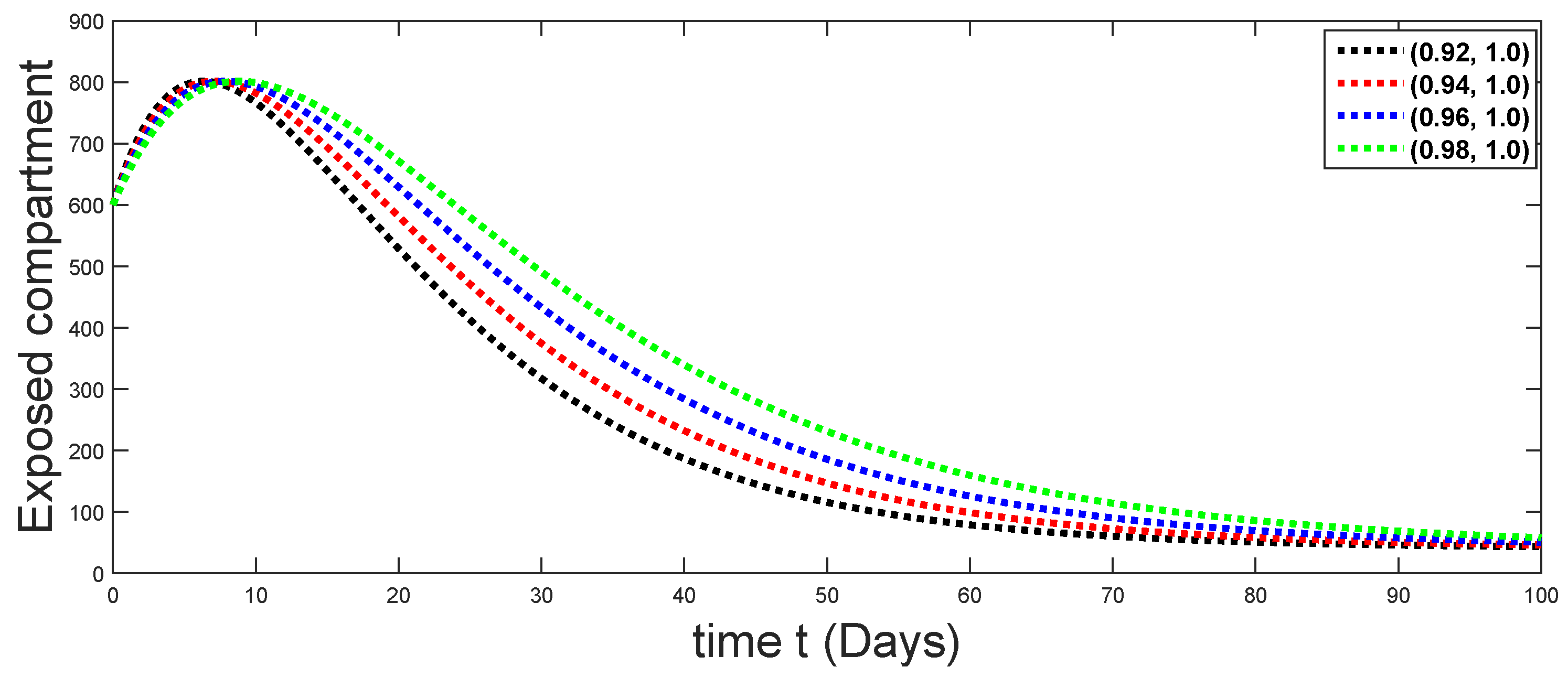
6. Numerical Presentation
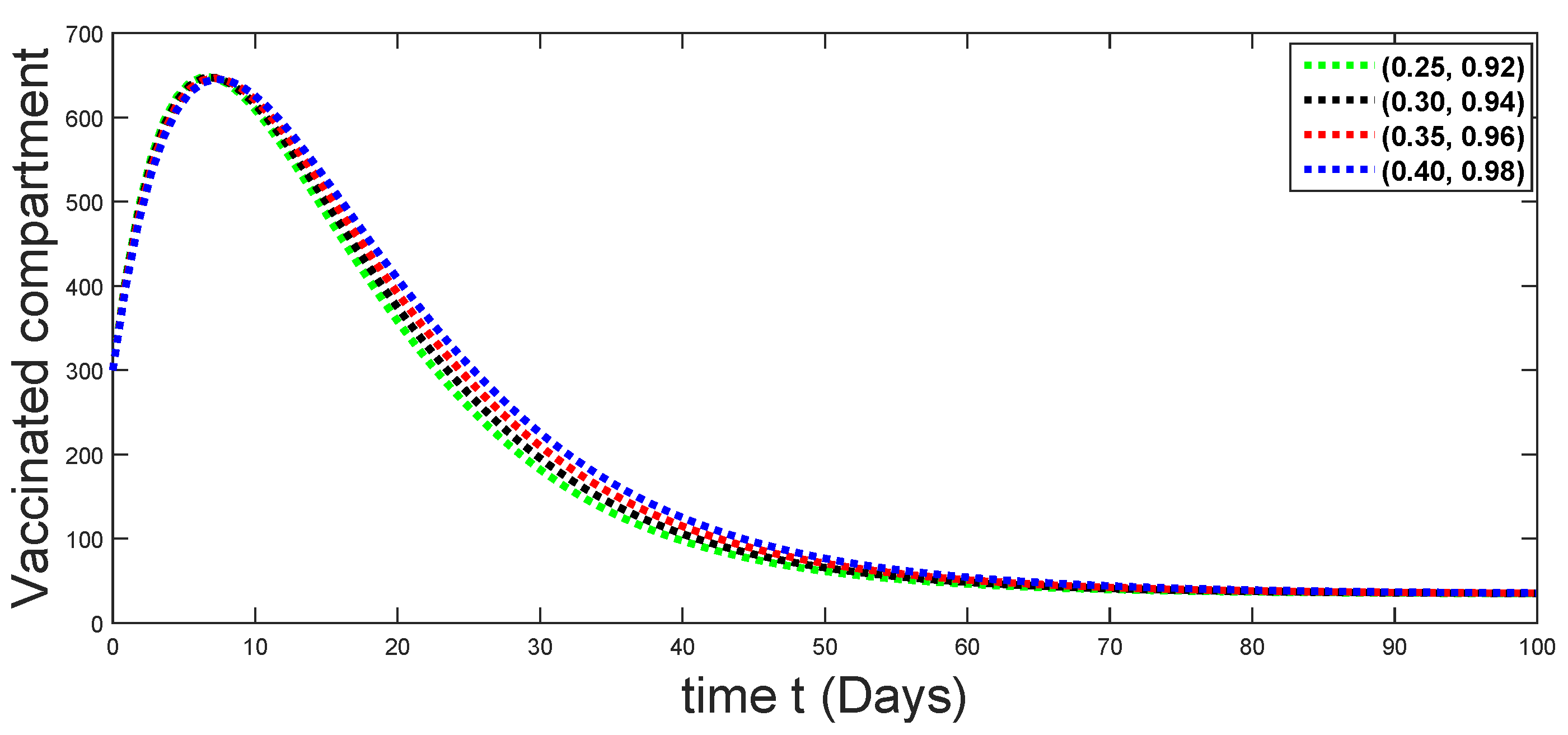
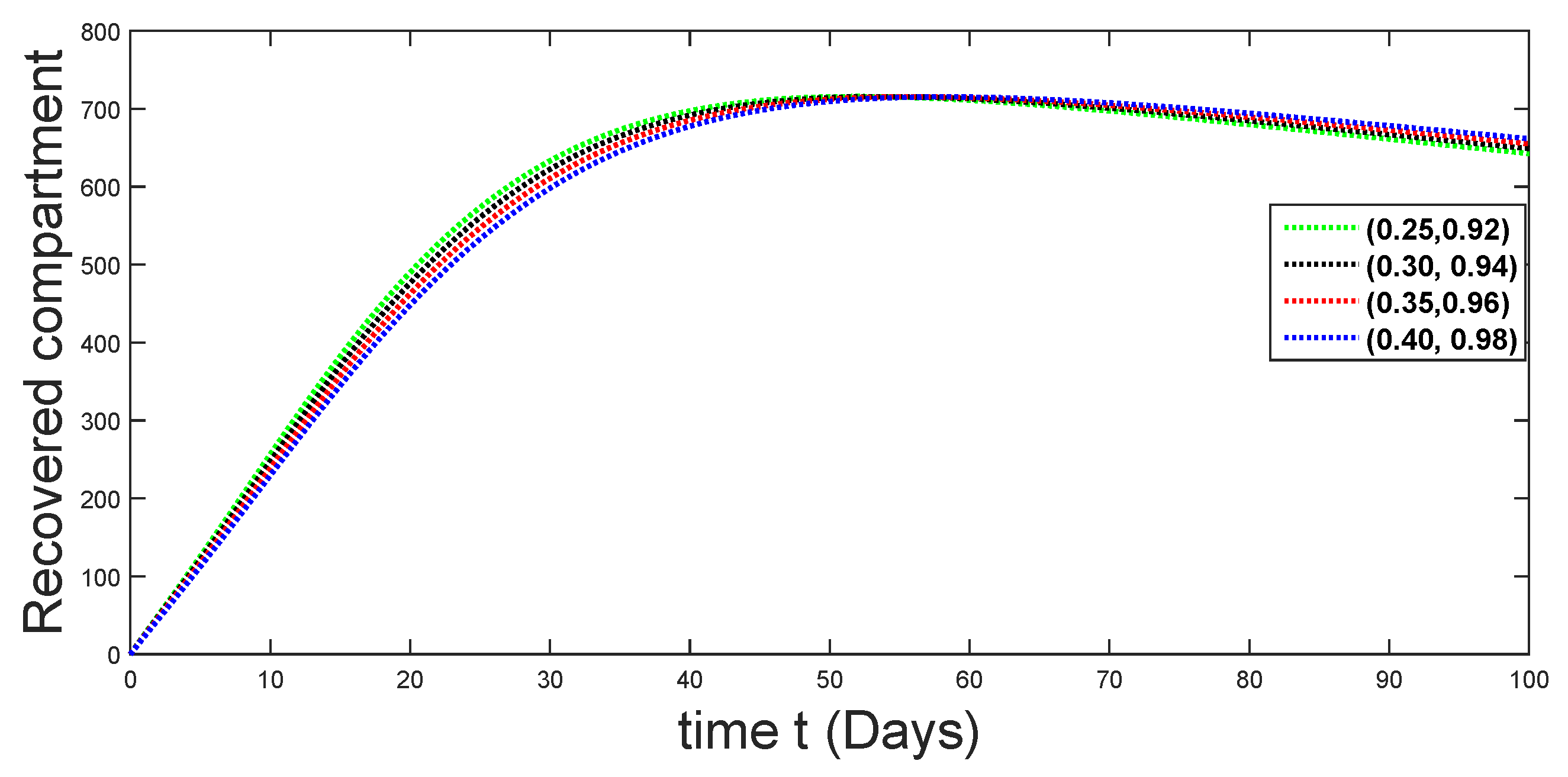
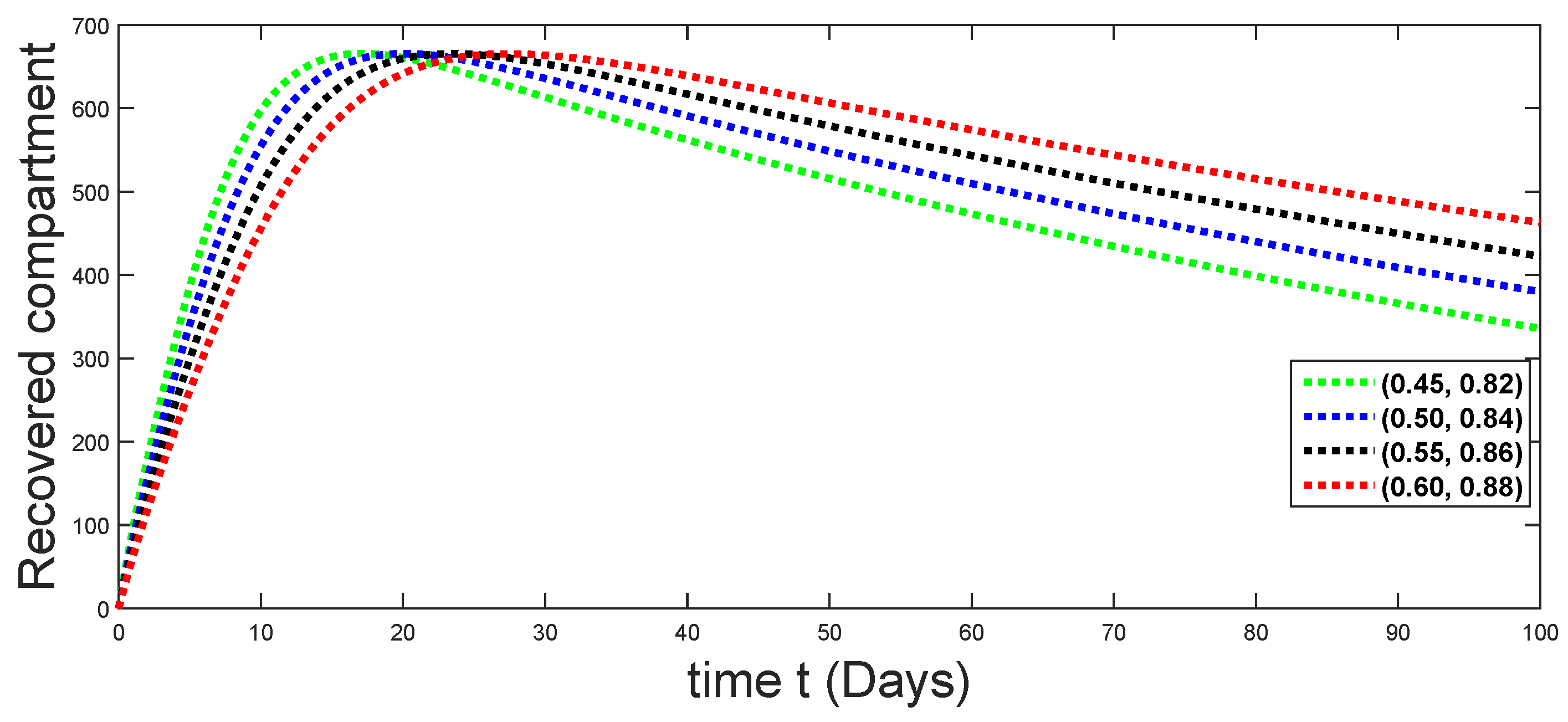
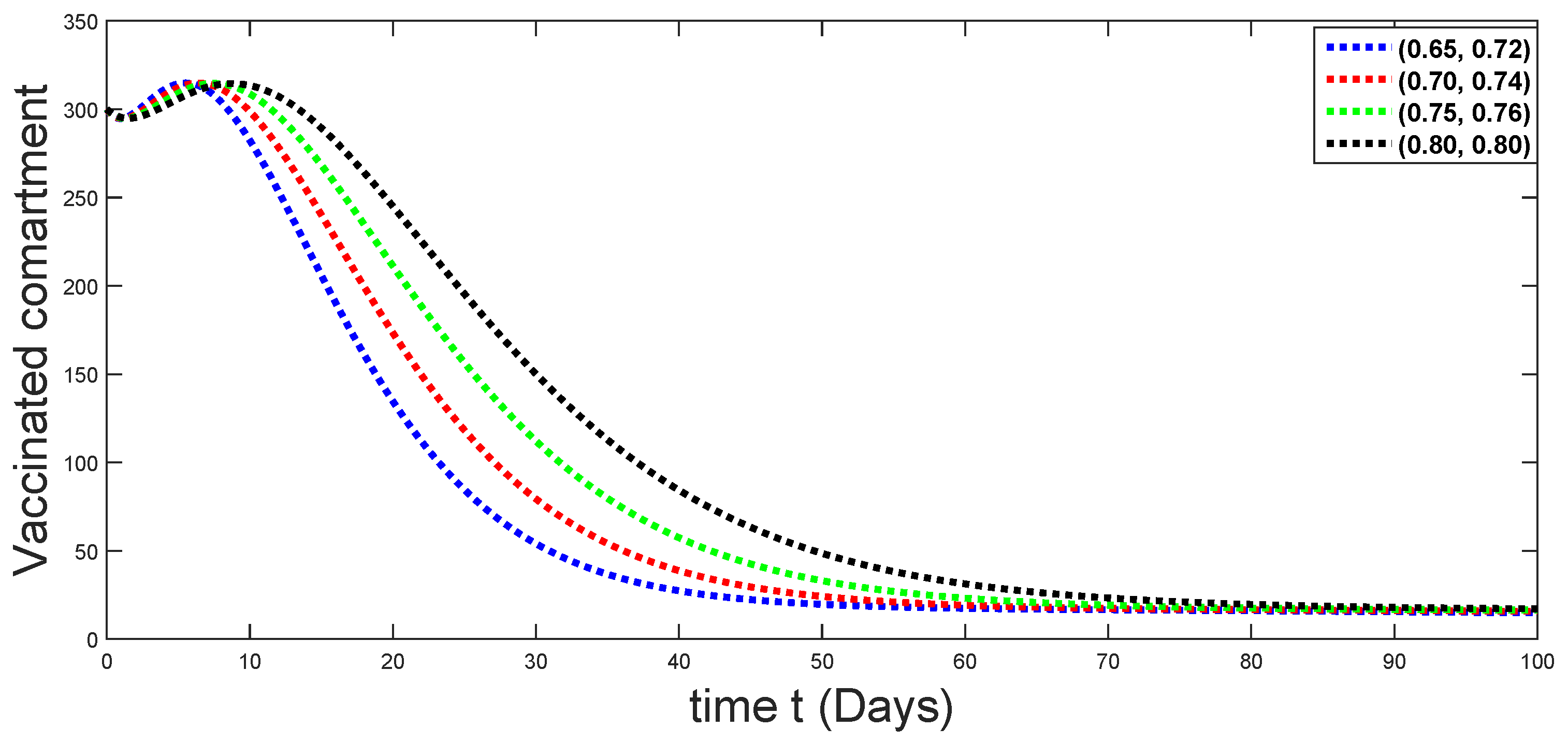
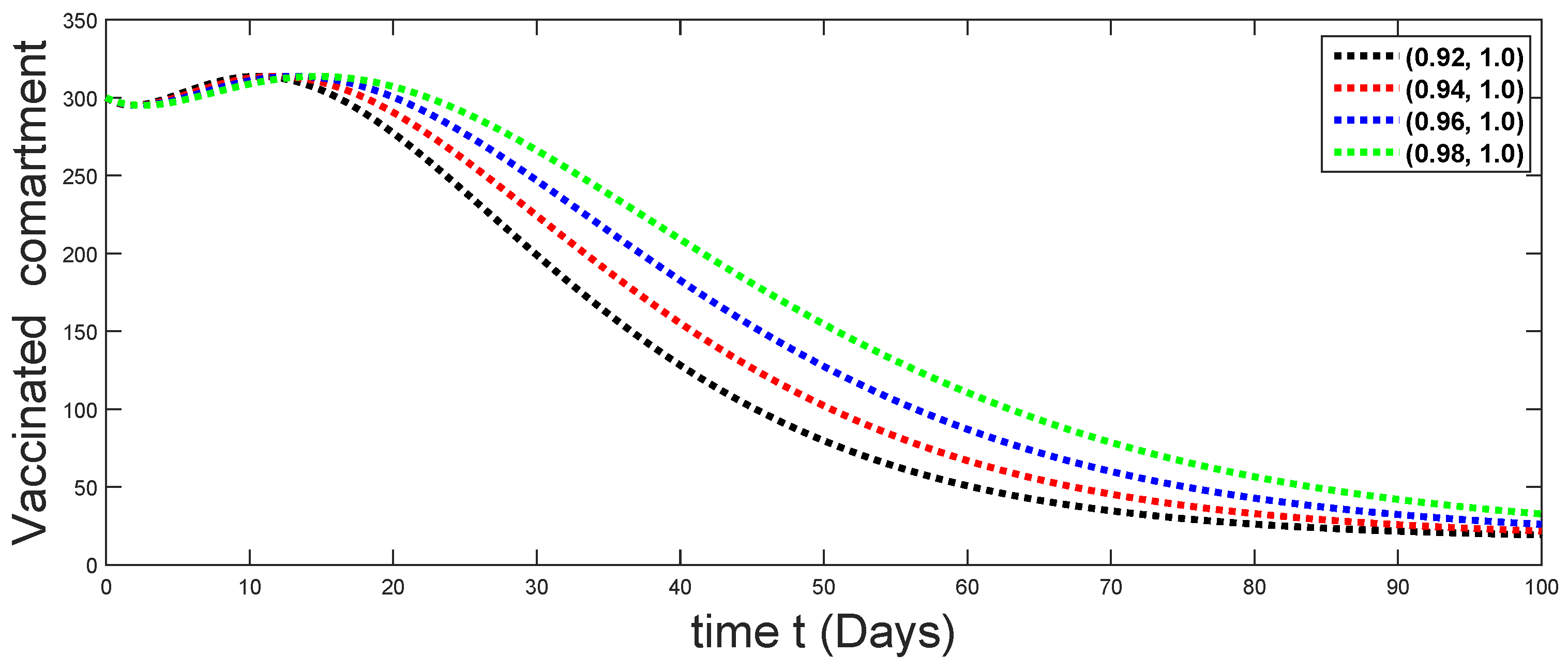
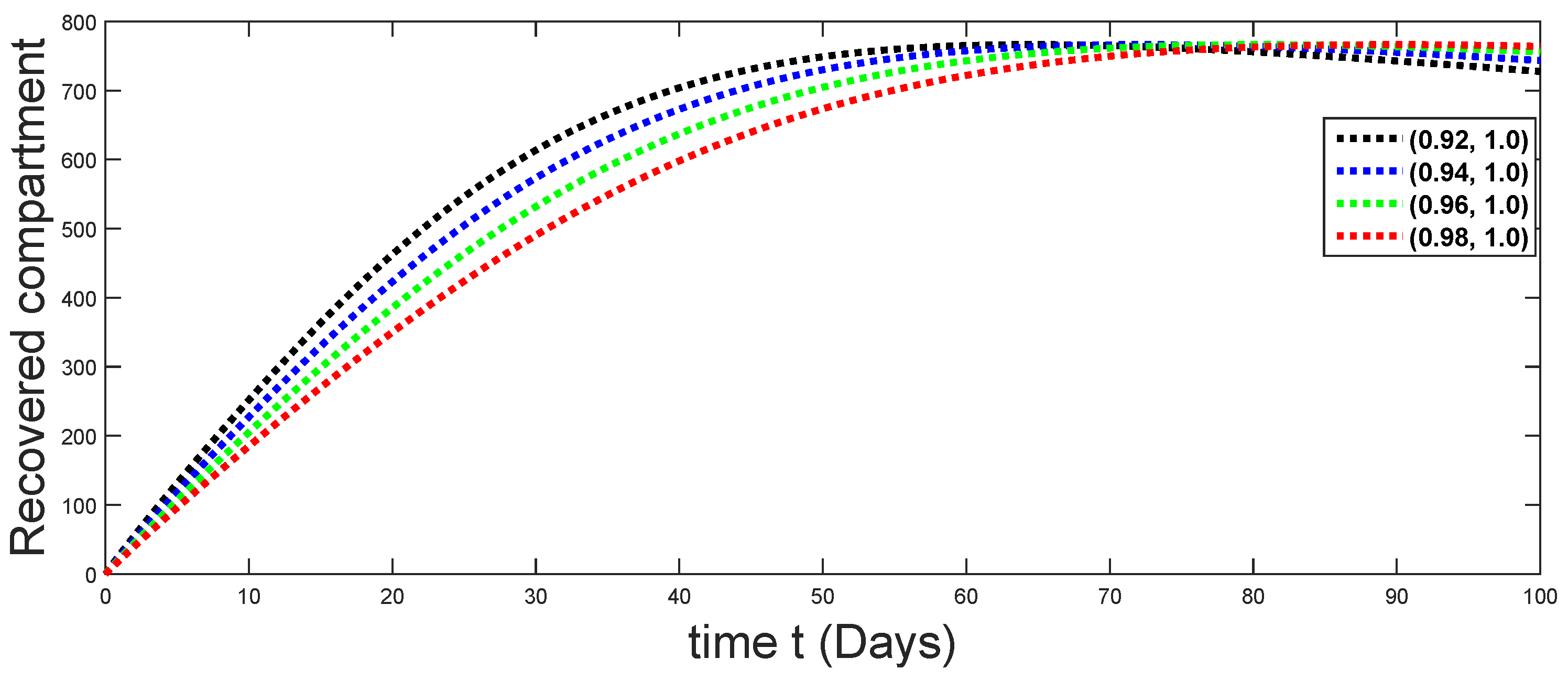
6.1. When
6.2. When
6.3. When
6.4. When
6.5. When
7. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Center for Disease Control (CDC). Conjunctivitis (Pink Eye). 2022. Available online: https://www.cdc.gov (accessed on 31 December 2023).
- Fehily, S.R.; Cross, G.B.; Fuller, A.J. Bilateral conjunctivitis in a returned traveller. PLoS Neglected Trop. 2015, 9, e0003351. [Google Scholar] [CrossRef]
- Elliot, R.H. Conjunctivitis in the tropics. Br. Med. J. 1925, 1, 12–14. [Google Scholar] [CrossRef]
- Malu, K.N. Allergic conjunctivitis in Jos-Nigeria. Niger. Med. J. J. Niger. Med. Assoc. 2014, 55, 166–170. [Google Scholar] [CrossRef]
- Kimberlin, D.W. Red Book: 2018–2021 Report of the Committee on Infectious Diseases; American Academy of Pediatrics: Elk Grove Village, IL, USA, 2018; No. Ed. 31. [Google Scholar]
- Chowell, G.; Shim, E.; Brauer, F.; Diaz-Dueas, P.; Hyman, J.M.; Castillo-Chavez, C. Modelling the transmission dynamics of acute haemorrhagic conjunctivitis: Application to the 2003 outbreak in Mexico. Stat. Med. 2006, 25, 1840–1857. [Google Scholar] [CrossRef]
- Murray, J.D. Mathematical Biology I; Springer: Berlin, Germany, 2003. [Google Scholar]
- Ohlsson, F.; Borgqvist, J.; Cvijovic, M. Symmetry structures in dynamic models of biochemical systems. J. R. Soc. Interface 2020, 17, 20200204. [Google Scholar] [CrossRef]
- Wilson, H.R.; Wilkinson, F. Symmetry perception: A novel approach for biological shapes. Vis. Res. 2002, 42, 589–597. [Google Scholar] [CrossRef]
- Almeida, R.; Malinowska, A.B.; Monteiro, M.T.T. Fractional differential equations with a Caputo derivative with respect to a kernel function and their applications. Math. Methods Appl. Sci. 2018, 41, 336–352. [Google Scholar] [CrossRef]
- Das, S.; Pan, I. Fractional Order Signal Processing: Introductory Concepts and Applications; Springer Science & Business Media: Berlin, Germnay, 2011. [Google Scholar]
- Araz, S.İ. Analysis of a COVID-19 model: Optimal control, stability and simulations. Alex. Eng. J. 2021, 60, 647–658. [Google Scholar] [CrossRef]
- Awadalla, M.; Yameni, Y. Modeling exponential growth and exponential decay real phenomena by ψ-Caputo fractional derivative. J. Adv. Math. Comput. Sci. 2018, 28, 1–13. [Google Scholar] [CrossRef]
- Atangana, A.; İğret Araz, S. Mathematical model of COVID-19 spread in Turkey and South Africa: Theory, methods, and applications. Adv. Differ. Equ. 2020, 2020, 659. [Google Scholar] [CrossRef]
- Ahmed, S.; Ahmed, A.; Mansoor, I.; Junejo, F.; Saeed, A. Output feedback adaptive fractional-order super-twisting sliding mode control of robotic manipulator. Iran. J. Sci. Technol. Trans. Electr. Eng. 2021, 45, 335–347. [Google Scholar] [CrossRef]
- Shah, K.; Jarad, F.; Abdeljawad, T. On a nonlinear fractional order model of dengue fever disease under Caputo-Fabrizio derivative. Alex. Eng. J. 2020, 59, 2305–2313. [Google Scholar] [CrossRef]
- Ahmed, S.; Wang, H.; Aslam, M.S.; Ghous, I.; Qaisar, I. Robust adaptive control of robotic manipulator with input time-varying delay. Int. J. Control Autom. Syst. 2019, 17, 2193–2202. [Google Scholar] [CrossRef]
- Shaikh, A.; Nisar, K.S.; Jadhav, V.; Elagan, S.K.; Zakarya, M. Dynamical behaviour of HIV/AIDS model using fractional derivative with Mittag-Leffler kernel. Alex. Eng. J. 2022, 61, 2601–2610. [Google Scholar] [CrossRef]
- Peter, O.J.; Shaikh, A.S.; Ibrahim, M.O.; Nisar, K.S.; Baleanu, D.; Khan, I.; Abioye, A.I. Analysis and dynamics of fractional order mathematical model of COVID-19 in Nigeria using atangana-baleanu operator. Comput. Mater. Contin. 2021, 66, 1823–1848. [Google Scholar] [CrossRef]
- Shaikh, A.S.; Shaikh, I.N.; Nisar, K.S. A mathematical model of COVID-19 using fractional derivative: Outbreak in India with dynamics of transmission and control. Adv. Differ. Equ. 2020, 2020, 373. [Google Scholar] [CrossRef] [PubMed]
- Teodoro, G.S.; Machado, J.T.; De Oliveira, E.C. A review of definitions of fractional derivatives and other operators. J. Comput. Phys. 2019, 388, 195–208. [Google Scholar] [CrossRef]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Hilfer, R. (Ed.) Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Kilbas, A.A. Hadamard-type fractional calculus. J. Korean Math. Soc. 2001, 38, 1191–1204. [Google Scholar]
- Zhang, T.; Li, Y. Global exponential stability of discrete-time almost automorphic Caputo-Fabrizio BAM fuzzy neural networks via exponential Euler technique. Knowl.-Based Syst. 2022, 246, 108675. [Google Scholar] [CrossRef]
- Khan, M.; Ahmad, Z.; Ali, F.; Khan, N.; Khan, I.; Nisar, K.S. Dynamics of two-step reversible enzymatic reaction under fractional derivative with Mittag-Leffler Kernel. PLoS ONE 2023, 18, e0277806. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. Applications of new time and spatial fractional derivatives with exponential kernels. Prog. Fract. Differ. Appl. 2016, 2, 1–11. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Losada, J.; Nieto, J.J. Properties of a new fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 87–92. [Google Scholar]
- Gul, R.; Sarwar, M.; Shah, K.; Abdeljawad, T.; Jarad, F. Qualitative analysis of implicit Dirichlet boundary value problem for Caputo-Fabrizio fractional differential equations. J. Funct. Spaces 2020, 2020, 4714032. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Xu, C.; Liu, Z.; Pang, Y.; Saifullah, S.; Inc, M. Oscillatory, crossover behavior and chaos analysis of HIV-1 infection model using piece-wise Atangana–Baleanu fractional operator: Real data approach. Chaos Solitons Fractals 2022, 164, 112662. [Google Scholar] [CrossRef]
- Saifullah, S.; Ali, A.; Irfan, M.; Shah, K. Time-fractional Klein–Gordon equation with solitary/shock waves solutions. Math. Probl. Eng. 2021, 2021, 6858592. [Google Scholar] [CrossRef]
- Alomari, A.K.; Abdeljawad, T.; Baleanu, D.; Saad, K.M.; Al-Mdallal, Q.M. Numerical solutions of fractional parabolic equations with generalized Mittag-Leffler kernels. Numer. Methods Partial. Differ. Equ. 2024, 40, e22699. [Google Scholar] [CrossRef]
- Saad Alshehry, A.; Imran, M.; Shah, R.; Weera, W. Fractional-View Analysis of Fokker-Planck equations by ZZ Transform with Mittag-Leffler Kernel. Symmetry 2022, 14, 1513. [Google Scholar] [CrossRef]
- Atangana, A. Fractal-fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fractals 2017, 102, 396–406. [Google Scholar] [CrossRef]
- He, J.H. Fractal calculus and its geometrical explanation. Results Phys. 2018, 10, 272–276. [Google Scholar] [CrossRef]
- Hu, Y.; He, J.H. On fractal space-time and fractional calculus. Therm. Sci. 2016, 20, 773–777. [Google Scholar] [CrossRef]
- Qureshi, S.; Atangana, A. Fractal-fractional differentiation for the modeling and mathematical analysis of nonlinear diarrhea transmission dynamics under the use of real data. Chaos Solitons Fractals 2020, 136, 109812. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Saad, K.M. Numerical simulation of the fractal-fractional Ebola virus. Fractal Fract. 2020, 4, 49. [Google Scholar] [CrossRef]
- Xiao, B.; Huang, Q.; Chen, H.; Chen, X.; Long, G. A fractal model for capillary flow through a single tortuous capillary with roughened surfaces in fibrous porous media. Fractals 2021, 29, 2150017. [Google Scholar] [CrossRef]
- Liang, M.; Liu, Y.; Xiao, B.; Yang, S.; Wang, Z.; Han, H. An analytical model for the transverse permeability of gas diffusion layer with electrical double layer effects in proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2018, 43, 17880–17888. [Google Scholar] [CrossRef]
- Yu, X.; Xu, H.; Zhai, C.; Regenauer-Lieb, K.; Sang, S.; Sun, Y.; Jing, Y. Characterization of water migration behavior during spontaneous imbibition in coal: From the perspective of fractal theory and NMR. Fuel 2024, 355, 129499. [Google Scholar] [CrossRef]
- Ahmad, I.; Ahmad, N.; Shah, K.; Abdeljawad, T. Some appropriate results for the existence theory and numerical solutions of fractals-fractional order malaria disease mathematical model. Results Control. Optim. 2024, 14, 100386. [Google Scholar] [CrossRef]
- Abro, K.A. Role of fractal–fractional derivative on ferromagnetic fluid via fractal Laplace transform: A first problem via fractal-fractional differential operator. Eur. J. Mech.-B/Fluids 2021, 85, 76–81. [Google Scholar] [CrossRef]
- Atangana, A.; Goufo, E.F.D. Cauchy problems with fractal-fractional operators and applications to groundwater dynamics. Fractals 2020, 28, 2040043. [Google Scholar] [CrossRef]
- Atangana, A.; Qureshi, S. Modeling attractors of chaotic dynamical systems with fractal–fractional operators. Chaos Solitons Fractals 2019, 123, 320–337. [Google Scholar] [CrossRef]
- Sangsawang, S.; Tanutpanit, T.; Mumtong, W.; Pongsumpun, P. Local stability analysis of mathematical model for hemorrhagic conjunctivitis disease. Curr. Appl. Sci. Technol. 2012, 12, 189–197. [Google Scholar]
- Javed, F.; Ahmad, A.; Ali, A.H.; Hincal, E.; Amjad, A. Investigation of conjunctivitis adenovirus spread in human eyes by using bifurcation tool and numerical treatment approach. Phys. Scr. 2024, 99, 085253. [Google Scholar] [CrossRef]
- Fatunla, S.O. Numerical Methods for Initial Value Problems in Ordinary Differential Equations; Academic Press: New York, NY, USA, 2014. [Google Scholar]
- Khan, M.A.; Atangana, A. Numerical Methods for Fractal-Fractional Differential Equations and Engineering: Simulations and Modeling; CRC Press: New York, NY, USA, 2023. [Google Scholar]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Further notes on the basic reproduction number. Math. Epidemiol. 2008, 2008, 159–178. [Google Scholar]
- DeJesus, E.X.; Kaufman, C. Routh-Hurwitz criterion in the examination of eigenvalues of a system of nonlinear ordinary differential equations. Phys. Rev. A 1987, 35, 5288. [Google Scholar] [CrossRef] [PubMed]
- Castillo-Chavez, C.; Blower, S.; van den Driessche, P.; Kirschner, D.; Yakubu, A.A. (Eds.) Mathematical Approaches for Emerging and Reemerging Infectious Diseases: Models, Methods, and Theory; Springer Science & Business Media: New York, NY, USA, 2002; Volume 126. [Google Scholar]
- Arriola, L.M.; Hyman, J.M. Being sensitive to uncertainty. Comput. Sci. Eng. 2007, 9, 10–20. [Google Scholar] [CrossRef]
- Khan, A.; Zarin, R.; Hussain, G.; Usman, A.H.; Humphries, U.W.; Gomez-Aguilar, J.F. Modeling and sensitivity analysis of HBV epidemic model with convex incidence rate. Results Phys. 2021, 22, 103836. [Google Scholar] [CrossRef]
- Hyers, D.H. On the stability of the linear functional equation. Proc. Natl. Acad. Sci. USA 1941, 27, 222–224. [Google Scholar] [CrossRef]
- Rassias, T.M. On the stability of the linear mapping in Banach spaces. Proc. Natl. Acad. Sci. USA 1978, 72, 297–300. [Google Scholar] [CrossRef]
- Sher, M.; Shah, K.; Rassias, J. On qualitative theory of fractional order delay evolution equation via the prior estimate method. Math. Methods Appl. Sci. 2020, 43, 6464–6475. [Google Scholar] [CrossRef]
- Yanagiwara, H.I.R.O.K.I. On the Stability of a Multistep Method. In Proceedings of the Sixth International Colloquim on Differential Equations, Plovdiv, Bulgaria, 18–23 August 1995; pp. 369–376. [Google Scholar]
- Sehnalová, P. Stability and convergence of numerical computations. Inf. Sci. Technol. Bull. Acm Slovak. 2011, 3, 26–35. [Google Scholar]
- Li, C.; Tao, C. On the fractional Adams method. Comput. Math. Appl. 2009, 58, 1573–1588. [Google Scholar] [CrossRef]









| Parameters | Numerical Value | Parameters | Value |
|---|---|---|---|
| R | |||
| (assumed) | n | 2000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeelani, M.B.; Alharthi, N.H. On a Symmetry-Based Structural Deterministic Fractal Fractional Order Mathematical Model to Investigate Conjunctivitis Adenovirus Disease. Symmetry 2024, 16, 1284. https://doi.org/10.3390/sym16101284
Jeelani MB, Alharthi NH. On a Symmetry-Based Structural Deterministic Fractal Fractional Order Mathematical Model to Investigate Conjunctivitis Adenovirus Disease. Symmetry. 2024; 16(10):1284. https://doi.org/10.3390/sym16101284
Chicago/Turabian StyleJeelani, Mdi Begum, and Nadiyah Hussain Alharthi. 2024. "On a Symmetry-Based Structural Deterministic Fractal Fractional Order Mathematical Model to Investigate Conjunctivitis Adenovirus Disease" Symmetry 16, no. 10: 1284. https://doi.org/10.3390/sym16101284






