Bivariate Log-Symmetric Regression Models Applied to Newborn Data
Abstract
:1. Introduction
2. Motivating Example
2.1. Anthropometric Measurements
2.2. The Dataset
- : weight (in hectograms);
- : length (crown-heel length, in centimeters),
- and the corresponding covariates are:
- : sex (0 for female, 1 for male);
- : gestational age at birth (in weeks);
- : mother’s age (in years);
- : father’s age (in years).
3. Preliminaries
- (medians);
- (dispersion); and
- (correlation)
- for , and density generator [15], denoted by , if its probability density function (PDF) is given by the following:whereand is a partition function given by the following:The variance–covariance matrix, when it exists, of a random vector is given by for some matrix function , where denotes the set of all real matrices, and
4. Bivariate Log-Symmetric Regression Models
4.1. Bivariate Regression
4.2. Maximum Likelihood Estimation
4.3. Residual Analysis
5. Monte Carlo Simulation
- Scenario 1: , , , and –low correlation–.
- Scenario 2: , , , and –moderate correlation–.
- Scenario 3: , , , and –high correlation–.
- The sample sizes for all three simulation scenarios are , with 500 Monte Carlo replications for each combination of above given parameters.
6. Application to Newborn Data
7. Concluding Remarks
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Elements of Observed Fisher Information Matrix
References
- Jones, M.C. On reciprocal symmetry. J. Stat. Plan. Inference 2008, 138, 3039–3043. [Google Scholar] [CrossRef]
- Vila, R.; Balakrishnan, N.; Saulo, H.; Protazio, A. Bivariate log-symmetric models: Distributional properties, parameter estimation and an application to public spending data. Braz. J. Probab. Stat. 2023, 37, 619–642. [Google Scholar] [CrossRef]
- Vanegas, L.H.; Paula, G.A. Log-symmetric distributions: Statistical properties and parameter es timation. Braz. J. Probab. Stat. 2016, 30, 196–220. [Google Scholar] [CrossRef]
- Marchant, C.; Leiva, V.; Cysneiros, F. A Multivariate Log-Linear Model for Birnbaum-Saunders Distributions. IEEE Trans. Reliab. 2016, 65, 816–827. [Google Scholar] [CrossRef]
- Kaombe, T.; Banda, J.; Hamuza, G.; Muula, A. Bivariate logistic regression model diagnostics applied to analysis of outlier cancer patients with comorbid diabetes and hypertension in Malawi. Sci. Rep. 2023, 13, 8340. [Google Scholar] [CrossRef]
- Khan, M.; Olivier, J. Regression to the mean: Estimation and adjustment under the bivariate normal distribution. Commun. Stat.-Theory Methods 2023, 52, 6972–6990. [Google Scholar] [CrossRef]
- Umair, M.; Khan, M.; Olivier, J. Accounting for regression to the mean under the bivariate t-distribution. Stat. Methods Med. Res. 2024. [Google Scholar] [CrossRef]
- Saulo, H.; Leão, J.; Leiva, V.; Vila, R.; Tiomazella, V. A bivariate fatigue-life regression model and its application to fracture of metallic tools. Braz. J. Probab. Stat. 2021, 35, 119–137. [Google Scholar] [CrossRef]
- Saulo, H.; Leão, J.; Vila, R.; Leiva, V.; Tiomazella, V. On mean-based bivariate Birnbaum-Saunders distributions: Properties, inference and application. Commun. Stat.-Theory Methods 2020, 49, 6032–6056. [Google Scholar] [CrossRef]
- Paulsen, C.; Nielsen, B.; Msemo, O.; Møller, S.; Ekmann, J.; Theander, T.; Bygbjerg, I.; Lusingu, J.; Minja, T.; Schmiegelow, C. Anthropometric measurements can identify small for gestational age newborns: A cohort study in rural Tanzania. BMC Pediatr. 2019, 19, 120. [Google Scholar] [CrossRef] [PubMed]
- Fenton, T.R.; Kim, J.H. A systematic review and meta-analysis to revisethe Fenton growth chart for preterm infants. BMC Pediatr. 2013, 13, 59. [Google Scholar] [CrossRef] [PubMed]
- Haksari, E.; Lafeber, H.; Hakimi, M.; Pawirohartono, E.; Nyström, L. Reference curves of birth weight, length, and head circumference for gestational ages in Yogyakarta, Indonesia. BMC Pediatr. 2016, 16, 188. [Google Scholar] [CrossRef] [PubMed]
- Rashidi, A.A.; Kiani, O.; Heidarzadeh, M.; Imani, B.; Nematy, M.; Taghipour, A.; Sadr, M.; Norouzy, A. Reference Curves of Birth Weight, Length, and Head Circumference for Gestational Age in Iranian Singleton Births. Iran. J. Pediatr. 2018, 28, e66291. [Google Scholar] [CrossRef]
- Morán-Vásquez, R.; Mazo-Lopera, M.; Ferrari, S. Quantile modeling through multivariate log-normal/independent linear regression models with application to newborn data. Biom. J. 2021, 63, 1290–1308. [Google Scholar] [CrossRef] [PubMed]
- Fang, K.T.; Kotz, S.; Ng, K.W. Symmetric Multivariate and Related Distributions; Chapman and Hall: London, UK, 1990. [Google Scholar]
- Kotz, S.; Kozubowski, T.J.; Podgórski, K. The Laplace Distribution and Generalizations; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Mäkeläinen, T.; Schmidt, K.; Styan, G. On the existence and uniqueness of the maximum likelihood estimate of a vector-valued parameter in fixed-size samples. Ann. Stat. 1981, 9, 758–767. [Google Scholar] [CrossRef]
- Cramér, H. Mathematical Methods of Statistics; Princeton University Press: Princeton, NJ, USA, 1946. [Google Scholar]
- Efron, B.; Hinkley, D. Assessing the accuracy of the maximum likelihood estimator: Observed versus expected Fisher Information. Biometrika 1978, 65, 457–487. [Google Scholar] [CrossRef]
- Hu, S.; Murphy, T.B.; O’Hagan, A. Bivariate Gamma Mixture of Experts Models for Joint Insurance Claims Modeling. arXiv 2019. [Google Scholar] [CrossRef]
- Yoo, S.H. Analysing household bottled water and water purifier expenditures: Simultaneous equation bivariate Tobit model. Appl. Econ. Lett. 2005, 12, 297–301. [Google Scholar] [CrossRef]
- Saulo, H.; Dasilva, A.; Leiva, V.; Sánchez, L.; de la Fuente-Mella, H. Log-symmetric quantile regression models. Stat. Neerl. 2022, 76, 124–163. [Google Scholar] [CrossRef]
- Song, P.X.K.; Li, M.; Yuan, Y. Joint Regression Analysis of Correlated Data Using Gaussian Copulas. Biometrics 2009, 65, 60–68. [Google Scholar] [CrossRef] [PubMed]

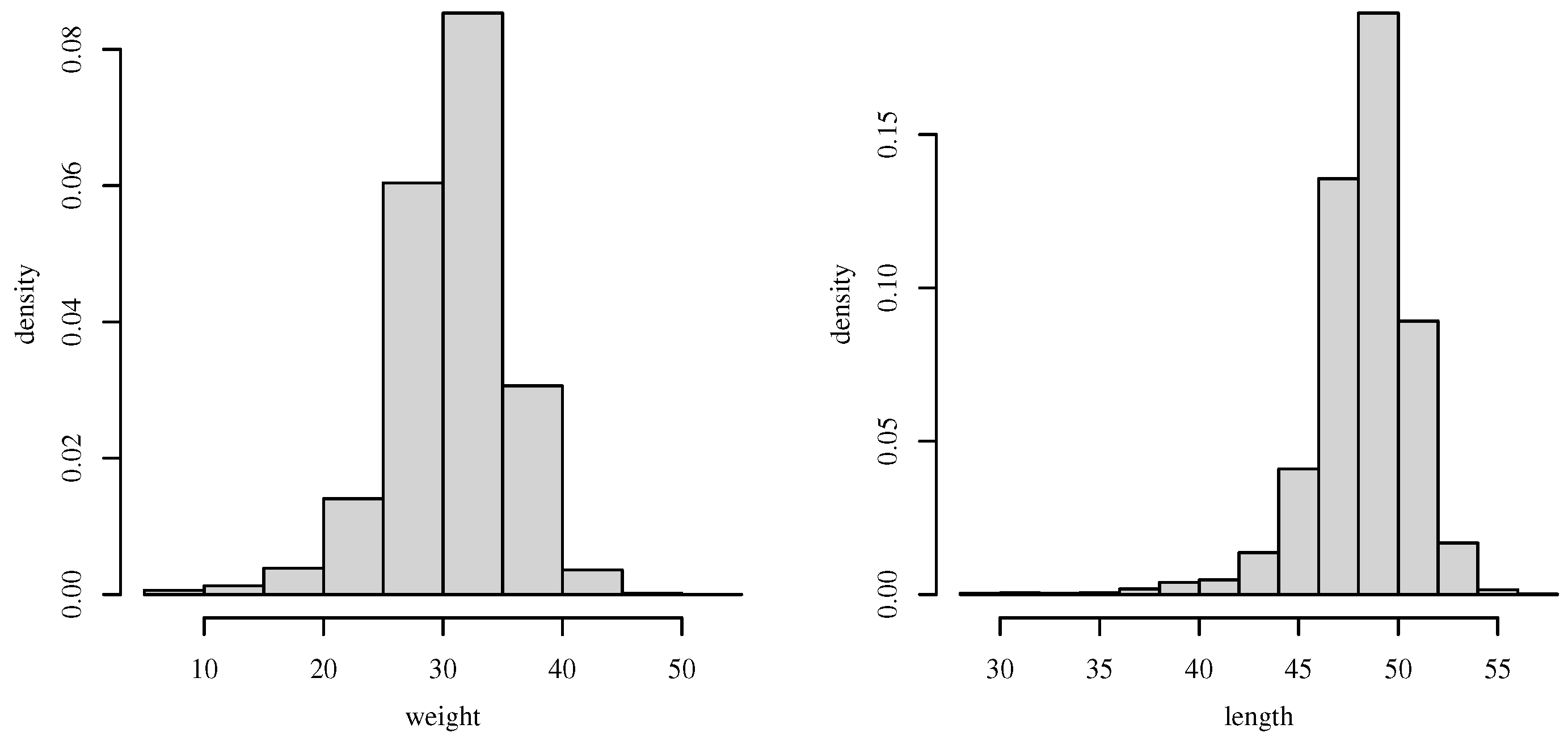
| Variables | n | Minimum | Median | Mean | Maximum | SD | CV | CS | CK |
|---|---|---|---|---|---|---|---|---|---|
| 6714 | 5.4 | 31.1 | 30.791 | 50.9 | 4.931 | 16.015 | −0.747 | 2.168 | |
| 6714 | 28 | 49 | 48.72 | 58 | 2.634 | 5.406 | −1.609 | 6.816 |
| Bivariate Distribution | Extra Parameter | ||
|---|---|---|---|
| Log-normal | − | ||
| Log-Student-t | |||
| Log-hyperbolic | |||
| Log-Laplace | − | ||
| Log-slash | |||
| Log-power-exponential | |||
| Log-logistic | − |
| Scenario 1 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 0.0505 | 0.0548 | 0.0226 | 0.0686 | 0.0605 | 0.0241 | 0.0313 | 0.0572 | 0.1552 | 0.0923 | 0.1538 | 0.0975 | 0.2758 | 0.2204 |
| 500 | 0.0203 | 0.0188 | 0.0086 | 0.0294 | 0.0265 | 0.0094 | 0.0126 | 0.0219 | 0.0627 | 0.0337 | 0.0618 | 0.0368 | 0.1188 | 0.0701 |
| 1000 | 0.0153 | 0.0129 | 0.0067 | 0.0197 | 0.0171 | 0.0061 | 0.0082 | 0.0163 | 0.0420 | 0.0221 | 0.0449 | 0.0221 | 0.0814 | 0.0508 |
| Scenario 2 | ||||||||||||||
| 100 | 0.0394 | 0.0314 | 0.0078 | 0.0229 | 0.0485 | 0.0146 | 0.0108 | 0.0189 | 0.2779 | 0.1108 | 0.2775 | 0.1114 | 0.0414 | 0.0654 |
| 500 | 0.0077 | 0.0048 | 0.0010 | 0.0029 | 0.0095 | 0.0022 | 0.0013 | 0.0025 | 0.1122 | 0.0433 | 0.1125 | 0.0433 | 0.0176 | 0.0167 |
| 1000 | 0.0040 | 0.0023 | 0.0004 | 0.0013 | 0.0049 | 0.0011 | 0.0006 | 0.0011 | 0.0795 | 0.0297 | 0.0795 | 0.0298 | 0.0121 | 0.0101 |
| Scenario 3 | ||||||||||||||
| 100 | 0.0166 | 0.0136 | 0.0028 | 0.0080 | 0.0201 | 0.0065 | 0.0036 | 0.0070 | 0.5120 | 0.1078 | 0.5101 | 0.1084 | 0.0797 | 0.0633 |
| 500 | 0.0023 | 0.0016 | 0.0003 | 0.0009 | 0.0030 | 0.0007 | 0.0004 | 0.0008 | 0.2097 | 0.0441 | 0.2097 | 0.0442 | 0.0318 | 0.0145 |
| 1000 | 0.0012 | 0.0007 | 0.0001 | 0.0004 | 0.0014 | 0.0003 | 0.0002 | 0.0003 | 0.1591 | 0.0315 | 0.1587 | 0.0315 | 0.0216 | 0.0091 |
| Scenario 1 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 0.0692 | 0.0496 | 0.0432 | 0.0433 | 0.0695 | 0.0493 | 0.0436 | 0.0438 | 0.0787 | 0.0813 | 0.0768 | 0.0867 | 0.1045 | 0.1397 |
| 500 | 0.0282 | 0.0167 | 0.0163 | 0.0187 | 0.0304 | 0.0181 | 0.0171 | 0.0166 | 0.0311 | 0.0303 | 0.0314 | 0.0324 | 0.0449 | 0.0442 |
| 1000 | 0.0211 | 0.0114 | 0.0123 | 0.0121 | 0.0195 | 0.0112 | 0.0114 | 0.0124 | 0.0211 | 0.0195 | 0.0226 | 0.0193 | 0.0304 | 0.0315 |
| Scenario 2 | ||||||||||||||
| 100 | 0.0574 | 0.0298 | 0.0173 | 0.0166 | 0.0575 | 0.0295 | 0.0174 | 0.0166 | 0.0692 | 0.0699 | 0.0688 | 0.0699 | 0.1041 | 0.1964 |
| 500 | 0.0118 | 0.0048 | 0.0021 | 0.0022 | 0.0117 | 0.0048 | 0.0020 | 0.0022 | 0.0282 | 0.0269 | 0.0283 | 0.0269 | 0.0436 | 0.0515 |
| 1000 | 0.0057 | 0.0021 | 0.0009 | 0.0009 | 0.0058 | 0.0021 | 0.0009 | 0.0009 | 0.0200 | 0.0184 | 0.0199 | 0.0184 | 0.0303 | 0.0322 |
| Scenario 3 | ||||||||||||||
| 100 | 0.0256 | 0.0137 | 0.0060 | 0.0057 | 0.0252 | 0.0140 | 0.0057 | 0.0058 | 0.0638 | 0.0679 | 0.0636 | 0.0682 | 0.0992 | 0.2213 |
| 500 | 0.0034 | 0.0016 | 0.0006 | 0.0006 | 0.0037 | 0.0015 | 0.0006 | 0.0006 | 0.0264 | 0.0274 | 0.0264 | 0.0274 | 0.0401 | 0.0535 |
| 1000 | 0.0017 | 0.0006 | 0.0003 | 0.0003 | 0.0016 | 0.0006 | 0.0003 | 0.0003 | 0.0204 | 0.0199 | 0.0203 | 0.0199 | 0.0275 | 0.0339 |
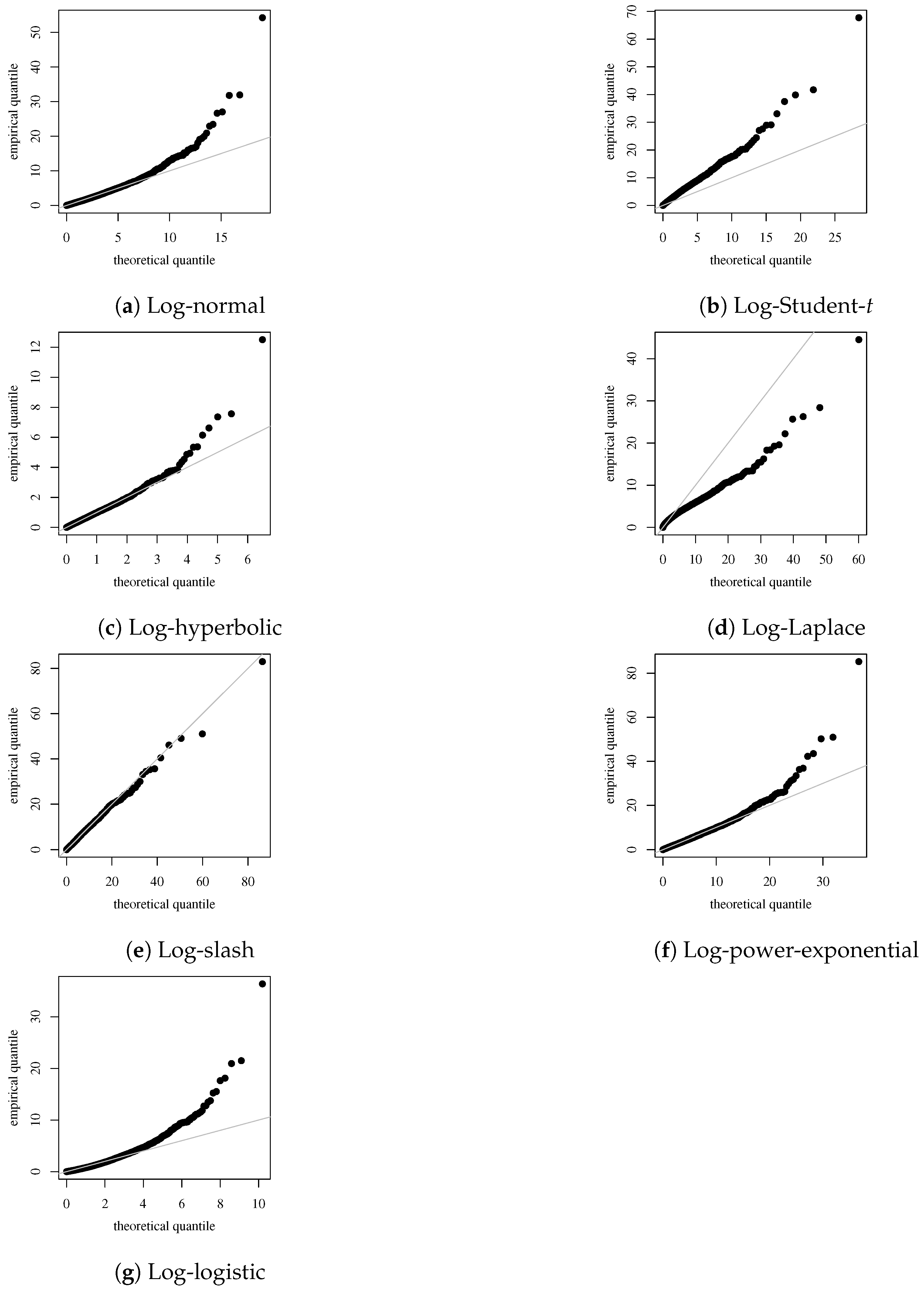
| Distribution | Log-Likelihood | AIC | BIC |
|---|---|---|---|
| Log-normal | −30,300.5199 | 60,651.0398 | 60,821.3385 |
| Log-Student-t | −30,236.8269 | 60,523.6538 | 60,693.9526 |
| Log-hyperbolic | −30,230.5438 | 60,511.0876 | 60,681.3864 |
| Log-Laplace | −30,814.1601 | 61,678.3202 | 61,848.6189 |
| Log-slash | −30,220.9040 | 60,491.8080 | 60,662.1068 |
| Log-power-exponential | −30,249.1342 | 60,548.2684 | 60,718.5672 |
| Log-logistic | −30,606.7447 | 61,263.4893 | 61,433.7881 |
| Coefficients for | ||||
|---|---|---|---|---|
| Parameter | Estimate | SE | -Value | -Value |
| 1.0757653 | 0.0436945 | 24.620 | < *** | |
| 0.0303725 | 0.0028133 | 10.796 | < *** | |
| 0.0592572 | 0.0011096 | 53.405 | < *** | |
| 0.0018078 | 0.0002887 | 6.263 | *** | |
| 0.0001755 | 0.0002369 | 0.741 | 0.459 | |
| Coefficients for | ||||
| Parameter | Estimate | SE | -Value | -Value |
| *** | ||||
| *** | ||||
| *** | ||||
| *** | ||||
| Coefficients for | ||||
| Parameter | Estimate | SE | t-Value | p-Value |
| *** | ||||
| *** | ||||
| *** | ||||
| Coefficients for | ||||
| Parameter | Estimate | SE | t-Value | p-Value |
| ** | ||||
| *** | ||||
| ** | ||||
| ** | ||||
| Coefficients for | ||||
| Parameter | Estimate | SE | t-Value | p-Value |
| *** | ||||
| *** | ||||
| *** | ||||
| ** | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saulo, H.; Vila, R.; Souza, R. Bivariate Log-Symmetric Regression Models Applied to Newborn Data. Symmetry 2024, 16, 1315. https://doi.org/10.3390/sym16101315
Saulo H, Vila R, Souza R. Bivariate Log-Symmetric Regression Models Applied to Newborn Data. Symmetry. 2024; 16(10):1315. https://doi.org/10.3390/sym16101315
Chicago/Turabian StyleSaulo, Helton, Roberto Vila, and Rubens Souza. 2024. "Bivariate Log-Symmetric Regression Models Applied to Newborn Data" Symmetry 16, no. 10: 1315. https://doi.org/10.3390/sym16101315







