Hyperchaotic Oscillator with Line and Spherical Equilibria: Stability, Entropy, and Implementation for Random Number Generation
Abstract
:1. Introduction
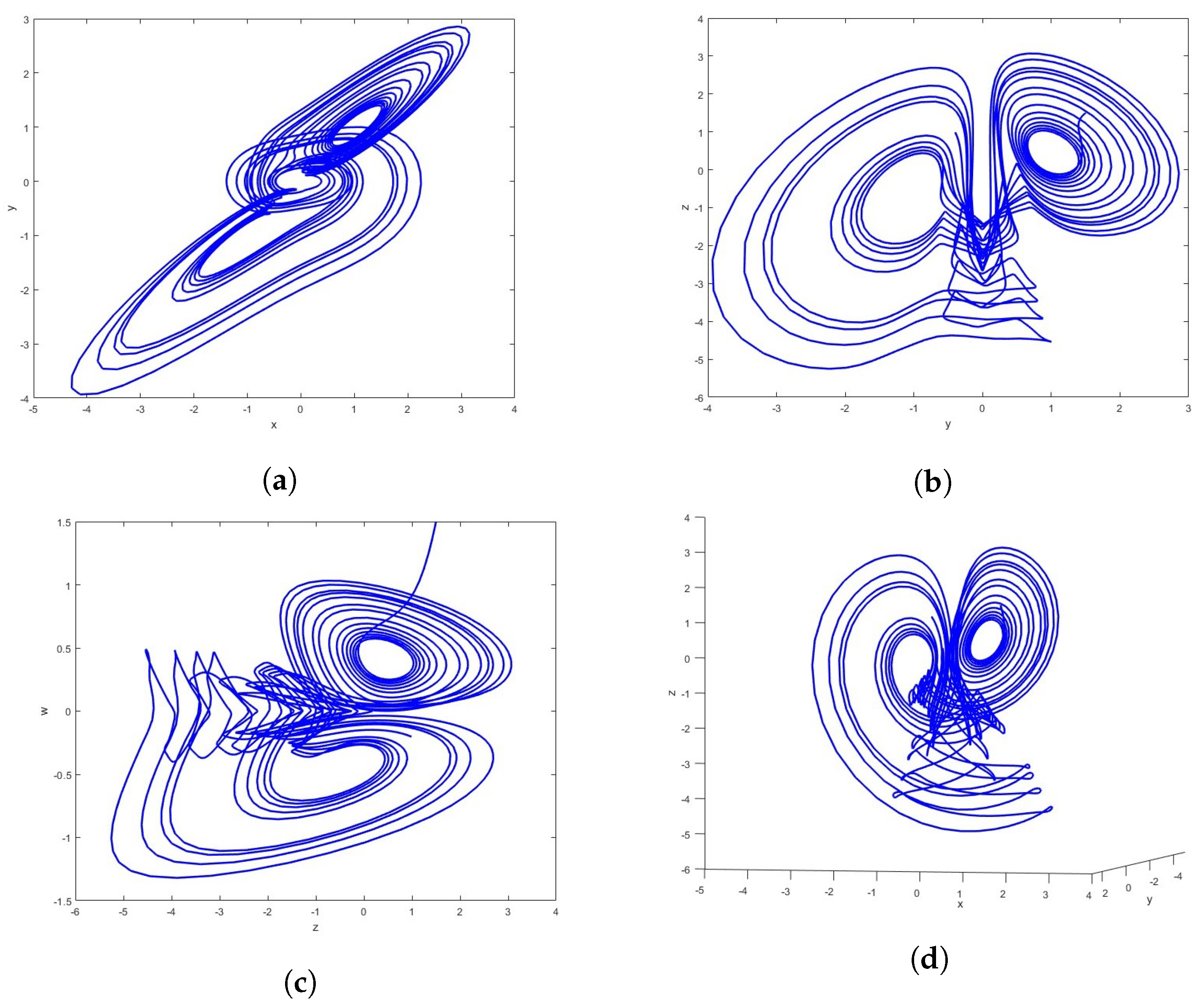
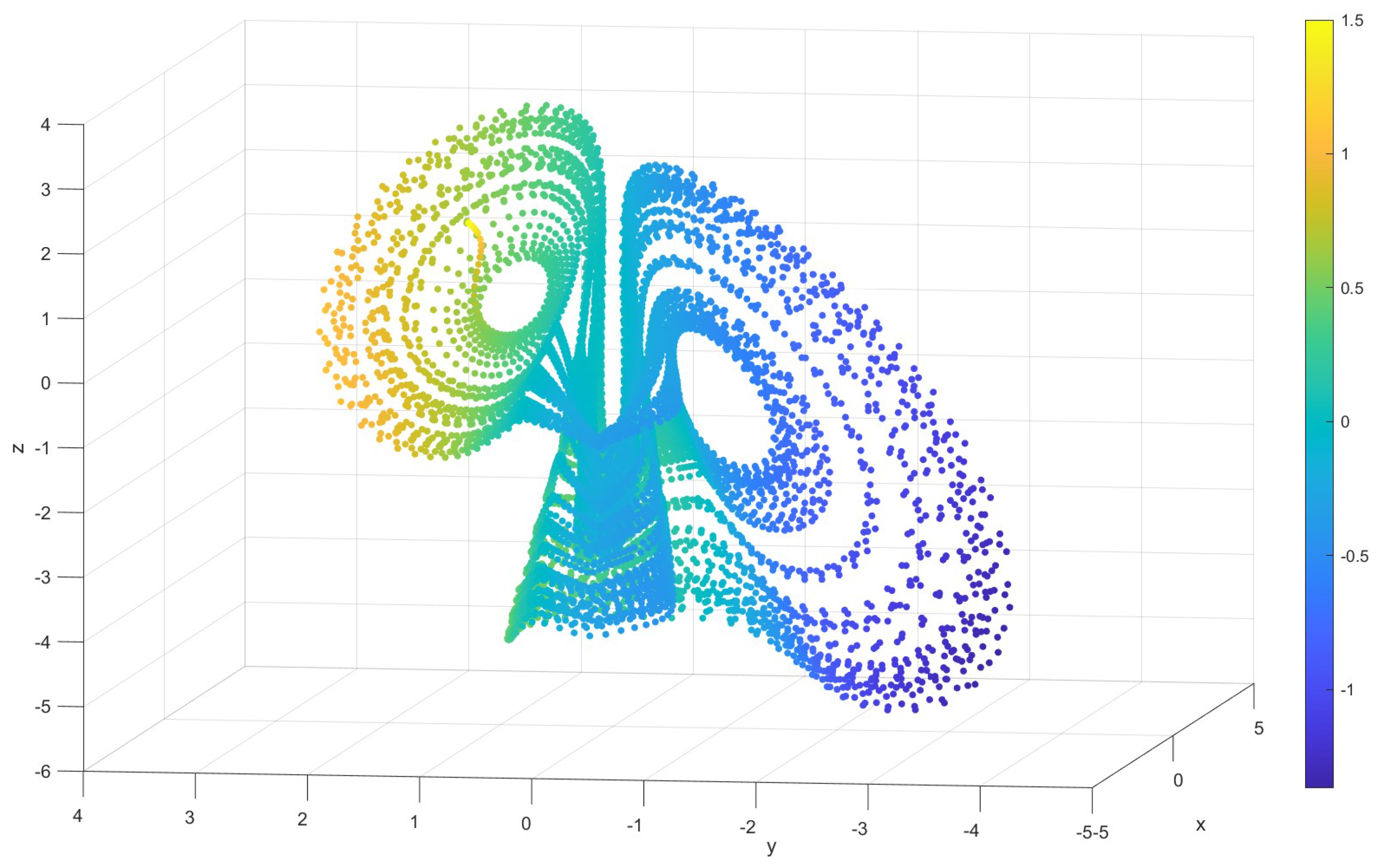
2. Model and Dynamics of the Oscillator
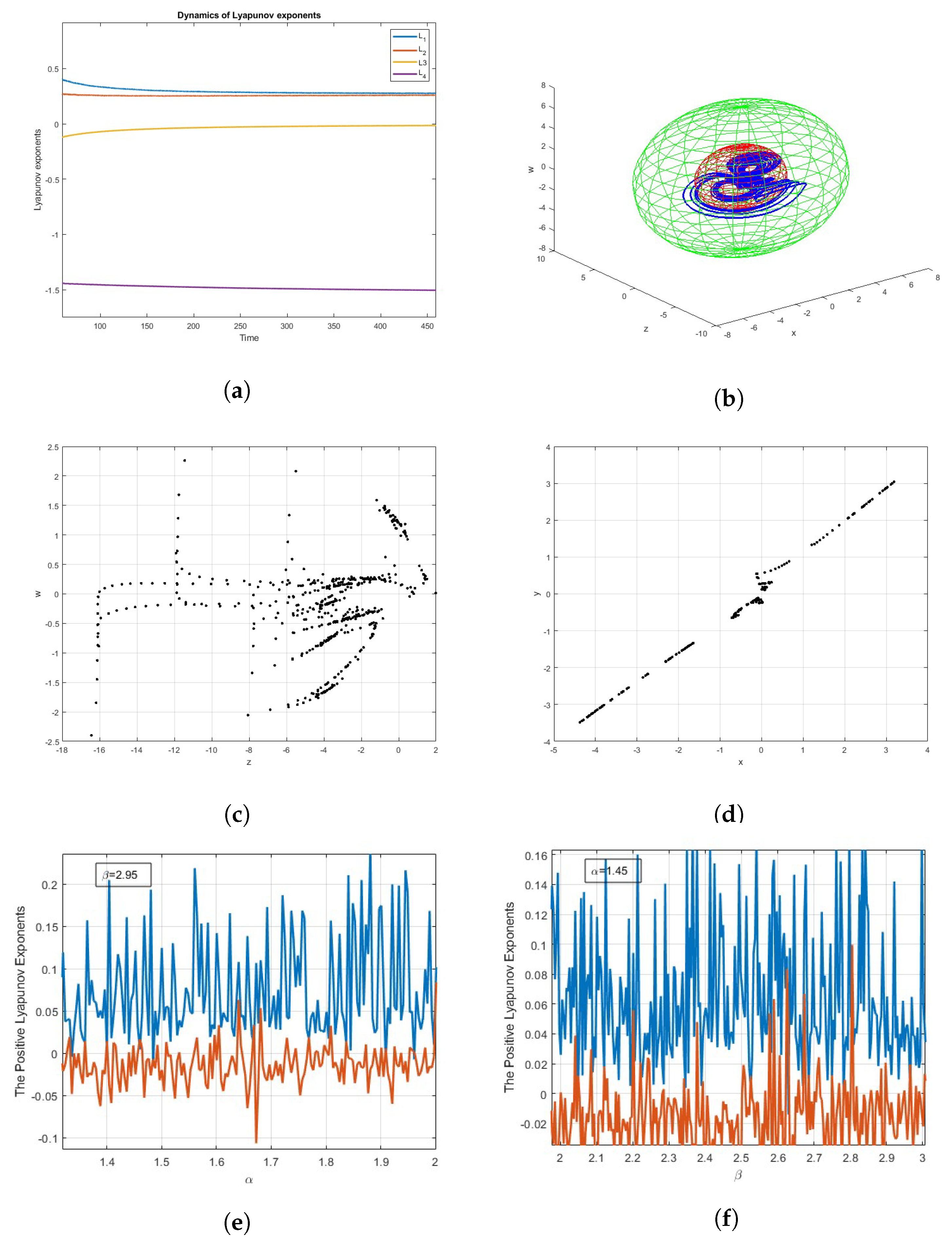
2.1. Stability Analysis
- I.
- The origin is the equilibrium point for the proposed oscillator.
- II.
- When and a line of equilibria appears as
- III.
- When , and we have spherical equilibria , where
2.2. Complexity of Oscillator (1)
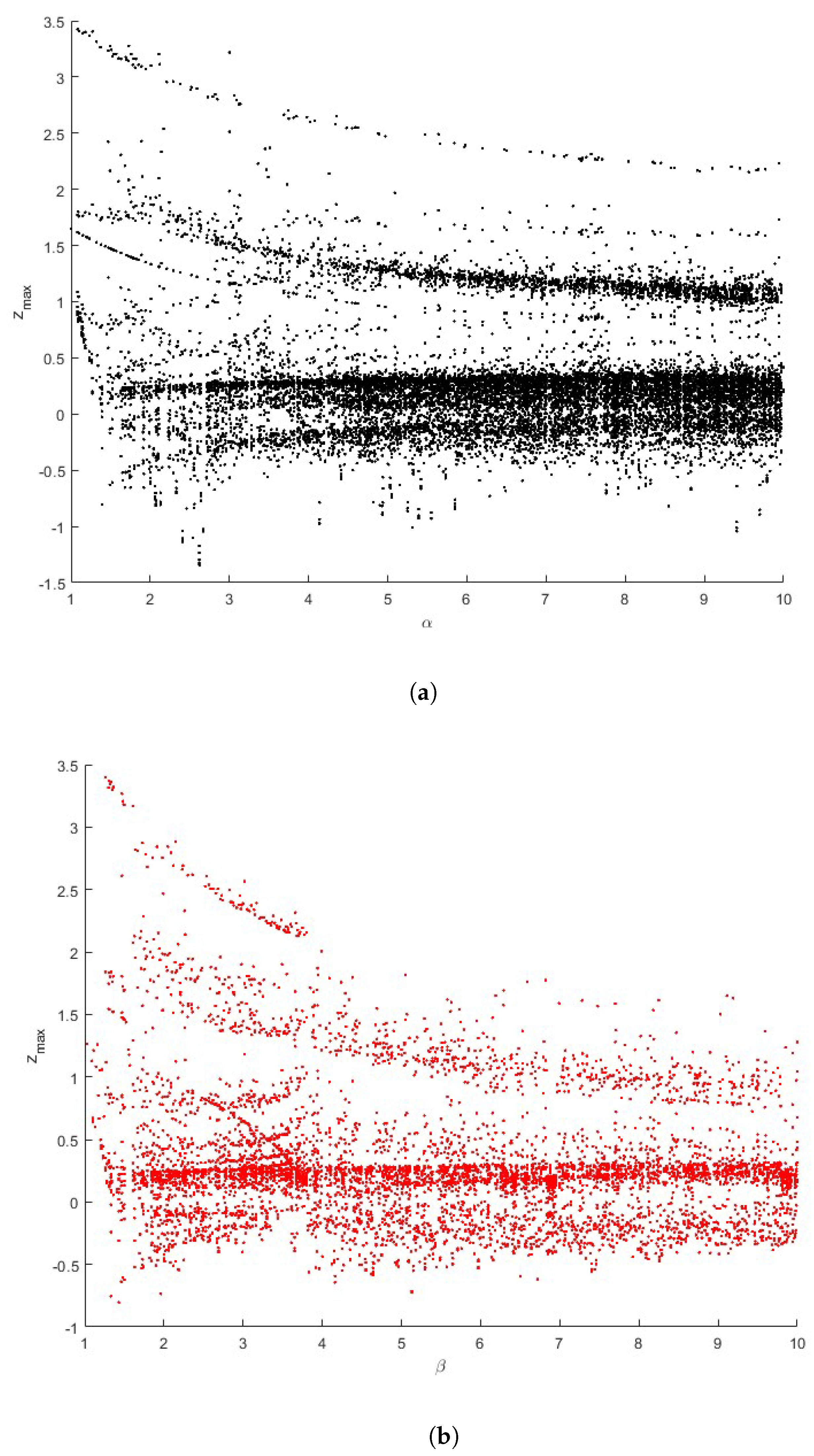
3. Bifurcation
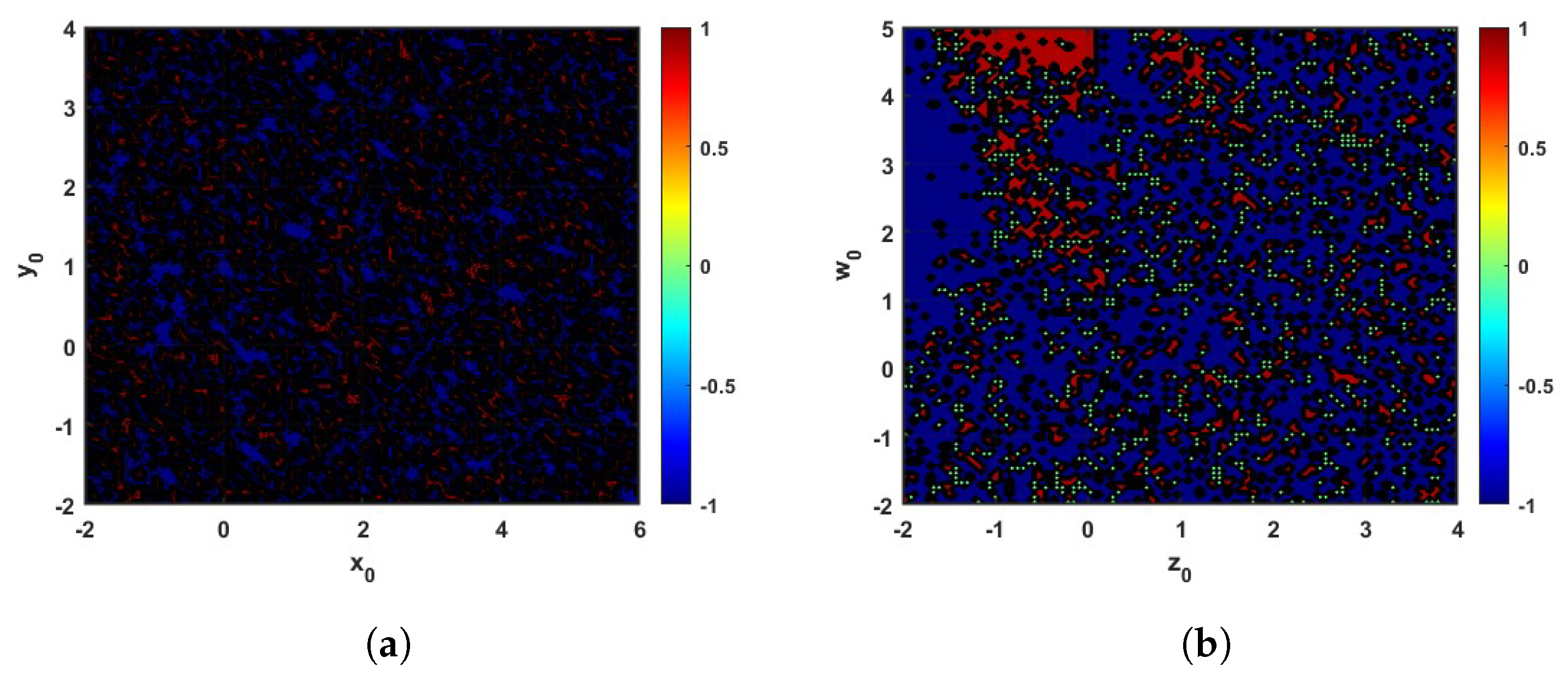
4. Poincaré Cross-Section
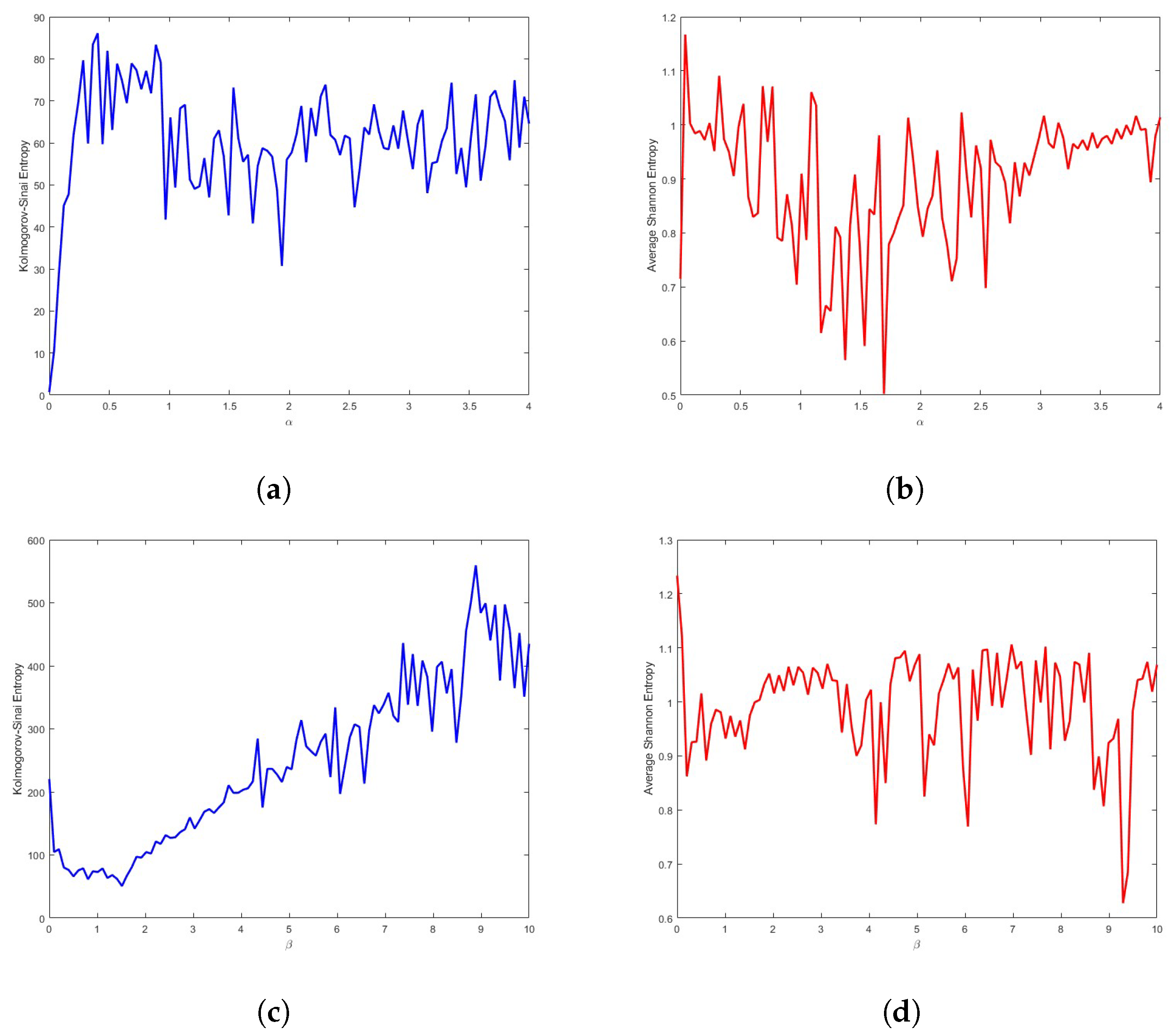
5. Entropy
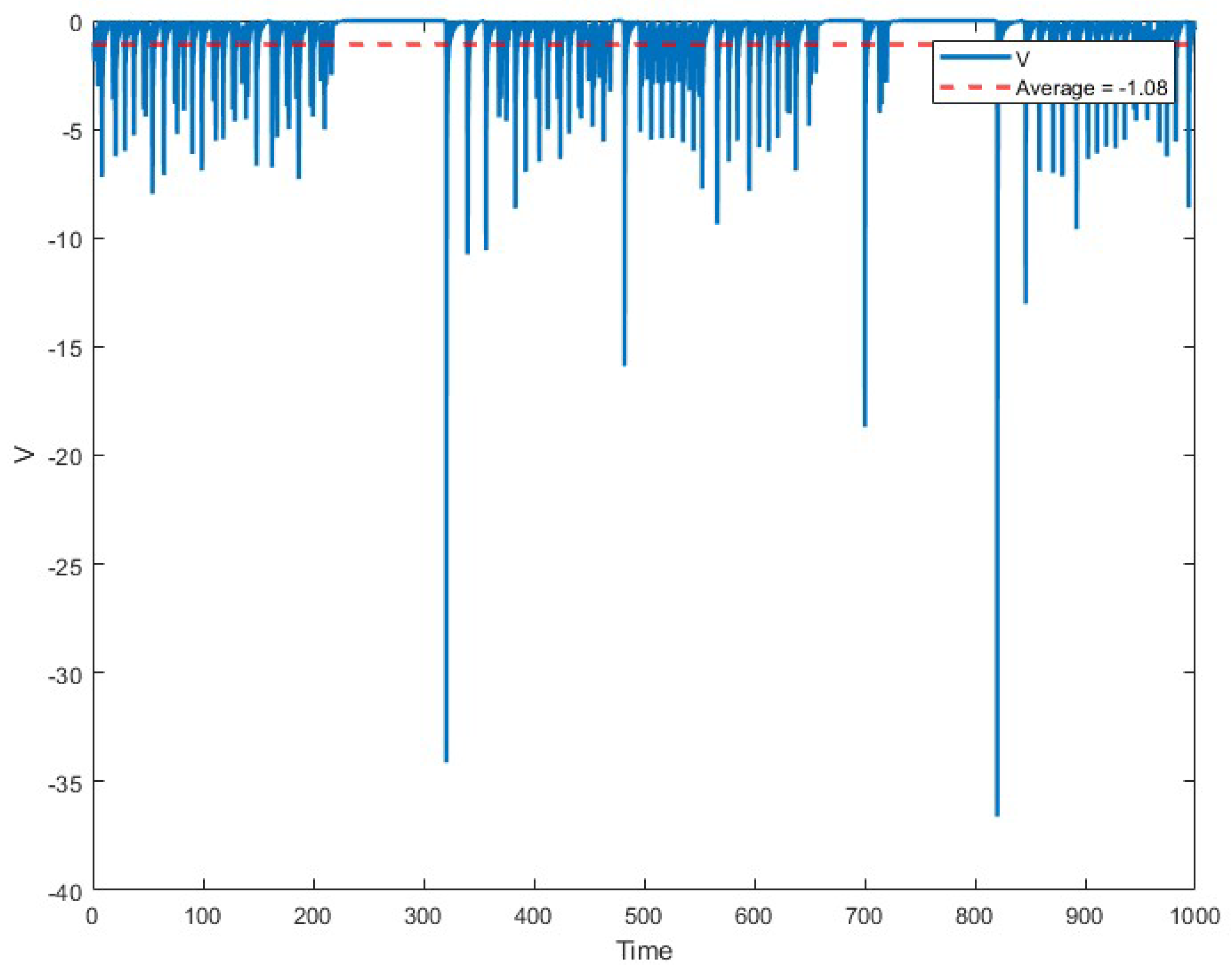
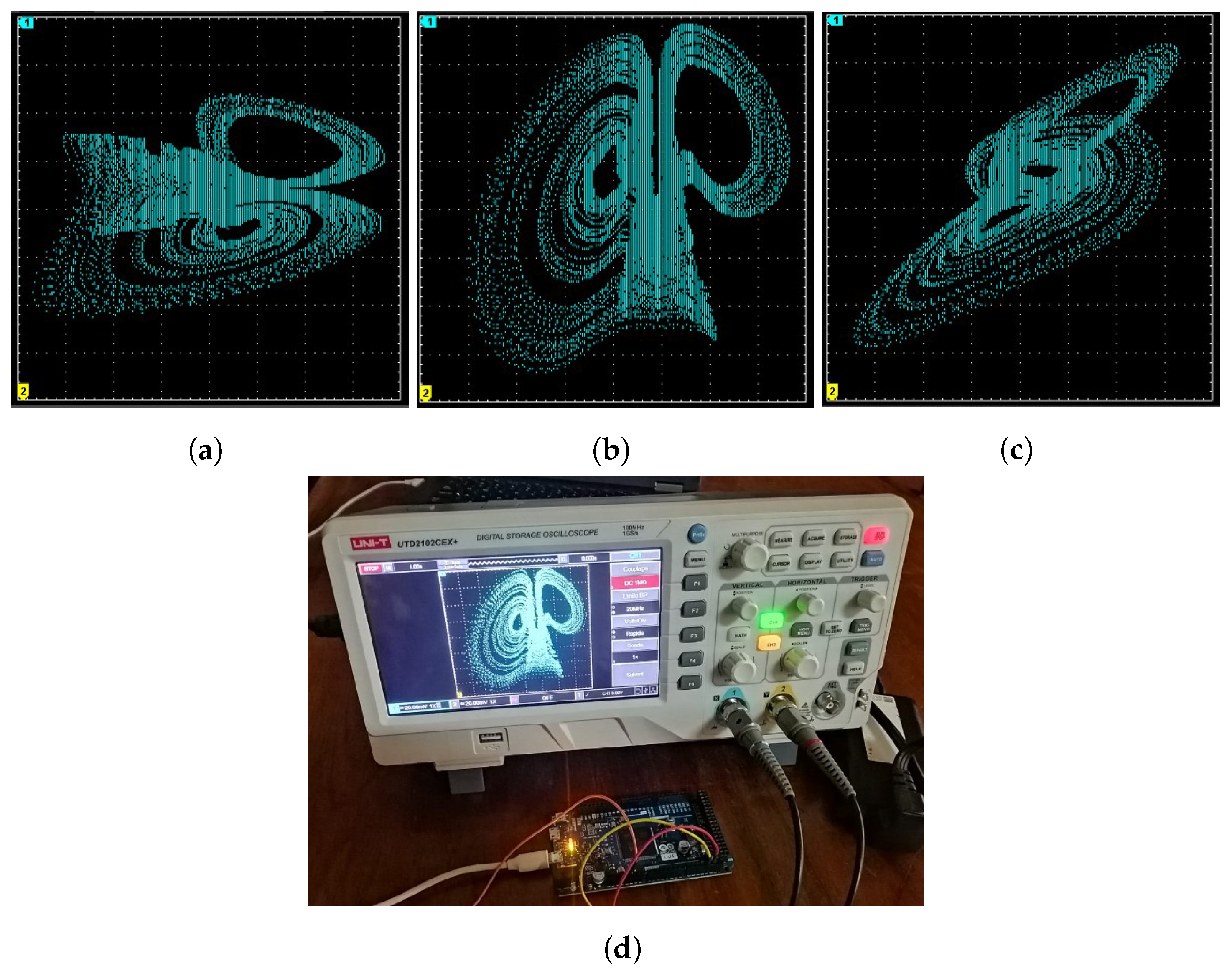
6. Microcontroller Implementation of 4D Oscillator
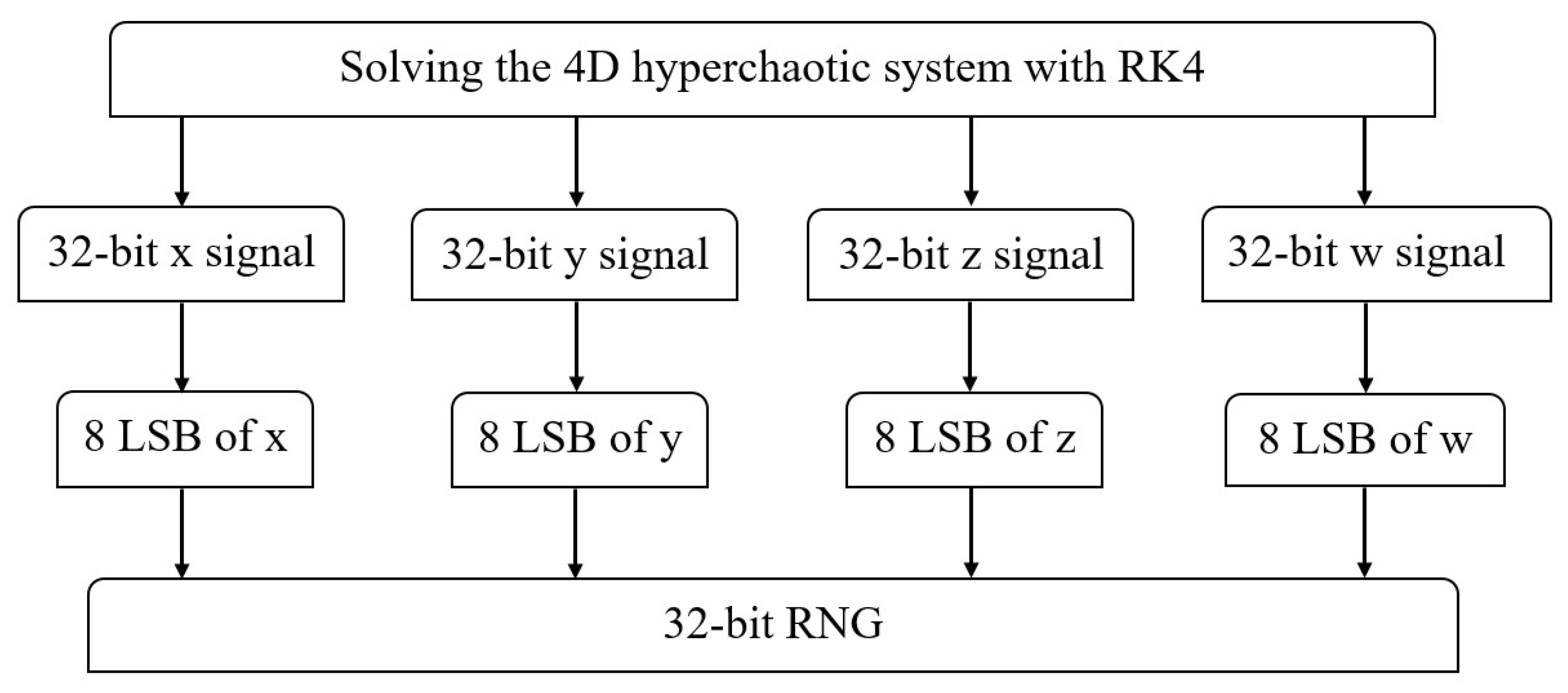
7. Implementation for RNG
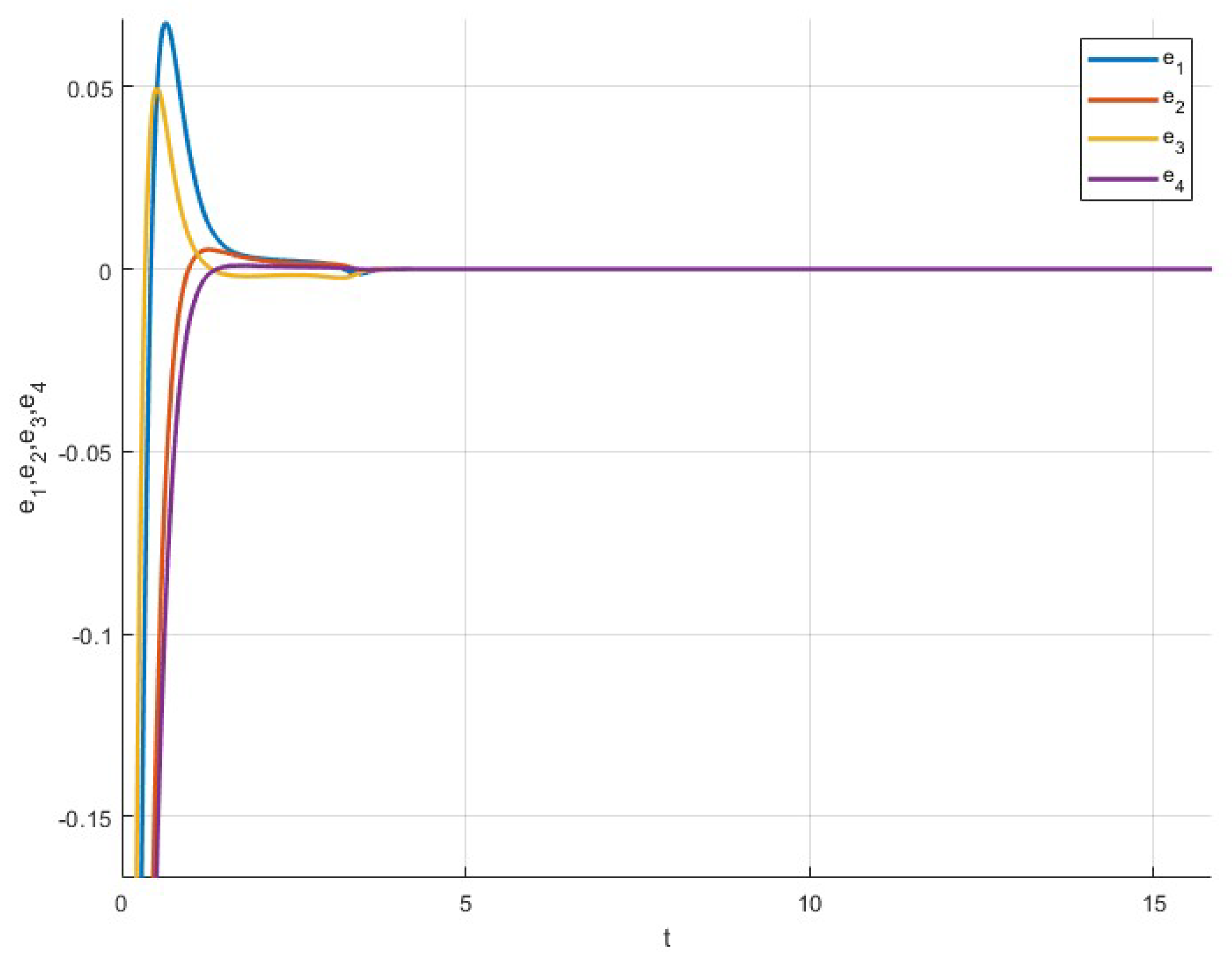
8. System Control
Numerical Simulation
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cicek, S.; Kocamaz, U.; Uyaroglu, Y. Secure communication with a chaotic system owning. Aeu Int. J. Electron. Commun. 2018, 88, 52–62. [Google Scholar] [CrossRef]
- Tamba, V.K.; Pham, V.; Shukur, A.A.; Grassi, G.; Momani, S. Oscillator without equilibrium and linear terms: Dynamics and application. Alex. Eng. J. 2024, 97, 376–384. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Yao, W.; Tan, Y. Chaotic dynamics in a neural network with different types of external stimuli. Commun. Nonlinear Sci. Numer. Simulat. 2020, 90, 105390. [Google Scholar] [CrossRef]
- Tan, Z.; Hepburn, B.S.; Tucker, C.; Ali, M.K. Pattern recognition using chaotic neural networks. Discret. Dyn. Nat. Soc. 1998, 2, 243–247. [Google Scholar]
- Wu, L.; Wang, D.; Zhang, C.; Mohammadzadeh, A. Chaotic Synchronization in Mobile Robots. Mathematics 2022, 10, 4568. [Google Scholar] [CrossRef]
- Korolj, A.; Wu, H.T.; Radisic, M. A healthy dose of chaos: Using fractal frameworks for engineering higher-fidelity biomedical systems. Biomaterials 2019, 219, 119363. [Google Scholar] [CrossRef] [PubMed]
- Lorenz, E.N. Deterministic Nonperiodic Flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.; Golpayegani, S.M.R.H. Elementary quadratic chaotic flows with no equilibria. Phys. Lett. A 2013, 377, 699–702. [Google Scholar] [CrossRef]
- Wei, Z. Dynamical behaviors of a chaotic system with no equilibria. Phys. Lett. A 2011, 376, 102–108. [Google Scholar] [CrossRef]
- Lao, S.K.; Shekofteh, Y.; Jafari, S.; Sprott, J. Cost function based on Gaussian mixture model for parameter estimation of a chaotic circuit with a hidden attractor. Int. J. Bifurc. Chaos 2014, 24, 1450010. [Google Scholar] [CrossRef]
- Wang, X.; Chen, G. A chaotic system with only one stable equilibrium. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1264–1272. [Google Scholar] [CrossRef]
- Kapitaniak, T.; Mohammadi, S.A.; Mekhilef, S.; Alsaadi, F.E.; Hayat, T.; Pham, V.T. A New Chaotic System with Stable Equilibrium: Entropy Analysis, Parameter Estimation, and Circuit Design. Entropy 2018, 20, 670. [Google Scholar] [CrossRef] [PubMed]
- Jafari, S.; Sprott, J. Simple chaotic flows with a line equilibrium. Chaos Solitons Fractals 2013, 57, 79–84. [Google Scholar] [CrossRef]
- Rajagopal, K.; Karthikeyan, A.; Srinivasan, A. Bifurcation and chaos in time delayed fractional order chaotic oscillator and its sliding mode synchronization with uncertainties. Chaos Solitons Fractals 2017, 103, 347–356. [Google Scholar] [CrossRef]
- Barati, K.; Jafari, S.; Sprott, J.C.; Pham, V.T. Simple Chaotic Flows with a Curve of Equilibria. Int. J. Bifurc. Chaos 2016, 26, 1630034. [Google Scholar] [CrossRef]
- Tolba, M.F.; Said, L.A.; Madian, A.H.; Radwan, A.G. FPGA implementation of fractional-order integrator and differentiator based on Grunwald Letnikov’s definition. In Proceedings of the 29th International Conference on Microelectronics (ICM), Beirut, Lebanon, 10–13 December 2017; pp. 1–4. [Google Scholar]
- Ismail, S.M.; Said, L.A.; Rezk, A.A.; Radwan, A.G.; Madian, A.H.; Abu-Elyazeed, M.F.; Soliman, A.M. Generalized fractional logistic map encryption system based on FPGA. EU-Int. J. Electron. Commun. 2017, 80, 114–126. [Google Scholar] [CrossRef]
- Leonov, G.; Kuznetsov, N.; Mokaev, T. Hidden attractor and homoclinic orbit in Lorenz-like system describing convective fluid motion in rotating cavity. Commun. Nonlinear Sci. Numer. Simul. 2015, 28, 166–174. [Google Scholar] [CrossRef]
- Rossler, O. An equation for hyperchaos. Phys. Lett. A 1979, 71, 155–157. [Google Scholar] [CrossRef]
- Barboza, R. Dynamics of a hyperchoatic Lorenz system. Int. J. Bifurc. Chaos 2007, 17, 4285–4290. [Google Scholar] [CrossRef]
- Neimark, Y.; Shilnikov, L. A condition for the generation of periodic motions. Sov. Math. Docklady 1963, 163, 1261–1264. [Google Scholar]
- Benkouider, K.; Vaidyanathan, S.; Sambas, A.; Cuautle, E.; Abd EL-latif, A.; Abd-EL-Atty, B.; Bermudez-Marquez, C.; Sulaman, I.; Awwal, A.; Kuman, P. A New 5-D Multistable Hyperchaotic System With Three Positive Lyapunov Exponents: Bifurcation Analysis, Circuit Design, FPGA Realization and Image Encryption. IEEE Access 2022, 10, 90111–90132. [Google Scholar] [CrossRef]
- Peng, Z.; Yu, W.; Wang, J.; Zhou, Z.; Chen, J.; Zhong, G. Secure communication based on microcontroller unit with a novel five-dimensional hyperchaotic system. Arabian J. Sci. Eng. 2021, 47, 813–828. [Google Scholar] [CrossRef]
- Vaidyanathan, S. A Novel 5-D Hyperchaotic System with a Line of Equilibrium Points and Its Adaptive Control. Advances and Applications in Chaotic Systems. Stud. Comput. Intell. 2016, 636, 471–494. [Google Scholar]
- Chunbiao, L.; Sprott, J.C.; Wesley, T. Bistability in a Hyperchaotic System with a Line Equilibrium. J. Exp. Theor. Phys. 2014, 118, 494–500. [Google Scholar]
- Singh, J.; Roy, B.K. The simplest 4-D chaotic system with line of equilibria, chaotic 2-torus and 3-torus behaviour. Nonlinear Dyn. 2017, 89, 1845–1862. [Google Scholar] [CrossRef]
- Singh, J.; Jafari, K.R.S. New family of 4-D hyperchaotic and chaotic systems with quadric surfaces of equilibria. Chaos Solitons Fractals 2018, 106, 243–257. [Google Scholar] [CrossRef]
- Yuming, C.; Qigui, Y. A new Lorenz-type hyperchaotic system with a curve of equilibria. Math. Comput. Simul. 2015, 112, 40–55. [Google Scholar]
- Wang, Z.; Xu, Z.; Mliki, E.; Agkgu, A.; Pham, V.-T.; Jafari, S. A new chaotic attractor around a pre-located ring. J. Int. Bifurc. Chaos 2017, 27, 1–10. [Google Scholar] [CrossRef]
- Diffie, W.; Hellman, M.E. Multiuser cryptographic techniques. In Proceedings of the June 7–10, 1976, National Computer Conference and Exposition; ACM: New York, NY, USA, 1976; pp. 109–112. [Google Scholar]
| Ref. | Dimensions | Equilibria | No. of Terms |
|---|---|---|---|
| [24] | 5D | Line | fifteen |
| [25] | 4D | Line | eight |
| [26] | 4D | Line | eight |
| [27] | 4D | Quadratic surfaces | six |
| [28] | 4D | Curve | thirteen |
| This work | 4D | Single, line, and sphere | nine |
| Test Name | p-Value (x) | p-Value (y) | p-Value (z) | p-Value (w) | Results |
|---|---|---|---|---|---|
| Frequency | 0.25345 | 0.70692 | 0.85872 | 0.92034 | demonstrated |
| Block frequency | 0.44118 | 0.93263 | 0.19375 | 0.28412 | demonstrated |
| Runs | 0.41489 | 0.55394 | 0.90287 | 0.07540 | demonstrated |
| Longest run of ones | 0.97984 | 0.97531 | 0.11504 | 0.21060 | demonstrated |
| Rank | 0.74427 | 0.47236 | 0.76575 | 0.46079 | demonstrated |
| DFT | 0.50292 | 0.06783 | 0.37834 | 0.77604 | demonstrated |
| No overlapping templates | 0.30195 | 0.05616 | 0.02864 | 0.10238 | demonstrated |
| Overlapping templates | 0.78749 | 0.77395 | 0.90626 | 0.81761 | demonstrated |
| Universal | 0.97158 | 0.15981 | 0.46365 | 0.62048 | demonstrated |
| Linear complexity | 0.18993 | 0.23150 | 0.92968 | 0.06544 | demonstrated |
| Serial test 1 | 0.38527 | 0.67854 | 0.17562 | 0.72572 | demonstrated |
| Serial test 2 | 0.48301 | 0.71068 | 0.53014 | 0.64265 | demonstrated |
| Approximate entropy | 0.14177 | 0.61022 | 0.37092 | 0.94487 | demonstrated |
| Cumulative sums (forward) | 0.30197 | 0.86374 | 0.51721 | 0.64392 | demonstrated |
| Random excursions x = 2 | 0.50579 | 0.57193 | 0.99671 | 0.41986 | demonstrated |
| Random excursion variant x = 8 | 0.72471 | 0.03628 | 0.59473 | 0.91573 | demonstrated |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shukur, A.A.; Pham, V.-T.; Tamba, V.K.; Grassi, G. Hyperchaotic Oscillator with Line and Spherical Equilibria: Stability, Entropy, and Implementation for Random Number Generation. Symmetry 2024, 16, 1341. https://doi.org/10.3390/sym16101341
Shukur AA, Pham V-T, Tamba VK, Grassi G. Hyperchaotic Oscillator with Line and Spherical Equilibria: Stability, Entropy, and Implementation for Random Number Generation. Symmetry. 2024; 16(10):1341. https://doi.org/10.3390/sym16101341
Chicago/Turabian StyleShukur, Ali A., Viet-Thanh Pham, Victor Kamdoum Tamba, and Giuseppe Grassi. 2024. "Hyperchaotic Oscillator with Line and Spherical Equilibria: Stability, Entropy, and Implementation for Random Number Generation" Symmetry 16, no. 10: 1341. https://doi.org/10.3390/sym16101341






