Parameter Estimation of Uncertain Differential Equations Driven by Threshold Ornstein–Uhlenbeck Process with Application to U.S. Treasury Rate Analysis
Abstract
:1. Introduction
1.1. Background and Motivation
1.2. Literature Review
1.3. Contribution
1.4. Organization of the Paper
2. Preliminaries
- Normality axiom: for the universal set Γ.
- Duality axiom: for any event
- Subadditivity axiom: For every countable sequence of events , we have
- Product axiom: Let be uncertainty spaces for . Then, the product uncertain measure error is an uncertain measure satisfyingwhere are arbitrary chosen events from for respectively.
- 1.
- and almost all sample paths are Lipschitz continuous;
- 2.
- has stationary and independent increments;
- 3.
- The increment .
3. Parameter Estimation of Uncertain TOU Process
3.1. Uncertain Threshold Ornstein–Uhlenbeck Process
3.2. Parameter Estimation of Uncertain TOU Process for with Maximum Likelihood Estimation
3.3. Parameter Estimation of Uncertain TOU Process for by Method of Moments
3.4. Hypothesis Test Based on the Residuals
4. Numerical Examples
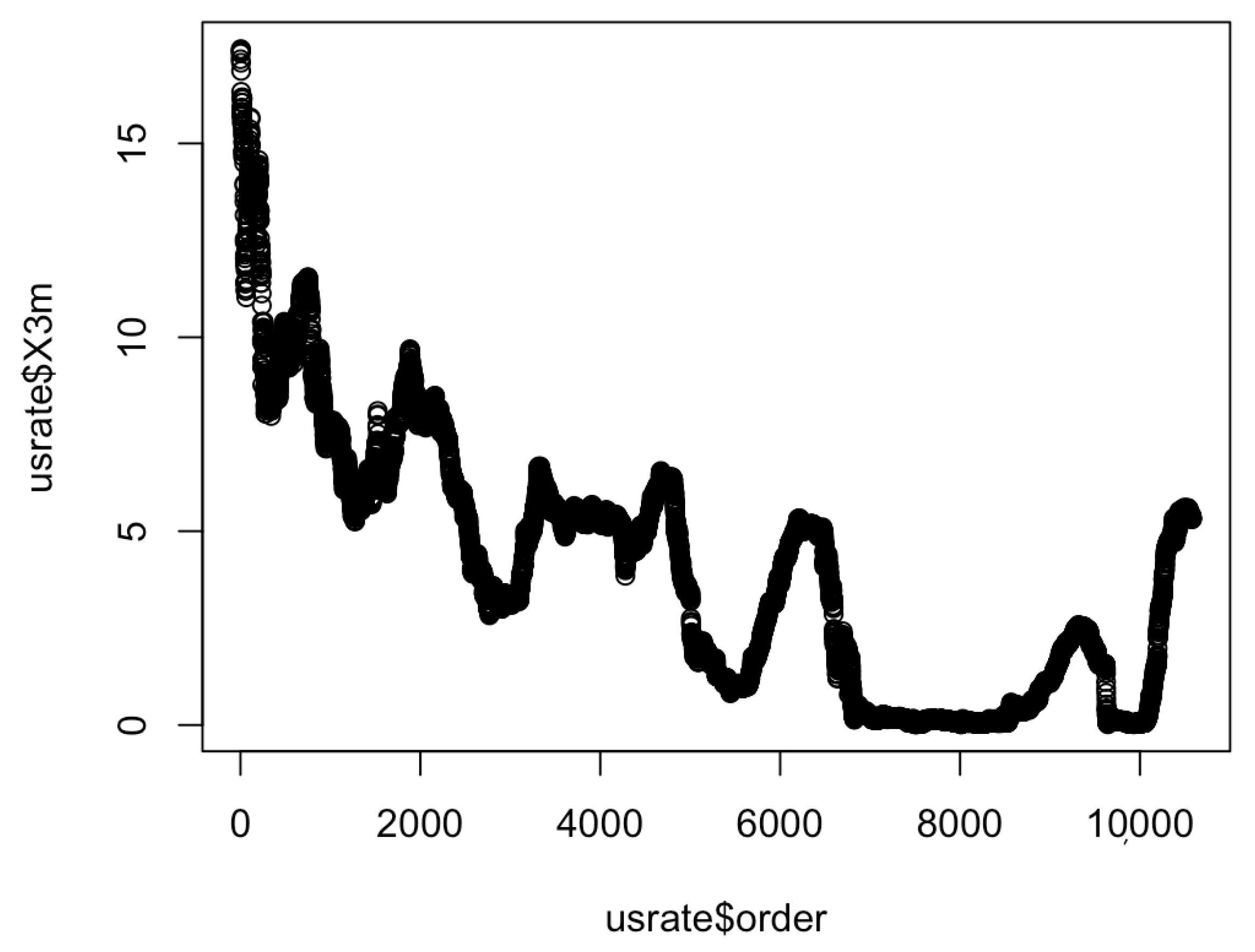
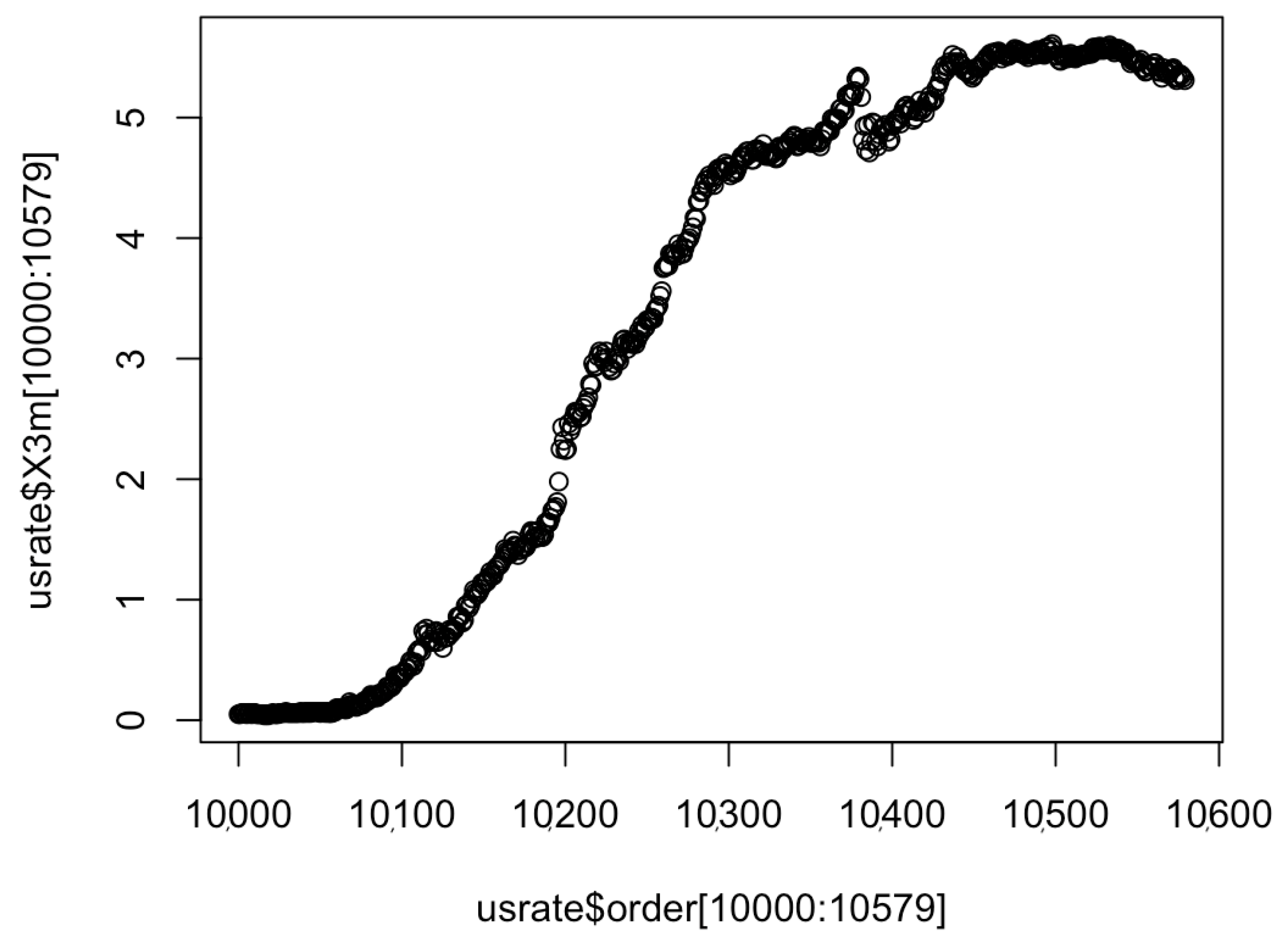
5. An Empirical Study on U.S. Treasury Rates
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Itô, K. Stochastic integral. Proc. Imp. Acad. 1944, 20, 519–524. [Google Scholar] [CrossRef]
- Karatzas, I.; Shreve, S. Methods of Mathematical Finance; Springer: New York, NY, USA, 1998; Volume 39. [Google Scholar]
- Shreve, S. Stochastic Calculus for Finance II: Continuous-Time Models; Springer: New York, NY, USA, 2004; Volume 11. [Google Scholar]
- Shreve, S. Stochastic Calculus for Finance I: The Binomial Asset Pricing Model; Springer: Pittsburgh, PA, USA, 2005. [Google Scholar]
- Liu, B. Uncertainty Theory; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Liu, B. Toward uncertain finance theory. J. Uncertainty Anal. Appl. 2013, 1, 1–15. [Google Scholar] [CrossRef]
- Liu, B. Some research problems in uncertainty theory. J. Uncertain Syst. 2009, 3, 3–10. [Google Scholar]
- Chen, X.; Liu, B. Existence and uniqueness theorem for uncertain differential equations. Fuzzy Optim. Decis. Mak. 2010, 9, 69–81. [Google Scholar] [CrossRef]
- Sheng, Y.; Gao, J. Exponential stability of uncertain differential equation. Soft Comput. 2016, 20, 3673–3678. [Google Scholar] [CrossRef]
- Sheng, Y.; Wang, C. Stability in p-th moment for uncertain differential equation. J. Intell. Fuzzy Syst. 2014, 26, 1263–1271. [Google Scholar] [CrossRef]
- Yao, K.; Ke, H.; Sheng, Y. Stability in mean for uncertain differential equation. Fuzzy Optim. Decis. Mak. 2015, 14, 365–379. [Google Scholar] [CrossRef]
- Wang, X.; Ning, Y.; Moughal, A.; Chen, X. Adams–simpson method for solving uncertain differential equation. Appl. Math. Comput. 2015, 271, 209–219. [Google Scholar] [CrossRef]
- Yang, X.; Ralescu, A. Adams method for solving uncertain differential equations. Appl. Math. Comput. 2015, 270, 993–1003. [Google Scholar] [CrossRef]
- Yang, X.; Shen, Y. Runge-kutta method for solving uncertain differential equations. J. Uncertainty Anal. Appl. 2015, 3, 1–12. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, J.; Huang, Z. Hamming method for solving uncertain differential equations. Appl. Math. Comput. 2017, 313, 331–341. [Google Scholar] [CrossRef]
- Gao, R. Milne method for solving uncertain differential equations. Appl. Math. Comput. 2016, 274, 774–785. [Google Scholar] [CrossRef]
- Cheng, Y.; Hu, Y.; Long, H. Generalized moment estimators for α-stable ornstein–uhlenbeck motions from discrete observations. Stat. Inference Stoch. Process. 2020, 23, 53–81. [Google Scholar] [CrossRef]
- Hu, Y.; Song, J. Parameter estimation for fractional ornstein–uhlenbeck processes with discrete observations. In Malliavin Calculus and Stochastic Analysis: A Festschrift in Honor of David Nualart; Springer: Boston, MA, USA, 2013; pp. 427–442. [Google Scholar]
- Wang, S.; Song, S.; Wang, Y. Skew ornstein–uhlenbeck processes and their financial applications. J. Comput. Appl. Math. 2015, 273, 363–382. [Google Scholar] [CrossRef]
- Chen, X.; Gao, J. Uncertain term structure model of interest rate. Soft Comput. 2013, 17, 597–604. [Google Scholar] [CrossRef]
- Yang, X.; Ke, H. Uncertain interest rate model for shanghai interbank offered rate and pricing of american swaption. Fuzzy Optim. Decis. Mak. 2023, 22, 447–462. [Google Scholar] [CrossRef]
- Yao, K. Uncertain Differential Equations; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Chen, X. American option pricing formula for uncertain financial market. Int. J. Oper. Res. 2011, 8, 32–37. [Google Scholar]
- Liu, Y.; Chen, X.; Ralescu, A. Uncertain currency model and currency option pricing. Int. J. Intell. Syst. 2015, 30, 40–51. [Google Scholar] [CrossRef]
- Li, H.; Yang, X.; Ni, Y. Pricing of shout option in uncertain financial market. Fuzzy Optim. Decis. Mak. 2024, 23, 449–467. [Google Scholar] [CrossRef]
- Jia, L.; Li, D.; Guo, F.; Liu, Y. Knock-out options pricing formulas in uncertain financial market with floating interest rate. Soft Comput. 2024, 1–14. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Y. Pricing and valuation of carbon swap in uncertain finance market. Fuzzy Optim. Decis. Mak. 2024, 23, 319–336. [Google Scholar] [CrossRef]
- Sheng, Y.; Yao, K.; Chen, X. Least squares estimation in uncertain differential equations. IEEE Trans. Fuzzy Syst. 2019, 28, 2651–2655. [Google Scholar] [CrossRef]
- Yao, K.; Liu, B. Parameter estimation in uncertain differential equations. Fuzzy Optim. Decis. Mak. 2020, 19, 1–12. [Google Scholar] [CrossRef]
- Liu, Z. Generalized moment estimation for uncertain differential equations. Appl. Math. Comput. 2021, 392, 125724. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, B. Estimating unknown parameters in uncertain differential equation by maximum likelihood estimation. Soft Comput. 2022, 26, 2773–2780. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Y.; Park, G.-K. Parameter estimation of uncertain differential equation with application to financial market. Chaos Solitons Fractals 2020, 139, 110026. [Google Scholar] [CrossRef]
- Li, A.; Xia, Y. Parameter estimation of uncertain differential equations with estimating functions. Soft Comput. 2024, 28, 77–86. [Google Scholar] [CrossRef]
- Wang, J.; Gong, H.; Li, A. On weighted threshold moment estimation of uncertain differential equations with applications in interbank rates analysis. J. Ambient Intell. Humaniz. Comput. 2024, 15, 3509–3518. [Google Scholar] [CrossRef]
- He, L.; Zhu, Y.; Gu, Y. Nonparametric estimation for uncertain differential equations. Fuzzy Optim. Decis. Mak. 2023, 22, 697–715. [Google Scholar] [CrossRef]
- Li, A.; Xia, Y. The Nadaraya–Watson Estimation of Uncertain Differential Equations; Technical Report; Springer: Cham, Switzerland, 2023; pp. 1–20. [Google Scholar]
- Liu, B. Fuzzy process, hybrid process and uncertain process. J. Uncertain Syst. 2008, 2, 3–16. [Google Scholar]
- Liu, Y.; Liu, B. Residual analysis and parameter estimation of uncertain differential equations. Fuzzy Optim. Decis. Mak. 2022, 21, 513–530. [Google Scholar] [CrossRef]
- Ye, T.; Liu, B. Uncertain hypothesis test for uncertain differential equations. Fuzzy Optim. Decis. Mak. 2022, 22, 195–211. [Google Scholar] [CrossRef]
- Su, F.; Chan, K. Quasi-likelihood estimation of a threshold diffusion process. J. Econom. 2015, 189, 473–484. [Google Scholar] [CrossRef]
| Author | Research | Year |
|---|---|---|
| Chen [23] | American option pricing | 2011 |
| Chen and Gao [20] | Uncertain term structure model | 2013 |
| Liu et al. [24] | Uncertain currency model | 2015 |
| Liu and Li [27] | Carbon swap | 2024 |
| Jia et al. [26] | Knock-out option | 2024 |
| Yang and Ke [21] | Uncertain interest rate model | 2024 |
| Author | Method | Year |
|---|---|---|
| Sheng et al. [28] | Least squares | 2019 |
| Yao and Liu [29] | Moment method | 2020 |
| Yang et al. [32] | Minimum cover estimation | 2020 |
| Liu [30] | Generalized moment method | 2021 |
| Liu and Liu [31] | Maximum likelihood estimation | 2022 |
| He et al. [35] | Nonparametric method | 2023 |
| Li and Xia [36] | Nadaraya–Watson method | 2023 |
| Li and Xia [33] | Estimation function method | 2024 |
| Wang et al. [34] | Threshold weighted moment method | 2024 |
| n | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | |
| 1.00 | 1.14 | 1.16 | 1.47 | 1.79 | 2.25 | |
| n | 7 | 8 | 9 | 10 | 11 | 12 |
| 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | 1.1 | |
| 2.59 | 2.77 | 3.24 | 2.77 | 3.46 | 4.78 | |
| n | 13 | 14 | 15 | 16 | 17 | 18 |
| 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | |
| 5.10 | 5.92 | 6.95 | 7.98 | 8.73 | 9.60 | |
| n | 19 | 20 | 21 | 22 | 23 | 24 |
| 1.8 | 1.9 | 2.0 | 2.1 | 2.2 | 2.3 | |
| 10.13 | 11.60 | 13.74 | 14.91 | 16.46 | 18.72 |
| i | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| 0.1373 | 0.2945 | 0.6356 | 0.5662 | 0.1484 | |
| n | 7 | 8 | 9 | 10 | 11 |
| 0.6378 | 0.2275 | 0.6393 | 0.6186 | 0.3312 | |
| n | 12 | 13 | 14 | 15 | 16 |
| 0.2375 | 0.2077 | 0.3203 | 0.2340 | 0.2591 | |
| n | 17 | 18 | 19 | 20 | 21 |
| 0.4190 | 0.0070 | 0.3617 | 0.4906 | 0.3345 | |
| n | 22 | 23 | 24 | ||
| 0.3301 | 0.8130 | 0.7046 |
| n | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 0.00 | 0.09 | 0.18 | 0.33 | |
| 0.0000 | 0.1252 | 0.1348 | 0.4350 | |
| n | 5 | 6 | 7 | 8 |
| 0.48 | 0.60 | 0.69 | 0.78 | |
| 0.6647 | 0.9104 | 1.0464 | 1.1049 | |
| n | 9 | 10 | 11 | 12 |
| 0.87 | 1.02 | 1.14 | 1.29 | |
| 1.2181 | 1.4125 | 1.4971 | 1.8163 | |
| n | 13 | 14 | 15 | 16 |
| 1.38 | 1.50 | 1.56 | 1.71 | |
| 1.9469 | 2.1097 | 2.2322 | 2.2517 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, A.; Wang, J.; Zhou, L. Parameter Estimation of Uncertain Differential Equations Driven by Threshold Ornstein–Uhlenbeck Process with Application to U.S. Treasury Rate Analysis. Symmetry 2024, 16, 1372. https://doi.org/10.3390/sym16101372
Li A, Wang J, Zhou L. Parameter Estimation of Uncertain Differential Equations Driven by Threshold Ornstein–Uhlenbeck Process with Application to U.S. Treasury Rate Analysis. Symmetry. 2024; 16(10):1372. https://doi.org/10.3390/sym16101372
Chicago/Turabian StyleLi, Anshui, Jiajia Wang, and Lianlian Zhou. 2024. "Parameter Estimation of Uncertain Differential Equations Driven by Threshold Ornstein–Uhlenbeck Process with Application to U.S. Treasury Rate Analysis" Symmetry 16, no. 10: 1372. https://doi.org/10.3390/sym16101372
APA StyleLi, A., Wang, J., & Zhou, L. (2024). Parameter Estimation of Uncertain Differential Equations Driven by Threshold Ornstein–Uhlenbeck Process with Application to U.S. Treasury Rate Analysis. Symmetry, 16(10), 1372. https://doi.org/10.3390/sym16101372






