Non-Periodic Quantized Model Predictive Control Method for Underwater Dynamic Docking
Abstract
1. Introduction
- A novel autonomous docking control system framework for underwater mobile terminals was proposed, featuring a 4-DOF model predictive docking controller designed to enhance the robustness of trajectory tracking under complex disturbances. This controller addressed the bounded docking disturbances, thruster saturation constraints, and system-state constraints.
- A novel ETQMPC control method was proposed for the UUV docking trajectory tracking, with the designed event-triggering mechanism adaptively adjusting the triggering interval based on the position and velocity tracking errors. This non-periodic control approach effectively reduced the number of iterations in the optimization algorithm while maintaining the docking control performance, thereby achieving an optimal balance between control efficiency and computational demands.
- To address the limited bandwidth of state feedback transmission, a state feedback quantified control algorithm was proposed, incorporating a hysteresis quantizer to manage the feedback of eight state quantities. This approach converted the continuous signals into discrete signals, ensuring the sufficient control accuracy while reducing the communication frequency and channel pressure.
2. Problem Formulation
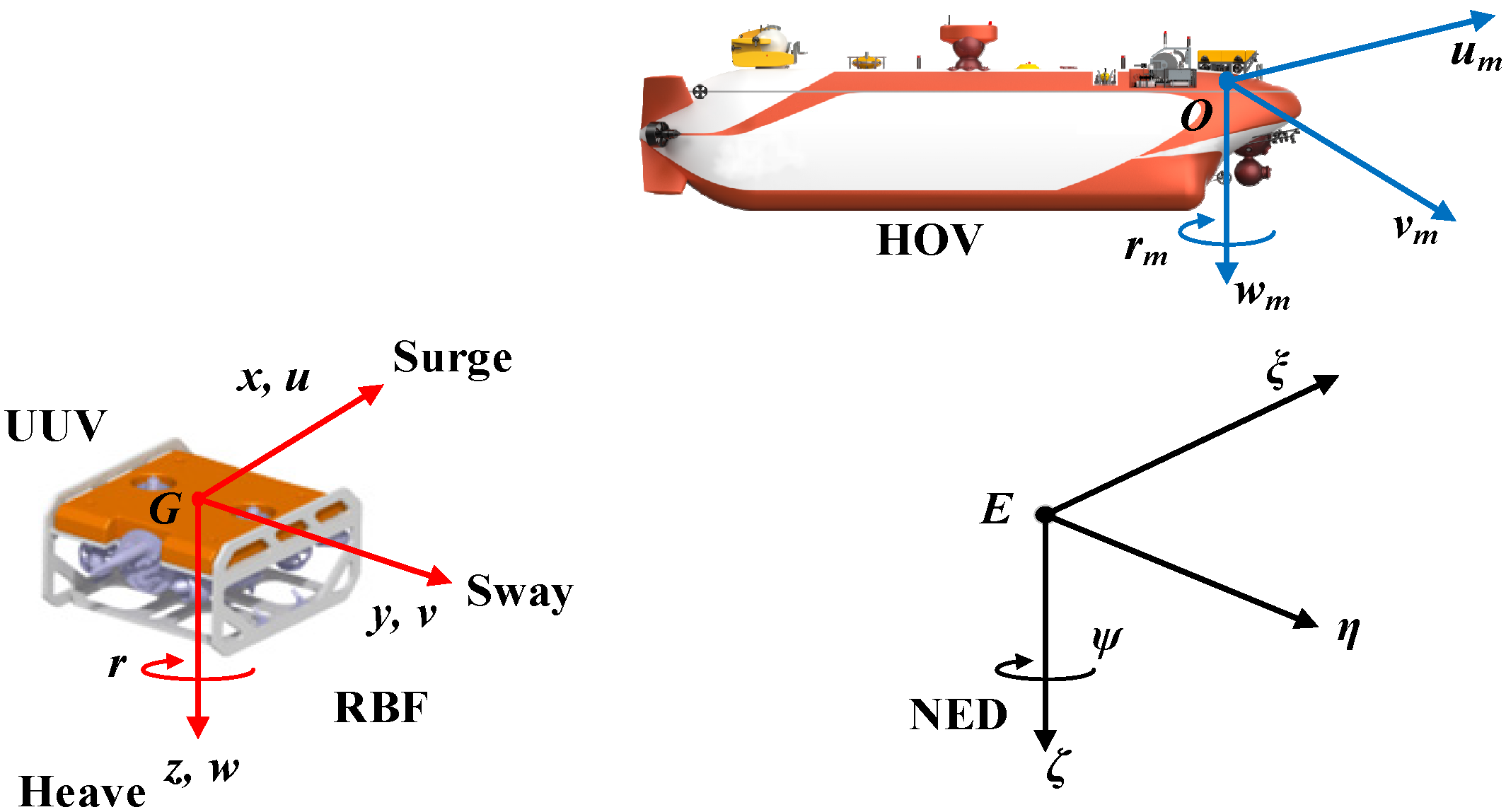
2.1. Notations
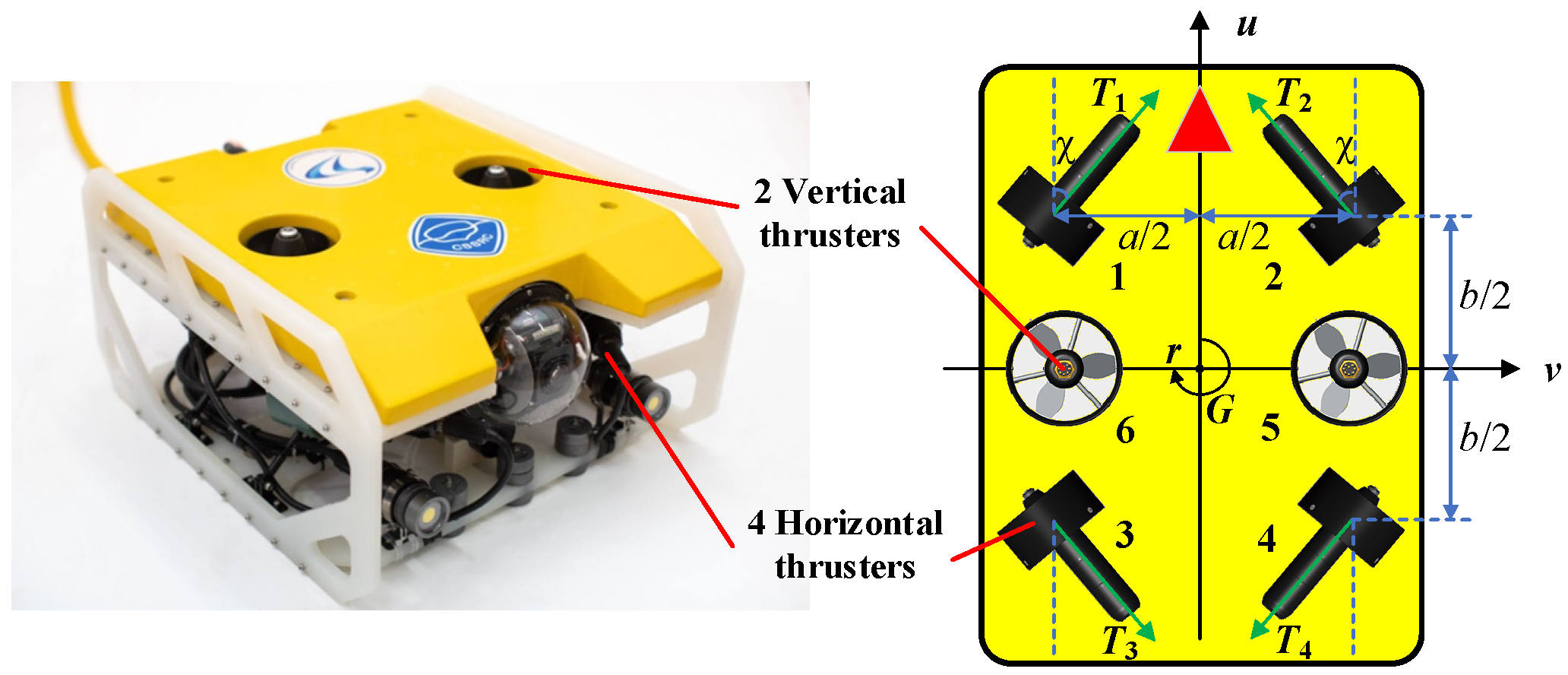
2.2. Docking Model
2.3. Docking Controller Design
2.4. Docking Trajectory Planning
3. Docking Control Method
3.1. Optimization Problem
- Control Input Constraint: Given the thrust saturation constraint on the thrusters, it is necessary to impose a bound on the control input amplitude, leading to the formulation of the control input constraint: , where represents the upper limit of the preset control input.
- State error tightening constraint: , where , and . The state constraint is introduced into the optimization problem to ensure the robustness of the algorithm.
- Terminal state constraint: , .
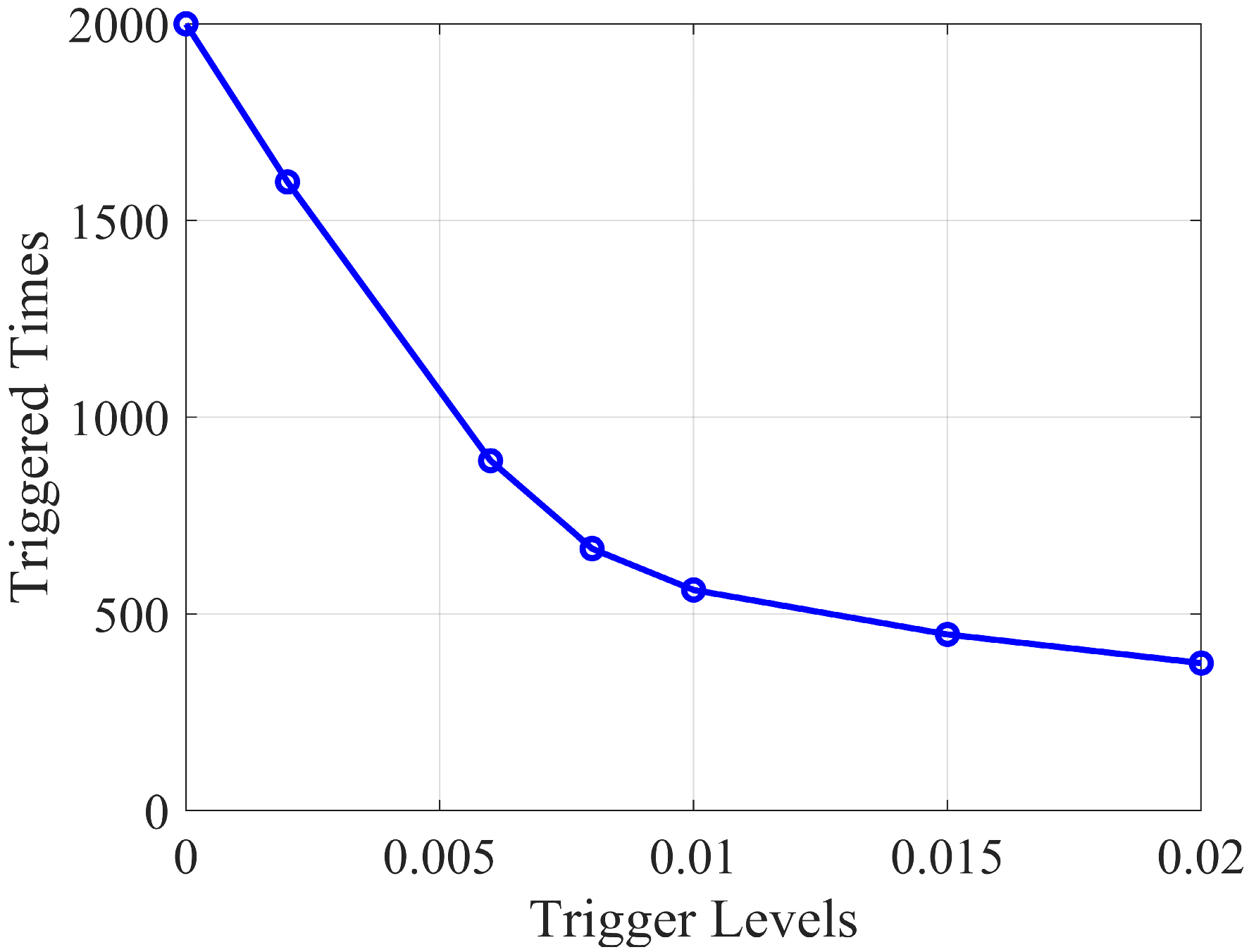
3.2. Event Triggering Mechanism
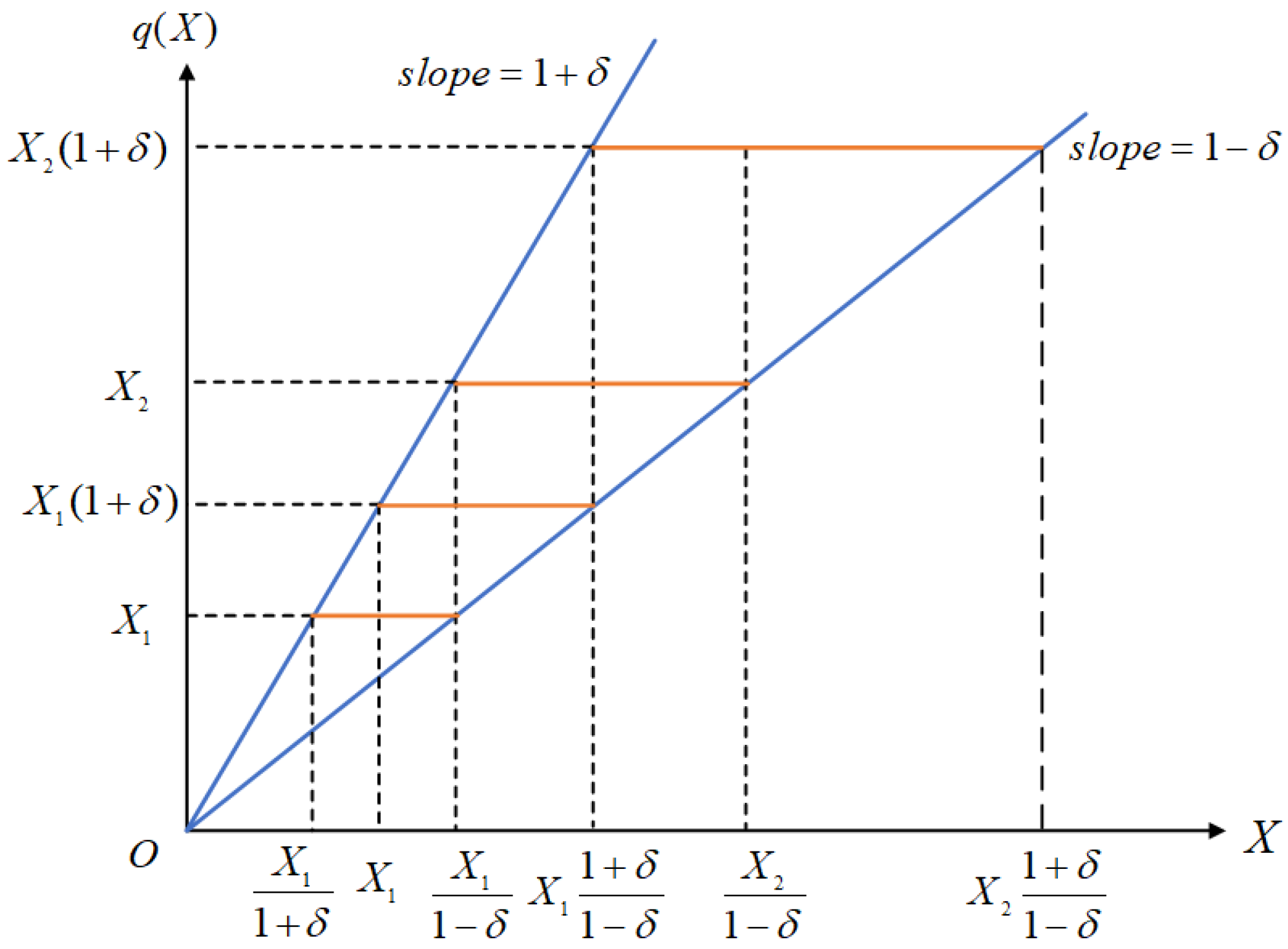
3.3. Quantizer Feedback
3.4. ETQMPC Algorithm
| Algorithm 1: ETQMPC Algorithm |
| Input: Prediction horizon ; triggering level ; local stabilizing gain ; weighting matrices Q, R and P; terminal constraints ; index . Output: 1: Obtain the status of the HOV; 2: Calculate the reference state with (12)–(17); 3: Sampling current system state ; 4: while do 5: Solve the optimization problem in (19); 6: while is not triggered do 7: Let denote the (sub-) optimal solution and apply control input; 8: end while 9: Generate quantized state feedback with (24), and calculate ; 10: Solve the optimization problem in (19); 11: ; 12: end while 13: Apply the locally stabilizing law 14: Repeat the above process until the end of docking. |
3.5. Feasibility and Stability Analysis
3.5.1. Feasibility Analysis
3.5.2. Stability Analysis
4. Results and Discussion
4.1. Parameter Selection
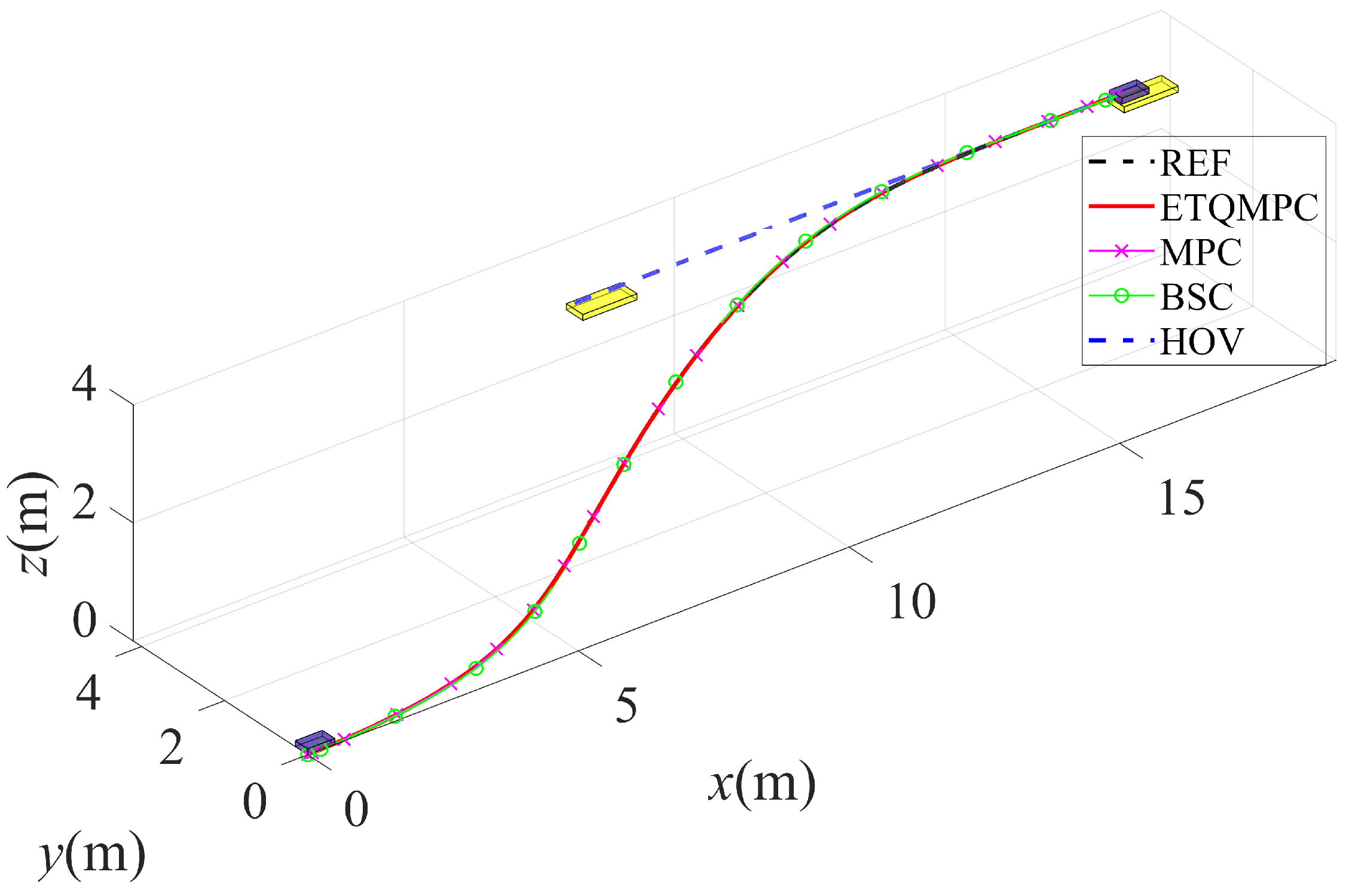
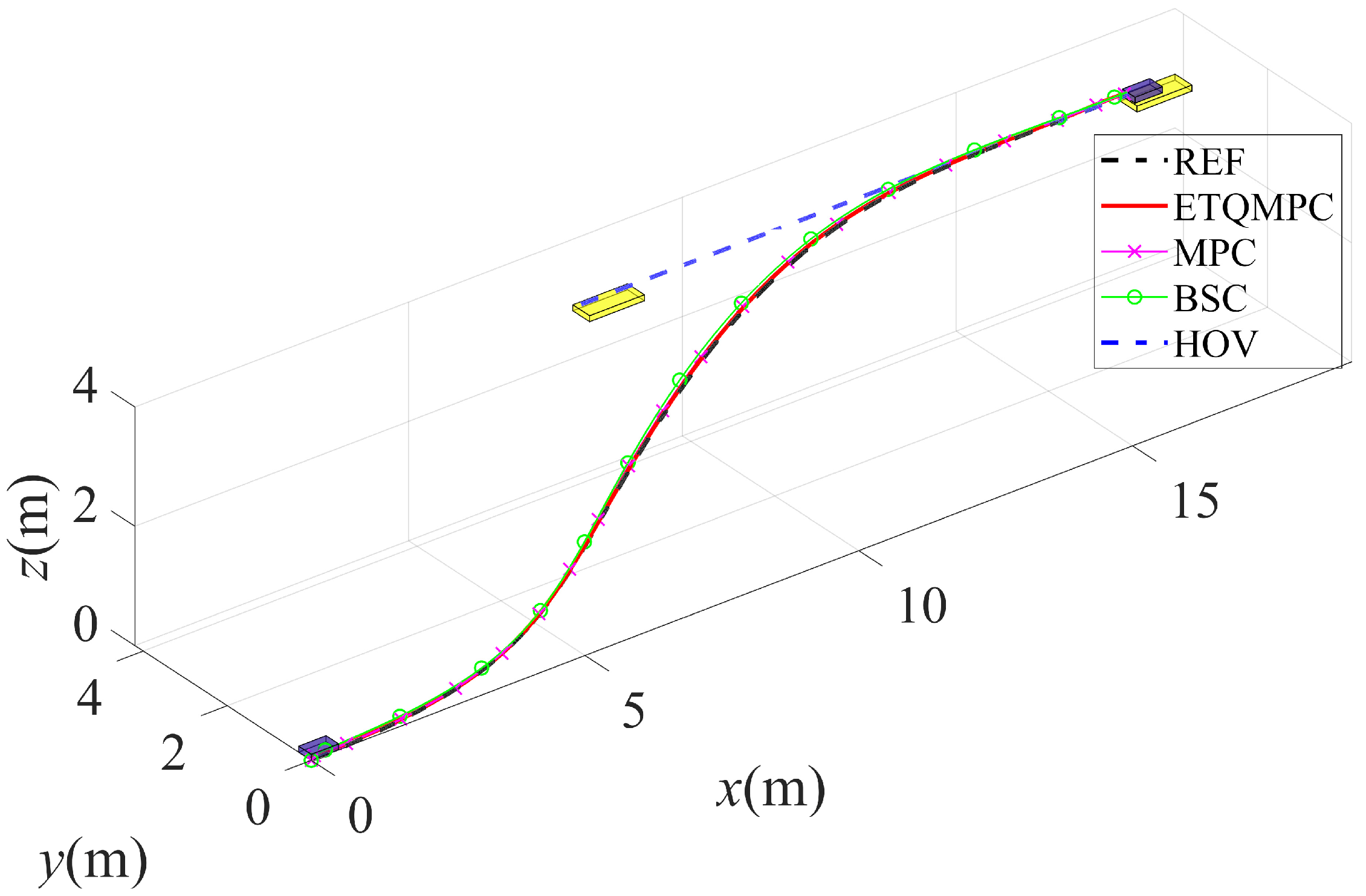
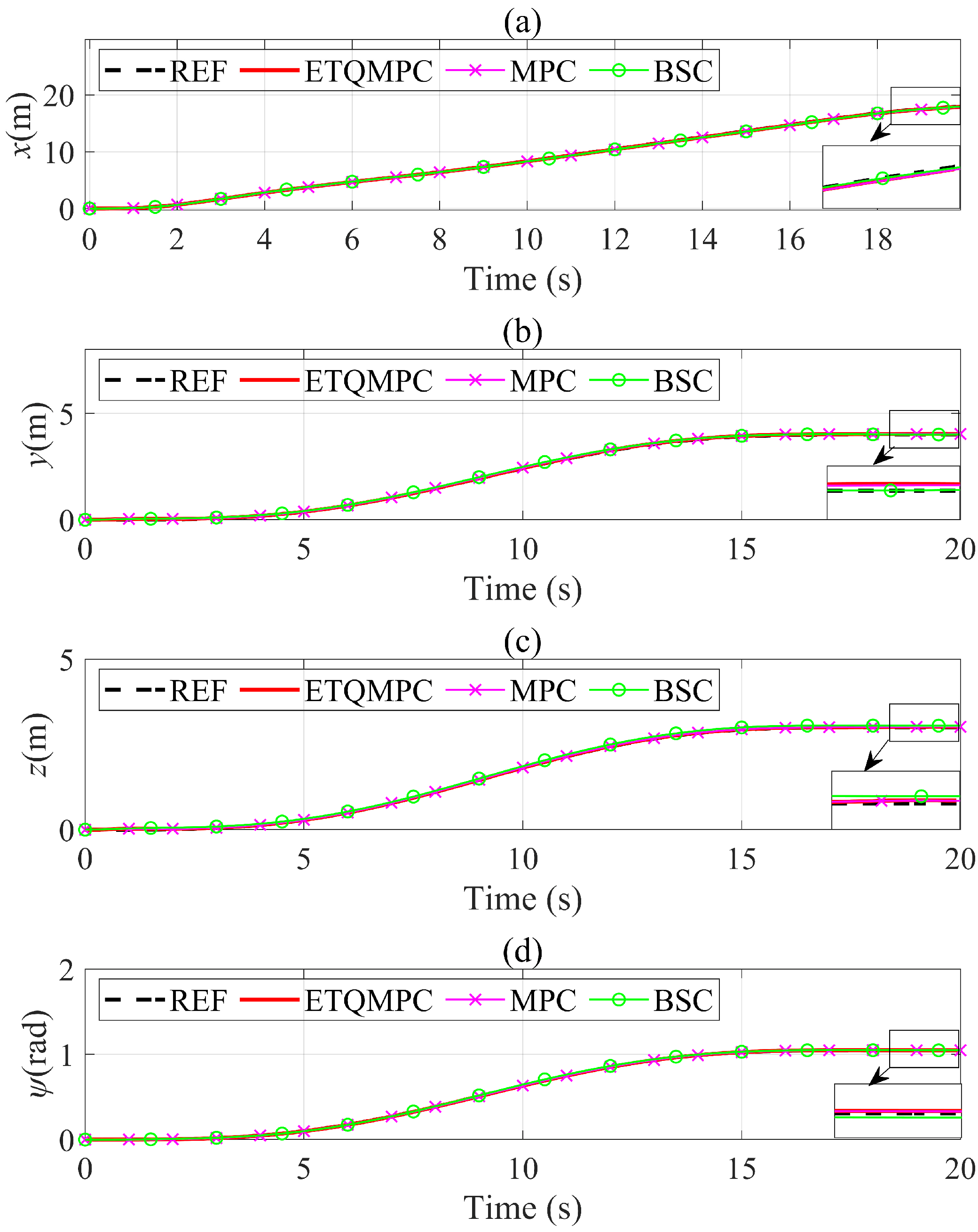
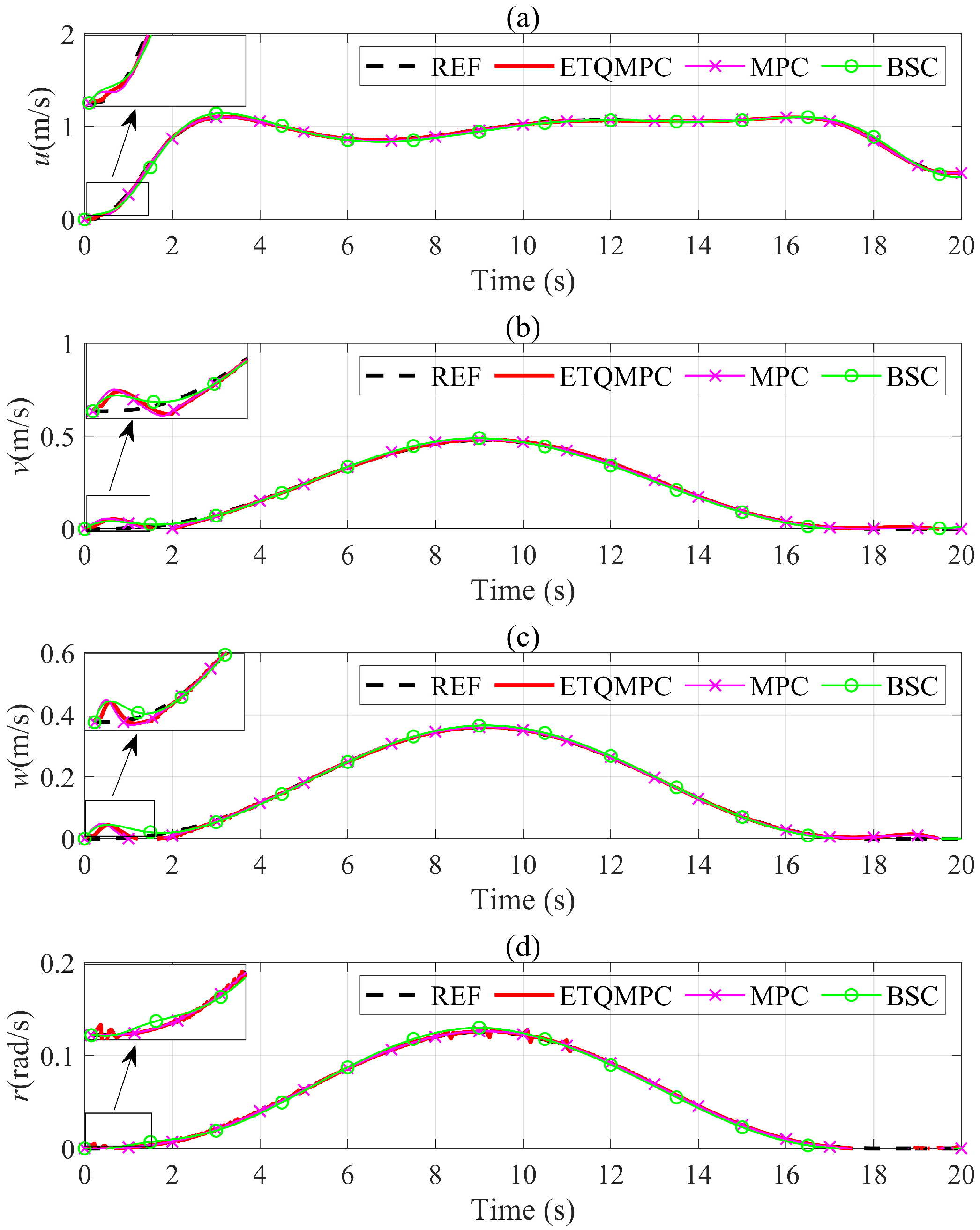
4.2. Tracking Performance Simulation
4.3. Robust Performance Simulation
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
- that satisfies the input constraints.
- 2.
- , which satisfies the tightening state constraint.
- 3.
- , which satisfies the terminal constraint.
Appendix C
- 1.
- First, if , it can converge to in a finite amount of time.
- 2.
- Second, the set can be proven to be a robust positive invariant set, and if , it can remain within this set.
Appendix D
| Feature | Values | Feature | Values |
|---|---|---|---|
| 116 kg | 0 | ||
| 116 kg | 3.0 | ||
| 4.9 | |||
| −167.6 | 3.5 | ||
| −477.2 | 241. 3 | ||
| −383 | 503.8 | ||
| −11.6 | 265.6 | ||
| −15.5 | 101.6 | ||
| −15.9 | 59.9 | ||
| 26.9 | 76.9 | ||
| 35.8 |
References
- Zhang, Y.; Gao, J.; Chen, Y.; Bian, C.; Zhang, F.; Liang, Q. Adaptive neural network control for visual docking of an autonomous underwater vehicle using command filtered backstepping. Int. J. Robust Nonlinear Control 2022, 32, 4716–4738. [Google Scholar] [CrossRef]
- Wang, T.; Sun, Z.; Ke, Y.; Li, C.; Hu, J. Two-Step Adaptive Control for Planar Type Docking of Autonomous Underwater Vehicle. Mathematics 2023, 11, 3467. [Google Scholar] [CrossRef]
- Lwin, K.N.; Myint, M.; Mukada, N.; Yamada, D.; Matsuno, T.; Saitou, K.; Godou, W.; Sakamoto, T.; Minami, M. Sea docking by dual-eye pose estimation with optimized genetic algorithm parameters. J. Intell. Robot. Syst. 2019, 96, 245–266. [Google Scholar] [CrossRef]
- Page, B.R.; Lambert, R.; Chavez-Galaviz, J.; Mahmoudian, N. Underwater Docking Approach and Homing to Enable Persistent Operation. Front. Robot. AI 2021, 8, 621755. [Google Scholar] [CrossRef]
- Xie, T.; Li, Y.; Jiang, Y.; Pang, S.; Xu, X. Three-dimensional mobile docking control method of an underactuated autonomous underwater vehicle. Ocean. Eng. 2022, 265, 112634. [Google Scholar] [CrossRef]
- Thuyen, N.A.; Anh, H.P.H. A new docking method for autonomous underwater vehicle using adaptive integral terminal sliding mode control. Int. J. Dyn. Control 2023, 11, 2354–2367. [Google Scholar] [CrossRef]
- Zuo, M.; Wang, G.; Xiao, Y.; Xiang, G. A Unified Approach for Underwater Homing and Docking of over-Actuated AUV. J. Mar. Sci. Eng. 2021, 9, 884. [Google Scholar] [CrossRef]
- Guo, L.; Liu, W.; Li, L.; Xu, J.; Zhang, K.; Zhang, Y. Fast Finite-Time Super-Twisting Sliding Mode Control with an Extended State Higher-Order Sliding Mode Observer for UUV Trajectory Tracking. Drones 2024, 8, 41. [Google Scholar] [CrossRef]
- Sahoo, A.; Dwivedy, S.K.; Robi, P. Adaptive Neuro Fuzzy PID Controller for A Compact Autonomous Underwater Vehicle. In Proceedings of the OCEANS 2022, Hampton Roads, Virginia Beach, VA, USA, 17–20 October 2022; pp. 1–5. [Google Scholar]
- Bingül, Ö.; Yıldız, A. Fuzzy logic and proportional integral derivative based multi-objective optimization of active suspension system of a 4 × 4 in-wheel motor driven electrical vehicle. J. Vib. Control 2023, 29, 1366–1386. [Google Scholar] [CrossRef]
- Liu, T.; Zhao, J.; Huang, J. A Gaussian-Process-Based Model Predictive Control Approach for Trajectory Tracking and Obstacle Avoidance in Autonomous Underwater Vehicles. J. Mar. Sci. Eng. 2024, 12, 676. [Google Scholar] [CrossRef]
- Hu, Y.; Li, B.; Jiang, B.; Han, J.; Wen, C.-Y. Disturbance Observer-Based Model Predictive Control for an Unmanned Underwater Vehicle. J. Mar. Sci. Eng. 2024, 12, 94. [Google Scholar] [CrossRef]
- Martinsen, A.B.; Lekkas, A.M.; Gros, S. Autonomous docking using direct optimal control. IFAC-PapersOnLine 2019, 52, 97–102. [Google Scholar] [CrossRef]
- Heshmati-Alamdari, S.; Nikou, A.; Dimarogonas, D.V. Robust trajectory tracking control for underactuated autonomous underwater vehicles in uncertain environments. IEEE Trans. Autom. Sci. Eng. 2020, 18, 1288–1301. [Google Scholar] [CrossRef]
- Uchihori, H.; Cavanini, L.; Tasaki, M.; Majecki, P.; Yashiro, Y.; Grimble, M.J.; Yamamoto, I.; Van der Molen, G.M.; Morinaga, A.; Eguchi, K. Linear parameter-varying model predictive control of AUV for docking scenarios. Appl. Sci. 2021, 11, 4368. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Luo, M.; Yang, C. MPC-based 3-D trajectory tracking for an autonomous underwater vehicle with constraints in complex ocean environments. Ocean. Eng. 2019, 189, 106309. [Google Scholar] [CrossRef]
- Gong, P.; Yan, Z.; Zhang, W.; Tang, J. Lyapunov-based model predictive control trajectory tracking for an autonomous underwater vehicle with external disturbances. Ocean. Eng. 2021, 232, 109010. [Google Scholar] [CrossRef]
- Li, S.; Zhu, Y.; Bai, J.; Guo, G. Dynamic obstacle avoidance of unmanned ship based on event-triggered adaptive nonlinear model predictive control. Ocean. Eng. 2023, 286, 115626. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, X.; Liang, C.; Han, X. An improved model predictive control for path-following of USV based on global course constraint and event-triggered mechanism. IEEE Access 2021, 9, 79725–79734. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, Q.; Wu, W.; Du, X.; Zhang, Y.; Han, P. Event-trigger NMPC for 3-D trajectory tracking of UUV with external disturbances. Ocean. Eng. 2023, 283, 115050. [Google Scholar] [CrossRef]
- Yuan, S.; Liu, Z.; Zheng, L.; Sun, Y.; Wang, Z. Event-based adaptive horizon nonlinear model predictive control for trajectory tracking of marine surface vessel. Ocean. Eng. 2022, 258, 111082. [Google Scholar] [CrossRef]
- Zhang, P.; Hao, L.-Y.; Wang, R. Self-triggered MPC for trajectory tracking of an Autonomous Underwater Vehicle with additive disturbance. In Proceedings of the 2023 IEEE 2nd Industrial Electronics Society Annual On-Line Conference (ONCON), Online Virtual, 8–10 December 2023; pp. 1–6. [Google Scholar]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Li, H.; Shi, Y. Event-triggered robust model predictive control of continuous-time nonlinear systems. Automatica 2014, 50, 1507–1513. [Google Scholar] [CrossRef]
- Liu, C.; Gao, J.; Li, H.; Xu, D. Aperiodic robust model predictive control for constrained continuous-time nonlinear systems: An event-triggered approach. IEEE Trans. Cybern. 2017, 48, 1397–1405. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Wu, W.; Lin, Y.; Shen, S. Online Safe Trajectory Generation for Quadrotors Using Fast Marching Method and Bernstein Basis Polynomial. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 344–351. [Google Scholar]
- Kulathunga, G.; Klimchik, A. Survey on Motion Planning for Multirotor Aerial Vehicles in Plan-Based Control Paradigm. Remote Sens. 2023, 15, 5237. [Google Scholar] [CrossRef]
- Chen, J.; Liu, T.; Shen, S. Online generation of collision-free trajectories for quadrotor flight in unknown cluttered environments. In Proceedings of the IEEE International Conference on Robotics & Automation, Stockholm, Sweden, 16–21 May 2016. [Google Scholar]
- Park, Y.; Kim, W.; Moon, H. Time-Continuous Real-Time Trajectory Generation for Safe Autonomous Flight of a Quadrotor in Unknown Environment. Appl. Sci. 2021, 11, 3238. [Google Scholar] [CrossRef]
- Li, P.; Wang, S.; Yang, H.; Zhao, H. Trajectory tracking and obstacle avoidance for wheeled mobile robots based on EMPC with an adaptive prediction horizon. IEEE Trans. Cybern. 2021, 52, 13536–13545. [Google Scholar] [CrossRef]
- Kavala Sen, D.; Yildiz, A.; Kopmaz, O. Optimal Design of a Five-Bar Planar Manipulator and Its Controller by Using Different Algorithms for Minimum Shaking Forces and Moments for the Largest Trajectory in a Usable Workspace. Machines 2022, 10, 971. [Google Scholar] [CrossRef]
- Tabuada, P. Event-triggered real-time scheduling of stabilizing control tasks. IEEE Trans. Autom. Control 2007, 52, 1680–1685. [Google Scholar] [CrossRef]
- Liu, W.; Ma, Q.; Xu, S.; Zhang, Z. State quantized output feedback control for nonlinear systems via event-triggered sampling. IEEE Trans. Autom. Control 2021, 67, 6810–6817. [Google Scholar] [CrossRef]
- Zhou, J.; Wen, C.; Yang, G. Adaptive backstepping stabilization of nonlinear uncertain systems with quantized input signal. IEEE Trans. Autom. Control 2013, 59, 460–464. [Google Scholar] [CrossRef]
- Luan, T.; Tan, Z.; Sun, M.; Wang, H.; Li, M.; Yao, H. Double-mode robust model predictive control of ship dynamic positioning system based on event-triggered mechanism. Ocean. Eng. 2023, 286, 115536. [Google Scholar] [CrossRef]
- Cho, G.R.; Park, D.-G.; Kang, H.; Lee, M.-J.; Li, J.-H. Horizontal trajectory tracking of underactuated auv using backstepping approach. IFAC-PapersOnLine 2019, 52, 174–179. [Google Scholar] [CrossRef]
- Liu, H.; Wei, Y.; Zhou, X.; Li, G. Operated ROV thrust distribution control system based on adaptive back-stepping controller. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 4633–4639. [Google Scholar]
- Shen, C.; Shi, Y.; Buckham, B. Trajectory Tracking Control of an Autonomous Underwater Vehicle Using Lyapunov-Based Model Predictive Control. IEEE Trans. Ind. Electron. 2018, 65, 5796–5805. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems; Michigan State University: Upper Saddle River, NJ, USA, 2002; Volume 38, pp. 1091–1093. [Google Scholar]
- Chen, H.; Allgöwer, F. A quasi-infinite horizon nonlinear model predictive control scheme with guaranteed stability. Automatica 1998, 34, 1205–1217. [Google Scholar] [CrossRef]
- Michalska, H.; Mayne, D.Q. Robust receding horizon control of constrained nonlinear systems. IEEE Trans. Autom. Control 1993, 38, 1623–1633. [Google Scholar] [CrossRef]
- Li, B.; Lu, P.; Du, C.; Liu, H. Event-Triggered Model Predictive Control for Linear Systems with Bounded Disturbance. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; pp. 279–284. [Google Scholar]

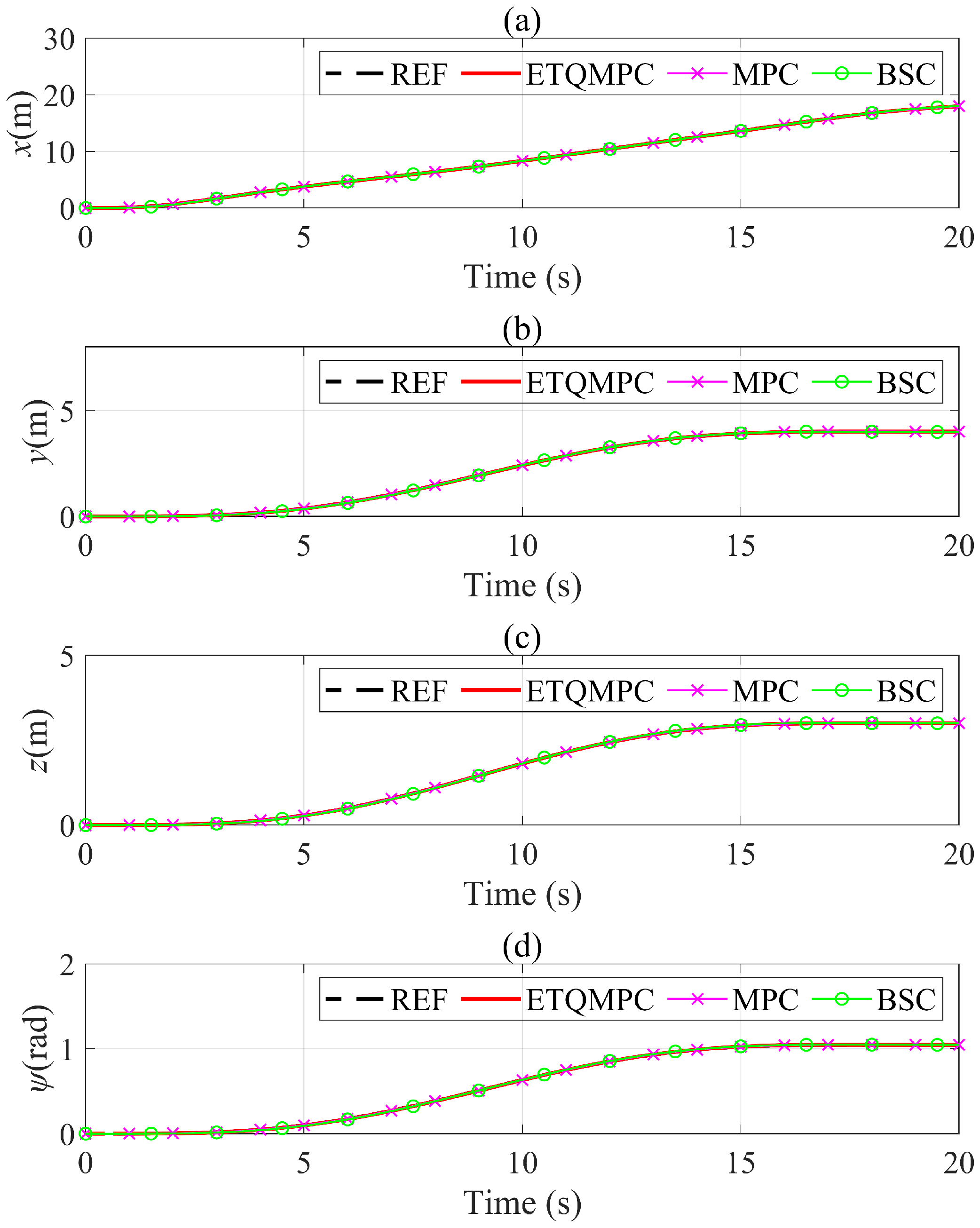
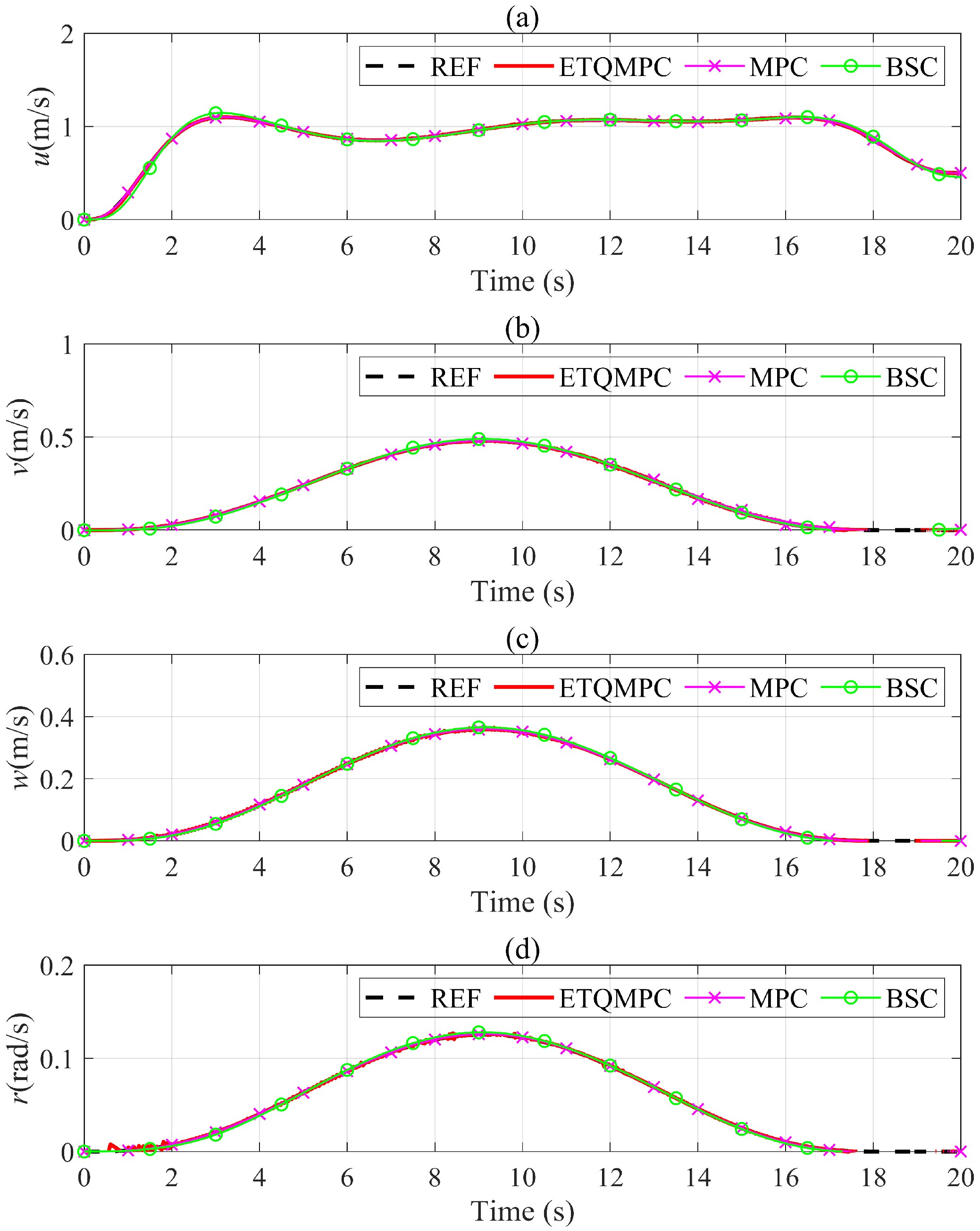

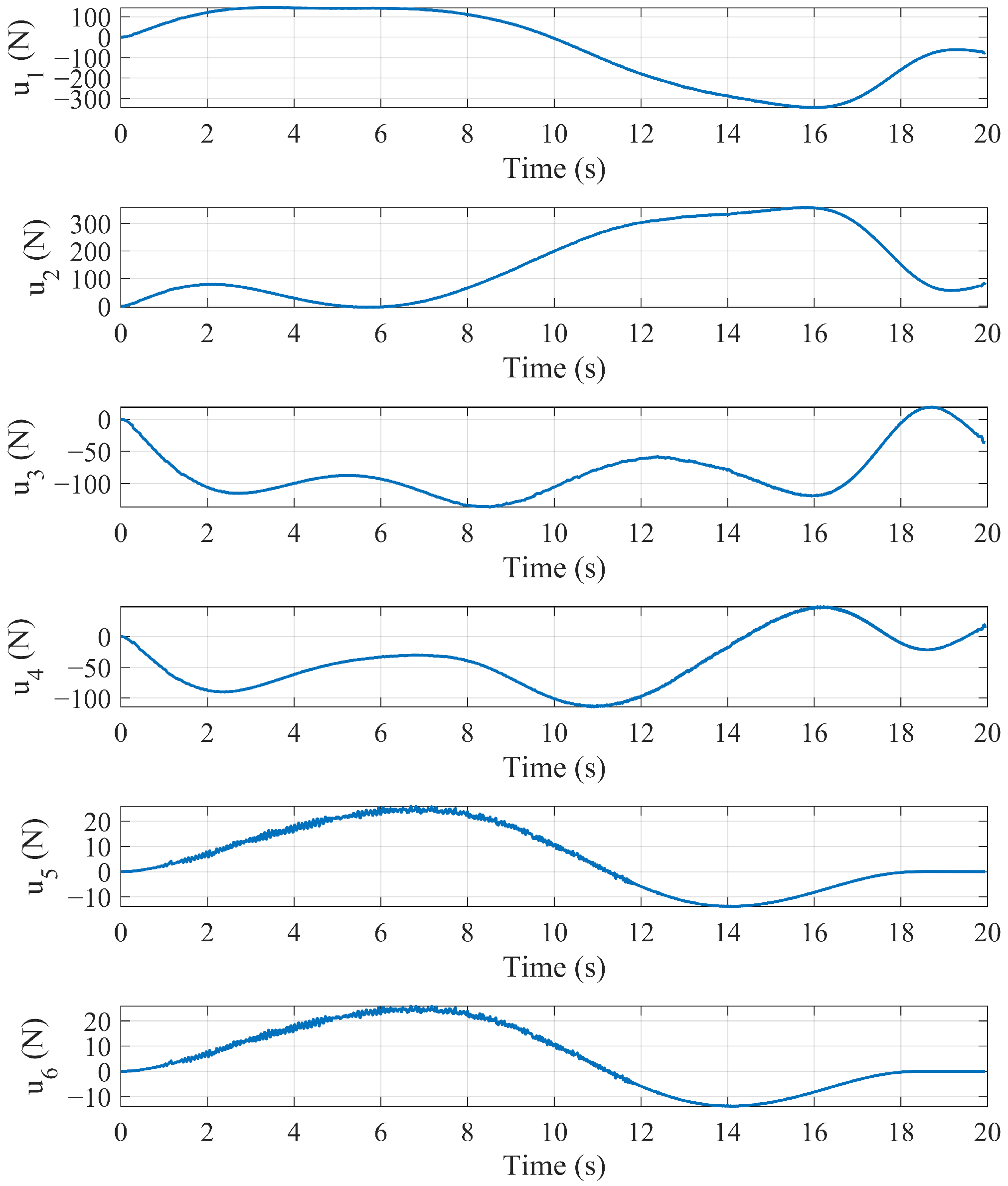
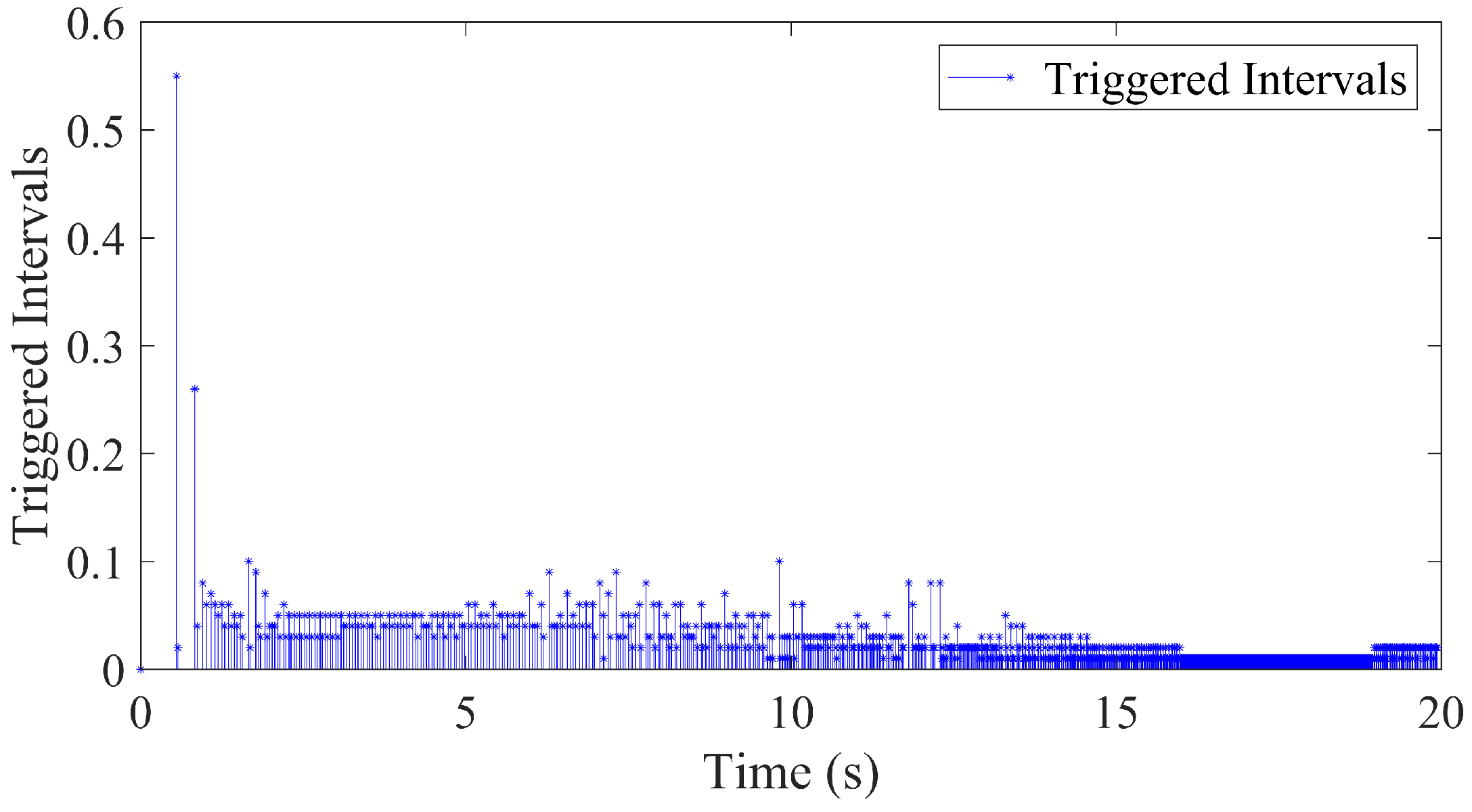
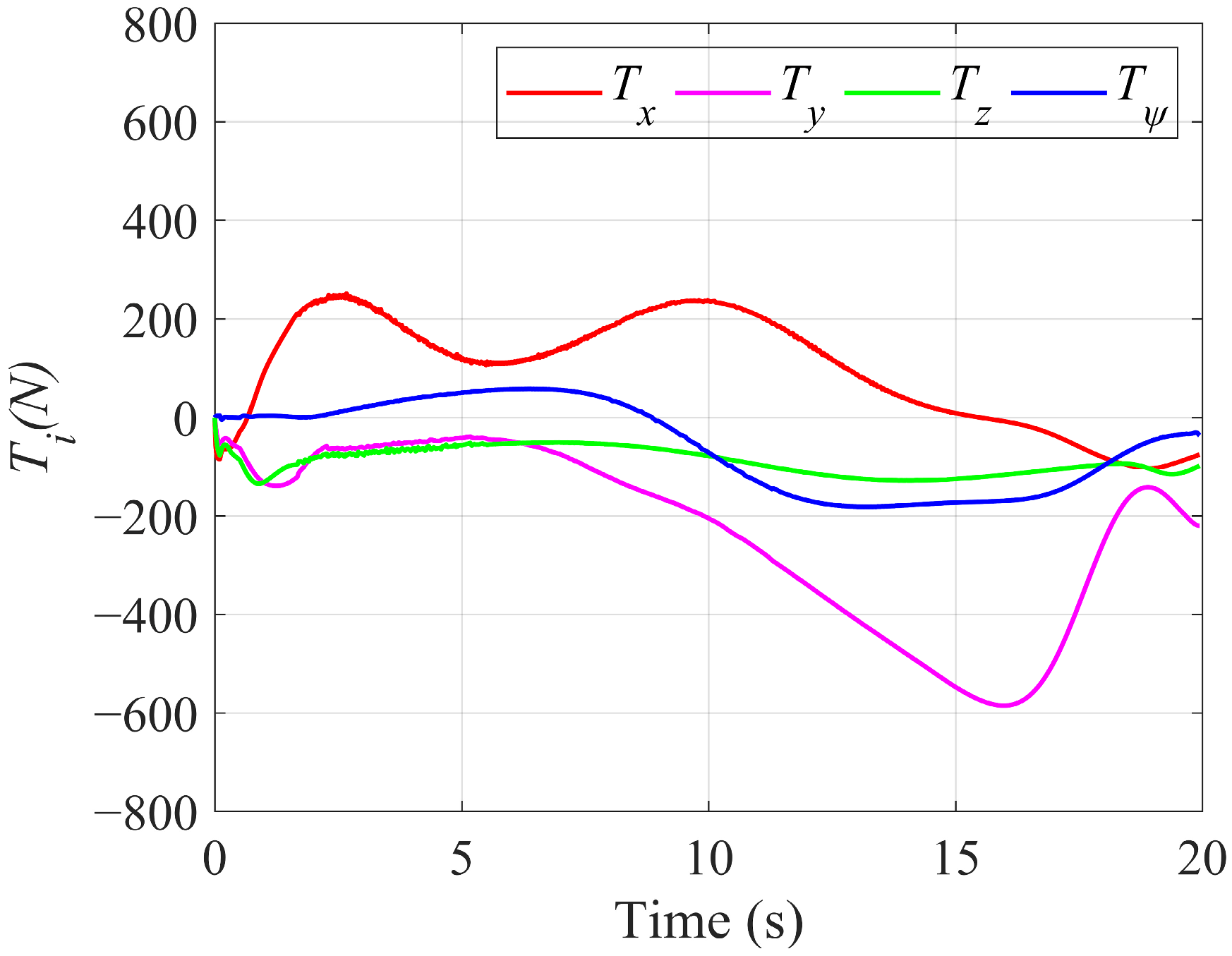


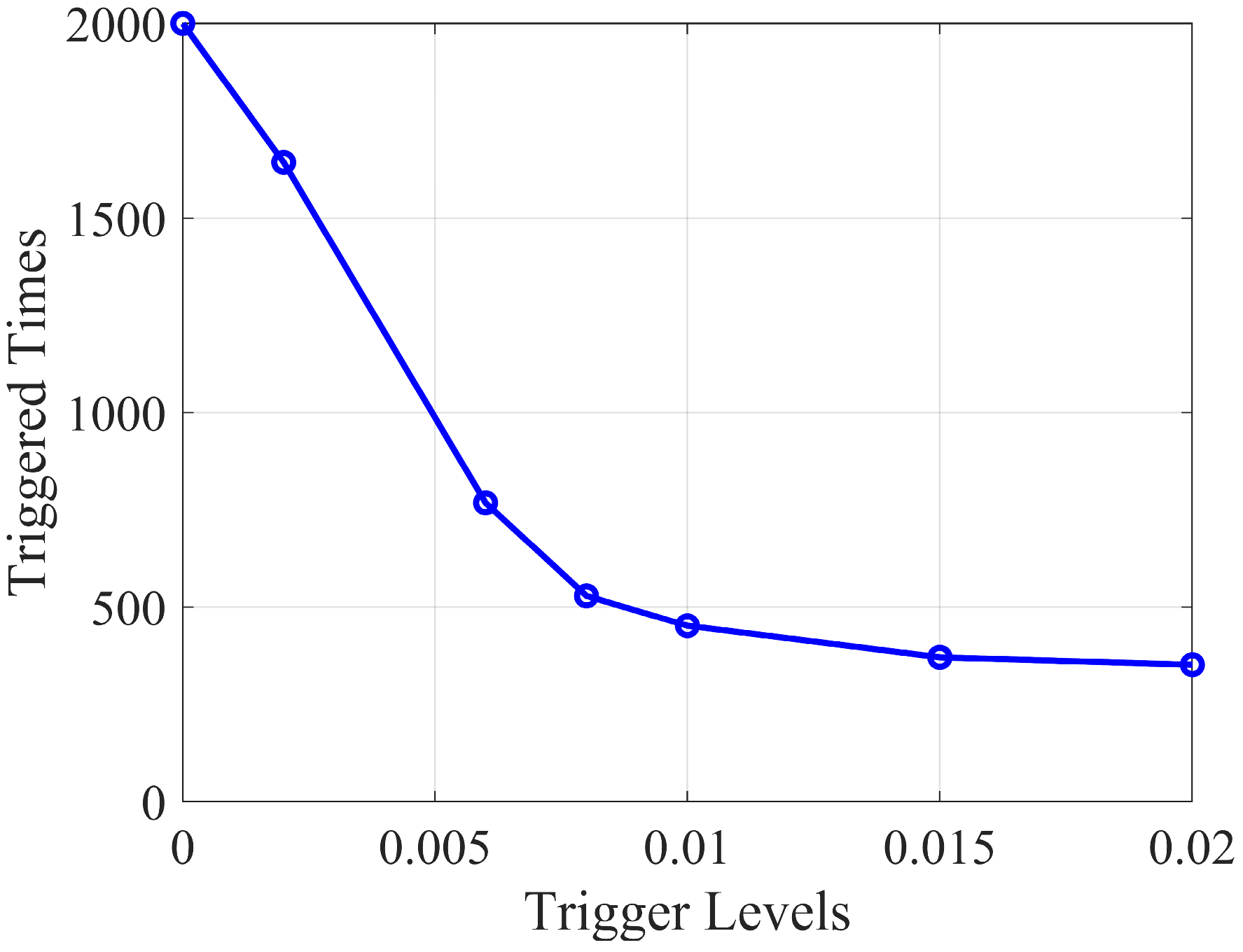
| MSEs | ETQMPC | MPC | BSC |
|---|---|---|---|
| x | 9.502 | 5.777 | 7.043 |
| y | 5.808 | 2.992 | 1.856 |
| z | 1.141 | 2.635 | 1.111 |
| ψ | 1.015 | 9.163 | 1.402 |
| u | 6.908 | 1.379 | 5.070 |
| v | 3.249 | 1.604 | 3.376 |
| w | 1.500 | 6.328 | 1.443 |
| r | 9.251 | 8.469 | 2.092 |
| MSEs | ETQMPC | MPC | BSC |
|---|---|---|---|
| x | 7.200 | 1.200 | 1.600 |
| y | 3.824 | 5.918 | 1.600 |
| z | 8.255 | 1.294 | 2.400 |
| ψ | 1.081 | 1.006 | 4.251 |
| u | 4.084 | 6.443 | 4.903 |
| v | 1.230 | 1.383 | 1.169 |
| w | 5.808 | 6.705 | 9.346 |
| r | 1.090 | 9.847 | 5.058 |
| Performance Improvement | Case I | Case II | ||
|---|---|---|---|---|
| MPC | BSC | MPC | BSC | |
| Position tracking | −11.4% | 881.8% | 62.1% | 372.6% |
| Yaw tracking | −9.7% | 1281.8% | −6.9% | 3834.1% |
| Velocity tracking | 161.3% | 4662.4% | 21.6% | 215.7% |
| Computing | 125.0% | 125.0% | 160.4% | 160.4% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ni, T.; Sima, C.; Qi, L.; Xu, M.; Wang, J.; Tang, R.; Zhang, L. Non-Periodic Quantized Model Predictive Control Method for Underwater Dynamic Docking. Symmetry 2024, 16, 1392. https://doi.org/10.3390/sym16101392
Ni T, Sima C, Qi L, Xu M, Wang J, Tang R, Zhang L. Non-Periodic Quantized Model Predictive Control Method for Underwater Dynamic Docking. Symmetry. 2024; 16(10):1392. https://doi.org/10.3390/sym16101392
Chicago/Turabian StyleNi, Tian, Can Sima, Liang Qi, Minghao Xu, Junlin Wang, Runkang Tang, and Lindan Zhang. 2024. "Non-Periodic Quantized Model Predictive Control Method for Underwater Dynamic Docking" Symmetry 16, no. 10: 1392. https://doi.org/10.3390/sym16101392
APA StyleNi, T., Sima, C., Qi, L., Xu, M., Wang, J., Tang, R., & Zhang, L. (2024). Non-Periodic Quantized Model Predictive Control Method for Underwater Dynamic Docking. Symmetry, 16(10), 1392. https://doi.org/10.3390/sym16101392







