Multilinear Variable Separation Approach in (4+1)-Dimensional Boiti–Leon–Manna–Pempinelli Equation

Abstract

In this paper, we use the multilinear variable separation approach involving two arbitrary variable separation functions to construct a new variable separation solution of the (4+1)-dimensional Boiti–Leon–Manna–Pempinelli equation. Through considering different parameters, three types of local excitations including dromions, lumps, and ring solitons are constructed. Dromion molecules, lump molecules, ring soliton molecules, and their interactions are analyzed through the velocity resonance mechanism. In addition, the results reveal the elastic and inelastic interactions between solitons. We discuss some dynamical properties of these solitons and soliton molecules obtained analytically. Three-dimensional diagrams and contour plots of the solution are given to help understand the physical mechanism of the solutions.

1. Introduction

Nonlinear partial differential equations (NLPDEs) have a wide range of applications in a number of scientific fields, including fluid dynamics, plasma physics, nonlinear optics, and condensed matter physics [1,2,3]. So far, many methods for solving NLPDEs have been established, such as the inverse scattering transform, Darboux transformation, the Hirota bilinear method, and various feasible approaches [4,5,6,7,8,9,10,11]. Among them, the multilinear variable separation approach (MLVSA), developed by Lou and Tang, is considered to be a fundamental and efficient method for solving NLPDEs [12,13]. It has been applied to a large number of important (2+1)- and (3+1)-dimensional nonlinear physical models, such as the (3+1)-dimensional Burgers equation, the (2+1)-dimensional Korteweg–de Vries equation, the (2+1)-dimensional Sawada–Kotera equation, and so on [14,15,16].

With the continuous advancement of modern fiber optic technology, soliton molecules are observed experimentally through the use of ultrashort pulse lasers and advanced optical equipment [17,18]. In addition, the study of soliton molecules has become a hot topic in recent years due to their practical applications. They are not limited to optical systems, and can be found in other areas of physics as well, such as acoustics, semiconductor physics, hydrodynamics, and so on [19,20,21,22]. A soliton refers to a stable, localized wave packet that maintains shape during propagation. A soliton molecule describes a composite structure formed by multiple interacting solitons, similar to a molecule composed of atoms [23]. Soliton molecules usually consist of several individual solitons that combine and propagate in parallel as a whole [24,25]. A velocity resonance mechanism has been proposed to search for soliton molecules [26,27]. In the case of velocity resonance, the repulsive and attractive forces between the solitons are balanced so that the velocities of the solitons become progressively equal [28,29]. This interaction may lead to the formation of soliton molecule. Based on velocity resonance, many nonlinear systems have been found to excite soliton molecules [30,31].

In this study, we endeavored to seek new variable separation solutions and novel nonlinear localized excitations for the following (4+1)-dimensional Boiti–Leon–Manna–Pempinelli (BLMP) equation [32,33,34]:

$$\begin{array}{c}\hfill u_{yt}+u_{zt}+u_{st}+u_{xxxy}+u_{xxxz}+u_{xxxs}-3u_x(u_{xy}+u_{xz}+u_{xs})-3u_{xx}(u_y+u_z+u_s)=0.\end{array}$$

(1)

The BLMP equation is a mathematical model that has important applications in nonlinear wave theory. As a result, this model has attracted considerable attention in mathematics and physics. The (2+1)-BMLP equation is part of the family of KdV equations. The KP equation can be considered an extension of the KdV equation. So, the (4+1)-dimensional BLMP, which extends the (2+1)-dimensional BLMP equation, is also associated with the extended KP model [35]. The study of the (4+1)-dimensional BLMP equation has focused on the integrable properties, soliton solutions, and numerical methods for the solution [36]. Through the Hirota bilinear method and other methods, scholars have obtained multiple soliton solutions of the BLMP equation and analyzed the complex dynamical behaviours [37,38]. An exact unique solution of the (4+1)-dimensional BLMP equation has been studied via a novel condition assertion [39]. Kuo et al. studied the resonant multi-soliton solutions for the (4+1)-dimensional BLMP equation using a simplified linear superposition method [40]. Ma et al. obtained a set of rational wave solutions using the corresponding Hirota bilinear form and proved the existence of a special wave structure for the (4+1)-dimensional BLMP equation [41]. It should be noted that dromions, lumps, ring solitons, and their corresponding molecules are analyzed using the variable separation approach and velocity resonance mechanism, which is a departure from previous approaches.

This paper is organised as follows. In Section 2, new variable separation solutions of the equations are constructed using the MLVSA involving two arbitrary variable separation functions p and q. In Section 3, we choose different parameters for the variable separation functions p and q to obtain several corresponding nonlinear excitations, including the dromions, lumps, and ring solitons. According to the velocity resonance mechanism, soliton molecules can be obtained by adjusting the velocity of the solitons. In particular, we analyze the elastic interactions for the three types of local excitations graphically. Finally, the conclusion and summary will be presented.

2. Variable Separation Solutions

MLVSA is widely applied to multidimensional nonlinear systems. Diverse local excitations of the (4+1)-dimensional BLMP equation are found using MLVSA. The method achieves the function of independent variables relative to traditional methods. Meanwhile, MLVSA enriches local waves through the construction of arbitrary functions. In contrast to the inverse scattering method, MLVSA not only deals with integrable nonlinear systems but also solves nonintegrable nonlinear systems efficiently. In the following, MLVSA is applied to the (4+1)-dimensional BLMP equation to find the solution. In order to multilinearize the nonlinear system to obtain the variable separation solutions, we first utilize the following Bäcklund transformation:

$$u=-2{\left(\ln f\right)}_x+u_0+u_1,$$

(2)

where $u_0\equiv u_0\left(t\right)$ and $u_1\equiv u_1(y,z,s)$ are arbitrary seed solutions of (1), and u is a function of $x,y,z,s$, and t. Under this transformation, the Hirota bilinear form of (1) is obtained as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}& (D_y{D}_t+D_z{D}_t+D_s{D}_t+D_y{D}_x^3+D_z{D}_x^3+D_s{D}_x^3-3(u_{1y}+u_{1z}+u_{1s})D_x^2\hfill \\ & -h_0-h_1)f·f=0,\hfill \end{array}\end{array}$$

(3)

where $h_0\equiv h_0\left(t\right)$ and $h_1\equiv h_1(y,z,s)$ are two arbitrary functions of the indicated arguments, and $D_i(i=x,y,z,s,t)$ is the widely known Hirota’s bilinear operator [42] defined by

$$\begin{array}{c}\hfill \begin{array}{cc}& D_x^m{D}_y^n{D}_z^j{D}_s^k{D}_t^l(f·g)\hfill \\ & ={({\partial }_x-{\partial }_{x^{\prime }})}^m{({\partial }_y-{\partial }_{y^{\prime }})}^n{({\partial }_z-{\partial }_{z^{\prime }})}^j{({\partial }_s-{\partial }_{s^{\prime }})}^k{({\partial }_t-{\partial }_{t^{\prime }})}^l\hfill \\ & f(x,y,z,s,t)·g(x^{\prime },y^{\prime },z^{\prime },s^{\prime },t^{\prime }){|}_{x^{\prime }=x,y^{\prime }=y,z^{\prime }=z,s^{\prime }=s,t^{\prime }=t},\hfill \end{array}\end{array}$$

(4)

where $m,n,j,k$, and l are non-negative integers. In this case, we find the new nonlinear variable separation solution for the nonlinear model (1) by assuming the expansion function f as follows:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill f=a_0+a_{1}p+a_{2}q+a_{3}pq,\end{array}\end{array}$$

(5)

where $a_0,a_1,a_2$, and $a_3$ are arbitrary constants, and $p\equiv p(x,t)$ and $q\equiv q(y,z,s,t)$ are arbitrary functions of the given arguments. Substituting (5) into (3) leads to

$$\begin{array}{c}\hfill \begin{array}{cc}& 2(a_0{a}_3-a_1{a}_2)(q_s+q_y+q_z)(p_t+p_{xxx})+6(q{a}_3+a_1)(u_{1y}+u_{1z}+u_{1s})(p_x^2(q{a}_3+a_1)\hfill \\ & -f{p}_{xx})+2f(p{a}_3+a_2)(q_{st}+q_{yt}+q_{zt})-2{(p{a}_3+a_2)}^2(q_s+q_y+q_z)q_t-(h_0+h_1)f^2=0.\hfill \end{array}\end{array}$$

(6)

We can easily confirm that Equation (6) is identically satisfied in the following case:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill h_0\left(t\right)=h_1(y,z,s)=0,q=q\left[{\displaystyle \frac{1}{2}}y+{\displaystyle \frac{1}{2}}z-s,t\right],u_1=u_1\left[{\displaystyle \frac{1}{2}}y+{\displaystyle \frac{1}{2}}z-s,t\right].\end{array}\end{array}$$

(7)

Finally, the new variable separation solution of (1) reads

$$\begin{array}{c}\hfill \begin{array}{c}\hfill u={\displaystyle \frac{-2(q{a}_3+a_1)p_x}{a_0+a_{1}p+a_{2}q+a_{3}pq}}+u_0+u_1,\end{array}\end{array}$$

(8)

which is an analytical solution. In particular, the different choices of arbitrary functions p, q, $u_0$, and $u_1$ involved in Equation (8) allow us to construct a wide variety of nonlinear excitation solutions for the (4+1)-dimensional BLMP equation. Additionally, it is noticed that the potential field of this model is

$$\begin{array}{c}\hfill \begin{array}{c}\hfill U\equiv u_y={\displaystyle \frac{-2(a_0{a}_3-a_1{a}_2)\left(p_x{q}_y\right)}{{(a_0+a_{1}p+a_{2}q+a_{3}pq)}^2}}+u_{1y}.\end{array}\end{array}$$

(9)

Here, both u and U are functions of $x,y,z,s$, and t. The different values of p and q taken by (9) are visualized in Table 1.

Table 1. Five different choices of arbitrary functions p and q in (10)–(14), respectively.

Dromions, dromion molecules, and their interactions in Figure 1, Figure 2 and Figure 3.	Lumps, lump molecules, and their interactions in Figure 4 and Figure 5.
${\displaystyle p=\exp \left[\sum _{i=1}^N{b}_i\tanh (k_i(v_{i}t+x)+{\omega }_i)\right],}$	$p=c+{\sum }_{i=1}^N{\displaystyle \frac{h_i}{{\omega }_i+{\left[k_{i}x+t{v}_i+b_i\right]}^2}},$
$q=\exp \left[{\sum }_{j=1}^M{C}_j\tanh (K_j(V_{j}t-y+z+s)+{\Omega }_j)\right].$	$q=C+{\sum }_{j=1}^M{\displaystyle \frac{H_j}{{\Omega }_j+{\left[K_{j}s+B_j\right]}^2+L_{j}z+y}}.$
Ring solitons, ring soliton molecules, and their interactions in Figure 6 and Figure 7.	The interactions between ring molecules and special oscillating lumps in Figure 8 and Figure 9.
${\displaystyle p=c+\exp \left[\sum _{i=1}^N{\omega }_i-{(k_{i}x+v_{i}t+b_i)}^2\right],}$	$p=\exp \left[{\sum }_{i=1}^N{\omega }_i-{(k_{i}x+v_{i}t+b_i)}^2\right]+{\displaystyle \frac{d}{1+{\left[(x-ct)(\cos (x-ct)+h)\right]}^2}},$
$q=C+{\sum }_{j=1}^M\cosh \left[{\Omega }_j+{(K_{j}x+V_{j}z+B_j+s)}^2)\right].$	$q={\sum }_{j=1}^M\cosh \left[{\Omega }_j+{(K_{j}x+V_{j}z+B_j+s)}^2)\right]+{\displaystyle \frac{1}{y^2+1}}.$
The interaction between lumps and dromion molecules Figure 10 and Figure 11.
${\displaystyle p=\exp \left[\sum _{i=1}^N{b}_i\tanh (k_i(v_{i}t+x)+{\omega }_i)\right]+\sum _{i=1}^M\frac{h_i^{\prime }}{{\omega }_i^{\prime }+{\left[k_i^{\prime }x+t{v}_i^{\prime }+b_i^{\prime }\right]}^2},}$
$q=\exp \left[{\sum }_{j=1}^N{C}_j\tanh (K_j(V_{j}t-y+z+s)+{\Omega }_j)\right]+{\sum }_{j=1}^M{\displaystyle \frac{H_j^{\prime }}{{\Omega }_j^{\prime }+{\left[K_j^{\prime }y+B_j^{\prime }\right]}^2+L_j^{\prime }z+s}}.$

Table 1. Five different choices of arbitrary functions p and q in (10)–(14), respectively.

Dromions, dromion molecules, and their interactions in Figure 1, Figure 2 and Figure 3.	Lumps, lump molecules, and their interactions in Figure 4 and Figure 5.
${\displaystyle p=\exp \left[\sum _{i=1}^N{b}_i\tanh (k_i(v_{i}t+x)+{\omega }_i)\right],}$	$p=c+{\sum }_{i=1}^N{\displaystyle \frac{h_i}{{\omega }_i+{\left[k_{i}x+t{v}_i+b_i\right]}^2}},$
$q=\exp \left[{\sum }_{j=1}^M{C}_j\tanh (K_j(V_{j}t-y+z+s)+{\Omega }_j)\right].$	$q=C+{\sum }_{j=1}^M{\displaystyle \frac{H_j}{{\Omega }_j+{\left[K_{j}s+B_j\right]}^2+L_{j}z+y}}.$
Ring solitons, ring soliton molecules, and their interactions in Figure 6 and Figure 7.	The interactions between ring molecules and special oscillating lumps in Figure 8 and Figure 9.
${\displaystyle p=c+\exp \left[\sum _{i=1}^N{\omega }_i-{(k_{i}x+v_{i}t+b_i)}^2\right],}$	$p=\exp \left[{\sum }_{i=1}^N{\omega }_i-{(k_{i}x+v_{i}t+b_i)}^2\right]+{\displaystyle \frac{d}{1+{\left[(x-ct)(\cos (x-ct)+h)\right]}^2}},$
$q=C+{\sum }_{j=1}^M\cosh \left[{\Omega }_j+{(K_{j}x+V_{j}z+B_j+s)}^2)\right].$	$q={\sum }_{j=1}^M\cosh \left[{\Omega }_j+{(K_{j}x+V_{j}z+B_j+s)}^2)\right]+{\displaystyle \frac{1}{y^2+1}}.$
The interaction between lumps and dromion molecules Figure 10 and Figure 11.
${\displaystyle p=\exp \left[\sum _{i=1}^N{b}_i\tanh (k_i(v_{i}t+x)+{\omega }_i)\right]+\sum _{i=1}^M\frac{h_i^{\prime }}{{\omega }_i^{\prime }+{\left[k_i^{\prime }x+t{v}_i^{\prime }+b_i^{\prime }\right]}^2},}$
$q=\exp \left[{\sum }_{j=1}^N{C}_j\tanh (K_j(V_{j}t-y+z+s)+{\Omega }_j)\right]+{\sum }_{j=1}^M{\displaystyle \frac{H_j^{\prime }}{{\Omega }_j^{\prime }+{\left[K_j^{\prime }y+B_j^{\prime }\right]}^2+L_j^{\prime }z+s}}.$

Figure 1. The elastic interaction between dromions and dromion molecule at times (a) $t=-80$, (b) $t=0$, and (c) $t=120$.

Figure 1. The elastic interaction between dromions and dromion molecule at times (a) $t=-80$, (b) $t=0$, and (c) $t=120$.

Figure 2. The elastic interaction between two dromion molecules at times (a) $t=-1$, (b) $t=1$, and (c) $t=3$.

Figure 2. The elastic interaction between two dromion molecules at times (a) $t=-1$, (b) $t=1$, and (c) $t=3$.

Figure 3. The contour plot of the elastic interaction between two dromion molecules at times (d) $t=-1$, (e) $t=1$, and (f) $t=3$.

Figure 3. The contour plot of the elastic interaction between two dromion molecules at times (d) $t=-1$, (e) $t=1$, and (f) $t=3$.

Figure 4. The elastic interaction between two lumps at times (a) $t=-6$, (b) $t=3$, and (c) $t=12$.

Figure 4. The elastic interaction between two lumps at times (a) $t=-6$, (b) $t=3$, and (c) $t=12$.

Figure 5. The elastic interaction between lumps and lump molecule at times (a) $t=-12$, (b) $t=2$, and (c) $t=17$.

Figure 5. The elastic interaction between lumps and lump molecule at times (a) $t=-12$, (b) $t=2$, and (c) $t=17$.

Figure 6. The elastic interaction between two ring solitons at times (a) $t=-40$, (b) $t=-5$, and (c) $t=-28$.

Figure 6. The elastic interaction between two ring solitons at times (a) $t=-40$, (b) $t=-5$, and (c) $t=-28$.

Figure 7. The elastic interaction between ring solitons and ring soliton molecules at times (a) $t=-10$, (b) $t=5/2$, and (c) $t=15$.

Figure 7. The elastic interaction between ring solitons and ring soliton molecules at times (a) $t=-10$, (b) $t=5/2$, and (c) $t=15$.

Figure 8. The interaction between the special oscillating lumps and ring soliton molecules at times (a) $t=-10$, (b) $t=5$, and (c) $t=20$.

Figure 8. The interaction between the special oscillating lumps and ring soliton molecules at times (a) $t=-10$, (b) $t=5$, and (c) $t=20$.

Figure 9. The contour plots of the interaction between the special oscillating lumps and ring soliton molecules at times (d) $t=-10$, (e) $t=5$, and (f) $t=20$.

Figure 9. The contour plots of the interaction between the special oscillating lumps and ring soliton molecules at times (d) $t=-10$, (e) $t=5$, and (f) $t=20$.

Figure 10. The interaction between the $2\times 2$ dromion molecules and lumps at times (a) $t=5$, (b) $t=-12$, and (c) $t=-24$.

Figure 10. The interaction between the $2\times 2$ dromion molecules and lumps at times (a) $t=5$, (b) $t=-12$, and (c) $t=-24$.

Figure 11. The contour plots of the interaction between the $2\times 2$ dromion molecules and lumps at times (d) $t=5$, (e) $t=-12$, and (f) $t=-24$.

Figure 11. The contour plots of the interaction between the $2\times 2$ dromion molecules and lumps at times (d) $t=5$, (e) $t=-12$, and (f) $t=-24$.

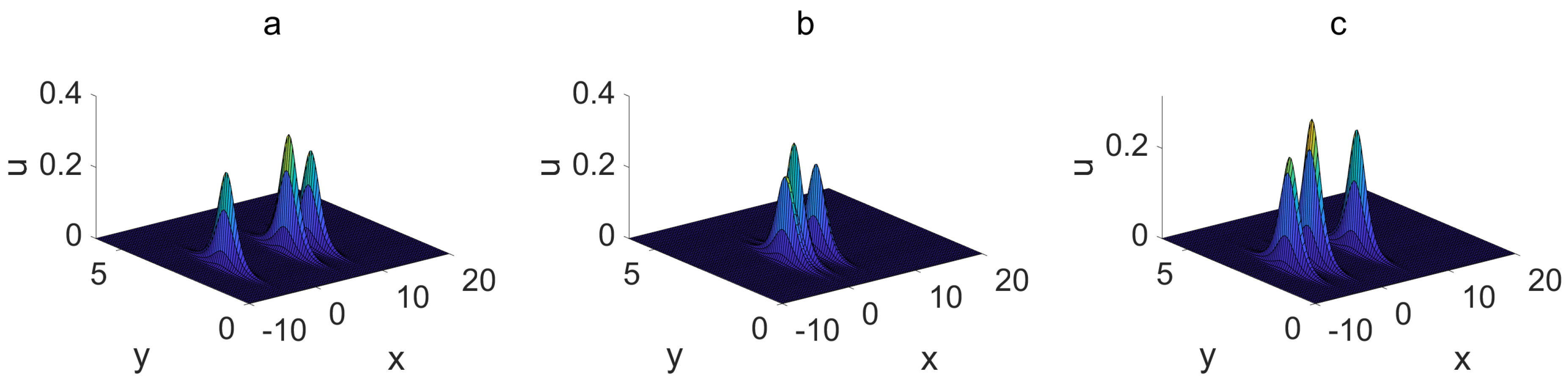
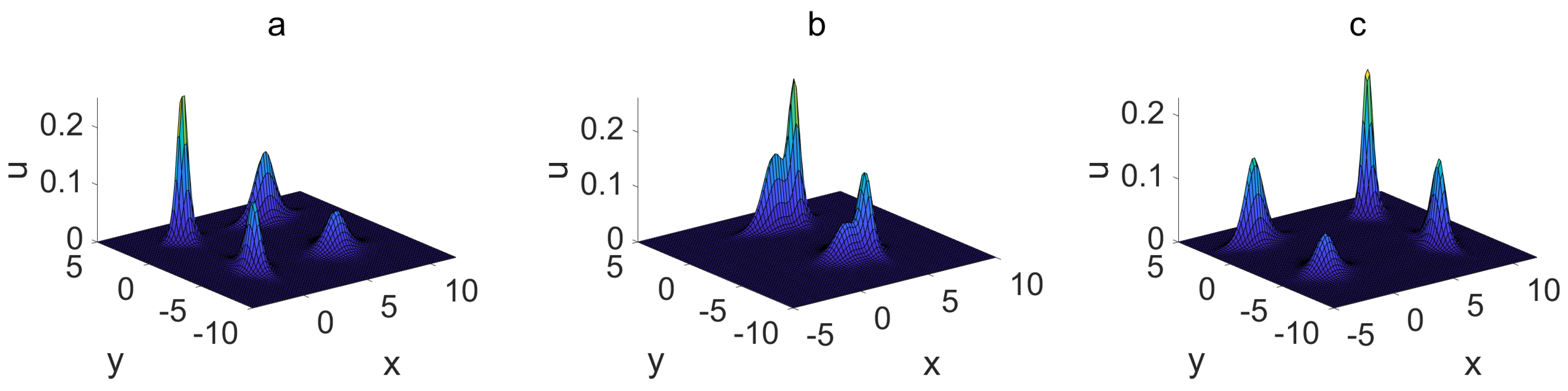
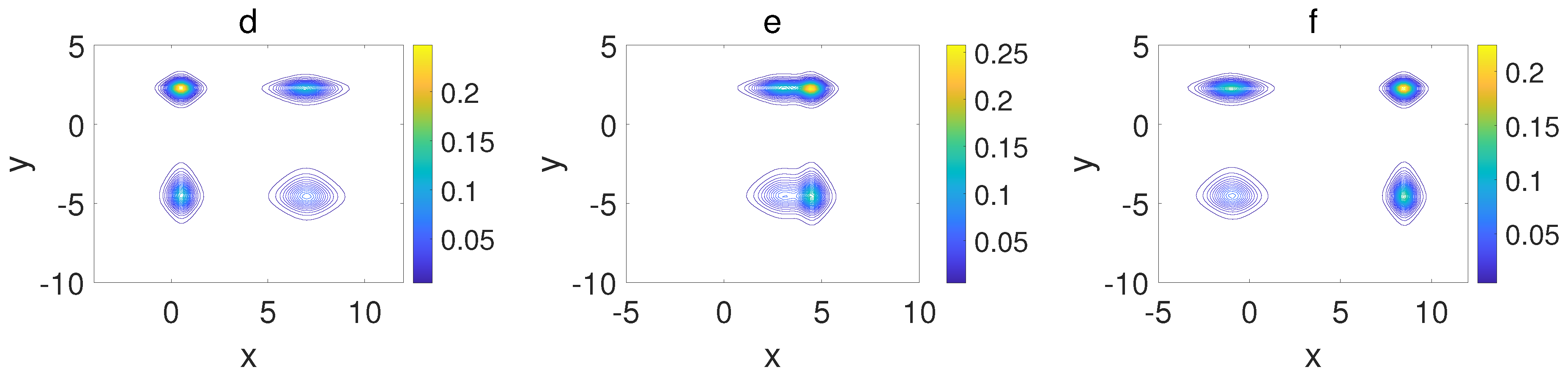
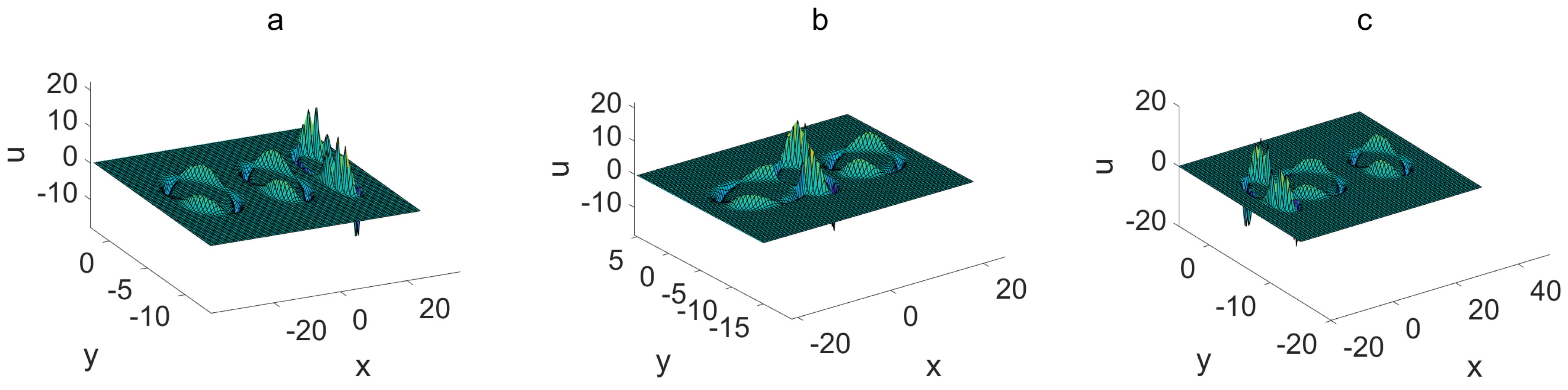
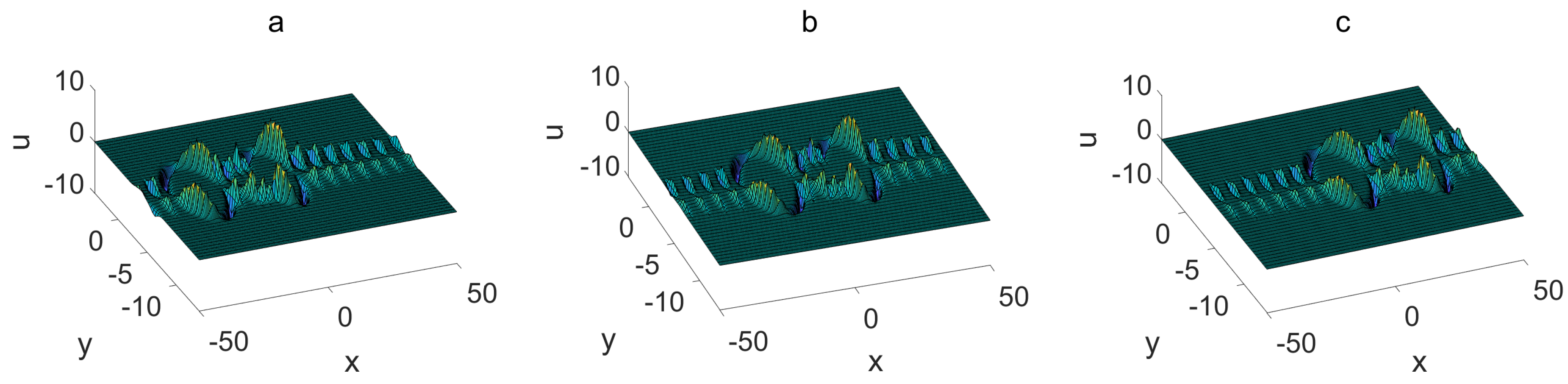
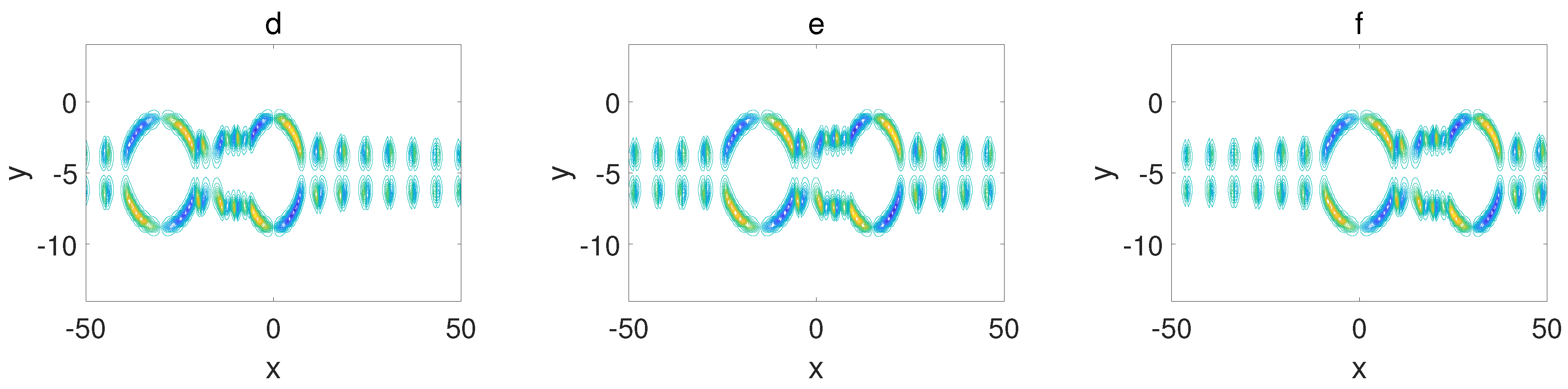
3. Nonlinear Excitations and Their Interactions

3.1. Dromions, Dromion Molecules, and Their Interactions

A dromion solution typically emerges at the intersection of two solitons traveling along non-parallel paths [43]. This subsection is dedicated to deriving dromion excitations for the (4+1)-dimensional BLMP equation. Hence, we restrict the variable-separating functions p and q as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}& p=\exp \left[\sum _{i=1}^N{b}_i\tanh (k_i(v_{i}t+x)+{\omega }_i)\right],\hfill \\ & q=\exp \left[\sum _{j=1}^M{C}_j\tanh (K_j(V_{j}t-y+z+s)+{\Omega }_j)\right],\hfill \end{array}\end{array}$$

(10)

where the variables ${\omega }_i,k_i,v_i,b_i,C_j,{\Omega }_j,K_j$, and $V_j$ are arbitrary constants. In this condition, the potential field U described by (9) and (10) captures the interactions with different dromions. To facilitate the graphical representation of the interactions between the different dromions, we set $z=0$, $s=0$, and $u_1=0$. Two cases involving dromion–dromion interactions and dromion–dromion molecule interactions are given below with $\{a_0,a_1,a_2,a_3\}=\{2,1,1,2\}$.

3.1.1. Dromion–Dromion Interactions

We take $M=3$ and $N=1$ and set the parameters as $b_1=b_2=b_3={\displaystyle \frac{1}{2}}$, $k_1=k_2=k_3=2$, $v_1=-v_2=-v_3=-{\displaystyle \frac{1}{20}},{\omega }_1=0,{\omega }_2=-3,{\omega }_3=-10,C_1=1,K_1=2,V_1=0,$ and ${\Omega }_1=5$. Then, the dromion molecule and a single dromion can be obtained, the interactions between which are shown in Figure 1. The diagrams reveal that the dromion molecule is asymmetric under the condition of ${\omega }_2\ne {\omega }_3$. Moreover, the dromion molecule moves in the negative x-axis direction, which is opposite to the single dromion. After the interaction, they both recover their respective shapes and velocities. Therefore, it can be deduced that their interactions are elastic.

3.1.2. Dromion–Dromion Molecule Interactions

We take $N=M=2$ to describe the interactions for two sets of dromion molecules by taking $b_1=b_2={\displaystyle \frac{1}{3}},k_1=-2,k_2=-1,v_1=-v_2=-2,{\omega }_1={\omega }_2=5$, $c_1=c_2=2$, $K_1=2,K_2=1,V_1=V_2=0,$ and ${\Omega }_1=-{\Omega }_2=5$. From Figure 2 and Figure 3, the two sets of dromion molecules gradually approach each other along the x-axis. Moreover, the distance of the two dromions within each dromion molecule remains constant with the evolution of time. After the collision, they maintain their original shapes and velocities but become farther apart. So we can infer that their interactions are perfectly elastic.

3.2. Lumps, Lump Molecules, and Their Interactions

In nonlinear systems, a lump is a special type of local structure that usually manifests itself as a rational function in all directions of spaces [44]. In this subsection, to find the lump excitations of the (4+1)-dimensional BLMP equation, the constraints on the variable separation functions p and q are

$$\begin{array}{c}\hfill \begin{array}{cc}& p=c+\sum _{i=1}^N{\displaystyle \frac{h_i}{{\omega }_i+{\left[k_{i}x+t{v}_i+b_i\right]}^2}},\hfill \\ & q=C+\sum _{j=1}^M{\displaystyle \frac{H_j}{{\Omega }_j+{\left[K_{j}s+B_j\right]}^2+L_{j}z+y}},\hfill \end{array}\end{array}$$

(11)

where the variables ${\omega }_i,k_i,v_i,b_i,h_i,{\Omega }_j,B_j,L_j,K_j,H_j,V_j,c$, and C are arbitrary constants. The potential U, determined by (9) and (11), can be constructed to describe the dynamical behaviour of the lumps by adjusting the velocity and shape. Furthermore, when two lumps satisfy ${\displaystyle \frac{v_i}{k_i}}={\displaystyle \frac{v_j}{k_j}}$, they can resonate to form a lump molecule. For ease of description, we set $\{a_0,a_1,a_2,a_3\}$ = $\{2,1,1,4\}$, $y=0,z=1$, and $u_1=0$ to demonstrate the interactions of lumps. Two cases involving lump–lump interactions and lump–lump molecule interactions are derived below.

3.2.1. Lump–Lump Interactions

We set $N=2$ and $M=1$ and the parameters chosen as $h_1=h_2=2,{\omega }_1={\omega }_2={\displaystyle \frac{1}{2}}$, $k_1={\displaystyle \frac{3}{2}}$, $k_2={\displaystyle \frac{3}{4}},v_1=2,v_2=-1,b_1=-2,b_2=5,c=1,H_1=4,{\Omega }_1={\displaystyle \frac{1}{3}},K_1=3$, $B_1=-8$, $L_1=1,$ and $C=0$. Two specific lumps can be obtained. Their interaction behaviors are shown in Figure 4. As time evolves, the figures reveal that two lumps collide roughly at $t=3$ according to the general interaction time formula ${\displaystyle \frac{b_1{k}_2-b_2{k}_1}{v_2{k}_1-v_1{k}_2}}$. After the collision, their shapes and velocities remain unchanged, indicating that their interactions are elastic.

3.2.2. Lump–Lump Molecule Interactions

According to the velocity resonance mechanism, we can obtain a lump molecule by setting two lumps to the same velocity. By taking $N=3$ and $M=1$, we obtain the interaction diagrams for a lump and lump molecule in the setting of the following parameters: $v_1=-1$, $v_2=2,v_3=1,k_1=1,k_2={\displaystyle \frac{3}{2}},k_3={\displaystyle \frac{3}{4}},h_1=3,h_2={\displaystyle \frac{3}{2}},h_3={\displaystyle \frac{5}{2}},b_1=4,b_2=-10$, $b_3=2$, ${\omega }_1={\displaystyle \frac{1}{4}},{\omega }_2={\omega }_3={\displaystyle \frac{1}{2}},c=1,H_1=5,{\Omega }_1={\displaystyle \frac{1}{2}},K_1=2,B_1=-8,L_1=1,$ and $C=0$. As shown in Figure 5, the single lump propagates positively along the x-axis, while the lump molecule moves in the opposite direction. According to the general interaction time formula, the single lump interacts sequentially with the first lump and the second lump in the lump molecule at $t=0$ and $t=4/7$ as time progresses. After the collision, they continue to propagate without changing shapes or velocities. Hence, their interactions are also elastic.

3.3. Ring Solitons, Ring Soliton Molecules, and Their Interactions

The feature of the ring soliton is the circular or ring-shaped waveform, with energy concentrated along the circular path. This ring structure distinguishes ring solitons from other solitons. Now, we assume the form of p and q to be

$$\begin{array}{c}\hfill \begin{array}{cc}& p=c+\exp \left[\sum _{i=1}^N{\omega }_i-{(k_{i}x+v_{i}t+b_i)}^2\right],\hfill \\ & q=C+\sum _{j=1}^M\cosh \left[{\Omega }_j+{(K_{j}x+V_{j}z+B_j+s)}^2)\right],\hfill \end{array}\end{array}$$

(12)

where the variables ${\omega }_i,k_i,v_i,b_i,{\Omega }_j,B_j,K_j,V_j,c$, and C are arbitrary constants. It is noted that ${\omega }_i$ and $b_i$ determine the size and position of the ring soliton, while ${\displaystyle \frac{v_i}{k_i}}$ determines its velocity. We take $\{a_0,a_1,a_2,a_3\}=\{2,1,1,0\}$, $z=s=0$, and $u_1=0$ to describe the interactions among ring solitons. Two cases of ring–ring interactions and ring–ring molecule interactions are written below.

3.3.1. Ring–Ring Interactions

In taking $N=2$ and $M=1$ and using the parameters ${\omega }_1=7,{\omega }_2=10,k_1=k_2={\displaystyle \frac{1}{8}}$, $v_1={\displaystyle \frac{1}{5}}$, $v_2=-{\displaystyle \frac{1}{4}},b_1=-b_2=5,c=2,{\Omega }_1=K_1=V_1=C=1,$ and $B_1=5$, two ring solitons can be obtained. As can be seen in Figure 6, the two ring solitons move in opposite directions along the x-axis and collide around at $t=-5$. After the collision, they continue to move without changing their shapes or velocities. So, the interactions of ring solitons are elastic.

3.3.2. Ring–Ring Molecule Interactions

We set $N=3$ and $M=1$ and choose the parameters as ${\omega }_1={\omega }_2=10,{\omega }_3=15$, $k_1={\displaystyle \frac{2}{5}}$, $k_2={\displaystyle \frac{1}{2}},k_3=1,v_1=-{\displaystyle \frac{2}{5}},v_2=-{\displaystyle \frac{1}{2}},v_3=1,b_1=5,b_2=b_3=-5,{\Omega }_1=1,K_1=1$, $V_1=1$, $B_1=5,c=0,$ and $C=0$. The elastic interactions between a ring soliton and ring soliton molecule can be observed in Figure 7. It can be easily seen from Figure 7 that the two ring solitons in the ring molecule are asymmetric. As time evolves, according to the general interaction time formula, the single ring soliton collides with the first ring soliton and the second ring soliton in the ring molecule at $t={\displaystyle \frac{35}{4}}$ and $t={\displaystyle \frac{5}{2}}$, respectively. Figure 7 also graphically shows that the shapes and velocities of the ring solitons remain constant after the interaction. Clearly, this demonstrates the elastic interactions.

3.4. Ring Solitons, Lumps, Dromions, and Their Interactions

3.4.1. The Interactions Between Ring Molecules and Special Oscillating Lumps

An oscillating lump is a localized structure that moves in a nonlinear system, with its shape oscillating or changing over time [45]. Assume the functions p and q as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}& p=\exp \left[\sum _{i=1}^N{\omega }_i-{(k_{i}x+v_{i}t+b_i)}^2\right]+{\displaystyle \frac{d}{1+{\left[(x-ct)(\cos (x-ct)+h)\right]}^2}},\hfill \\ & q=\sum _{j=1}^M\cosh \left[{\Omega }_j+{(K_{j}x+V_{j}z+B_j+s)}^2)\right]+{\displaystyle \frac{1}{y^2+1}},\hfill \end{array}\end{array}$$

(13)

where the variables ${\omega }_i,k_i,v_i,b_i,{\Omega }_j,B_j,K_j,V_j,c,d$, and h are arbitrary constants. For ease of graphical observation, we set $N=2,M=1$, and $u_1=0$. Setting the parameters as ${\omega }_1={\omega }_2=15,k_1={\displaystyle \frac{2}{5}},k_2={\displaystyle \frac{1}{2}},v_1=-{\displaystyle \frac{2}{5}},v_2=-{\displaystyle \frac{1}{2}},b_1=8,b_2=-5,d=900,{\Omega }_1=1$, $K_1=1$, $V_1=1,B_1=5,c=1,h={\displaystyle \frac{5}{4}},z=s=0$, and $\{a_0,a_1,a_2,a_3\}=\{2,1,1,0\}$, we can obtain the dynamical behavior of the interaction between a ring molecule and special oscillating lumps, as shown in Figure 8 and Figure 9. As depicted in the figures, the ring soliton molecule is composed of two symmetric ring solitons that moves in the positive direction along the x-axis while maintaining the shape and velocity. At the same time, the oscillating lumps also propagate along the x-axis. During the movement, the shapes of the oscillating lumps show periodic oscillations.

3.4.2. The Interaction Between Lump and Dromion Molecules

In this section, we set p and q to

$$\begin{array}{c}\hfill \begin{array}{cc}& p=\exp \left[\sum _{i=1}^N{b}_i\tanh (k_i(v_{i}t+x)+{\omega }_i)\right]+\sum _{i=1}^M{\displaystyle \frac{h_i^{\prime }}{{\omega }_i^{\prime }+{\left[k_i^{\prime }x+t{v}_i^{\prime }+b_i^{\prime }\right]}^2}},\hfill \\ & q=\exp \left[\sum _{j=1}^N{C}_j\tanh (K_j(V_{j}t-y+z+s)+{\Omega }_j)\right]+\sum _{j=1}^M{\displaystyle \frac{H_j^{\prime }}{{\Omega }_j^{\prime }+{\left[K_j^{\prime }y+B_j^{\prime }\right]}^2+L_j^{\prime }z+s}},\hfill \end{array}\end{array}$$

(14)

where the variables $b_i,k_i,v_i,{\omega }_i,C_j,K_j,V_j,{\Omega }_j,h_i^{\prime },{\omega }_i^{\prime },k_i^{\prime },b_i^{\prime },H_i^{\prime },{\Omega }_j^{\prime },B_j^{\prime },K_j^{\prime },$ and $L_j^{\prime }$ are arbitrary constants. We set $N=2$, $M=1$, and $u_1=0$ and the parameters as $b_1=b_2=2,k_1=k_2=1$, $v_1=v_2=-1$, ${\omega }_1=-10,{\omega }_2=-20,C_1=C_2=1,K_1=K_2=2,V_1=V_2=0$, ${\Omega }_1=0$, ${\Omega }_2=-5,h_1^{\prime }=3,{\omega }_1^{\prime }=2,k_1^{\prime }={\displaystyle \frac{2}{3}},b_1^{\prime }=5,H_1^{\prime }=5,{\Omega }_1^{\prime }=1,B_1^{\prime }=8,K_1^{\prime }=2,L_1^{\prime }=1,$ and $z=s=0$. For the sake of observation, we select $\{a_0,a_1,a_2,a_3\}$ as $\{2,1,1,4\}$. Figure 10 adn Figure 11 show the interaction between the lump and the $2\times 2$ dromion molecules. Here, the dromion molecules consist of two rows and two columns of dromions. As seen in the figures, they collide around at $t=-12$. After the collision, the lump and dromion molecules fuse their energy. As can be seen from the contour plot, the lump gradually dissipates. Thus, their interactions are clearly inelastic.

4. Conclusions

In summary, the study of the BLMP equation contributes to a better understanding of wave phenomena in nonlinear systems and provides theoretical support for practical applications. In this paper, we use the MLVSA to construct new variable separation solutions for the (4+1)-dimensional BLMP Equation (1). The result is that various local excitations of the BLMP equation can be obtained by constructing arbitrary functions. Then, three different choices of arbitrary variable separation functions p and q are made to describe different solutions, including dromions, lumps, and ring solitons. As can be seen from the figures, the three types of local excitations are distinctly different in shapes and symmetries. According to the velocity resonance mechanism, the soliton molecules and their interactions are obtained through the modulation of soliton velocities. In analyzing the diagram, it is known that the interactions of these localized excitations are elastic. The elastic interactions demonstrate soliton stability and shape preservation. Additionally, this work demonstrates that the interactions between a ring soliton molecule and special oscillating lumps are elastic. The interaction behavior between dromion molecules and a lump is inelastic.

The above results amply reveal that the variable separation functions p and q, as well as the choice of parameters, have a profound effect on the class of localized excitations and the propagation properties of solitons. This work discusses the local excitations of the (4+1)-dimensional BLMP equation. We analyze the interactions between a ring molecule and special oscillating lumps, which were not mentioned in previous work. Further research on the dynamics of the nonlocal form of the (4+1)-dimensional BLMP equation will be carried out in future work [35]. Since soliton structures can be diverse, there are many questions that deserve further study. We can observe soliton molecules with a number of methods; we still lack understanding of the physical mechanism of soliton molecule production. And more soliton molecules with other wave structures need in-depth study.