Implications of Asymptomatic Carriers for Tuberculosis Transmission and Control in Thailand: A Modelling Approach
Abstract
1. Introduction
2. Methods and Materials
3. System Properties
3.1. Existence of Equilibria
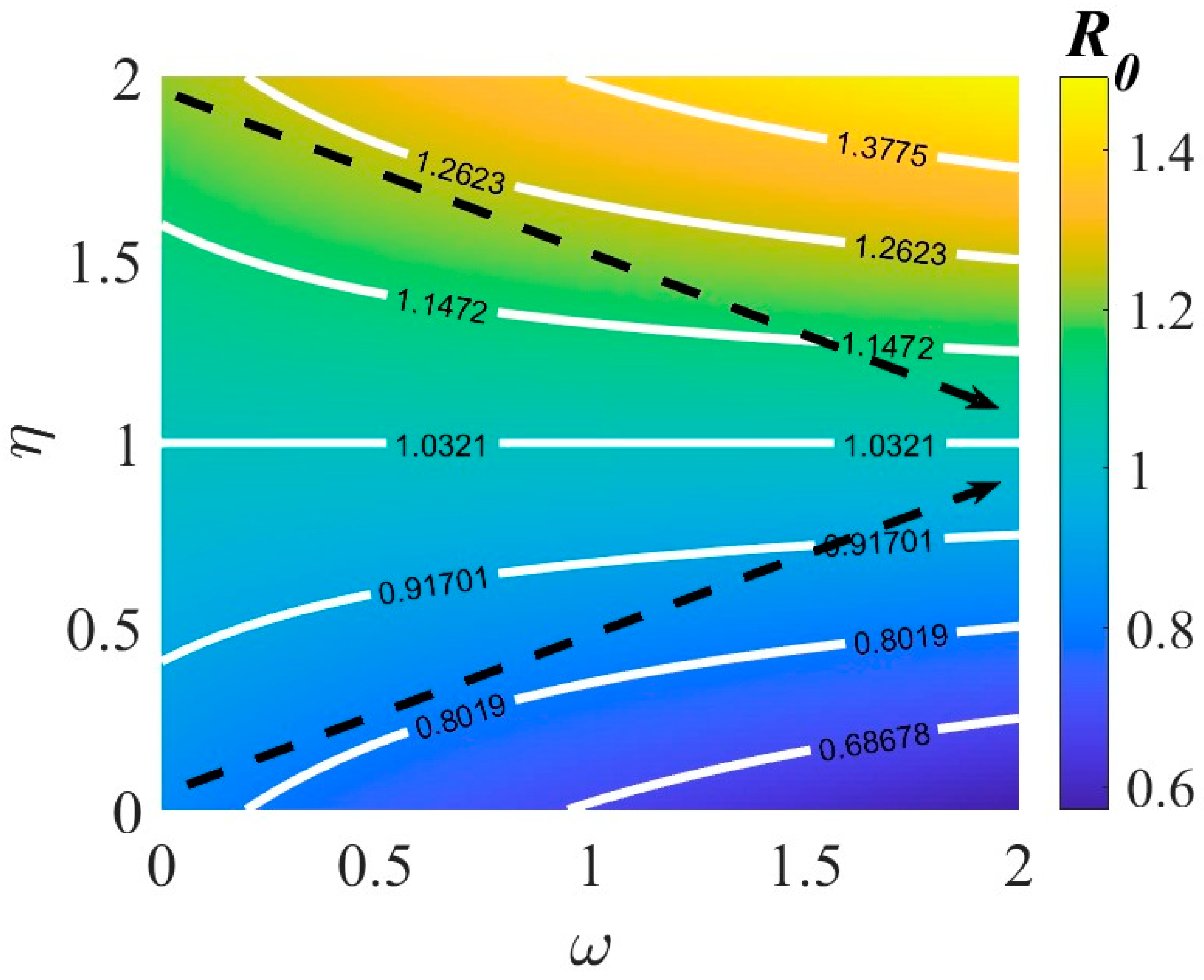
3.2. Basic Reproduction Number
3.3. Parameters Estimation
4. Results
4.1. Calculating Asymptomatic Carries and Symptomatic Infection
- where ,
- ,
- , and
- .
4.2. Asymptomatic Carriers Are Essential to the Spread of TB Transmission
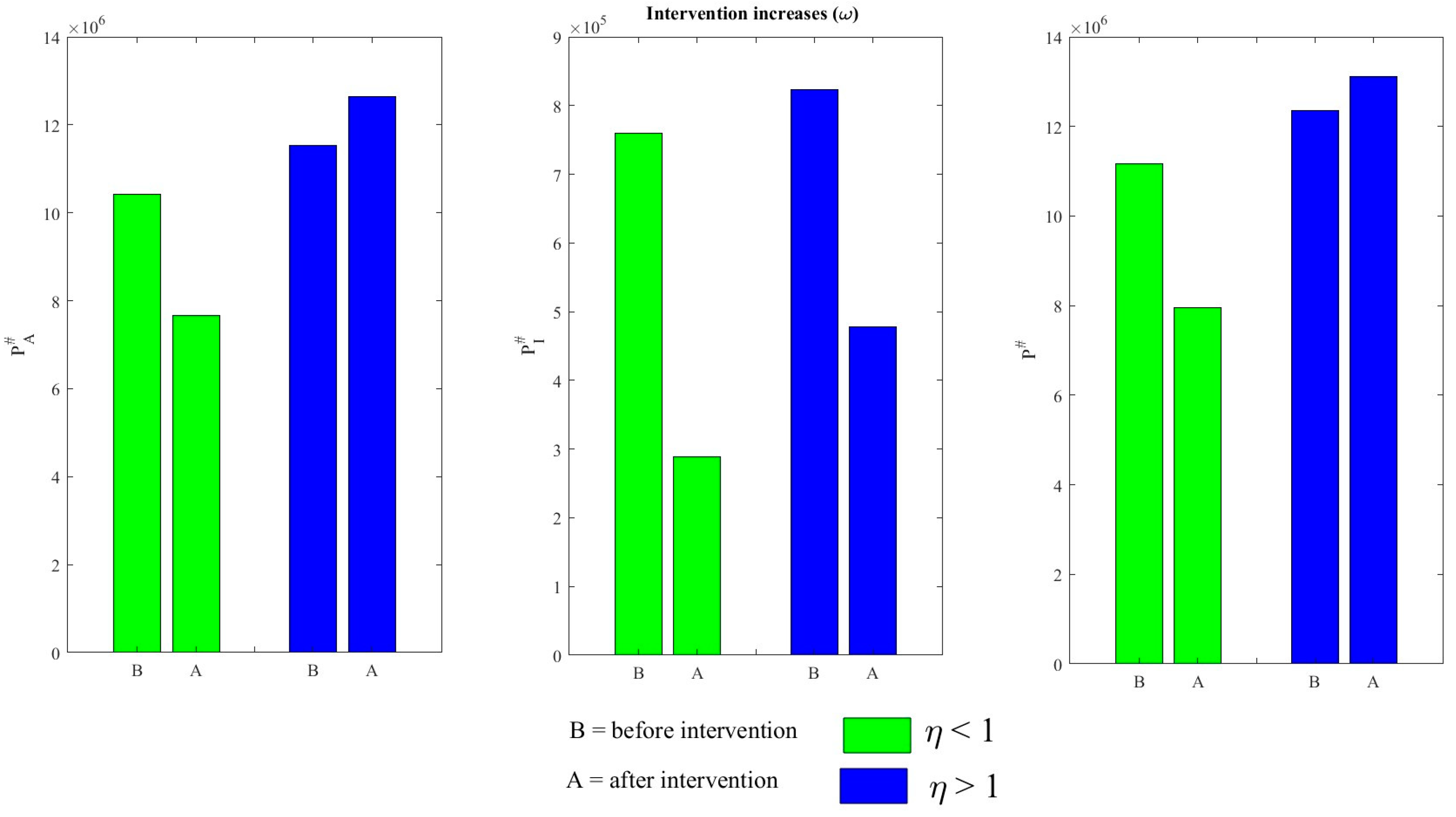
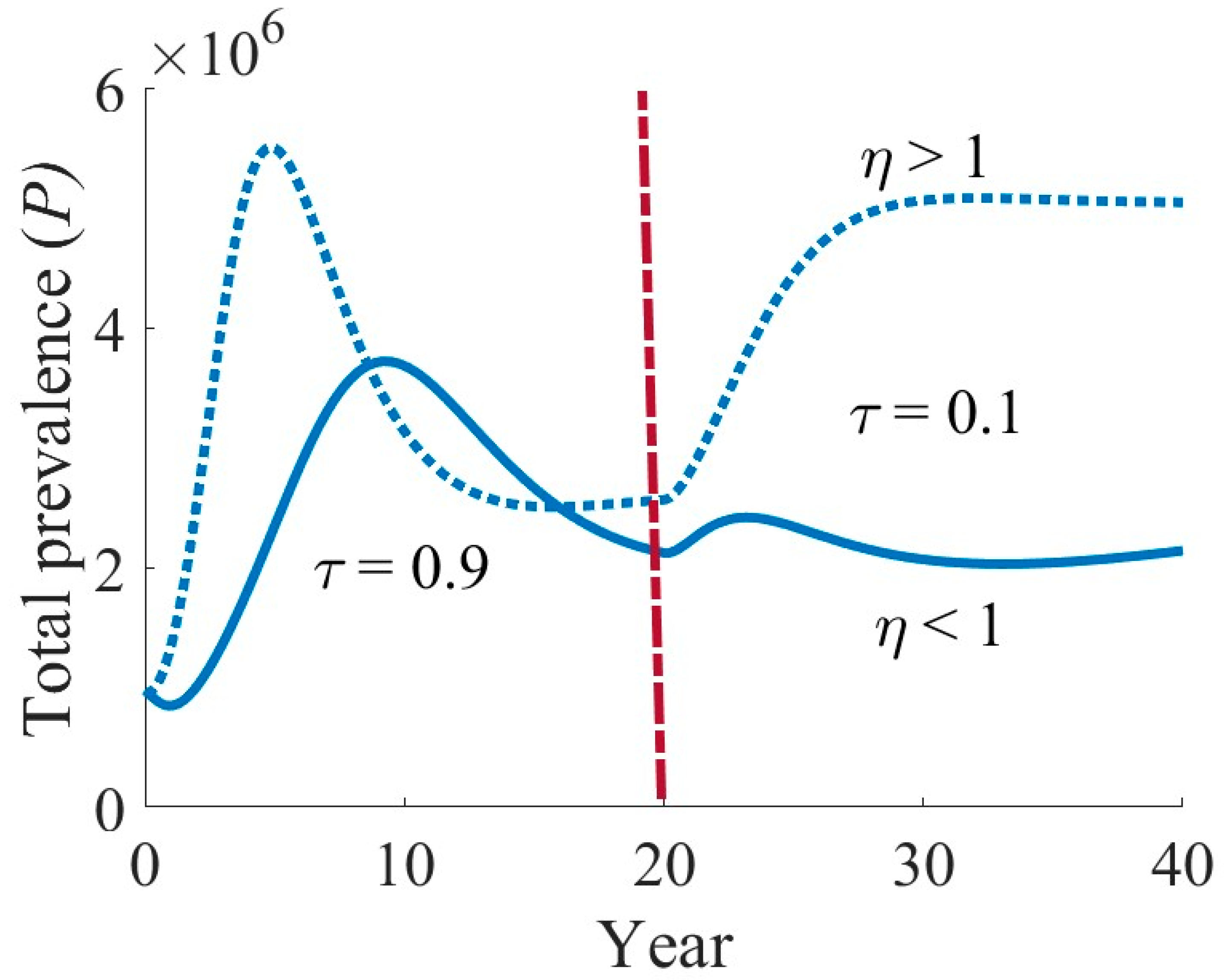
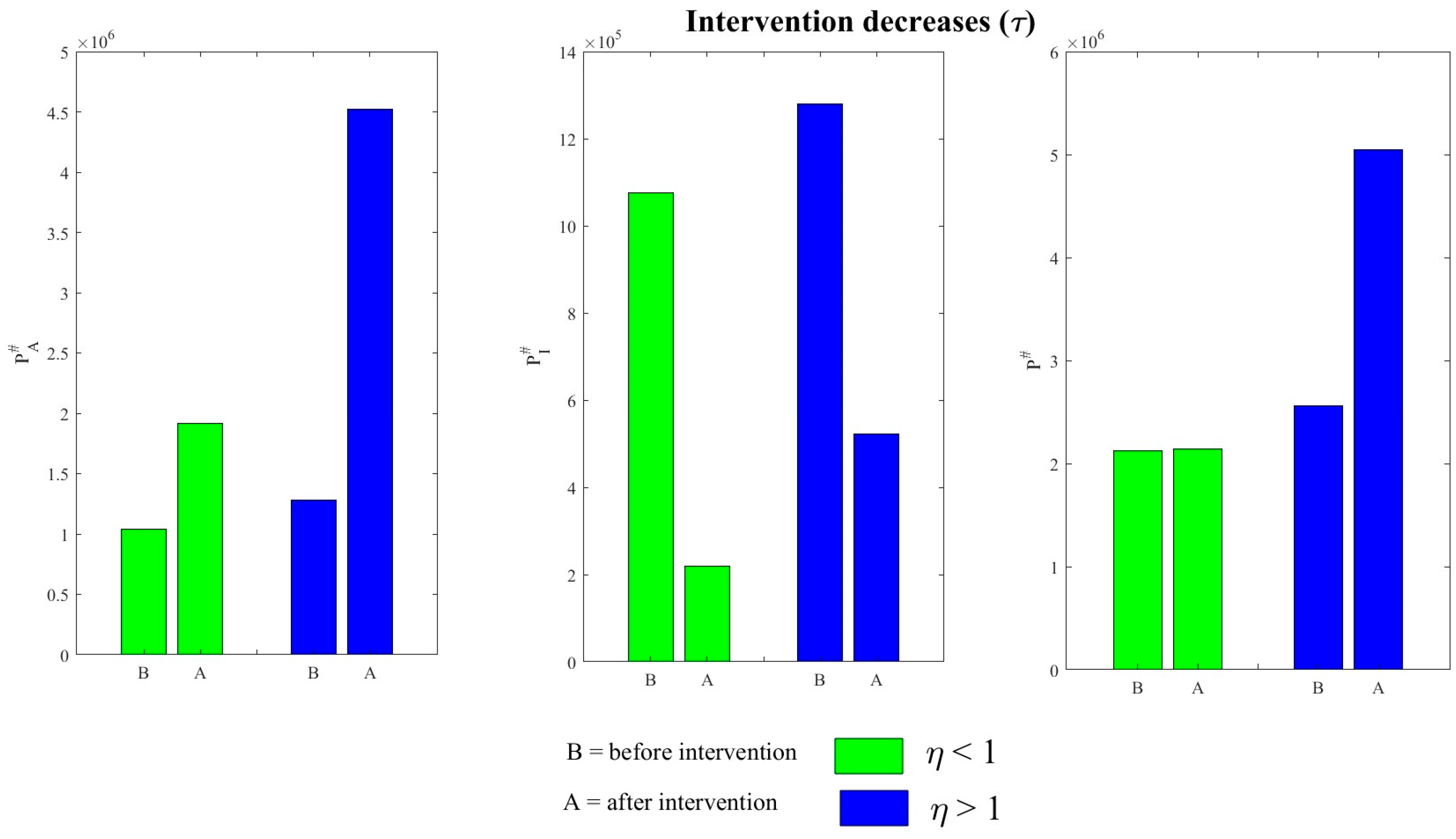
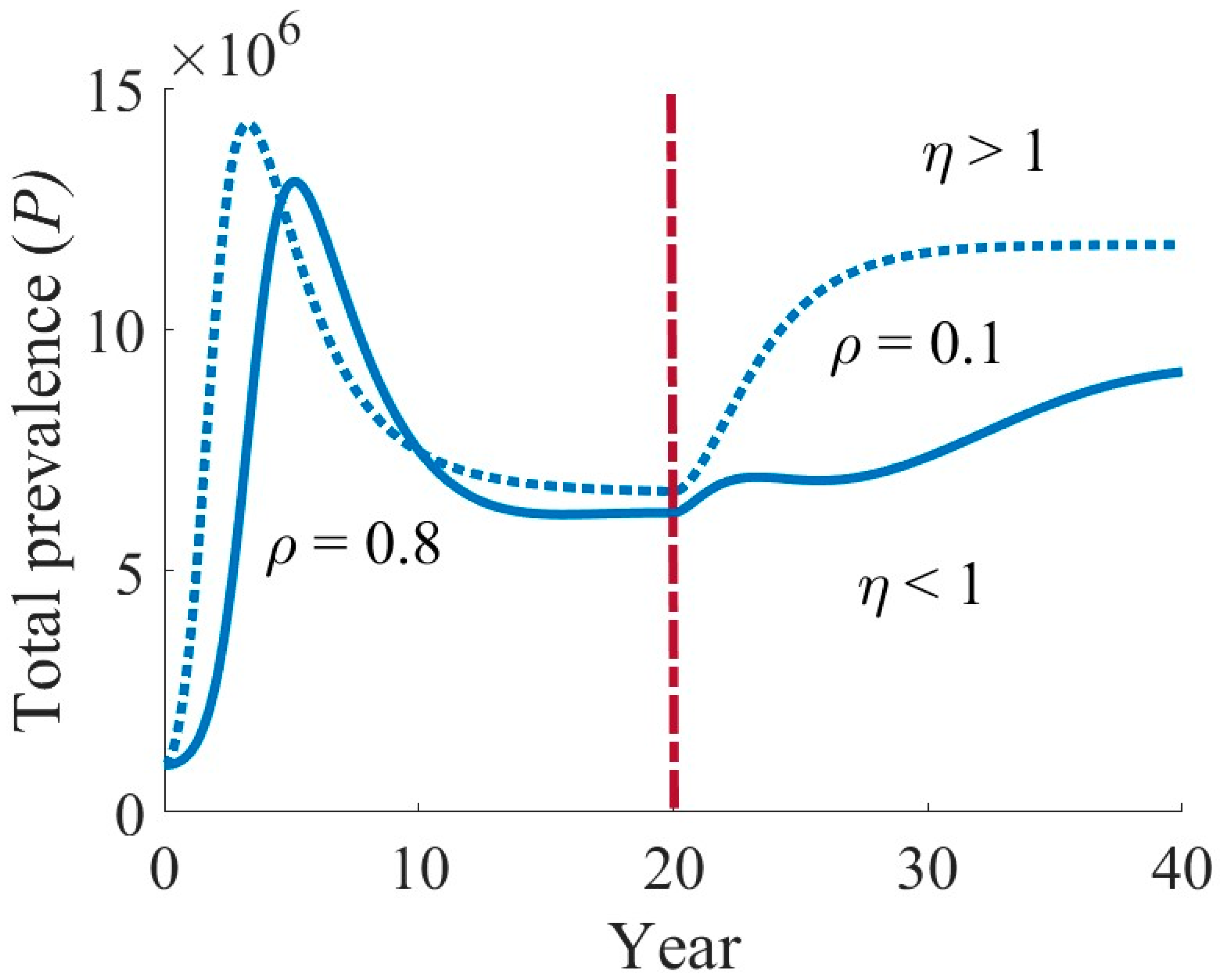
4.3. Effects of Various Interventions on TB Dynamics
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Floyd, K.; Raviglione, M.C.; Glaziou, P. Global epidemiology of tuberculosis. Semin. Respir. Crit. Care Med. 2018, 39, 271–285. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Global Tuberculosis Report; WHO: Geneva, Switzerland, 2020. [Google Scholar]
- Antonucci, G.; Girardi, E.; Raviglione, M.C.; Ippolito, G. Risk factors for tuberculosis in HIV-infected persons. A prospective cohort studies. The Gruppo Italiano di Studio Tubercolosi e AIDS (GISTA). JAMA 1995, 274, 143–148. [Google Scholar] [CrossRef] [PubMed]
- Cowie, R.L. The epidemiology of tuberculosis in gold miners with silicosis. Am. J. Respir. Crit. Care Med. 1994, 150, 1460–1462. [Google Scholar] [CrossRef]
- Rieder, H.L.; Cauthen, G.M.; Comstock, G.W.; Snider, D.E. Epidemiology of tuberculosis in the United States. Epidemiologic Rev. 1989, 11, 79–98. [Google Scholar] [CrossRef]
- Narasimhan, P.; Wood, J.; Macintyre, C.R.; Mathai, D. Risk factors for tuberculosis. Pulm. Med. 2013, 2013, 828939. [Google Scholar] [CrossRef]
- Lenaerts, A.; Barry, C.E.; Dartois, V. Heterogeneity in tuberculosis pathology, microenvironments and therapeutic responses. Immunol. Rev. 2015, 264, 288–307. [Google Scholar] [CrossRef]
- Drain, P.K.; Bajema, K.L.; Dowdy, D.; Dheda, K.; Naidoo, K.; Schumacher, S.G.; Ma, S.; Meermeier, E.; Lewinsohn, D.M.; Sherman, D.R. Incipient and Subclinical Tuberculosis: A Clinical Review of Early Stages and Progression of Infection. Clin. Microbiol. Rev. 2018, 31, e00021-18. [Google Scholar] [CrossRef]
- Bajema, K.L.; Bassett, I.V.; Coleman, S.M.; Ross, D.; Freedberg, K.A.; Wald, A.; Drain, P.K. Subclinical tuberculosis among adults with HIV: Clinical features and outcomes in a South African cohort. BMC Infect. Dis. 2019, 19, 14. [Google Scholar] [CrossRef]
- Kendall, E.A.; Shrestha, S.; Dowdy, D.W. The epidemiological importance of subclinical tuberculosis. A critical reappraisal. Am. J. Respir. Crit. Care Med. 2021, 203, 168–174. [Google Scholar] [CrossRef]
- Xu, Y.; Cancino-Muñoz, I.; Torres-Puente, M.; Villamayor, L.M.; Borrás, R.; Borrás-Máñez, M.; Bosque, M.; Camarena, J.J.; Colomer-Roig, E.; Colomina, J.; et al. High-resolution mapping of tuberculosis transmission: Whole genome sequencing and phylogenetic modelling of a cohort from Valencia Region, Spain. PLOS Med. 2019, 16, e1002961. [Google Scholar] [CrossRef]
- Global Tuberculosis Report 2019: World Health Organization. Available online: https://www.who.int/publications/i/item/global-tuberculosis-report-2019 (accessed on 3 June 2021).
- Pichanon, M.; Leilani, P.; Kamon, K.; Pirapon, J.O.; Gompol, S. Tuberculosis at a university hospital, Thailand: A surprising incidence of TB among a new generation of highly exposed health care workers who may be asymptomatic. PLoS ONE 2022, 17, e0273027. [Google Scholar]
- Joshi, R.; Reingold, A.L.; Menzies, D.; Pai, M. Tuberculosis among health-care workers in low- and middle-income countries: A sys-tematic review. PLoS Med. 2006, 3, e494. [Google Scholar] [CrossRef] [PubMed]
- Baussano, I.; Nunn, P.; Williams, B.; Pivetta, E.; Bugiani, M.; Scano, F. Tuberculosis among health care workers. Emerg. Infect. Dis. 2011, 17, 488–494. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, H.; Ruan, Y.; Chin, D.P.; Xia, Y.; Cheng, S.; Chen, M.; Zhao, Y.; Jiang, S.; Du, X.; et al. Tuberculosis prevalence in China, 1990–2010; a longitudinal analysis of national survey data. Lancet 2014, 383, 2057–2064. [Google Scholar] [CrossRef]
- Blaser, N.; Zahnd, C.; Hermans, S.; Salazar-Vizcaya, L.; Estill, J.; Morrow, C.; Egger, M.; Keiser, O.; Wood, R. Tuberculosis in Cape Town: An age-structured transmission model. Epidemics 2016, 14, 54–61. [Google Scholar] [CrossRef]
- Bhunu, C.P.; Garira, W.; Mukandavire, Z.; Zimba, M. Tuberculosis transmission model with chemoprophylaxis and treatment. Bull. Math. Biol. 2008, 70, 1163–1191. [Google Scholar] [CrossRef]
- Songkram, S. Samakhom Prab Wannarok Hang Prathetthai Nai Phra Borom Rachupatham [The Anti-Tuberculosis Association of Thailand Under the Royal Patronage of His Majesty the King], 5th ed.; Banyat, P., Chaivej, N., Songkram, S., Eds.; Wannarok. Anti-Tuberculosis Association of Thailand: Bangkok, Thailand, 2003; pp. 26–30. [Google Scholar]
- World Health Organization. TB: A Global Emergency; World Health Organization: Geneva, Switzerland, 1994. [Google Scholar]
- Inchai, J.; Liwsrisakun, C.; Bumroongkit, C.; Euathrongchit, J.; Tajarernmuang, P.; Pothirat, C. Tuberculosis among Healthcare Workers at Chiang Mai University Hospital, Thailand: Clinical and Microbiological Characteristics and Treatment Outcomes. Jpn. J. Infect. Dis. 2018, 71, 214–219. [Google Scholar] [CrossRef]
- Jiamjarasrangsi, W.; Hirunsuthikul, N.; Kamolratanakul, P. Tuberculosis among health care workers at King Chulalongkorn Memorial Hospital, 1988–2002. Int. J. Tuberc Lung Dis. 2005, 9, 1253–1258. [Google Scholar]
- Pongwittayapanu, P.; Anothaisintawee, T.; Malathum, K.; Wongrathanandha, C. Incidence of Newly Diagnosed Tuberculosis among Healthcare Workers in a Teaching Hospital, Thailand. Ann. Glob. Health 2018, 84, 342–347. [Google Scholar] [CrossRef]
- Department of Disease Control. Panyutthasat Wannarok Radabchat Por. Sor. 2560–2564 [National Strategic Plan on Tuberculosis B.E. 2560–2564]; Department of Disease Control, Ministry of Public Health: Bangkok, Thailand, 2017. [Google Scholar]
- Blower, S.M.; Small, P.M.; Hopewell, P.C. Control strategies for tuberculosis epidemics: New models for old problems. Science 1996, 273, 497–500. [Google Scholar] [CrossRef]
- Fatmawati; Tasman, H. An optimal treatment control of TB-HIV coinfection. Int. J. Math. Math. Sci. 2016, 2016, 8261208. [Google Scholar] [CrossRef]
- Hickson, R.I.; Mercer, G.N.; Lokuge, K.M. A metapopulation model of tuberculosis transmission with a case study from high to low burden areas. PLoS ONE 2012, 7, e34411. [Google Scholar] [CrossRef]
- Houben, R.M.G.J.; Sumner, T.; Grant, A.D.; White, R.G. Ability of preventive therapy to cure latent Mycobacterium tuberculosis infection in HIV-infected individuals in high-burden settings. Proc. Natl. Acad. Sci. USA 2014, 111, 5325–5330. [Google Scholar] [CrossRef]
- Kaplan, R.; Caldwell, J.; Middelkoop, K.; Bekker, L.G.; Wood, R. Impact of ART on TB case fatality stratified by CD4 count for HIV-positive TB patients in Cape Town, South Africa (2009–2011). JAIDS J. Acquir. Immune Defic. Syndr. 2014, 66, 487–494. [Google Scholar] [CrossRef]
- Purwati, U.D.; Riyudha, F.; Tasman, H. Optimal control of a discrete age-structured model for tuberculosis transmission. Heliyon 2020, 6, e03030. [Google Scholar] [CrossRef]
- Childs, L.M.; Abuelezam, N.N.; Dye, C.; Gupta, S.; Murray, M.B.; Williams, B.G.; Buckee, C.O. Modelling challenges in context: Lessons from malaria, HIV, and tuberculosis. Epidemics 2015, 10, 102–107. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.A.P.; Roberts, M.G. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 2009, 7, 873–885. [Google Scholar] [CrossRef]
- van den Driessche, P. Reproduction numbers of infectious disease models. Infect. Dis. Model. 2017, 2, 288–303. [Google Scholar] [CrossRef]
- Shuai, Z.; van den Driessche, P. Global Stability of Infectious Disease Models Using Lyapunov Functions. SIAM J. Appl. Math. 2013, 73, 1513–1532. [Google Scholar] [CrossRef]
- Data Commons. Place Explorer Thailand. Available online: https://datacommons.org/place/country/THA/?utm_medium=explore&mprop=lifeExpectancy&popt=Person&hl=en (accessed on 23 December 2023).
- Chisholm, R.H.; Campbell, P.T.; Wu, Y.; Tong, S.Y.C.; McVernon, J.; Geard, N. Implications of asymptomatic carriers for infectious disease transmission and control. R. Soc. Open Sci. 2018, 5, 172341. [Google Scholar] [CrossRef]
- Shaweno, D.; Trauer, J.M.; Denholm, J.T.; McBryde, E.S. The role of geospatial hotspots in the spatial spread of tuberculosis in rural Ethiopia: A mathematical model. R. Soc. Open Sci. 2018, 5, 180887. [Google Scholar] [CrossRef] [PubMed]
- Kuddus, A.; Meehan, M.T.; White, L.J.; McBryde, E.S.; Adekunle, A.I. Modeling drug-resistant tuberculosis amplification rates and intervention strategies in Bangladesh. PLoS ONE 2020, 15, e0236112. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Global Tuberculosis Programme. Available online: https://www.who.int/teams/global-tuberculosis-programme/tb-reports (accessed on 10 June 2023).
- Furuya-Kanamori, L.; Cox, M.; Milinovich, G.J.; Magalhaes, R.J.S.; Mackay, I.M.; Yakob, L. Heterogeneous and dynamic prevalence of asymptomatic influenza virus infections. Emerg. Infect. Dis. 2016, 22, 1052–1056. [Google Scholar] [CrossRef] [PubMed]
- DeMuri, G.P.; Wald, E.R. The group A streptococcal carrier state reviewed: Still an enigma. J. Pediatr. Infect. Dis. Soc. 2014, 3, 336–342. [Google Scholar] [CrossRef] [PubMed]
- Gerding, D.N.; Muto, C.A.; Owens, R.C., Jr. Measures to control and prevent Clostridium difficile infection. Clin. Infect. Dis. 2008, 46, S43–S49. [Google Scholar] [CrossRef]
- Robinson, M.; Stilianakis, N.I. A model for the emergence of drug resistance in the presence of asymptomatic infections. Math. Biosci. 2013, 243, 163–177. [Google Scholar] [CrossRef]
- Wang, X.; Panchanathan, S.; Chowell, G. A Data-driven mathematical model of ca-mrsa transmission among age groups: Evaluating the effect of control interventions. PLoS Comput. Biol. 2013, 9, e1003328. [Google Scholar] [CrossRef]









| Parameters | Description | Values | References |
|---|---|---|---|
| Populations in Thailand, 2021 | 72,000,000 | [35] | |
| Birth/mortality rate | [35] | ||
| Transmission rate | Fitted | ||
| The pace of advancement toward the asymptomatic carriage | 0.1 | [36] | |
| Rate of progression to symptomatic infection | [36] | ||
| Percentage of newly reported cases with symptoms | 0.02 | [36] | |
| Rate of progression | 0.36 | Fitting | |
| The rate at which latency is recovered | 0.3 | [36] | |
| The rate at which asymptomatic carriage recovers | 0.2 | [37] | |
| The recovery rate from symptomatic infection | 0.205 | [37] | |
| Relative infectious of carriers compared to symptomatically infected hosts | 0.0018 | Fitted | |
| Treatment rate of symptomatic infection | 0.60 | Fitted | |
| Rate of loss of immunity | 0.1 | [38] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuddus, M.A.; Tithi, S.K.; Theparod, T. Implications of Asymptomatic Carriers for Tuberculosis Transmission and Control in Thailand: A Modelling Approach. Symmetry 2024, 16, 1538. https://doi.org/10.3390/sym16111538
Kuddus MA, Tithi SK, Theparod T. Implications of Asymptomatic Carriers for Tuberculosis Transmission and Control in Thailand: A Modelling Approach. Symmetry. 2024; 16(11):1538. https://doi.org/10.3390/sym16111538
Chicago/Turabian StyleKuddus, Md Abdul, Sazia Khatun Tithi, and Thitiya Theparod. 2024. "Implications of Asymptomatic Carriers for Tuberculosis Transmission and Control in Thailand: A Modelling Approach" Symmetry 16, no. 11: 1538. https://doi.org/10.3390/sym16111538
APA StyleKuddus, M. A., Tithi, S. K., & Theparod, T. (2024). Implications of Asymptomatic Carriers for Tuberculosis Transmission and Control in Thailand: A Modelling Approach. Symmetry, 16(11), 1538. https://doi.org/10.3390/sym16111538







