A General Mollification Regularization Method to Solve a Cauchy Problem for the Multi-Dimensional Modified Helmholtz Equation
Abstract
:1. Introduction
2. Ill-Posedness Analysis of the Cauchy Problem
3. General Framework of the Convolution Kernel Function
- (1)
- ;
- (2)
- , where is a constant;
- (3)
- , where is a constant.
4. Parameter Choice Strategies and Error Estimations
- (1)
- ;
- (2)
- ;
- (3)
- ;
- (4)
- ;
- (5)
- .
4.1. A priori Parameter Choice Strategies and Error Estimations
4.2. A posteriori Parameter Choice Strategies and Error Estimations
- (a)
- and are continuous functions;
- (b)
- ;
- (c)
- and ;
- (d)
- and are strictly increasing functions.
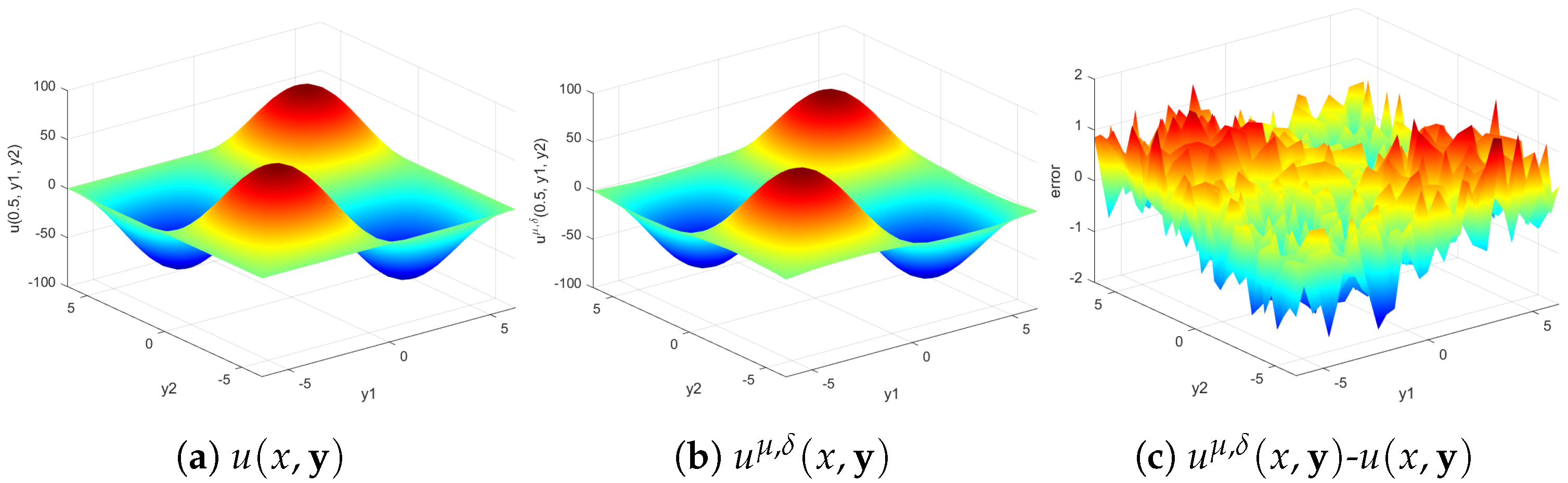
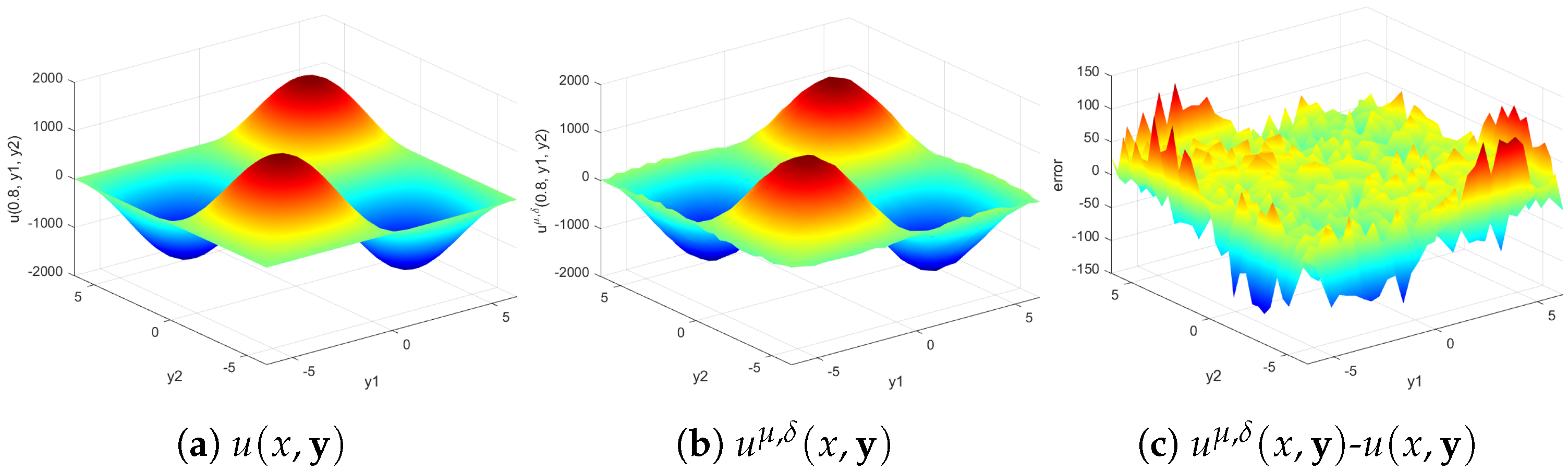
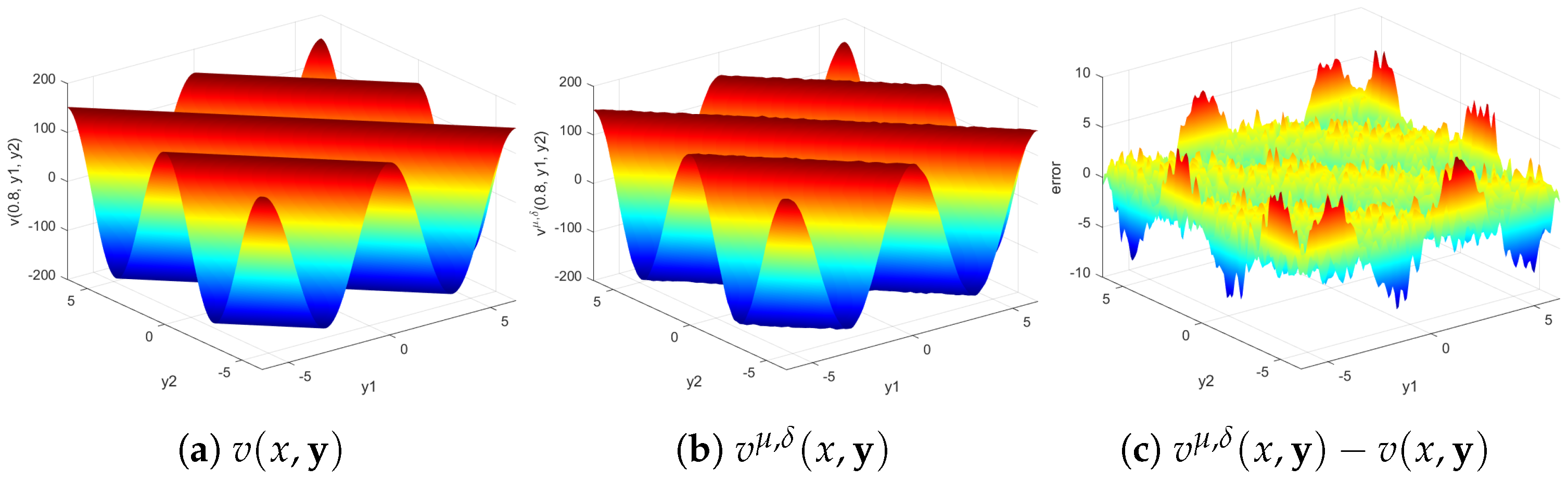
5. Numerical Experiments
- (1)
- The regularization solution is stable for both the a priori and a posteriori parameter choice strategy;
- (2)
- The results of the regularization solution are still well for high wave number k;
- (3)
- The results of the a posteriori choice strategy are better than those of the a priori choice strategy;
- (4)
- The Gaussian kernel function has a slight advantage over the other two kernel functions.
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nguyen, H.T.; Tran, Q.V.; Nguyen, V.T. Some remarks on a modified Helmholtz equation with inhomogeneous source. Appl. Math. Model. 2013, 37, 793–814. [Google Scholar] [CrossRef]
- Cheng, H.W.; Huang, J.F.; Leiterman, T.J. An adaptive fast solver for the modified Helmholtz equation in two dimensions. J. Comput. Phys. 2006, 211, 616–637. [Google Scholar] [CrossRef]
- Manoussakis, G. A new modified Helmholtz equation for the expression of the gravity gradient and the intensity of an electrostatic field in spherical harmonics. Mathematics 2023, 11, 4326. [Google Scholar] [CrossRef]
- Reginska, T.; Reginski, K. Approximate solution of a Cauchy problem for the Helmholtz equation. Inverse Probl. 2006, 22, 975–989. [Google Scholar] [CrossRef]
- Xiong, X.T.; Shi, W.X.; Fan, X.Y. Two numerical methods for a Cauchy problem for modified Helmholtz equation. Appl. Math. Model. 2011, 35, 4951–4964. [Google Scholar] [CrossRef]
- Marin, L.; Elliott, L.; Heggs, P.J.; Ingham, D.B.; Lesnic, D.; Wen, X. Conjugate gradient-boundary element solution to the Cauchy problem for Helmholtz-type equations. Comput. Mech. 2003, 31, 367–377. [Google Scholar] [CrossRef]
- Qin, H.H.; Wei, T. Quasi-reversibility and truncation methods to solve a Cauchy problem of the modified Helmholtz equation. Math. Comput. Simulat. 2009, 80, 352–366. [Google Scholar] [CrossRef]
- Cheng, H.; Zhu, P.; Gao, J. A regularization method for the cauchy problem of the modified Helmholtz equation. Math. Meth. Appl. Sci. 2015, 38, 3711–3719. [Google Scholar] [CrossRef]
- Chen, Y.G.; Yang, F.; Ding, Q. The Landweber iterative regularization method for solving the Cauchy problem of the modified Helmholtz equation. Symmetry 2022, 14, 1209. [Google Scholar] [CrossRef]
- Fu, C.L.; Feng, X.L.; Qian, Z. The Fourier regularization for solving the Cauchy problem for the Helmholtz equation. Appl. Numer. Math. 2009, 59, 2625–2640. [Google Scholar] [CrossRef]
- He, S.Q.; Feng, X.F. A regularization method to solve a Cauchy problem for the two-dimensional modified Helmholtz equation. Mathematics 2019, 7, 360. [Google Scholar] [CrossRef]
- Jday, F.; Omri, H. Adaptive Runge-Kutta regularization for a Cauchy problem of a modified Helmholtz equation. J. Inverse Ill-Posed Probl. 2023, 31, 351–374. [Google Scholar] [CrossRef]
- Hao, D.N. A mollification method for ill-posed problems. Numer. Math. 1994, 68, 469–506. [Google Scholar]
- Murio, D.A. The Mollification Method and the Numerical Solution of Ill-Posed Problems; Wiley-Interscience Publication: New York, NY, USA, 1993. [Google Scholar]
- Basu, M. Gaussian-based edge-detection methods—A survey. IEEE Trans Syst. Man Cybern. C 2002, 32, 252–260. [Google Scholar] [CrossRef]
- Yang, F.; Fu, C.L. A mollification regularization method for the inverse spatial-dependent heat source problem. J. Comput. Appl. Math. 2014, 255, 555–567. [Google Scholar] [CrossRef]
- He, S.Q.; Feng, X.F. A mollification regularization method with the Dirichlet Kernel for two Cauchy problems of three-dimensional Helmholtz equation. Int. J. Comput. Math. 2020, 97, 2320–2336. [Google Scholar] [CrossRef]
- Fu, C.L.; Ma, Y.J.; Zhang, Y.X.; Yang, F. A a posteriori regularization for the Cauchy problem for the Helmholtz equation with inhomogeneous Neumann data. Appl. Math. Model. 2015, 39, 4103–4120. [Google Scholar] [CrossRef]
- He, S.Q.; Di, C.N.; Yang, L. The mollification method based on a modified operator to the ill-posed problem for 3D Helmholtz equation with mixed boundary. Appl. Numer. Math. 2021, 160, 422–435. [Google Scholar] [CrossRef]
- Li, Z.P.; Xu, C.; Lan, M.; Qian, Z. A mollification method for a Cauchy problem for the Helmholtz equation. Int. J. Comput. Math. 2018, 95, 2256–2268. [Google Scholar] [CrossRef]
- Kirsch, A. An Introduction to the Mathematical Theory of Inverse Problems, 2nd ed.; Springer: New York, NY, USA, 2011. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Wang, B.; Zhou, D. A General Mollification Regularization Method to Solve a Cauchy Problem for the Multi-Dimensional Modified Helmholtz Equation. Symmetry 2024, 16, 1549. https://doi.org/10.3390/sym16111549
Xu H, Wang B, Zhou D. A General Mollification Regularization Method to Solve a Cauchy Problem for the Multi-Dimensional Modified Helmholtz Equation. Symmetry. 2024; 16(11):1549. https://doi.org/10.3390/sym16111549
Chicago/Turabian StyleXu, Huilin, Baoxia Wang, and Duanmei Zhou. 2024. "A General Mollification Regularization Method to Solve a Cauchy Problem for the Multi-Dimensional Modified Helmholtz Equation" Symmetry 16, no. 11: 1549. https://doi.org/10.3390/sym16111549
APA StyleXu, H., Wang, B., & Zhou, D. (2024). A General Mollification Regularization Method to Solve a Cauchy Problem for the Multi-Dimensional Modified Helmholtz Equation. Symmetry, 16(11), 1549. https://doi.org/10.3390/sym16111549






