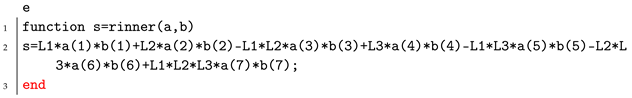On Matrices of Generalized Octonions (Cayley Numbers)
Abstract
1. Introduction
- When , this condition yields the real octonions [5].
- When , this condition yields the split octonions [6].
- When , this condition yields the semi octonions [7].
- When , this condition yields the split semi octonions [8].
- When , this condition yields the quasi octonions [9].
- When , this condition yields the split quasi octonions [10].
- When , this condition yields the para octonions [11].
2. The Inner Product Space
3. Some Properties of Generalized Octonion
- When , the Generalized Octonion c is said to have a spacelike vector part.
- When , the Generalized Octonion c is said to have a timelike vector part.
- When , the Generalized Octonion c is said to have a lightlike vector part.
4. De Moivre’s Formulas of Generalized Octonion
5. Roots of Generalized Octonion
6. An Application
- The product of and isand by taking we get
- The inner product of and is and by taking we get
- The norm of is and the norm of is By taking we get
- The inverse of does not exist and the inverse of isBy taking we get
- The inner product of the vector parts of is and by taking we get
- The vector product of the vector parts of is and by taking we get
- The right representation of the Generalized Octonion isand by taking we get
- The left representation of the Generalized Octonion isand by taking we get
- and By taking the inner product so is a lightlike Generalized Octonion. Thus, where Note that On the other hand, the inner product so is a spacelike Generalized Octonion. Also, so is a Generalized Octonion with spacelike vector part. Thus, where
- The 9th power of is . The right representation of is acquired from Theorem 12 case (iii) as follows:Then, the 9th power of is
- The 3-roots of the equation are follows:
7. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| The set of the Cayley numbers | |
| 3PGO | 3-parameter generalized octonions |
| Real part of the Generalized Octonion | |
| Vector part of the Generalized Octonion | |
| The conjugate of the Generalized Octonion | |
| The norm of the Generalized Octonion | |
| The inverse of the Generalized Octonion | |
| Inner product of 7-tuples vectors | |
| Vector product of 7-tuples vectors | |
| The right matrix representation of the Generalized Octonion | |
| The left matrix representation of the Generalized Octonion | |
| ker | The kernel of any transformation |
Appendix A
- The MATLAB function for multiplication of any two Generalized Octonion are as follows:
- The MATLAB codes for calculating the example above are written as:The other calculations are only given with the MATLAB functions. With similar way, one can run the calculation codes.
- The MATLAB function for inner product of any two Generalized Octonion are as follows:
- The MATLAB function for norm of any Generalized Octonion is defined as follows:
- The MATLAB function for inverse of any invertible Generalized Octonion is given as follows:
- The MATLAB function for vector inner product of vector parts of any two Generalized Octonion is defined as follows:
- The MATLAB function for calculating the vector products of vector parts of any two Generalized Octonion is as follows:
- The MATLAB function for the right representation of any Generalized Octonion is given as follows:
- The MATLAB function for the left representation of any Generalized Octonion is as follows:
- The MATLAB function for the n-power and m-root of any Generalized Octonion is as follows:
References
- Hamilton, W.R. Elements of Quaternions; Longmans, Green and Co: London, UK, 1866. [Google Scholar]
- Cayley, A. On Jacobi’s Elliptic Functions, in Reply to the Rev. B. Bronwin, and on Quaternions. Philos. Mag. 1845, 26, 208–211. [Google Scholar]
- Wikipedia. Available online: https://en.wikipedia.org/wiki/Octonion (accessed on 25 September 2024).
- Zhevlakov, K.A.; Slinko, A.; Shestakov, I.; Shirshov, A.I. Rings That Are Nearly Associative; Academic Press: London, UK, 1982. [Google Scholar]
- Baez, J. The octonions. Bull. Am. Math. Soc. 2002, 39, 145–205. [Google Scholar] [CrossRef]
- Carmody, K. Circular and hyperbolic quaternions, octonions, and sedenions. Appl. Math. Comput. 1988, 28, 47–72. [Google Scholar] [CrossRef]
- Jafari, M. A viewpoint on semi-octonion algebra. J. SelçUk Univ. Nat. Appl. Sci. 2015, 4, 46–53. [Google Scholar]
- Jafari, M. Introduction to Split Semi-Octonion: Algebra and Analysis. 2015. Available online: https://www.researchgate.net/publication/281454836_Introduction_to_Split_Semi-Octonion_Algebra_and_Analysis (accessed on 11 November 2024).
- Jafari, M. An Introduction to Quasi-Octonions and Their Representation. 2015. Available online: https://www.researchgate.net/publication/281202641_An_Introduction_to_Quasi-Octonions_and_Their_Representation (accessed on 11 November 2024).
- Jafari, M. The fundamental algebraic properties of split quasi-octonions. DUFED 2016, 5, 118–122. [Google Scholar]
- Jafari, M. On The Para-Octonions:A Non-Associative Normed Algebra. MFBD 2016, 28, 95–99. [Google Scholar]
- Schray, J.; Mongue, A.A. Octonionic Representations of Clifford Algebras and Triality. Found. Phys. 1996, 26, 17–70. [Google Scholar] [CrossRef]
- Alo, J.; Akbıyık, M. On split-octonionic curves. Log. J. Igpl 2024. [Google Scholar] [CrossRef]
- Tian, Y. Matrix representations of octonions and their applications. Adv. Appl. Clifford Algebras 2000, 10, 61–90. [Google Scholar] [CrossRef]
- Akbıyık, M. On Powers and Roots of Split Octonions. J. Math. 2023, 2023, 2314–4629. [Google Scholar] [CrossRef]
- Sabinin, L.V.; Sbitneva, L.; Shestakov, I.P. Non Associative Algebra and its Applications, 1st ed.; A Series of Lecture Notes in Pure and Applied Mathematics; Chapman& Hill, CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Gogberashvili, M. Octonionic geometry. Adv. Appl. Cliford Algebr. 2005, 15, 55–66. [Google Scholar] [CrossRef][Green Version]
- Flaut, C.; Shpakivskyi, V. An efficient method for solving equations in generalized quaternion and octonion algebras. Adv. Appl. Clifford Algebras 2015, 25, 337–350. [Google Scholar] [CrossRef]
- Leite, F.S.; Vitoria, J. Generalization of the De Moivre Formulas for Quaternions and Octonions; Math. Studies in the Honour of Luis de Albuquerque; Universidade de Coimbra: Coimbra, Portugal, 1994. [Google Scholar]
- Şentürk, T.D.; Ünal, Z. 3-Parameter Generalized Quaternions. Comput. Methods Funct. Theory 2022, 22, 575–608. [Google Scholar] [CrossRef]
- Schafer, R.D. An Introduction to Nonassociative Algebras; Academic Press: New York, NY, USA, 1966. [Google Scholar]
- Bektaş, Ö.; Yüce, S. De Moivre’s and Euler’s Formulas for the Matrices of Octonions. Proc. Natl. Acad. Sci. USA 2019, 89, 113–127. [Google Scholar] [CrossRef]
- Bektaş, Ö. Split-type octonion matrix. Math. Methods Appl. Sci. 2019, 42, 5215–5232. [Google Scholar] [CrossRef]
- Jafari, M. The Real Matrix Representations of Semi-Octonions. Anadolu Univ. J. Sci. Technol.-Theor. Sci. 2016, 4, 99–112. [Google Scholar] [CrossRef][Green Version]
| × | ||||||||
| × | 1 | |||||||
| 1 | 1 | |||||||
| Type of the Generalized Octonion | Polar Form | Conditions |
|---|---|---|
| c is spacelike and the vector part of c is timelike | ||
| c is spacelike and the vector part of c is spacelike | ||
| c is lightlike | , | |
| The vector part of c is lightlike |
| The Polar Form | n Is Even | n Is Odd |
|---|---|---|
| Real octonions [5] | Powers [18] Roots [18] Matrix representations [14] De Moivre of Matrix Representations [22] | |
| Split octonions [6] | Powers [15,18] Roots [15,18] Matrix representations [23] De Moivre of Matrix Representations [15] | |
| Semi octonions [7] | Powers [24] Roots [24] Matrix representations [7] De Moivre of Matrix Representations [7] | |
| Split semi octonions [8] | Powers [8] Roots [8] Matrix representations De Moivre of Matrix Representations | |
| Quasi octonions [9] | Powers [9] Roots [9] Matrix representations De Moivre of Matrix Representations | |
| Split quasi octonions [10] | Powers [10] Roots [10] Matrix representations De Moivre of Matrix Representations | |
| Para octonions [11] | Powers [11] Roots [11] Matrix representations De Moivre of Matrix Representations |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamaç Akbıyık, S. On Matrices of Generalized Octonions (Cayley Numbers). Symmetry 2024, 16, 1567. https://doi.org/10.3390/sym16121567
Yamaç Akbıyık S. On Matrices of Generalized Octonions (Cayley Numbers). Symmetry. 2024; 16(12):1567. https://doi.org/10.3390/sym16121567
Chicago/Turabian StyleYamaç Akbıyık, Seda. 2024. "On Matrices of Generalized Octonions (Cayley Numbers)" Symmetry 16, no. 12: 1567. https://doi.org/10.3390/sym16121567
APA StyleYamaç Akbıyık, S. (2024). On Matrices of Generalized Octonions (Cayley Numbers). Symmetry, 16(12), 1567. https://doi.org/10.3390/sym16121567