Conformational and Chiroptical Properties of Salicylamide-Based Peptidomimetics

Abstract

Optical rotation (OR), the most frequently used chiroptical method, is used for the characterization of newly synthesized or isolated compounds. Computational predictions of OR are, however, mainly used for the determination of the absolute configurations of chiral compounds, but they may also be used for the verification of conformational analysis results if the experimental values are known. Our computational study deals with the conformational analysis of flexible salicylamide-based peptidomimetics, starting with a conformation search, then a low-level ab initio preoptimization of the hundreds of conformations found, and, finally, a higher-level DFT optimization. For the resulting minima structures, Boltzmann populations were calculated, followed by OR calculations for all the populated conformers using the DFT method with various basis sets with diffuse functions. Weighted averages of the ORs were compared with experimental values, and the agreement, which ranged from excellent to moderate for various compounds, served as a verification of the conformational analysis results.

1. Introduction

Knowing the exact spatial arrangement of compounds, either newly synthetized or isolated from natural sources, is fundamental knowledge for the study of their properties not only in the pharmaceutical industry and medicine but also in organic chemistry, biochemistry, and materials science [1,2,3,4,5,6,7,8]. Furthermore, for chiral compounds, the absolute configuration must be known. Common structure determination techniques like NMR, IR, or MS spectroscopy cannot be used for this purpose, as two enantiomers provide the same spectral signals in all these spectroscopies. The only classical structural tool that can distinguish enantiomers is X-ray crystallography, which is, however, limited to crystalline compounds only. Here, the recently developed computational methods may be of use, as ab initio or DFT calculations of chiroptical properties may be used for the determination or confirmation of the absolute configurations of chiral compounds. And as optical rotation (OR) is a routinely measured property for new compounds, the calculation of OR is the most frequently used method for that purpose, making use of the fact that the ORs of both enantiomers E_R and E_S are of the same absolute value but of opposite signs:

$${\left[\alpha \right]}_{\nu }\left(E_R\right)={-\left[\alpha \right]}_{\nu }\left(E_S\right)$$

(1)

The theoretical quantum-mechanical background for optical rotation was derived long ago by Rosenfeld in 1928 [9], and the current methodology has been reviewed recently [10,11]. As a result, calculations of OR for rigid molecules are becoming routine. However, for conformationally flexible molecules, the situation is more complicated, and a detailed conformational analysis must be performed prior to OR calculations to obtain equilibrium populations of stable conformations and their relative free energies. The calculated OR is then a weighted average of the ORs of populated conformers:

$${\left[\alpha \right]}_{\nu }=\sum _i{\mathrm{x}}_i{\left[\alpha \right]}_{\nu }^i$$

(2)

where x_i is the molar fraction of the i-th conformer and ${\left[\alpha \right]}_{\nu }^i$ is the optical rotation of the i-th conformer.

OR is extremely sensitive to the shape of a molecule, and even different conformers of the same compound often have different signs of OR. Comparison of experimental and calculated value of OR can thus be used as a verification of the results of conformational analysis.

For our computational study, six compounds bearing the salicylic motif, which are interesting both for their structure and spectrum of biological activities, were selected. Salicylic acid is found, for example, in willow bark, from which it was isolated. In addition to fulfilling the function of a plant hormone [12], today, it is mainly used in dermatology [13]; however, its antimicrobial activity has also been described [14,15,16]. The best-known drugs derived from it are acetylsalicylic acid or Aspirin^®—with anti-inflammatory, antipyretic, and anticoagulant effects [17]—and mesalazine, which is used to treat inflammatory bowel diseases [18]. Salicylanilides, commercially available, e.g., as niclosamide [19], rafoxanide [20], or closantel [21], are anthelmintics, but in recent years, their other biological effects have been discovered, e.g., anticancer [22] or antiviral [23], stimulating scientific interest in these simple and small molecules [24,25,26,27,28,29,30,31,32]. In addition to anticancer activity [33], for example, their herbicidal activity [34] or ability to inhibit acetylcholinesterase [35,36,37] can be mentioned. However, the antimicrobial activity of salicylamides is the most described [24,25,38,39,40,41,42,43,44,45,46], and it can be multiplied by introducing a carbamate group to the free phenolic salicylic hydroxyl or by inserting an amino acid fragment between the salicylic and anilide parts of the molecule, i.e., by the preparation of diamides, namely, salicylamide-based peptidomimetics [30,47,48,49,50,51,52,53]. It is necessary to mention that salicylanilide-based peptidomimetics also show anticancer activity [54,55,56].

2. Materials and Methods

2.1. Compounds

Structures of all six salicylamides 1–6 under study are given in

Table 1. Structures of salicylamides.

Comp.	Structure	Name	Molecular Formula /Weight	Refs.
1		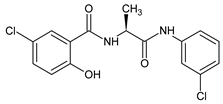5-chloro-N-{(2S)-1-[(3-chlorophenyl)amino]-1-oxopropan-2-yl}-2-hydroxybenzamide	C16H14Cl2N2O3 [353.200]	[30,47]
2		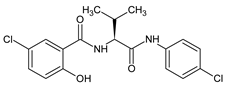5-chloro-N-{(2S)-1-[(4-chloro phenyl)amino]-3-methyl -1-oxobutan-2-yl}-2-hydroxybenzamide	C18H18Cl2N2O3 [381.253]	[47]
3		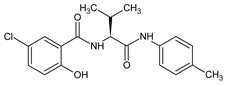5-chloro-2-hydroxy-N-{(2S) -3-methyl-1-[(4-methylphenyl)amino] -1-oxobutan-2-yl}benzamide	C19H21ClN2O3 [360.835]	[30,47]
4		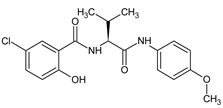5-chloro-2-hydroxy-N-{(2S)- 1-[(4-methoxyphenyl)amino]-3-methyl -1-oxobutan-2-yl}benzamide	C19H21ClN2O4 [376.834]	[30,47]
5		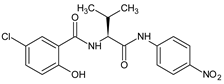5-chloro-2-hydroxy-N-{(2S) -3-methyl-1-[(4-nitrophenyl)amino] -1-oxobutan-2-yl}benzamide	C18H18ClN3O5 [391.806]	[30]
6		5-chloro-2-hydroxy-N-[(2S) -3-methyl-1-oxo-1-{[4-(trifluoromethyl)phenyl]amino}butan-2-yl]benzamide	C19H18ClF3N2O3 [414.806]	[30,47]

together with their systematic names generated using ACD/Name ver. 12.01 software [57]. Their synthesis, spectral data, optical rotations, and biological activities were described previously [30,47,52] (and refs. thereon).

2.2. Conformational Analysis and Geometry Optimizations

Low-energy conformers for all compounds 1–6 were searched using the Conformational Search routine of HyperChem ver. 8.0.3 software [58] at the molecular mechanics level using the MM+ forcefield. Found structures were preoptimized at the HF/4-31G level in a gas phase. Final optimization of all resulting geometries was performed at the DFT level using the hybrid B3PW91 [59,60] functional with 6-31G(d,p) basis set in chloroform using the CPCM [61,62] implicit solvation model. For comparison, final optimizations were also performed with the same DFT functional augmented with the D3 version of Grimme’s dispersion correction [63]. All minima were confirmed by a frequency calculation at the same level of theory, and Boltzmann populations of each conformer p_i were calculated using

$$p_i=\frac{\mathrm{e}\mathrm{x}\mathrm{p}(-\frac{{\epsilon }_i}{kT})}{\sum _i\mathrm{e}\mathrm{x}\mathrm{p}(-\frac{{\epsilon }_i}{kT})}$$

(3)

where ε_i is the Gibbs free energy of i-th conformer, k is the Boltzmann constant, and T is the absolute temperature. All DFT calculations were performed using the Gaussian 16 package [64].

2.3. Calculations of Optical Rotation

Experimental optical rotations were measured in ethyl acetate at the wavelength of sodium D line at 589 nm. Theoretical ORs were calculated in the same solvent and at the same wavelength using the B3PW91 functional and various basis sets with a polarization function.

3. Results and Discussion

3.1. Conformational Analysis

All salicylamides 1–6 are very flexible molecules with many freely rotatable bonds. Relevant low-energy conformations were searched using the conformation search utility in HyperChem software. The number of conformers found for each compound is given in

Table 2. Results of conformation search and preoptimization.

Comp.	Conformations after Conformation Search	Conformations after Preoptimization
1	268	22
2	349	25
3	1268	10
4	1219	22
5	1180	13
6	518	24

. At a minimum, several hundred conformations were found for each compound, with a maximum of 1268 for compound 3. For this reason, a low-level preoptimization was performed at the Hartree-Fock HF/4-31 level. This step reduced the number of conformations to about 20, and it is also given in Table 2.

Final geometry optimizations were performed at the B3PW91/6-31G(d,p) level. Originally, conformational analysis was intended for predictions of NMR and IR spectra, and chloroform was used as an implicit solvent using CPCM model. However, it was verified that there were only minor differences in the optimized geometries in ethyl acetate and in chloroform.

All local minima were verified through frequency calculations at the same theoretical level, and Boltzmann populations were calculated based on Gibbs free energies. Up to four populated conformers were found for compounds 1–6, and their geometries and populations are given in

Table 3. Populated conformers after conformational analysis.

Comp.	Conformer Designation	Geometry	Population
1	a		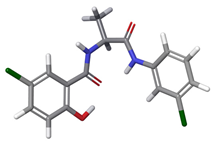99.95%
2	a		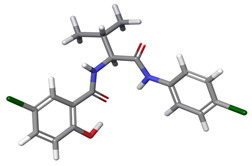60.74%
	b		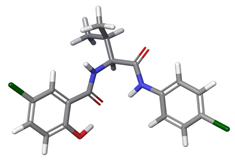23.13%
	c		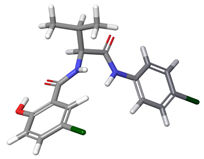16.09%
3	a		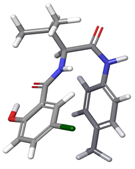79.29%
	b		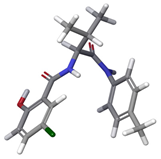16.40%
	c		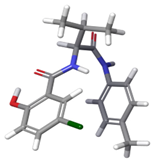4.30%
4	a		69.25% a
	b		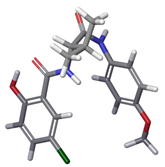17.52% a
	c		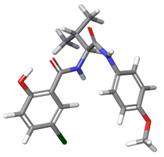7.54% a
5	a		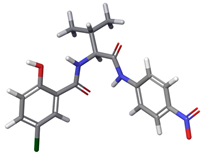67.90%
	b		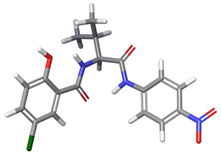32.09%
6	a		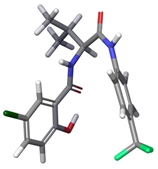34.50%
	b		33.11%
	c		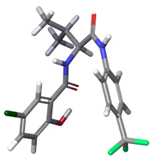27.79%
	d		14.10%

^a For the calculation of weighted averages of ORs, populations were normalized to 100%.

.

The various conformers of each compound differ mainly in the torsion angles connecting both aromatic rings. They are designated according to Figure 1 and, for a better quantitative characterization of the separate conformers, are listed in

Table 4. Torsion angles of populated conformers.

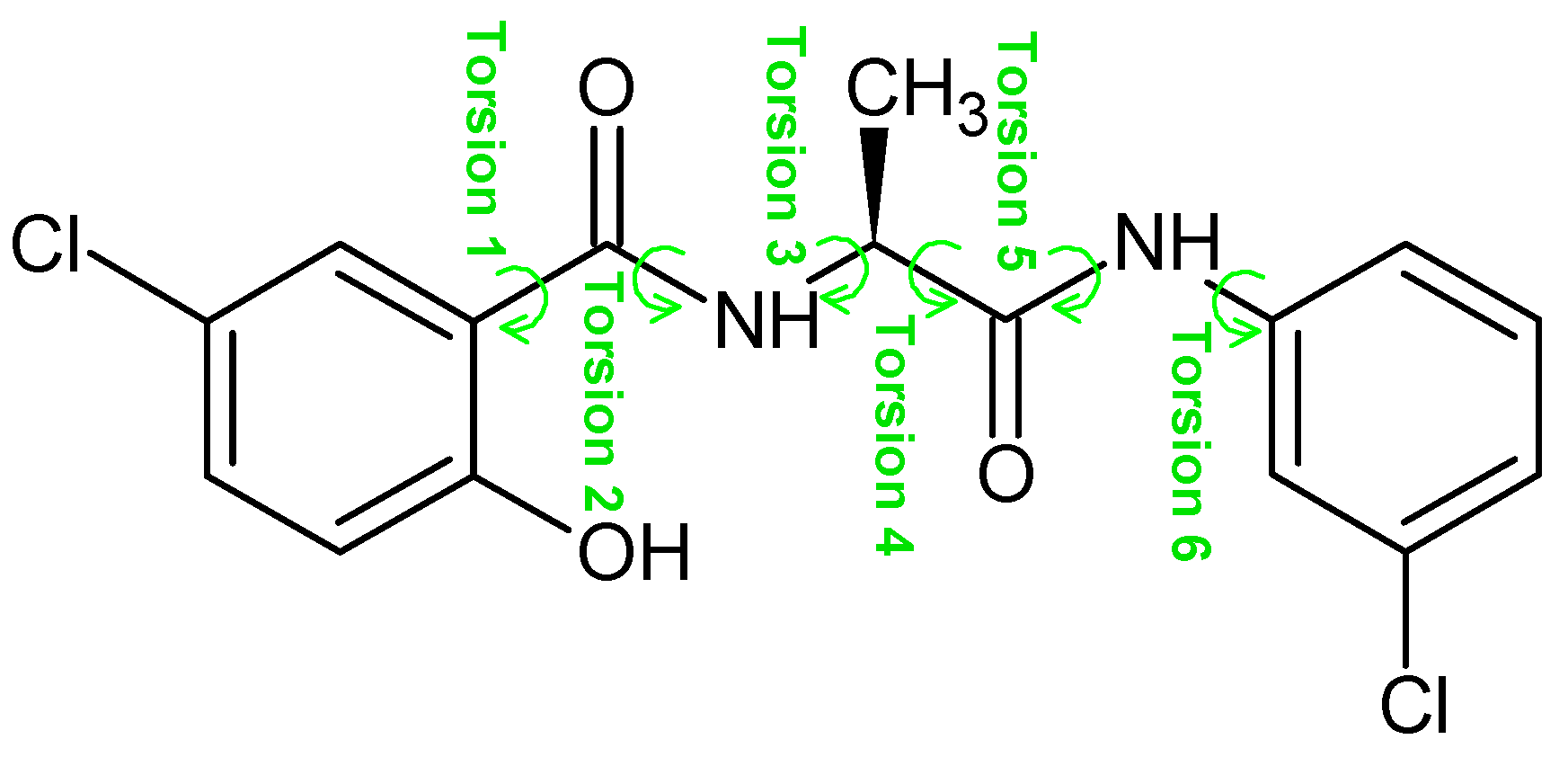
Conformer	Torsion 1	Torsion 2	Torsion 3	Torsion 4	Torsion 5	Torsion 6
1a	−169.7	−174.1	−87.4	67.0	−178.1	177.7
2a	−170.0	−177.6	−87.9	76.7	−176.4	174.6
2b	−168.7	−173.7	−88.1	61.4	−179.1	179.9
2c	172.9	−173.2	−117.5	12.8	176.7	−178.1
3a	173.1	−178.7	−132.6	41.4	16.1	51.4
3b	−173.7	−178.8	149.7	−37.1	−11.6	117.1
3c	−171.1	−174.1	−106.8	−3.6	−14.9	114.7
4a	−168.2	−178.6	−130.6	40.0	14.3	55.4
4b	−172.4	−178.1	−84.4	−43.2	−8.0	106.6
4c	−171.8	179.6	57.7	56.0	8.4	64.8
5a	1.3	−174.8	−86.8	72.1	−176.7	174.4
5b	0.4	−172.5	−85.9	60.0	−178.8	179.4
6a	−174.6	−176.2	−133.2	39.5	18.4	42.6
6b	174.0	−176.4	−133.8	39.4	16.9	43.7
6c	173.5	−176.9	−133.4	39.4	17.1	44.8
6d	171.2	176.2	55.2	51.5	6.8	52.4

.

To assess the effect of dispersion interactions, all final optimizations at the DFT level were also performed with the dispersion-corrected DFT method (DFT-D) [63] as included in Gaussian 16. This only led to minor changes in geometries and populations for compounds 1 and 2. However, for other compounds, the changes are more noticeable. Their populations and torsion angles are given in

Table 5. Populations and torsion angles of dispersion-corrected populated conformers.

Conformer	Population	Torsion 1	Torsion 2	Torsion 3	Torsion 4	Torsion 5	Torsion 6
1a	92.17%	−164.8	−175.9	−85.5	65.3	−174.6	170.2
2a	48.37%	−166.2	−178.0	−87.0	73.9	−172.8	167.4
2b	29.67%	−164.4	−174.1	−87.0	58.7	−176.2	174.6
2c	11.36%	−164.2	167.4	−124.0	34.3	15.2	53.9
2d	8.45%	170.0	−174.1	−125.7	17.0	177.8	−179.1
3a	90.63%	−163.1	169.0	−125.9	36.2	14.3	−124.3
3b	7.32%	−164.8	172.2	−75.6	−7.3	−5.6	112.2
4a	95.70%	−164.8	169.0	−125.0	34.7	12.3	−132.2
4b	4.20%	−162.3	170.3	−59.6	−33.2	2.1	109.2
5a	94.07%	−167.5	164.4	−124.9	31.9	13.9	−131.6
5b	2.44%	162.5	−164.9	36.4	42.7	−10.8	−122.6
6a	89.84%	−167.0	166.3	−124.3	32.6	14.8	−129.2
6d	7.47%	−160.3	169.4	−56.3	−30.8	1.1	115.5

.

3.2. Calculations of Optical Rotation

For the calculation of optical rotation, we used the time-dependent Density Functional Theory (TDDFT) [65,66,67,68] methodology with gauge-invariant atomic orbitals (GIAOs) as implemented in Gaussian 16 software. Using a standard B3PW91 functional, we sought to test several basis sets with diffuse functions (6-311++G(2d,p), aug-cc-pVDZ, aug-cc-pVTZ, and aug-cc-pVQZ). To allow us to compare our calculated optical rotations with the experimental ones, the calculations were performed at the sodium D line wavelength, i.e., 589 nm.

While the substitution of an implicit solvent in the CPCM solvent model plays only a minor role during geometry optimization calculations, we noticed that it plays a significant role during OR calculation. Optical rotations are thus sensitive to solvents [69], even of similar polarity. Differences between the calculated optical rotations in chloroform and ethyl acetate for compounds 1 and 2 and several basis sets are illustrated in

Table 6. Calculated optical rotations using different solvents and basis sets.

Comp.	Solvent	6-311++G(2d,p)	aug-cc-pVDZ	aug-cc-pVTZ
1	chloroform	−0.4	6.9	14.0
	ethyl acetate	1.7	22.6	31.5
2	chloroform	−90.3	−85.1	−78.8
	ethyl acetate	−81.1	−73.9	−70.2

. The same geometry is used in both calculations. For comparison, experimental optical rotations are listed in

Table 7. Experimental optical rotations in ethyl acetate.

Comp.	[α]d	Refs.
1	37.0 (c 1.6)	[30,47]
2	−71.7 (c 1.5)	[47]
3	−56.2 (c 0.3)	[30,47]
4	−63.2 (c 0.2)	[30,47]
5	−64.8 (c 0.2)	[30]
6	−73.8 (c 0.2)	[30,47]

.

It is obvious that the optical rotations calculated in ethyl acetate were in all cases in better agreement with the experimental values compared to those in chloroform.

The optical rotations of all the populated conformers and their Boltzmann weighted averages calculated in ethyl acetate with various basis sets are given in

Table 8. Calculated optical rotations in ethyl acetate.

Comp.	Conformer	6-311++G(2d,p)	aug-cc-pVDZ	aug-cc-pVTZ	aug-cc-pVQZ
1	a	1.7	22.6	31.5	32.2
2	a	−98.6	−90.3	−84.5	−86.1
	b	−214.9	−207.0	−200.6	−203.2
	c	177.2	179.1	179.9	180.8
	w. a. 1	−81.1	−73.9	−68.8	−70.2
3	a	−161.9	−158.7	−151.8	−132.8
	b	108.4	110.9	111.8	121.4
	c	238.3	236.7	239.9	239.9
	w. a.	−100.4	−97.5	−91.7	−75.1
4	a	−66.9	−60.1	−54.2	−53.8
	b	51.5	55.0	55.4	57.3
	c	−185.3	−185.2	−184.5	−201.7
	w. a.	−54.4	−48.7	−44.2	−45.0
5	a	−230.6	−225.0	−226.9	−228.0
	b	−363.8	−357.1	−356.8	−340.0
	w. a.	−273.3	−267.3	−268.6	−263.9
6	a	−247.0	−241.0	−234.3	−226.1
	b	−200.9	−202.2	−195.4	−187.6
	c	−188.9	−189.7	−183.6	−179.3
	d	160.7	161.5	159.1	167.3
	w. a.	−160.0	−158.7	−153.5	−146.4

¹ Weighted average for a compound.

.

The level of agreement of the calculated data with the experimental optical rotations differs for the various compounds. Structure 1, which is conformationally rigid and for which only one populated conformer was found, provides, with triple-ζ and quadruple-ζ basis sets, an excellent agreement with the experimental value of 37.0°. For compound 2, the best agreement was achieved even if it had three conformers, two of them having a negative value of ORs and one having a positive value. It is obvious that conformational analysis in this case provided an exact representation of the populated conformers. All the basis sets performed well for this structure, with, again, quadruple-ζ being the best. Compounds 3 and 4 showed similarly good agreement with the experimental values, with a difference of about 20°. Both compounds consist of three conformers of different signs of ORs, and the conformational analysis seems to provide an exact representation of the conformers. However, a trend of improving results with a larger basis set was not observed here. The worst agreement was observed for compounds 5 and 6, with a difference of about 200 and 70°, respectively. Both compounds consist of conformers with large negative values of OR (<−150°), and there is no way to achieve experimental values of about −70°. It is obvious that conformational analysis probably omitted some conformers with a more positive value of ORs for both compounds.

The inclusion of dispersion corrections into DFT calculations did not lead to a straightforward improvement of the calculated and experimental rotations. While they had a noticeable effect on the conformational analysis, the dispersion corrections did not affect the calculated ORs. For comparison, we recalculated optical rotations at the B3PW91/aug-cc-pVDZ level for dispersion-corrected geometries, and the results are given in

Table 9. Calculated optical rotations in ethyl acetate for dispersion-corrected geometries.

Comp.	Conformer	aug-cc-pVDZ
1	a	24.3
2	a	101.7
	b	−222.9
	c	−341.7
	d	185.5
	w. a. 1	−139.9
3	a	−26.0
	b	179.2
	w. a.	−10.6
4	a	−60.1
	b	55.0
	c	−185.2
	w. a.	−55.3
5	a	−257.2
	b	−191.6
	w. a.	−255.5
6	a	−335.4
	b	217.5
	w. a.	−292.9

¹ Weighted average for a compound.

.

While some minor improvement can be seen for compounds 1, 4, and 5, for the other compounds, the agreement between the calculated and experimental optical rotations worsened, most significantly for compound 6.

Comparing the basis sets used, it can be seen that the quadruple-ζ aug-cc-pVQZ basis set provides the best agreement between the calculated and experimental data. However, it is also the most time consuming.

Table 10. Average CPU task times for OR calculations.

Basis Set	Time [d]
6-311++G(2d,p)	0.5
aug-cc-pVDZ	0.5
aug-cc-pVTZ	10
aug-cc-pVQZ	>70

lists the average CPU task times for the basis sets used.

It is clear that the quadruple-ζ basis set is very expensive, even when used with multiple CPUs. For this reason, we concluded that the triple-ζ basis set has the best price/performance ratio for routine calculations of OR.

It must be emphasized that the signs of optical rotations were correctly predicted in all cases, and the calculations of OR can thus be used for the determination of absolute configurations, even for conformationally flexible compounds. Furthermore, it can be seen that optical rotations are extremely sensitive to minor changes in geometry and are suitable for the assessment of conformer populations during conformational analysis.

4. Conclusions

Based on successful applications of optical rotation calculations for the determination of the absolute configurations of various compounds, at least the rigid ones, we chose an opposite approach for the study of the conformational analysis of conformationally flexible molecules. As optical rotation is extremely sensitive to the 3D geometry of a compound, even small changes in the rotation of exocyclic groups can lead to dramatic changes in optical rotation. For this reason, we decided to use optical rotation as an evaluator of the conformational analysis results of conformationally flexible molecules. We performed a detailed computational conformational analysis of six flexible salicylamide-based compounds. In the initial step, we used the conformation search utility, which found hundreds of conformations for each compound. These were then optimized in two steps, and Boltzmann populations were calculated. This yielded 1–4 conformations for each molecule, and, finally, optical rotations were calculated as weighted averages of rotations for each populated conformer. For their DFT calculation, the B3PW91 functional was used with several basis sets including diffuse functions. If we assume that the optical rotations were calculated exactly, we employed an excellent tool for the assessment of conformational analysis. Of the six compounds for which experimental optical rotations were known, for two of them (1 and 2), the agreement between the calculated and experimental rotations were excellent. Compound 1 proved to be rigid and existed in one conformer only. For compound 2, three populated conformers were found, two of them having negative optical rotations and one having positive rotations. It is clear that the conformers and their populations were calculated exactly in this case. For compounds 3 and 4, the agreement between the experimental and calculated rotations was moderate. We can conclude that only minor discrepancies in populations occurred in this case. The worst agreement was found for compounds 5 and 6. All the populated conformers of these compounds had highly negative rotations, while the experimental values were only slightly negative, i.e., −64.8° and −73.8°, respectively. It is evident that changes in populations could not improve the agreement between the experimental and calculated values substantially in this case and that it is probable that some conformers with only slight negative optical rotations or positive ORs were missed during the conformational analysis. The inclusion of dispersion corrections into the DFT optimizations had a noticeable effect on the calculated geometries and their populations; however, a clear and straightforward improvement of the calculated optical rotations was not observed. Finally, we proved that the optical rotations calculated with the quadruple-ζ aug-cc-pVQZ basis set were the best but, unacceptably, too time consuming and that the triple-ζ basis set yielded optimum performance.