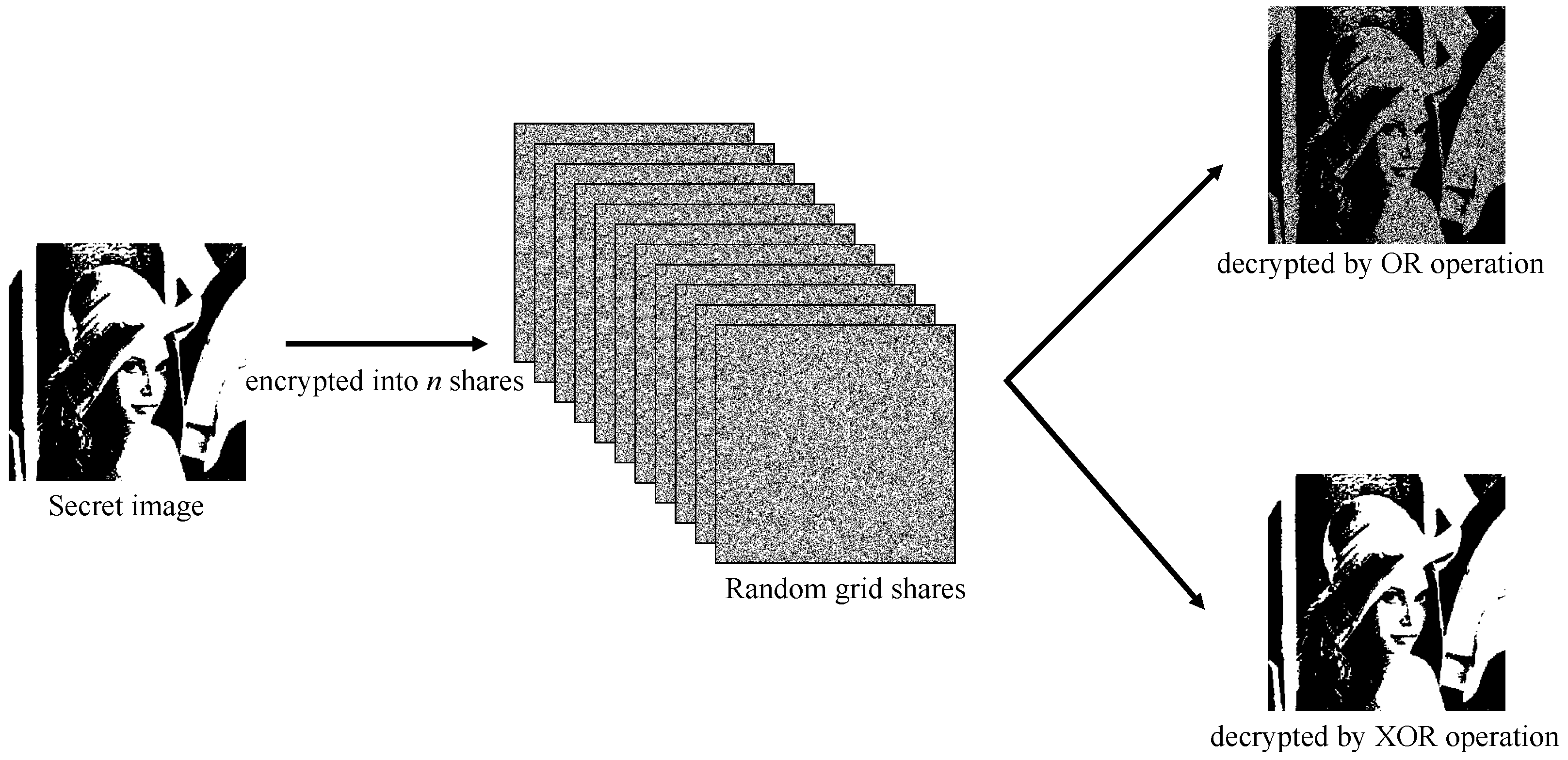
1. Introduction
Introduced in 1995 [
1], the visual cryptography scheme (VCS for short) was a new technique that involves encrypting a secret image into
n random grid images (also called “shares”) that can be stacked together to disclose the original secret image. To enhance this approach, a (
k,
n)-threshold visual cryptography scheme ((
k,
n) VCS for short) was presented. This method entails the encryption of a binary secret image into
n shares, with the condition that at least
k shares (where
k ≤
n) must be combined to reconstruct the original image. If fewer than
k shares are utilized, no clue about the original image can be discerned.
Generally speaking, cryptography systems in information security can be divided into symmetric cryptography systems and asymmetric cryptography systems. For VCS, if shares are regarded as the “key” and “ciphertext” generated by the encryption algorithm, then because at least k shares need to be collected to recover the ”plaintext”, the visual cipher can be regarded as a type of symmetric cryptosystem. Compared with traditional cryptography systems, VCS usually does not pursue the ability to completely restore the original secret. Instead, it focuses on the ability to use human vision to identify the original secret during restoration.
Looking back to 1987, Kafri and Keren [
2] were pioneers in the field of visual secret sharing (VSS for short) through the use of random grids (RG for short). In the field of visual cryptography, random grids are a technique used to divide a secret image into irregular grids or patterns. Each grid or pattern is designed to appear random when viewed individually and does not contain the original secret information, as shown in
Figure 1. The original secret image can only be reconstructed when these random grids or patterns are combined or superimposed. This innovative approach rectified the limitation of secret pixel expansion and eliminated the necessity for codebook designs, which were shortcomings in Naor and Shamir’s method [
1]. Although Kafri and Keren [
2] initially introduced the construction of (2, 2) RG-based VCS, it was not until 2009 that Shyu [
3], as well as Chen and Tsao [
4] independently proposed the first (
n,
n) RG-based VCS. In 2011, Chen and Tsao [
5] were pioneers in introducing (
k,
n) RG-based VCS.
Traditional VCS involves directly stacking two binary (black-and-white) images, which is equivalent to performing a logical OR operation just like the human visual system (HVS); we treat black pixels as 1 and white pixels as 0. In other words, it treats white pixels as transparent and black pixels as black. When the two images are superimposed, what the human eye perceives is the content of the OR-reconstructed image. In practice, it is equivalent to printing the share on a transparency separately. You can simply overlay those transparencies when restoring. However, this approach results in the image becoming progressively darker and makes it difficult to identify the original secret as more shares are stacked. Furthermore, it is impossible to completely restore the original secret. Therefore, a method for recovering the secret using an XOR operation was developed. By assigning 0 (white) when both pixels are the same and 1 (black) when they differ, as shown in
Table 1, this operation makes it possible to fully recover the secret, as shown in
Figure 1. In practice, it can be completed by using additional equipment to perform XOR operations. For example, using a copier that can print out black-and-white reverse images (inverting color, that is, a NOT operation logically) and a formula that converts the XOR operation into OR and NOT operations. Because the XOR operation needs extra cost or equipment, if the equipment cannot be obtained, the scheme can be more flexible if the secret can still be restored by using the OR operation (direct stacking). Currently, some scholars have studied a VCS that can restore the original image using both OR and XOR decryptions [
6,
7,
8].
In 2009, Wang proposed a region incrementing visual cryptography scheme (RIVCS for short) [
9], which enables a dealer to divide the content of a secret image
S into multiple regions and assign a level of secrecy to each region. In this
q-level scheme, the secrecy level of a region ranges from 1 to
q, with the first-level secret being the least significant and the
q-level secret being the most significant. The dealer has the flexibility to assign each region of
S a secrecy level that aligns with the specific needs of their application, reflecting the degree of secrecy required for that region. This level of regulation allows for more precise control over the distribution of secrets, ensuring that sensitive information remains highly protected while still allowing for the sharing of less sensitive information. Wang’s scheme [
9] utilizes the basic matrix proposed by Naor and Shamir [
1] for encryption. However, the encryption process results in pixel expansion and can only be restored using an OR operation. For the purpose of addressing the limitations of pixel expansion and the reliance on a single OR-based decryption, we have made improvements accordingly and propose an RG-based RIVCS with the abilities of OR and XOR decryption. While visual cryptography is considered symmetric due to the division between public and private keys, it is important to note that VC, including RIVCS, often does not rely on complex mathematical operations or key pairs like traditional symmetric encryption (e.g., AES or DES). Instead, it uses visual properties and simple pixel stacking techniques for decryption. After Wang, many scholars have continued research on RIVCS. Wang et al. [
10] proposed a (2, 3) RIVCS using random grids in 2010. In 2012, Shyu and Jiang [
11] focused on minimizing pixel expansion of basis matrices (2,
n) RIVCS, and Yang et al. [
12] concentrated on applying (
k,
n) RIVCS to color images. Kumar and Sharma [
13] proposed a (
k,
n) RIVCS using random grids in 2015. They gave three construction methods using the ideas of Kafri and Keren [
2], and the number of the secrecy levels is always equal to
n −
k + 1. Furthermore, in 2019, Yang et al. [
14] achieved progressive restoration in a (
k,
n) RIVCS.
Currently, many scholars are actively engaged in research on visual cryptography schemes. Each researcher brings a unique focus to their exploration of VCS. For example, Huang et al. emphasize generating meaningful encrypted images and utilizing the XOR operator for restoration [
15]. Chen and Juan specialize in encrypting grayscale and color images into meaningful encrypted images [
16]. Panchbhai and Varade focus on the research of a block-based progressive secret sharing scheme (BPVSS for short) for both grayscale and color images [
17]. Zhang et al. concentrate on a group secret sharing scheme [
18], where collaborative efforts within a group enable the recovery of secret information.
Therefore, the main contribution of this paper is to propose a new method for RIVCS. Compared with existing RIVCS, the proposed method not only has better visual quality in OR-based recovery in most cases (especially when stacking all shares), but also incorporates the function of XOR-based restoration. It supports OR and XOR operation decryption, making the decryption process flexible. This design allows users to use OR operations for decryption without the need for any specialized equipment, and users with additional equipment can use XOR operations to enhance the visual quality of the recovered images. To the best of our knowledge, this paper is the first to propose an innovative RIVCS that can use both OR and XOR operations for decryption.
The paper follows this structure: the subsequent section covers related work,
Section 3 introduces the main result of this paper, which is (
k,
n) 2D_RIVCS, and
Section 4 provides an analysis of this scheme, while
Section 5 and
Section 6 showcase the experimental results and comparison with other similar works, respectively. Finally,
Section 7 provides a summary and introduces some innovative ideas for future work.
4. Theoretical Analyses
In this section, we offer a theoretical discussion of the security and visual recognizability of the proposed scheme.
First, this paper will establish the security of Algorithm 3, verifying that each individual encrypted image is secure and that collecting fewer than
k encrypted images remains secure. Note that, to facilitate this proof, we will utilize
bi to represent the
ith image within the algorithm before rearrangement (Step 4 of Algorithm 4), while
Bi will denote the
ith image after rearrangement, with 1 ≤
i ≤
n. As used in the literature [
5], we also define that
b1⊕2⊕…⊕i =
b1⊕
b2⊕ …⊕
bi and
b1⊗2⊗…
⊗i =
b1⊗
b2⊗ …⊗
bi, with 1 ≤
i ≤
n.
Lemma 1. For each grid pixel b1, b2, …, bn generated based on the corresponding secret pixel of S in Algorithm 3,
Proof of Lemma 1. In Step 2 of Algorithm 3, we generate the
n grid pixels
b1,
b2, …,
bn with a value of 0 or 1 with equal probability. So, after executing Step 2, we obtain
Then,
bk,
bt and
bn will be changed in Steps 3, 4 and 5 of Algorithm 3 according to conditions for each corresponding secret pixel
s. For Step 3, because Prob(
b1⊕2⊕…⊕k−1 = 0) = Prob(
b1⊕2⊕…⊕k−1 = 1) =
and
bk =
b1 ⊕
b2…⊕
bk−1⊕
s, we have
After executing Step 3. For the same reason, we know Prob(
bt = 0) = Prob(
bt = 1) =
, with
k ≤
t ≤
n, after executing Steps 4 and 5. So, Prob(
bi = 0) = Prob(
bi = 1) =
with 1 ≤
i ≤
n, in the end. □
In the following, we define b[S(0)] (and b[S(1)]) to denote a pixel b in the recovered image corresponding to a transparent (opaque) pixel in the image S.
Lemma 2. For each grid pixel b1, b2, …, bn generated based on the corresponding secret pixel of S in Algorithm 3, stacking any p grid pixel {bi1, bi2, …, bip} from {b1, b2, …, bn}, for which p < k, we have Proof of Lemma 2. According to Lemma 1, Prob(bi = 0) = = Prob(bi =1), where 1 ≤ i ≤ n. However, based on the calculations of the algorithm and the properties of the XOR operation, when b1⊕b2⊕ …⊕bk = s and b1⊕b2⊕ …⊕bt = s, it results in bk+1⊕ …⊕bt = 0 for some k < t < n. Similarly, when b1⊕b2⊕ …⊕bt = s and b1⊕b2⊕ …⊕bn = s, it leads to bt+1⊕ …⊕bn = 0. Additionally, when b1⊕b2⊕ …⊕bk = s and b1⊕b2⊕ …⊕bn = s, it causes bk+1⊕ …⊕bn = 0. This situation occurs regardless of whether the secret is white or black, allowing us to determine that no matter the stacking of pixels by OR operation or XOR operation, T[bi1⊗bi2⊗ …⊗bip[S(0)]] = T[bi1⊗bi2⊗ …⊗bip[S(1)]], and T[bi1⊕bi2⊕ …⊕bip[S(0)]] = T[bi1⊕bi2⊕ …⊕bip[S(1)]]. □
Theorem 1. Algorithm 3 (k, n) 2D_VCS is secure.
Proof of Theorem 1. According to Lemma 1 and Lemma 2, we meet the security condition T[B[S(0)]] = T[B[S(1)]] when stacking any p shares for 1 ≤ p < k. Algorithm 3 guarantees the security of each individual encrypted image and ensures the maintenance of security in the scenario where fewer than k encrypted images are collected. □
Next, we will show the visual recognizability of Algorithm 3, which offers two decryption methods. We will separately prove the visual recognizability based on whether OR or XOR decryption is applied, theoretically ensuring that the contrast is visually recognizable in both cases. First, let us begin with the XOR part.
Lemma 3. Stacking k grid pixels {b1, b2, …, bk}, where b1, b2, …, bk are generated after executing Step 2 and Step 3 of Algorithm 3, we have Proof of Lemma 3. Based on Step 3 of Algorithm 3, we know that s = b1⊕b2⊕ …⊕bk. So, b1⊕b2⊕ …⊕bk = b1⊕b2⊕ …⊕bk−1 ⊕(b1⊕b2⊕ …⊕bk−1⊕s) = s. Therefore, T[b1⊕b2⊕ …⊕bk[S(0)]] = 1, and T[b1⊕b2⊕ …⊕bk[S(1)]] = 0. □
Lemma 4. Stacking p (k < p ≤n) grid pixels {b1, b2, …, bp}, where b1, b2, …, bp are generated after executing Step 4 of Algorithm 3, we have Proof of Lemma 4. For (10) and (11), according to Step 4 of Algorithm 3, we know the probability is for choosing bp from {bk+1, …, bn} to reset b1⊕b2⊕ …⊕bp = s. That is, the probability that the pixel is restored is ; otherwise, the pixel will be randomly turned transparent or opaque. □
Lemma 5. Stacking p (k < p ≤ n) grid pixels {b1, b2, …, bk, bn−p+k+1, bn−p+k+2, …, bn}, where b1, b2, …, bn are generated after executing Step 5 of Algorithm 3, we have Proof of Lemma 5. In Step 3 of Algorithm 3, we are aware that bk = s ⊕ b1 ⊕ b2 ⊕ … ⊕ bk−1. Furthermore, in Step 4 and Step 5 we have bt = s ⊕ b1 ⊕ b2 ⊕ … ⊕ bt−1 for some k < t ≤ n, and bn = s ⊕ b1 ⊕ b2 ⊕ … ⊕ bn−1. It implies s = b1⊕b2⊕…⊕bn = b1⊕b2⊕…⊕bt⊕bt+1⊕…⊕bn = s⊕bt+1⊕…⊕bn, so bt+1⊕…⊕bn = 0 for some k < t ≤ n with probability . When t = n − p + k, b1⊕b2⊕…⊕bk ⊕bn−p+k+1⊕…⊕bn = s. Hence, T[b1⊕b2⊕ …bn−p+k+1⊕…⊕bn [S(0)]] = + (1− )·, and T[b1⊕b2⊕ …bn−p+k+1⊕…⊕bn [S(0)]] = (1− )·. □
Lemma 6. Stacking p (1 ≤ p < n − k) grid pixels {bk+1, bk+2, …, bk+p}, where b1, b2, …, bn are generated after executing Step 5 of Algorithm 3, we have Proof of Lemma 6. We know b1 ⊕ b2 ⊕ …⊕ bk = s, and when t = k + p in Step 4 of Algorithm 3, b1⊕b2⊕ …⊕bk+p = s. So, bk+1⊕bk+2…⊕bk+p = 0 when t = k + p. □
Lemma 7. When p = n − k, stacking p grid pixels {bk+1, bk+2, …, bk+p = bn}, where b1, b2, …, bn are generated after executing Step 5 of Algorithm 3, we have Proof of Lemma 7. Because b1 ⊕ b2 ⊕ …⊕ bk = s, b1⊕b2⊕ …⊕bn = s (by Step 5 of Algorithm 3), and p = n − k, bk+1⊕bk+2…⊕bn = 0. □
Lemma 8. Stacking p (k < p < n) grid pixels {bn−p+1, bn−p+2, …, bn} where b1, b2, …, bn are generated after executing Step 5 of Algorithm 3, we have Proof of Lemma 8. We know b1 ⊕ b2 ⊕ …⊕bn = s, and when t = n − p in Step 4 of Algorithm 3, b1⊕b2⊕ …⊕bn−p = s. Hence, bn−p+1⊕b n−p+2…⊕bn = 0 when t = n − p. □
Lemma 9. In Algorithm 3, stacking any k shares {Bi1, Bi2, …, Bik} from {B1, B2, …, Bn}, we have Proof of Lemma 9. For k > n − k, we use Lemma 3; for k = n − k, apply Lemmas 3 and 7; and for k < n − k, Lemmas 3, 6 and 8 are corresponding. □
Lemma 10. In Algorithm 3, stacking any p (k< p < n) shares {Bi1, Bi2, …, Bip} from {B1, B2, …, Bn} we have Proof of Lemma 10. When we stack any p shares, we will meet one of three difference cases: (1) p > n − k; (2) p = n − k; and (3) p < n − k. In the first case we use Lemma 4 and Lemma 5 to prove it. In the second case we meet Lemmas 4, 5 and 7. When the third case happens, we use Lemmas 4, 5, 6 and 8. □
Theorem 2. Algorithm 3 (k, n) 2D_VCS has visual recognizability when using XOR decryption.
Proof of Theorem 2. To achieve visual recognizability as defined in Definition 4, it is necessary that
T[
B[
S(0)]] −
T[
B[
S(1)]] be greater than 0. According to Lemma 9 and Lemma 10, we can deduce the light transmission for restoring
p encrypted images using XOR, where
k ≤
p <
n. Therefore, we can calculate the following:
Based on the formula above, it is evident that Algorithm 3 for (
k,
n) 2D_VCS meets the condition of being visually recognizable when collecting
k shares or more. □
The contrast under various cases for (
k,
n) 2D_VCS for 2 ≤
k ≤
p ≤
n ≤ 6 using XOR decryption can be deduced from Lemma 9 and Lemma 10, as presented in
Table 3.
With the XOR decryption (⊕) part thoroughly addressed, this paper will proceed to discuss the visual recognizability when the OR decryption (⊗) method is applied. Before proceeding with the proof, let us introduce a variable s, for which 1 ≤ s ≤ n − k, representing the number of encrypted images (out of the total p) that are chosen for restoration and fall within the range of the (k + 1)th to the nth encrypted image. For instance, if we are restoring from 3 encrypted images and s is equal to 2, this implies that 1 encrypted image will be selected from {b1, b2, …, bk}, and 2 encrypted images will be chosen from {bk+1, bk+2, …, bn}. The following lemmas will be categorized based on the different cases of these s selected encrypted images.
Lemma 11. Stacking k grid pixels {b1, b2, …, bk}, where b1, b2, …, bk are generated after executing Step 2 and Step 3 of Algorithm 3, we have Proof of Lemma 11. According to Lemma 1, we know that
b1,
b2, …,
bk−1 are created randomly and independently; thus,
The corresponding pixel
bk is generated by
bk =
b1⊕
b2⊕ …⊕
bk−1⊕
s. So, we have
b1⊗
b2⊗ …⊗
bk =
b1⊗
b2⊗ …⊗
bk−1⊗(
b1⊕
b2⊕ …⊕
bk−1⊕
s). Hence,
When stacking p encrypted images using the OR decryption method, for which k ≤ p < n, the value of s will gradually increase from 1 to min{n − k − 1, p}. These s images will be consecutive encrypted images starting either from bk+1 exclusive-or counting backward from bn. For instance, in the case of (3, 6) 2D_VCS, when p is 3 and s is 1, the set of s images will be {b4} or {b6}, and when s is 2, the set of s images will be {b4, b5} or {b5, b6}. The maximum value for s is min{n − k − 1, p}, which is min{2, 3}, which is equal to 2. Based on the aforementioned conditions, when decrypting p encrypted images using the OR decryption method, the set of p images containing s consecutive encrypted images from {bk+1, bk+2, …, bn} starting either from bk+1 exclusive-or counting backward from bn, let the recovered image be referred to as Rp,1, and let the set of all possible Rp,1 be SR1.
Lemma 12. The light transmission of Rp,1 in SR1 can be derived as follows: Proof of Lemma 12. In Lemmas 5, 6 and 7, it can be observed that when selecting s consecutive pixels from {bk+1, bk+2, …, bn} starting either from bk+1 or counting backward from bn, there is a probability of obtaining white pixels. Next, based on the difference between p and s, we can divide the possible combination of the remaining p − s pixels of Rp,1 into three cases:
- (1)
p − s <
k: In this case, for each of the remaining
p −
s pixels, the probability of being black or white is
, resulting in
combinations. Here,
counts the number of pixels that can be selected from the initial
k and the remaining
pixels, except the
s consecutive pixels and the 2 pixels that could potentially continue the sequence or be against the definition of the exclusive-or. We multiply by 2 because there are two cases: starting from
bk+1 and counting backward from
bn. Hence, we can derive:
This simplifies to:
- (2)
p − s =
k: In this case, for the remaining
p −
s pixels that exactly match the initial
k pixels, there are
= 2 combinations. Similarly, there are
combinations for the remaining pixels that do not select the initial
k pixels completely. Hence, we can derive:
This simplifies to:
- (3)
p −
s >
k: In this case, for the remaining
p − s pixels that are greater than
k, there are
combinations which choose all of the first
k pixels completely. In addition, for the remaining cases, there are
combinations. Hence, we can derive:
This simplifies to:
Combining the three cases with variations in
s, we can obtain:
In the part of T[Rp,1[S(1)]], combinations of light transmission including the first k shares will all be 0. Therefore, we can obtain:
- (1)
when p − s < k, we have
- (2)
when p − s = k, we have
- (3)
when p − s > k, we have
Combining the three cases with variations in
s, we can obtain:
According to the above proof, (24) and (25) are established. □
Based on these conditions, when stacking p encrypted images using the OR decryption method, for which k ≤ p < n, the value of s will gradually increase from 2 to min{n − k − 1, p}. These s shares will be the sum of two sets of consecutive encrypted images, one counted from bk+1 forward and the other counted from bn backward. Let the recovered image be referred to Rp,2, and let the set of all possible Rp,2 be SR2. For example, in the (3, 7) 2D_VCS, when p is 3 and s is 2, these s shares will be {b4, b7}, and when s is 3, these s shares will be {b4, b5, b7} or {b4, b6, b7}.
Lemma 13. The light transmission of Rp,2 in SR2 can be derived as follows: Proof of Lemma 13. The proof process is similar to Lemma 12, as Lemmas 5, 6 and 7 have shown that there is a probability of white in {bk+1, …, bn} when counting from bk+1 or from bn backward. Unlike Lemma 12, where one set of s shares is chosen from {bk+1, …, bn}, Lemma 13 selects two sets that together add up to s shares. Similar to Lemma 12, it is divided into three cases, although the combination here does not need to be multiplied by 2. Instead, a variable i is used, and its range is from 1 to s. i represents the shares counted from bk+1, and the remaining s − i shares are counted from bn backward. Therefore, the three cases are as follows:
- (1)
when p − s < k, we have T[Rp,2[S(0)]] = , which simplifies to .
- (2)
when p − s = k, we have T[Rp,2[S(0)]] = , which simplifies to
- (3)
when p − s > k, we have T[Rp,2[S(0)]] = , which simplifies to .
Combining the three cases with variations in s, we can obtain (26). The proof for (27) T[Rp,2[S(1)]] is similar to the proof of (26); the results can be concluded. □
There is another possible combination when stacking p encrypted images using the OR decryption method for n − k ≤ p < n. That is, s equals n − k, indicating that {bk+1, …, bn} are all included in the p shares. Let the recovered image be referred to Rp,3 and the set of all possible Rp,3 be SR3.
Lemma 14. The light transmission of Rp,3 in SR3 can be derived as follows: Proof of Lemma 14. In the case of
Rp,3, the proof process is similar to Lemmas 12 and 13. When
s equals
n −
k, we have
bk+1⊕
bk+2⊕ …⊕
bn = 0. In this case, there is a probability of
that
t equals
n, and as a result, only
bn has been computed (not random) in
bk+1 to
bn. The remaining probability of
may select one pixel
bt from
bk+1 to
bn−1, such that both
bt and
bn have been computed. Furthermore, here
s =
n −
k and
p − s =
p − n +
k <
k because
p <
n. Therefore, we only need to consider
p −
s <
k, leading to the following:
Substituting
s =
n −
k yields and simplifies to:
When stacking p encrypted images using the OR decryption method, for which k ≤ p < n, and it always includes the first k encrypted images but excludes the condition as Rp,1 or Rp,2, let the recovered image be referred to Rp,4. In addition, let the set of all possible Rp,4 be SR4.
Lemma 15. The light transmission of Rp,4 in SR4 can be derived as follows: Proof of Lemma 15. There will be
combinations when taking
p out of
n, which are guaranteed to include the first
k pixels. However, we need to subtract the combinations already calculated in
Rp,1 and
Rp,2. In the case of
Rp,1 and when
p − s =
k and
p − s >
k, there are
combinations that include the first
k shares. In the case of
Rp,2 and when
p − s =
k and
p − s >
k, there are
combinations that include the first
k shares. So, the number of possible combinations for
Rp,4 is
Next, based on Lemma 11, we obtain the result of stacking the first k images, and the results can be concluded. □
At last, when stacking p encrypted images using the OR decryption method, for which k ≤ p < n, these are still some combinations not included in Rp,1, Rp,2, Rp,3 or Rp,4. Let the recovered image be referred to as Rp,5 and the set of all possible Rp,5 be SR5.
Lemma 16. The light transmission of Rp,5 in SR5 can be derived as follows: where
Proof of Lemma 16. There will be
combinations when taking
p out of
n. However, we need to subtract the combinations already calculated in
Rp,1,
Rp,2,
Rp,3 and
Rp,4. So, we obtain:
Then, based on Lemma 1, we obtain the result of stacking all of the p images in Rp,5, and the results can be concluded. □
Lemma 17. In Algorithm 3, stacking all n encrypted images from {B1, B2, …, Bn}, we have Proof of Lemma 17. When all the encrypted images are stacked together using the OR operator, it is known that the first
k images will be equal to
s, and all
n images will also be equal to
s. In the sixth step of Algorithm 3, the first
t images will also be equal to
s, but there is a
probability that
t will be equal to
n. Therefore, we can derive the following:
Lemma 18. In Algorithm 3, stacking any p (k≤ p≤ n) shares {Bi1, Bi2, …, Bip} from {B1, B2, …, Bn}, we have Proof of Lemma 18. Based on Lemma 11 to Lemma 18, we have considered all possible cases when using OR decryption in (k, n) 2D_VCS. Therefore, to calculate the light transmission (T), we simply need to sum them up. □
From Lemma 17 and Lemma 18, we can derive the contrast under different cases for OR decryption in (
k,
n) 2D_VCS, as illustrated in
Table 4.
Theorem 3. Algorithm 3 (k, n) 2D_VCS has visual recognizability when using OR decryption.
Proof of Theorem 3. From Lemma 17, Lemma 18, it can be observed that when collecting k or more encrypted images and using the OR decryption method, the contrast (α) is always greater than 0. A contrast greater than 0 implies that theoretically, the information of the secret image S is visible, and the decryption is successful, meeting the conditions for visual recognizability. Therefore, Theorem 3 is proven. □
Based on the aforementioned Lemmas and Theorems, it becomes evident that Algorithm 3 for (k, n) 2D_VCS is both secure and functional. This conclusion reaffirms that the system not only preserves the confidentiality of the secret image but also offers a practical approach to decrypting it, making it a robust and reliable solution for visual secret sharing.
Now, we will demonstrate the theoretical security and usability of Algorithm 4 presented in this paper for (k, n) 2D_RIVCS.
Theorem 4. Algorithm 4 for (k, n) 2D_RIVCS is secure and visually recognizable.
Proof of Theorem 4. According to Algorithm 4, (k, n) 2D_RIVCS is primarily constructed by repetitively employing (k, n) 2D_VCS to encrypt different secret levels Sld. Therefore, to establish the security and visual recognizability of Algorithm 4, it is necessary to first demonstrate the security and visual recognizability of Algorithm 3. As shown in Theorems 1, 2 and 3, the security and visual recognizability of Algorithm 3 have already been established. Consequently, it can be inferred that Algorithm 4 is secure and visually recognizable as well. □
As the secret levels Sl of the secret image S are arbitrarily determined by the user, the proportion of these levels can vary with each division. Consequently, the fidelity of the reconstruction may differ when different numbers of encrypted images p are collected. Therefore, it is impractical to establish a fixed contrast between the reconstructed image and the secret image S for each case. According to Theorem 1, it is evident that obtaining a minimum of k or more encrypted images enables the recovery of clues related to the secret image S. With fewer than k images, only a chaotic and indecipherable image can be obtained.
Next, this paper analyzes the time complexity of Algorithm 4. In steps 1~4 of Algorithm 4, it can be observed that, for each pixel (i, j), the steps from 2~4 in Algorithm 4 are repeated. The size of the secret image is , indicating that these steps will be repeated times. Note that the time complexity of Steps 2–5 of Algorithm 3 is O(k + t + n) = O(n). Therefore, the time complexity of Algorithm 4 is O(nWH). It is equal to the size of the output, so Algorithm 4 is a linear-time algorithm. Due to the nature of the algorithm, hardware devices and processor efficiency do not significantly impact the execution speed. Users can employ any hardware, software and programming language to implement the algorithm presented in this paper. However, we will provide detailed information about the specific software used in the experiments (in the next section), namely MATLAB R2022b.
Algorithm 4 combines Algorithm 3 and a region incrementing visual cryptography scheme (RIVCS), thus introducing a novel application for Algorithm 3 while affording a broader spectrum of use cases. This innovative approach leverages the inherent strengths of both Algorithm 3 and RIVCS, paving the way for the fusion of these two cryptographic techniques. As a result, Algorithm 4 is capable of addressing diverse scenarios, showcasing its adaptability and extending the realm of possibilities for secure and visually recognizable image encryption and decryption.