Robustness Analysis of Exponential Synchronization in Complex Dynamic Networks with Deviating Argumentsand Parameter Uncertainties
Abstract
:1. Introduction
- In the paper, we study the robust synchronization of CDNs with DAs. Compared with systems with ordinary time delays, the system discussed in this paper involves both delayed and advanced coupling, and we employ an unified model to describe the finite speed of signal propagation and to predict the behavior of nodes.
- We introduce upper bounds for the argument length and parameter size in CDNs by employing Gronwall inequalities and inequality techniques.
- Massive complex networks are scale-free, meaning that most nodes are disconnected, but a few have many connections. In addition, the connection matrix in the model of CDNs are all symmetric, i.e., if nodes i and j are connected and disconnected, the adjacency matrix parameters are 0 and 1, respectively. This matrix is described in the model establishment in Section 2 and the simulation in Section 4.
2. Preliminaries
2.1. Notation
2.2. Preliminary Preparation
3. Main Results
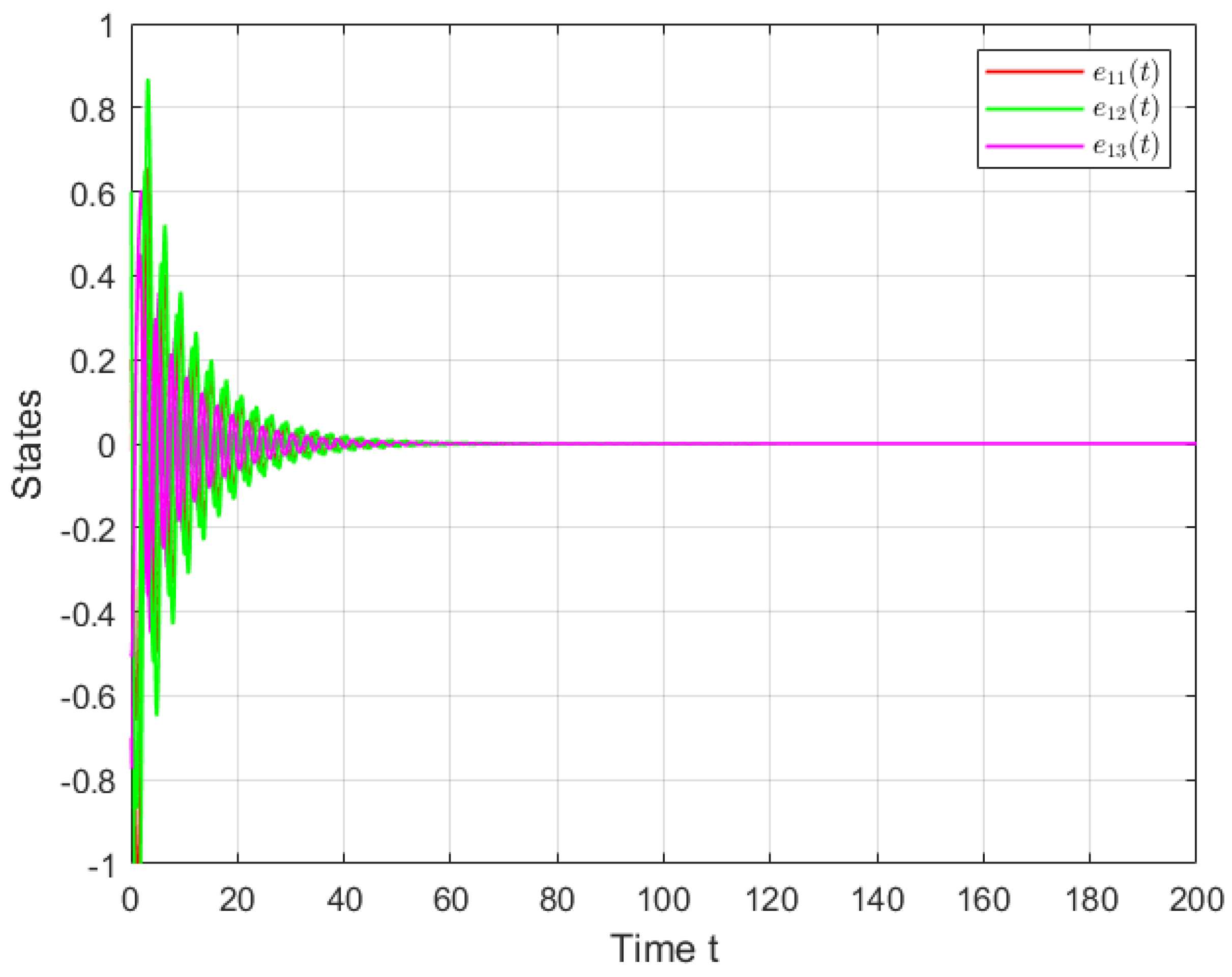
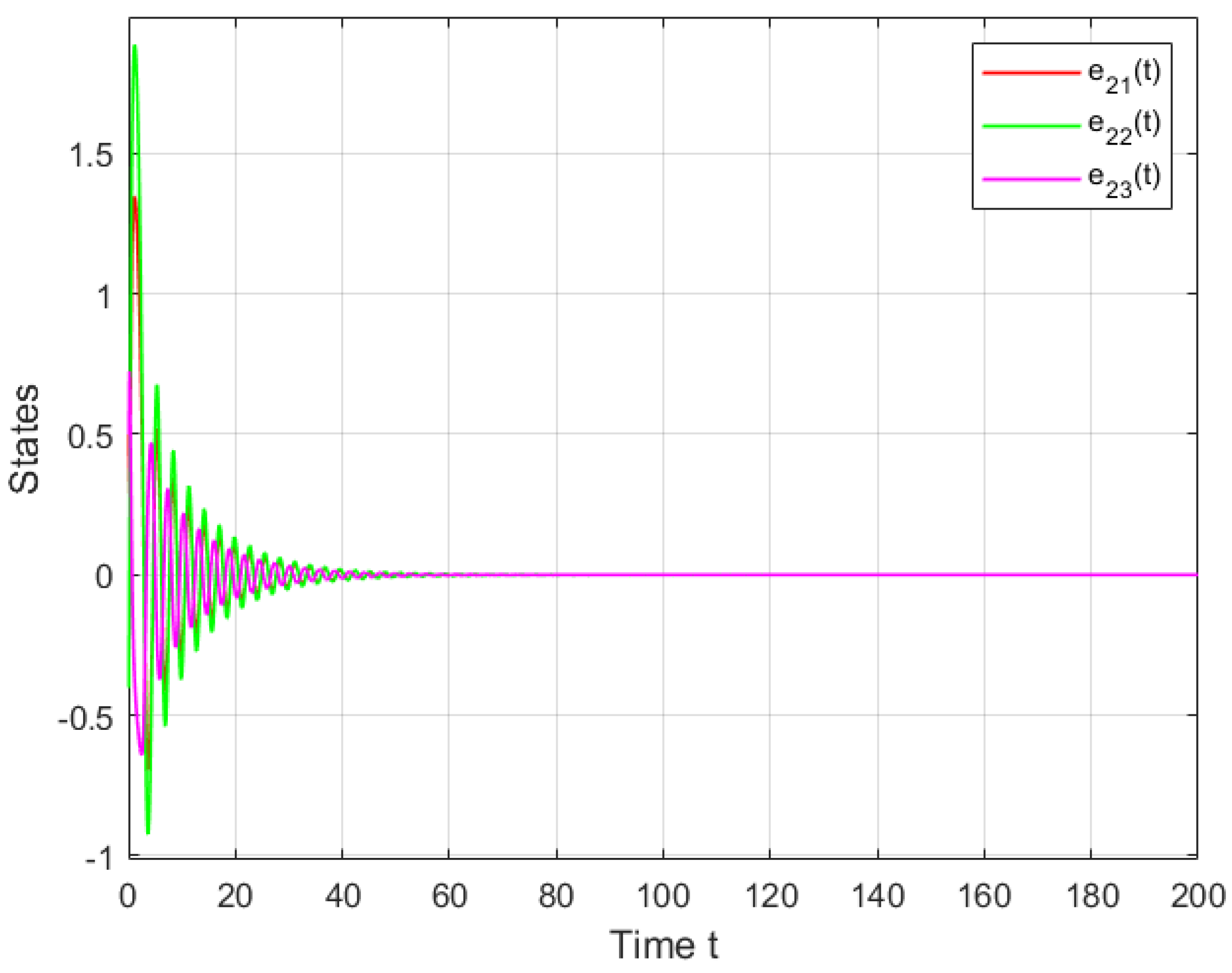
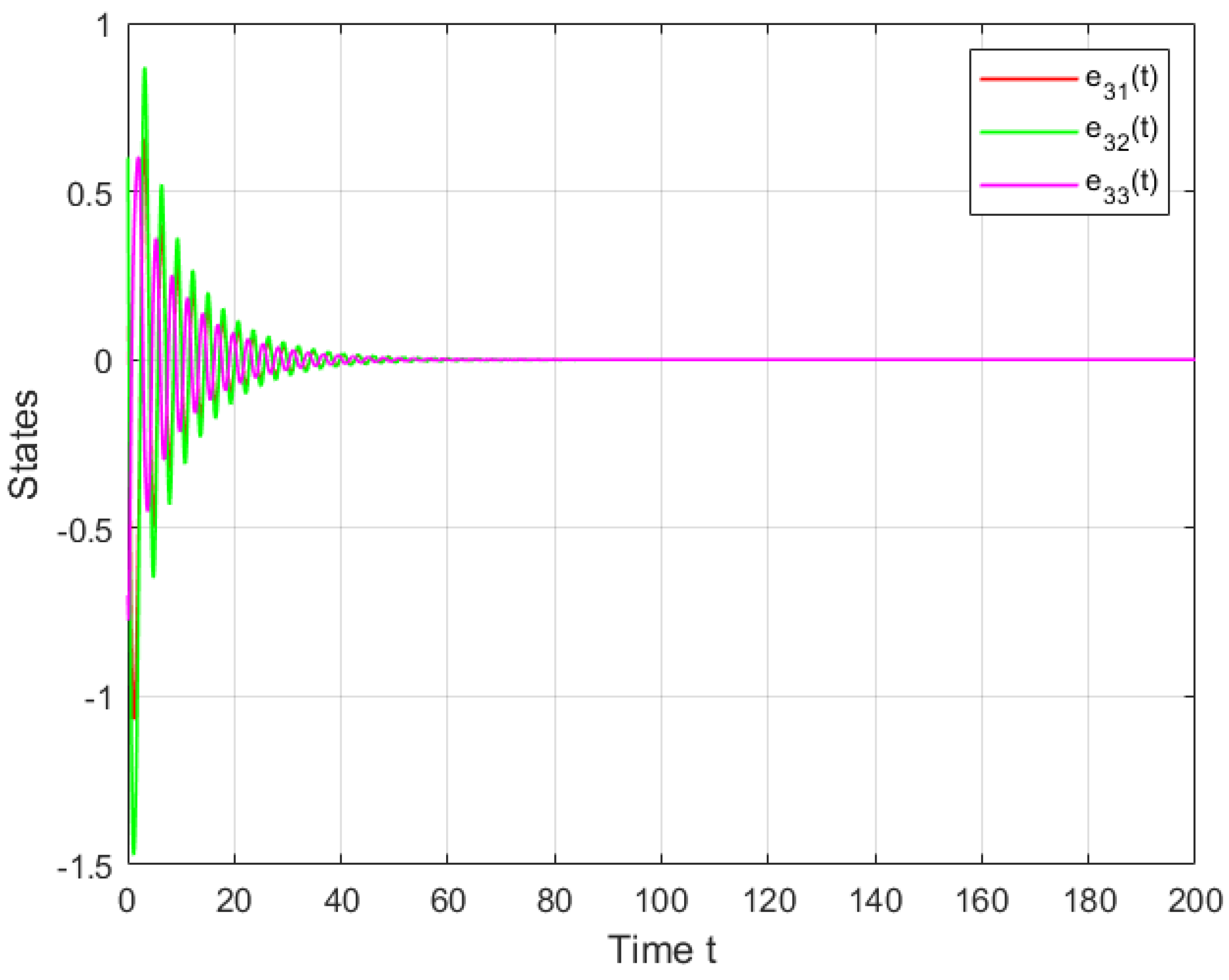
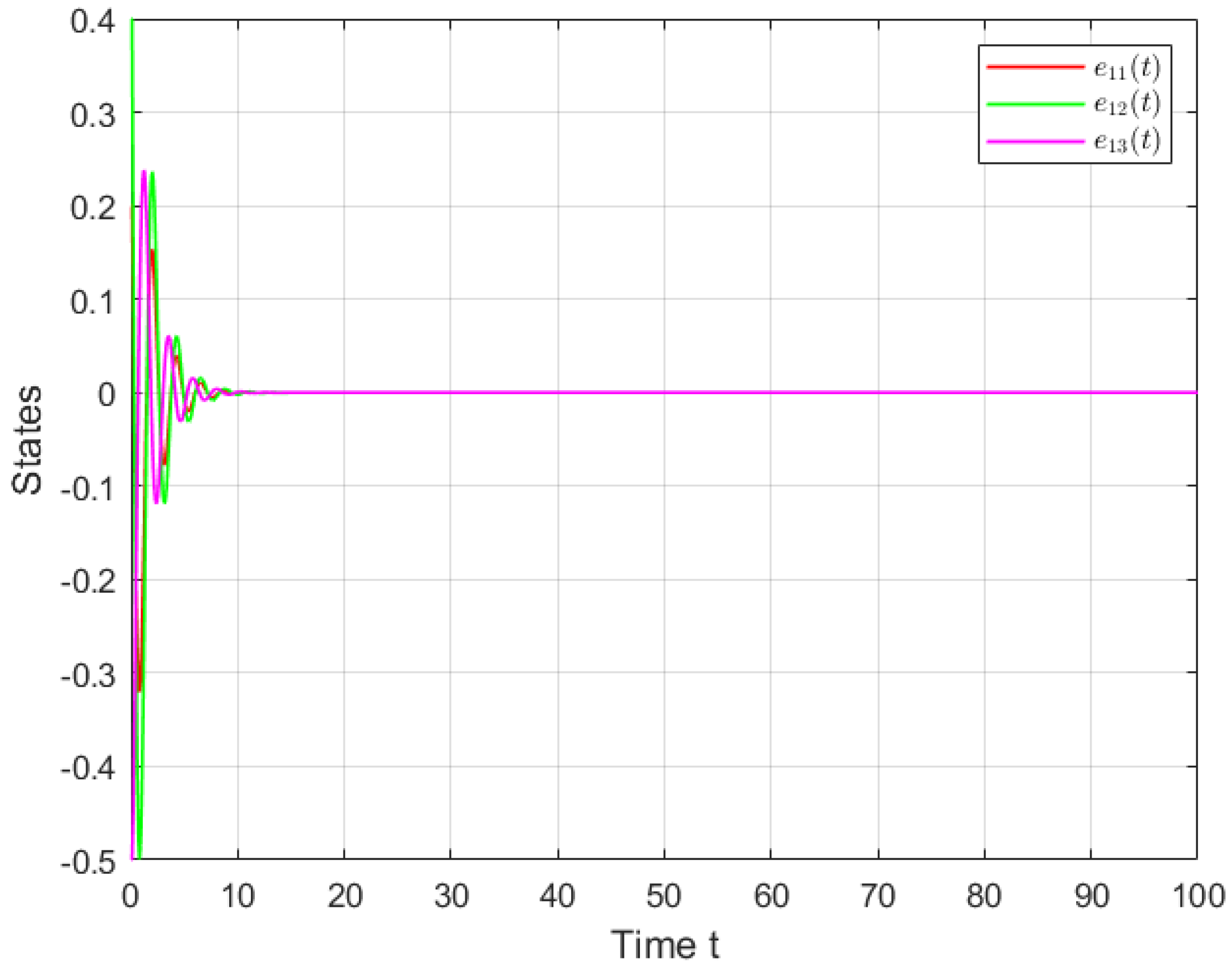
4. Simulations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, J.; Xiang, L.; Liu, Z. Synchronization in complex delayed dynamical networks with impulsive effects. Physica A 2007, 384, 684–692. [Google Scholar] [CrossRef]
- Yu, W.; Chen, G.; Lü, J. On pinning synchronization of complex dynamical networks. Automatica 2009, 45, 429–435. [Google Scholar] [CrossRef]
- Ali, M.S.; Usha, M.; Orman, Z.; Arik, S. Improved result on state estimation for complex dynamical networks with time varying delays and stochastic sampling via sampled-data control. Neural Netw. 2019, 114, 28–37. [Google Scholar]
- Wang, L.; Sun, Y.-X. Robustness of pinning a general complex dynamical network. Phys. Lett. A 2010, 374, 1699–1703. [Google Scholar] [CrossRef]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.-U. Complex networks: Structure and dynamics. Phys. Rep. 2023, 424, 175–308. [Google Scholar] [CrossRef]
- Gao, P.; Wang, Y.; Zhao, J.; Zhang, L.; Peng, Y. Links synchronization control for the complex dynamical network. Neurocomputing 2023, 515, 59–67. [Google Scholar] [CrossRef]
- Weng, T.; Chen, X.; Ren, Z.; Xu, J.; Yang, H. Multiple moving agents on complex networks: From intermittent synchronization to complete synchronization. Physica A 2023, 614, 128562. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J.; Lu, J.; Lou, J. Finite-time synchronization of complex networks with partial communication channels failure. Inf. Sci. 2023, 634, 539–549. [Google Scholar] [CrossRef]
- Li, B. Finite-time synchronization for complex dynamical networks with hybrid coupling and time-varying delay. Nonlinear Dyn. 2014, 76, 1603–1610. [Google Scholar] [CrossRef]
- Wang, J.; Ru, T.; Xia, J.; Wei, Y.; Wang, Z. Finite-time synchronization for complex dynamic networks with semi-markov switching topologies: An h∞ event-triggered control scheme. Appl. Math. Comput. 2019, 356, 235–251. [Google Scholar] [CrossRef]
- Shi, L.; Zhu, H.; Zhong, S.; Zeng, Y.; Cheng, J. Synchronization for time-varying complex networks based on control. J. Comput. Appl. Math. 2016, 301, 178–187. [Google Scholar] [CrossRef]
- Arbi, A.; Cao, J.; Alsaedi, A. Improved synchronization analysis of competitive neural networks with time-varying delays. Nonlinear Anal. Model. 2018, 23, 82–107. [Google Scholar] [CrossRef]
- Liu, X.; Yu, X.; Xi, H. Finite-time synchronization of neutral complex networks with markovian switching based on pinning controller. Neurocomputing 2015, 153, 148–158. [Google Scholar] [CrossRef]
- Xu, Z.; Li, X.; Duan, P. Synchronization of complex networks with time-varying delay of unknown bound via delayed impulsive control. Neural Netw. 2020, 125, 224–232. [Google Scholar] [CrossRef]
- Wu, Y.; Shen, B.; Ahn, C.K.; Li, W. Intermittent dynamic event-triggered control for synchronization of stochastic complex networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 2639–2650. [Google Scholar] [CrossRef]
- Zhu, Q.; Cao, J. Stability analysis of markovian jump stochastic bam neural networks with impulse control and mixed time delays. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 467–479. [Google Scholar]
- Akhmet, M.U.; Aruğaslan, D.; Yılmaz, E. Stability analysis of recurrent neural networks with piecewise constant argument of generalized type. Neural Netw. 2010, 23, 805–811. [Google Scholar] [CrossRef] [PubMed]
- Wu, A.; Liu, L.; Huang, T.; Zeng, Z. Mittag-leffler stability of fractional-order neural networks in the presence of generalized piecewise constant arguments. Neural Netw. 2017, 85, 118–127. [Google Scholar] [CrossRef] [PubMed]
- Shen, W.; Zeng, Z.; Wen, S. Synchronization of complex dynamical network with piecewise constant argument of generalized type. Neurocomputing 2016, 173, 671–675. [Google Scholar] [CrossRef]
- Fang, W.; Xie, T.; Li, B. Robustness analysis of fuzzy cellular neural network with deviating argument and stochastic disturbances. IEEE Access 2023, 11, 3717–3728. [Google Scholar]
- Fang, W.; Xie, T.; Li, B. Robustness analysis of bam cellular neural network with deviating arguments of generalized type. Discret. Dyn. Nat. Soc. 2023, 2023, 9570805. [Google Scholar] [CrossRef]
- Zhu, S.; Shen, Y. Robustness analysis for connection weight matrix of global exponential stability recurrent neural networks. Neurocomputing 2013, 101, 370–374. [Google Scholar] [CrossRef]
- Liu, S.; Yu, Y.; Zhang, S. Robust synchronization of memristor-based fractional-order hopfield neural networks with parameter uncertainties. Neural Comput. Appl. 2019, 31, 3533–3542. [Google Scholar] [CrossRef]
- Wong, W.K.; Li, H.; Leung, S. Robust synchronization of fractional-order complex dynamical networks with parametric uncertainties. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4877–4890. [Google Scholar] [CrossRef]
- Arbi, A. Robust model predictive control for fractional-order descriptor systems with uncertainty. Fract. Calc. Appl. Anal. 2023, 1–17. [Google Scholar] [CrossRef]
- Zeng, Z.; Wang, J.; Liao, X. Global exponential stability of a general class of recurrent neural networks with time-varying delays. IEEE Trans. Circuits Syst. 2003, 50, 1353–1358. [Google Scholar] [CrossRef]
- Bellman, R. The stability of solutions of linear differential equations. Duke Math. J. 1943, 10, 643–647. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, T.; Xiong, X. Robustness Analysis of Exponential Synchronization in Complex Dynamic Networks with Deviating Argumentsand Parameter Uncertainties. Symmetry 2024, 16, 158. https://doi.org/10.3390/sym16020158
Xie T, Xiong X. Robustness Analysis of Exponential Synchronization in Complex Dynamic Networks with Deviating Argumentsand Parameter Uncertainties. Symmetry. 2024; 16(2):158. https://doi.org/10.3390/sym16020158
Chicago/Turabian StyleXie, Tao, and Xing Xiong. 2024. "Robustness Analysis of Exponential Synchronization in Complex Dynamic Networks with Deviating Argumentsand Parameter Uncertainties" Symmetry 16, no. 2: 158. https://doi.org/10.3390/sym16020158
APA StyleXie, T., & Xiong, X. (2024). Robustness Analysis of Exponential Synchronization in Complex Dynamic Networks with Deviating Argumentsand Parameter Uncertainties. Symmetry, 16(2), 158. https://doi.org/10.3390/sym16020158






