Dynamics of Iterations of the Newton Map of sin(z)
Abstract
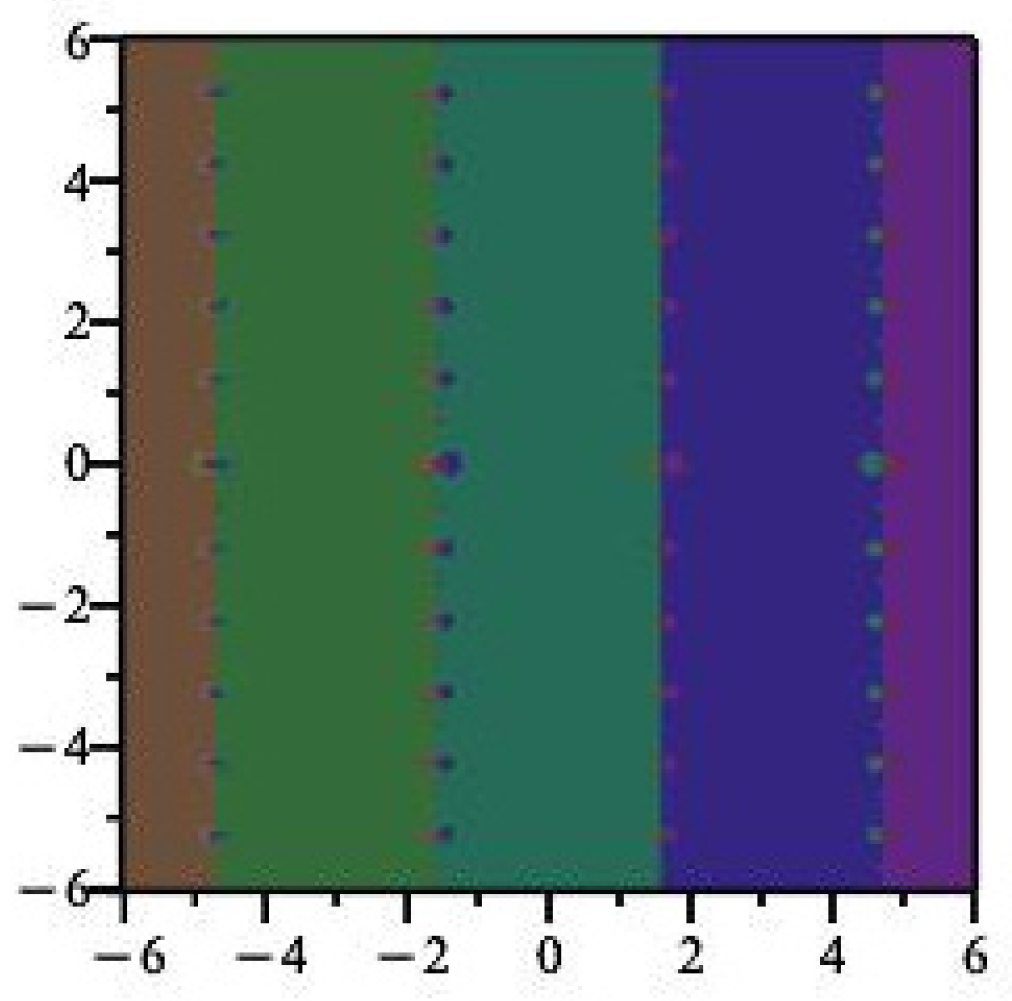
1. Introduction
2. Newton’s Method and
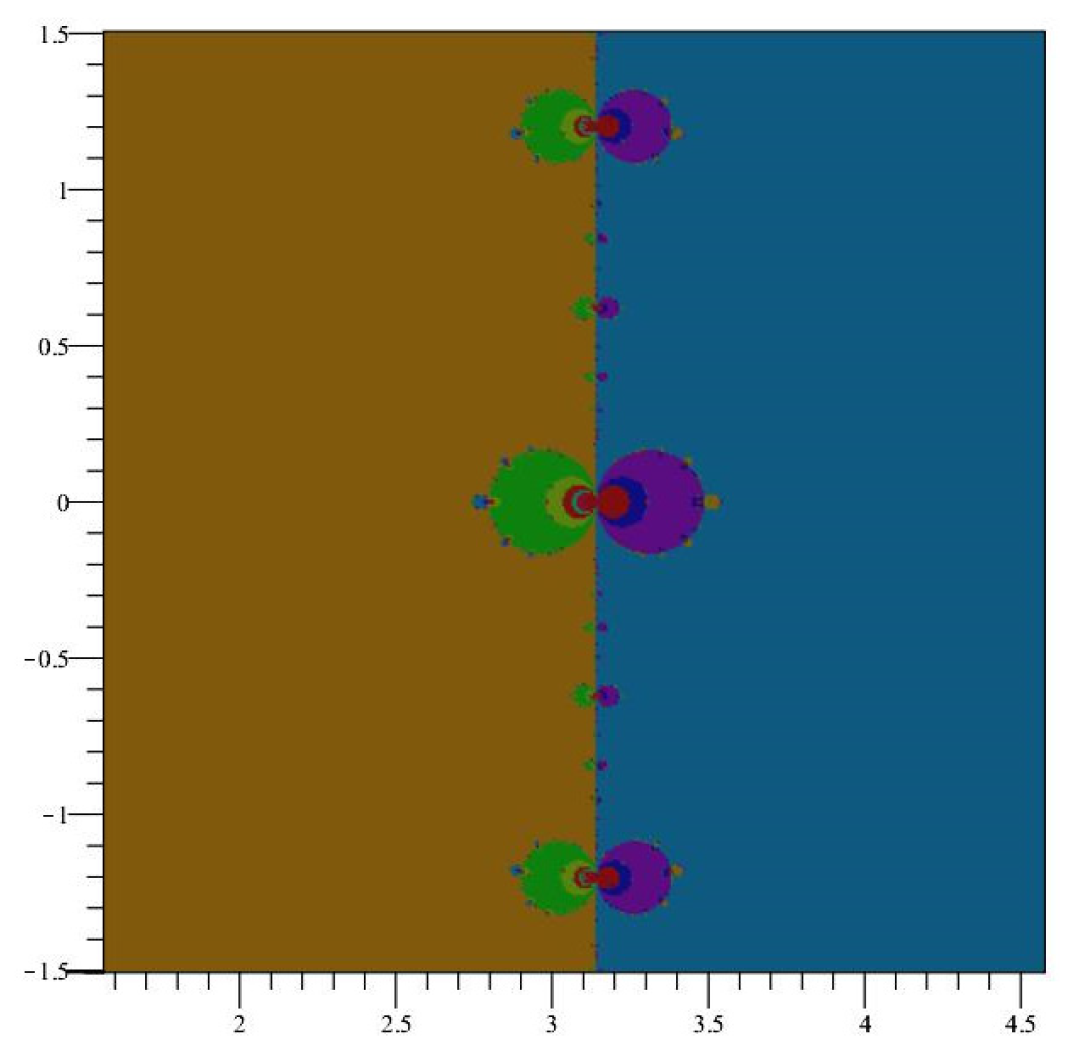
2.1. Introduction to the Dynamics of the Newton Map of sin(z)
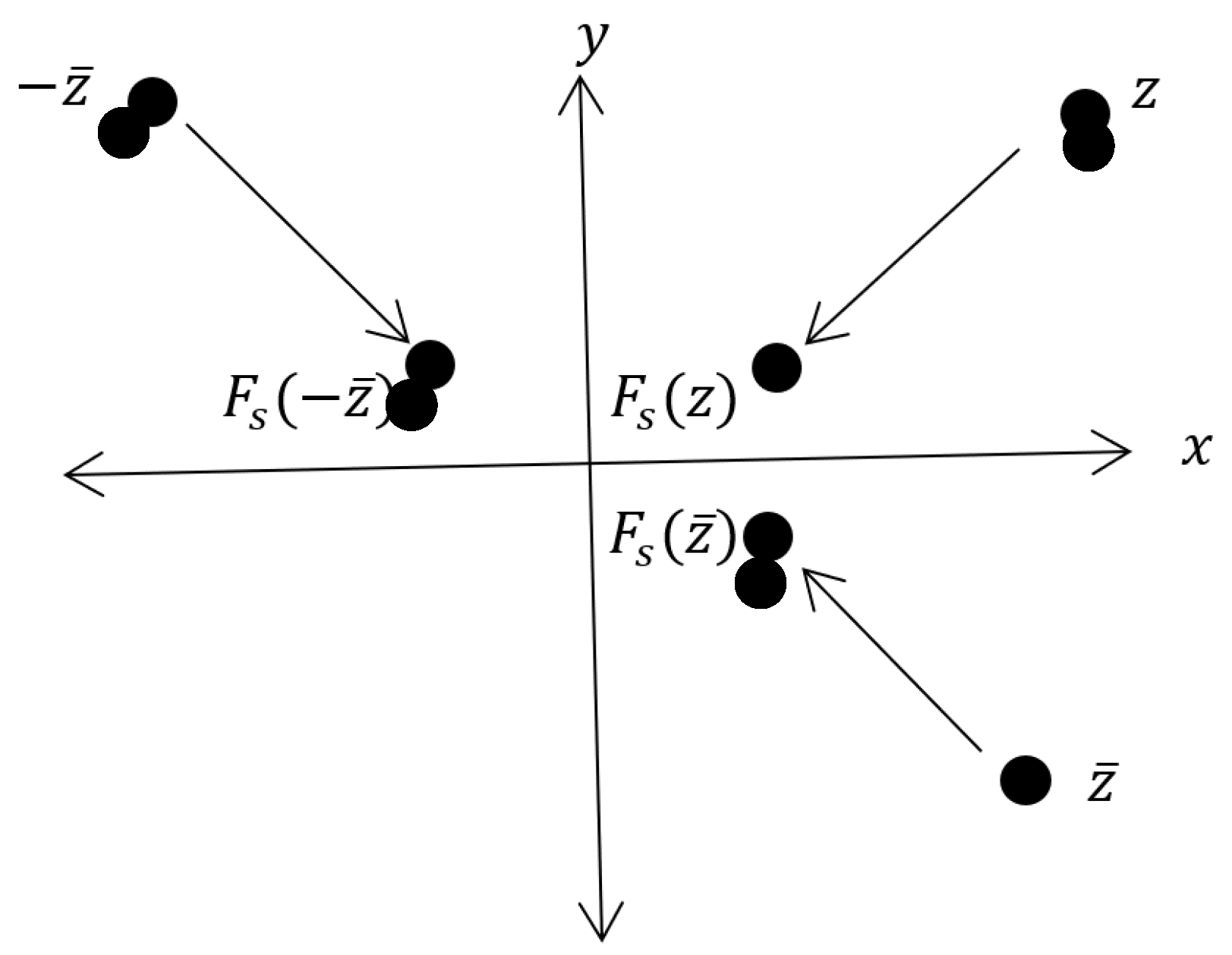
2.2. Symmetry of
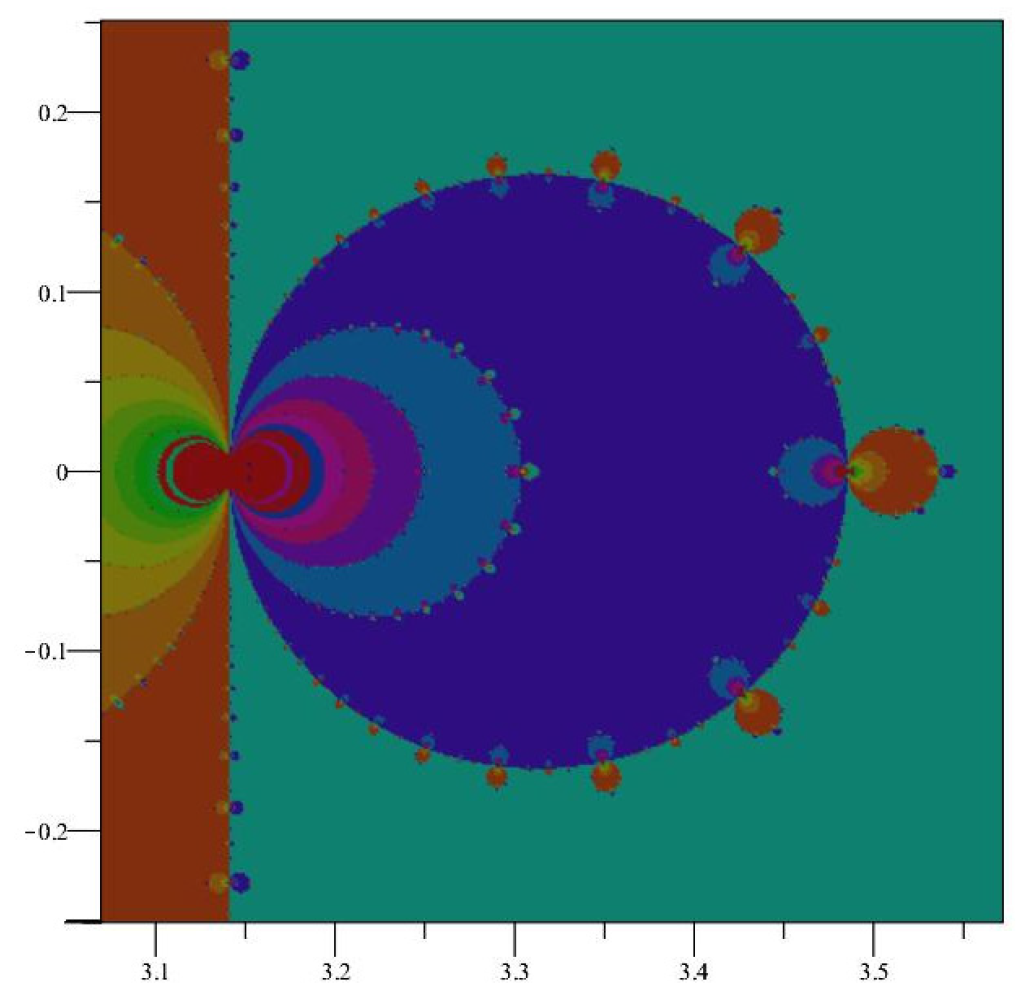
2.3. Bounding the Primary Basins
2.3.1. Bounds and Convergence along the x-Axis
2.3.2. Periodic Points along the x-Axis
2.3.3. Bounds along Vertical Lines
2.3.4. Convergence along Vertical Lines
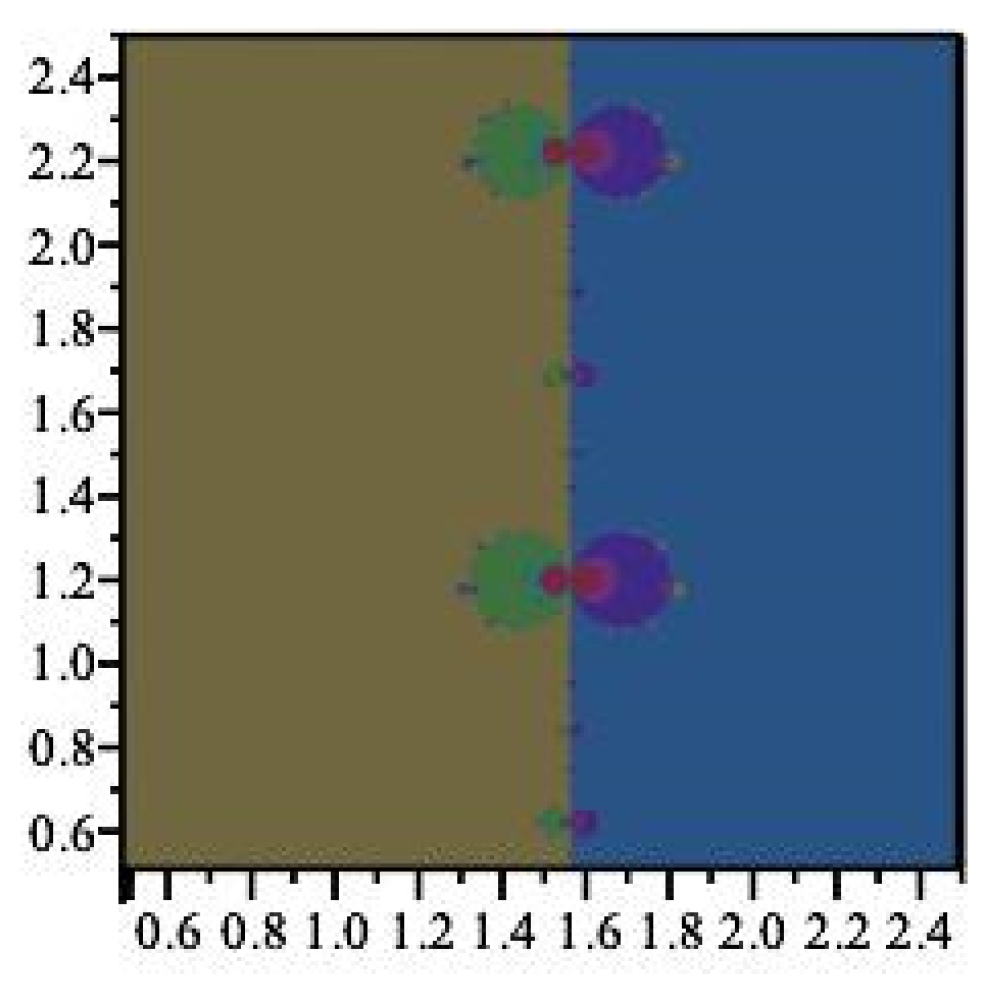
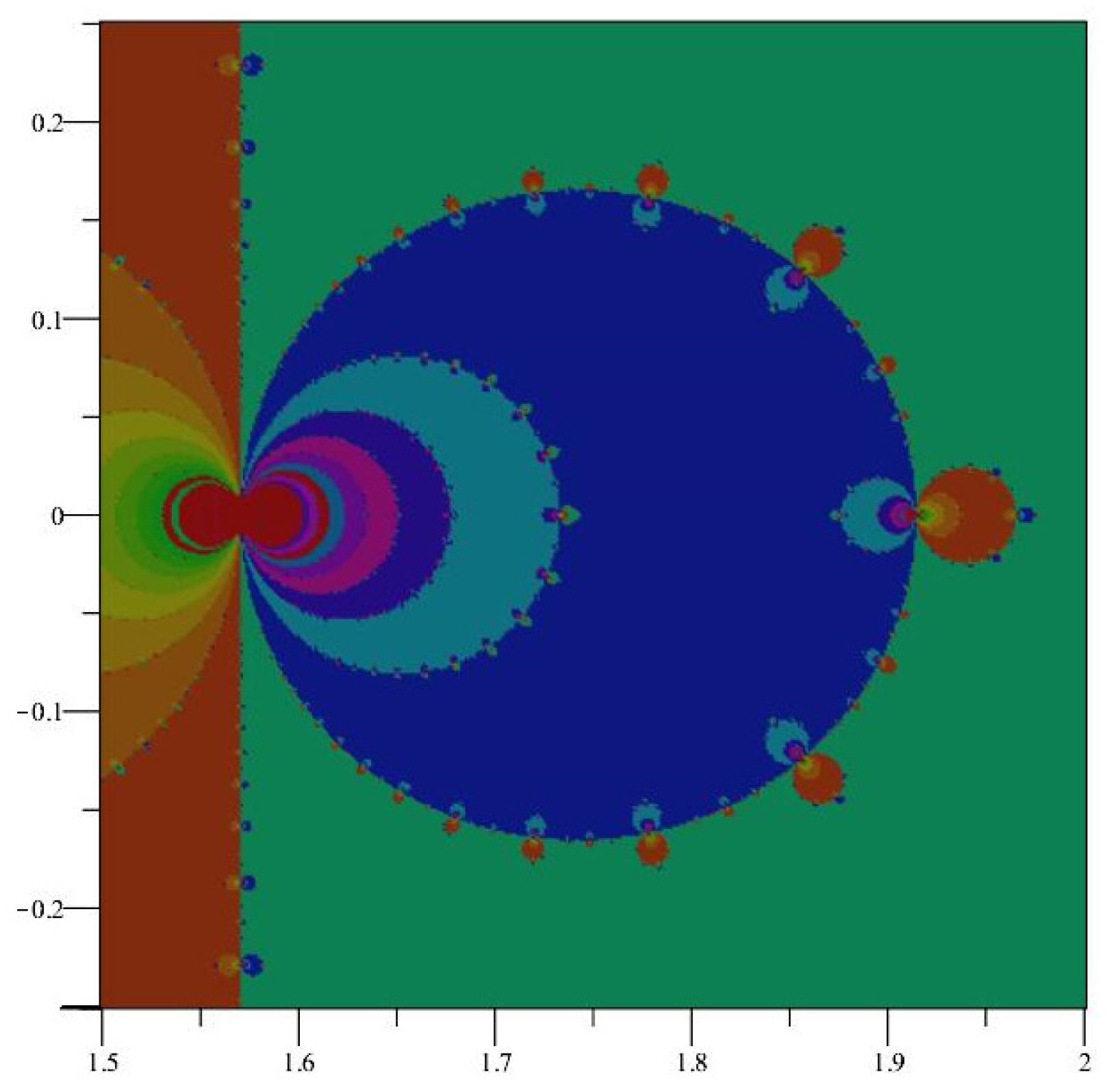
2.3.5. Convergence in the Complex Plane
3. Comparison of Newton Maps of sin(z) and cos(z)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gilbert, W. Newton’s Method for multiple roots. Comput. Graph. 1994, 18, 227–229. [Google Scholar] [CrossRef]
- Walsh, J. The Dynamics of Newton’s Method for Cubic Polynomials. Coll. Math. J. 1995, 26, 22–28. [Google Scholar] [CrossRef]
- Alexander, D.; Iavernaro, F.; Rosa, A. Early Days in Complex Dynamics: A History of Complex Dynamics in One Variable during 1906–1942; American Mathematical Society: Providence, RI, USA, 2012. [Google Scholar]
- Haeseler, F.; Peitgen, H. Newton’s method and complex dynamical systems. Acta Appl. Math. 1988, 13, 3–58. [Google Scholar] [CrossRef]
- Blanchard, P. The Dynamics of Newton’s Method. In Proceedings of the Symposia in Applied Mathematics, Cincinnati, OH, USA, January 1994; Complex Dynamical Systems: The Mathematics behind the Mandelbrot and Julia Sets. Devaney, R.L., Ed.; American Mathematical Society: Providence, RI, USA, 1994; Volume 49, pp. 139–154. [Google Scholar]
- Barnard, R.; Dwyer, J.; Williams, E.; Williams, G. Conjugacies of the Newton Maps of Rational Functions. Complex Var. Elliptic Equ. 2019, 64, 1666–1685. [Google Scholar] [CrossRef]
- Dwyer, J.; Barnard, R.; Cook, D.; Corte, J. Iteration of Complex Functions and Newton’s Method. Aust. Sr. Math. J. 2009, 23, 9–16. [Google Scholar]
- Bray, K.; Dwyer, J.; Barnard, R.; Williams, G. Fixed Points, Symmetries, and Bounds for Basins of Attraction of Complex Trigonometric Functions. Int. J. Math. Math. Sci. 2020, 2020, 1853467. [Google Scholar] [CrossRef]
- Saff, E.B.; Snider, A.D. Fundamentals of Complex Analysis for Mathematics, Science, and Engineering, 3rd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 2003. [Google Scholar]
- Stankewitz, R. Complex Dynamics: Chaos, Fractals, the Mandelbrot Set, and More. In Explorations in Complex Analysis; Mathematical Association of America: Washington, DC, USA, 2009. [Google Scholar]
- Conway, J. Functions of One Complex Variable I; Springer: New York, NY, USA, 1978. [Google Scholar]
- Li, T.Y.; Yorke, J.A. Period three implies chaos. Am. Math. Mon. 1975, 82, 985–992. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cloutier, A.; Dwyer, J.; Barnard, R.W.; Stone, W.D.; Williams, G.B. Dynamics of Iterations of the Newton Map of sin(z). Symmetry 2024, 16, 162. https://doi.org/10.3390/sym16020162
Cloutier A, Dwyer J, Barnard RW, Stone WD, Williams GB. Dynamics of Iterations of the Newton Map of sin(z). Symmetry. 2024; 16(2):162. https://doi.org/10.3390/sym16020162
Chicago/Turabian StyleCloutier, Aimée, Jerry Dwyer, Roger W. Barnard, William D. Stone, and G. Brock Williams. 2024. "Dynamics of Iterations of the Newton Map of sin(z)" Symmetry 16, no. 2: 162. https://doi.org/10.3390/sym16020162
APA StyleCloutier, A., Dwyer, J., Barnard, R. W., Stone, W. D., & Williams, G. B. (2024). Dynamics of Iterations of the Newton Map of sin(z). Symmetry, 16(2), 162. https://doi.org/10.3390/sym16020162






