Determining the Safest Anchoring Knot in a Fall Arrest System by Means of Static Tests
Abstract
:1. Introduction
2. Materials and Methods
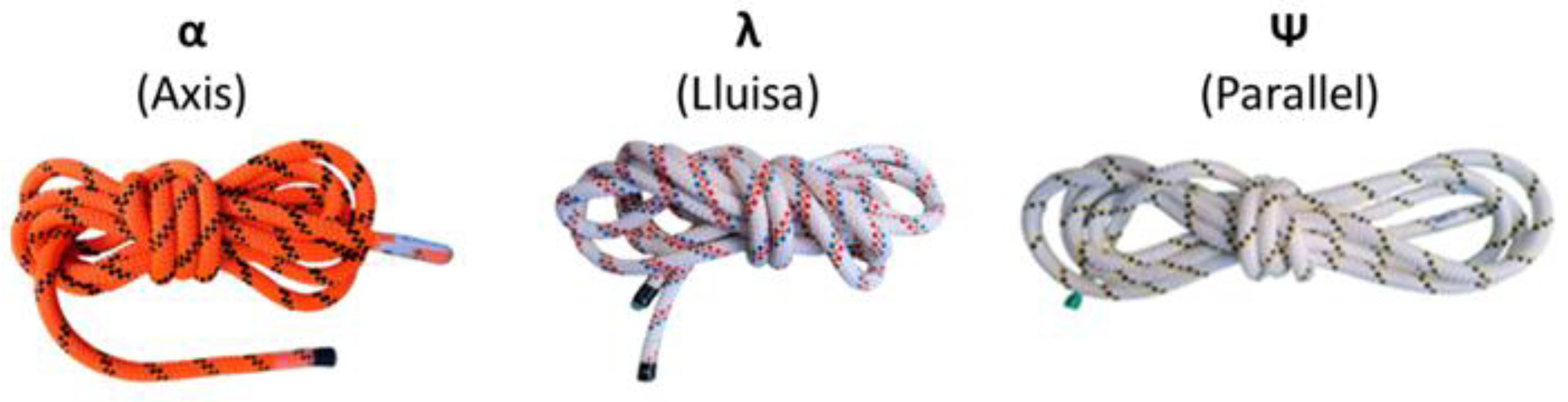
2.1. Ropes and Test Samples
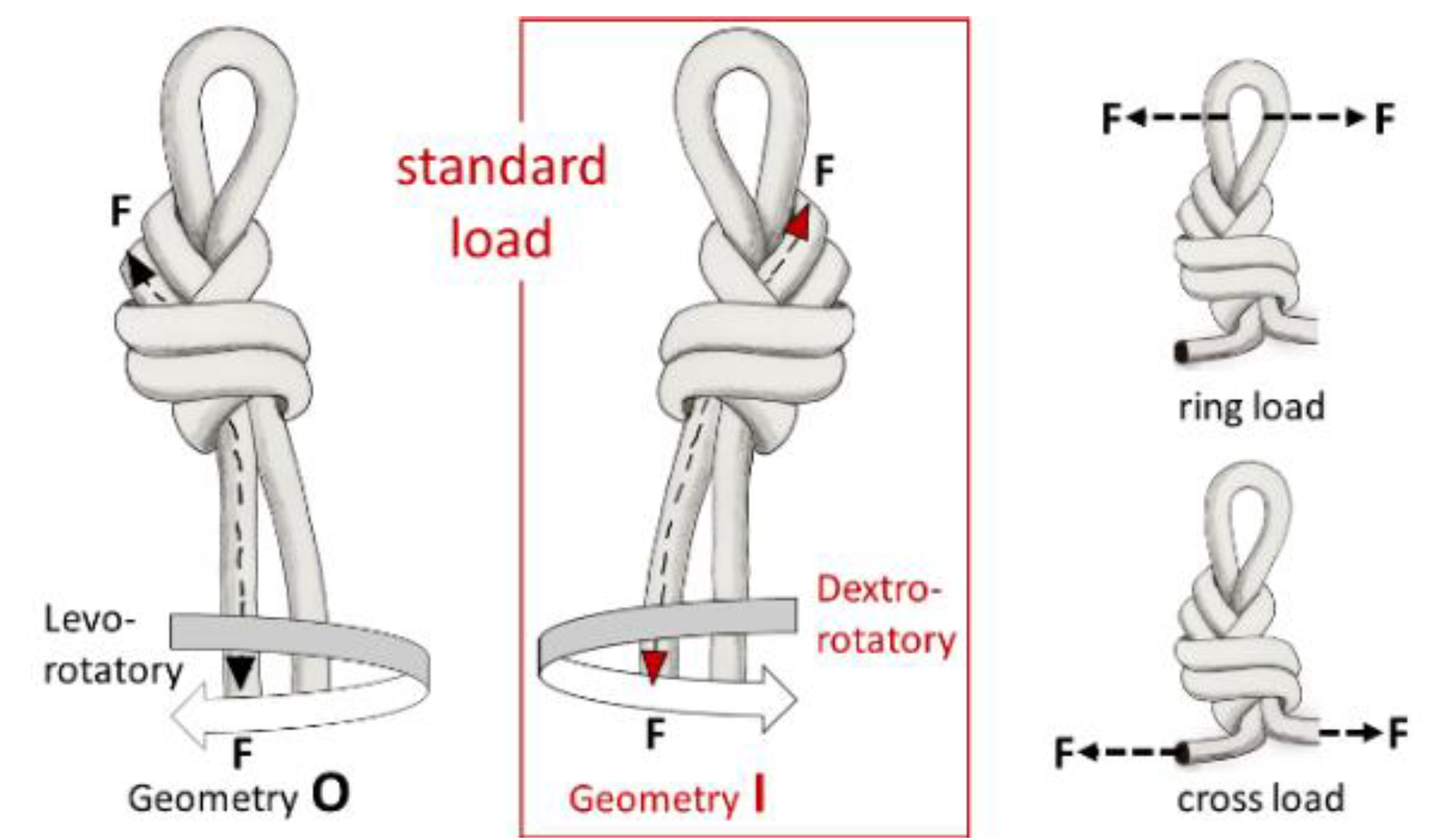
2.2. Knots
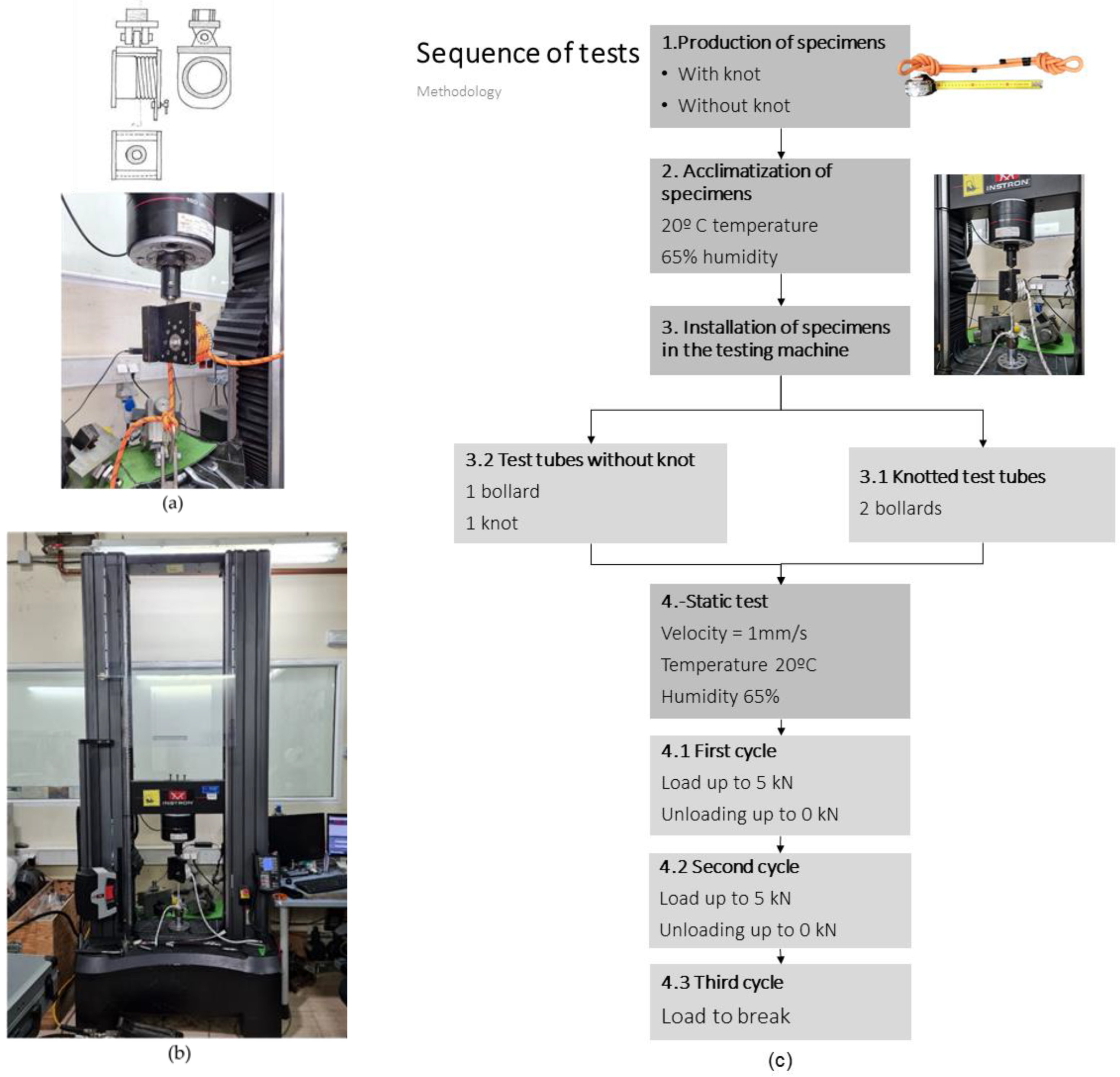
2.3. Experiment Setup and Procedure
3. Results and Discussion
3.1. Statistical Analysis
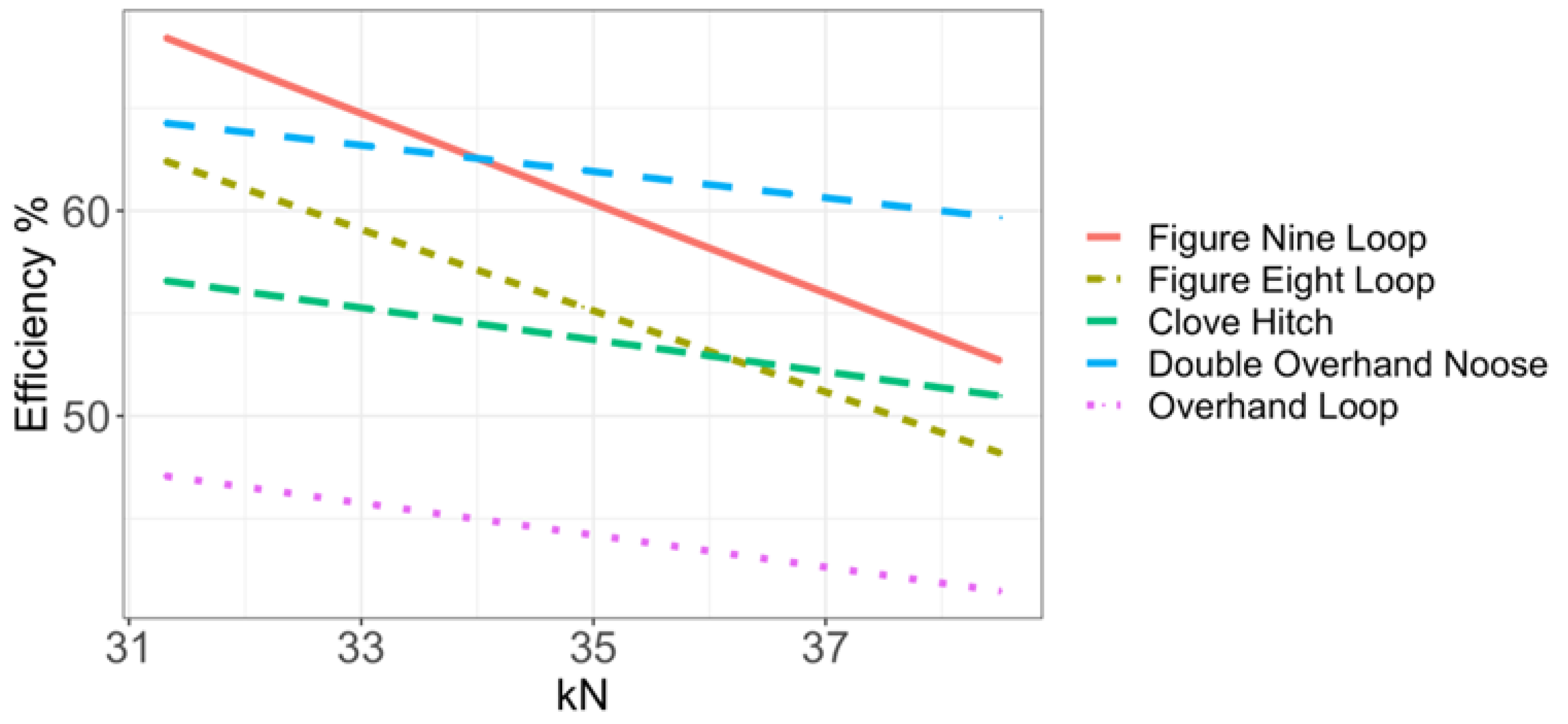
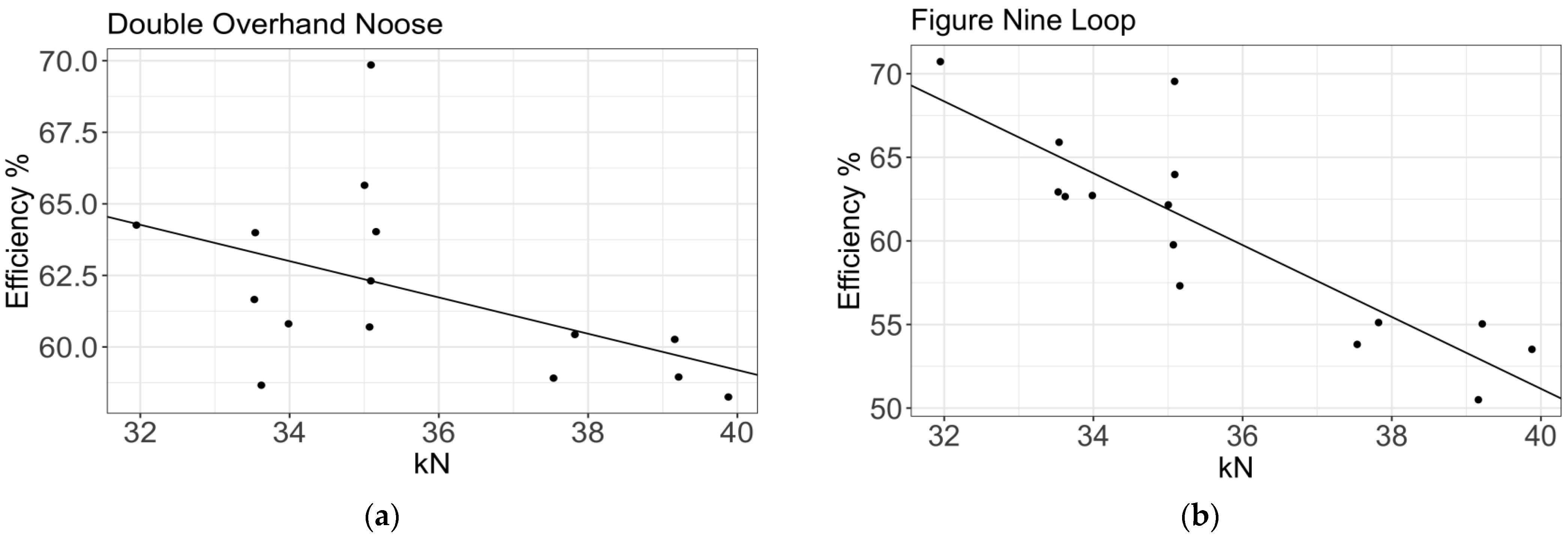
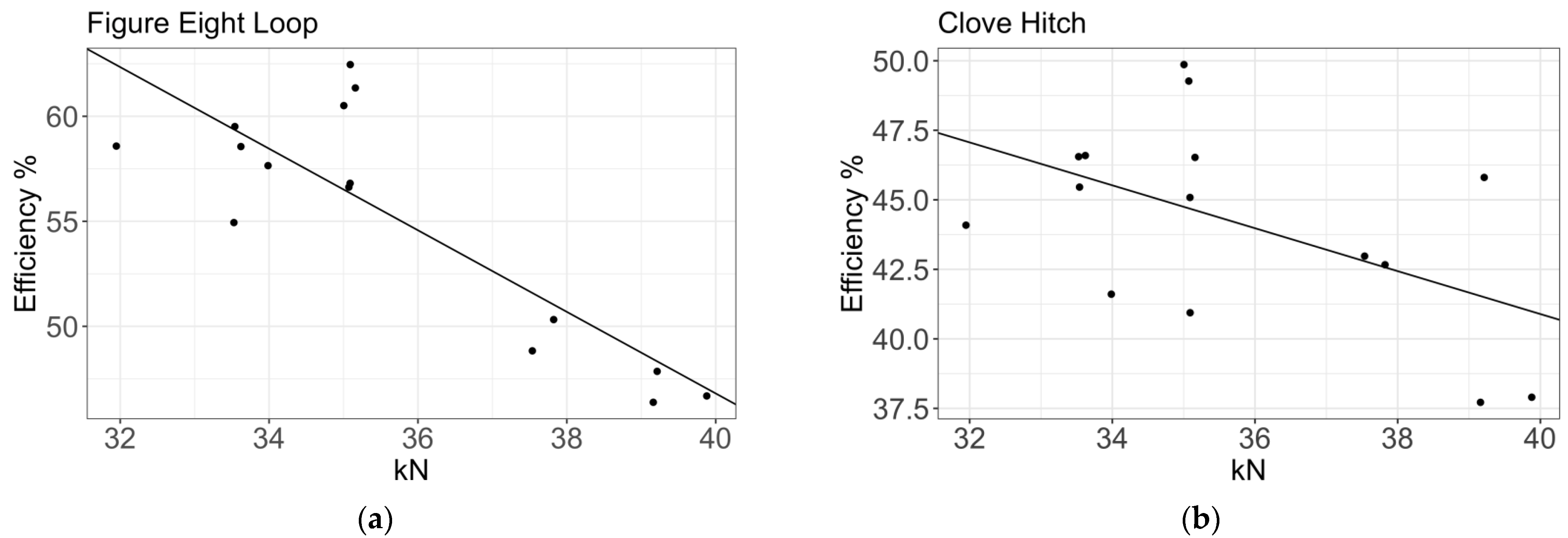
3.2. Knotless Rope Breaks: Efficiency
4. Conclusions and Contributions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Luo, F.; Li, R.Y.M.; Crabbe, M.J.C.; Pu, R. Economic development and construction safety research: A bibliometrics approach. Saf. Sci. 2022, 145, 105519. [Google Scholar] [CrossRef]
- Zeng, L.; Li, R.Y.M.; Yigitcanlar, T.; Zeng, H. Public Opinion Mining on Construction Health and Safety: Latent Dirichlet Allocation Approach. Buildings 2023, 13, 927. [Google Scholar] [CrossRef]
- Dong, X.S.; Brown, S.; Brooks, R.D. Trends of fatal falls in the U.S. Construction Industry. In Proceedings of the 21st Congress of the International Ergonomics Association (IEA 2021), Online, 13–18 June 2021; Volume 309. [Google Scholar] [CrossRef]
- Dong, X.S.; Largay, J.A.; Choi, S.D.; Wang, X.; Cain, C.T.; Romano, N. Fatal falls and PFAS use in the construction industry: Findings from the NIOSH FACE reports. Accid. Anal. Prev. 2017, 102, 136–143. [Google Scholar] [CrossRef]
- Dong, X.S.; Jackson, R.; Varda, D.; Bunting, J. Trends of Fall Injuries and Prevention in the Construction Industry. Available online: https://www.cpwr.com/wp-content/uploads/publications/Quarter2-QDR-2019.pdf (accessed on 8 March 2022).
- Safe Work Australia. Work-Related Injury Fatalities/Key WHS Statistics Australia. 2021. Available online: https://www.safeworkaustralia.gov.au/sites/default/files/2021-10/Key%20work%20health%20and%20safety%20statistics%20Australia%202021.pdf (accessed on 5 March 2022).
- Ministry of Labor and Social Economy (MITES). Occupational Accident Statistics. Available online: https://www.mites.gob.es/estadisticas/eat/eat20/Resumen_resultados_ATR_2020.pdf (accessed on 8 February 2022).
- Health and Safety Executive. Health and Safety in Construction in Great Britain (HSE). Construction Statistics in Great Britain. 2022. Available online: https://www.hse.gov.uk/statistics/industry/construction.pdf (accessed on 30 January 2022).
- EN-363:2018; Personal Fall Protection Equipment-Personal Fall Protection Systems. European Committee for Standardization: Brussels, Belgium, 2018.
- Carrión, E.A.; Menchacatorre, P.I.; García, R.T. Individual Fall Protection Systems: Legislation, Definitions and Equipment; Publications of the University of Alicante: Alicante, Spain, 2014; ISBN 978-84-9717-321-6. [Google Scholar]
- Garcia-Dils de la Vega, S.; Castaño Lacruz, J. Some notes on knots. Subterránea 2005, 23, 42–44. Available online: https://www.efiemer.com/wp-content/uploads/2019/02/Algunas_notas_sobre_nudos.pdf (accessed on 16 March 2022).
- Guinot, S.; Sáez, P. Sistemas de Protección Individual Contra Caídas en Bomberos; Ediciones Desnivel: Madrid, Spain, 2015; ISBN 978-84-9829-330-2. [Google Scholar]
- Tourte, B.; Marbach, G. Técnicas de Espeleologia Alpina; Ediciones Desnivel: Madrid, Spain, 2003; ISBN 978-84-9576-095-1. [Google Scholar]
- Sulowski, A.C. How good is the 8 kN Maximum Arrest Force limit in industrial Fall Arrest Systems. In Proceedings of the International Symposium on Fall Protection—IFPS’06, Seattle, WA, USA, 14–15 June 2006. [Google Scholar]
- Pomares, J.C.; Irles, R.; Segovia, E.; Ferrer, B. Acceleration and Deflection Analysis for Class C Edge Protection Systems in Construction Work. J. Constr. Eng. Manag. 2014, 8, 140. [Google Scholar] [CrossRef]
- Zuluaga, C.M.; Albert, A.; Winkel, M.A. Improving Safety, Efficiency, and Productivity: Evaluation of Fall Protection Systems for Bridge Work Using Wearable Technology and Utility Analysis. J. Constr. Eng. Manag. 2020, 146, 04019107. [Google Scholar] [CrossRef]
- Rico, S.; Matthew, H.; Rajagopalan, B.; Siddharth, B. Safety Risk Tolerance in the Construction Industry: Cross-Cultural Analysis. J. Constr. Eng. Manag. 2020, 146, 04020022. [Google Scholar] [CrossRef]
- Ashley, C.W. The Ashley Book of Knots, 12th ed.; Doubleday and Company, Inc.: New York, NY, USA, 1944. [Google Scholar]
- Marbach, G.; Tourte, B. Alpine Caving Techniques: A Complete Guide to Safe and Efficient Caving, 1st ed.; Speleo Projects: Allschwil, Switzerland, 2002. [Google Scholar]
- Turner, J.C.; Griend, P.V.; Warner, C. History and Science of Knot; Series on Knots and Everything; World Scientific Publishing Co Pte Ltd.: Singapore, 1996; p. 464. [Google Scholar]
- BEAL. Available online: https://www.beal-planet.com/en (accessed on 31 January 2022).
- Cuenot, S.; Bodeau, H. Petzl, la Promesse des Profondeurs; Guérin, Ed.; Editions Paulsen: Chamonix, France, 2012. [Google Scholar]
- MSA. The Safety Company. Available online: https://us.msasafety.com/Fall-Protection/Rescue-%26-Descent-Products/FP-Rescue-Ropes/p/000230001200001001 (accessed on 8 February 2022).
- PETZL. PETZL-Professional. Available online: https://www.petzl.com/GB/en/Professional/Ropes (accessed on 28 January 2022).
- Boron, K.; Obstalecki, M.; Kurath, P.; Horn, G.P. Utilizing Knots to Reduce Dynamic Loads in Fire Service Rope Systems. Conf. Proc. Soc. Exp. Mech. Ser. 2013, 1, 433–439. [Google Scholar] [CrossRef]
- Brown, A. The Strength of Knots in Dynamic Climbing Rope. Available online: http://personal.strath.ac.uk/andrew.mclaren/alasdair_brown_2008.pdf (accessed on 2 February 2022).
- Carrión, E.; Ferrer, B.; Monge, J.; Sáez, P.; Pomares, J.; González, A. Minimum Clearance Distance in Fall Arrest Systems with Energy Absorber Lanyards. Int. J. Environ. Res. Public Health 2021, 18, 5823. [Google Scholar] [CrossRef]
- López, E.; Julián, R.; Reising, M. Evaluation and analysis of climbing knots. In Proceedings of the 13th Argentine and 8th Latin American Congress of Physical Education and Sciences, Ensenada, Mexico, 30 September–4 October 2019; Available online: http://congresoeducacionfisica.fahce.unlp.edu.ar/ (accessed on 1 January 2023).
- Martin, D.A.; Boron, K.; Obstalecki, M.; Kurath, P.; Horn, G.P. Feasibility of Knots to Reduce the Maximum Dynamic Arresting Load in Rope Systems. J. Dyn. Behav. Mater. 2015, 1, 214–224. [Google Scholar] [CrossRef]
- Arai, Y.; Yasuda, R.; Akashi, K.-I.; Harada, Y.; Miyata, H.; Kinosita, K., Jr.; Itoh, H. Tying a molecular knot with optical tweezers. Nature 1999, 399, 446–448. [Google Scholar] [CrossRef]
- Marbach, G.; Rocourt, J.L. Techniques de la Spéléologie Alpine; Techniques Sportives Appliquées: Choranche, France, 1980. [Google Scholar]
- Pieranski, P.; Kasas, S.; Dietler, G.; Dubochet, J.; Stasiak, A. Localization of breakage points in knotted strings. New J. Phys. 2001, 3, 10. [Google Scholar] [CrossRef]
- Stasiak, A.; Dobay, A.; Dubochet, J. Knotted Fishing Line, Covalent Bonds, and Breaking Points. Science 1999, 286, 11. [Google Scholar] [CrossRef]
- Drohan, D. Preferred Knots for Use in Canyons. Available online: http://www.paci.com.au/downloads_public/knots/06_Joining-knots_DDrohan.pdf (accessed on 8 March 2022).
- Milne, K.A.; McLaren, A.J. An Assessment of the Strength of Knots and Splices Used as Eye Terminations in a Sailing Environment. Sports Eng. 2006, 9, 1–13. [Google Scholar] [CrossRef]
- Aldazabal, J.; Meizoso, A.M.; Muniategui, A.; Ibarzabal, A.; Urcaregui, M. Tensile Strength of Knotted Ropes. An. De La Mecánica De Fract. 2007, 2, 563–566. [Google Scholar]
- Nuñez, T. Los Mejores Nudos de Escalada; Ediciones Desnivel: Madrid, Spain, 2011. [Google Scholar]
- Merchant, D. Life on a Line. The Underground Rope Rescue Manual, 2nd ed.; Lulu Enterprises, UK Ltd.: North Wales, UK, 2007; Volume 2, Available online: http://www.lifeonaline.com/legal (accessed on 3 January 2023).
- Diamond, W. An Assessment of the Strength of Rope Splices and Knots in Sailing Ropes. Available online: http://Personal.Strath.Ac.Uk/Andrew.Mclaren/William_Diamond_2007.Pdf (accessed on 8 March 2022).
- Gómez, P. Breaking Knots, 2nd ed.; Valencian School of Speleology: Valencia, Spain, 2016. [Google Scholar]
- Šimon, J.; Dekýš, V.; Palcek, P. Revision of Commonly Used Loop Knots Efficiencies. Acta Phys. Pol. A 2020, 138, 404–420. [Google Scholar] [CrossRef]
- Nuñez, T. Something More about Knots; Ediciones Desnivel: Madrid, Spain, 1999. [Google Scholar]
- UNE-EN 1891; Personal Protective Equipment for the Prevention of Falls from a Height—Low Stretch Kernmantle Ropes. Asociación Española de Normalización: Madrid, Spain, 1999.
- EN 919:1995; Fibre Ropes for General Service. Determination of Certain Physical and Mechanical Properties. European Committee for Standardization: Brussels, Belgium, 1995.
- AS 4142.3; Fibre Ropes, Part 3: Man-Made Fibre Rope for Static Life Rescue Lines. Australia Standards: Homebush, Australia, 1993.
- EN 892:2012; Mountaineering Equipment-Dynamic Mountaineering Ropes-Safety Requirements and Test Methods. European Committee for Standardization: Brussels, Belgium, 2012.
- BS:3104:1970; Polyamide (Nylon) Mountaineering Ropes. British Standards Institution: London, UK, 1970.
- BS EN 892:2004; Mountaineering Equipment. Dynamic Mountaineering Ropes. Safety Requirements and Test Methods. British Standards Institution: London, UK, 2004.
- National Fire Protection Association. NFPA 1. Fire Code, 2012th ed.; NFPA Publications: Quincy, MA, USA, 2011. [Google Scholar]
- Saitta, A.M.; Soper, P.D.; Wasserman, E.; Klein, M.L. Influence of a knot on the strength of a polymer strand. Nature 1999, 399, 46–48. [Google Scholar] [CrossRef] [PubMed]
- Horn, G.P.; Kurath, P. In Failure of firefighter escape rope under dynamic loading and elevated temperatures. In Dynamic Behavior of Materials, Proceedings of the 2010 Annual Conference on Experimental and Applied Mechanics, Indianapolis, Indiana, 7–10 June 2010; Springer: New York, NY, USA, 2011; Volume 1, pp. 353–359. [Google Scholar] [CrossRef]
- Fontenot, N.; Stenvers, D.; Gilmore, J.; Solomon, A.; van Berkel, B.; Grabandt, O.; Kong, D. In Use of synthetic rope in high-temperature or fire environments. In OCEANS 2009; IEEE: Biloxi, MS, USA, 2009; pp. 1–6. [Google Scholar] [CrossRef]
- EN ISO 139:2005/A1; Textiles—Standard Atmospheres for Conditioning and Testing. European Committee for Standardization: Brussels, Belgium, 2005.
- Baszczyński, K. Effect of Repeated Loading on Textile Rope and Webbing Characteristics in Personal Equipment Protecting against Falls from a Height. Fibres Text. East. Eur. 2015, 23, 110–118. [Google Scholar] [CrossRef]
- European Parliament and the Council of the European Union. Directive 2001/45/EC of the European Parliament and of the Council of 27 June 2001. Amending Council Directive 89/655/EEC Concerning the Minimum Safety and Health Requirements for the Use of Work Equipment by Workers at Work; Official Journal of the European Communities: Luxembourg, 2001. [Google Scholar]
- European Parliament and the Council of the European Union. Regulation (EU) 2016/425 of the European Parliament and of the Council of 9 March 2016 on Personal Protective Equipment and Repealing Council Directive 89/686/EEC. Available online: http://data.europa.eu/eli/reg/2016/425/oj (accessed on 28 January 2024).
- Carrión, E.; Sáez, P.; Pomares, J.; González, A. Average Force of Deployment and Maximum Arrest Force of Energy Absorbers Lanyards. Int. J. Environ. Res. Public Health 2020, 17, 7647. [Google Scholar] [CrossRef] [PubMed]
- Eurasian Economic Union (EAC). Available online: https://www.ccis-expertise.com/en/eurasian-economic-union-export (accessed on 19 January 2024).
- UIAA 107; Safety Standards. Available online: https://www.theuiaa.org/safety/safety-standards/ (accessed on 8 May 2023).
- EN-364/AC; Personal Protective Equipment against Falls from a Height Test Methods. European Committee for Standardization: Brussels, Belgium, 1993.
- EN ISO 7500-1:2018; Metallic Materials. Calibration and Verification of Static Uniaxial Testing Machines. Part 1: Tension/Compression Testing Machines. Calibration and Verification of the Force-Measuring System. European Committee for Standardization: Brussels, Belgium, 2018.
- Šimon, J.; Ftorek, B. Basic Statistical Properties of the Knot Efficiency. Symmetry 2022, 14, 1926. [Google Scholar] [CrossRef]
- Zhu, X.; Li, R.Y.M.; Crabbe, M.J.C.; Sukpascharoen, K. Can a chatbot enhance hazard awareness in the construction industry? Front. Public Health 2022, 10, 993700. [Google Scholar] [CrossRef] [PubMed]
- Marturello, D.M.; McFadden, M.S.; Bennett, R.A.; Ragetly, G.R.; Horn, G. Knot Security and Tensile Strength of Suture Materials. Vet. Surg. 2014, 43, 73–79. [Google Scholar] [CrossRef] [PubMed]
- Muffly, T.M.; Boyce, J.; Kieweg, S.L.; Bonham, A.J. Tensile Strength of a Surgeon’s or a Square Knot. J. Surg. Educ. 2010, 67, 222–226. [Google Scholar] [CrossRef] [PubMed]



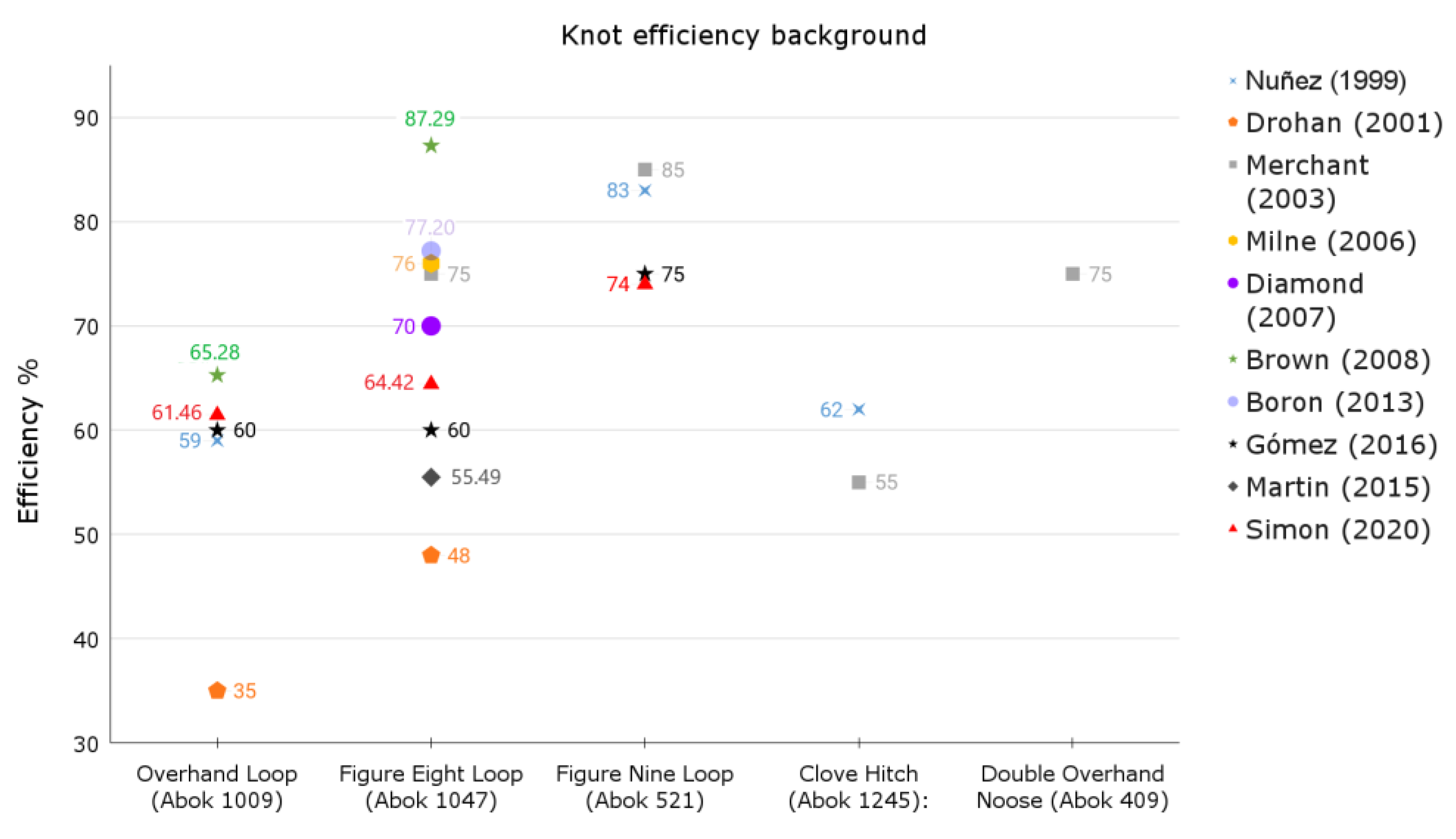
| Author | Rope Type | Standards | Experimental Procedure | Breaking Load without Knot |
|---|---|---|---|---|
| Nuñez (1999) [42] | New low-stretch kernmantle rope Polyamides and polyester | EN 1891:1999 [43] | Number of tests: 153 Sample conditioning according to the standard EN 919 [44] | No record |
| Drohan (2001) [34] | Canyoning 11 mm Used rope | AS 4142.3 (1993) [45] | Number of trials: 48 Number of tests per knot type: 6 Speed = 0.67 mm/s Sample conditioning: 20 °C /65% humidity Minimum breaking strength (MBS) = mean − 2sd Prebreak load cycles: no | Obtained from manufacturer’s data |
| Merchant (2007) [38] | 11 mm ropes for caving Used kernmantle rope Nylon-6,6 polyamides | EN 1891:1999 [43] | Distinguish between different knot configurations Not stated: number of tests, speed, specimen conditioning, and applied load cycles | Obtained from manufacturer’s data |
| Milne-Laren (2006) [35] | Sailing New ropes | EN 892 with adaptations [46] | Number of trials: 180 (3 trials with no knot) Number of trials per scenario: 5 Speed = 1 mm/s Sample conditioning: no Load cycles prior to breakage: 3 cycles at a 10% breaking load Knots tied by three different people (to simulate the human factor in knot tying) | Obtained from our own tests |
| Aldazabal (2007) [36] | Beal cord, 5 mm New rope | EN 1891:1999 [43] | Number of trials: 45 Number of rehearsals per stage: 5 Speed = 1 mm/s Sample conditioning: no Prebreak load cycles: no Data logging at frequency = 0.5 Hz | Obtained from our own tests |
| Diamond (2007) [39] | Sailing Polyester Ø, 8 and 10 mm; Dyneema 8 mm It is not stated whether the rope was new or used. | Number of tests: 158 No cycles Steel bollard ropes with three turns of a drum (for holding ropes without a knot) Test tubes of 2.3 m (knotless), 1.64 m (bowline knot), and 1.75 m (figure eight knot) Not stated: test speed, acclimatisation samples | Obtained from manufacturer’s data | |
| Brown (2008) [26] | Dynamic climbing10 mm Beal Tiger It is not stated whether the rope is new or used. | BS 3104 [47] BS 892 [48] | Number of tests: 60 All labelled test tubes are 2 m No load cycles Not stated: test speed, sample acclimatisation, new or used rope | Obtained from our own tests |
| Boron (2013) [25] | Escape rope Technora–Technora Technora–nylon Nylon–nylon New ropes | NFPA 1983 CI 1801 [49] | Number of tests: not determined Number of rehearsals per stage: 5 Speed = 5.4 mm/s Sample conditioning: room temperature [50,51,52] Minimum breaking strength (MBS) = mean − 3sd Prebreak load cycles: two preload cycles, the first of 130 N and the second of 830 N. | Obtained from manufacturer’s data |
| Martin (2015) [29] | Escape rope Technora–Technora Technora–nylon New ropes | NFPA 1983 CI 1801 [49] | Number of tests: 27 Number of rehearsals per scenario: 3 Speed = 5.4 mm/s Sample conditioning: at room temperature and humidity Minimum breaking strength (MBS) = mean − 3sd Prebreak load cycles: no Data logging at frequency = 10 Hz | Not provided |
| Gomez (2016) [40] | Low-stretch kernmantle rope Polyamide (PA) polyester (PES) Ø 10 mm New and used ropes | EN 1891:1999 [43] | Distinguish between different configurations of symmetrical knots (levorotatory and dextrorotatory) Number of tests: 216 Speed > 5 mm/s 3 tests each per scenario (sample set) knots Long = not defined 0 cycles Knots made by cavers No sample acclimatisation | Obtained from manufacturer’s data |
| Šimon (2020) [41] | Low-stretch kernmantle rope Polyamide New and used ropes | EN 1891:1999 [43] | Number of trials: 81 (figure light, ABOK 1047) + 66 (double figure eight loop, ABOK 1085) + 19 (figure nine loop, ABOK 521) + 180 (overhand, ABOK 1009) + 153 (bowline, ABOK 1010) + 50 (alpine butterfly, ABOK 1053) Minimum number of rehearsals per scenario: 12 Speed = 3 mm/s Sample conditioning: tests carried out at ambient laboratory temperature Prebreak load cycles: no | Obtained from our own tests |
| Performance | α Model Axis (PETZL) | λ Model Lluisa (KORDA’S) | Ψ Model Parallel (PETZL) |
|---|---|---|---|
| Standards | EN 1891 type A [43] EAC NFPA 1983 [49] UIAA 107 [59] | EN 1891 type A [43] EN892 + A12016 [46] simple dynamic rope | EN 1891 type A [43] EAC NFPA 1983 [49] UIAA 107 [59] |
| Diameter (mm) | 11 | 10.6 | 10.5 |
| Sheath slippage (%) | 1.3 | 0 | 1 |
| Elongation between 50 and 150 daN (%) | 3 | 3.8 | 3.4 |
| Mass of the sheath (%)/mass of the core (%) | 41/59 | 37.5/62.5 | 45/55 |
| Mass per unit length (g/m) | 82 | 77 | 75 |
| Static strength without knots (kN) | 30 | 32.3 | 27 |
| Static strength with figure eight loop knots at ends (kN) | 19 | complies | 15 |
| Static strength with sewn termination | 22 | complies | 22 |
| Shrinkage (%) | 2 | −0.2 | 2 |
| Numbers of carriers | 32 | 32 | |
| Number of falls with an FF = 1 | 20 | >5 | 10 |
| Material | polyester/polyamide | polyamide | polyester/polyamide |
| Rope Model | α (11 mm) kp | λ (10.6 mm) kp | ψ (10.5 mm) kp |
|---|---|---|---|
| Maximum and minimum breaking values obtained during tests | 3830–3605 | 3264–3068.30 | 3376.67–3362 |
| Value provided by the manufacturer (knotless) | 3059.15 | 3293.68 | 2753.23 |
| Terminal Type | Breaking Values Obtained during Tests (kp) | ||
Figure eight loop (Abok 1047) | 1827.89 | 1916.98 | 2071.61 |
| 1760.43 | 1797.44 | 2034.17 | |
| 1802.25 | 1769.06 | 1907.32 | |
| 1788.05 | 1881.73 | 2105.00 | |
| 1744.45 | 1890.86 | 1914.43 | |
Figure nine loop (Abok 521) | 2002.10 | 2122.77 | 1935.31 |
| 1939.82 | 2170.00 | 2089.50 | |
| 2072.60 | 2026.20 | 2013.04 | |
| 2049.60 | 2047.00 | 2155.89 | |
| 1899.21 | 2023.00 | 2343.49 | |
Double overhand noose (Abok 409) | 2195.26 | 2061.33 | 2161.99 |
| 2123.73 | 1971.58 | 2206.95 | |
| 2220.04 | 1985.39 | 2044.48 | |
| 2231.04 | 1984.79 | 2354.07 | |
| 2266.53 | 1894.23 | 2099.72 | |
Overhand loop (Abook 1009) | 1792.37 | 1824.00 | 1885.09 |
| 1954.57 | 1493.00 | 1877.44 | |
| 1856.44 | 1697.00 | 1855.71 | |
| 1878.20 | 1748.00 | 1938.64 | |
| 1907.51 | 2016.65 | 1848.78 | |
| Clove hitch (Abok 1245) | 1549.81 | 1464.26 | 1570.99 |
 | 1549.23 | 1352.74 | 1676.28 |
| 1724.99 | 1498.98 | 1659.56 | |
| 1451.55 | 1358.01 | 1379.70 | |
| 1418.52 | 1504.47 | 1519.30 | |
Knotless rope | 3632.50 | 3221.20 | 3376.67 |
| 3605.00 | 3068.30 | 3361.80 | |
| 3766.00 | 3220.00 | 3368.30 | |
| 3830.00 | 3264.00 | 3370.10 | |
| 3761.00 | 3229.00 | 3369.90 | |
| ANOVA | df | SS | MS | F Value | p-Value |
|---|---|---|---|---|---|
| Knot | 4 | 2924.1 | 731.0 | 83.99 | <0.0001 |
| Rope | 2 | 765.2 | 382.6 | 43.96 | <0.0001 |
| Knot × Rope | 8 | 191.5 | 23.9 | 2.75 | 0.0118 |
| Residuals | 60 | 522.2 | 8.7 | ||
| R2 = 0.8814 | |||||
| Differences between Knots | Effects (%) |
|---|---|
| Figure nine loop–figure eight loop | +5.24% |
| Clove hitch–figure eight loop | −10.93% |
| Double overhand noose–figure eight loop | +6.78% |
| Overhand loop–figure eight loop | −1.42% |
| Differences between Ropes | Effects (%) |
| λ–ψ | −0.88% |
| α–ψ | −7.17% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sáez, P.I.; Carrión, E.Á.; Ferrer, B.; García, E.; Monge, J.F. Determining the Safest Anchoring Knot in a Fall Arrest System by Means of Static Tests. Symmetry 2024, 16, 167. https://doi.org/10.3390/sym16020167
Sáez PI, Carrión EÁ, Ferrer B, García E, Monge JF. Determining the Safest Anchoring Knot in a Fall Arrest System by Means of Static Tests. Symmetry. 2024; 16(2):167. https://doi.org/10.3390/sym16020167
Chicago/Turabian StyleSáez, Pedro Ignacio, Elena Ángela Carrión, Belén Ferrer, Encarnación García, and Juan Francisco Monge. 2024. "Determining the Safest Anchoring Knot in a Fall Arrest System by Means of Static Tests" Symmetry 16, no. 2: 167. https://doi.org/10.3390/sym16020167
APA StyleSáez, P. I., Carrión, E. Á., Ferrer, B., García, E., & Monge, J. F. (2024). Determining the Safest Anchoring Knot in a Fall Arrest System by Means of Static Tests. Symmetry, 16(2), 167. https://doi.org/10.3390/sym16020167