Abstract
The structures and bonding of selected neutral M(CO)6 complexes (M = Sc, Y, La, Lu, Ac and U) have been studied by density functional theory calculations. The calculations revealed the preference for C2v symmetry and low-spin electronic state for most of these complexes. The relative stability of the low-symmetry species increases gradually with the size of the metal atom. While the characteristic Oh hexa-coordinated structure is favored in the high-spin electronic state of the smaller metals, for heavier metals, important advantages of the C2v vs. Oh structures include larger charge transfer interactions in terms of transferred electrons as well as better steric conditions. Our joint experimental–theoretical analysis detected and confirmed the Oh structure of the Sc(CO)6 complex in cryogenic CO/Ar matrices.
1. Introduction
Metal carbonyls are best known for their complexes with transition metals (TM), which have numerous applications like industrial catalysts or precursors for exotic compounds. They were extensively studied in the 1970s, using mostly matrix isolation trapping, spectroscopy and photochemical excitation [1,2,3,4,5,6,7], resulting in substantial amounts of experimental physicochemical data.
In the past two decades, numerous experimental studies were performed on gaseous ionic carbonyl complexes of f elements [8,9,10,11,12,13,14,15], heavy alkaline-earth (Ca, Sr, Ba) [16,17,18], rare-earth (Sc, Y) [19] and heavy transition metals (Zr, Hf) [20]. While the latter studies focused on the highest coordinated species (mostly eight, but in a few cases even nine, like Tm(CO)9−, Lu(CO)9− [14] and La(CO)9+, Ce(CO)9+ [11]), lower coordinations were also documented in the mass spectra. A very recent study targeting the highest-coordination neutral carbonyl complexes of Sc, Y and La using gas-phase-size-specific infrared–vacuum ultraviolet spectroscopy reported Sc(CO)7, Y(CO)8 and La(CO)8 as the highest-coordination species [21].
Quantum chemical calculations over the decades focused on the electronic structure, geometry and bonding interactions—revealing several interesting features [6,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37].
The best-characterized neutral TM hexacarbonyls are those of group VI (Cr, Mo, W). They are stable (crystalline) at room temperature and have a highly symmetric octahedral structure [24,38,39,40,41,42,43,44]. Their high stability has been attributed to their saturated valence shell following the so-called 18-electron rule [27,37,45,46,47]. However, the adjacent V(CO)6 is also stable and octahedral [48,49], although it only has 17 valence electrons. The Ti(CO)6 complex was found to be unstable; therefore it could only be detected and characterized under matrix isolation conditions [50].
Beyond neutral complexes, several ionic hexacarbonyl species stabilized by counterions have been synthesized in the solid phase [51,52,53,54,55]. The characteristic single absorption band of the CO stretching in the IR spectra provided strong evidence for the octahedral structure of these molecules [51,52,53,54,55].
Neutral lanthanide carbonyls were reported recently from a matrix isolation FT-IR study [56], where the interpretation of the spectra was facilitated by Density Functional Theory (DFT) calculations. The most abundant species in the cryogenic CO matrix proved to be Ln(CO)8, but in a few cases, Ln(CO)7 and Ln(CO)6 could also be identified. Surprisingly, the DFT calculations indicated the preference of lower-symmetry C2v structures (Figure 1) for those Ln(CO)6 molecules—in contrast to the expected Oh symmetry based on the known TM(CO)6 complexes [29,35,37].
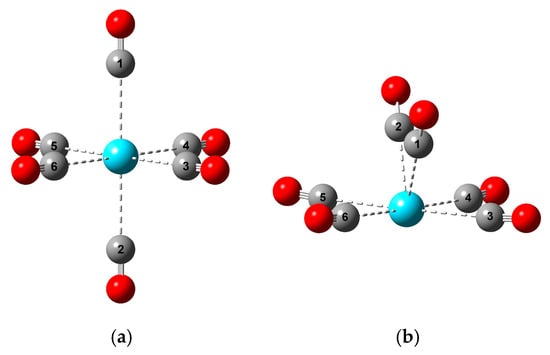
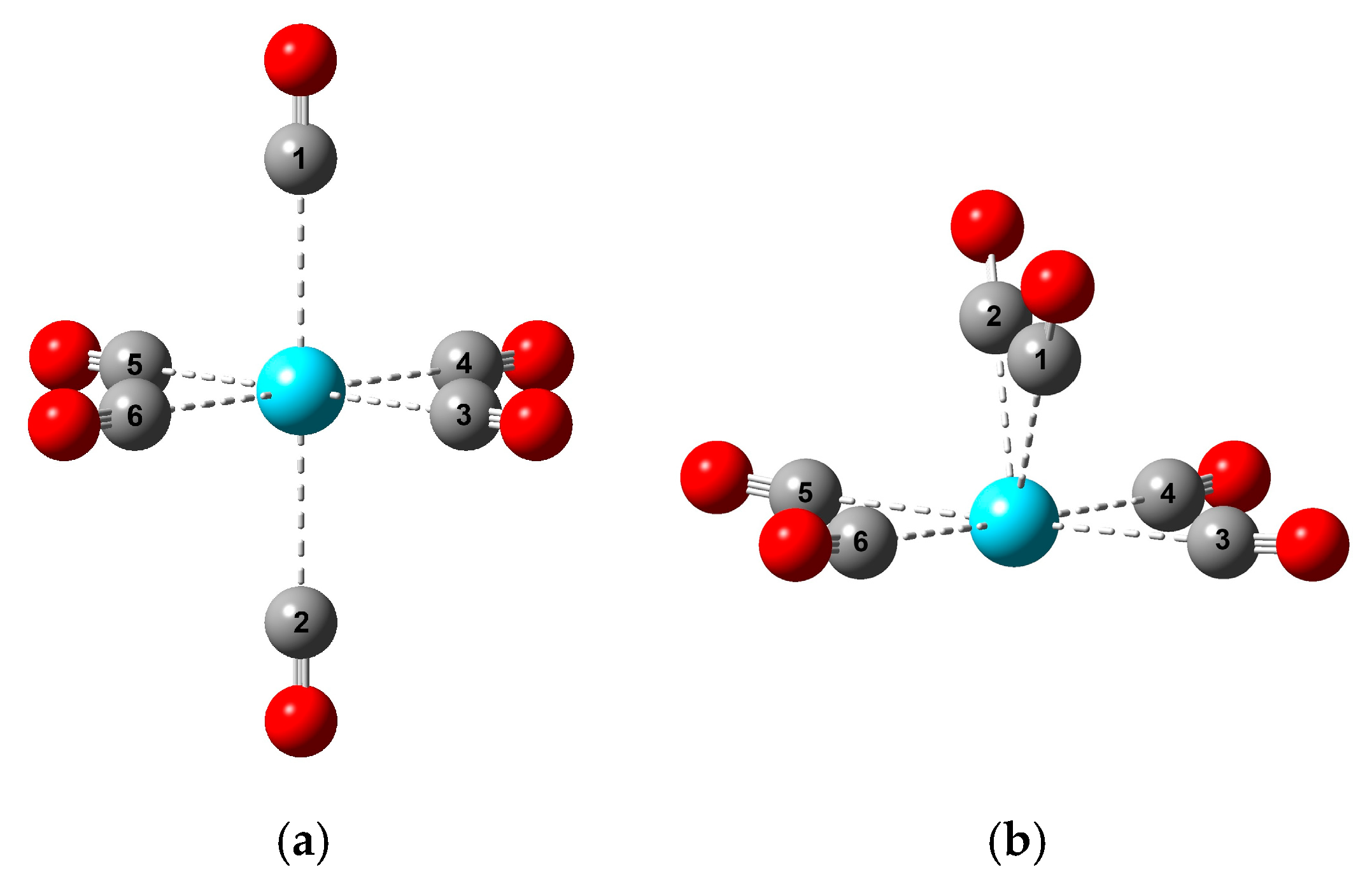
Figure 1.
The main characteristic structures of M(CO)6 complexes discussed in this paper: (a) Oh (D4h); (b) C2v (Cs). The meaning of the colors is: cyan, M; gray, C; red, O. The numbering of C atoms serves the definition of bond angles in Section 3.2.
The aim of the present study is to clarify how far the preference for lower symmetry goes in the rare-earth and f element groups of the periodic system and to uncover their bonding characteristics. This study is performed by means of DFT calculations extended with a Natural Bond Orbital (NBO) analysis [57,58,59,60,61] of the donor-acceptor interactions.
2. Computational and Experimental Details
2.1. Computational Details
The DFT computations were performed with the Gaussian09 suite of programs [62] using the hybrid B3LYP [63,64,65] exchange–correlation functional in conjunction with the correlation consistent cc-pVTZ basis sets for the light atoms C, O [66] and Sc [67]. For the heavy atoms, the quasi-relativistic small-core (4/5f-in-valence) pseudopotentials were applied: (i) for Y, La and Lu the one denoted as ECP28MWB [68,69] with contracted valence basis sets of (8s7p6d2f1g)/(6s5p3d2f1g) for Y [70] and (14s13p10d8f6g)/(10s8p5d4f3g) for La and Lu [71], and (ii) for Ac and U, the one named ECP60MWB [72,73] in conjunction with (14s13p10d8f6g)/(10s9p5d4f3g) valence bases [73,74].
In order to account for dispersion effects, the D3 version of Grimme’s empirical correction using the original damping [75] was utilized. Though somewhat old, the B3LYP exchange–correlation functional in conjunction with a triple-zeta basis set and proper dispersion correction belongs to the recommended methods for geometries and vibrational frequencies [76]. The predicted relative energies of the structural isomers were confirmed by calculations on selected complexes with the more robust PBE0 hybrid functional [77], in conjunction with the same basis set and other technical parameters as in the B3LYP jobs. (The PBE0 relative energies are given in Table S1 in the Supplementary Materials). Because of the weak character of coordination interactions, the integration accuracy was set to SuperFine grid. The ground states of the computed molecules were verified using the STABLE keyword. The spin-contaminations of the open-shell systems were checked in each calculation: the calculated <Ŝ2> eigenvalues proved to be consistent with the theoretical ones (cf. Table S1).
The single- vs. multireference character of the studied complexes was probed by populations of natural molecular orbitals, generated from the unrestricted B3LYP wavefunctions using the guess=(read, only, save, naturalorbitals) keyword. Significant deviations from double-, single- and/or unoccupation would point to a multireference character. For all the complexes, we obtained only negligible deviations from the reference values (2 or 1) of the occupied orbitals. Accordingly, the population of the virtual orbitals was also negligible, with the largest being 0.006 e in the case of quintet U(CO)6.
Single-point relativistic complete active space self-consistent field (CASSCF) [78] calculations on the B3LYP reference geometries of the significant low- and high-spin structures were carried out by means of the MOLCAS 8.2 code [79,80], applying C1 symmetry. The scalar relativistic effects were taken into account with the second-order Douglas–Kroll–Hess Hamiltonian [81,82]. The used atomic natural-orbital-type all-electron basis sets valence of the triple-zeta plus polarization quality developed for relativistic calculations (ANO-RCC) had the contraction schemes of [21s15p10d6f4g2h]/[6s5p3d2f1g] for Sc and [21s18p13d6f4g2h]/[7s6p4d2f1g] for Y [83], [24s21p15d5f3g2h]/[8s7p5d2f1g] for La and [25s22p15d11f4g2h]/[8s7p4d3f2g1h] for Lu [84], [27s24p18d14f6g3h]/[9s8p6d4f2g1h] for Ac and [26s23p17d13f5g3h]/[9s8p6d5f2g1h] for U [85] and [14s9p4d3f2g]/[4s3p2d1f] for C and O [86].
The active space consisted of the valence electrons and orbitals of the metals, viz. 3e/9o (electron/orbital) for Sc, Y and Lu and 3e/13o for La, Ac and U. The most stable electronic state was selected from the results of state-averaged 5-root calculations. Subsequent second-order perturbation theory calculations on the basis of the CASSCF wave functions (CASPT2) [87,88] accounted for dynamic electron correlation.
The CASSCF data confirmed a very slight multireference character of the studied complexes: the contribution of the main electron configuration was between 87–93%, and the populations of the 2- and 1-electron orbitals were between 1.83–1.88 and 0.93–0.98 e, respectively, while that of the most populated virtual orbital was 0.05 e.
An analysis of the intramolecular interactions was performed on the basis of the B3LYP calculations. The atomic charges and valence orbital populations of the metals were evaluated using the Natural Bond Orbital (NBO) model [57,58,59,60,61] by means of the NBO 6.0 code [89,90]. Due to the deficiency of NBO 6.0 for g functions, for this analysis, the g polarization functions were omitted from the metal basis sets. The DFT steric energy was estimated according to Shubin Liu’s energy decomposition analysis [91] using the Multiwfn code [92].
2.2. Matrix Isolation Spectroscopy
As described in detail previously [56,93], basically, a Displex closed-cycle helium refrigerator was used to cool a NaCl optical window to 10 K in a specialized vacuum system. Monoatomic scandium and yttrium vapors were generated by direct resistive heating of a metal filament (Goodfellow 0.25 mm, 99%) in a water-cooled oven, and high-purity gases were obtained from Messer-Griesheim (Ar 5.7, CO 4.7). Infrared spectra were recorded on Perkin-Elmer FT-IR spectrometers equipped with data collection computers and UV–visible spectra on computer-controlled double-beam Perkin-Elmer Hitachi 320 on the same sample within a few minutes. For narrow-band irradiations, the light of a 1000 W Hg/Xe lamp was selected by a monochromator system. The purpose of the UV–vis measurements was to check for impurities and to follow the progress of the Sc + CO reaction by the vanishing sharp peaks of the isolated Sc atoms. Representative IR and UV–vis spectra are given in Figures S2 and S3 of the Supplementary Materials.
3. Results and Discussion
3.1. Characteristic Structures
In the calculations on the M(CO)6 complexes (M = Sc, Y, La, Lu, Ac, U), all the reasonable spin states were probed. The ground-state electron configurations of the studied group IIIB metals are ns1(n−1)d2 and ns2(n−1)d1 for the high- and low-spin states, respectively. They correspond to spin multiplicities of 4 and 2, respectively, for Sc, Y, La, Lu and Ac. Due to the additional (n−2)f3 subshell of U, the possible spin multiplicities are 7, 5, 3 and 1. The obtained characteristic stationary points on the potential energy surfaces are given in Table 1.

Table 1.
Characteristic stationary points of the studied M(CO)6 complexes from geometry optimizations.
The data in Table 1 reveal that the preferred structure of the high-spin (quartet) M(CO)6 complexes is the octahedral one. Interestingly, by contrast, the octahedral structure of the highest-spin septet U(CO)6 is unstable—it is a third-order saddle point which, upon further optimization, converged to a C2 minimum on the potential energy surface. The many unpaired U 5f electrons (partly participating in the bonding) result in a deformed electron density distribution influencing also the bonding directions.
The data in Table 1 show also that the octahedral symmetry is not stable for the low-spin M(CO)6 complexes. Due to the Jahn–Teller effect, the Oh structures were distorted slightly in the geometry optimizations to D4h—which proved to be local minima for M = Sc and Lu, whereas they are second-order saddle points in the case of the other M. Our calculations resulted in C2v global minimum structures for most of the low-spin M(CO)6 complexes. The exception is Ac with the largest radius, where the C2v structure distorted slightly to a Cs minimum with a marginal (0.3 kJ/mol) energy difference.
The stability relations of the octahedral high-spin and lower symmetry low-spin species are important for the goal of the present study. In terms of the present B3LYP electronic energies, the high-spin Oh complex is preferred in the case of the small Sc—but in the case of the other metals, the lowest-energy forms are the low-spin states with C2v/Cs structure. This trend is essentially confirmed by the PBE0 and CASPT2 results (given in Table S1), just the two forms of Sc(CO)6 are energetically nearly identical at the latter theoretical levels.
The thermal effects increase the relative stabilities of the high-spin Oh/D4h structures by a few kJ/mol. At low temperature (10 K), the calculated energy order of the different structures was preserved, but at room temperature, the energy order of Lu(CO)6 and Y(CO)6 changed in favor of the high-spin structures at the applied B3LYP level (see ΔG10K and ΔG298K in Table 1). In any case, the small energy differences in the Sc, Lu and Y hexacarbonyls indicate comparable stabilities of the high- and low-symmetry forms.
It should be noted that the relative energies of the studied open-shell complexes can be sensitive to the applied theoretical model. In an earlier CCSD(T) study of the Sc(CO)6 complex using single-point calculations on BP86-optimized geometries, the preference for the low-spin C2v structure was predicted [33]. Our matrix isolation IR results are discussed below in Section 3.4; however, they support our DFT predictions for the preference of the high-spin Oh structure, at least in the cryogenic Ar matrix. In view of the different order from CCSD(T)—though the energy differences are small—one could speculate whether the Ar matrix would stabilize the Oh structure, and in this way, turn over the stability relation of the two species. In order to estimate the effect of the matrix, we performed geometry optimizations using the polarized-continuum (PCM) solvation model [94,95] with Ar as a solvent on the low- and high-spin species of Sc(CO)6. These calculations predicted a relative stabilization of the low-spin C2v vs. the high-spin Oh structure by 3.4 kJ/mol and thus do not support a turn-over from C2v to Oh in the Ar matrix. Altogether, it seems that for the slightly multiconfigurational open-shell Sc(CO)6 complex, the less sophisticated DFT provided results closer to the experiment than the more sophisticated CCSD(T).
The computed B3LYP energies in Table 1 reveal a gradual increase in stability in the low-symmetry forms with increasing M size. This implies a definite role of steric effects for this property (which is elaborated in a later section of this paper).
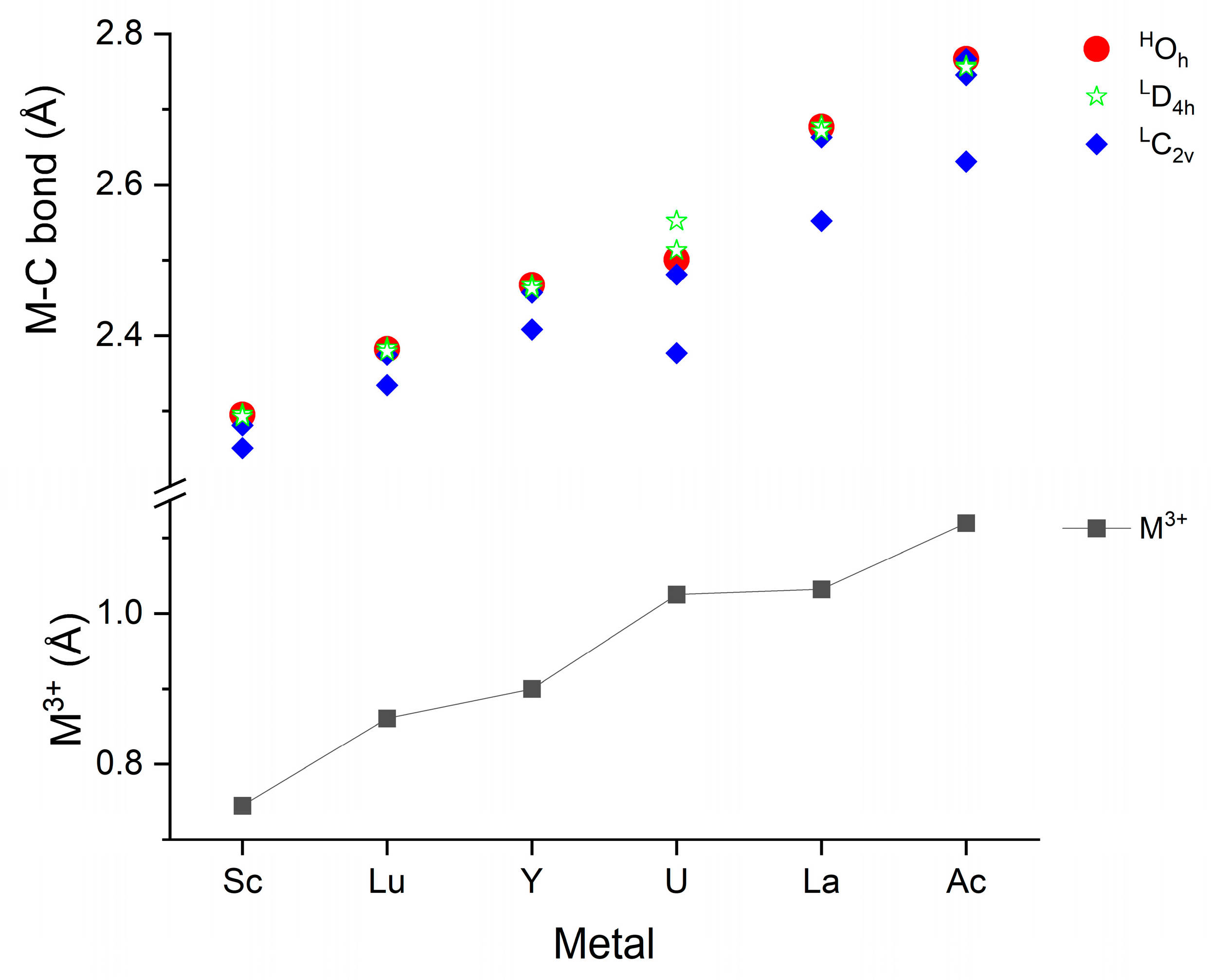
Besides the symmetry, characteristic geometrical information is provided by the M-C bond distances of the M(CO)6 complexes depicted in Figure 2. The first such information is the good correlation between the M3+ effective ionic radii [96] and the computed M-C bond distances. The only significant deviation can be observed for U, where the bonding interactions are more complex than in the cases of the other metals due to the involvement of 5f valence electrons. Because of the neutral character of the complexes, available empirical neutral M radii [97] were also considered in the above comparison. They have some deviations from the trend in the M3+ radii; thus, the agreement with the calculated M-C distances was worse (cf. Table S2).
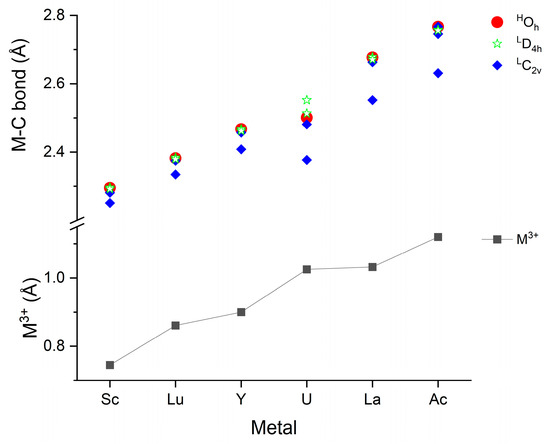
Figure 2.
Compilation of computed M-C bond distances of the M(CO)6 complexes shown with the M3+ 6-coordinate effective ionic radii [96]. The superscripts H and L indicate the high- and low-spin states (7 and 5 for U), respectively. The presented values are given in Table S2 of the Supplementary Materials.
The most important message of Figure 2 is, however, the characteristic differences in the M-C bond distances in the various structures. These bonds in the high-spin Oh and low-spin (from Oh slightly distorted) D4h structures are nearly identical in the studied set of M(CO)6 complexes. Also, the four equatorial M-C bonds in the C2v structures (see Figure 1b) remain close to the six M-C bond distances of the symmetric Oh and D4h isomers. In contrast, the two axial M-C bonds become gradually shorter with increasing M size. They correlate well with the above-mentioned increasing C2v stability, implying the significant role of the axial ligands in the stability relations.
3.2. Steric Conditions
Steric interactions are closely related to the above-discussed structural properties and are determined by the particular structures and the size of M. Due to the fixed bond angles of 90/180 degrees in the Oh and D4h structures, in these structures, steric relaxation can only occur by the elongation of the M-C bond distances. In contrast, in the C2v structures, both the axial and equatorial C-M-C angles can vary, as presented in Figure 3.
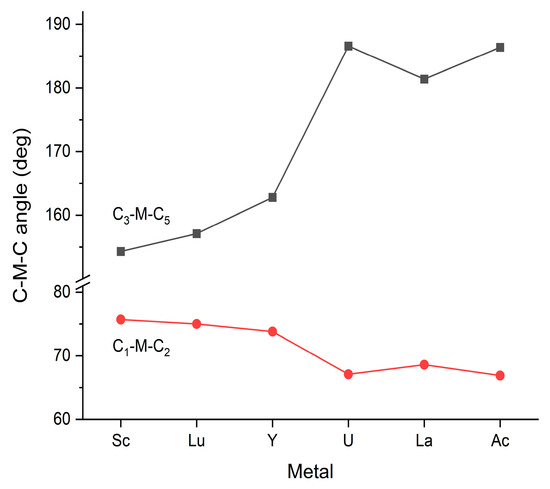
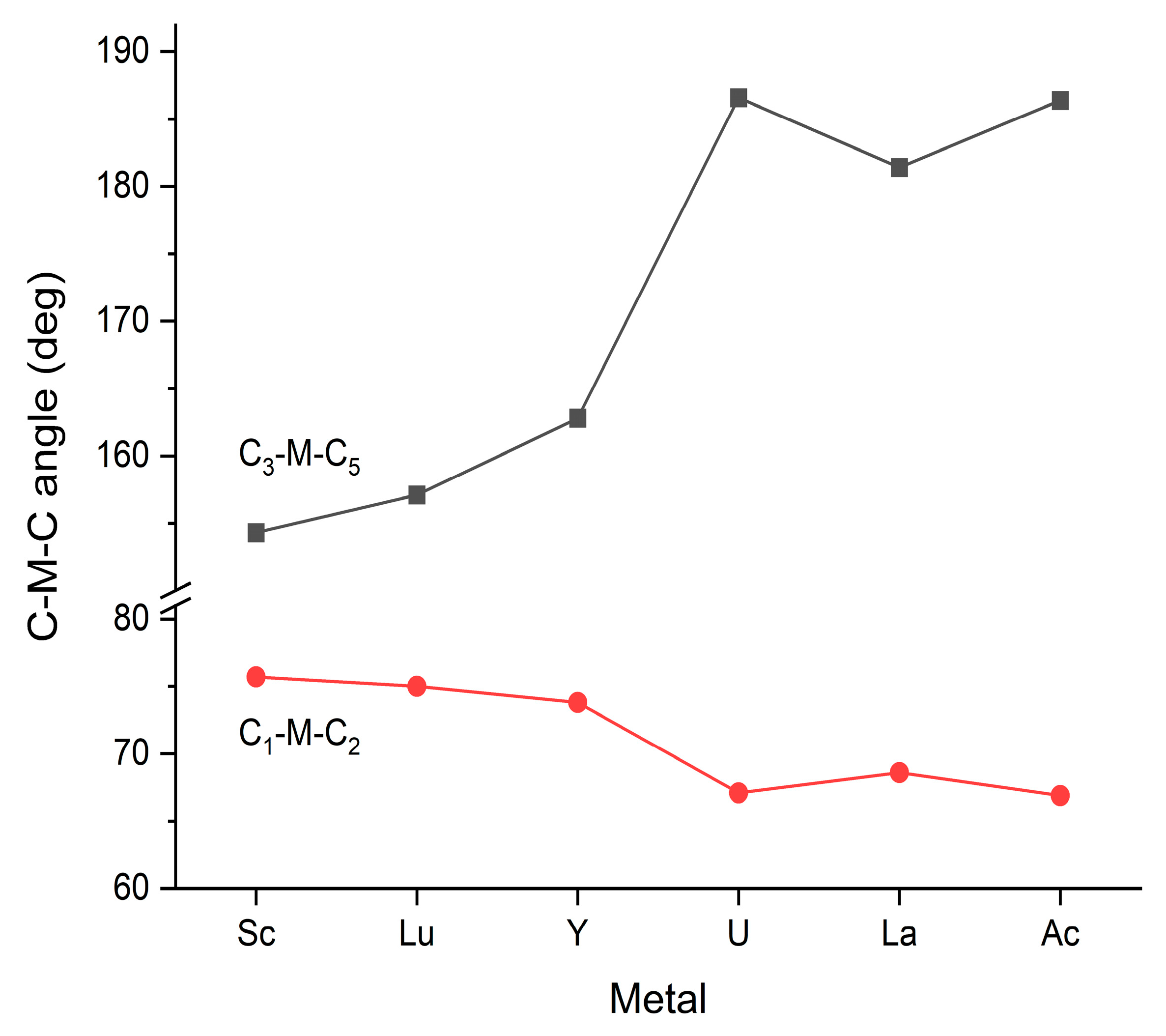
Figure 3.
Selected C-M-C bond angles of the optimized M(CO)6 C2v structures. The C1-M-C2 and C3-M-C5 ones correspond to the angles between the axial and equatorial ligands, respectively (see Figure 1b). The presented values are given in Table S3 of the Supplementary Materials.
The presented bond angles show a reasonable correlation with the M3+ radii (cf. Figure 2). The C1-M-C2 angles decrease gently with increasing axial M-C bond distances—as allowed by the decreasing steric repulsion of these adjacent groups. The similarly decreasing steric interaction between the axial and equatorial CO groups can be followed in the C3-M-C5 angles. In the case of the smaller Sc, Lu and Y metals, the equatorial CO groups are considerably bent away from the axial CO groups (downwards in Figure 1b). In the U, La and Ac complexes, however, the equatorial CO groups are slightly bent toward the axial ones (upwards in Figure 1b, indicated by the >180 deg. values for C3-M-C5), facilitated by the decreased steric repulsion. Accordingly, in these latter structures, there is more free place for the coordination of additional (hepta-, octa-) ligands at the bottom side of the structure.
The steric interactions in the complexes are characterized by means of a steric analysis adapted from S. Liu [91,98]. In fact, the DFT steric energy of Liu corresponds to the Weizsäcker kinetic energy [99] representing spatial effects, but it lacks additional effects related to the Pauli exclusion. Nevertheless, this model has been successfully applied to study conformational changes [100], the anomeric effect [101] and chemical reactions [102].
The evaluated DFT steric energies (Table S4) were used to assess the relative order of repulsive steric effects in the characteristic Oh, D4h and C2v structures. Particularly interesting is the comparison of the D4h and C2v structures of the same (low) spin states. As discussed above, the C2v structures proved to be more stable than D4h in terms of electronic energy for all the studied M(CO)6 complexes. The calculated DFT steric energies showed a significant steric preference of C2v vs. D4h (>600 kJ/mol, cf. Table S4). The spatial steric effect in the high-spin Oh structures is even larger. This steric strain supports the distortion of the low-spin D4h structures to C2v. Moreover, the steric preference of the low-spin C2v structures can also be a significant factor for their higher stability compared with the high-spin Oh ones in the cases of the larger metals. A further important factor is the donor–acceptor interaction, discussed in the following subsection.
3.3. Donor–Acceptor Interactions
The metal–ligand interactions in carbonyl complexes involve very interesting bonding features and therefore have been investigated extensively [34,35,36,37,103,104,105,106]. They consist of CO→M σ donation and M→CO π backdonation, the σ and π notations representing the σ and π characters of the orbitals participating in these interactions.
Several studies have focused on the shifts in CO vibrational stretching frequencies, which are caused by the elongation or contraction of the CO bond depending on the nature of the donor–acceptor interaction. In neutral and most ionic M(CO)x complexes, shifts to the lower wavenumbers (red shift) occur, originating from elongation of the CO bond upon backdonation from M to the π* orbitals of CO. This characteristic red shift has been used to characterize the strength of interaction [105], as well as to clarify coordination numbers [9,107,108,109,110,111,112].
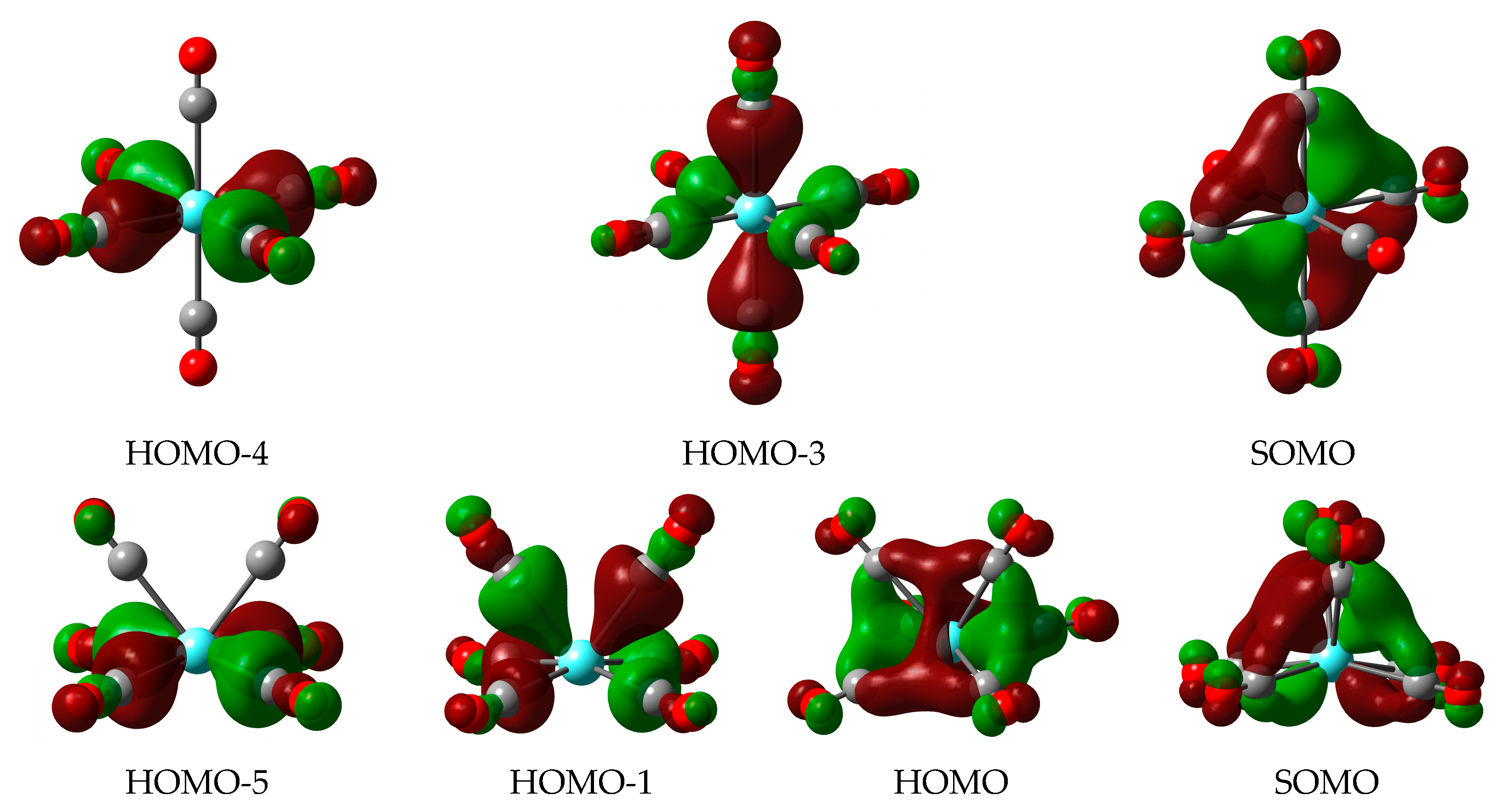
The main bonding orbitals in the Oh and C2v structures are demonstrated in Figure 4 by those of Y(CO)6. In the high-spin Oh structure, the σ donation is manifested in two 2-electron orbitals: one involving an equatorial Y 4d acceptor orbital (upper row HOMO-4) and the other formed with the axial Y 4d acceptor orbital (upper row HOMO-3). The π backdonation interactions occur from three orthogonal singly occupied 4d orbitals of the Y atom (e.g., upper row SOMO). The low-spin C2v isomer is formed by three 2-electron orbitals from which the σ donation from the equatorial and axial CO groups is distinguished (bottom row HOMO-5 and HOMO-1). The two π backdonation orbitals (bottom row HOMO and SOMO) are delocalized over the six CO groups.
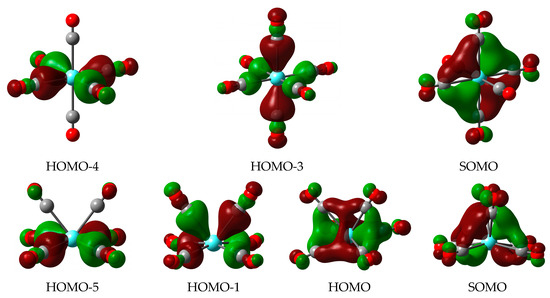
Figure 4.
Selected Kohn–Sham orbitals of Y(CO)6 demonstrating the donor–acceptor interactions in the two characteristic structures: 4Oh (top), 2C2v (bottom). The applied isovalue corresponds to 0.03 (electrons/(Bohr)3)1/2.
Some quantitative information on the electrons participating in the donor–acceptor interactions can be provided by NBO analysis [57]. Selected NBO results on the studied complexes are compiled in Table 2, together with the Allred–Rochow electronegativities [113].

Table 2.
NBO analysis results on the charge transfer (CT) interactions 1 in selected M(CO)6 complexes.
The net natural charge of M (qM) corresponds to the difference in CT to and from M. A negative qM means that the number of donated electrons exceeds the backdonated ones—a case reported recently for several neutral and ionic metal carbonyls [37,56]. It can occur with a sufficiently large number of donor CO groups, while the surrounded M has only a limited number of electrons for backdonation.
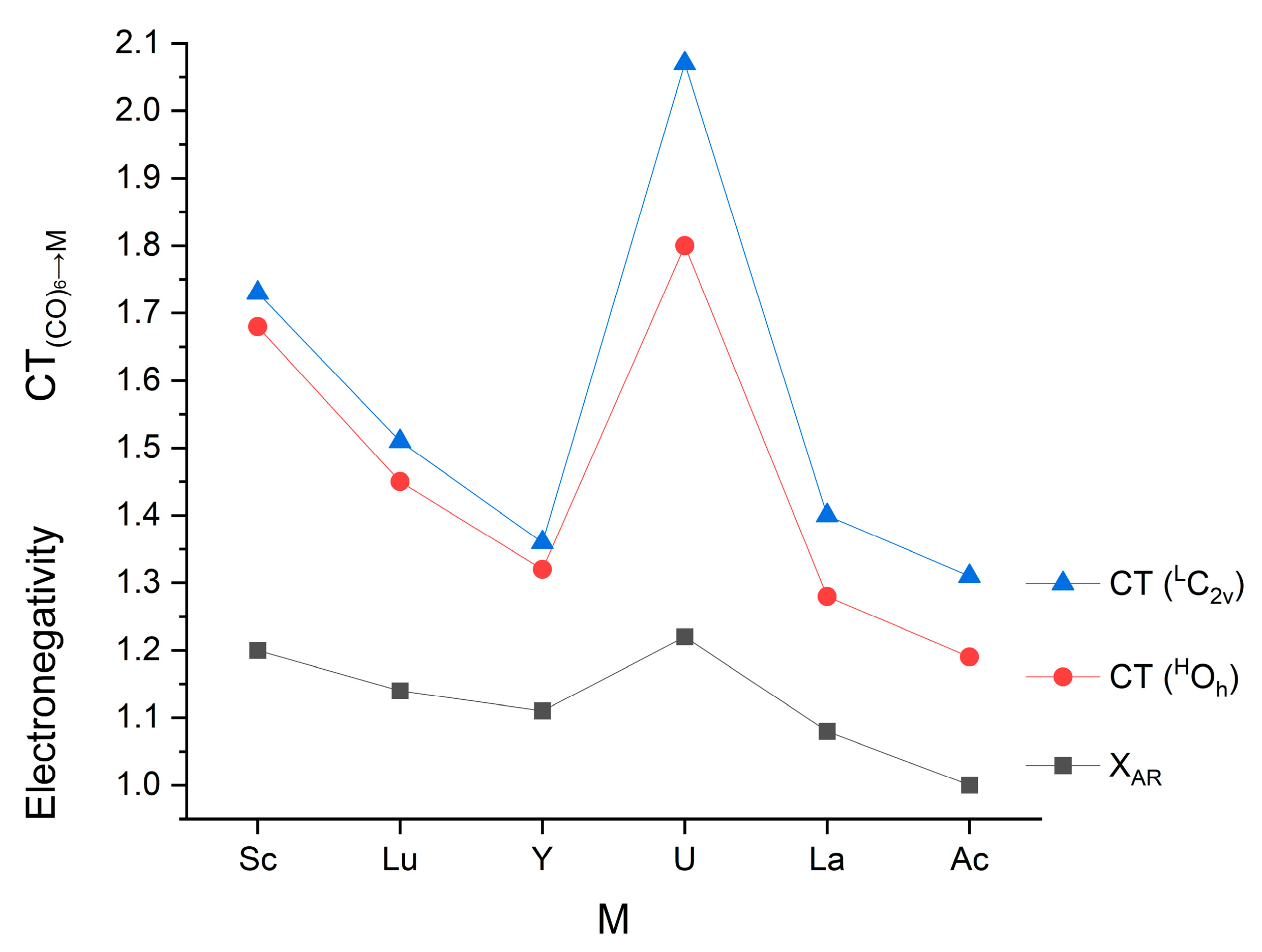
Among the present complexes, a negative qM was obtained for Sc and U. In the complexes of the other metals, the M→ (CO)6 backdonation exceeded the (CO)6→M donation. This feature is in accordance with the electronegativities of Sc and U being the largest in the present set (cf. Table 2). In general, there is a good correlation between the number of electrons transferred from (CO)6 to M and the Allred–Rochow electronegativities (cf. Figure 5), suggesting a dominant role of electronegativity in this process. In contrast, no trend in the M→ (CO)6 backdonation can be recognized (cf. Table 2), implying the comparable importance of electronegativity, spatial conditions and relative energies of the interacting orbitals.
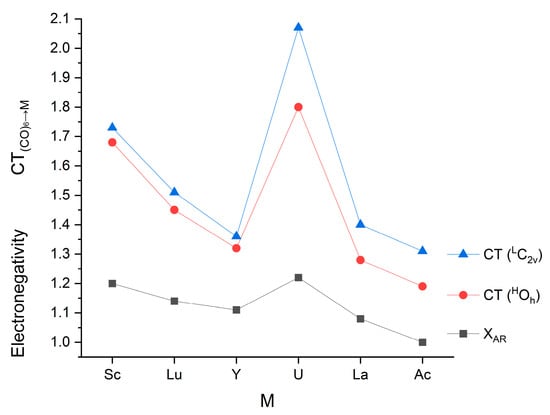
Figure 5.
Relation of Allred–Rochow electronegativities (in Pauling units) [113] and the (CO)6→M charge transfers (e) in the M(CO)6 complexes.
The sum of the donated and backdonated electrons (ΣCT) is around 3 e, which means covalent M-C bond orders of ca. 0.5 pro CO group. The somewhat larger value of U(CO)6 is the result of the above-noted larger donation and backdonation interactions.
A very important observation in the presented CT data is that they are consistently larger in the low-spin C2v structures than in the high-spin Oh ones (cf. Table 2 and Figure 5). Obviously, they are strongly related to the consistently shorter (both equatorial and axial) M-C bond distances in the former structures (cf. Figure 2).
The ground-state electron configurations of the studied metals are ns1(n−1)d2 and ns2(n−1)d1 for the high- and low-spin states, respectively. In the case of U, it is extended with the (n−2)f3 subconfiguration. The metal valence orbital populations of the complexes in Table 2 are in agreement with extensive promotions of the valence s electrons to d orbitals as a prerequisite of complex formation. At the same time, the data confirm the dominant role of valence d orbitals, as is usual for d and f elements. The populations of valence f orbitals in the f elements are generally very small, indicating their small role in the bonding.
The excess of the 5f population with respect to the (n−2)f3 subconfiguration of U has a somewhat larger value for the C2v isomer of U(CO)6 (0.15 e), indicating enhanced contribution to bonding in the form of 6d/5f hybrid orbitals. An inspection of the molecular orbitals of U(CO)6 also revealed a slight backdonation from the 1-electron 5f orbitals to the antibonding orbitals of the CO groups (Figure S4). The valence s populations are around 0.4 e in the complexes: they are manifested mainly in nonbonding lower-energy molecular orbitals, while a small bonding contribution was detected as d/s hybrid in M acceptor orbitals.
Looking back at Table 1, we can recognize slightly (but consistently) higher energies in the low-spin D4h species with respect to the high-spin Oh ones. This seems to be in contradiction with the M-C bond distances being marginally smaller in the low-spin D4h forms (cf. Figure 2). The smaller bond distance results in (marginally) larger CT data for the low-spin D4h form with respect to those of the high-spin Oh one—as seen for the Sc(CO)6 complex in Table 2. Altogether, the marginal differences between the CT properties of the D4h and Oh species suggest that the change in spin state does not cause any significant difference in the electron transfer in these very similar structures. On the other hand, nonmarginal differences in the energies of the donor and acceptor orbitals in the two spin states cannot be excluded.
Visual inspection of the bonding molecular orbitals did not show any difference for the low-spin D4h or high-spin Oh species (cf. Figure 4). The difference in the spin state, i.e., one of the 1-electron orbitals in the D4h species has a spin opposite to the orthogonally oriented other two 1-electron orbitals, had no viewable effect on the shape of the molecular orbital. The very close atomic charges and visually identical molecular orbitals imply very similar charge distribution in the two complex forms. Accordingly, the change in spin state likely does not cause any significant difference in the electrostatic interactions.
Another significant contribution to the energetics of bonding is the Pauli repulsion, i.e., the repulsion of the electrons with the same spin. This can result in the lower stability of the high-spin Oh form, where there are three orthogonal 1-electron orbitals of the same spin (e.g., SOMO in Figure 4 upper row).
Finally, the promotion process should be mentioned, i.e., the energy needed to promote the M atoms from their ground states to the excited states with the right orbital populations for the donor–acceptor interactions. In the above arguments, we showed that most metal–ligand interactions seem to be more favorable for the low-spin C2v structure than for the high-spin Oh one. Yet, among the studied complexes, Sc(CO)6 prefers the high-spin Oh form in terms of electronic energy (cf. Table 1). In view of the above considerations, a lower promotion energy of the quartet (4s13d2) Sc atom with respect to the doublet (4s23d1) one may be the key factor for that.
3.4. Matrix Isolation IR
We analyzed earlier recorded unpublished matrix isolation IR spectra of Sc carbonyl complexes in order to find experimental evidence on the Sc(CO)6 complex and its structure. The spectra revealed a mixture of various coordinations. Annealing and irradiation experiments clarified the relation of the bands, and these data are compiled in Table S5 of the Supplementary Materials. The assignments are based on the computed vibrational frequencies and IR intensities, as presented in Figure 6. In order to facilitate an easier visual overview, the overestimated B3LYP frequencies were corrected by the scale factor 0.96 from ref. [56].
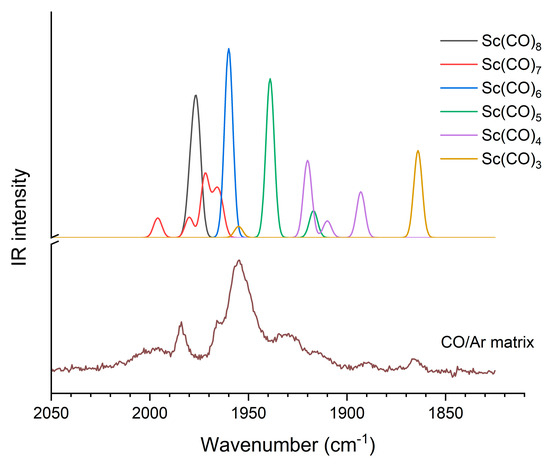
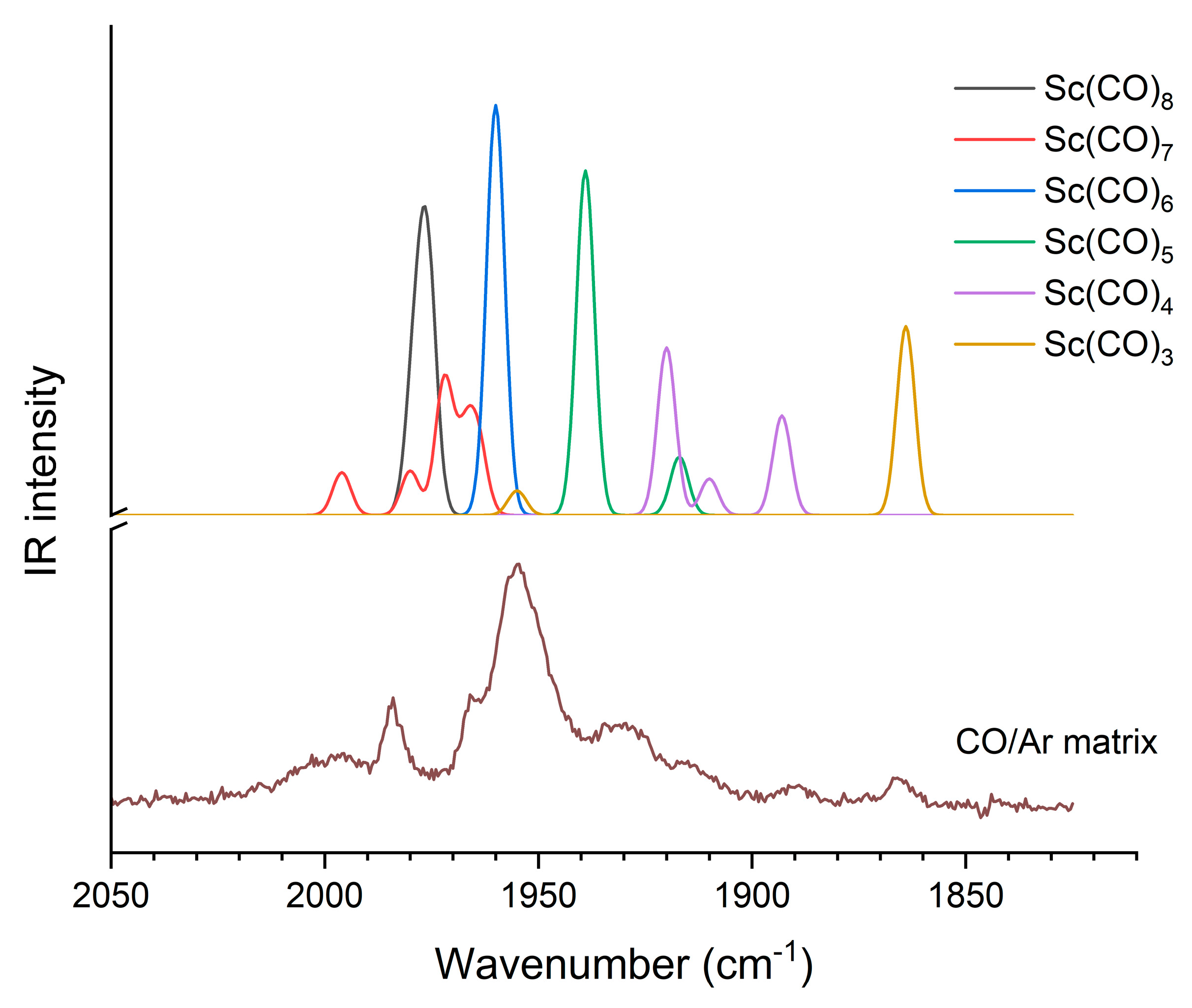
Figure 6.
Computed (scaled B3LYP) and experimental CO/Ar matrix isolation IR spectra of Sc(CO)x complexes.
The bands of Sc(CO)x complexes at 1984, 1965, 1955, 1930, 1980 and 1866 cm−1 observed in the CO/Ar matrix can be attributed to the complexes with coordination numbers of 8, 7, 6, 5, 4 and 3, respectively (cf. Figure 6 and Table S5). The observed bands of the octa- and heptacarbonyl species complement a previous report on the [Sc(CO)8]− [13] and [Sc(CO)8]+ ions [19] observed in the gaseous phase by mass spectrometry and confirm the possibility of octa-coordination as the highest one for neutral scandium atoms too.
The main message from this section is the assignment of the strong 1955 cm−1 absorption to Sc(CO)6 on the basis of the present B3LYP vibrational data. In the annealing and irradiation experiments, its intensity changed independently (cf. Table S5), confirming the single-band character of this absorption. According to the B3LYP calculations, the less symmetric C2v form can be expected to give four bands of comparable intensity within a range of ca. 30 cm−1; thus, the single absorption band confirms the high-spin Oh structure of the Sc(CO)6 complex.
The IR spectra of low-coordinated Sc(CO)x complexes trapped in solid Ar and Ne have been reported by Zhou and Andrews [6]. From their crowded spectrum (due to the formation of numerous excited-state byproducts upon high-energy laser evaporation), the absorptions at 1865.4 and around 1890 cm−1 are in good agreement with our weak bands at 1866 and 1890 cm−1 (cf. Table S5). Here, we revised the literature assignments of the former bands based on unscaled BP86 frequencies with rather poor agreements [33].
4. Conclusions
The main question of this study was the preference of the (low-spin) low-symmetry C2v structure vs. the (high-spin) high-symmetry Oh one. The computed electronic energies supported this stability for most M in the present study, the exception being the smallest Sc. The Oh structure of Sc(CO)6 was confirmed by the here-reported matrix isolation IR results.
The computations clarified several advantages of the C2v species vs. the Oh/D4h ones:
- (i)
- Closer M-C distances, implying stronger bonding interactions;
- (ii)
- Weaker steric effects, particularly in the cases of larger M-s;
- (iii)
- Generally stronger CT interactions in terms of transferred electrons,
- (iv)
- Less Pauli repulsion because of the low-spin character.
On the other hand, orbital overlaps seem to be less advantageous in the C2v structures of small M, where the equatorial {C3,C4,C5,C6,M} moieties are considerably distorted from planarity in contrast to the planar features in the Oh and D4h structures.
An unknown but important factor is the promotion energy getting the electronic structure of M optimal for donor–acceptor interactions—this can be considerably different for the high- and low-spin states.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/sym16020178/s1, Spin contamination data and PBE0 and CASPT2 relative energies (Table S1); data presented in Figure 2 and Figure 3 of the paper (Table S2: optimized M-C distances; Table S3 C-M-C angles); estimated steric energies (Table S4); MI-IR data of Sc(CO)x (Table S5); selected structures of U(CO)6 (Figure S1); selected IR spectra of Sc(CO)x (Figure S2); selected UV–vis spectra of Sc(CO)x (Figure S3); bonding molecular orbitals of the quintet C2v global minimum of U(CO)6 (Figure S4); Cartesian coordinates of the optimized B3LYP structures with electronic energies.
Author Contributions
Conceptualization, A.K.; methodology, A.K. and W.K.; investigation, A.K. and W.K; writing—original draft preparation, A.K. and W.K.; writing—review and editing, A.K. and W.K.; supervision, A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article and supplementary materials.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hallam, H.E. Vibrational Spectroscopy of Trapped Species Infrared and Raman Studies of Matrix-Isolated Molecules, Radicals and Ions; John Wiley & Sons Ltd.: New York, NY, USA, 1973. [Google Scholar]
- Moskovits, M.; Ozin, G.A. Cryochemistry; Wiley: Hoboken, NJ, USA, 1976. [Google Scholar]
- Turner, J.J.; Burdett, J.K.; Perutz, R.N.; Poliakoff, M. Matrix photochemistry of metal carbonyls. Pure Appl. Chem. 1977, 49, 271–285. [Google Scholar] [CrossRef]
- Burdett, J.K. Matrix isolation studies on transition metal carbonyls and related species. Coord. Chem. Rev. 1978, 27, 1–58. [Google Scholar] [CrossRef]
- Perutz, R.N. Matrix Photochemistry of Transition Metal Complexes: Principles, Applications and Links to Other Methods. In Low Temperature Molecular Spectroscopy; NATO ASI Series, 483; Fausto, R., Ed.; Springer: Dordrecht, The Netherlands, 1996; pp. 95–124. [Google Scholar] [CrossRef]
- Zhou, M.; Andrews, L. Matrix Infrared Spectra and Density Functional Calculations of ScCO, ScCO−, and ScCO+. J. Phys. Chem. A 1999, 103, 2964–2971. [Google Scholar] [CrossRef]
- Turner, J.J.; George, M.W.; Poliakoff, M.; Perutz, R.N. Photochemistry of transition metal carbonyls. Chem. Soc. Rev. 2022, 51, 5300–5329. [Google Scholar] [CrossRef]
- Jin, X.; Jiang, L.; Xu, Q.; Zhou, M. Reactions of Gadolinium Atoms and Dimers with CO: Formation of Gadolinium Carbonyls and Photoconversion to CO Activated Molecules. J. Phys. Chem. A 2006, 110, 12585–12591. [Google Scholar] [CrossRef]
- Jiang, L.; Xu, Q. Reactions of Laser-Ablated La and Y Atoms with CO: Matrix Infrared Spectra and DFT Calculations of the M(CO)x and MCO+ (M = La, Y; x = 1−4) Molecules. J. Phys. Chem. A 2007, 111, 3271–3277. [Google Scholar] [CrossRef]
- Ricks, A.M.; Gagliardi, L.; Duncan, M.A. Infrared Spectroscopy of Extreme Coordination: The Carbonyls of U+ and UO2+. J. Am. Chem. Soc. 2010, 132, 15905–15907. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.; Wang, J.; Qin, Z.; Shi, L.; Tang, Z.; Xing, X. Octacoordinate Metal Carbonyls of Lanthanum and Cerium: Experimental Observation and Theoretical Calculation. J. Phys. Chem. A 2014, 118, 9380–9385. [Google Scholar] [CrossRef] [PubMed]
- Brathwaite, A.D.; Maner, J.A.; Duncan, M.A. Testing the Limits of the 18-Electron Rule: The Gas-Phase Carbonyls of Sc+ and Y+. Inorg. Chem. 2014, 53, 1166–1169. [Google Scholar] [CrossRef]
- Jin, J.; Yang, T.; Xin, K.; Wang, G.; Jin, X.; Zhou, M.; Frenking, G. Octacarbonyl Anion Complexes of Group Three Transition Metals [TM(CO)8]− (TM=Sc, Y, La) and the 18-Electron Rule. Angew. Chem. Int. Ed. 2018, 57, 6236–6241. [Google Scholar] [CrossRef] [PubMed]
- Jin, J.; Pan, S.; Jin, X.; Lei, S.; Zhao, L.; Frenking, G.; Zhou, M. Octacarbonyl Anion Complexes of the Late Lanthanides Ln(CO)8− (Ln = Tm, Yb, Lu) and the 32-Electron Rule. Chem. Eur. J. 2019, 25, 3229–3234. [Google Scholar] [CrossRef]
- Chi, C.; Pan, S.; Jin, J.; Meng, L.; Luo, M.; Zhao, L.; Zhou, M.; Frenking, G. Octacarbonyl Ion Complexes of Actinides [An(CO)8]+/− (An = Th, U) and the Role of f Orbitals in Metal–Ligand Bonding. Chem. Eur. J. 2019, 25, 11772–11784. [Google Scholar] [CrossRef]
- Wu, X.; Zhao, L.; Jin, J.; Pan, S.; Li, W.; Jin, X.; Wang, G.; Zhou, M.; Frenking, G. Observation of alkaline earth complexes M(CO)8 (M = Ca, Sr, or Ba) that mimic transition metals. Science 2018, 361, 912–916. [Google Scholar] [CrossRef]
- Bettens, T.; Pan, S.; De Proft, F.; Frenking, G.; Geerlings, P. Alkaline Earth Metals Activate N2 and CO in Cubic Complexes Just Like Transition Metals: A Conceptual Density Functional Theory and Energy Decomposition Analysis Study. Chem. Eur. J. 2020, 26, 12785–12793. [Google Scholar] [CrossRef]
- Yang, X. The 18-electron rule for main-group alkaline earth octacarbonyl complexes. Nat. Sci. Rev. 2019, 6, 8–9. [Google Scholar] [CrossRef]
- Xing, X.; Wang, J.; Xie, H.; Liu, Z.; Qin, Z.; Zhao, L.; Tang, Z. Octacoordinate metal carbonyls of scandium and yttrium: Theoretical calculations and experimental observation. Rapid Commun. Mass Spectrom. 2013, 27, 1403–1409. [Google Scholar] [CrossRef]
- Deng, G.; Lei, S.; Pan, S.; Jin, J.; Wang, G.; Zhao, L.; Zhou, M.; Frenking, G. Filling a Gap: The Coordinatively Saturated Group 4 Carbonyl Complexes TM(CO)8 (TM = Zr, Hf) and Ti(CO)7. Chem. Eur. J. 2020, 26, 10487–10500. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Tian, C.-Y.; Zhao, Y.; Jiang, S.; Wang, T.; Zheng, H.; Yan, W.; Li, G.; Xie, H.; Li, J.; et al. Observation of Confinement-Free Neutral Group Three Transition Metal Carbonyls Sc(CO)7 and TM(CO)8 (TM=Y, La). Angew. Chem. Int. Ed. 2023, 62, e202305490. [Google Scholar] [CrossRef] [PubMed]
- Hillier, I.H.; Saunders, V.R. Ab initio molecular orbital calculations of transition metal complexes. Mol. Phys. 1971, 22, 1025–1034. [Google Scholar] [CrossRef]
- Baerends, E.J.; Ros, P. The electronic structure of transition metal carbonyl complexes. Mol. Phys. 1975, 30, 1735–1747. [Google Scholar] [CrossRef]
- Rees, B.; Mitschler, A. Electronic structure of chromium hexacarbonyl at liquid nitrogen temperature. 2. Experimental study (x-ray and neutron diffraction) of σ and π bonding. J. Am. Chem. Soc. 1976, 98, 7918–7924. [Google Scholar] [CrossRef]
- Arratia-Perez, R.; Yang, C.Y. Bonding in metal hexacarbonyls. J. Chem. Phys. 1985, 83, 4005–4014. [Google Scholar] [CrossRef][Green Version]
- Barnes, L.A.; Bauschlicher, C.W., Jr. Theoretical studies of the transition metal–carbonyl systems MCO and M(CO)2, M=Ti, Sc, and V. J. Chem. Phys. 1989, 91, 314–330. [Google Scholar] [CrossRef]
- Davidson, E.R.; Kunze, K.L.; Machado, F.B.C.; Chakravorty, S.J. The transition metal-carbonyl bond. Acc. Chem. Res. 1993, 26, 628–635. [Google Scholar] [CrossRef]
- Fournier, R. Theoretical study of the monocarbonyls of first-row transition metal atoms. J. Chem. Phys. 1993, 99, 1801–1815. [Google Scholar] [CrossRef]
- Ehlers, A.W.; Frenking, G. Structures and Bond Energies of the Transition Metal Hexacarbonyls M(CO)6 (M = Cr, Mo, W). A Theoretical Study. J. Am. Chem. Soc. 1994, 116, 1514–1520. [Google Scholar] [CrossRef]
- Adamo, C.; Lelj, F. A hybrid density functional study of the first-row transition-metal monocarbonyls. J. Chem. Phys. 1995, 103, 10605–10613. [Google Scholar] [CrossRef]
- Jonas, V.; Thiel, W. Theoretical study of the vibrational spectra of the transition metal carbonyls M(CO)6 [M=Cr, Mo, W], M(CO)5 [M=Fe, Ru, Os], and M(CO)4 [M=Ni, Pd, Pt]. J. Chem. Phys. 1995, 102, 8474–8484. [Google Scholar] [CrossRef]
- Koukounas, C.; Kardahakis, S.; Mavridis, A. Electronic and geometric structure of the 3d-transition metal monocarbonyls MCO, M=Sc, Ti, V, and Cr. J. Chem. Phys. 2005, 123, 074327. [Google Scholar] [CrossRef]
- Gao, S.-M.; Guo, W.-P.; Jin, L.; Ding, Y.-H. Maximum carbonyl-coordination number of scandium. Computational study of Sc(CO)n (n = 1–7), Sc(CO)7− and Sc(CO)63−. Int. J. Quantum Chem. 2013, 113, 1192–1199. [Google Scholar] [CrossRef]
- van der Lubbe, S.C.C.; Vermeeren, P.; Fonseca Guerra, C.; Bickelhaupt, F.M. The Nature of Nonclassical Carbonyl Ligands Explained by Kohn–Sham Molecular Orbital Theory. Chem. Eur. J. 2020, 26, 15690–15699. [Google Scholar] [CrossRef]
- Frenking, G.; Fröhlich, N. The Nature of the Bonding in Transition-Metal Compounds. Chem. Rev. 2000, 100, 717–774. [Google Scholar] [CrossRef]
- Frenking, G. Understanding the nature of the bonding in transition metal complexes: From Dewar’s molecular orbital model to an energy partitioning analysis of the metal–ligand bond. J. Organomet. Chem. 2001, 635, 9–23. [Google Scholar] [CrossRef]
- Frenking, G.; Fernández, I.; Holzmann, N.; Pan, S.; Krossing, I.; Zhou, M. Metal–CO Bonding in Mononuclear Transition Metal Carbonyl Complexes. JACS Au 2021, 1, 623–645. [Google Scholar] [CrossRef]
- Brockway, L.O.; Ewens, R.V.C.; Lister, M. An electron diffraction investigation of the hexacarbonyls of chromium, molybdenum and tungsten. Trans. Faraday Soc. 1938, 34, 1350–1357. [Google Scholar] [CrossRef]
- Jones, L.H. Vibrational spectra and force constants of the hexacarbonyls of chromium, molybdenum and tungsten. Spectrochim. Acta 1963, 19, 329–338. [Google Scholar] [CrossRef]
- Arnesen, S.P.; Seip, H.M. Studies on the Failure of the First Born Approximation in Electron Diffraction. V. Molybdenum- and Tungsten Hexacarbonyl. Acta Chem. Scand. 1966, 20, 2711–2727. [Google Scholar] [CrossRef]
- Jost, A.; Rees, B.; Yelon, W.B. Electronic structure of chromium hexacarbonyl at 78 K. I. Neutron diffraction study. Acta Cryst. Sect. B 1975, 31, 2649–2658. [Google Scholar] [CrossRef]
- Tevault, D.; Nakamoto, K. Matrix isolation and computer simulation spectra of chromium hexacarbonyl Cr(CO)6 and molybdenum hexacarbonyl Mo(CO)6. Inorg. Chem. 1975, 14, 2371–2373. [Google Scholar] [CrossRef]
- Perutz, R.N.; Turner, J.J. Photochemistry of the Group VI hexacarbonyls in low-temperature matrices. II. Infrared spectra and structures of carbon-13 monoxide-enriched hexacarbonyls and pentacarbonyls of chromium, molybdenum, and tungsten. Inorg. Chem. 1975, 14, 262–270. [Google Scholar] [CrossRef]
- Hawkins, N.J.; Mattraw, H.C.; Sabol, W.W.; Carpenter, D.R. Spectroscopy of Gaseous Carbonyls. I. Infrared Spectra and Thermodynamic Properties of Chromium and Molybdenum Hexacarbonyls. J. Chem. Phys. 2004, 23, 2422–2427. [Google Scholar] [CrossRef]
- Langmuir, I. Types of Valence. Science 1921, 54, 59–67. [Google Scholar] [CrossRef]
- Tolman, C.A. The 16 and 18 electron rule in organometallic chemistry and homogeneous catalysis. Chem. Soc. Rev. 1972, 1, 337–353. [Google Scholar] [CrossRef]
- Jensen, W.B. The Origin of the 18-Electron Rule. J. Chem. Educ. 2005, 82, 28. [Google Scholar] [CrossRef]
- Bellard, S.; Rubinson, K.A.; Sheldrick, G.M. Crystal and molecular structure of vanadium hexacarbonyl. Acta Cryst. Sect. B 1979, 35, 271–274. [Google Scholar] [CrossRef]
- Elschenbroich, C.; Salzer, A. Organometallics: A Concise Introduction, 2nd ed.; Wiley-VCH: Weinheim, Germany, 1992. [Google Scholar]
- Busby, R.; Klotzbuecher, W.; Ozin, G.A. Titanium hexacarbonyl, Ti(CO)6, and titanium hexadinitrogen, Ti(N2)6. 1. Synthesis using titanium atoms and characterization by matrix infrared and ultraviolet-visible spectroscopy. Inorg. Chem. 1977, 16, 822–828. [Google Scholar] [CrossRef]
- Calderazzo, F.; Englert, U.; Pampaloni, G.; Pelizzi, G.; Zamboni, R. Studies on carbonyl derivatives of early transition elements. A convenient method for the preparation of the [Nb(CO)6]- anion at atmospheric pressure and room temperature. Crystal and molecular structure of [M(CO)6]- (M = Nb, Ta) as their bis(triphenylphosphine) nitrogen(1+) derivatives. Inorg. Chem. 1983, 22, 1865–1870. [Google Scholar] [CrossRef]
- Holloway, J.H.; Senior, J.B.; Szary, A.C. Rhenium carbonyl fluorides: Preparation of [Re(CO)6][ReF6] and some reactions of [Re(CO)5F·ReF5]. J. Chem. Soc. Dalton Trans. 1987, 741–745. [Google Scholar] [CrossRef]
- Ellis, J.E.; Chi, K.M. Highly reduced organometallics. 28. Synthesis, isolation, and characterization of [K(cryptand 2.2.2)]2[Hf(CO)6], the first substance to contain hafnium in a negative oxidation state. Structural characterization of [K(cryptand 2.2.2)]2[M(CO)6]•pyridine (M = Ti, Zr, and Hf). J. Am. Chem. Soc. 1990, 112, 6022–6025. [Google Scholar] [CrossRef]
- Bernhardt, E.; Bach, C.; Bley, B.; Wartchow, R.; Westphal, U.; Sham, I.H.T.; von Ahsen, B.; Wang, C.; Willner, H.; Thompson, R.C.; et al. Homoleptic, σ-Bonded Octahedral [M(CO)6]2+ Cations of Iron(II), Ruthenium(II), and Osmium(II): Part 1: Syntheses, Thermochemical and Vibrational Characterizations, and Molecular Structures as [Sb2F11]− and [SbF6]− Salts. A Comprehensive, Comparative Study. Inorg. Chem. 2005, 44, 4189–4205. [Google Scholar] [CrossRef] [PubMed]
- Geier, J.; Willner, H.; Lehmann, C.W.; Aubke, F. Formation of Hexacarbonylmanganese(I) Salts, [Mn(CO)6]+X-, in Anhydrous HF. Inorg. Chem. 2007, 46, 7210–7214. [Google Scholar] [CrossRef] [PubMed]
- Kovács, A.; Klotzbücher, W. A DFT and Matrix-Isolation IR/UV-Visible Study of High-Coordinated Lanthanide-CO Complexes. Molecules 2023, 28, 5043. [Google Scholar] [CrossRef] [PubMed]
- Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
- Weinhold, F.; Landis, C.R. Valency and Bonding: A Natural Bond Orbital Donor-Acceptor Perspective; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar] [CrossRef]
- Glendening, E.D.; Landis, C.R.; Weinhold, F. Natural bond orbital methods. WIREs Comput. Mol. Sci. 2012, 2, 1–42. [Google Scholar] [CrossRef]
- Weinhold, F. Natural bond orbital analysis: A critical overview of relationships to alternative bonding perspectives. J. Comput. Chem. 2012, 33, 2363–2379. [Google Scholar] [CrossRef]
- Weinhold, F.; Landis, C.R.; Glendening, E.D. What is NBO analysis and how is it useful? Int. Rev. Phys. Chem. 2016, 35, 399–440. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2010. [Google Scholar]
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Balabanov, N.B.; Peterson, K.A. Systematically convergent basis sets for transition metals. I. All-electron correlation consistent basis sets for the 3d elements Sc–Zn. J. Chem. Phys. 2005, 123, 064107. [Google Scholar] [CrossRef] [PubMed]
- Andrae, D.; Haeussermann, U.; Dolg, M.; Stoll, H.; Preuss, H. Energy-adjusted ab initio pseudopotentials for the second and third row transition elements. Theor. Chim. Acta 1990, 77, 123–141. [Google Scholar] [CrossRef]
- Dolg, M.; Stoll, H.; Preuss, H. Energy-adjusted ab initio pseudopotentials for the rare earth elements. J. Chem. Phys. 1989, 90, 1730–1734. [Google Scholar] [CrossRef]
- Martin, J.M.L.; Sundermann, A. Correlation consistent valence basis sets for use with the Stuttgart–Dresden–Bonn relativistic effective core potentials: The atoms Ga–Kr and In–Xe. J. Chem. Phys. 2001, 114, 3408–3420. [Google Scholar] [CrossRef]
- Cao, X.; Dolg, M. Segmented contraction scheme for small-core lanthanide pseudopotential basis sets. J. Mol. Struct. Theochem 2002, 581, 139–147. [Google Scholar] [CrossRef]
- Küchle, W.; Dolg, M.; Stoll, H.; Preuss, H. Energy-Adjusted Pseudopotentials for the Actinides. Parameter Sets and Test Calculations for Thorium and Thorium Monoxide. J. Chem. Phys. 1994, 100, 7535–7542. [Google Scholar] [CrossRef]
- Cao, X.; Dolg, M.; Stoll, H. Valence basis sets for relativistic energy-consistent small-core actinide pseudopotentials. J. Chem. Phys. 2003, 118, 487–496. [Google Scholar] [CrossRef]
- Cao, X.; Dolg, M. Segmented contraction scheme for small-core actinide pseudopotential basis sets. J. Mol. Struct. Theochem 2004, 673, 203–209. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parameterization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Bursch, M.; Mewes, J.-M.; Hansen, A.; Grimme, S. Best-Practice DFT Protocols for Basic Molecular Computational Chemistry. Angew. Chem. Int. Ed. 2022, 61, e202205735. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6169. [Google Scholar] [CrossRef]
- Roos, B.O. Advances in Chemical Physics, Ab Initio Methods in Quantum Chemistry—II; Lawley, K.P., Ed.; John Wiley & Sons Ltd.: Chichester, UK, 1987; pp. 399–446. [Google Scholar]
- Karlström, G.; Lindh, R.; Malmqvist, P.-Å.; Roos, B.O.; Ryde, U.; Veryazov, V.; Widmark, P.-O.; Cossi, M.; Schimmelpfennig, B.; Neogrady, P.; et al. MOLCAS: A Program Package for Computational Chemistry. Comput. Mat. Sci. 2003, 28, 222–239. [Google Scholar] [CrossRef]
- Aquilante, F.; Autschbach, J.; Carlson, R.K.; Chibotaru, L.F.; Delcey, M.G.; De Vico, L.; Galván, I.F.; Ferré, N.; Frutos, L.M.; Gagliardi, L.; et al. MOLCAS 8: New Capabilities for Multiconfigurational Quantum Chemical Calculations Across the Periodic Table. J. Comput. Chem. 2016, 37, 506–541. [Google Scholar] [CrossRef] [PubMed]
- Douglas, N.; Kroll, N.M. Quantum Electrodynamical Corrections to the Fine Structure of Helium. Ann. Phys. 1974, 82, 89–155. [Google Scholar] [CrossRef]
- Hess, B.A. Relativistic Electronic-Structure Calculations Employing a Two-Component No-Pair Formalism with External-Field Projection Operators. Phys. Rev. A 1986, 33, 3742–3748. [Google Scholar] [CrossRef] [PubMed]
- Roos, B.O.; Lindh, R.; Malmqvist, P.-Å.; Veryazov, V.; Widmark, P.-O. New Relativistic ANO Basis Sets for Transition Metal Atoms. J. Phys. Chem. A 2005, 109, 6575–6579. [Google Scholar] [CrossRef] [PubMed]
- Roos, B.O.; Lindh, R.; Malmqvist, P.-Å.; Veryazov, V.; Widmark, P.-O. New Relativistic Atomic Natural Orbital Basis Sets for Lanthanide Atoms with Applications to the Ce Diatom and LuF3. J. Phys. Chem. A 2008, 112, 11431–11435. [Google Scholar] [CrossRef]
- Roos, B.O.; Lindh, R.; Malmqvist, P.-Å.; Veryazov, V.; Widmark, P.-O. New Relativistic ANO Basis Sets for Actinide Atoms. Chem. Phys. Lett. 2005, 409, 295–299. [Google Scholar] [CrossRef]
- Roos, B.O.; Lindh, R.; Malmqvist, P.-Å.; Veryazov, V.; Widmark, P.-O. Main Group Atoms and Dimers Studied with a New Relativistic ANO Basis Set. J. Phys. Chem. A 2004, 108, 2851–2858. [Google Scholar] [CrossRef]
- Andersson, K.; Malmqvist, P.-Å.; Roos, B.O.; Sadlej, A.; Wolinski, K. Second-Order Perturbation Theory with a CASSCF Reference Function. J. Phys. Chem. 1990, 94, 5483–5488. [Google Scholar] [CrossRef]
- Andersson, K.; Malmqvist, P.-Å.; Roos, B.O. Second-Order Perturbation Theory with a Complete Active Space Self-Consistent Field Reference Function. J. Chem. Phys. 1992, 96, 1218–1226. [Google Scholar] [CrossRef]
- Glendening, E.D.; Badenhoop, J.K.; Reed, A.E.; Carpenter, J.E.; Bohmann, J.A.; Morales, C.M.; Landis, C.R.; Weinhold, F. NBO 6.0; Theoretical Chemistry Institute, University of Wisconsin: Madison, WI, USA, 2013. [Google Scholar]
- Glendening, E.D.; Landis, C.R.; Weinhold, F. NBO 6.0: Natural Bond Orbital Analysis Program. J. Comput. Chem. 2013, 34, 1429–1437. [Google Scholar] [CrossRef] [PubMed]
- Fang, D.; Piquemal, J.-P.; Liu, S.; Cisneros, G.A. DFT-steric-based energy decomposition analysis of intermolecular interactions. Theor. Chem. Acc. 2014, 133, 1484. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Kovács, A.; Klotzbücher, W. Octa-coordination in complexes of lanthanides with N2 confirmed by matrix-isolation IR spectroscopy and DFT calculations. J. Mol. Struct. 2023, 1272, 134222. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev. 2005, 105, 2999–3093. [Google Scholar] [CrossRef]
- Scalmani, G.; Frisch, M.J. Continuous surface charge polarizable continuum models of solvation. I. General formalism. J. Chem. Phys. 2010, 132, 114110. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Cryst. 1976, A32, 751–767. [Google Scholar] [CrossRef]
- Slater, J.C. Atomic Radii in Crystals. J. Chem. Phys. 2004, 41, 3199–3204. [Google Scholar] [CrossRef]
- Liu, S. Steric effect: A quantitative description from density functional theory. J. Chem. Phys. 2007, 126, 244103. [Google Scholar] [CrossRef]
- Weizsäcker, C.F.v. Zur Theorie der Kernmassen. Z. Phys. 1935, 96, 431–458. [Google Scholar] [CrossRef]
- Liu, S.; Govind, N. Toward Understanding the Nature of Internal Rotation Barriers with a New Energy Partition Scheme: Ethane and n-Butane. J. Phys. Chem. A 2008, 112, 6690–6699. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Zhong, A.-G.; Yang, Q.; Liu, S. Origin of anomeric effect: A density functional steric analysis. J. Chem. Phys. 2011, 134, 084103. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Hu, H.; Pedersen, L.G. Steric, Quantum, and Electrostatic Effects on SN2 Reaction Barriers in Gas Phase. J. Phys. Chem. A 2010, 114, 5913–5918. [Google Scholar] [CrossRef] [PubMed]
- Goldman, A.S.; Krogh-Jespersen, K. Why Do Cationic Carbon Monoxide Complexes Have High C−O Stretching Force Constants and Short C−O Bonds? Electrostatic Effects, Not σ-Bonding. J. Am. Chem. Soc. 1996, 118, 12159–12166. [Google Scholar] [CrossRef]
- Lupinetti, A.J.; Frenking, G.; Strauss, S.H. Nonclassical Metal Carbonyls: Appropriate Definitions with a Theoretical Justification. Angew. Chem. Int. Ed. 1998, 37, 2113–2116. [Google Scholar] [CrossRef]
- Lupinetti, A.J.; Jonas, V.; Thiel, W.; Strauss, S.H.; Frenking, G. Trends in Molecular Geometries and Bond Strengths of the Homoleptic d10 Metal Carbonyl Cations [M(CO)n]x+ (Mx+=Cu+, Ag+, Au+, Zn2+, Cd2+, Hg2+; n=1–6): A Theoretical Study. Chem. Eur. J. 1999, 5, 2573–2583. [Google Scholar] [CrossRef]
- Willner, H.; Aubke, F. σ-Bonded Metal Carbonyl Cations and Their Derivatives: Syntheses and Structural, Spectroscopic, and Bonding Principles. Organometallics 2003, 22, 3612–3633. [Google Scholar] [CrossRef]
- Slater, J.L.; De Vore, T.C.; Calder, V. Detection of neodymium and ytterbium carbonyls using matrix isolation. Inorg. Chem. 1973, 12, 1918–1921. [Google Scholar] [CrossRef]
- Slater, J.L.; DeVore, T.C.; Calder, V. Detection of praseodymium, europium, gadolinium, and holmium carbonyls using matrix isolation. Inorg. Chem. 1974, 13, 1808–1812. [Google Scholar] [CrossRef]
- Klotzbücher, W.E.; Petrukhina, M.A.; Sergeev, G.B. Reactions of Samarium Atoms in Inert and Reactive Matrices. Mendeleev Commun. 1994, 4, 5–7. [Google Scholar] [CrossRef]
- Ermilov, A.Y.; Nemukhin, A.V.; Kovba, V.M. Characterization of structures and spectra of holmium complexes formed in the CO and N2 matrices. Mendeleev Commun. 1999, 9, 88–89. [Google Scholar] [CrossRef]
- Zhou, M.; Andrews, L.; Li, J.; Bursten, B.E. Reactions of Th Atoms with CO: The First Thorium Carbonyl Complex and an Unprecedented Bent Triplet Insertion Product. J. Am. Chem. Soc. 1999, 121, 12188–12189. [Google Scholar] [CrossRef]
- Zhou, M.; Andrews, L.; Li, J.; Bursten, B.E. Reaction of Laser-Ablated Uranium Atoms with CO: Infrared Spectra of the CUO, CUO-, OUCCO, (η2-C2)UO2, and U(CO)x (x = 1−6) Molecules in Solid Neon. J. Am. Chem. Soc. 1999, 121, 9712–9721. [Google Scholar] [CrossRef]
- Allred, A.L.; Rochow, E.G. A scale of electronegativity based on electrostatic force. J. Inorg. Nucl. Chem. 1958, 5, 264–268. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).