On Conformable Fractional Milne-Type Inequalities
Abstract
:1. Introduction
2. Main Results
3. Applications
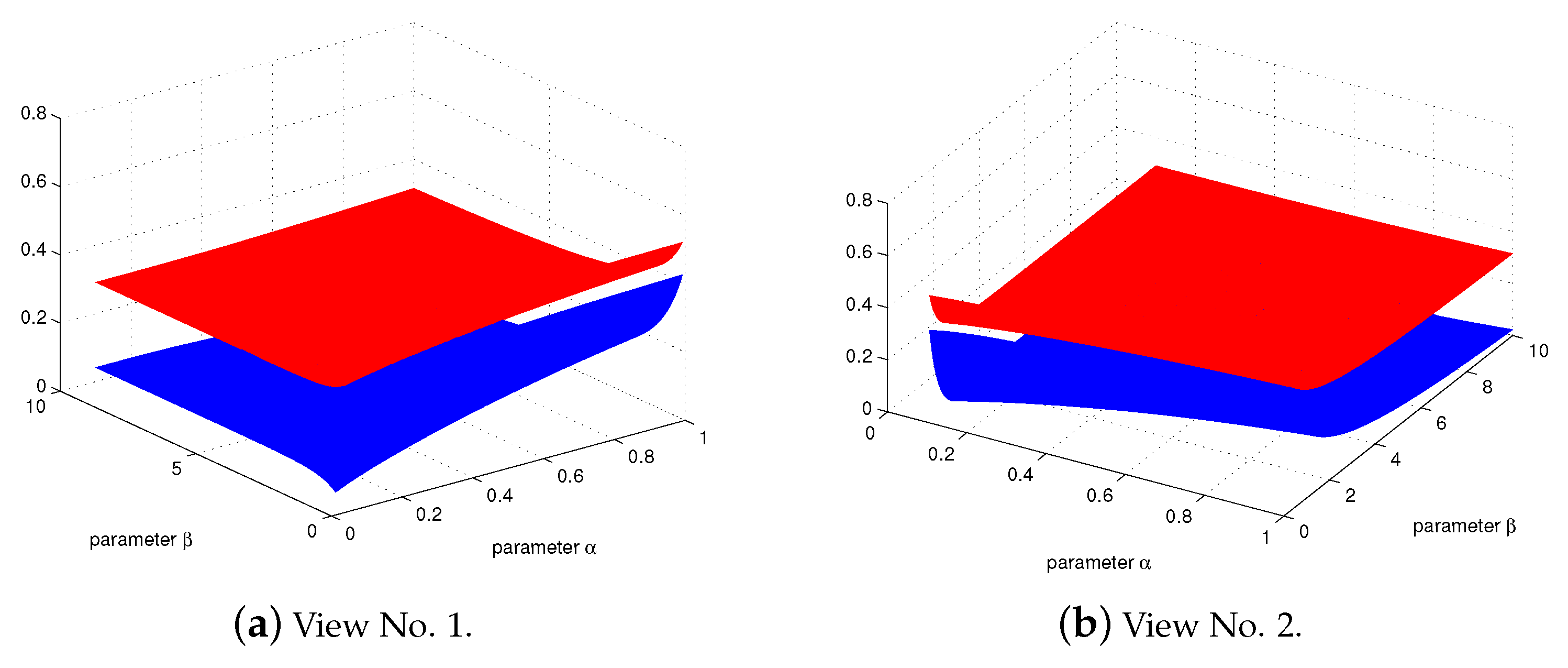
Application to Composite Quadrature Formula
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jensen, J.L.W.V. Sur les fonctions convexes et les inégalités entre les valeurs moyennes. Acta Math. 1906, 30, 175–193. [Google Scholar] [CrossRef]
- Rockafellar, R.T.; Wets, R.J.B. Variational Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; Volume 317. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004; pp. 14–716. [Google Scholar]
- Osborne, M.J.; Rubinstein, A. A Course in Game Theory; MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Khan, A.M.; Khurshid, Y.; Du, T.S.; Chu, Y.M. Generalization of Hermite-Hadamard type inequalities via conformable fractional integrals. J. Funct. Spaces 2018, 2018, 5357463. [Google Scholar]
- Kashuri, A.; Du, T.S.; Liko, R. On some new integral inequalities concerning twice differentiable generalized relative semi–(m, h)–preinvex mappings. Stud. Univ. Babes-Bolyai Math. 2019, 64, 43–61. [Google Scholar] [CrossRef]
- Meftah, B.; Lakhdari, A.; Saleh, W.; Kiliçman, A. Some new fractal Milne type integral inequalities via generalized convexity with applications. Fractal Fract. 2023, 7, 166. [Google Scholar] [CrossRef]
- Niculescu, C.P.; Persson, L.-E. Convex functions and their applications. A contemporary approach. In CMS Books in Mathematics/Ouvrages de Mathé Matiques de la SMC; Springer: New York, NY, USA, 2006; Volume 23. [Google Scholar]
- Dragomir, S.S.; Pearce, C.E.M. Selected Topics on Hermite-Hadamard Inequalities and Applications; RGMIA Monographs, Victoria University: Melbourne, VI, USA, 2000. [Google Scholar]
- Mitrinović, D.S.; Lacković, I.B. Hermite and convexity. Aequationes Math. 1985, 28, 229–232. [Google Scholar] [CrossRef]
- Booth, A.D. Numerical Methods, 3rd ed.; Butterworths: La Canada Flintrige, CA, USA, 1966. [Google Scholar]
- Djenaoui, M.; Meftah, B. Milne type inequalities for differentiable s-convex functions. Honam Math. J. 2022, 44, 325–338. [Google Scholar]
- Ullah, M.I.; Ain, Q.T.; Khan, A.; Abdeljawad, T.; Alqudah, M.A. Fractional approach to solar heating model using extended ODE system. Alex. Eng. J. 2023, 81, 405–418. [Google Scholar] [CrossRef]
- Thirthar, A.A.; Nazmul, S.K.; Mondal, B.; Alqudah, M.A.; Abdeljawad, T. Utilizing memory effects to enhance resilience in disease-driven prey-predator systems under the influence of global warming. J. Appl. Math. Comput. 2023, 69, 4617–4643. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional integrals and derivatives. In Theory and Applications; Edited and with a foreword by S. M. Nikol’skiĭ; Translated from the 1987 Russian Original; Revised by the authors; Gordon and Breach Science Publishers: Yverdon, Switzerland, 1993. [Google Scholar]
- Kashuri, A.; Meftah, B.; Mohammed, P.O.; Lupa, A.A.; Abdalla, B.; Hamed, Y.S.; Abdeljawad, T. Fractional weighted Ostrowski-Type inequalities and their applications. Symmetry 2021, 13, 968. [Google Scholar] [CrossRef]
- Lakhdari, A.; Meftah, B. Some fractional weighted trapezoid type inequalities for preinvex functions. Int. J. Nonlinear Anal. Appl. 2022, 13, 3567–3587. [Google Scholar]
- Meftah, B. Fractional Hermite-Hadamard type integral inequalities for functions whose modulus of derivatives are co-ordinated log-preinvex. Punjab Univ. J. Math. 2019, 51, 21–37. [Google Scholar]
- Saleh, W.; Lakhdari, A.; Kiliçman, A.; Frioui, A.; Meftah, B. Some new fractional Hermite-Hadamard type inequalities for functions with co-ordinated extended (s,m)-prequasiinvex mixed partial derivatives. Alex. Eng. J. 2023, 72, 261–267. [Google Scholar] [CrossRef]
- Saleh, W.; Lakhdari, A.; Abdeljawad, T.; Meftah, B. On fractional biparameterized Newton-type inequalities. J. Inequalities Appl. 2023, 2023, 122. [Google Scholar] [CrossRef]
- Budak, H.; Kösem, P.; Kara, H.H. On new Milne-type inequalities for fractional integrals. J. Inequal. Appl. 2023, 2023, 10. [Google Scholar] [CrossRef]
- Mitrinović, D.S.; Pečarić, J.E.; Fink, A.M. Classical and new inequalities in analysis. In Mathematics and its Applications (East European Series); Kluwer Academic Publishers Group: Dordrecht, Germany, 1993; Volume 61. [Google Scholar]
- Bullen, P.S.; Mitrinović, S.D.; Vasić, P.M. Means and their inequalities. In Mathematics and its Applications (East European Series); Translated and revised from the Serbo-Croatian; D. Reidel Publishing Co.: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Hyder, A.; Soliman, A.H. A new generalized θ-conformable calculus and its applications in mathematical physics. Phys. Scr. 2020, 96, 15208. [Google Scholar] [CrossRef]
- Zhao, D.; Luo, M. General conformable fractional derivative and its physical interpretation. Calcolo 2017, 54, 903–917. [Google Scholar] [CrossRef]
- Jarad, F.; Uğurlu, E.; Abdeljawad, T.; Baleanu, D. On a new class of fractional operators. Adv. Differ. Equ. 2017, 2017, 247. [Google Scholar] [CrossRef]
- Set, E.; Choi, J.; Gözpınar, A. Hermite-Hadamard type inequalities involving nonlocal conformable fractional integrals. Malays. J. Math. Sci. 2021, 15, 33–43. [Google Scholar]
- Set, E.; Akdemir, A.O.; Gözpınar, A.; Jarad, F. Ostrowski type inequalities via new fractional conformable integrals. AIMS Math. 2019, 4, 1684–1697. [Google Scholar] [CrossRef]
- Hyder, A.A.; Budak, H.; Almoneef, A.A. Further midpoint inequalities via generalized fractional operators in Riemann–Liouville sense. Fractal Fract. 2022, 6, 496. [Google Scholar] [CrossRef]
- Kara, H.; Budak, H.; Etemad, S.; Rezapour, S.; Ahmad, H.; Kaabar, M.K.A. A study on the new class of inequalities of midpoint-type and trapezoidal-type based on twice differentiable functions with conformable operators. J. Funct. Spaces 2023, 2023, 4624604. [Google Scholar] [CrossRef]
- Hezenci, F.; Budak, H. Simpson-type inequalities for conformable fractional operators with respect to twice-differentiable functions. J. Math. Ext. 2023, 17. [Google Scholar]
- Ünal, C.; Hezenci, F.; Budak, H. Conformable fractional Newton-type inequalities with respect to differentiable convex functions. J. Inequal. Appl. 2023, 2023, 85. [Google Scholar] [CrossRef]
- Rashid, S.; Akdemir, A.O.; Nisar, K.S.; Abdeljawad, T.; Rahman, G. New generalized reverse Minkowski and related integral inequalities involving generalized fractional conformable integrals. J. Inequal. Appl. 2020, 2020, 177. [Google Scholar] [CrossRef]
- Rahman, G.; Nisar, K.S.; Qi, F. Some new inequalities of the Grüss type for conformable fractional integrals. AIMS Math. 2018, 3, 575–583. [Google Scholar] [CrossRef]
- Rahman, G.; Ullah, Z.; Khan, A.; Set, E.; Nisar, K.S. Certain Chebyshev-type inequalities involving fractional conformable integral operators. Mathematics 2019, 7, 364. [Google Scholar] [CrossRef]
- Nisar, K.S.; Tassaddiq, A.; Gauhar, R.; Khan, A. Some inequalities via fractional conformable integral operators. J. Inequal. Appl. 2019, 2019, 217. [Google Scholar] [CrossRef]
- Butt, S.I.; Akdemir, A.O.; Nasir, J.; Jarad, F. Some Hermite-Jensen-Mercer like inequalities for convex functions through a certain generalized fractional integrals and related results. Miskolc Math. Notes 2020, 21, 689–715. [Google Scholar] [CrossRef]
- Akdemir, A.O.; Ekinci, A.; Set, E. Conformable fractional integrals and related new integral inequalities. J. Nonlinear Convex Anal. 2017, 18, 661–674. [Google Scholar]
- AlNemer, G.; Kenawy, M.; Zakarya, M.; Cesarano, C.; Rezk, H.M. Generalizations of Hardy’s type inequalities via conformable calculus. Symmetry 2021, 13, 242. [Google Scholar] [CrossRef]
- AlNemer, G.; Kenawy, M.R.; Rezk, H.M.; El-Deeb, A.A.; Zakarya, M. Fractional Leindler’s Inequalities via Conformable Calculus. Symmetry 2022, 14, 1958. [Google Scholar] [CrossRef]
- AlNemer, G.; Zakarya, M.; Butush, R.; Rezk, H.M. Some New Bennett–Leindler Type Inequalities via Conformable Fractional Nabla Calculus. Symmetry 2022, 14, 2183. [Google Scholar] [CrossRef]
- Hezenci, F.; Budak, H. Novel results on trapezoid-type inequalities for conformable fractional integrals. Turkish J. Math. 2023, 47, 425–438. [Google Scholar] [CrossRef]
- Hezenci, F.; Kara, H.; Budak, H. Conformable fractional versions of Hermite-Hadamard-type inequalities for twice-differentiable functions. Bound. Value Probl. 2023, 2023, 48. [Google Scholar] [CrossRef]
- Hyder, A.A.; Barakat, M.A.; Fathallah, A.; Cesarano, C. Further Integral Inequalities through Some Generalized Fractional Integral Operators. Fractal Fract. 2021, 5, 282. [Google Scholar] [CrossRef]
- Rezk, H.M.; Albalawi, W.; El-Hamid, H.A.A.; Saied, A.I.; Bazighifan, O.; Mohamed, M.S.; Zakarya, M. Hardy-Leindler-type inequalities via conformable delta fractional calculus. J. Funct. Spaces 2022, 2022, 2399182. [Google Scholar] [CrossRef]
- Zakarya, M.; Altanji, M.; AlNemer, G.; El-Hamid, H.A.A.; Cesarano, C.; Rezk, H.M. Fractional reverse coposnís inequalities via conformable calculus on time scales. Symmetry 2021, 13, 542. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ying, R.; Lakhdari, A.; Xu, H.; Saleh, W.; Meftah, B. On Conformable Fractional Milne-Type Inequalities. Symmetry 2024, 16, 196. https://doi.org/10.3390/sym16020196
Ying R, Lakhdari A, Xu H, Saleh W, Meftah B. On Conformable Fractional Milne-Type Inequalities. Symmetry. 2024; 16(2):196. https://doi.org/10.3390/sym16020196
Chicago/Turabian StyleYing, Rui, Abdelghani Lakhdari, Hongyan Xu, Wedad Saleh, and Badreddine Meftah. 2024. "On Conformable Fractional Milne-Type Inequalities" Symmetry 16, no. 2: 196. https://doi.org/10.3390/sym16020196




