On the Entire Harmonic Index and Entire Harmonic Polynomial of Graphs
Abstract
:1. Introduction
2. The Informative Power for Chemical Modeling
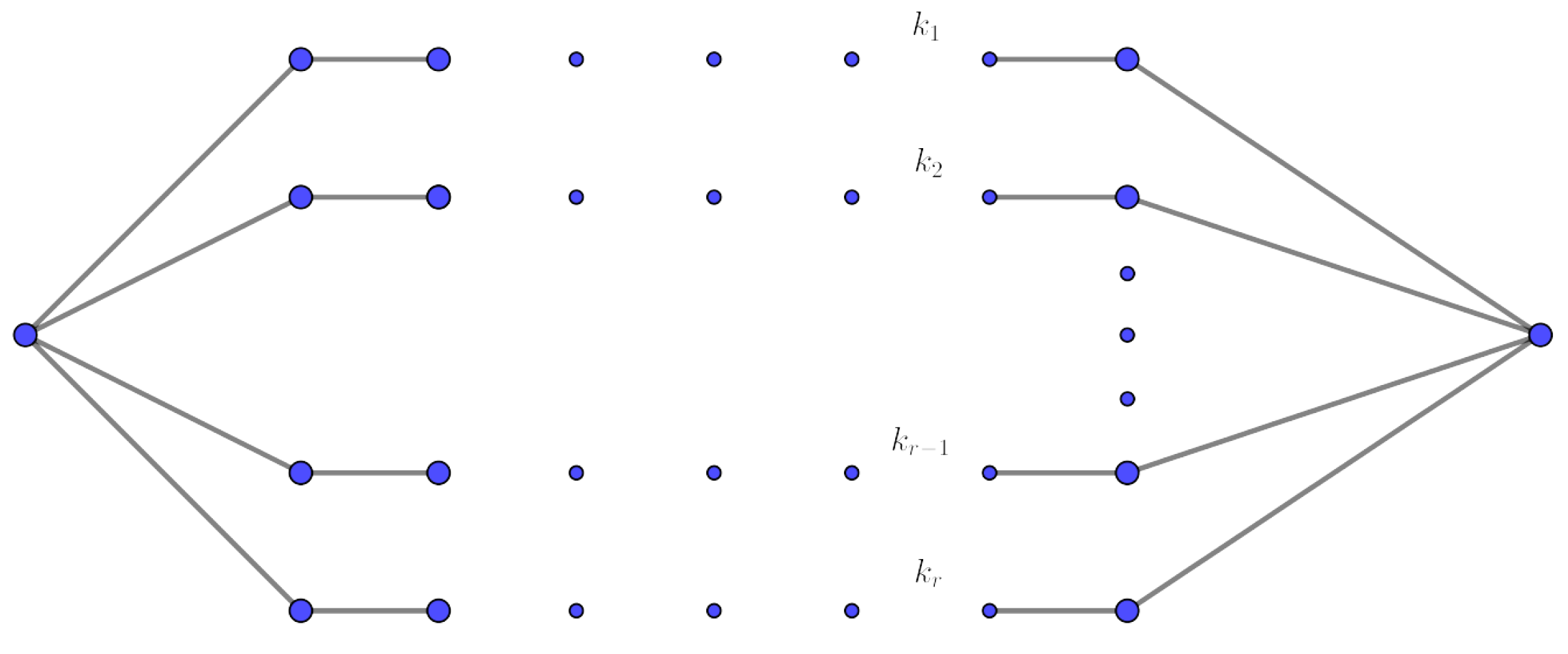
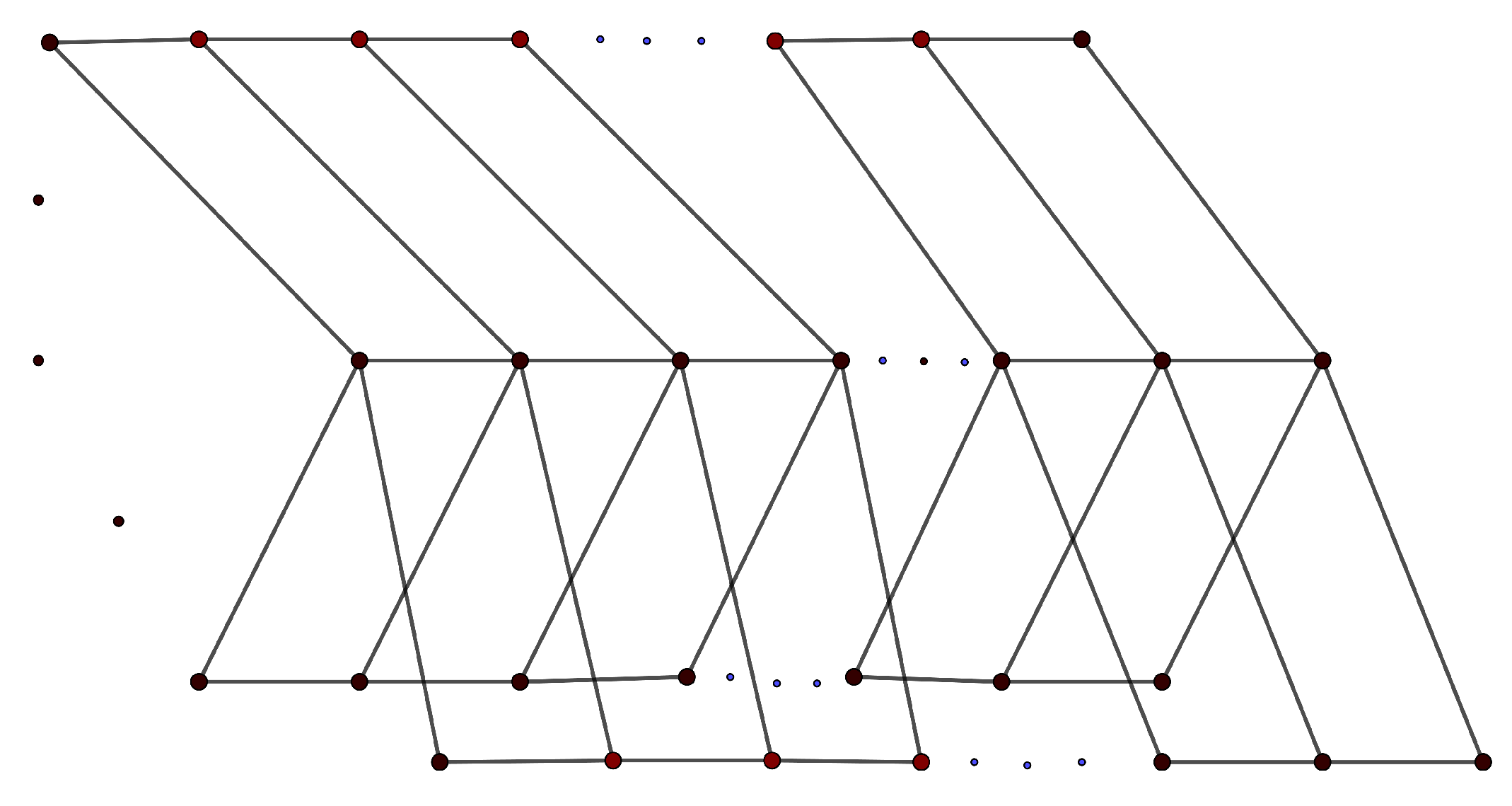
3. Mathematical Results on Some Significant Families of Graphs
- 1.
- 2.
- .
- 3.
- i.
- ii.
- 1.
- .
- 2.
- .
- 3.
- .
- 4.
- .
- 1.
- .
- 2.
- .
- , if there is an edge between u and v.
- , if edges e and f share both endpoints and have degrees a and b, respectively.
- , if vertex v and edge f are incident and have degrees a and b, respectively.
4. Entire Harmonic Index under Some Common Graph Operations
5. Relationships between the Entire Harmonic Index and Other Indices
6. Conclusions
- More mathematical study for this new index to discover its relations with the other graph parameters;
- Investigation of the broader applicability of this new index across diverse network types, including social networks, biological networks, and technological networks;
- Exploration of the potential of this index in various domains, such as drug discovery in medicine and material design in engineering.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harary, F. Graph Theory; Addison-Wesley, Reading Mass: Boston, MA, USA, 1969. [Google Scholar]
- Wiener, H. Structural determination of paraffin boiling points. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar] [CrossRef]
- Gutman, I.; Trinajstic, N. Graph theory and molecular orbitals, Total π-electron energy of alternant hydrocarbons. Chem. Phys. Lett. 1972, 17, 535–538. [Google Scholar] [CrossRef]
- Dobrynin, A.A.; Kochetova, A.A. Degree distance of a graph: A degree analog of the Wiener index. J. Chem. Inf. Comput. Sci. 1994, 34, 1082–1086. [Google Scholar] [CrossRef]
- Gutman, I. Selected properties of the Schultz molecular topological index. J. Chem. Inf. Comput. Sci. 1994, 34, 1087–1089. [Google Scholar] [CrossRef]
- Das, K.C.; Gutman, I. On Wiener and multiplicative Wiener indices of graphs. Discret. Appl. Math. 2016, 206, 9–14. [Google Scholar] [CrossRef]
- Das, K.C.; Gutman, I.; Nadjafi-Arani, M.J. Relations between distance-based and degree-based topological indices. Appl. Math. Comput. 2015, 270, 142–147. [Google Scholar] [CrossRef]
- Gutman, I. Degree-based topological indices. Croat. Chem. Acta 2013, 86, 351–361. [Google Scholar] [CrossRef]
- Ali, A.; Trinajstić, N. A novel/old modification of the first Zagreb index. Mol. Inform. 2018, 37, 1800008. [Google Scholar] [CrossRef] [PubMed]
- Javaid, M.; Ali, U.; Siddiqui, K. Novel connection based Zagreb indices of several wheel-related graphs. Comput. J. Comb. Math. 2021, 1, 1–28. [Google Scholar]
- Javaid, M.; Siddique, M.K.; Bonyah, E. Computing gutman connection index of thorn graphs. J. Math. 2021, 2021, 2289514. [Google Scholar] [CrossRef]
- Deng, H.; Sarala, D.; Ayyaswamy, S.K.; Balachandran, S. The Zagreb indices of four operations on graphs. Appl. Math. Comput. 2016, 275, 422–431. [Google Scholar] [CrossRef]
- Ahmed, H.; Saleh, A.; Ismail, R.; Alameri, A. Computational analysis for eccentric neighborhood Zagreb indices and their significance. Heliyon 2023, 9, e17998. [Google Scholar] [CrossRef] [PubMed]
- Wazzan, S.; Saleh, A. New Versions of Locating Indices and Their Significance in Predicting the Physicochemical Properties of Benzenoid Hydrocarbons. Symmetry 2022, 14, 1022. [Google Scholar] [CrossRef]
- da Fonseca, C.M.; Stevanovic, D. Further properties of the second Zagreb index. MATCH Commun. Math. Comput. Chem. 2014, 72, 655–668. [Google Scholar]
- Gutman, I.; Das, K.C. The first Zagreb index 30 years after. MATCH Commun. Math. Comput. Chem. 2004, 50, 83–92. [Google Scholar]
- Khalifeh, M.H.; Yousefi-Azari, H.; Ashrafi, A.R. The first and second Zagreb indices of some graph operations. Discret. Appl. Math. 2009, 157, 804–811. [Google Scholar] [CrossRef]
- Sarala, D.; Deng, H.; Ayyaswamy, S.K.; Balachandran, S. The Zagreb indices of graphs based on four new operations related to the lexicographic product. Appl. Math. Comput. 2017, 309, 156–169. [Google Scholar] [CrossRef]
- Sarkar, P.; De, N.; Pal, A. The Zagreb indices of graphs based on new operations related to the join of graphs. J. Int. Math. Virtual Inst. 2017, 7, 181–209. [Google Scholar]
- Ullah, A.; Zaman, S.; Hamraz, A.; Saeedi, G. Network-based modeling of the molecular topology of fuchsine acid dye with respect to some irregular molecular descriptors. J. Chem. 2022, 2022, 8131276. [Google Scholar] [CrossRef]
- Hakeem, A.; Ullah, A.; Zaman, S. Computation of some important degree-based topological indices for γ-graphyne and Zigzag graphyne nanoribbon. Mol. Phys. 2023, 121, e2211403. [Google Scholar] [CrossRef]
- Ullah, A.; Zaman, S.; Hamraz, A. Zagreb connection topological descriptors and structural property of the triangular chain structures. Phys. Scr. 2023, 98, 025009. [Google Scholar] [CrossRef]
- Zhou, B.; Gutman, I. Further properties of Zagreb indices. MATCH Commun. Math. Comput. Chem. 2005, 54, 233–239. [Google Scholar]
- Alqesmah, A.; Alwardi, A.; Rangarajan, R. On the Distance Eccentricity Zagreb Indices of Graphs. Int. J. Math. Combin. 2017, 4, 110–120. [Google Scholar]
- Alwardi, A.; Alqesmah, A.; Rangarajan, R.; Cangul, I.N. Entire Zagreb indices of graphs. Discret. Math. Algorithms Appl. 2018, 10, 1850037. [Google Scholar] [CrossRef]
- Saleh, A.; Aqeel, A.; Cangul, I.N. On the entire ABC index of graphs. Proc. Jangjeon Math. Soc. 2020, 23, 39–51. [Google Scholar]
- Saleh, A.; Cangul, I.N. On the entire Randic index of graphs. Adv. Appl. Math. Sci. 2021, 20, 1559–1569. [Google Scholar]
- Ghalav, A.; Ashrafi, A.R. Bounds on the entire Zagreb indices of graphs. MATCH Commun. Math. Comput. Chem. 2019, 81, 371–381. [Google Scholar]
- Gutman, I. On vertex and edge degree-based topological indices. Vojnoteh. Glas. Mil. Tech. Cour. 2023, 71, 855–863. [Google Scholar] [CrossRef]
- Randic, M. Characterization of molecular branching. J. Am. Chem. Soc. 1975, 97, 6609–6615. [Google Scholar] [CrossRef]
- Zhong, L. The harmonic index for graphs. Appl. Math. Lett. 2012, 25, 561–566. [Google Scholar] [CrossRef]
- Zhou, B.; Nenad, T. On a novel connectivity index. J. Math. Chem. 2009, 46, 1252–1270. [Google Scholar] [CrossRef]
- Iranmanesh, M.A.; Mahboubeh, S. On the Harmonic Index and Harmonic Polynomial of Caterpillars with Diameter Four. Iran. J. Math. Chem. 2015, 5, 35–43. [Google Scholar]
- Randić, M.; Nenad, T. In search for graph invariants of chemical interes. J. Mol. Struct. 1993, 300, 551–571. [Google Scholar] [CrossRef]
- NIST Standard Reference Database. Available online: http://webbook.nist.gov/chemistry/ (accessed on 18 November 2023).
- Hayat, S.; Arif, A.; Zada, L.; Khan, A.; Zhong, Y. Mathematical Properties of a Novel Graph-Theoretic Irregularity Index with Potential Applicability in QSPR Modeling. Mathematics 2022, 10, 4377. [Google Scholar] [CrossRef]
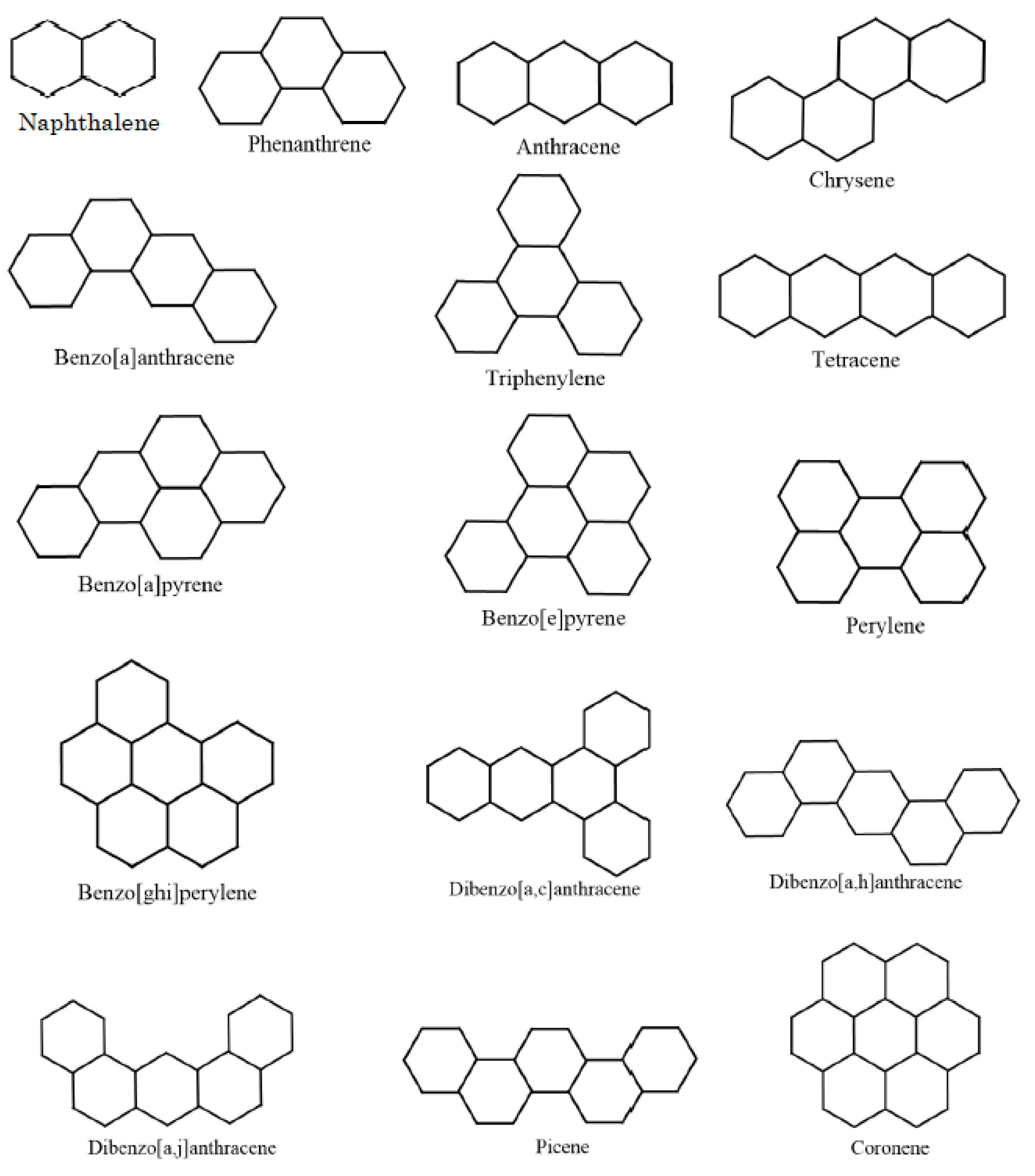
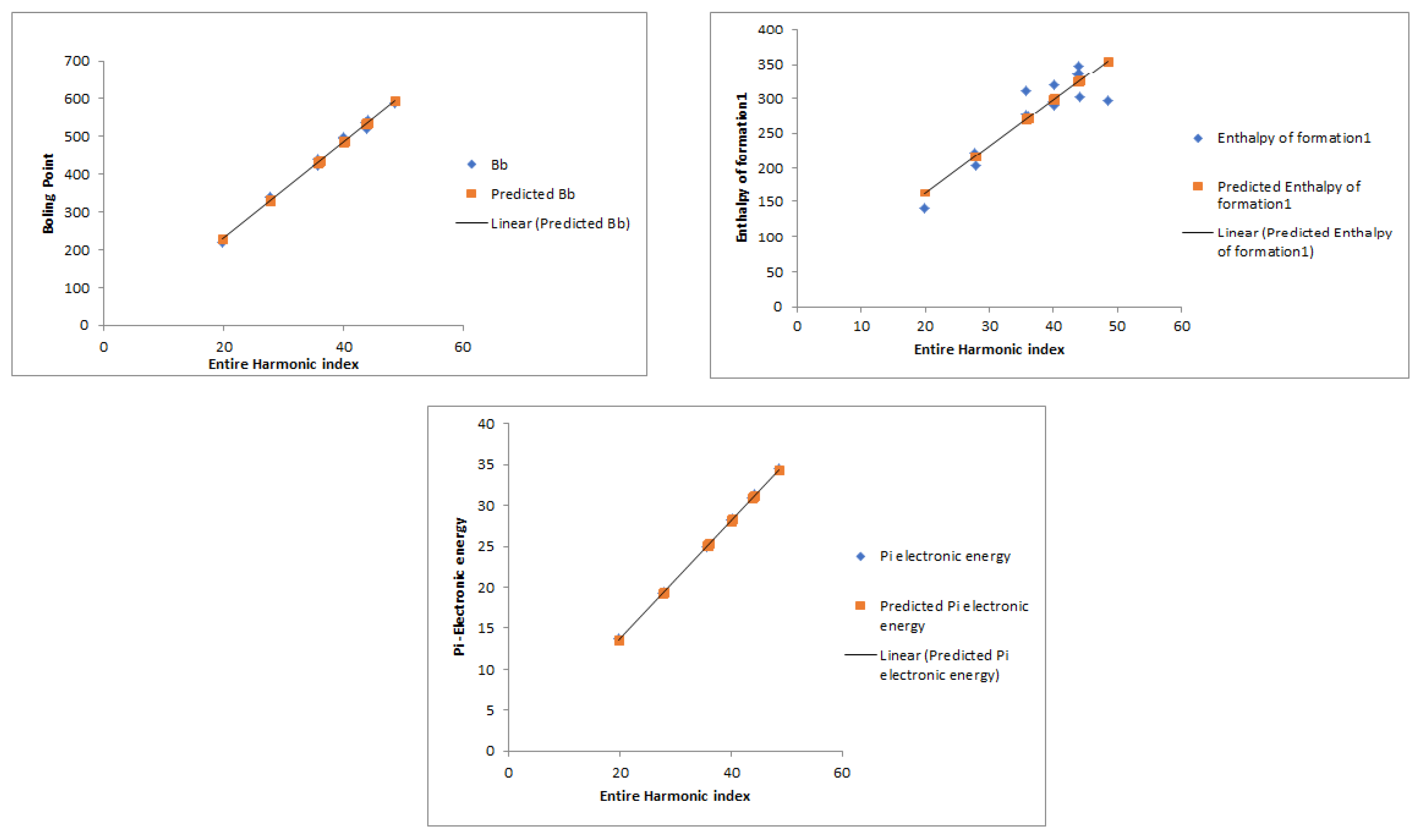

| SN | The Compounds | H | R | |||||
|---|---|---|---|---|---|---|---|---|
| 1 | naphthalene | 13.6832 | 141 | 218 | 19.8475 | 4.9333 | 4.9663 | 5.1971 |
| 2 | phenanthrene | 19.4483 | 202.7 | 338 | 27.8665 | 6.8999 | 6.9495 | 7.408 |
| 3 | anthracene | 19.3137 | 222.6 | 340 | 27.7618 | 6.8666 | 6.9327 | 7.3942 |
| 4 | chrysene | 25.1922 | 271.1 | 431 | 35.8856 | 8.8666 | 8.9327 | 9.619 |
| 5 | tetraphene or Benz(a)anthracene | 25.1012 | 277.1 | 425 | 35.78 | 8.8333 | 8.9158 | 9.6051 |
| 6 | triphenylene | 25.2745 | 275.1 | 429 | 36.057 | 8.8999 | 8.9495 | 9.6328 |
| 7 | naphthacene or TETRACENE | 24.9308 | 310.5 | 440 | 35.6761 | 9.7999 | 8.899 | 9.5913 |
| 8 | benzo[a]pyrene | 28.222 | 296 | 496 | 39.9618 | 9.8333 | 9.9158 | 10.8299 |
| 9 | benzo[e]pyrene | 28.3361 | 289.9 | 493 | 40.1998 | 9.8666 | 9.9327 | 10.8437 |
| 10 | perylene | 28.2453 | 319.2 | 497 | 40.0998 | 9.8666 | 9.9327 | 10.8437 |
| 11 | benzo[ghi]perylene | 31.4251 | 301.2 | 542 | 44.1428 | 10.8333 | 10.9158 | 12.0546 |
| 12 | dibenzo[a,c]anthracene | 30.9418 | 348 | 535 | 43.9713 | 10.8333 | 10.9158 | 11.8299 |
| 13 | dibenz[a,h]anthracene | 30.8805 | 335 | 536 | 43.7999 | 10.7999 | 10.899 | 11.8161 |
| 14 | dibenz[a,j]anthracene | 30.8795 | 336.3 | 531 | 44.0618 | 10.7999 | 10.899 | 11.8161 |
| 15 | picene | 30.9432 | 336.9 | 519 | 43.9046 | 10.8333 | 10.9158 | 11.8299 |
| 16 | coronene | 34.5718 | 296.7 | 590 | 48.5189 | 11.8 | 11.899 | 13.2655 |
| Boiling Point | Enthalpy of Formation | Pi Electronic Energy | |
|---|---|---|---|
| Entire Harmonic index | 1 | ||
| Harmonic index | |||
| Randić index | |||
| The sum-connectivity index | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saleh, A.; Alsulami, S.H. On the Entire Harmonic Index and Entire Harmonic Polynomial of Graphs. Symmetry 2024, 16, 208. https://doi.org/10.3390/sym16020208
Saleh A, Alsulami SH. On the Entire Harmonic Index and Entire Harmonic Polynomial of Graphs. Symmetry. 2024; 16(2):208. https://doi.org/10.3390/sym16020208
Chicago/Turabian StyleSaleh, Anwar, and Samirah H. Alsulami. 2024. "On the Entire Harmonic Index and Entire Harmonic Polynomial of Graphs" Symmetry 16, no. 2: 208. https://doi.org/10.3390/sym16020208






